A Numerical Study of the Influence of Channel-Scale Secondary Circulation on Mixing Processes Downstream of River Junctions
Abstract
:1. Introduction
1.1. Near Field Processes—Secondary Circulation and Shear-Driven Turbulence
1.2. Implications for Mixing
2. Case Study and Methods
2.1. Case-Study
2.2. Numerical Simulation
2.3. Analysis of Model Outputs
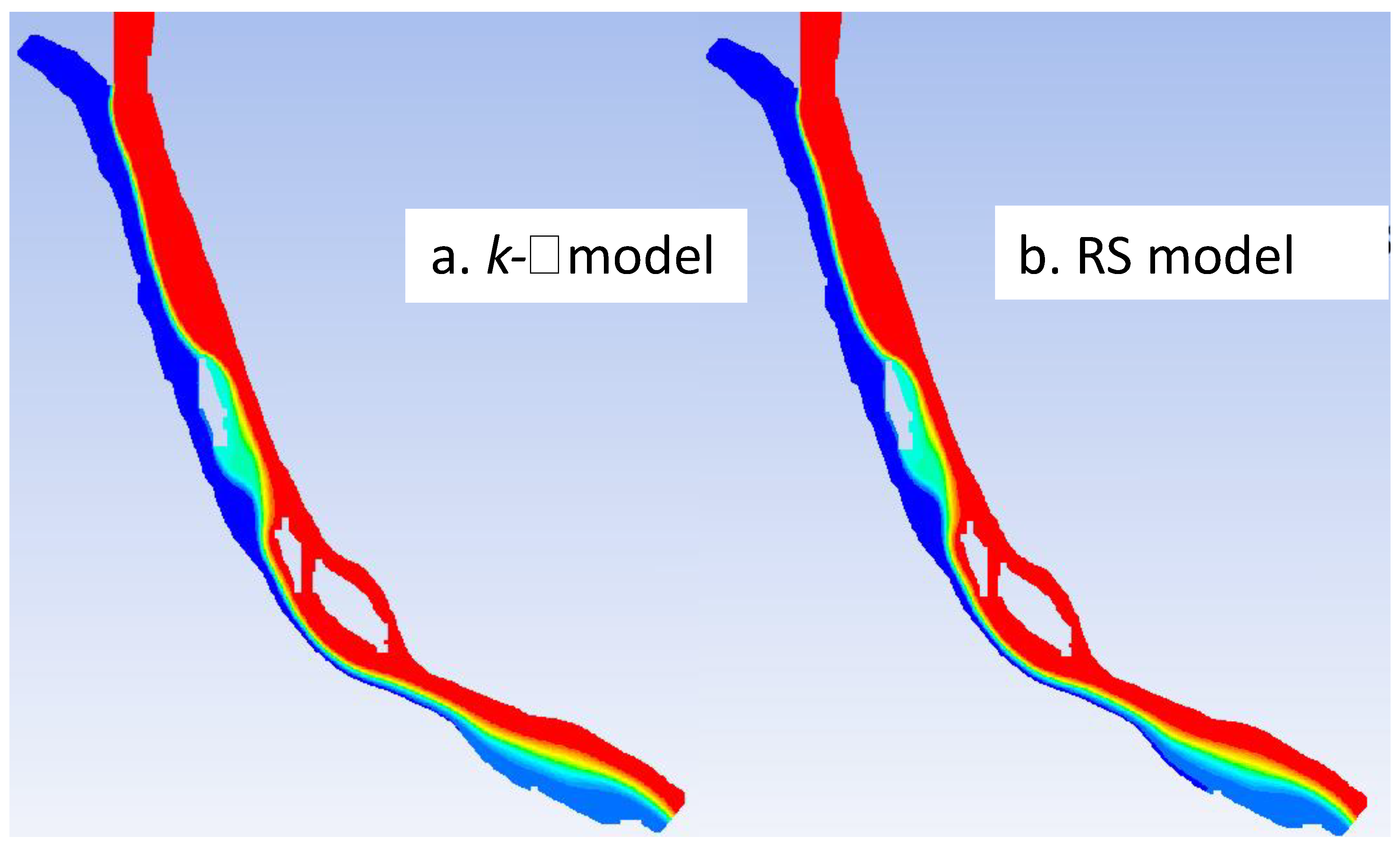
2.4. Mesh Sensitivity and Validation
3. Results
3.1. R Simulations: Regular Planform and Bathymetry
3.2. P Simulations: Natural Planform, Regular Bathymetry
3.3. N Simulations: Natural Planform and Bathymetry
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MacKay, J.R. Lateral mixing of the Laird and Mackenzie rivers downstream from their confluence. Can. J. Earth Sci. 1970, 7, 111–124. [Google Scholar] [CrossRef]
- Matsui, E.; Salati, F.; Friedman, I.; Brinkman, W.L.F. Isotopic hydrology of the Amazonia, 2, Relative discharge of the Negro and Solimões rivers through 18O concentrations. Water Resour. Res. 1976, 12, 781–785. [Google Scholar] [CrossRef]
- Weibezahn, F.H. Downstream natural mixing of water from the Orinoco, Atabapo and Guaviare rivers. Eos Trans. AGU 1983, 644, 699. [Google Scholar]
- Stallard, R.F. Cross-channel mixing and its effect on sedimentation in the Orinoco River. Water Resour. Res. 1987, 23, 1977–1986. [Google Scholar] [CrossRef]
- Lane, S.N.; Parsons, D.R.; Best, J.L.; Orfeo, O.; Kostaschuk, R.; Hardy, R.J. Causes of rapid mixing at a junction of two large rivers: Río Paraná and Río Paraguay, Argentina. J. Geophys. Res. Earth Surf. 2008, 113, F02019. [Google Scholar] [CrossRef] [Green Version]
- Laraque, A.; Guyot, J.; Filizola, N. Mixing processes in the Amazon River at the confluences of the Negro and Solimões Rivers, Encontro das Aguas, Brazil. Hydrol. Process. 2009, 23, 3131–3140. [Google Scholar] [CrossRef]
- Bouchez, J.; Lajeunesse, E.; Gaillardet, J.; France-Lanord, C.; Dutra-Maia, P.; Maurice, L. Turbulent mixing in the Amazon River: The isotopic memory of confluences. Earth Planet. Sci. Lett. 2010, 290, 37–43. [Google Scholar] [CrossRef]
- Gualtieri, C.; Filizola, N.; Oliveira, M.; Santos, A.M.; Ianniruberto, M. A field study of the confluence between Negro and Solimões Rivers. Part 1: Hydrodynamics and sediment transport. C. R. Geosci. 2018, 350, 31–42. [Google Scholar] [CrossRef]
- Gualtieri, C.; Ianniruberto, M.; Filizola, N. On the mixing of rivers with a difference in density: The case of the Negro/Solimões confluence, Brazil. J. Hydrol. 2019, 578, 124029. [Google Scholar] [CrossRef]
- Schmidt, W. Der Massenaustausch in Freier Luft und Verwandte Erscheinugen; H. Grandamburg: Hamburg, Germany, 1925. [Google Scholar]
- Makkaveev, V.M. On the distribution of solutions in the turbulent flow and the chemical method of measuring the flow. Zap. GGI 1933, 10, 229–246. [Google Scholar]
- Fischer, H.B. Dispersion predictions in natural streams. J. Sanit. Eng. Div. 1968, 94, 927–943. [Google Scholar]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: Cambridge, MA, USA, 1979; 483p. [Google Scholar]
- Rutherford, J. River Mixing; Wiley: Chichester, UK, 1994. [Google Scholar]
- Taylor, E.H. Flow characteristics at rectangular open-channel junctions. Trans. Am. Soc. Civ. Eng. 1944, 109, 893–912. [Google Scholar]
- Einstein, A. The cause of the formation of meanders in the courses of rivers and of the so-called Baer’s Law. In Ideas and Opinions; Bonanza Books: New York, NY, USA, 1954; pp. 249–253. [Google Scholar]
- Rhoads, B.L.; Kenworthy, S.T. Flow structure at an asymmetrical stream confluence. Geomorphology 1995, 11, 273–293. [Google Scholar] [CrossRef]
- Mosley, M.P. An experimental study of channel confluences. J. Geol. 1976, 84, 535–562. [Google Scholar] [CrossRef]
- Ashmore, P.E.; Ferguson, R.I.; Prestegaard, K.L.; Ashworth, P.J.; Paola, C. Secondary flow in anabranch confluences of a braided, gravel-bed stream. Earth Surf. Process. Landf. 1992, 17, 299–311. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Lane, S.N.; Richards, K.S.; Biron, P.M.; Roy, A.G. Flow structures and mixing at an asymmetrical open-channel confluence: A numerical study. J. Hydraul. Eng. 2001, 127, 351–368. [Google Scholar] [CrossRef]
- Huang, J.C.; Weber, L.J.; Lai, Y.G. Three-dimensional numerical study of flows in open-channel junctions. J. Hydraul. Eng. 2002, 128, 268–280. [Google Scholar] [CrossRef]
- Kennedy, B.A. On Playfair’s law of accordant junctions. Earth Surf. Process. Landf. 1984, 9, 153–173. [Google Scholar] [CrossRef]
- Best, J.L. The morphology of river channel confluences. Prog. Phys. Geogr. 1986, 10, 157–174. [Google Scholar] [CrossRef]
- Best, J.L. Flow dynamics at river channel confluences: Implications for sediment transport and bed morphology. In Recent Developments in Fluvial Sedimentology; Special Publication; SEPM Society of Sedimentary Geology: Tulsa, OK, USA, 1987; pp. 27–35. [Google Scholar]
- Best, J.L. Sediment transport and bed morphology at river channel confluences. Sedimentology 1988, 35, 481–498. [Google Scholar] [CrossRef]
- Best, J.L.; Roy, A.G. Mixing layer distortion at the confluence of channels of unequal depth. Nature 1991, 350, 411–413. [Google Scholar] [CrossRef]
- Biron, P.M.; Best, J.L.; Roy, A.G. Effects of bed discordance on flow dynamics at open channel confluences. J. Hydraul. Eng. 1996, 122, 676–682. [Google Scholar] [CrossRef]
- Biron, P.M.; Roy, A.G.; Best, J.L. Turbulent flow structure at concordant and discordant open-channel confluences. Exp. Fluids 1996, 21, 437–446. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Biron, P.; Lane, S.N.; Richards, K.S.; Roy, A.G. Investigation of controls on secondary circulation and mixing processes in a simple confluence geometry using a three-dimensional numerical model. Hydrol. Process. 1998, 12, 1371–1396. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Sukhodolov, A.N. Spatial and temporal structure of shear layer turbulence at a stream confluence. Water Resour. Res. 2004, 40, W06304. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Sukhodolov, A.N. Lateral momentum flux and the spatial evolution of flow within a confluence mixing interface. Water Resour. Res. 2008, 44, W08440. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Sukhodolov, A.N. Field investigation of three-dimensional flow structure at stream confluences, Spatial and temporal structure of shear layer turbulence at a stream confluence. Water Resour. Res. 2001, 37, 2393–2410. [Google Scholar] [CrossRef]
- Cushman-Roisin, B.; Constantinescu, G.S. Dynamical adjustment of two streams past their confluence. J. Hydraul. Res. 2020, 58, 305–313. [Google Scholar] [CrossRef]
- Konsoer, K.M.; Rhoads, B.L. Spatial-temporal structure of mixing interface turbulence at two large river confluences. Environ. Fluid Mech. 2014, 14, 1043–1070. [Google Scholar] [CrossRef]
- Gaudet, J.M.; Roy, A.G. Effect of bed morphology on flow mixing length at river confluences. Nature 1995, 373, 138–139. [Google Scholar] [CrossRef]
- Biron, P.M.; Ramamurthy, A.S.; Han, S. Three-dimensional numerical modeling of mixing at river confluences. J. Hydraul. Eng. 2004, 130, 243–253. [Google Scholar] [CrossRef]
- Lyubimova, T.; Lepikhin, A.; Parshakova, Y.; Konovalov, V.; Tiunov, A. Formation of the density currents in the zone of confluence of two rivers. J. Hydrol. 2014, 508, 328–342. [Google Scholar] [CrossRef]
- Ramon, C.L.; Armengol, J.; Dolz, J.; Prats, J.; Rueda, F.J. Mixing dynamics at the confluence of two large rivers undergoing weak density variations. J. Geophys. Res. Ocean. 2014, 119, 2386–2402. [Google Scholar] [CrossRef]
- Ramon, C.L.; Prats, J.; Rueda, F.J. The influence of flow inertia, buoyancy, wind, and flow unsteadiness on mixing at the asymmetrical confluence of two large rivers. J. Hydrol. 2016, 539, 11–26. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Rhoads, B.L. Rates and patterns of thermal mixing at a small stream confluence under variable incoming flow conditions. Hydrol. Process. 2015, 29, 4442–4456. [Google Scholar] [CrossRef]
- Herrero, S.H.; Jose, M.D.L.; Garcia, M.G.; Ricardo, N.S.; Best, J.L.; Mariana, P. The influence of tributary flow density differences on the hydrodynamic behavior of a confluent meander bend and implications for flow mixing. Geomorphology 2018, 304, 99–112. [Google Scholar] [CrossRef]
- Cheng, Z.; Constantinescu, G. Stratification effects on flow hydrodynamics and mixing at a confluence with a highly discordant bed and a relatively low velocity ratio. Water Resour. Res. 2018, 54, 4537–4562. [Google Scholar] [CrossRef]
- Constantinescu, G.; Miyawaki, S.; Rhoads, B.; Sukhodolov, A. Numerical evaluation of the effects of planform geometry and inflow conditions on flow, turbulence structure, and bed shear velocity at a stream confluence with a concordant bed. J. Geophys. Res. Earth Surf. 2014, 119, 2079–2097. [Google Scholar] [CrossRef]
- Constantinescu, G.; Miyawaki, S.; Rhoads, B.; Sukhodolov, A. Influence of planform geometry and momentum ratio on thermal mixing at a stream confluence with a concordant bed. Environ. Fluid Mech. 2016, 16, 845–873. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, D.Z.; Steffler, P.M. Secondary currents induced mixing at channel confluences. Can. J. Civ. Eng. 2017, 44, 1071–1083. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Zhang, H.; Yuan, S. Hydrodynamics and contaminant transport on a degraded bed at a 90-degree channel confluence. Environ. Fluid Mech. 2018, 18, 443–463. [Google Scholar] [CrossRef]
- Parsons, D.R.; Best, J.L.; Lane, S.N.; Orfeo, O.; Hardy, R.J.; Kostaschuk, R. Form roughness and the absence of secondary flow in a large confluence-diffluence, Paraná River, Argentina. Earth Surf. Process. Landf. 2007, 32, 155–162. [Google Scholar] [CrossRef]
- Szupiany, R.N.; Amsler, M.L.; Parsons, D.R.; Best, J.L. Morphology, flow structure, and suspended bed sediment transport at two large braid-bar confluences. Water Resour. Res. 2009, 45, W05415. [Google Scholar] [CrossRef] [Green Version]
- Hickin, E.J. Mean flow structure in meanders of the Squamish River, British Columbia. Can. J. Earth Sci. 1978, 15, 1833–1849. [Google Scholar] [CrossRef] [Green Version]
- Kashyap, S.; Constantinescu, G.; Rennie, C.D.; Post, G.; Townsend, R. Influence of channel aspect ratio and curvature on flow, secondary circulation, and bed shear stress in a rectangular channel bend. J. Hydraul. Eng. 2012, 138, 1045–1059. [Google Scholar] [CrossRef]
- Dietrich, W.E.; Smith, J.D. Influence of the point bar on flow through curved channels. Water Resour. Res. 1983, 19, 1173–1192. [Google Scholar] [CrossRef]
- Shakibaeinia, A.; Tabatabai, M.R.M.; Zarrati, A.R. Three-dimensional numerical study of flow structure in channel confluences. Can. J. Civ. Eng. 2010, 37, 772–781. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Zhu, W. Combining flow in 90° junctions of rectangular conduit. J. Hydraul. Eng. 1997, 123, 1012–1019. [Google Scholar] [CrossRef]
- Schindfessel, L.; Creelle, S.; De Mulder, T. How different cross-sectional shapes influence the separation zone of an open-channel confluence. J. Hydraul. Eng. 2017, 143, 04017036. [Google Scholar] [CrossRef]
- ASME. Statement upon the control of numerical accuracy. J. Fluids Eng. 1993, 115, 339–340. [Google Scholar]
- ASME. Perspective: Journal of Fluids Engineering Editorial Policy Statement on the Control of Numerical Accuracy. J. Fluids Eng. 2009, 115, 339–340. [Google Scholar]
- Lane, S.N.; Hardy, R.J.; Ferguson, R.I.; Parsons, D.R. A framework for model verification and validation of CFD schemes in natural open channel flows. In Computational Fluid Dynamics: Applications in Environmental Hydraulics; Bates, P.D., Lane, S.N., Ferguson, R.I., Eds.; John Wiley & Sons: Chichester, UK, 2005. [Google Scholar]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to computational fluid dynamics for environmental fluid mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Blanckaert, K.; de Vriend, H.J. Secondary flow in sharp open-channel bends. J. Fluid Mech. 2004, 498, 353–380. [Google Scholar] [CrossRef] [Green Version]
- Hua, C.W.; Yu, M.H.; Wei, H.Y.; Liu, C.J. The mechanisms of energy transformation in sharp open-channel bends: Analysis based on experiments in a laboratory flume. J. Hydrol. 2019, 571, 723–739. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S. Reynolds stress modelling of rectangular open-channel flow. Int. J. Numer. Methods Fluids 2006, 51, 1319–1334. [Google Scholar] [CrossRef]
- Choi, S.-U.; Park, M.; Kang, H. Numerical simulations of cellular secondary currents and suspended sediment transport in open-channel flows over smooth-rough bed strips. J. Hydraul. Res. 2007, 45, 829–840. [Google Scholar] [CrossRef]
- Wu, L.; Long, T.; Lu, X. Improvement of separation efficiency and production capacity of a hydrocyclone. Water Sci. Technol. Water Supply 2012, 12, 281–299. [Google Scholar] [CrossRef]
- Han, S.S.; Biron, P.M.; Ramamurthy, A.S. Three-dimensional modelling of flow in sharp open-channel bends with vanes. J. Hydraul. Res. 2011, 49, 64–72. [Google Scholar] [CrossRef]
- Safarzadeh, A.; Brevis, W. Assessment of 3D-RANS models for the simulation of topographically forced shallow flows. J. Hydrol. Hydromech. 2016, 64, 83–90. [Google Scholar] [CrossRef] [Green Version]
- Blanckaert, K. Flow separation at convex banks in open channels. J. Fluid Mech. 2015, 779, 432–467. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.A.; Jha, S.; Stoesser, T. On the values for the turbulent Schmidt number in environmental flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- Paik, J.; Sotiropoulos, F. Coherent structure dynamics upstream of a long rectangular block at the side of a large aspect ratio channel. Phys. Fluids 2005, 17, 115104. [Google Scholar] [CrossRef]
- Lane, S.N.; Bradbrook, K.F.; Richards, K.S.; Biron, P.M.; Roy, A.G. Secondary circulation in river channel confluences: Measurement myth or coherent flow structure? Hydrol. Process. 2000, 14, 2047–2071. [Google Scholar] [CrossRef]
- Arfken, G.B.; Weber, H.J. Mathematical Methods for Physicists, 4th ed.; Academic Press: San Diego, CA, USA, 1995; pp. 92–93. [Google Scholar]
- Rhoads, B.L.; Johnson, K.K. Three-dimensional flow structure, morphodynamics, suspended sediment, and thermal mixing at an asymmetrical river confluence of a straight tributary and curving main channel. Geomorphology 2018, 323, 51–69. [Google Scholar] [CrossRef]
- Fischer, H.B. The effect of bends on dispersion in streams. Water Resour. Res. 1969, 5, 496–506. [Google Scholar] [CrossRef]
- Fukuoka, S.; Sayre, W.W. Longitudinal dispersion in sinuous channels. J. Hydraul. Div. 1973, 99, 195–217. [Google Scholar]
- Yotsukura, N.; Sayre, W.W. Transverse mixing in natural channels. Water Resour. Res. 1976, 12, 695–704. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Lane, S.N.; Richards, K.S. Numerical simulation of time-averaged flow structure at river channel confluences. Water Resour. Res. 2000, 36, 2731–2746. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flow. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
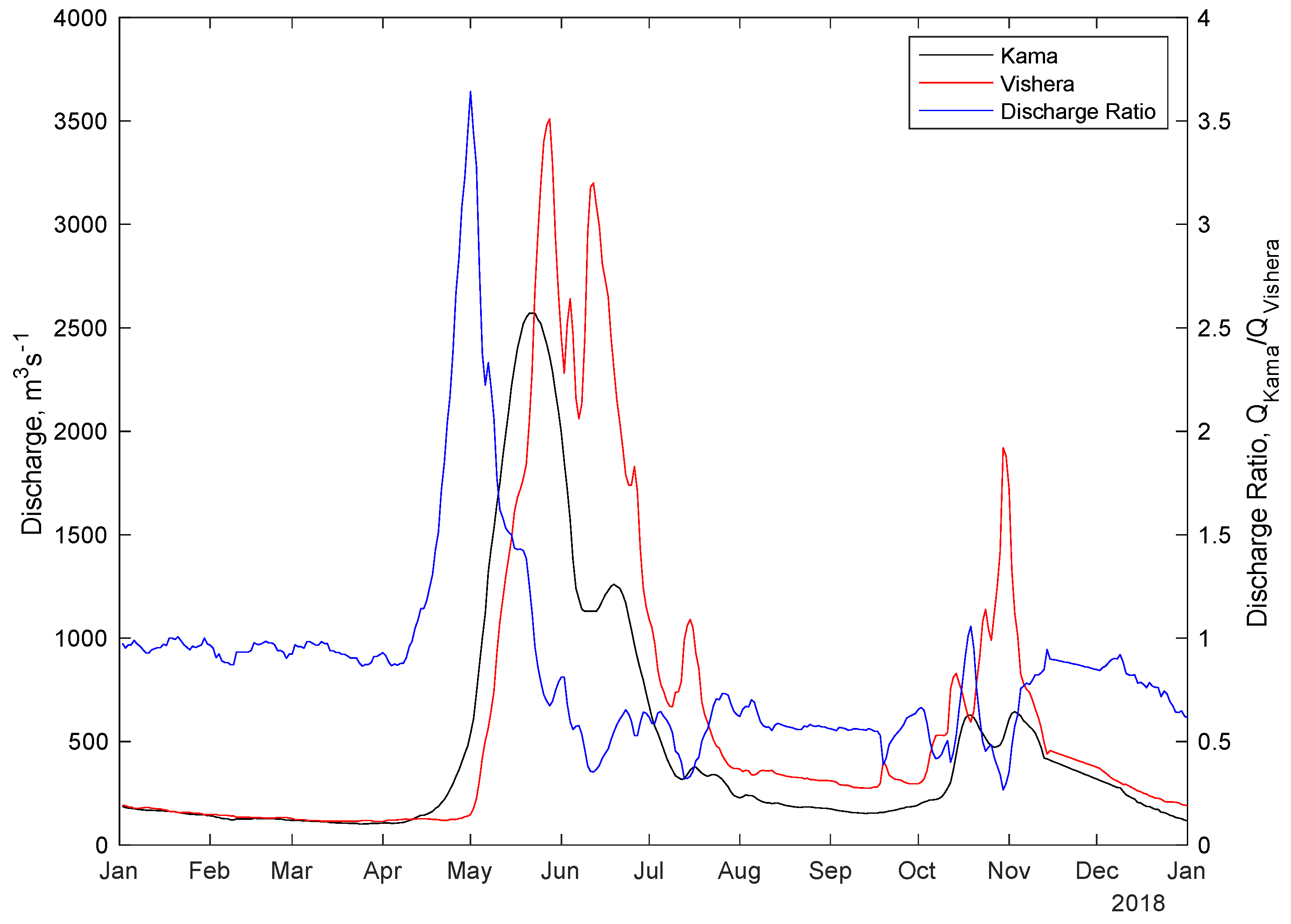
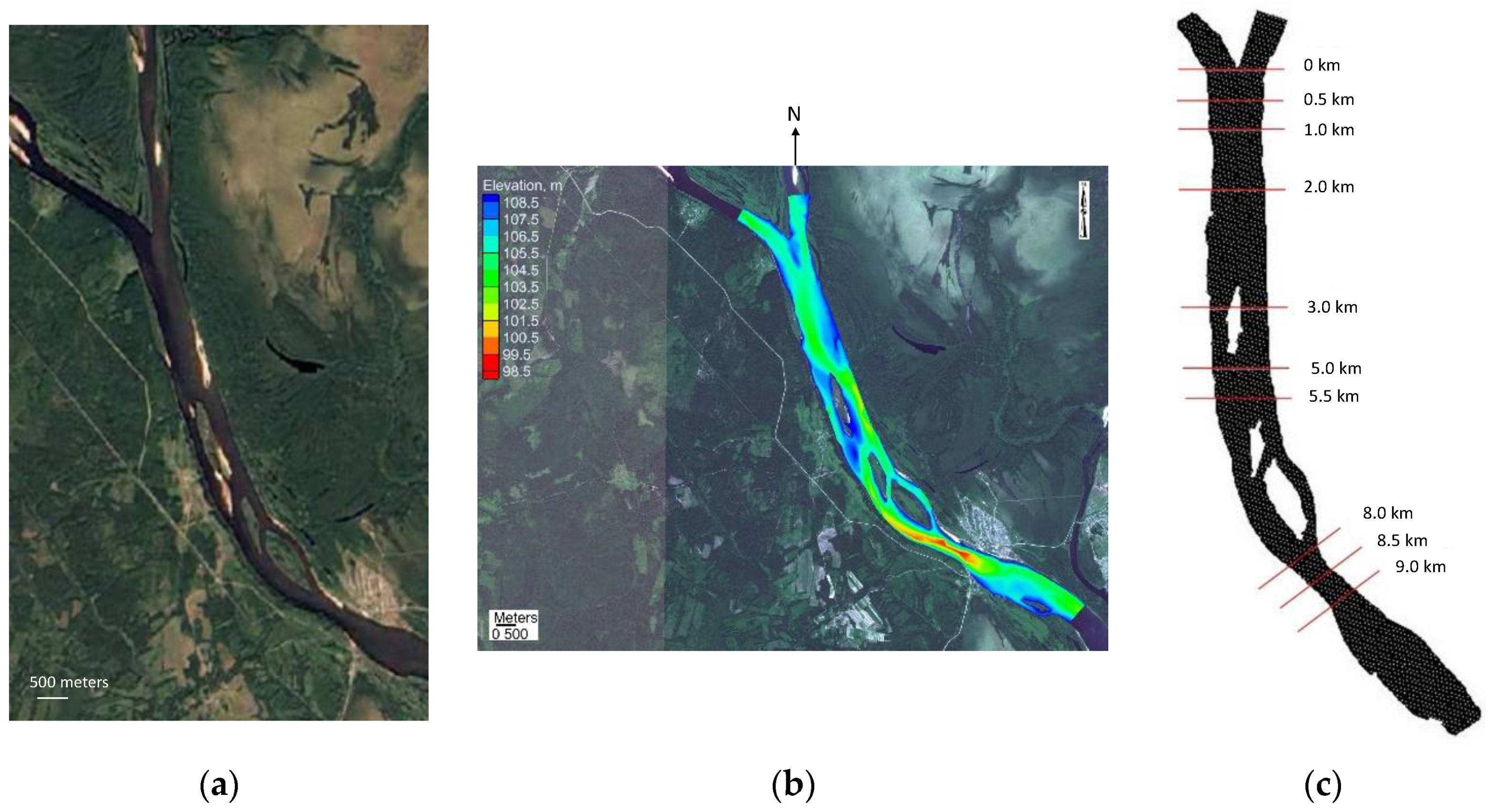
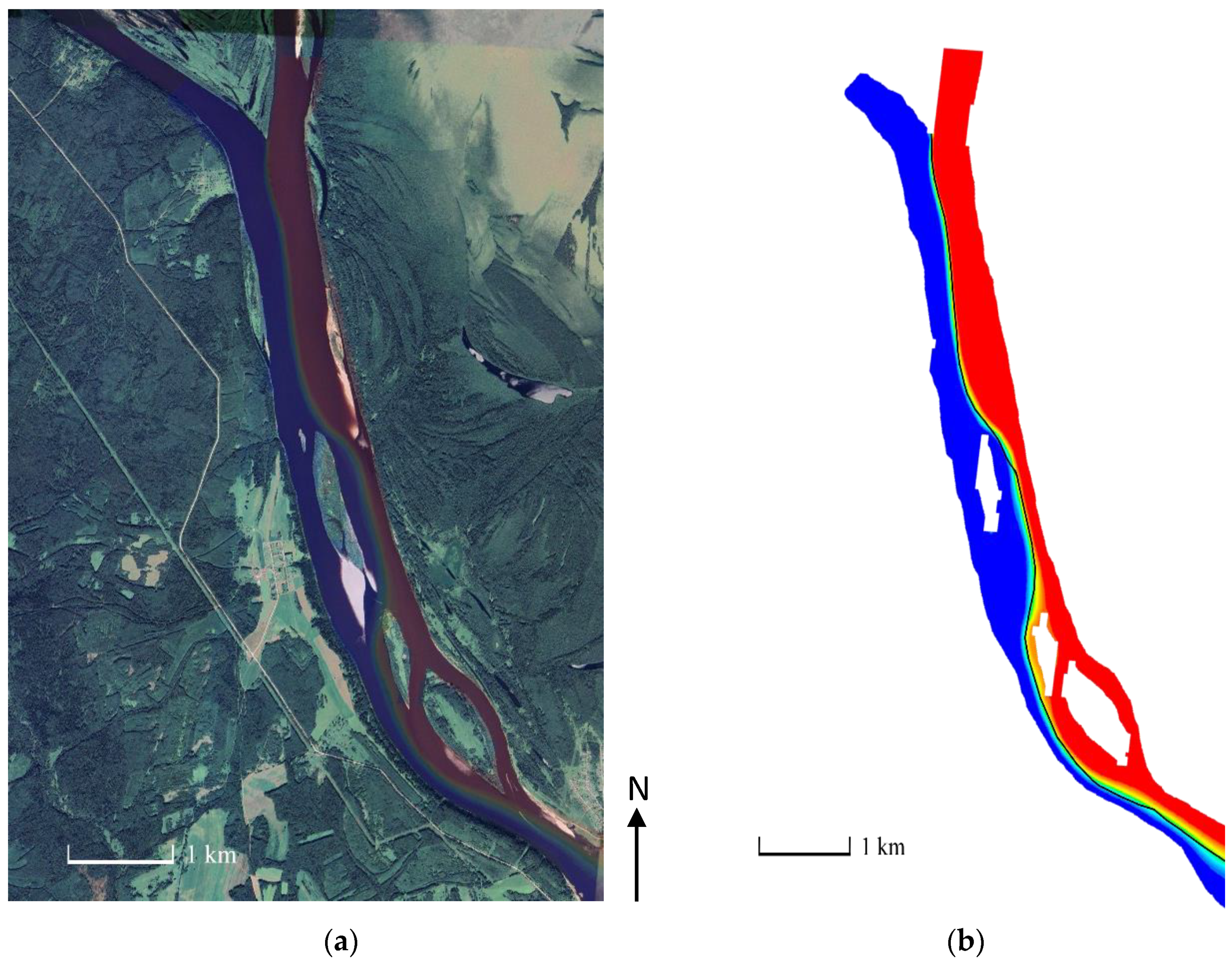
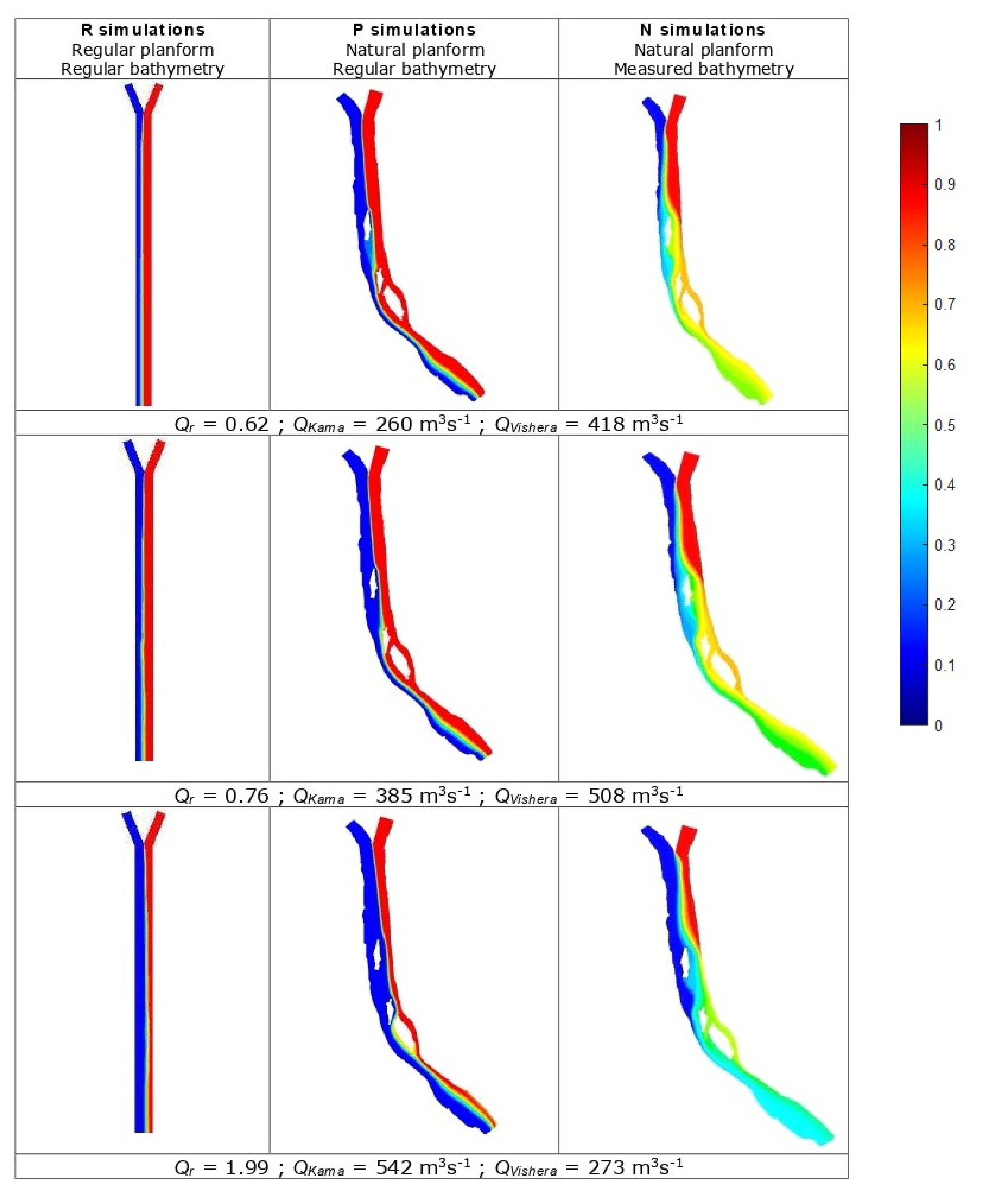
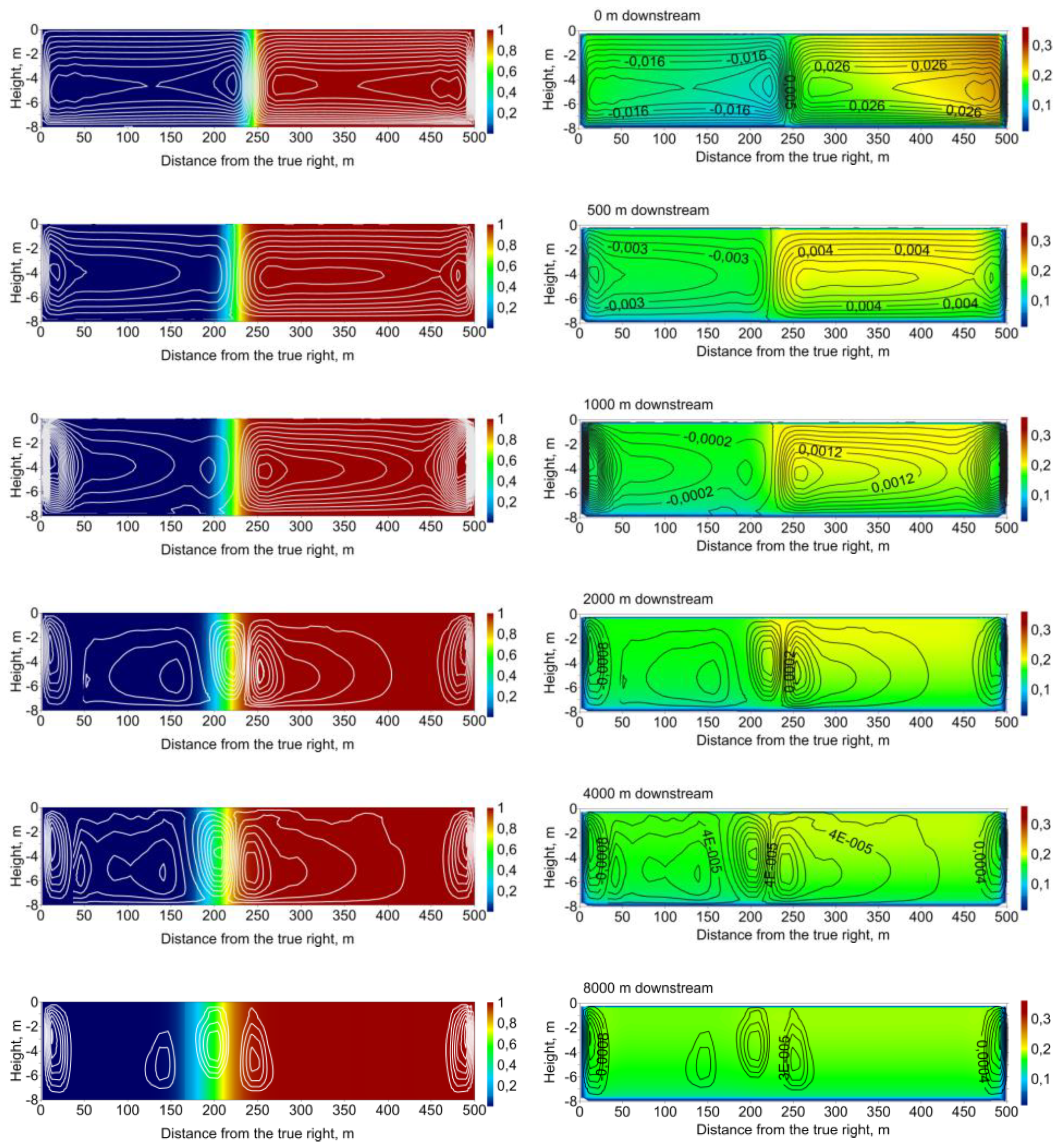
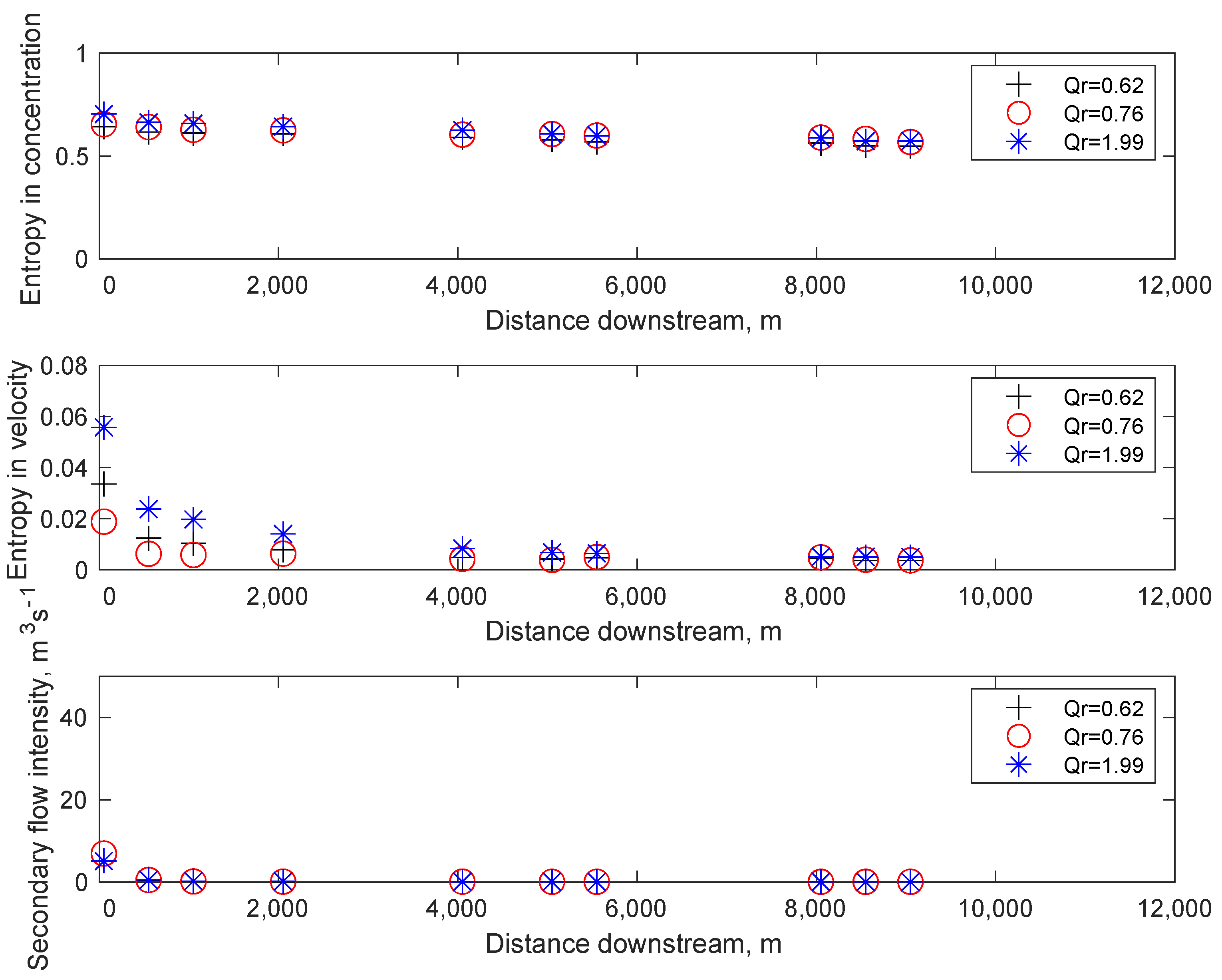
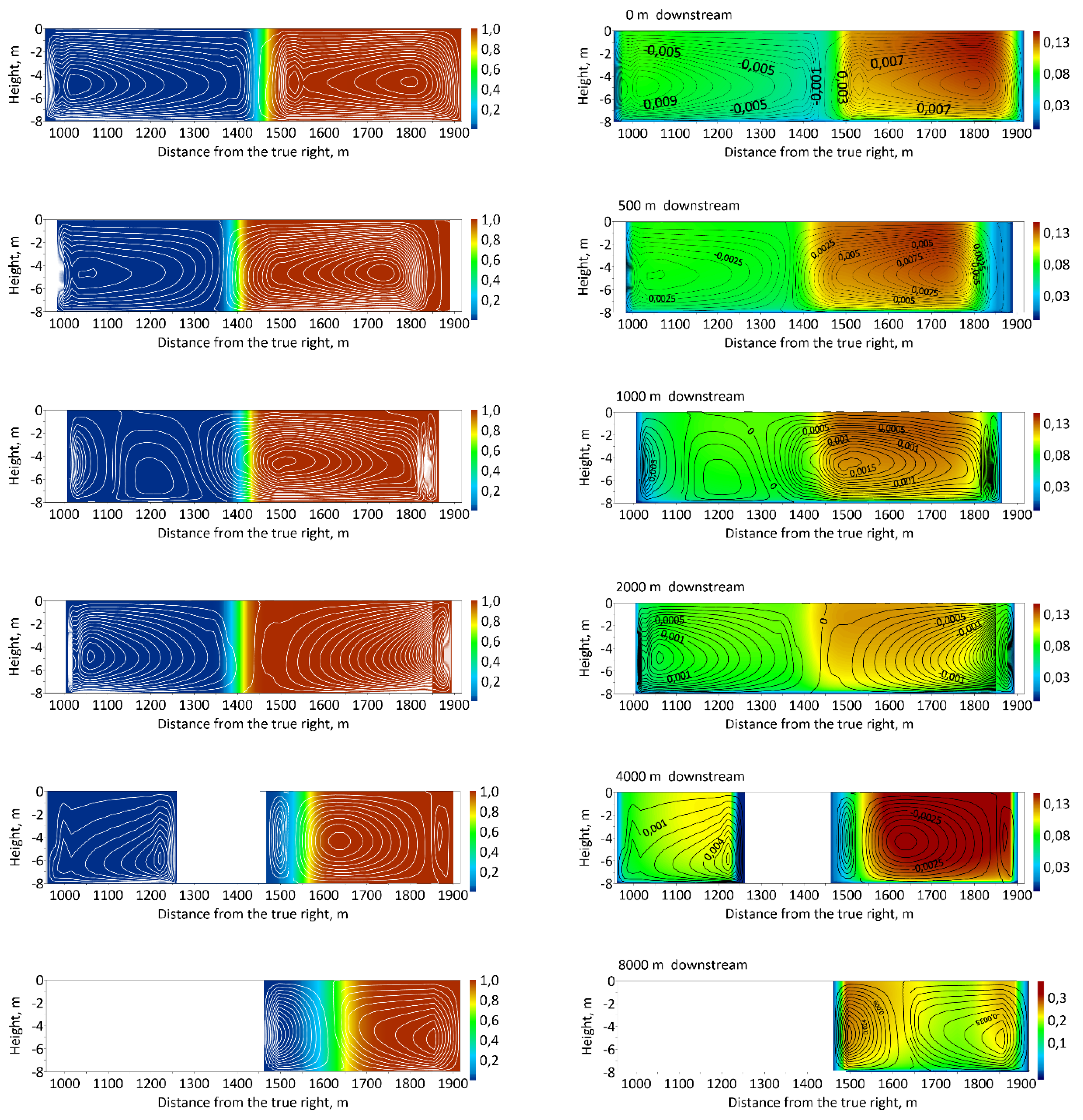
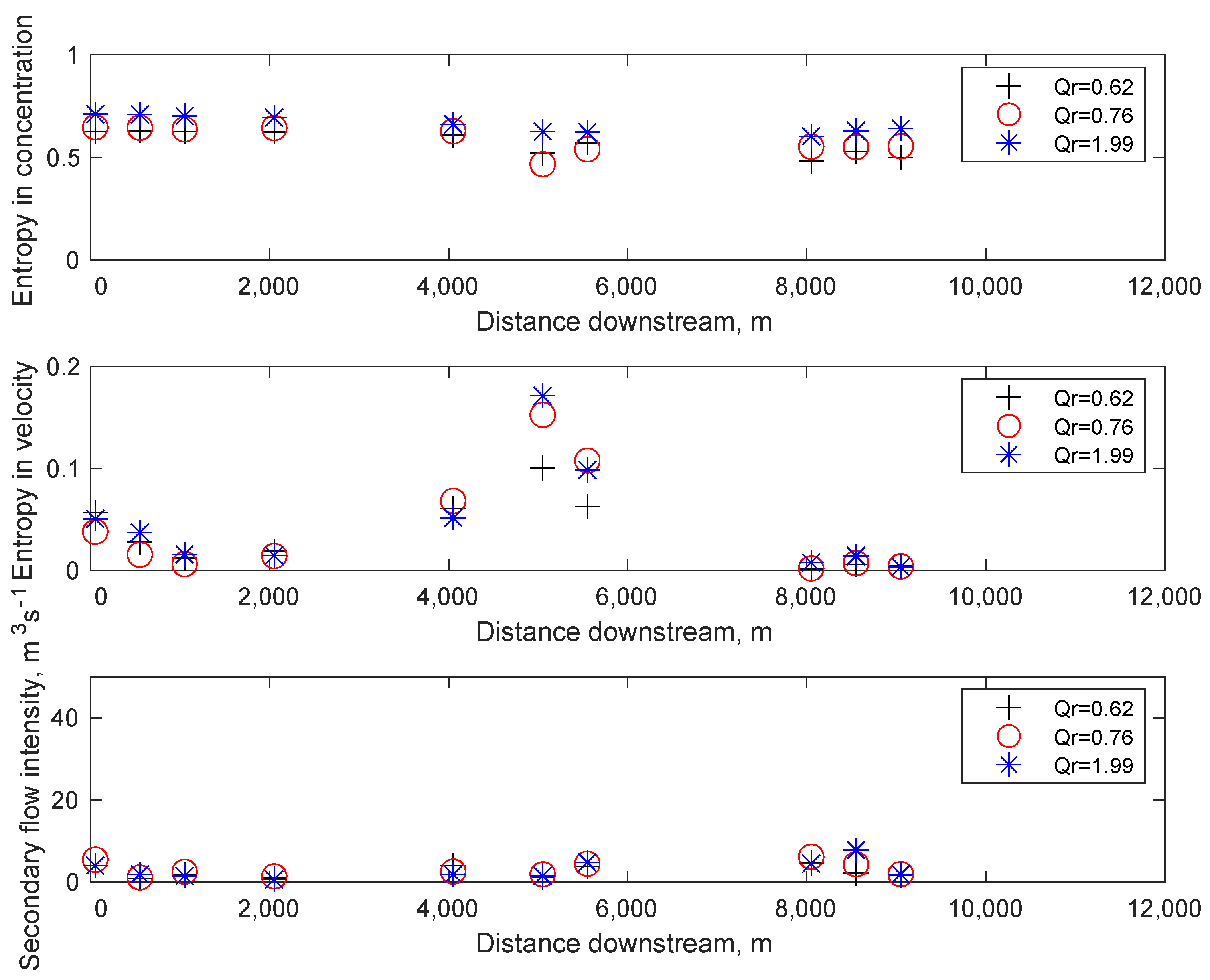
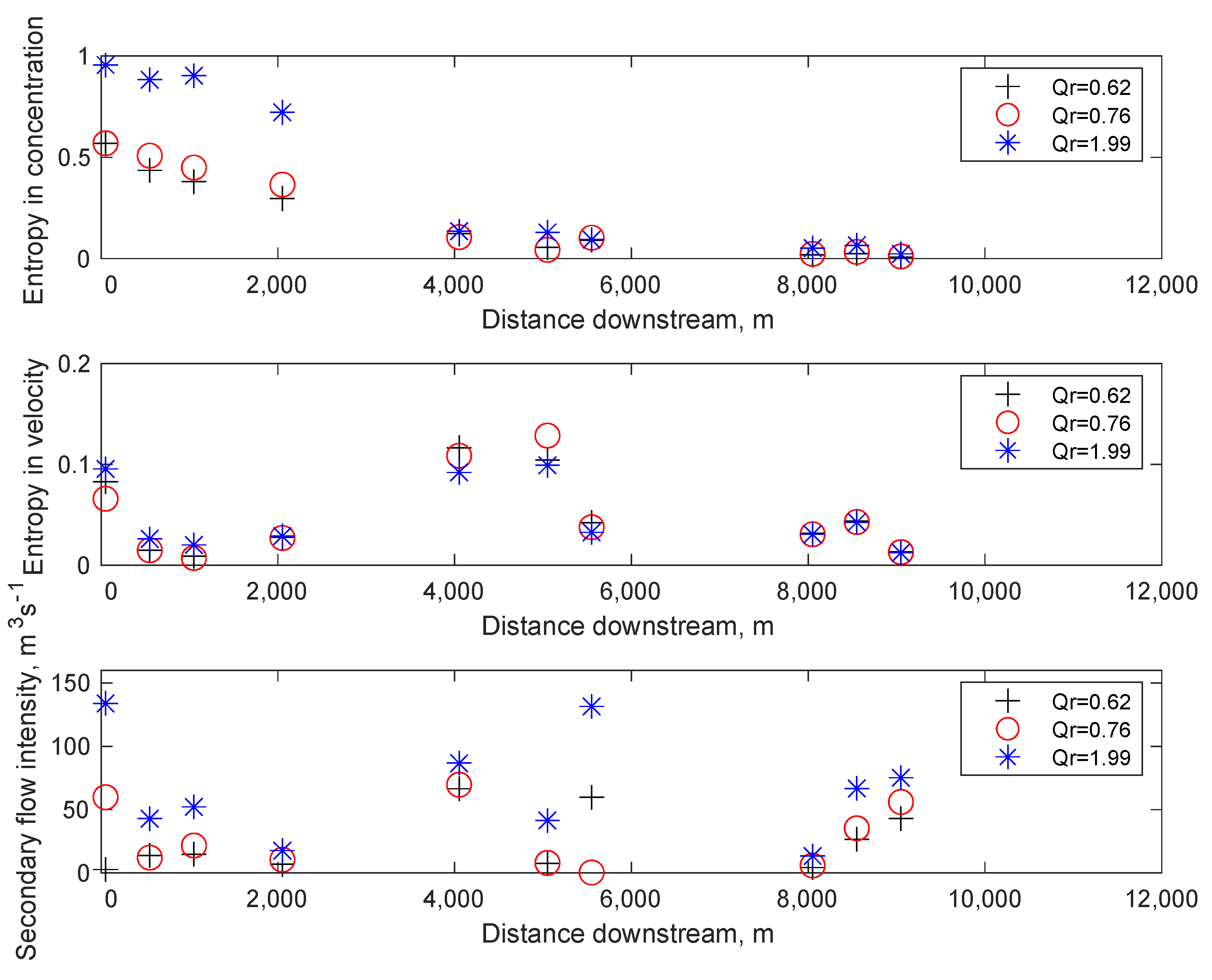
| Sample | Discharge Kama (QKama) m3·s−1 | Discharge Vishera (QVishera) m3·s−1 | Discharge Ratio (QKama/QVishera) |
|---|---|---|---|
| 30 July 2018 | 260 | 418 | 0.62 |
| 22 July 2018 | 385 | 508 | 0.76 |
| 10 September 2018 | 542 | 273 | 1.99 |
| Validation data, 19 July 2019 | 1010 | 1170 | 0.86 |
| Parameter | 0 km −20.5% | 0 km −6.9% | 0 km Base Mesh | 0.5 km −20.5% | 0.5 km −6.9% | 0.5 km Base Mesh |
|---|---|---|---|---|---|---|
| Entropy in concentration | 0.596 | 0.601 | 0.601 | 0.539 | 0.572 | 0.572 |
| Entropy in velocity | 0.032 | 0.031 | 0.031 | 0.010 | 0.016 | 0.016 |
| Secondary circulation intensity (m3·s−1) | 1.390 | 1.502 | 1.761 | 0.051 | 0.055 | 0.055 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyubimova, T.P.; Lepikhin, A.P.; Parshakova, Y.N.; Kolchanov, V.Y.; Gualtieri, C.; Roux, B.; Lane, S.N. A Numerical Study of the Influence of Channel-Scale Secondary Circulation on Mixing Processes Downstream of River Junctions. Water 2020, 12, 2969. https://doi.org/10.3390/w12112969
Lyubimova TP, Lepikhin AP, Parshakova YN, Kolchanov VY, Gualtieri C, Roux B, Lane SN. A Numerical Study of the Influence of Channel-Scale Secondary Circulation on Mixing Processes Downstream of River Junctions. Water. 2020; 12(11):2969. https://doi.org/10.3390/w12112969
Chicago/Turabian StyleLyubimova, Tatyana P., Anatoly P. Lepikhin, Yanina N. Parshakova, Vadim Y. Kolchanov, Carlo Gualtieri, Bernard Roux, and Stuart N. Lane. 2020. "A Numerical Study of the Influence of Channel-Scale Secondary Circulation on Mixing Processes Downstream of River Junctions" Water 12, no. 11: 2969. https://doi.org/10.3390/w12112969
APA StyleLyubimova, T. P., Lepikhin, A. P., Parshakova, Y. N., Kolchanov, V. Y., Gualtieri, C., Roux, B., & Lane, S. N. (2020). A Numerical Study of the Influence of Channel-Scale Secondary Circulation on Mixing Processes Downstream of River Junctions. Water, 12(11), 2969. https://doi.org/10.3390/w12112969








