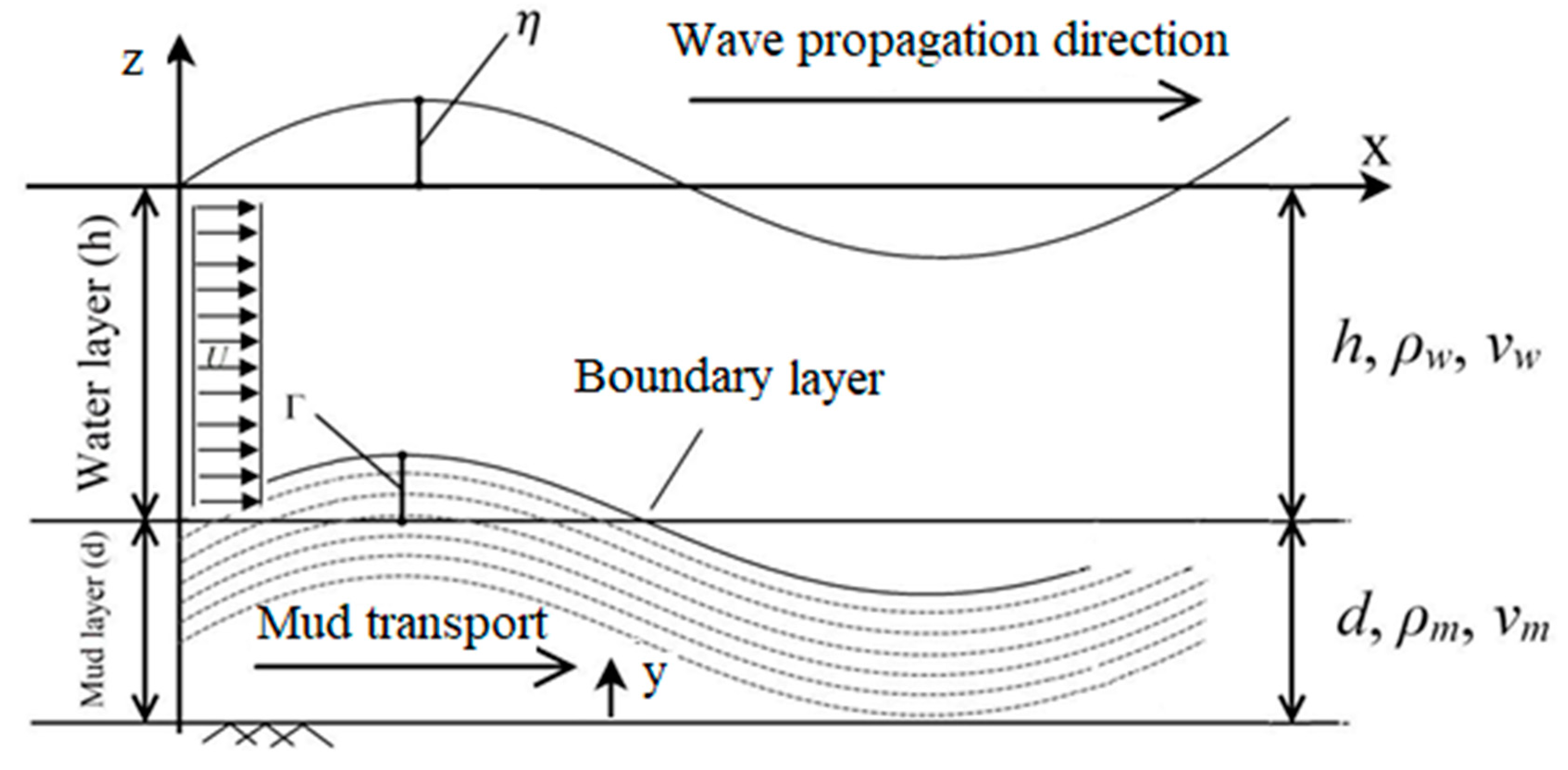
1. Introduction
Phenomena relevant to the water–sediment systems are of great importance in the coastal zones all over the world. Therefore, water–sediment interaction should be studied from different perspectives, e.g., coastal protection, land reclamation, and water quality management [
1]. Some parts of the coasts including estuaries and mouths of large rivers are mainly covered by the soft mud (Lousiana coast [
2]; Brazil [
3]; South Korea [
4]; and Iran [
5]). The current exists in most of the cases in the fields of water-mud systems, especially in the confluences of large rivers and estuaries (e.g., Ems estuary [
6]; Southampton water estuary [
7]). The current substantially affects the two major aspects of wave mud interaction: wave attenuation, and mud mass transport, which are highly influential in the coastal systems in the environmental, engineering, and management aspects [
1]. While both wave attenuation and mud transport affect the designing of the harbors and ports [
8], the mud mass transport may also cause some environmental issues by carrying the pollutant species toward the coasts [
9]. The current influences a wave field by shifting the frequency and changing the amplitude, and it plays a significant role in the development of the waves of unusual character. Current can also refract waves, change the direction of wave propagation, and consequently affect the nearshore hydrodynamics [
10].
Wave–mud interactions have been widely studied in several aspects including wave height attenuation ([
11,
12,
13]), mud mass transport as the bed load ([
8,
9,
14,
15,
16] among many others), stratified two-phase flows ([
12,
17]), and, suspended load (e.g., the most recent ones are [
18,
19]). Many analytical and experimental studies have been carried to reveal the unknown aspects of the wave-mud interactions (e.g., wave attenuation and mud mass transport). One of the most pioneering among them was Gade [
20], who provided analytical solutions to wave attenuation induced by mud mechanical responses to the waves. Dalrymple and Liu [
11] developed a two-layer fluid model to study the attenuation of waves over a muddy bottom, which was characterized as a laminar viscous fluid. The models were considered with different assumptions for the mud mechanical behavior, e.g., potential flows or fully shear flows, including appropriate solutions for each assumption. Neither the second-order mud mechanical behaviors (e.g., mass transport), nor the current, were considered in the model. Applying a matched asymptotic expansion, Dore [
14] investigated the mud mass transport in a two-layer water-mud system mathematically. Piedra-Cueva [
21] provided an analytical solution for the mud mass transport in a closed channel with an unbounded domain. Assuming that the mud thickness is in the same order as its Stokes’ boundary layer thickness, Ng [
15] presented an analytical perturbation solution for the first and second-order (mean) velocities inside the mud and water layers. Considering the same assumption as Ng [
15], Liu and Chan [
22] presented a new model on wave attenuation. The model was applied to a viscoelastic muddy bed, and the wave attenuation rate, water–mud interfacial interaction, velocity profile, and effects of viscosity, and the impacts of elasticity were all investigated and discussed. The theoretical results were checked with available experimental data and other existing numerical results, providing good agreements. Kranenburg et al. [
23] implemented a dispersion relation obtained from a viscous two-layer model in the wave-forecasting model SWAN (Simulating Wave Nearshore) to simulate wave damping in coastal areas by fluid mud deposits. The dispersion relation was derived for an inviscid upper layer and a viscous lower layer. The model was shown to be highly applicable in the natural conditions, assessing the two-dimensional evolution of wave fields in coastal areas. Neither Liu and Chan [
22] nor Kranenburg et al. [
23] provided formulations for the mud mass transport. Neither of the mentioned studies has investigated the effects of current on wave mud interactions. Some other analytical attempts have been made to formulate the mud mass transport due to the rheological behaviors (e.g., [
9,
24]). The simple assumption of applying the apparent viscosity in viscoelastic mud-adopted by many researchers (e.g., [
22])-was criticized by Ng and Zhang [
24]. In addition to the theoretical studies, there have also been some efforts to measure the mud mass transport rates through experimental tests (e.g., [
8,
25,
26] and more recently [
10]). There have also been a few numerical model developments for wave–mud interaction reported in the literature (e.g., [
27,
28]).
Despite numerous research efforts on wave-mud interactions ([
9,
16,
29,
30,
31,
32,
33,
34] in addition to the above-mentioned studies), very few analytical and numerical studies have been carried to formulate the effects of current on the wave–mud interactions. Nakano [
35] employed an extended multi-layered fluid system to model wave–current–mud interaction. The model did not include a straightforward formula for the mass transport induced by wave-current interactions. An and Shibayama [
26] conducted some laboratory wave flume experiments to observe wave–mud interaction with the current. Wave height attenuation rates and vertical distributions of mean velocities were measured. The numerical model and laboratory experiments revealed that both the wave attenuation rate and mud mass transport, decrease in the following current and increase when an opposing current is applied. Zhao et al. [
1] presented a numerical and experimental study on wave–current–mud interactions. It was assumed that the mud is soft, the shear stress is capable of moving the mud particles, and the current penetrates the mud layer. Therefore, it was mentioned that the mud mass transport is increased by the following current and vice versa. More recently, Soltanpour et al. [
10] provided a combined experimental and semi-analytical study to investigate the current effects on wave–mud interactions. It was assumed that in the ranges of the viscosities applied in their study (e.g., mud viscosity,
νm = O (0.01 N/m
2)), the current does not penetrate the mud layer, and the measurements confirmed such an assumption.
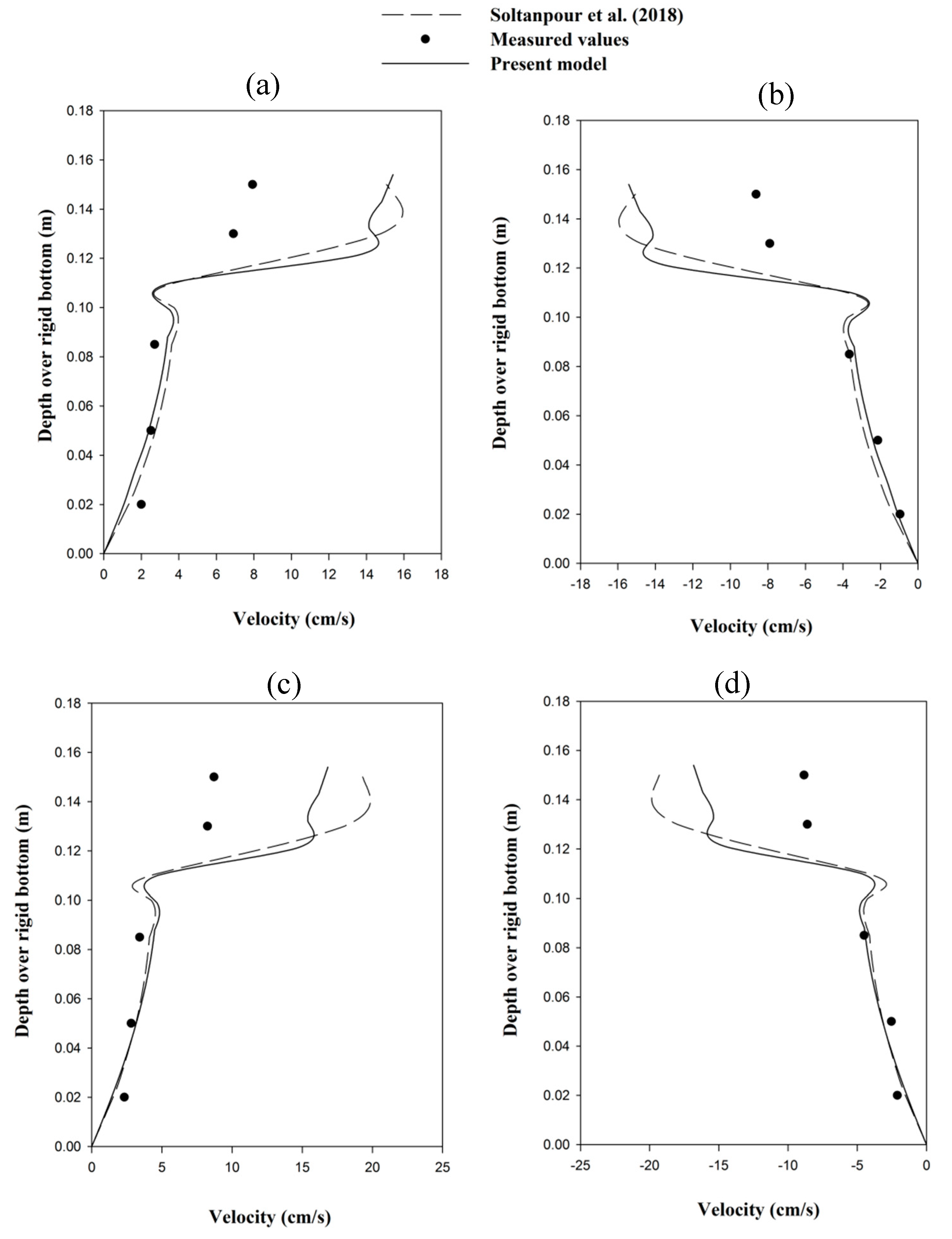
The literature lacks a solution to the first and second order for the dynamic responses of the mud layer to the waves and current interaction. The semi-analytical model presented in Soltanpour et al. [
10] does not provide explicit relations for the dispersion, particle velocities, and mud mass transport. The mud layer was considered as a thick layer, which is contrary to the assumptions of the present study and does not match the real physical conditions of a highly viscous layer of mud. The initial purpose of the present study was to provide formulations, analysis, and investigations for the complicated phenomena of wave–current–mud interaction. In this regard, the present study offers analytical investigations of wave–current–mud interactions to the second-order by the assist of the perturbation method, assuming that the mud layer thickness is of the same order as the mud boundary layer thickness. Straightforward solutions have been obtained for the dissipation rates, phase shift, particle velocities, and mud mass transport induced by wave–current–mud interactions. The effects of current on the dynamics of mud in response to the coaction of regular wave and current have been discussed. Besides, the results of the model have been compared with the measurements of Soltanpour et al. [
10], and An and Shibayama [
26] where good agreements were achieved.
4. Conclusions
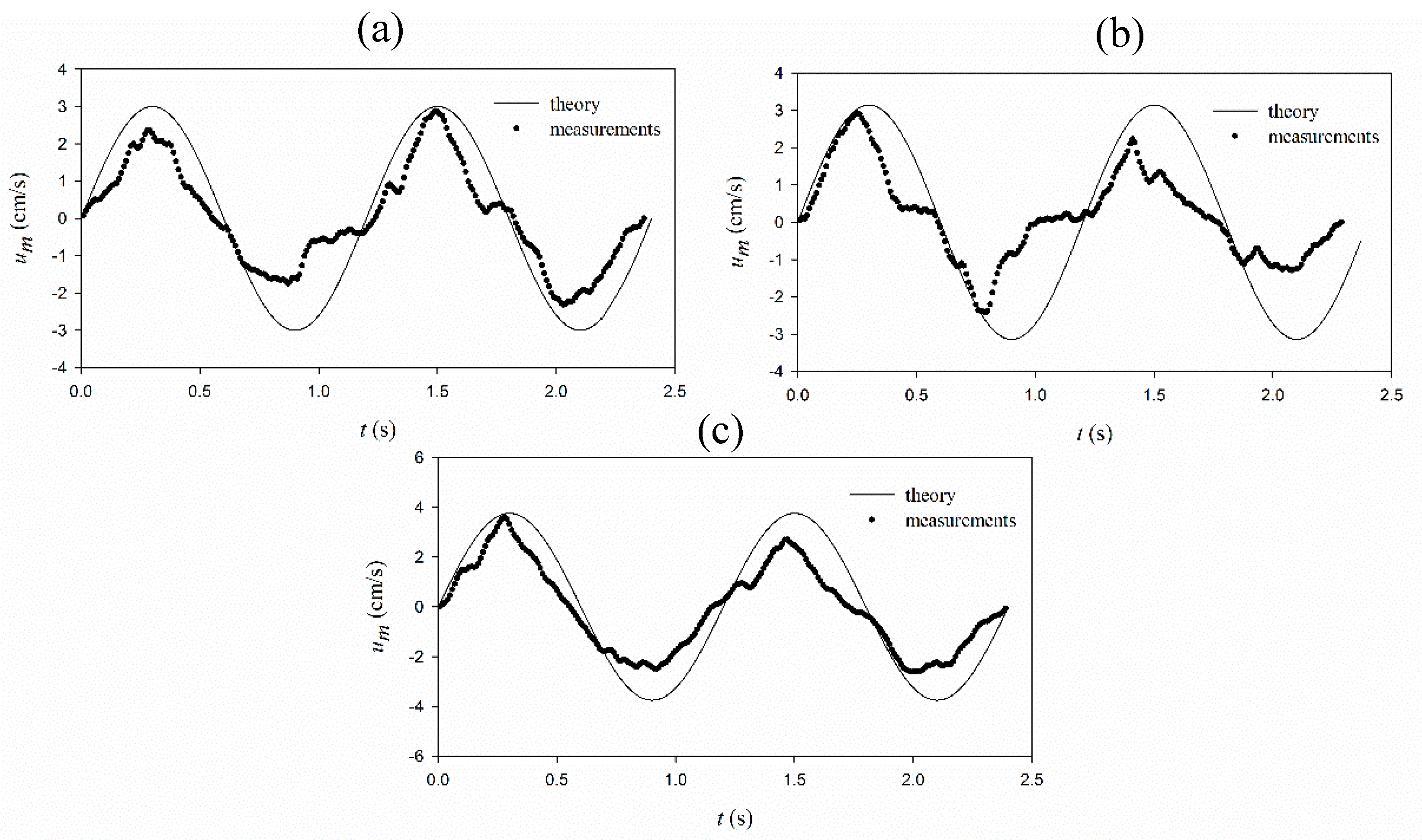
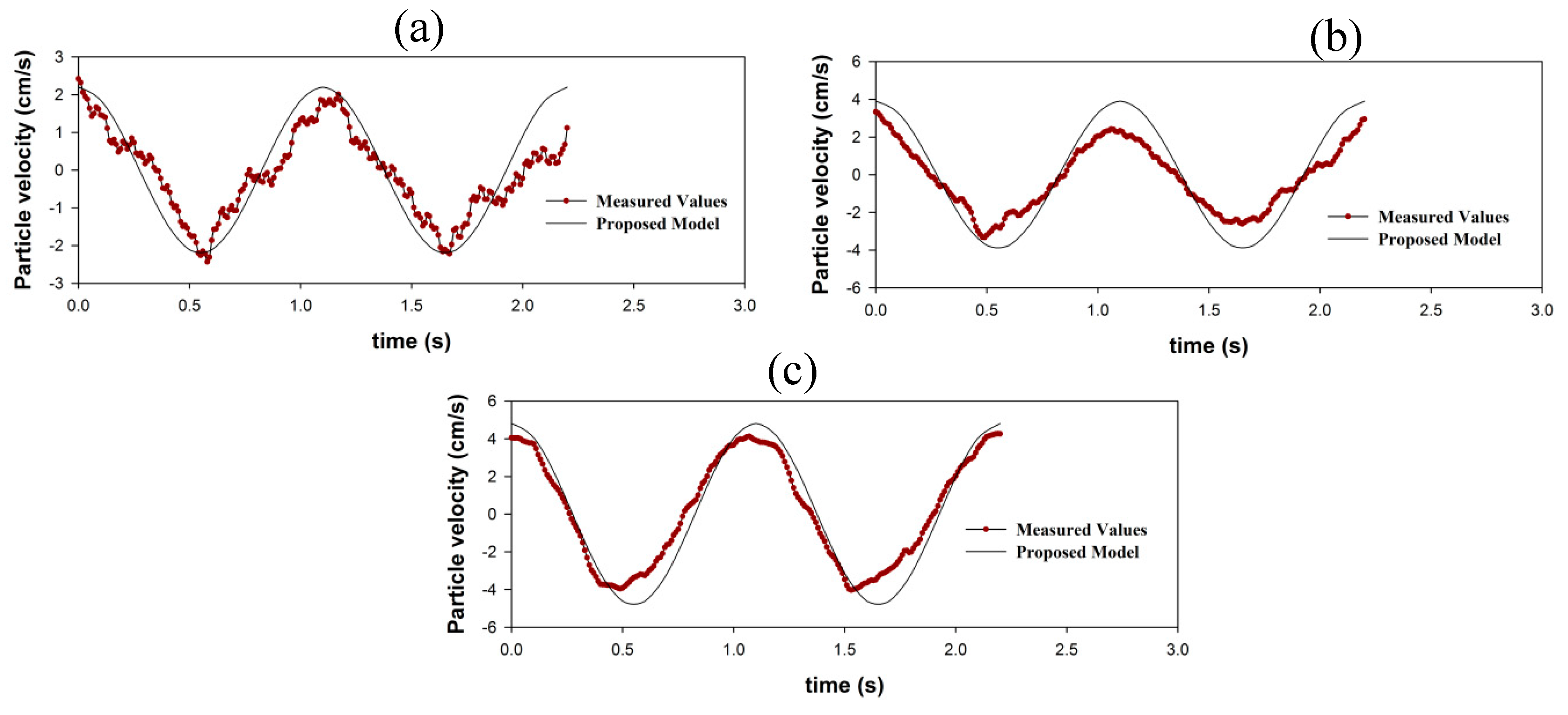
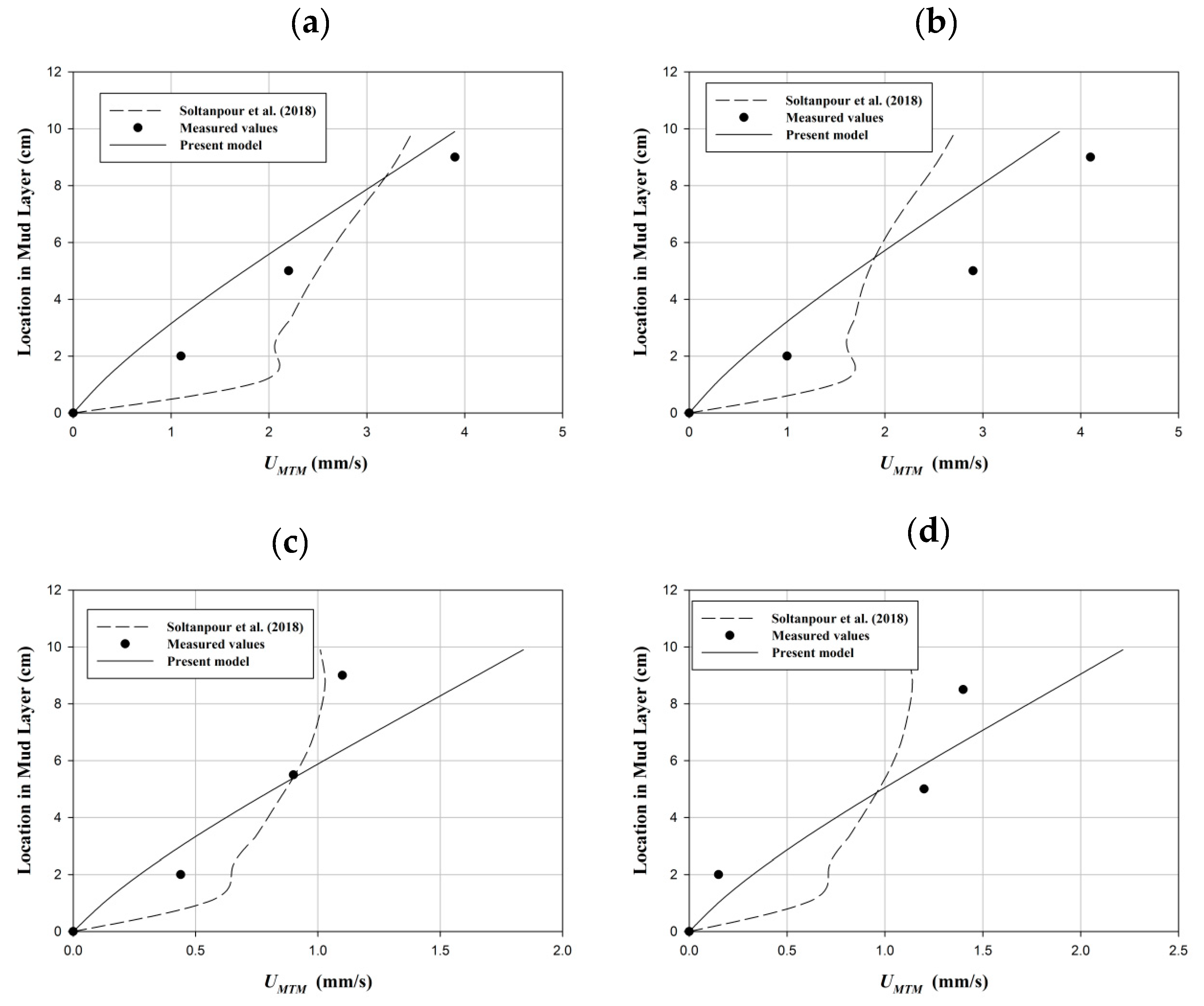
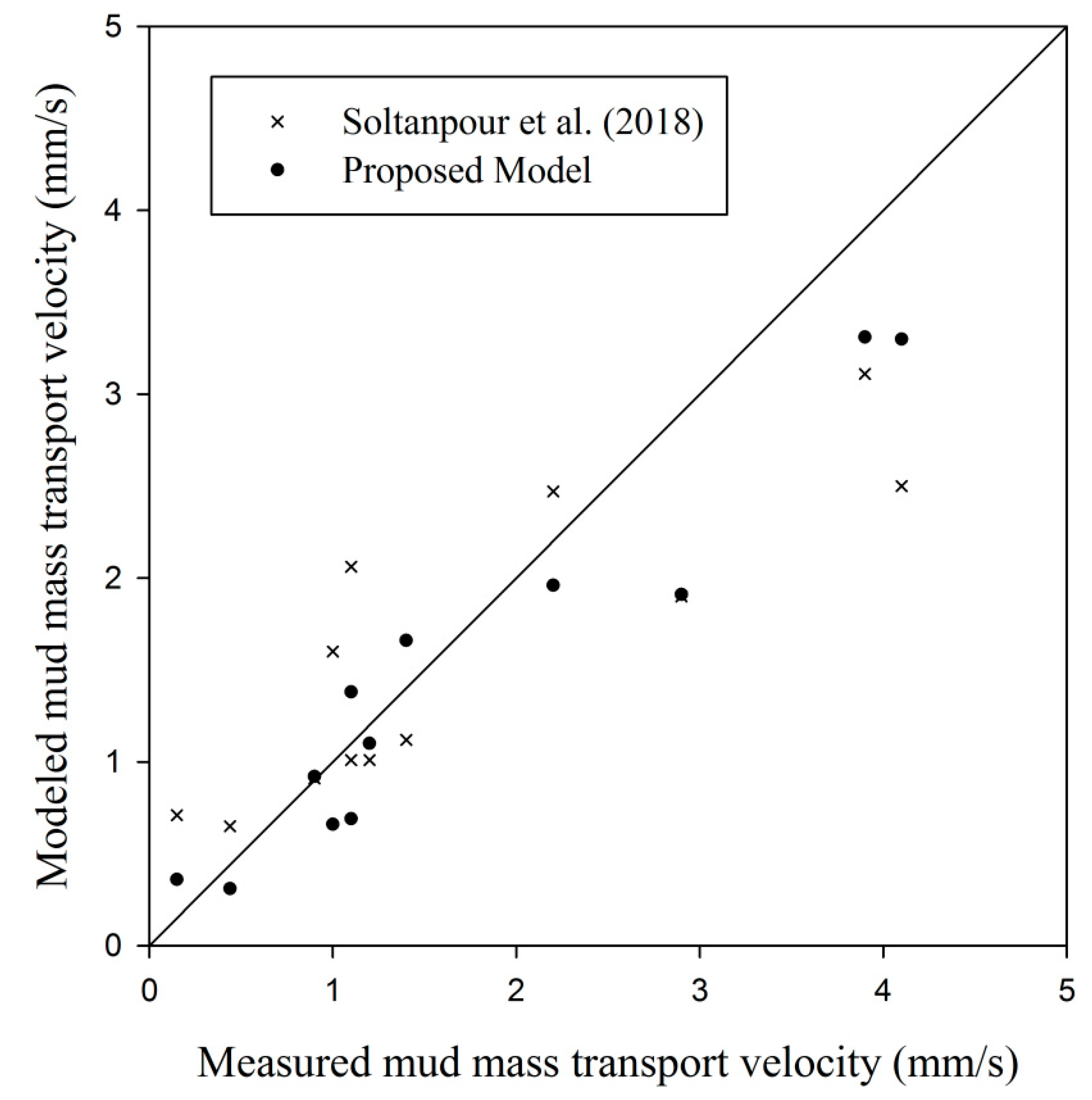
This study provides an analytical investigation of wave–current–mud interaction. The proposed model can be used in the prediction of mud transport where the waves and currents coexist (e.g., confluences of rivers, estuaries, and seas). By the estimation of the mud transport over several periods, pollutant species transports can be calculated, and dredging volumes are estimated that both help the environmental/water scientists and engineers to preserve and manage the coasts and ports. The perturbation approach was adopted to solve the water–mud system of equations to the second order. The effects of current on particle velocity, dissipation rates, and phase shift in the first order and the mass transport and mean velocity in the second-order were investigated. The results of the model have been compared with the measured values of Soltanpour et al. [
10], and An and Shibayama [
26]. In addition to the fact that the proposed model provides explicit and straightforward expressions for the mud particle and mass transport velocities for the first time, the results show that the proposed model has superiority to the model of Soltanpour et al. [
10] in the calculation of mud mass transport velocity. Good agreements are achieved in the calculations of the mud induced wave height attenuation in the presence of currents when compared with the measurements of An and Shibayama [
26]. The following results were achieved from the present study:
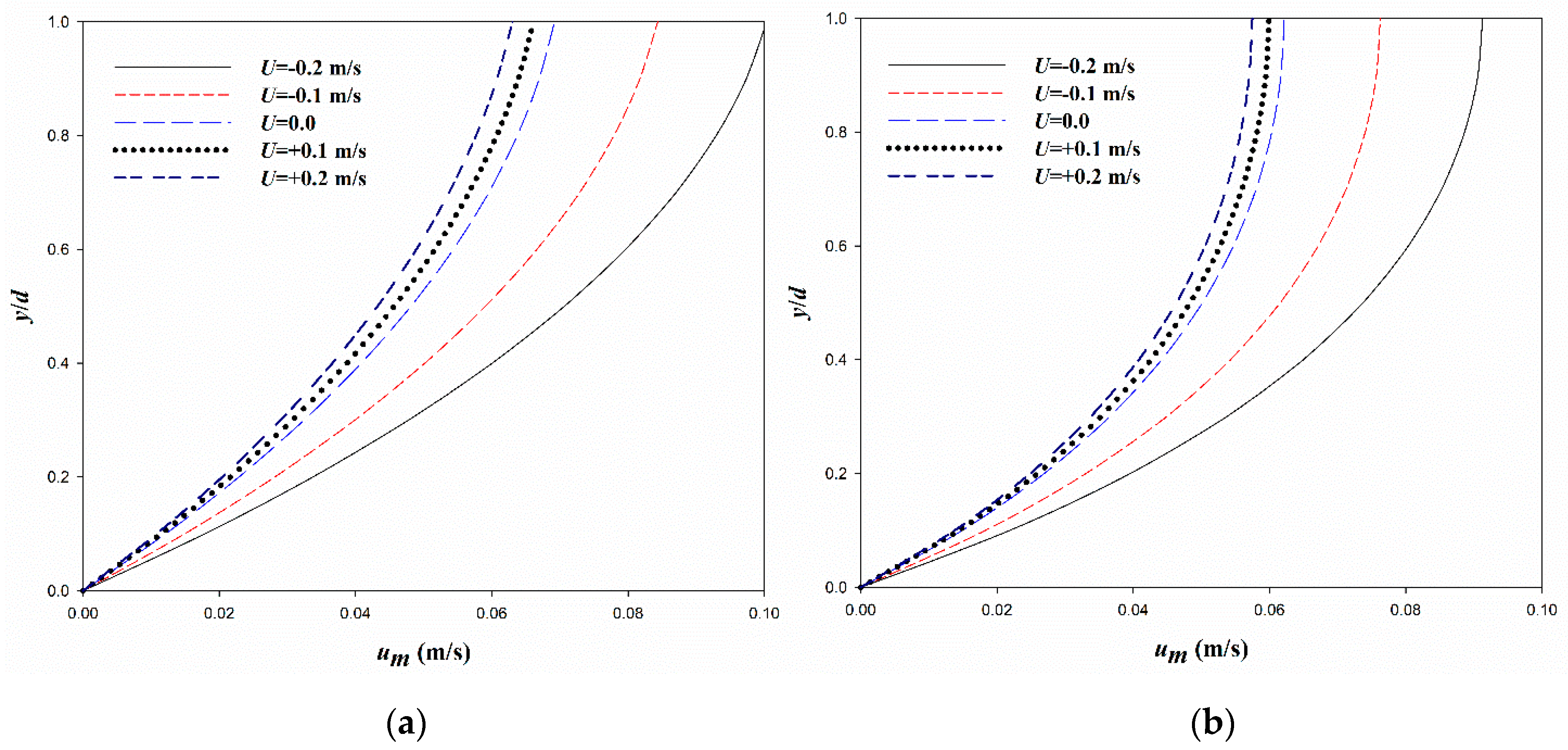
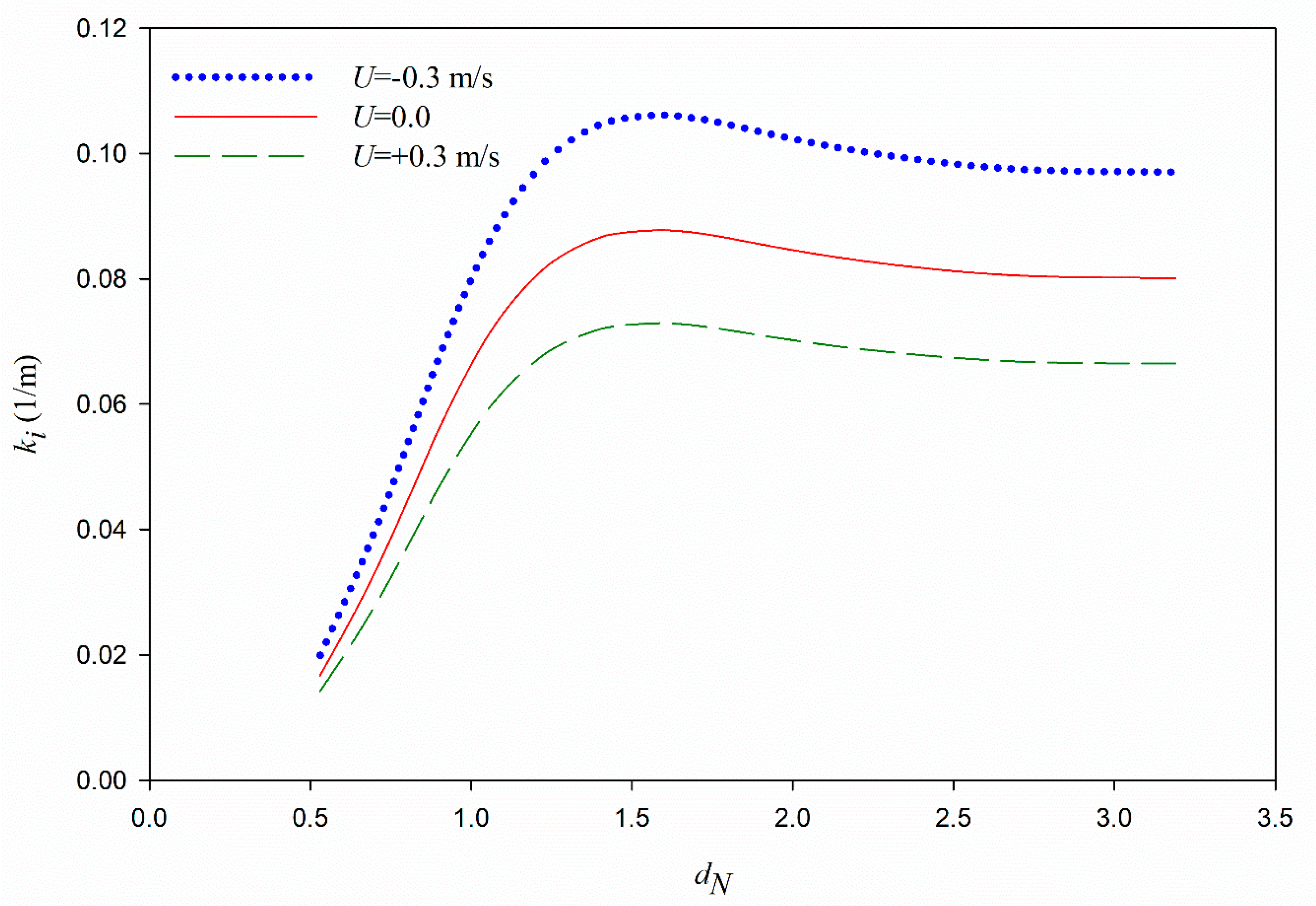
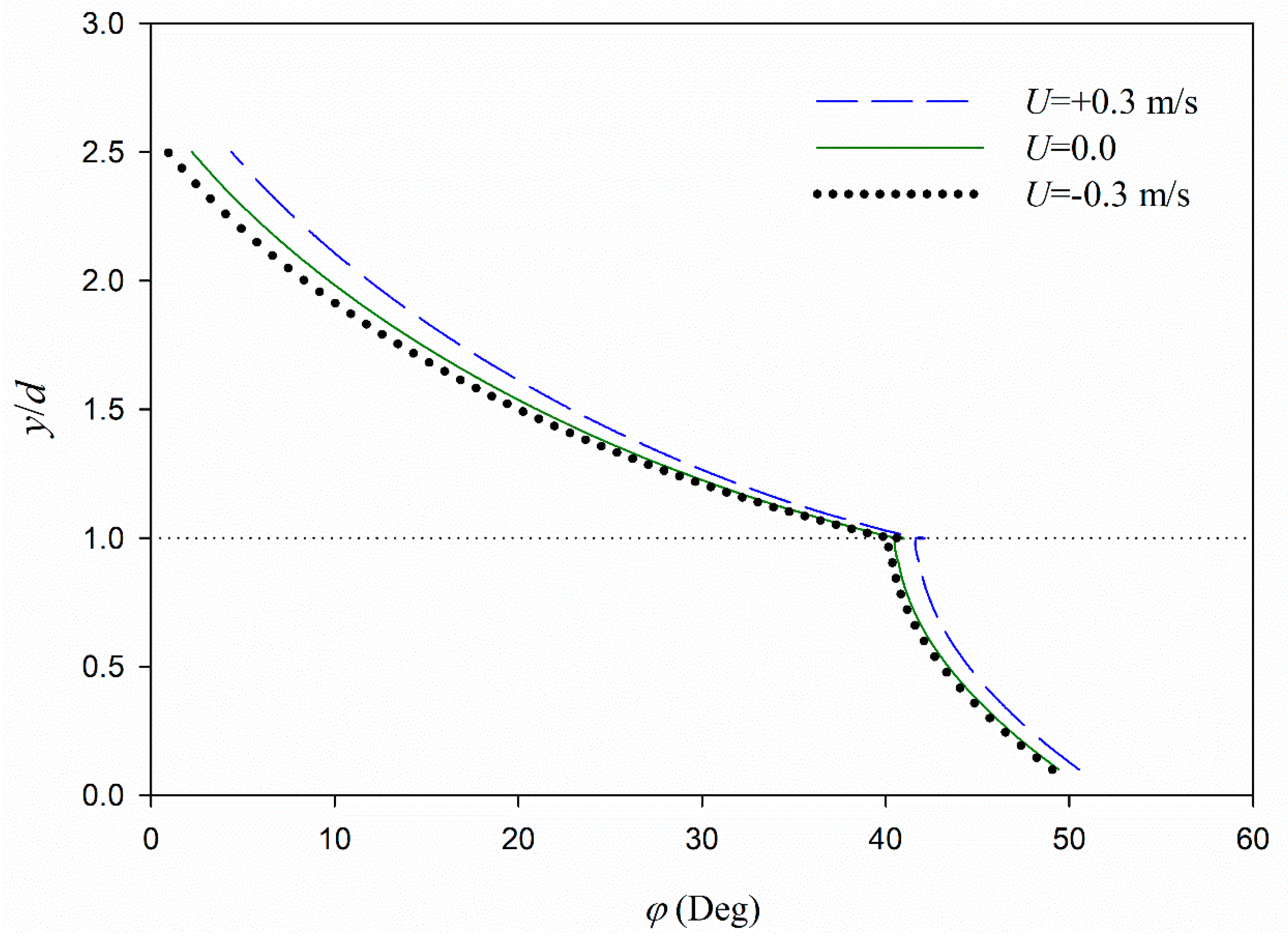
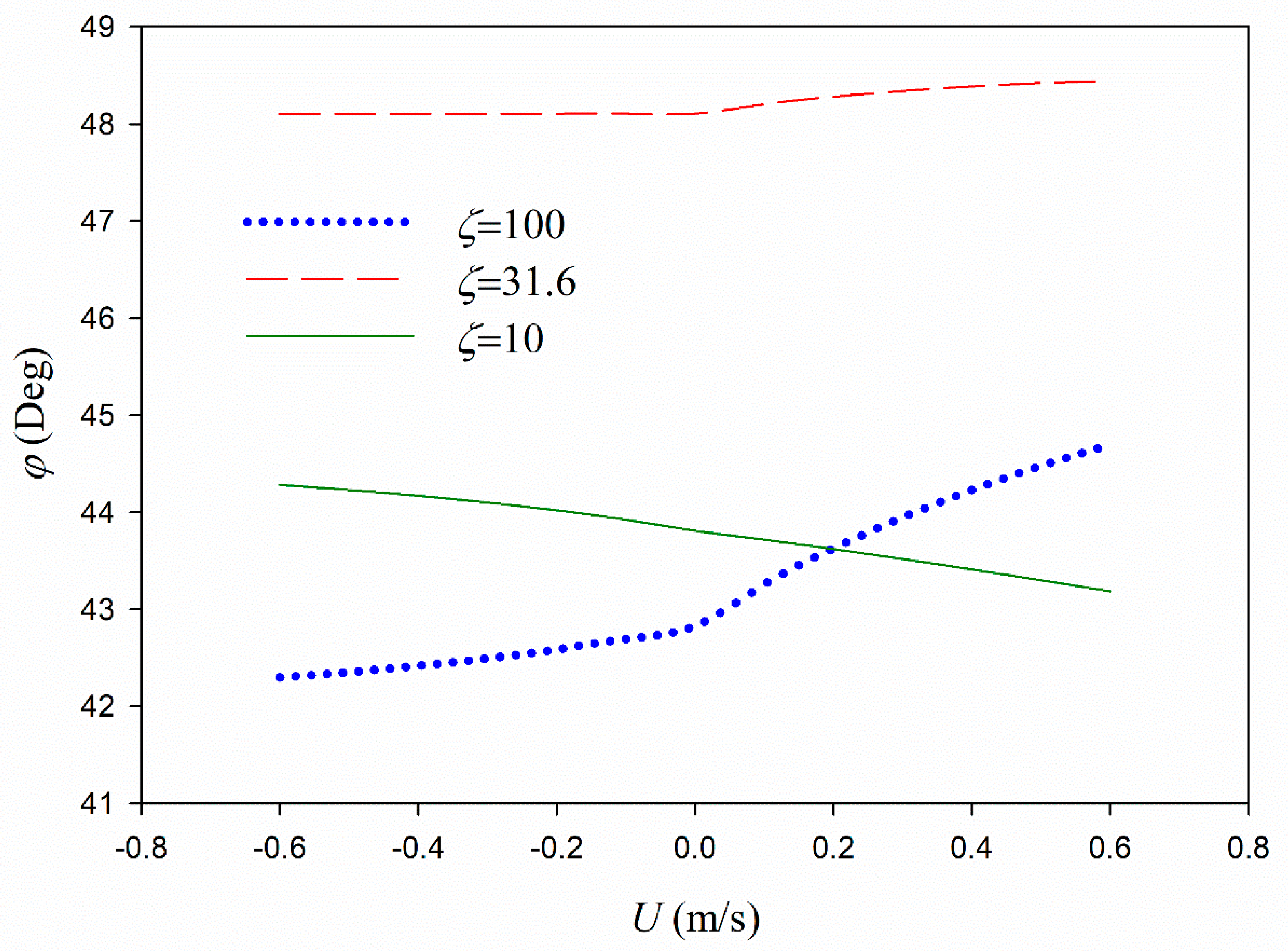
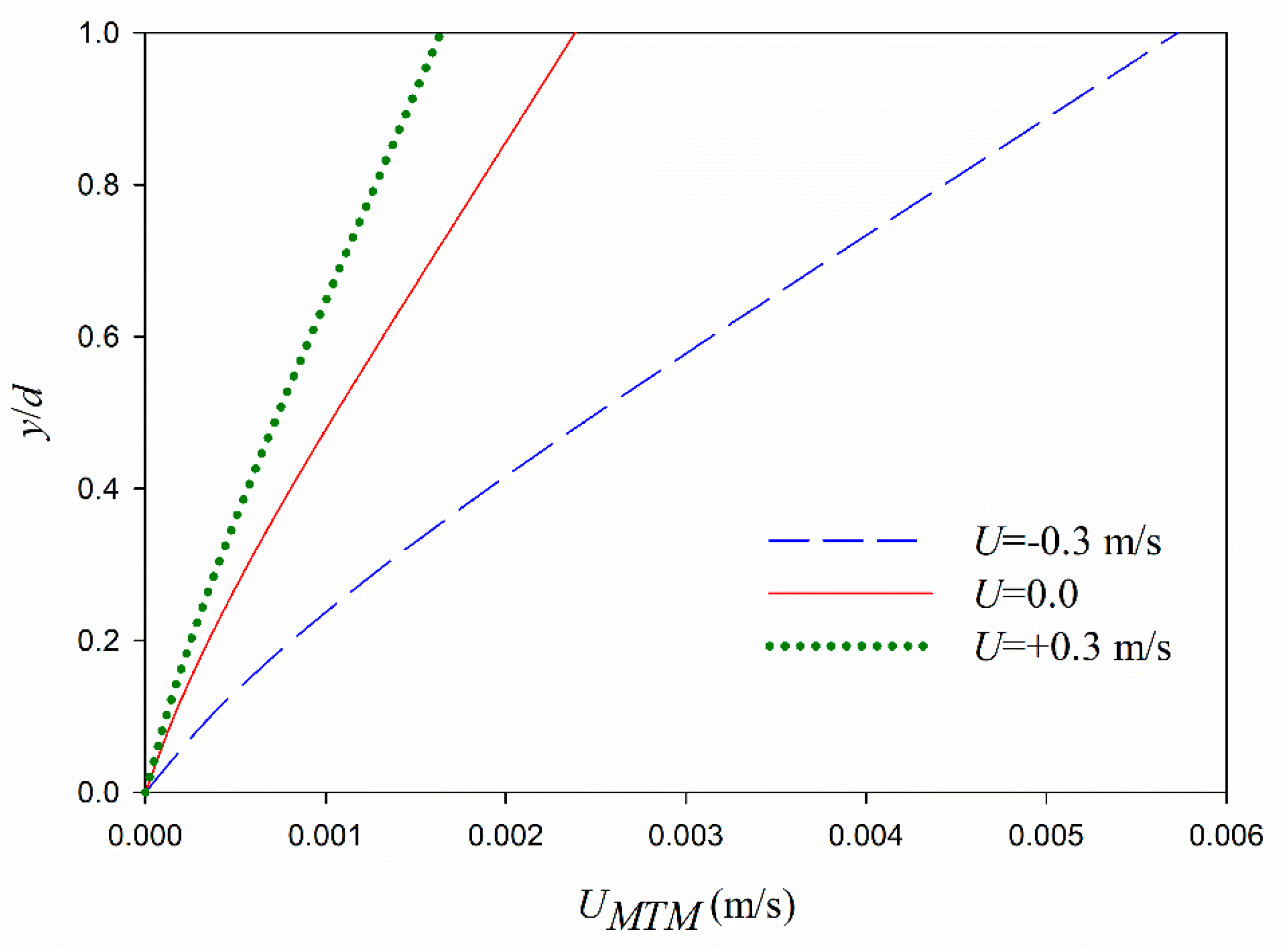
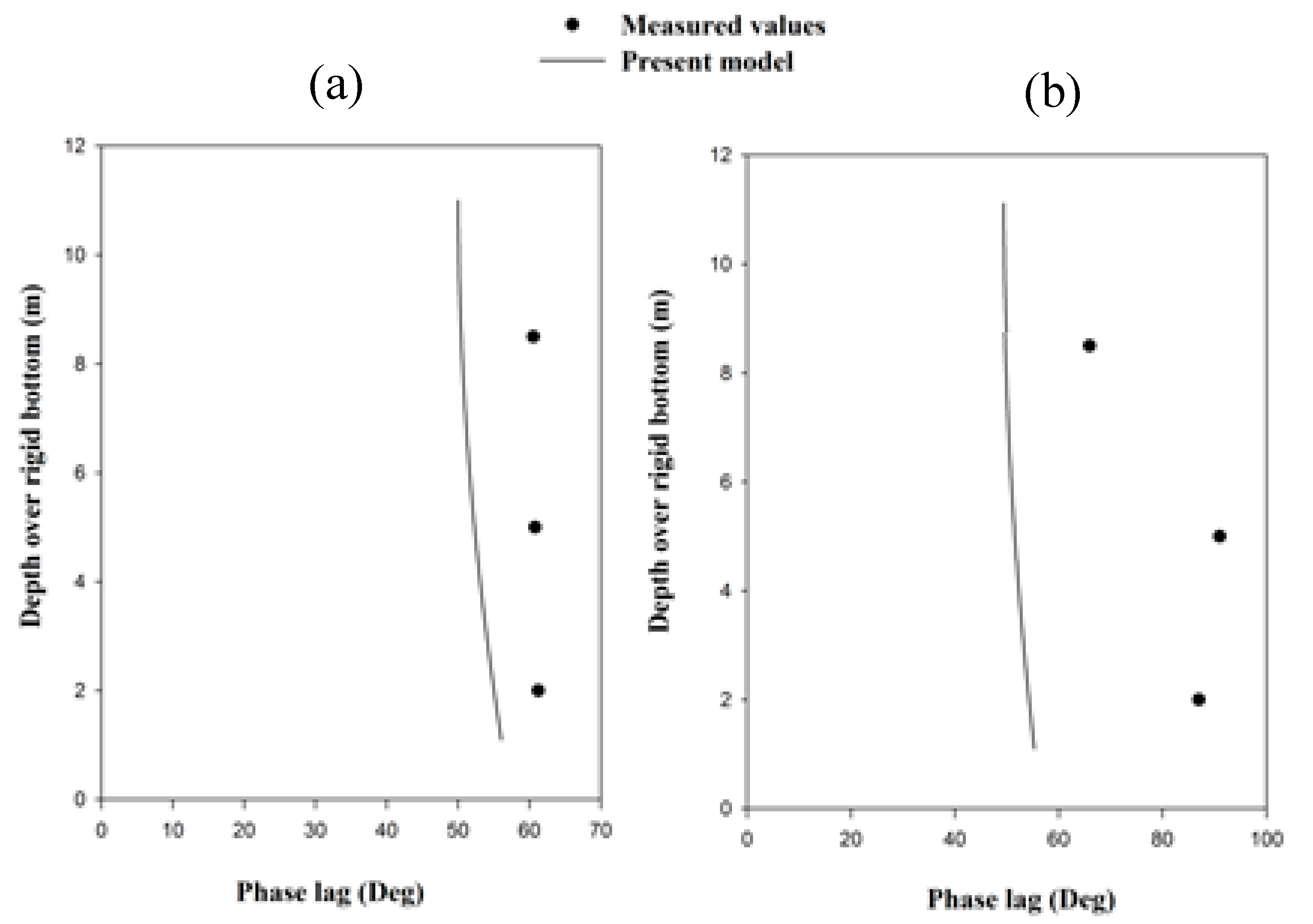
The following current decreases the particle velocity and dissipation rates, while the phase shift may increase, decrease, or be constant by moving from the opposing current to the following current.
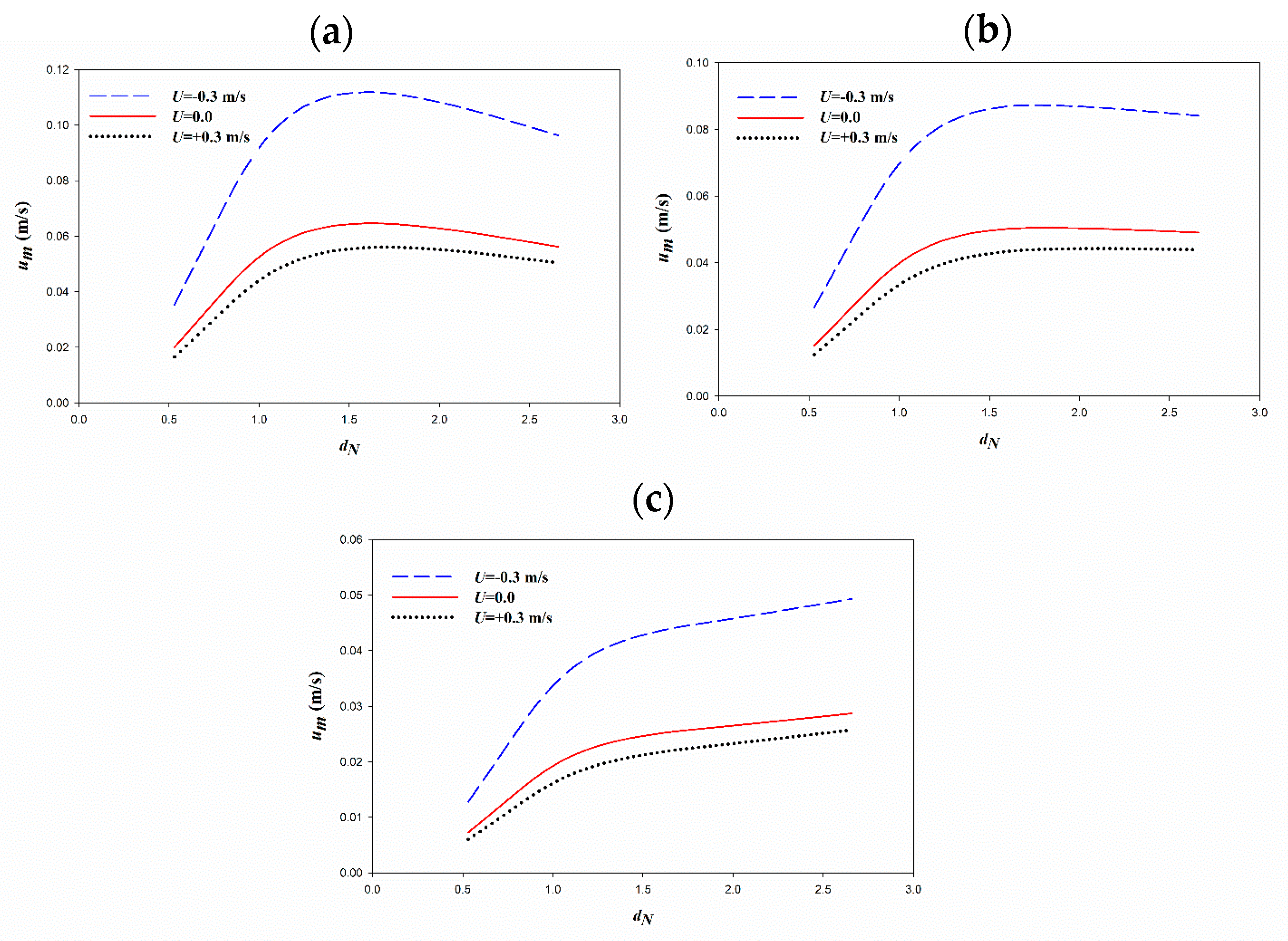
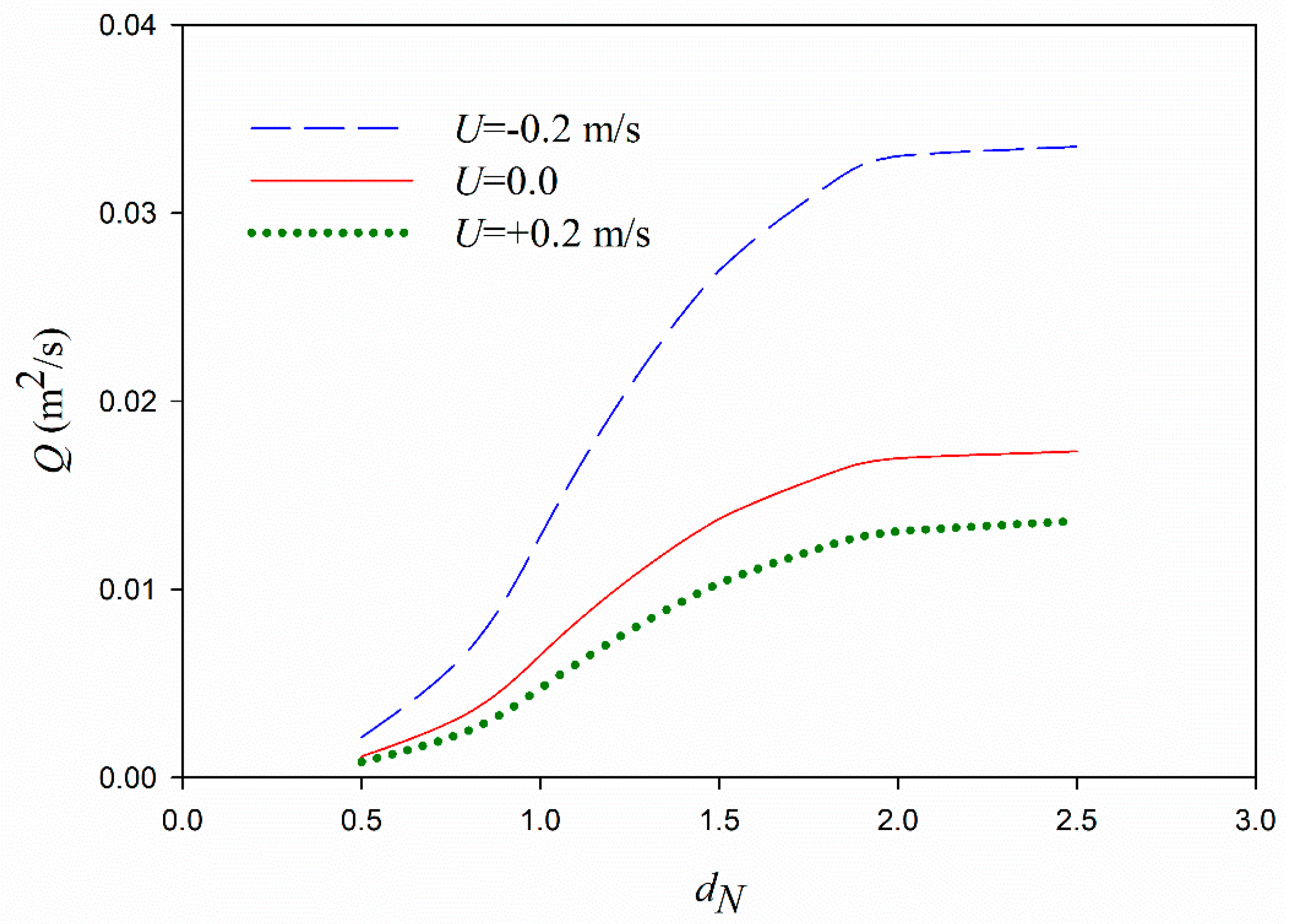
In the second-order, the mud mass transport is increased by a shift from opposing to following currents.
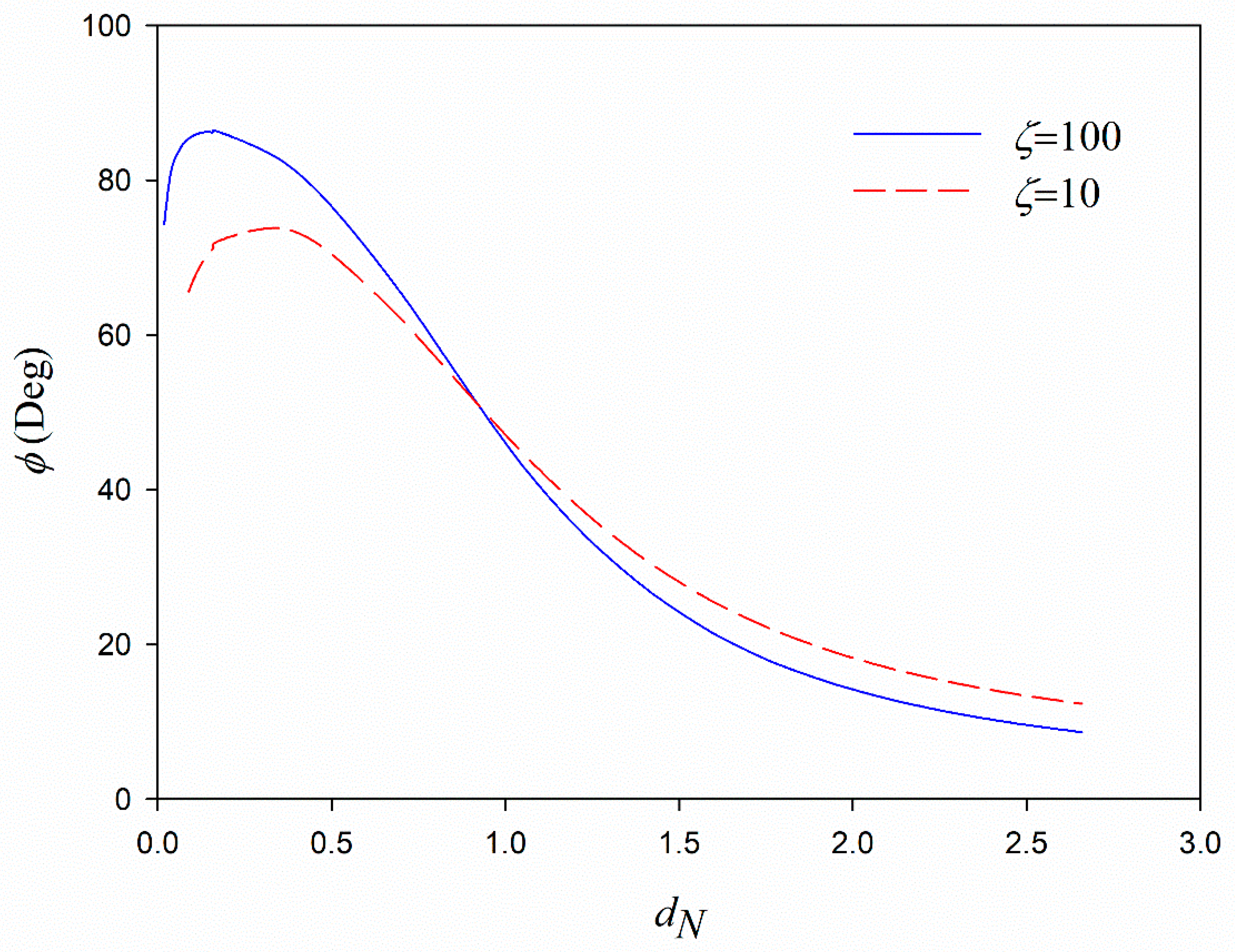
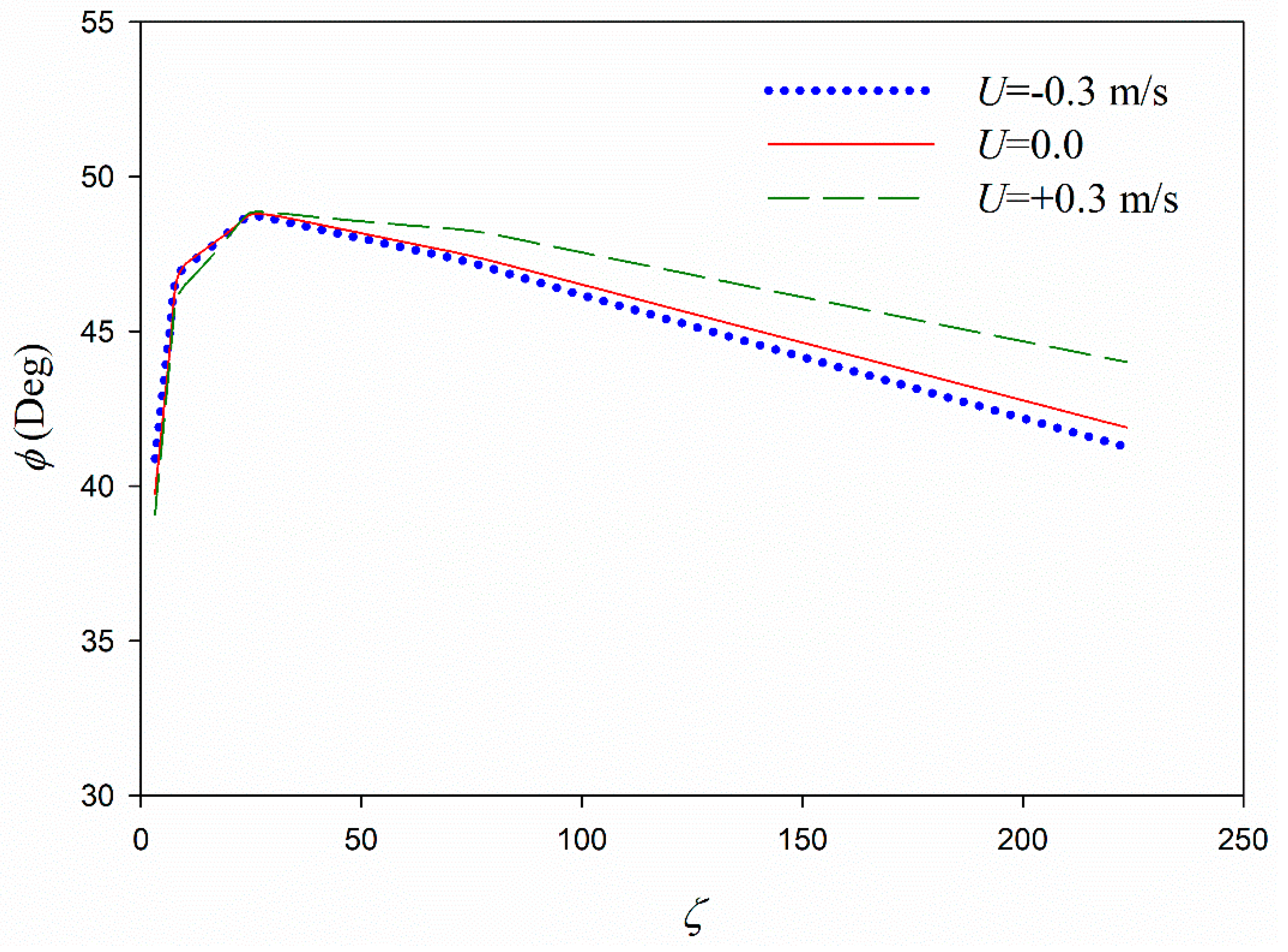
Particle velocity, dissipation rates, and phase shift show a local peak versus the dimensionless mud thickness.
The proposed assumption of a thin mud layer, which depth is in the same order as its boundary layer thickness matches better with the laboratory data in the mud viscosity of the orders of (0.01 N/m2) compared to the models in the literature.
A more general study must be carried to investigate the effects of the lower values of current velocities on mud mass transport (e.g., when the current velocity is of the same order as the wave-induced velocities). Attempts also must be made to generalize the present study assumption to find the ranges of viscosity that make the mud softer and the current to penetrate the mud layer.