A New Optimization Method for the Layout of Pumping Wells in Oases: Application in the Qira Oasis, Northwest China
Abstract
:1. Introduction
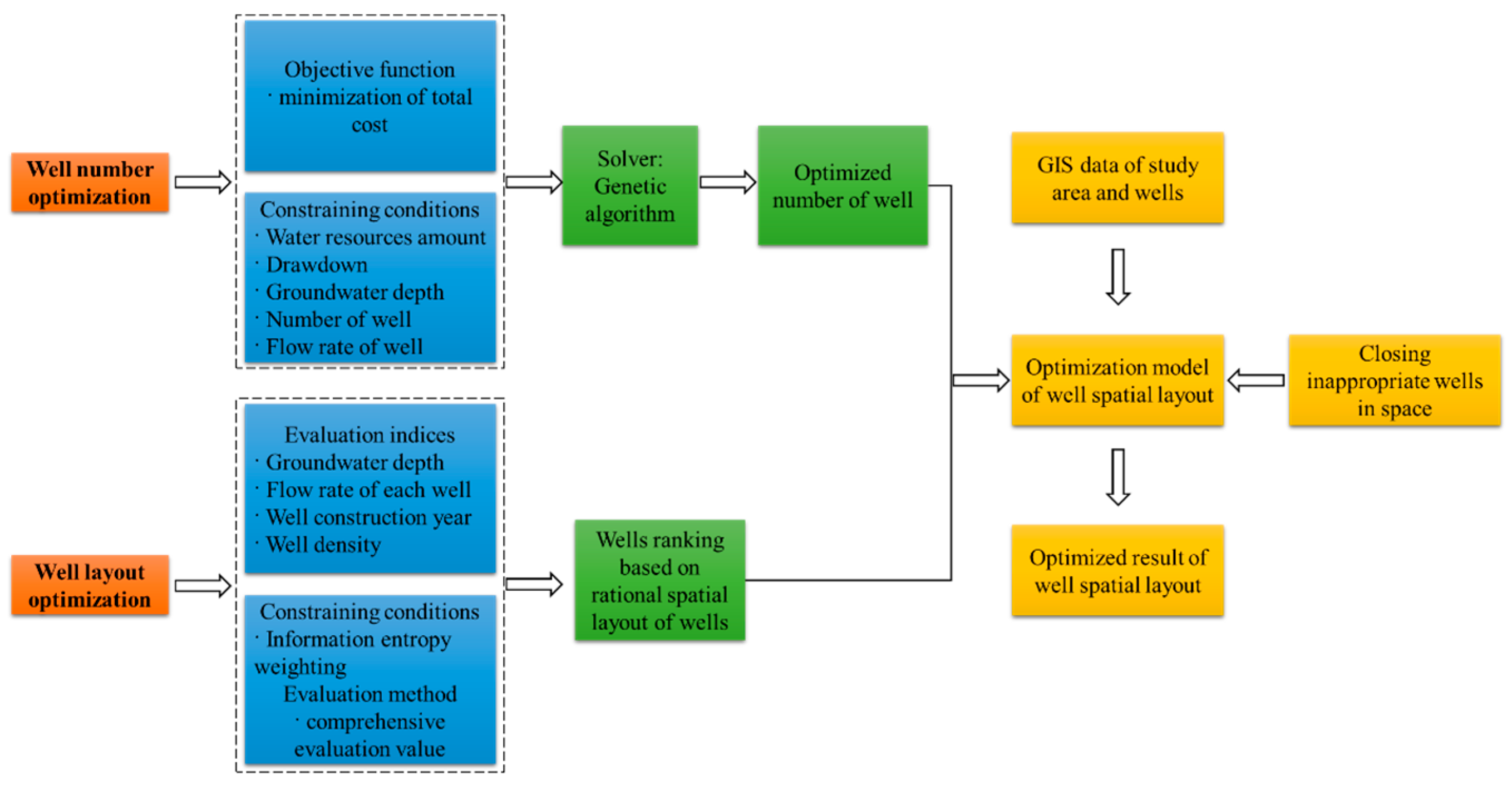
2. Methods
2.1. The Number of Wells Optimization
2.1.1. Nonlinear Programming Methodology
2.1.2. Nonlinear Programming Application
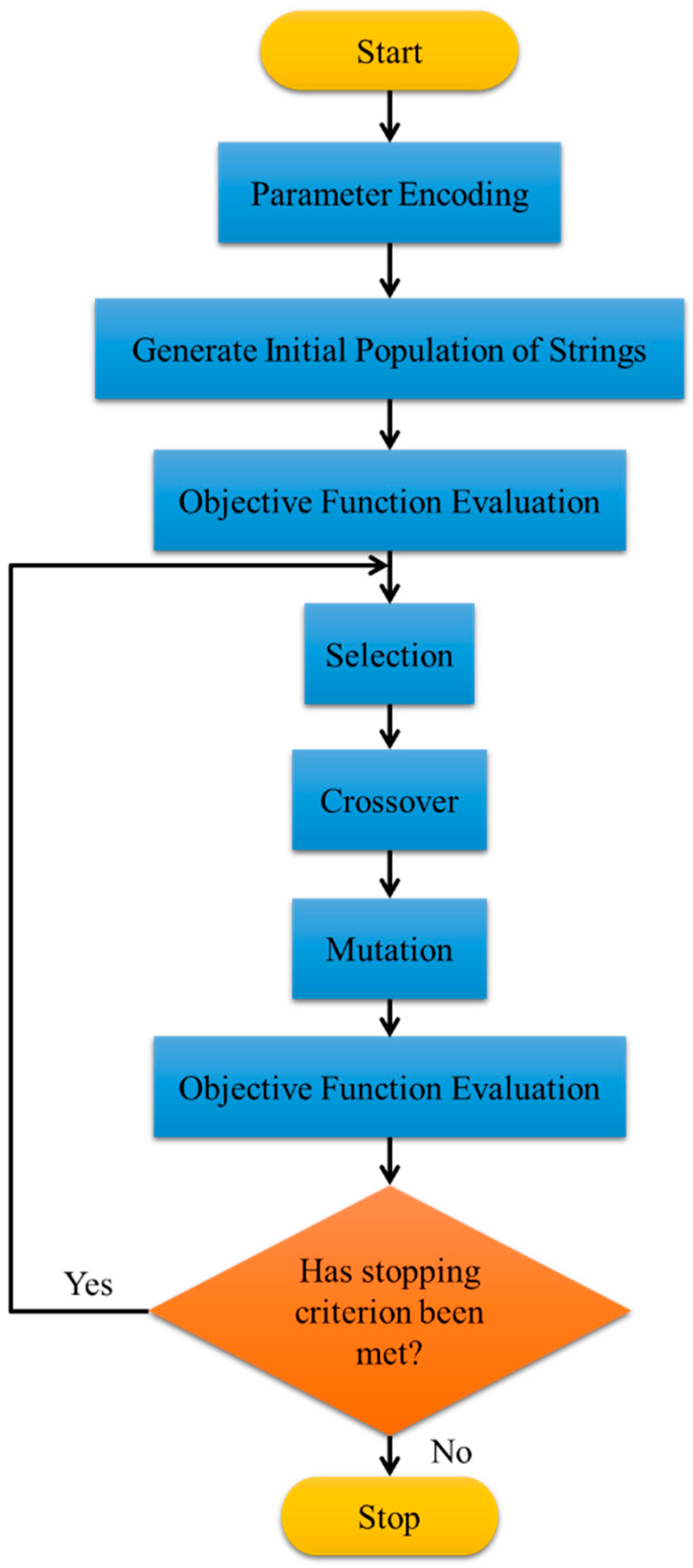
2.1.3. Genetic Algorithm
2.2. Well Layout Optimization
- (1)
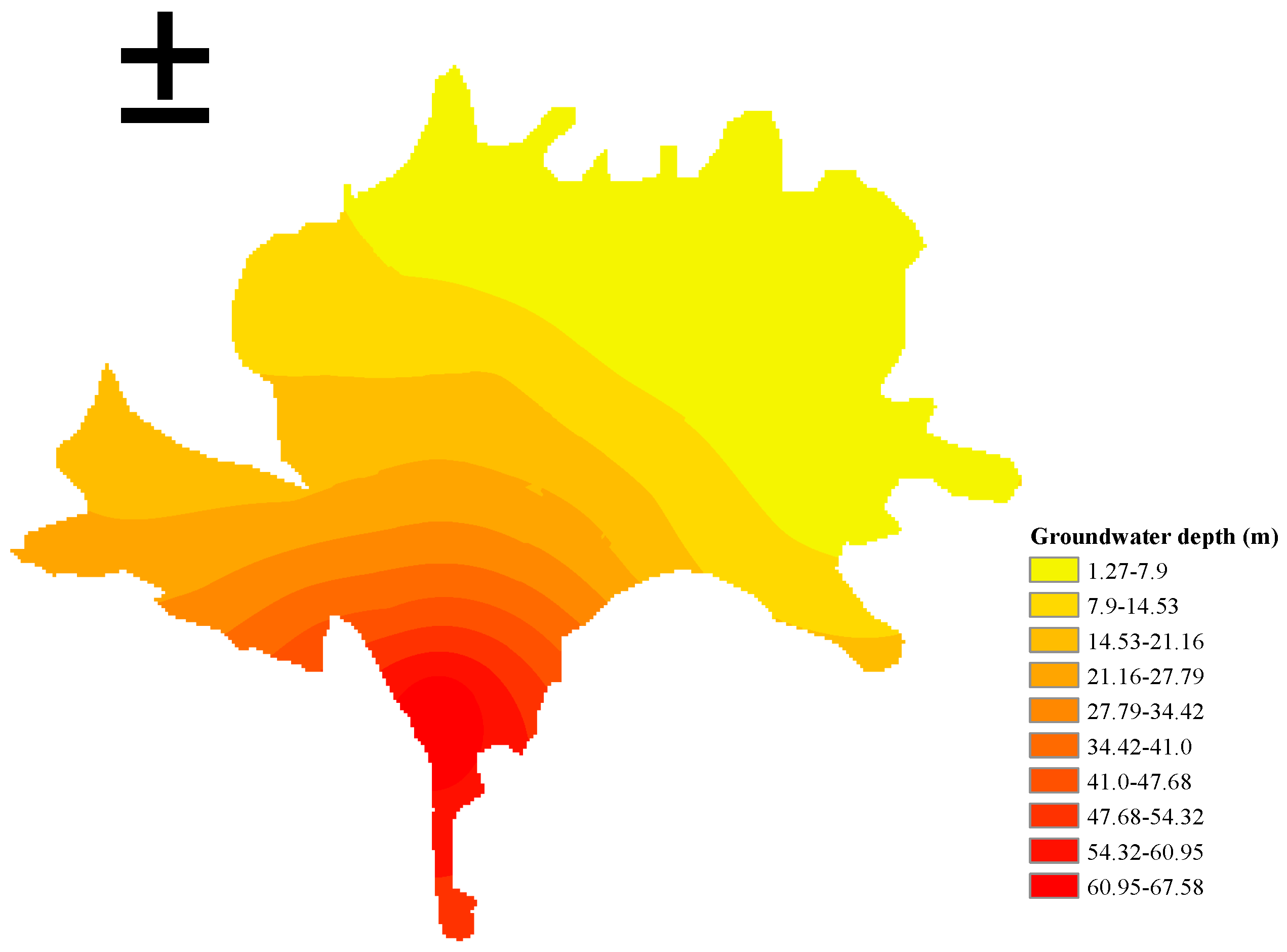
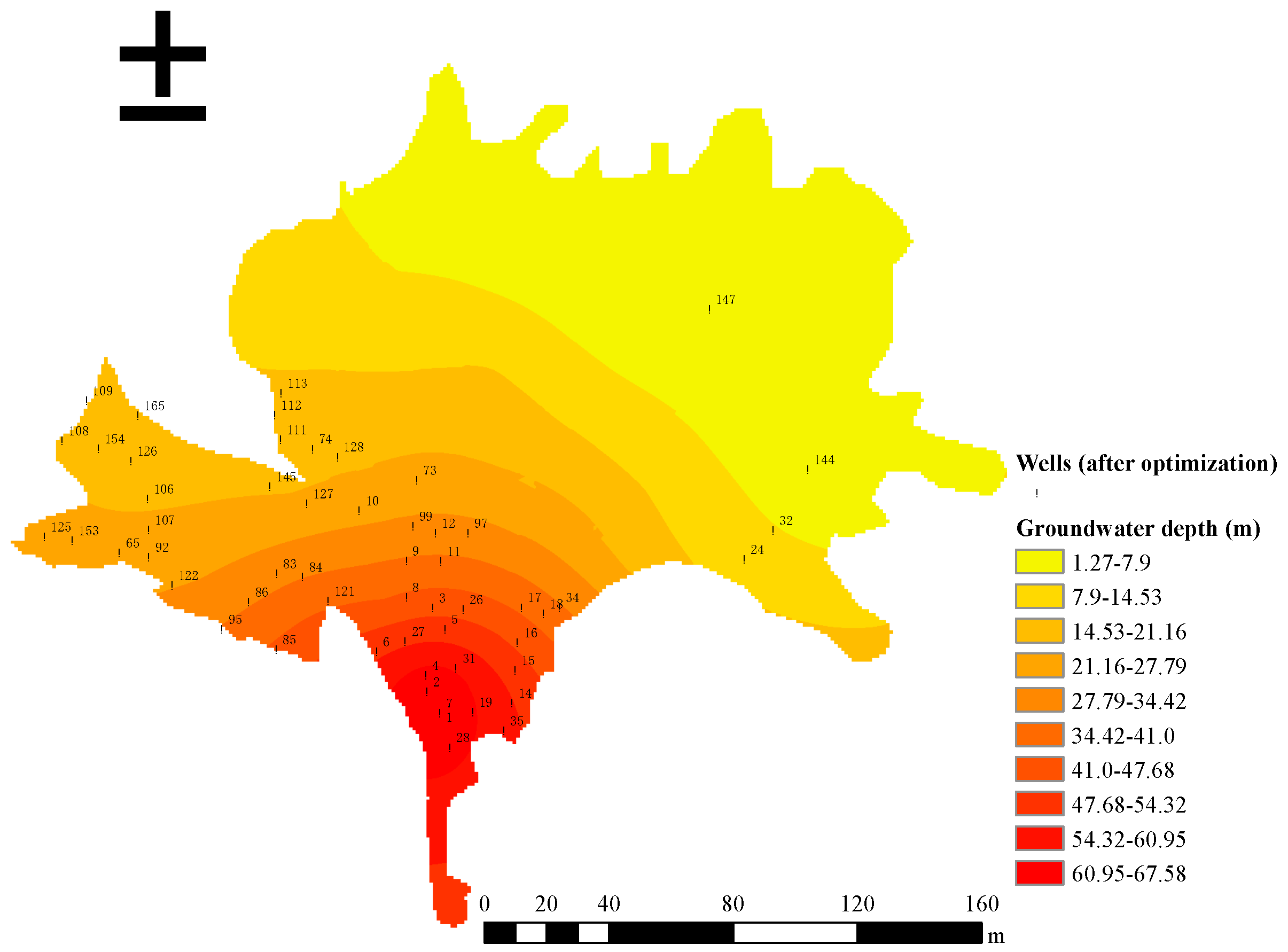
- Normalization of the assessment matrix to resolve the multidimensional indices and multiple data units for different indices:where is the normalized value of the original evaluation matrix, ; and in the evaluation index j, is the minimum value and is the maximum value. For i = 1, 2, …, 166, represents the value of the land type indicator for each well, as measured by unit area demand for groundwater resources shown in Table 6, which is a benefit type index. The maximum and minimum values of are 1504.71 and 394.46, respectively; represents the value of the groundwater depth indicator for each well, as measured by the mean of the groundwater depth interval in the distribution area of the well shown in Figure 4, which is a cost type index. For example, if the well is distributed in an area where the groundwater depth is in the interval [0, 10], then . The maximum and minimum values of are 55 and 10, respectively; represents the value of the well density indicator for each well, as measured by the theoretical well distance, which is a benefit type index. The maximum and minimum values of are 589.38 and 294.69, respectively; represents the value of the well density indicator for each well, which is a cost type index. The maximum and minimum values of are 2000 and 30, respectively. A larger “Benefit type index” value indicates more expensive benefits, while the “Cost type index” indicates the opposite.
- (2)
- Calculation of the entropy value of index j:where is the proportion of the evaluation index j within different values of i, (), , and [41].
- (3)
- Calculation of the deviation coefficient of index j:
- (4)
- Calculation of the weight of index j:
3. Case Study
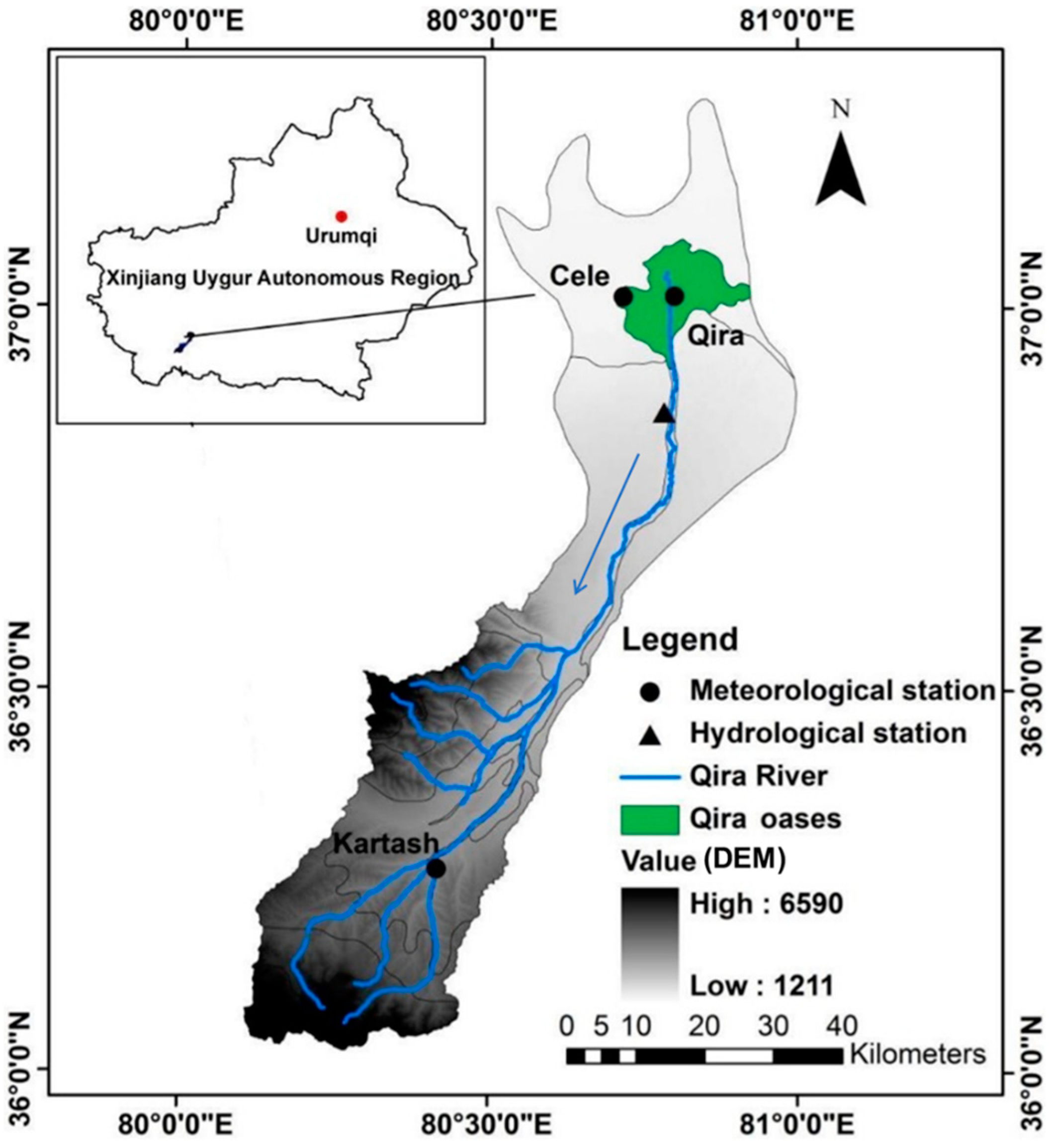
3.1. Study Area
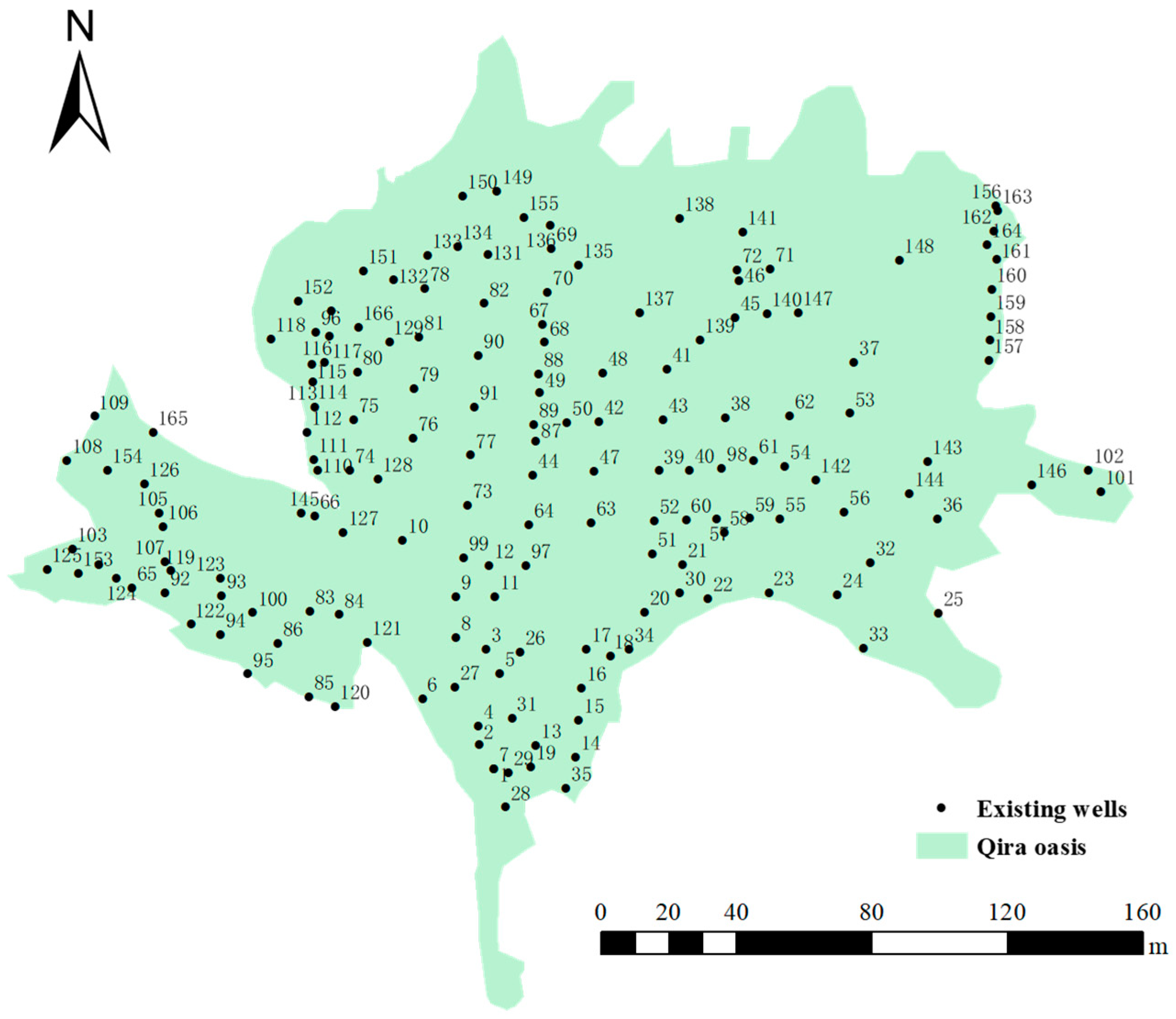
3.2. Data Description
4. Results
4.1. Well-Number Optimization
4.2. Well Spatial-Layout Optimization
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
The Calculation of Well Flow Rate Based on Dupuit Assumption
- (1)
- The aquifer is homogeneous and isotropic.
- (2)
- The groundwater obeys Darcy Law.
- (3)
- The phreatic water to wells can be considered as horizontal.
- (4)
- The flow rate of the wells equals to the discharge of groundwater.
References
- Storm, H.; Heckelei, T.; Heidecke, C. Estimating irrigation water demand in the Moroccan Drâa Valley using contingent valuation. J. Environ. Manag. 2011, 92, 2803–2809. [Google Scholar] [CrossRef]
- García-Garizábal, I.; Causapé, J.; Abrahao, R. Application of the Irrigation Land Environmental Evaluation Tool for flood irrigation management and evaluation of water use. CATENA 2011, 87, 260–267. [Google Scholar] [CrossRef]
- Rivers, M.; Coles, N.; Zia, H.; Harris, N.R.; Yates, R.; Harvey, H.W. How could sensor networks help with agricultural water management issues? Optimizing irrigation scheduling through networked soil-moisture sensors. In Proceedings of the 2015 IEEE Sensors Applications Symposium, Zadar, Croatia, 13–15 April 2015. [Google Scholar]
- Chu, Y.; Shen, Y.; Yuan, Z. Water footprint of crop production for different crop structures in the Hebei southern plain, North China. Hydrol. Earth Syst. Sci. 2017, 21, 3061–3069. [Google Scholar] [CrossRef] [Green Version]
- Xin, L.; Wang, S.; Huo, Z.; Li, F.; Hao, X. Optimizing layout of pumping well in irrigation district for groundwater sustainable use in northwest China. Hydrol. Process. 2015, 29, 4188–4198. [Google Scholar]
- Ling, H.; Xu, H.; Shi, W.; Zhang, Q. Regional climate change and its effects on the runoff of Manas River, Xinjiang, China. Environ. Earth Sci. 2011, 64, 2203–2213. [Google Scholar] [CrossRef]
- Bekri, E.; Disse, M.; Yannopoulos, P. Optimizing Water Allocation under Uncertain System Conditions for Water and Agriculture Future Scenarios in Alfeios River Basin (Greece)—Part B: Fuzzy-Boundary Intervals Combined with Multi-Stage Stochastic Programming Model. Water 2015, 7, 6427–6466. [Google Scholar] [CrossRef] [Green Version]
- Campana, P.E.; Olsson, A.; Li, H.; Yan, J. An economic analysis of photovoltaic water pumping irrigation systems. Int. J. Green Energy 2016, 13, 831–839. [Google Scholar] [CrossRef]
- Ketabchi, H.; Ataie-Ashtiani, B. Review: Coastal groundwater optimization—Advances, challenges, and practical solutions. Hydrogeol. J. 2015, 23, 1129–1154. [Google Scholar] [CrossRef]
- Gaur, S.; Chahar, B.R.; Graillot, D. Analytic elements method and particle swarm optimization based simulation–optimization model for groundwater management. J. Hydrol. 2011, 402, 217–227. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B. Identification of groundwater pollution sources using GA-based linked simulation optimization model. J. Hydrol. Eng. 2006, 11, 101–110. [Google Scholar] [CrossRef]
- Ayvaz, M.T.; Karahan, H. A simulation/optimization model for the identification of unknown groundwater well locations and pumping rates. J. Hydrol. 2008, 357, 76–92. [Google Scholar] [CrossRef]
- Sidiropoulos, E.; Tolikas, P. Well Locations and Constraint Handling in Groundwater Pumping Cost Minimization via Genetic Algorithms. Water Air Soil Pollut. Focus 2004, 4, 227–239. [Google Scholar] [CrossRef]
- Gorelick, S. A review of distributed parameter groundwater management modeling method. Water Resour. Res. 1983, 19, 305–319. [Google Scholar] [CrossRef]
- Bouwer, H. Integrated water management: Emerging issues and challenges. Agric. Water Manag. 2000, 45, 217–228. [Google Scholar] [CrossRef]
- Monaghan, R.M.; Wilcock, R.J.; Smith, L.C.; Tikkisetty, B.; Thorrold, B.S.; Costall, D. Linkages between land management activities and water quality in an intensively farmed catchment in southern New Zealand. Agric. Ecosyst. Environ. 2007, 118, 211–222. [Google Scholar] [CrossRef]
- Stanko, Z.P.; Boyce, S.E.; Yeh, W.G. Nonlinear model reduction of unconfined groundwater flow using POD and DEIM. Adv. Water Resour. 2016, 97, 130–143. [Google Scholar] [CrossRef] [Green Version]
- Aral, M.M.; Guan, J. Genetic Algorithms in Search of Groundwater Pollution Sources. In Advances in Groundwater Pollution Control and Remediation; Springer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; U Michigan Press: Oxford, UK, 1975; Volume viii, p. 183. [Google Scholar]
- Kirkpatrick, S.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kennedy, J. Particle Swarm Optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 2011; Volume 1944, pp. 1942–1948. [Google Scholar]
- Huang, C.; Mayer, A.S. Pump-and-treat optimization using well locations and pumping rates as decision variables. Water Resour. Res. 1997, 33, 1001–1012. [Google Scholar] [CrossRef] [Green Version]
- Fragoso, T.; da Conceição Cunha, M.; Lobo-Ferreira, J.O.P. Optimal pumping from Palmela water supply wells (Portugal) using simulated annealing. Hydrogeol. J. 2009, 17, 1935–1948. [Google Scholar] [CrossRef]
- Milnes, E. Process-based groundwater salinisation risk assessment methodology: Application to the Akrotiri aquifer (Southern Cyprus). J. Hydrol. 2011, 399, 29–47. [Google Scholar] [CrossRef] [Green Version]
- Bayer, P.; Duran, E.; Baumann, R.; Finkel, M. Optimized groundwater drawdown in a subsiding urban mining area. J. Hydrol. 2009, 365, 95–104. [Google Scholar] [CrossRef]
- Tang, H.; Huang, B.G.; Dao-Xuan, L.I.; Zeng, F.H. Determing water driving effectiveness of oil reservoir with fuzzy comprehensive evaluation method. Pet. Explor. Dev. 2002, 29, 97–99. [Google Scholar]
- Wang, H.F.; Dong, Z.C. Application of Analytic Hierarchy Process(AHP)Method in Regional Water Resources Sustainable Development Evaluation. Water Power 2002, 7, 2–14. [Google Scholar]
- Pan, X.A. Study on Village Reclamation Suitability Evaluation Based on the Index Method. Mod. Agric. Sci. Technol. 2013, 2, 340–342. [Google Scholar]
- Ziadat, F.M. Land suitability classification using different sources of information: Soil maps and predicted soil attributes in Jordan. Geoderma 2007, 140, 73–80. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Sarmadian, F.; Ahmadi, A. Spatially-based model of land suitability analysis using block kriging. Aust. J. Crop Sci. 2011, 5, 1533–1541. [Google Scholar]
- Liu, X.; Wang, S.; Hao, X. Suitability assessment on spatial layout of pumping wells in Hongyashan irrigation district. Trans. Chin. Soc. Agric. Eng. 2013, 29, 101–109. [Google Scholar]
- Jie, X.; Gui, D.; Lei, J.; Zeng, F.; Mao, D.; Zhang, Z. Model development of a participatory Bayesian network for coupling ecosystem services into integrated water resources management. J. Hydrol. 2017, 554, 50–65. [Google Scholar]
- Technical Code for Water Wells. PRC, N.S.o. GB/T 50625-2010. 2010. Available online: http://www.gbstandards.org/mobile/GB_List-m.asp?id=82800 (accessed on 18 August 2010).
- Ahlfeld, D.P.; Sawyer, C.S. Well Location in Capture Zone Design Using Simulation and Optimization Techniques. Groundwater 1990, 28, 507–512. [Google Scholar] [CrossRef]
- Guan, J.; Aral, M.M. Optimal remediation with well locations and pumping rates selected as continuous decision variables. J. Hydrol. 1999, 221, 20–42. [Google Scholar] [CrossRef]
- Lin, H.-T.; Tan, Y.-C.; Chen, C.-H.; Lin, W.-S.; Liu, C.-W. Multivariate approaches optimize locations of groundwater pumping facilities for different hydrogeological scales. Hydrol. Process. 2012, 26, 2985–2996. [Google Scholar] [CrossRef]
- Maas, C. Groundwater flow to a well in a layered porous medium: 1. Steady flow. Water Resour. Res. 1987, 23, 1675–1681. [Google Scholar] [CrossRef]
- Kanemoto, Y.; Sugawara, R.; Ohmura, M. A genetic algorithm for the rectilinear Steiner tree in 3-D VLSI layout design. In Proceedings of the 2004 47th Midwest Symposium on Circuits and Systems, Hiroshima, Japan, 25–28 July 2004. [Google Scholar]
- Li, X.; Wang, K.; Liu, L.; Xin, J.; Yang, H.; Gao, C. Application of the Entropy Weight and TOPSIS Method in Safety Evaluation of Coal Mines. Procedia Eng. 2011, 26, 2085–2091. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Gu, C.L.; Gu, L.W.; Zhang, Y. The evaluation of tourism destination competitiveness by TOPSIS & information entropy—A case in the Yangtze River Delta of China. Tour. Manag. 2011, 32, 443–451. [Google Scholar]
- Chen, R.J.; Qian, H.L.; Kan, H.D.; Yuan, D. A Review of Comprehensive Index Methods in Water Quality Assessment. J. Environ. Occup. Med. 2009, 26, 581–584. [Google Scholar]
- Qian, J.; Zhao, J.; Gui, D.; Feng, X. Effeccts of ecological water use and irrigation on groundwater depth in Cele Oasis. Bull. Soil Water Conserv. 2018, 38, 96–102. [Google Scholar]
| Name of Method | Reference | Example of Application |
|---|---|---|
| Genetic Algorithm (GA) | Holland, 1975 | Huang et al. [23] optimized the total cost and number of pumping wells applying GA method. |
| Simulated Annealing (SA) | Kirkpatrick et al., 1983 | Fragoso et al. [24] regarded the pipe costs, the well installation, and pumping costs as the objective function applying SA method. |
| Particle Swarm Optimization (PSO) | Kennedy and Eberhart, 1995 | Gaur et al. [10] made pumping water amount maximum and the total cost minimum using PSO method. |
| Target | Evaluation Indexes |
|---|---|
| Evaluation model of wells spatial layout | 1. Type of land use |
| 2. Depth of groundwater | |
| 3. Flow rate of each well | |
| 4. Density of a well |
| Crop | Irrigated Area (ha) | Net Irrigation Water Demand (m3/ha·a) | Water Demand (m3/a) |
|---|---|---|---|
| Wheat | 1336 | 5587 | 7.46 × 106 |
| Maize | 1345 | 4680 | 6.29 × 106 |
| Pomegranate | 669.5 | 13,550 | 9.07 × 106 |
| Red date | 1987 | 10,650 | 2.12 × 107 |
| Walnut | 1371 | 10,600 | 1.45 × 107 |
| Sum of values | 6708.5 | 45,067 | 5.85 × 107 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Extractable amount of groundwater | Ps | m3/a | 1500.4 × 104 |
| Return water of irrigation and ecology | Prw | 213.5 × 104 | |
| Industrial water demand | Pir | 104.3 × 104 | |
| Domestic water demand | Pdr | 172.84 × 104 | |
| Required amount of ecological water | Per | 438.6 × 104 | |
| Difference of lateral discharge and recharge | Plr-Pld | 1500.4 × 104 | |
| Discharge from evaporation | Ped | 0 | |
| Recharge due to precipitation | Ppr | 0 | |
| Surface water resources for irrigation | Psw | 5815.5 × 104 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| The well management and maintenance cost coefficient | a | RMB | 23.72 × 104 |
| The number of wells | n | 20 | |
| The annual average operating days | T | d | 70 |
| The daily average operating hours | t | h/d | 12 |
| Groundwater price per cubic meter | rg | RMB/m3 | 0.20 |
| Net pumping lift | h’ | m | 22.5 |
| Cost of electricity per | re | 0.15 | |
| Allowed maximum drawdown | Smax | m | 5.00 |
| Permeability coefficient | K | m/h | 0.72 |
| Distance from the bottom elevation of the unconfined aquifer to the phreatic free surface | H | m | 55.00 |
| Radius of influence of the pumping well | R | m | 400 |
| Radius of the pumping well | r0 | m | 0.175 |
| abatement coefficient of total discharge | α | 0.03 | |
| Maximum value of the well flow rate | Qmax | m3/h | 200 |
| Existing number of wells | Ne | 166 | |
| Degree of groundwater recharge | μ | 0.25 |
| Type of Land Use | Area (ha) | Unit Area Demand for Groundwater Resources (mm) |
|---|---|---|
| Towns and villages | 176.5 | 394.46 |
| Woodland | 4027.5 | 1504.71 |
| Dryland plain | 2681.0 | 654.22 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Shen, M.; Zhao, J.; Dai, H.; Gui, D.; Feng, X.; Ju, J.; Sang, S.; Zhang, X.; Hu, B. A New Optimization Method for the Layout of Pumping Wells in Oases: Application in the Qira Oasis, Northwest China. Water 2019, 11, 970. https://doi.org/10.3390/w11050970
Liu Y, Shen M, Zhao J, Dai H, Gui D, Feng X, Ju J, Sang S, Zhang X, Hu B. A New Optimization Method for the Layout of Pumping Wells in Oases: Application in the Qira Oasis, Northwest China. Water. 2019; 11(5):970. https://doi.org/10.3390/w11050970
Chicago/Turabian StyleLiu, Yi, Mengyang Shen, Jianping Zhao, Heng Dai, Dongwei Gui, Xinlong Feng, Jiali Ju, Shilei Sang, Xiaoying Zhang, and Bill Hu. 2019. "A New Optimization Method for the Layout of Pumping Wells in Oases: Application in the Qira Oasis, Northwest China" Water 11, no. 5: 970. https://doi.org/10.3390/w11050970
APA StyleLiu, Y., Shen, M., Zhao, J., Dai, H., Gui, D., Feng, X., Ju, J., Sang, S., Zhang, X., & Hu, B. (2019). A New Optimization Method for the Layout of Pumping Wells in Oases: Application in the Qira Oasis, Northwest China. Water, 11(5), 970. https://doi.org/10.3390/w11050970






