On the Use of NLDAS2 Weather Data for Hydrologic Modeling in the Upper Mississippi River Basin
Abstract
1. Introduction
2. Materials and Methods
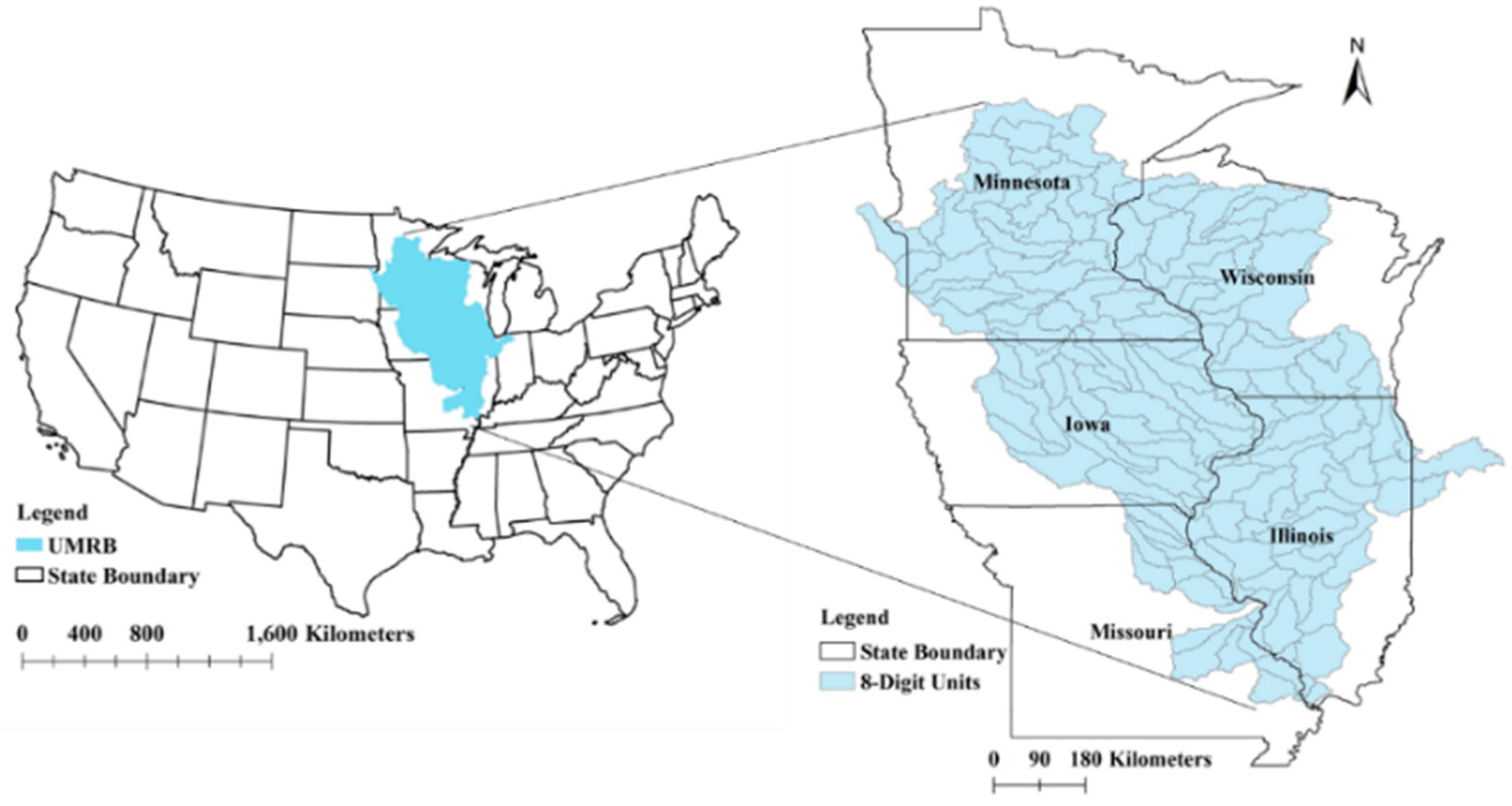
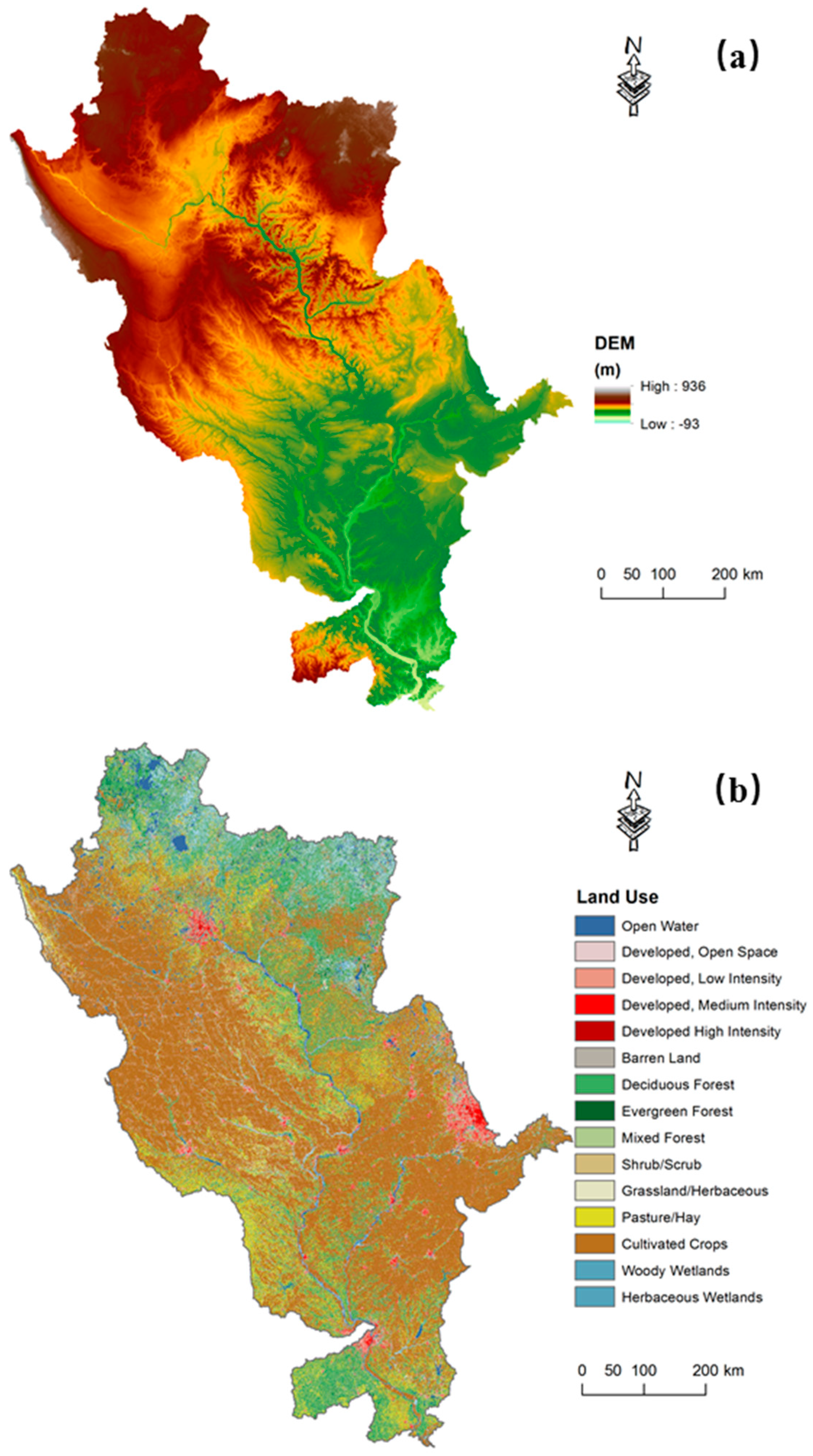
2.1. Study Area
2.2. SWAT Model Setup
2.3. NLDAS2 Dataset
2.4. Three Simulation Scenarios
2.5. Model Calibration, Sensitivity, and Uncertainty Analysis
2.6. Model Evaluation
3. Results and Discussion
3.1. Parameter Sensivity Analysis
3.2. Model Performance Evaluation
3.3. Model Uncertainty Analysis
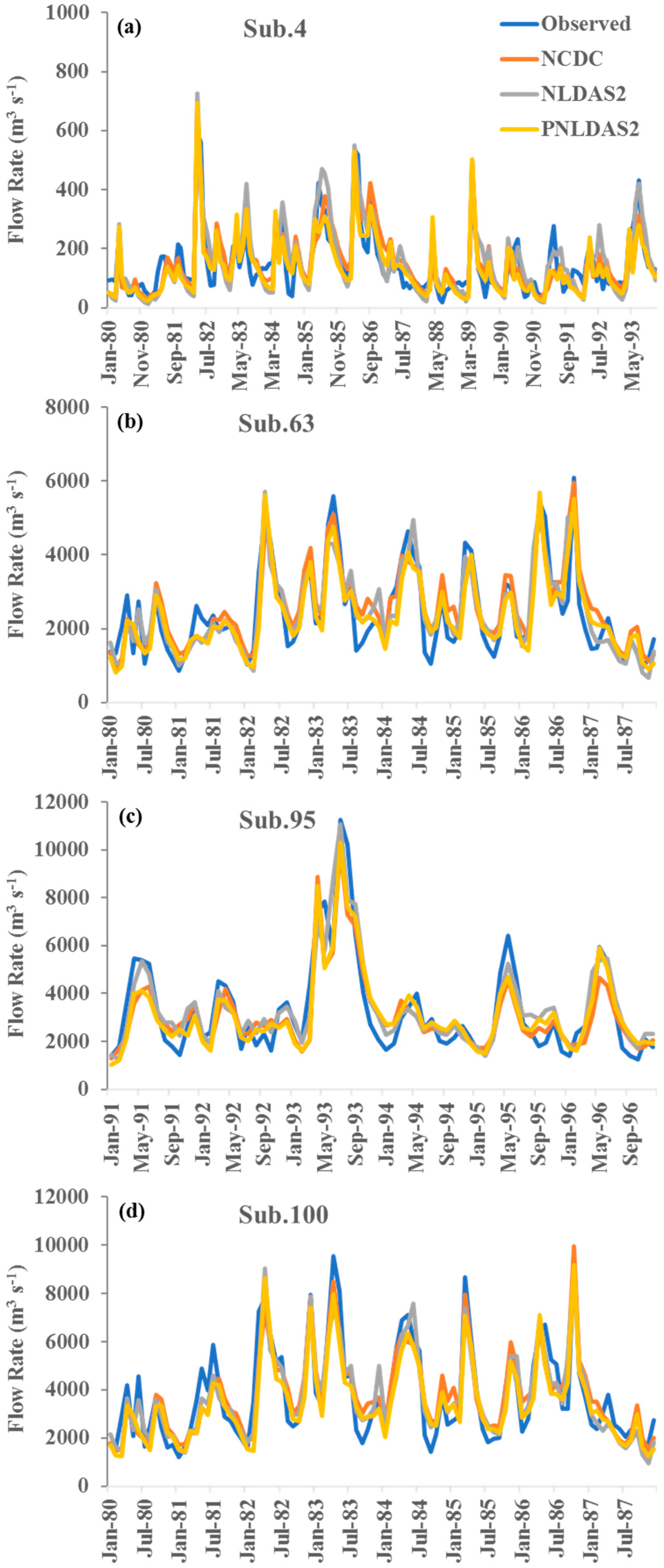
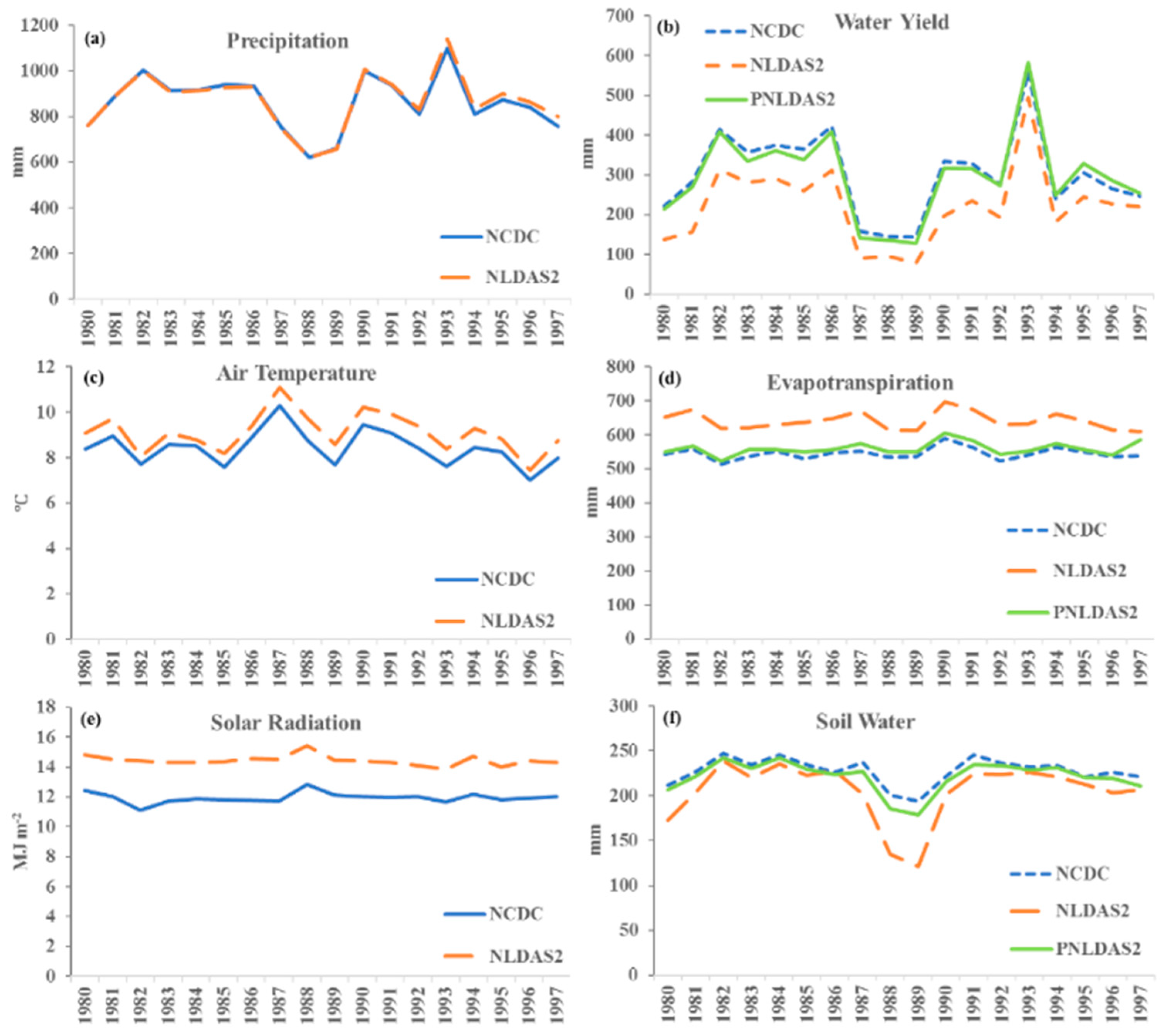
3.4. Weather Data Impacts on Stream Flow Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Parmele, L.H. Errors in output of hydrologic models due to errors in input potential evapotranspiration. Water Resour. Res. 1972, 8, 348–359. [Google Scholar] [CrossRef]
- Xia, J.; Chen, J.; Weng, J.; Yu, L.; Qi, J.; Liao, Q. Vulnerability of water resources and its spatial heterogeneity in Haihe River Basin, China. Chin. Geogr. Sci. 2014, 24, 525–539. [Google Scholar] [CrossRef]
- Sun, L.; Yang, F.; Wang, J.; Fang, H.; Qi, J. Impacts of forest types on soil C, N and DOC loss in runoff in the laterite hilly region of southern China. Environ. Earth Sci. 2015, 74, 1391–1402. [Google Scholar]
- Clark, M.P.; Fan, Y.; Lawrence, D.M.; Adam, J.C.; Bolster, D.; Gochis, D.J.; Hooper, R.P.; Kumar, M.; Leung, L.R.; Mackay, D.S. Improving the representation of hydrologic processes in Earth System Models. Water Resour. Res. 2015, 51, 5929–5956. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Williams, J.R.; Arnold, J.G.; Kiniry, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Grassland, Soil and Water Research Service: Temple, TX, USA, 2011.
- Zhang, C.; Li, S.; Qi, J.; Xing, Z.; Meng, F. Assessing impacts of riparian buffer zones on sediment and nutrient loadings into streams at watershed scale using an integrated REMM-SWAT model. Hydrol. Process. 2017, 31, 916–924. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Li, Q.; Xing, Z.; Bourque, C.P.-A.; Meng, F.-R. A new soil-temperature module for SWAT application in regions with seasonal snow cover. J. Hydrol. 2016, 538, 863–877. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Yang, Q.; Xing, Z.; Meng, F.-R. SWAT Setup with Long-term detailed landuse and management records and modification for a micro-watershed influenced by freeze-thaw cycles. Water Resour. Manag. 2017, 31, 3953–3974. [Google Scholar] [CrossRef]
- Li, Q.; Qi, J.; Xing, Z.; Li, S.; Jiang, Y.; Danielescu, S.; Zhu, H.; Wei, X.; Meng, F.-R. An approach for assessing impact of land use and biophysical conditions across landscape on recharge rate and nitrogen loading of groundwater. Agric. Ecosyst. Environ. 2014, 196, 114–124. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; McCarty, G.W.; Sadeghi, A.M.; Cosh, M.H.; Zeng, X.; Gao, F.; Daughtry, C.S.; Huang, C.; Lang, M.W. Assessing the performance of a physically-based soil moisture module integrated within the Soil and Water Assessment Tool. Environ. Model. Softw. 2018, 109, 329–341. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Bourque, C.P.; Xing, Z.; Fan-Rui, M. Developing a decision support tool for assessing land use change and BMPs in ungauged watersheds based on decision rules provided by SWAT simulation. Hydrol. Earth Syst. Sci. 2018, 22, 3789–3806. [Google Scholar] [CrossRef]
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Obled, C.; Wendling, J.; Beven, K. The sensitivity of hydrological models to spatial rainfall patterns: an evaluation using observed data. J. Hydrol. 1994, 159, 305–333. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: an application in the Blue Nile River Basin. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Di Luzio, M.; Johnson, G.L.; Daly, C.; Eischeid, J.K.; Arnold, J.G. Constructing retrospective gridded daily precipitation and temperature datasets for the conterminous United States. J. Appl. Meteorol. Clim. 2008, 47, 475–497. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R. GIS-Based spatial precipitation estimation: a comparison of geostatistical approaches. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 894–906. [Google Scholar] [CrossRef]
- Kyriakidis, P.C.; Kim, J.; Miller, N.L. Geostatistical mapping of precipitation from rain gauge data using atmospheric and terrain characteristics. J. Appl. Meteorol. 2001, 40, 1855–1877. [Google Scholar] [CrossRef]
- Piper, S.C.; Stewart, E.F. A gridded global data set of daily temperature and precipitation for terrestrial biospheric modeling. Glob. Biogeochem. Cycles 1996, 10, 757–782. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Clim. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kouwen, N.; Danard, M.; Bingeman, A.; Luo, W.; Seglenieks, F.R.; Soulis, E.D. Case study: watershed modeling with distributed weather model data. J. Hydrol. Eng. 2005, 10, 23–38. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Piechota, T.C. Ensemble streamflow prediction: climate signal weighting methods vs. climate forecast system reanalysis. J. Hydrol. 2012, 442, 105–116. [Google Scholar] [CrossRef]
- Smith, R.A.; Kummerow, C.D. A comparison of in situ, reanalysis, and satellite water budgets over the Upper Colorado River Basin. J. Hydrometeorol. 2013, 14, 888–905. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, X. Impact of bias-correction methods on effectiveness of assimilating SMAP soil moisture data into NCEP global forecast system using the ensemble Kalman filter. IEEE Geosci. Remote Sens. Lett. 2018, 15, 659–663. [Google Scholar] [CrossRef]
- Mitchell, K.E.; Lohmann, D.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.; Luo, L. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wu, J.; Tanaka, K. Reducing nitrogen runoff from the upper Mississippi River basin to control hypoxia in the Gulf of Mexico: easements or taxes? Marine Resour. Econ. 2005, 20, 121–144. [Google Scholar] [CrossRef]
- Jha, M.; Gassman, P.W.; Secchi, S.; Gu, R.; Arnold, J. Effect of watershed subdivision on swat flow, sediment, and nutrient predictions. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 811–825. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Wang, Q. Improving hydrological simulation in the Upper Mississippi River Basin through enhanced freeze-thaw cycle representation. J. Hydrol. 2019, 571, 605–618. [Google Scholar] [CrossRef]
- Homer, C.; Huang, C.; Yang, L.; Wylie, B.; Coan, M. Development of a 2001 national land-cover database for the United States. Photogramm. Eng. Remote Sens. 2004, 70, 829–840. [Google Scholar] [CrossRef]
- USDA-NRCS. State Soil Geographic (STATSGO) Database Misc. Pub. 1492; USDA-NRCS National Soil Survey Center: Lincoln, NE, USA, 1995.
- Ek, M.; Mitchell, K.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. Energy and Water Balance Calculations in the Mosaic LSM; National Aeronautics and Space Administration, Goddard Space Flight Center, Laboratory for Atmospheres, Data Assimilation Office; Laboratory for Hydrospheric Processes: Washington, DC, USA, 1996.
- Burnash, R.; Ferral, R.; McGuire, R. A Generalized Streamflow Simulation System—Conceptual Modeling for Digital Computers; US National Weather Service, State of California, Dept. of Water Resources: Sacramento, CA, USA, 1973.
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Jamieson, R.; Hebb, D.; Xing, Z.; Meng, F.-R. Modifying SWAT with an energy balance module to simulate snowmelt for maritime regions. Environ. Model. Softw. 2017, 93, 146–160. [Google Scholar] [CrossRef]
- Sharpley, A.N.; Williams, J.R. EPIC-Erosion/Productivity Impact Calculator: 1, Model Documentation; USDA-ARS. Technical Bulletin. USDA. Agricultural Research Service: Beltsville, MA, USA, 1990; p. 127.
- Leta, O.T.; van Griensven, A.; Bauwens, W. Effect of single and multisite calibration techniques on the parameter estimation, performance, and output of a SWAT model of a spatially heterogeneous catchment. J. Hydrol. Eng. 2016, 22, 05016036. [Google Scholar] [CrossRef]
- Abbaspour, K.; Vejdani, M.; Haghighat, S. SWAT-CUP calibration and uncertainty programs for SWAT. In Proceedings of the MODSIM 2007 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand, Christchurch, New Zealand, 10–13 December 2007. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Singh, A.; Imtiyaz, M.; Isaac, R.; Denis, D. Assessing the performance and uncertainty analysis of the SWAT and RBNN models for simulation of sediment yield in the Nagwa watershed, India. Hydrol. Sci. J. 2014, 59, 351–364. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Li, Q.; Xing, Z.; Bourque, C.P.-A.; Meng, F.-R. Assessing an enhanced version of SWAT on water quantity and quality simulation in regions with seasonal snow cover. Water Resour. Manag. 2016, 30, 5021–5037. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Cosh, M.H. Modeling soil temperature in a temperate region: A comparison between empirical and physically based methods in SWAT. Ecol. Eng. 2019, 129, 134–143. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Hao, F. Predicting hydrologic response to climate change in the Luohe River basin using the SWAT model. Trans. ASABE 2007, 50, 901–910. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP 2012: SWAT Calibration and Uncertainty Programs—A User Manual; Eawag: Dübendorf, Switzerland, 2013. [Google Scholar]
- Gao, J.; Sheshukov, A.Y.; Yen, H.; White, M.J. Impacts of alternative climate information on hydrologic processes with SWAT: A comparison of NCDC, PRISM and NEXRAD datasets. Catena 2017, 156, 353–364. [Google Scholar] [CrossRef]
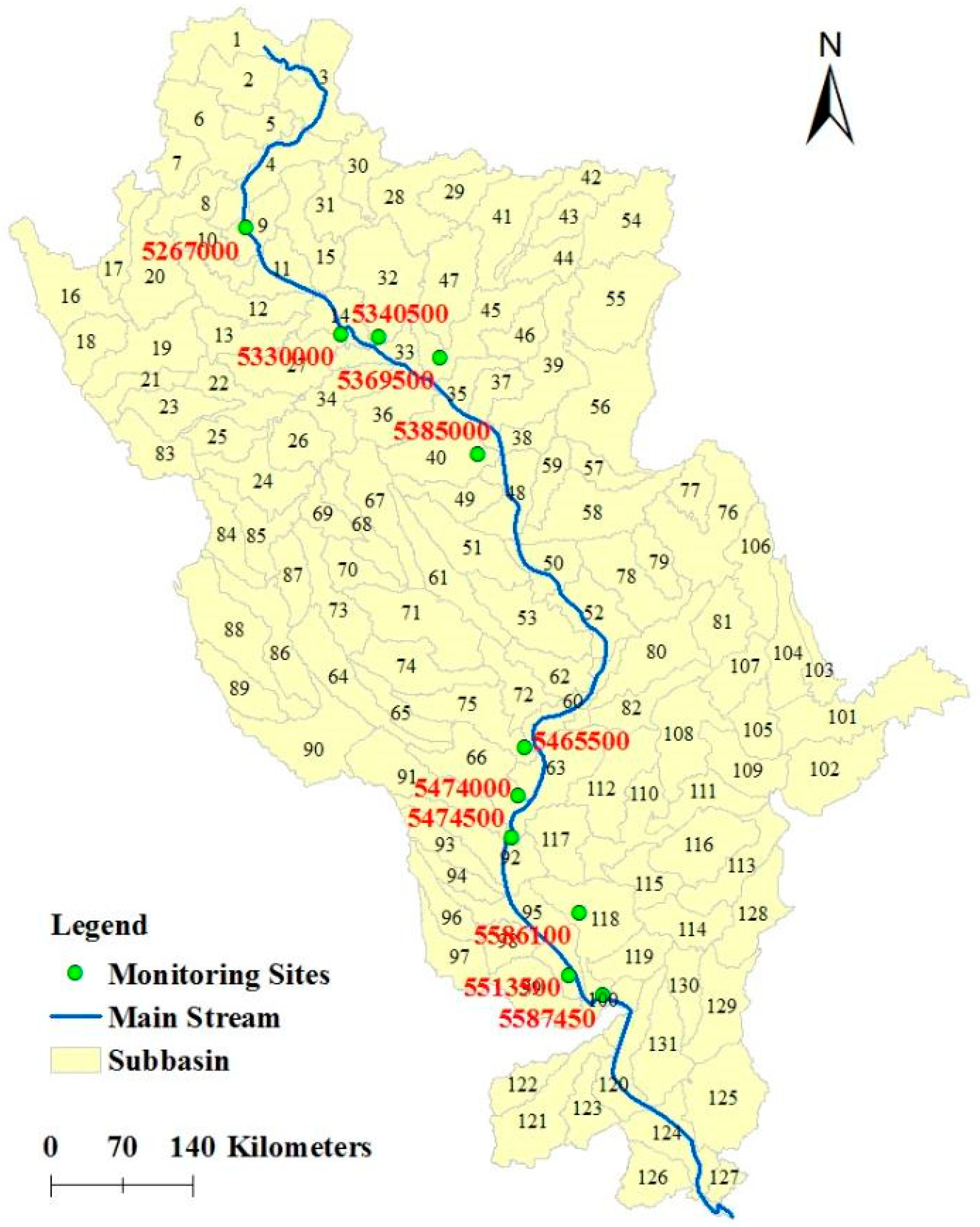
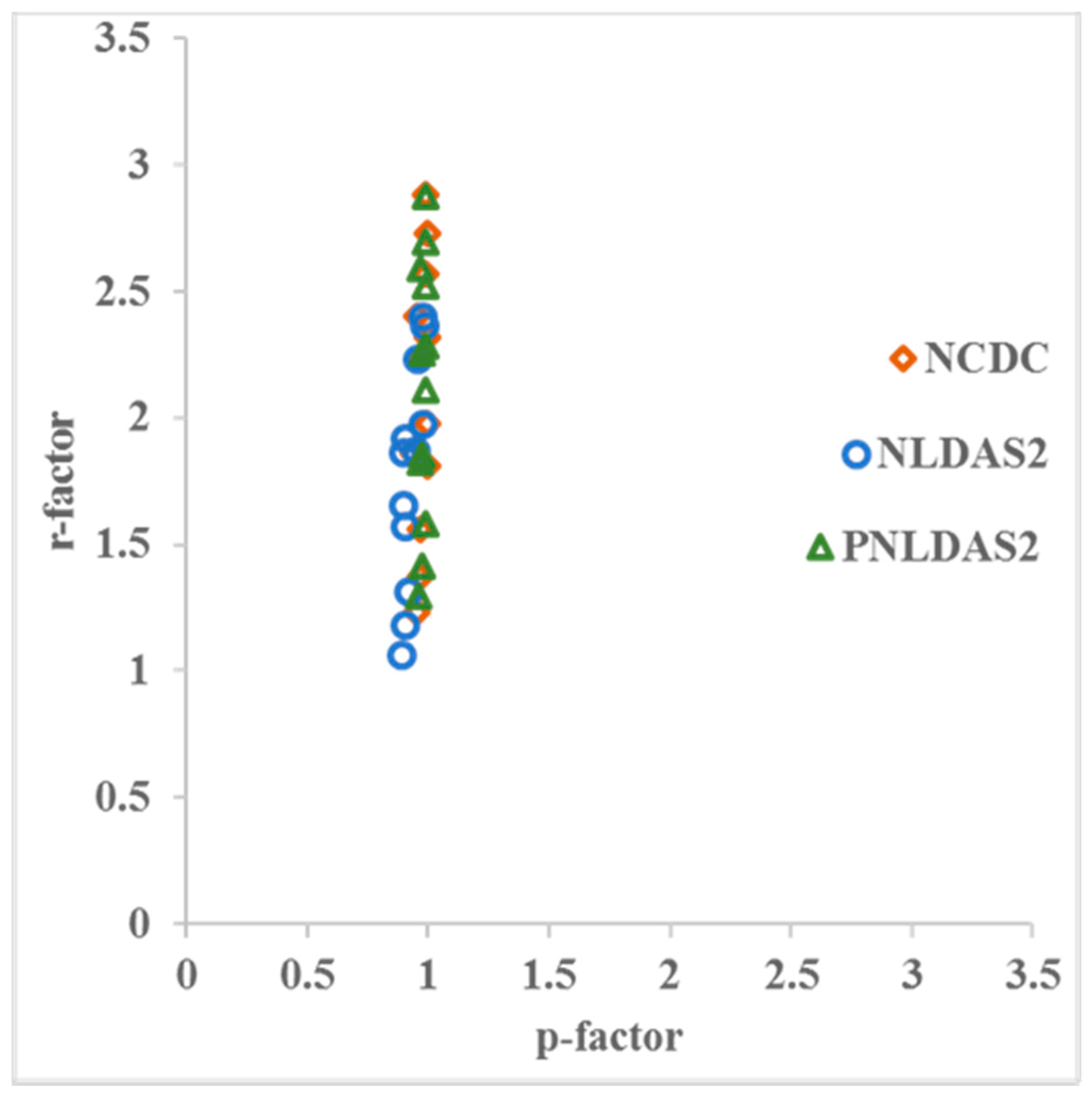
| Sub-Basin No. | USGS ID | HUC8 | SWAT Area (km3) | USGS Area (km3) | SWAT Area/USGS Area | Calibration | Validation |
|---|---|---|---|---|---|---|---|
| 4 | 5267000 | 7010104 | 30,180 | 29,696 | 1.02 | 1980–1987 | 1988–1993 |
| 27 | 5330000 | 7020012 | 43,720 | 43,126 | 1.01 | 1980–1987 | 1988–1996 |
| 32 | 5340500 | 7030005 | 20,030 | 19,768 | 1.01 | 1980–1987 | 1988–1996 |
| 40 | 5385000 | 7040008 | 4301 | 4250 | 1.01 | 1991–1993 | 1994–1996 |
| 45 | 5369500 | 7050005 | 24,720 | 24,338 | 1.02 | 1991–1993 | 1994–1996 |
| 63 | 5474500 | 7080104 | 309,400 | 304,640 | 1.02 | 1980–1983 | 1984–1987 |
| 66 | 5474000 | 7080107 | 11,250 | 11,016 | 1.02 | 1980–1987 | 1988–1995 |
| 75 | 5465500 | 7080209 | 32,800 | 31,997 | 1.03 | 1980–1987 | 1988–1995 |
| 95 | 5513500 | 7110004 | 368,000 | 363,643 | 1.01 | 1991–1993 | 1994–1996 |
| 100 | 5587450 | 7110009 | 447,500 | 438,528 | 1.02 | 1980–1983 | 1984–1988 |
| 118 | 5586100 | 7140203 | 74,600 | 73,656 | 1.01 | 1991–1993 | 1994–1996 |
| Ranking | NCDC-SWAT | NLDAS2-SWAT | PNLDAS2-SWAT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | p-Value | Used | Parameter | p-Value | Used | Parameter | p-Value | Used | |
| 1 | V__ALPHA_BF | 0.000 | 0.2829 | V__ALPHA_BF | 0.000 | 0.2223 | V__ALPHA_BF | 0.000 | 0.2829 |
| 2 | V__ESCO | 0.000 | 0.421 | V__ESCO | 0.000 | 0.937 | V__ESCO | 0.000 | 0.421 |
| 3 | V__GW_DELAY | 0.000 | 186.2 | R__CN2 | 0.000 | −0.0345 | V__GW_DELAY | 0.000 | 186.2 |
| 4 | V__CH_K2 | 0.000 | 84.1 | V__SMTMP | 0.000 | 3.23 | V__CH_K2 | 0.000 | 84.1 |
| 5 | V__SMTMP | 0.000 | 3.53 | V__CH_K2 | 0.000 | 34.5 | V__SMTMP | 0.013 | 3.53 |
| 6 | V__SURLAG | 0.102 | 0.505 | V__SURLAG | 0.033 | 1.995 | V__SURLAG | 0.080 | 0.505 |
| 7 | R__CN2 | 0.552 | −0.0465 | V__GW_DELAY | 0.184 | 96.2 | V__SFTMP | 0.212 | 2.23 |
| 8 | V__SFTMP | 0.584 | 2.23 | V__SFTMP | 0.321 | −3.21 | R__SOL_K | 0.803 | −0.1345 |
| 9 | R__SOL_K | 0.922 | −0.1345 | R__SOL_K | 0.946 | 0.0475 | R__CN2 | 0.896 | −0.0465 |
| Sub-Basin | NCDC-SWAT | NLDAS2-SWAT | PNLDAS2-SWAT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | NS | Pbias | R2 | NS | Pbias | R2 | NS | Pbias | |
| 4 | 0.73 | 0.71 | −6.7 | 0.76 | 0.65 | −5.9 | 0.76 | 0.75 | 4.9 |
| 27 | 0.76 | 0.73 | −6.2 | 0.78 | 0.68 | −12.2 | 0.74 | 0.71 | 4.7 |
| 32 | 0.76 | 0.73 | 0.4 | 0.75 | 0.72 | 8.8 | 0.78 | 0.72 | 12.3 |
| 40 | 0.81 | 0.70 | −20.6 | 0.82 | 0.70 | −21.1 | 0.76 | 0.73 | −9.8 |
| 45 | 0.61 | 0.59 | −6.2 | 0.66 | 0.65 | −2.5 | 0.64 | 0.61 | −4.1 |
| 63 | 0.77 | 0.76 | −3.6 | 0.80 | 0.80 | −0.7 | 0.79 | 0.78 | 4.0 |
| 66 | 0.75 | 0.74 | −3.0 | 0.75 | 0.74 | −3.8 | 0.72 | 0.72 | 1.4 |
| 75 | 0.74 | 0.72 | 6.2 | 0.80 | 0.79 | 3.7 | 0.78 | 0.73 | 12.9 |
| 95 | 0.79 | 0.78 | 6.5 | 0.84 | 0.84 | −0.9 | 0.81 | 0.79 | 9.6 |
| 100 | 0.80 | 0.79 | 2.7 | 0.83 | 0.83 | 2.5 | 0.79 | 0.76 | 9.2 |
| 118 | 0.82 | 0.77 | 10.4 | 0.86 | 0.81 | 5.1 | 0.82 | 0.75 | 10.6 |
| Sub-Basin | NCDC-SWAT | NLDAS2-SWAT | PNLDAS2-SWAT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | NS | Pbias | R2 | NS | Pbias | R2 | NS | Pbias | |
| 4 | 0.57 | 0.54 | 4.4 | 0.63 | 0.48 | −9.1 | 0.62 | 0.54 | 11.4 |
| 27 | 0.85 | 0.78 | 22.5 | 0.81 | 0.80 | −0.3 | 0.81 | 0.76 | 22.2 |
| 32 | 0.67 | 0.64 | 8.9 | 0.66 | 0.65 | 1.1 | 0.71 | 0.68 | 11.5 |
| 40 | 0.46 | 0.44 | −2.0 | 0.58 | 0.35 | 15.1 | 0.38 | 0.25 | 10.1 |
| 45 | 0.83 | 0.81 | −1.3 | 0.79 | 0.65 | −9.1 | 0.76 | 0.50 | −17.0 |
| 63 | 0.78 | 0.75 | −8.9 | 0.79 | 0.79 | −2.2 | 0.82 | 0.81 | 0.6 |
| 66 | 0.86 | 0.83 | 5.3 | 0.87 | 0.86 | −7.8 | 0.82 | 0.82 | −2.8 |
| 75 | 0.85 | 0.80 | 13.1 | 0.88 | 0.86 | 5.0 | 0.85 | 0.81 | 12.3 |
| 95 | 0.80 | 0.71 | 2.4 | 0.77 | 0.74 | −6.7 | 0.79 | 0.76 | −4.7 |
| 100 | 0.86 | 0.85 | −5.5 | 0.87 | 0.87 | 1.9 | 0.88 | 0.87 | 3.9 |
| 118 | 0.92 | 0.83 | 13.0 | 0.95 | 0.91 | 5.3 | 0.88 | 0.78 | 15.3 |
| Sub-Basin | NCDC-SWAT | NLDAS2-SWAT | PNLDAS2-SWAT | |||
|---|---|---|---|---|---|---|
| p-Factor | r-Factor | p-Factor | r-Factor | p-Factor | r-Factor | |
| 4 | 0.99 | 2.57 | 0.91 | 1.86 | 1.00 | 2.52 |
| 27 | 0.97 | 1.56 | 0.93 | 1.31 | 1.00 | 1.58 |
| 32 | 0.94 | 1.86 | 0.92 | 1.57 | 0.98 | 1.82 |
| 40 | 0.96 | 2.23 | 0.99 | 1.97 | 0.99 | 2.25 |
| 45 | 0.95 | 2.40 | 1.00 | 2.36 | 0.98 | 2.59 |
| 63 | 1.00 | 2.73 | 0.97 | 2.23 | 1.00 | 2.69 |
| 66 | 0.95 | 1.23 | 0.90 | 1.06 | 0.97 | 1.29 |
| 75 | 0.97 | 1.37 | 0.92 | 1.18 | 0.99 | 1.41 |
| 95 | 1.00 | 1.98 | 0.96 | 1.87 | 1.00 | 2.11 |
| 100 | 1.00 | 2.32 | 0.92 | 1.92 | 1.00 | 2.28 |
| 118 | 1.00 | 1.81 | 0.91 | 1.65 | 0.99 | 1.85 |
| Model | Scenario | Participation | Surface Runoff | Lateral Flow | Baseflow | Percolation | Tile Flow | Soil Water | ET | PET | Water Yield |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Uncali. | NCDC-SWAT | 863 | 126 | 13 | 145 | 146 | 34 | 228 | 545 | 792 | 303 |
| NLDAS2-SWAT | 871 | 113 | 10 | 91 | 91 | 20 | 206 | 641 | 996 | 223 | |
| PNLDAS2-SWAT | 871 | 133 | 12 | 134 | 135 | 31 | 221 | 560 | 838 | 297 | |
| Cali. | NCDC-SWAT | 863 | 95 | 11 | 127 | 120 | 29 | 210 | 608 | 780 | 247 |
| NLDAS2-SWAT | 871 | 98 | 12 | 127 | 124 | 30 | 219 | 612 | 996 | 254 | |
| PNLDAS2-SWAT | 871 | 94 | 11 | 118 | 111 | 26 | 202 | 630 | 830 | 235 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, J.; Wang, Q.; Zhang, X. On the Use of NLDAS2 Weather Data for Hydrologic Modeling in the Upper Mississippi River Basin. Water 2019, 11, 960. https://doi.org/10.3390/w11050960
Qi J, Wang Q, Zhang X. On the Use of NLDAS2 Weather Data for Hydrologic Modeling in the Upper Mississippi River Basin. Water. 2019; 11(5):960. https://doi.org/10.3390/w11050960
Chicago/Turabian StyleQi, Junyu, Qianfeng Wang, and Xuesong Zhang. 2019. "On the Use of NLDAS2 Weather Data for Hydrologic Modeling in the Upper Mississippi River Basin" Water 11, no. 5: 960. https://doi.org/10.3390/w11050960
APA StyleQi, J., Wang, Q., & Zhang, X. (2019). On the Use of NLDAS2 Weather Data for Hydrologic Modeling in the Upper Mississippi River Basin. Water, 11(5), 960. https://doi.org/10.3390/w11050960






