Influences of Catchment and River Channel Characteristics on the Magnitude and Dynamics of Storage and Re-Suspension of Fine Sediments in River Beds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Sites and Data Sources
2.2. Model Description
2.2.1. Fine Sediment Accumulation
2.2.2. Fine Sediment Re-Suspension
2.2.3. Fine Sediment Accumulation during Flood Recession
2.2.4. Model Simulation
2.3. Determination of the Model Parameters
2.4. Model Evaluation
3. Results
3.1. Model Parameters
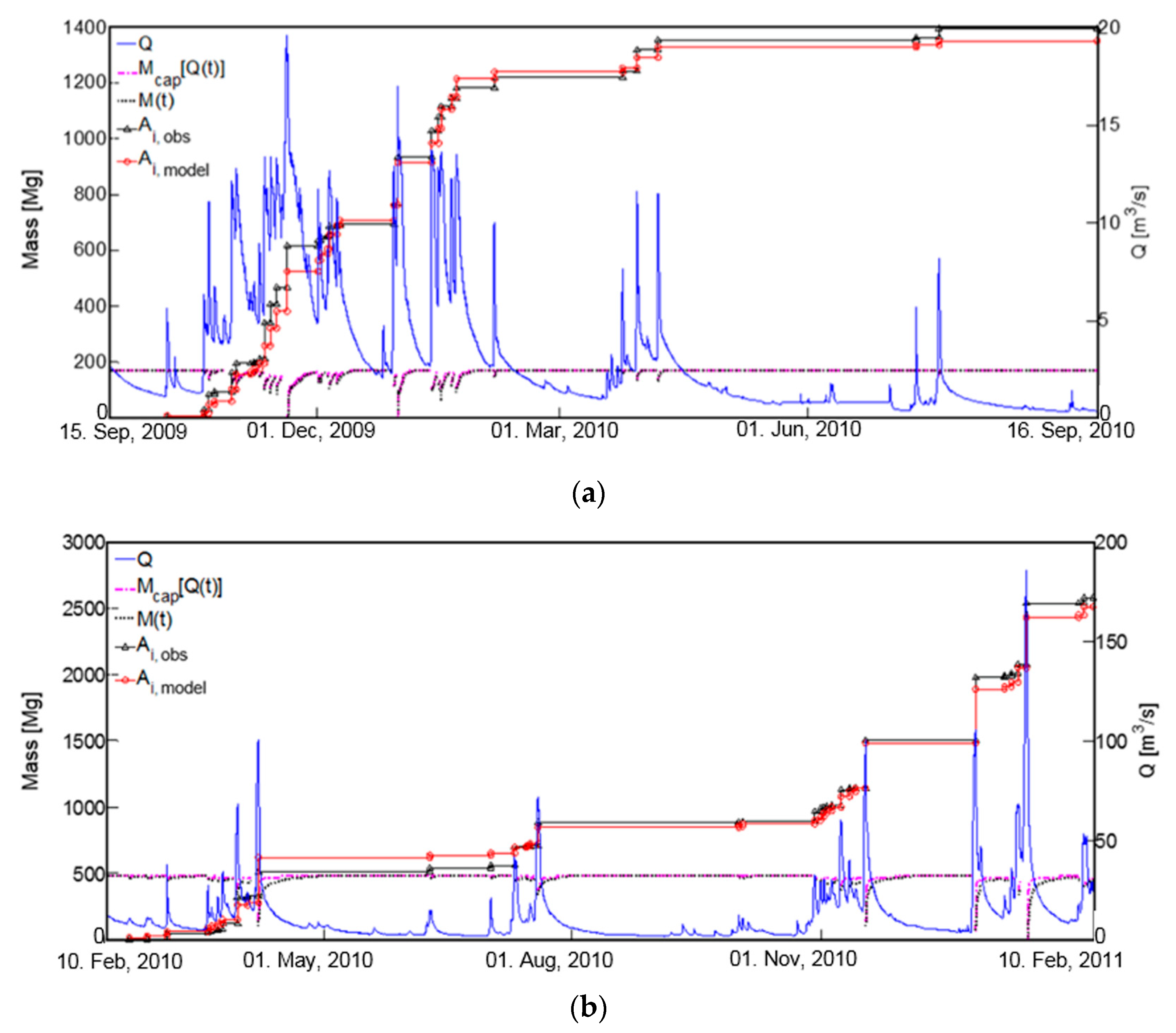
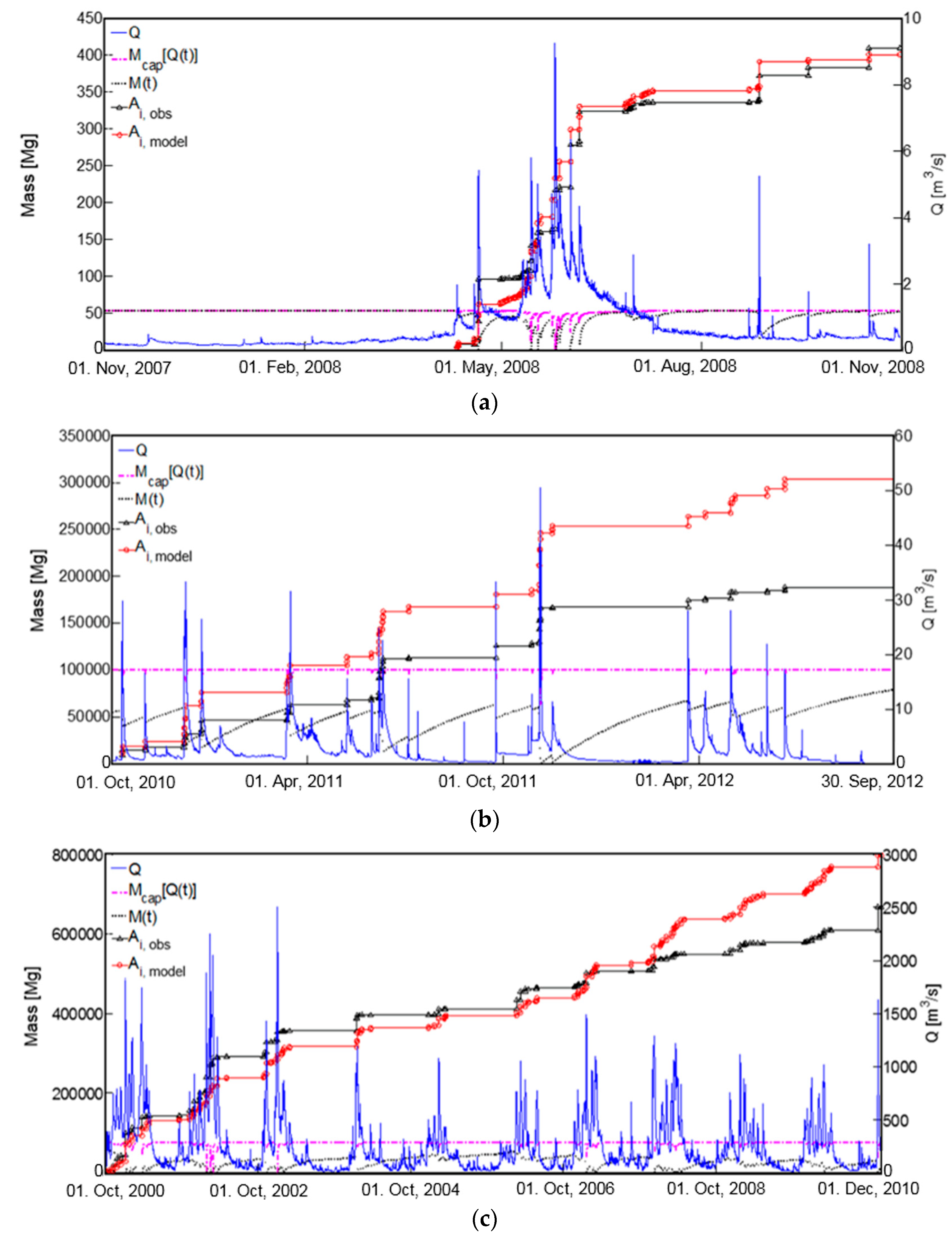
3.2. Model Calibration
3.3. Model Validation
3.4. Model Parameter Dependence on Catchment Characteristics
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| M | mass |
| L | length |
| T | time |
| Mg | megagram (equal to 1000 km) |
| Q (L3/T) | water discharge |
| Qs (M/T) | fine sediment loading rate |
| Qc (L3/T) | critical flow rate required to initiate the mobilization of sediment bed material |
| Qpeak (L3/T) | peak flow rate of a flood event |
| Qmax (L3/T) | maximum recorded flow rate during the observation period |
| C (M/L3) | concentration of fine sediments within the water column |
| (M/L3) | background suspended sediment concentration from the catchment |
| (M) | mass of fine sediments accumulated within the pore space of the sediment bed |
| (M) | maximum mass of fine sediments accumulated within the pore space of the sediment bed, representing the capacity of the sediment bed for fine sediments accumulation |
| (M) | Observed mass of fine sediments released from the sediment bed into the water column |
| (M) | model-estimated mass of fine sediments released from the sediment bed into the water column |
| (M) | capacity for fine sediment storage in the sediment bed |
| (M) | observed cumulative mass of fine sediments released in the first i flood events of the season |
| (M) | model-estimated cumulative mass of fine sediments released in the first i flood events of the season |
| α (L3/T) | sediment removal parameter representing filtration and settling of fine sediments within the sediment bed of the catchment |
| dimensionless sediment bed erosion parameter | |
| (T) | time at the start of a flood event i |
| (T) | time at the peak flow rate of a flood event i |
Appendix A. Details of Model Description
Appendix A1. Fine Sediment Re-Suspension
Appendix A2. Fine Sediment Accumulation during Flood Recession
References
- Droppo, I.G.; Liss, S.N.; Williams, D.; Nelson, T.; Jaskot, C.; Trapp, B. Dynamic existence of waterborne pathogens within river sediment compartments. Implications for water quality regulatory affairs. Environ. Sci. Technol. 2009, 43, 1737–1743. [Google Scholar] [CrossRef] [PubMed]
- Søndergaard, M.; Jensen, J.P.; Jeppesen, E. Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia 2003, 506, 135–145. [Google Scholar] [CrossRef]
- Singer, M.B.; Aalto, R.; James, L.A.; Kilham, N.E.; Higson, J.L.; Ghoshal, S. Enduring legacy of a toxic fan via episodic redistribution of California gold mining debris. Proc. Natl. Acad. Sci. USA 2013, 110, 18436–18441. [Google Scholar] [CrossRef]
- Herrero, A.; Vila, J.; Eljarrat, E.; Ginebreda, A.; Sabater, S.; Batalla, R.J.; Barceló, D. Transport of sediment borne contaminants in a Mediterranean river during a high flow event. Sci. Total Environ. 2018, 633, 1392–1402. [Google Scholar] [CrossRef] [PubMed]
- Quesada, S.; Tena, A.; Guillén, D.; Ginebreda, A.; Vericat, D.; Martínez, E.; Navarro-Ortega, A.; Batalla, R.J.; Barceló, D. Dynamics of suspended sediment borne persistent organic pollutants in a large regulated Mediterranean river (Ebro, NE Spain). Sci. Total Environ. 2014, 473, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Suttle, K.B.; Power, M.E.; Levine, J.M.; McNeely, C. How fine sediment in riverbeds impairs growth and survival of juvenile salmonids. Ecol. Appl. 2004, 14, 969–974. [Google Scholar] [CrossRef]
- Béjar, M.; Gibbins, C.; Vericat, D.; Batalla, R.J. Effects of suspended sediment transport on invertebrate drift. River Res. Appl. 2017, 33, 1655–1666. [Google Scholar] [CrossRef]
- Buendia, C.; Gibbins, C.N.; Vericat, D.; Batalla, R.J.; Douglas, A. Detecting the structural and functional impacts of fine sediment on stream invertebrates. Ecol. Indic. 2013, 25, 184–196. [Google Scholar] [CrossRef]
- Buendia, C.; Gibbins, C.N.; Vericat, D.; Batalla, R.J. Effects of flow and fine sediment dynamics on the turnover of stream invertebrate assemblages. Ecohydrology 2014, 7, 1105–1123. [Google Scholar] [CrossRef]
- Pelletier, J.D. A spatially distributed model for the long-term suspended sediment discharge and delivery ratio of drainage basins. J. Geophys. Res. 2012, 117, F2. [Google Scholar] [CrossRef]
- Warrick, J.A.; Mertes, L.A.K. Sediment yield from the tectonically active semiarid Western Transverse Ranges of California. Geol. Soc. Am. Bull. 2009, 121, 1054–1070. [Google Scholar] [CrossRef]
- Syvitski, J.P.; Morehead, M.D.; Bahr, D.B.; Mulder, T. Estimating fluvial sediment transport: The rating parameters. Water Resour. Res. 2000, 36, 2747–2760. [Google Scholar] [CrossRef]
- Gao, P.; Nearing, M.A.; Commons, M. Suspended sediment transport at the instantaneous and event time scales in semiarid watersheds of southeastern Arizona, USA. Water Resour. Res. 2013, 49, 6857–6870. [Google Scholar] [CrossRef]
- Warrick, J.A.; Madej, M.A.; Goni, M.A.; Wheatcroft, R.A. Trends in the suspended-sediment yields of coastal rivers of northern California, 1955-2010. J. Hydrol. 2013, 489, 108–123. [Google Scholar] [CrossRef]
- Alexandrov, Y.; Laronne, J.B.; Reid, I. Intra-event and inter-seasonal behaviour of suspended sediment in flash floods of the semi-arid northern Negev, Israel. Geomorphology 2007, 85, 85–97. [Google Scholar] [CrossRef]
- Harrington, S.T.; Harrington, J.R. An assessment of the suspended sediment rating curve approach for load estimation on the Rivers Bandon and Owenabue, Ireland. Geomorphology 2013, 185, 27–38. [Google Scholar] [CrossRef]
- Klein, M. Anti clockwise hysteresis in suspended sediment concentration during individual storms: Holbeck catchment, Yorkshire England. Catena 1984, 11, 251–257. [Google Scholar] [CrossRef]
- Carson, M.A.; Taylor, C.H.; Grey, B.J. Sediment production in a small Appalachian watershed during spring runoff: the Eaton Basin, 1970-1972. Can. J. Earth Sci. 1973, 10, 1707–1734. [Google Scholar] [CrossRef]
- Williams, G.P. Sediment concentration versus water discharge during single hydrologic events in rivers. J. Hydrol. 1989, 111, 89–106. [Google Scholar] [CrossRef]
- Harvey, J.W.; Drummond, J.D.; Martin, R.L.; McPhillips, L.E.; Packman, A.I.; Jerolmack, D.J.; Stonedahl, S.H.; Aubeneau, A.F.; Sawyer, A.H.; Larsen, L.G.; et al. Hydrogeomorphology of the hyporheic zone: Stream solute and fine particle interactions with a dynamic streambed. J. Geophys. Res. 2012, 117, G00N11. [Google Scholar] [CrossRef]
- Cantalice, J.R.B.; Cunha, M.; Stosic, B.D.; Piscoya, V.C.; Guerra, S.M.S.; Singh, V.P. Relationship between bedload and suspended sediment in the sand-bed Exu River, in the semi-arid region of Brazil. Hydrol. Sci. J. 2013, 58, 1789–1802. [Google Scholar] [CrossRef]
- Piqué, G.; López-Tarazón, J.A.; Batalla, R.J. Variability of in-channel sediment storage in a river draining highly erodible areas (the Isábena, Ebro Basin). J. Soil. Sediment. 2014, 14, 2031–2044. [Google Scholar] [CrossRef]
- Yang, C.C.; Lee, K.T. Analysis of flow-sediment rating curve hysteresis based on flow and sediment travel time estimations. Int. J. Sediment Res. 2018, 33, 171–182. [Google Scholar] [CrossRef]
- Juez, C.; Hassan, M.A.; Franca, M.J. The origin of fine sediment determines the observations of suspended sediment fluxes under unsteady flow conditions. Water Resour. Res. 2018, 54, 5654–5669. [Google Scholar] [CrossRef]
- Walling, D.E. The sediment delivery problem. J. Hydrol. 1983, 65, 209–237. [Google Scholar] [CrossRef]
- Negev, M. Analysis of Data on Suspended Sediment Discharge in Several Streams in Israel; Hydrological Paper No. 12; Israel Hydrological Service: Jerusalem, Israel, 1969; pp. 8–17. [Google Scholar]
- Alexandrov, Y.; Cohen, H.; Laronne, J.B.; Reid, I. Suspended sediment load, bed load, and dissolved load yields from a semiarid drainage basin: A 15-year study. Water Resour. Res. 2009, 45, W08408. [Google Scholar] [CrossRef]
- Brasington, J.; Richards, K. Turbidity and suspended sediment dynamics in small catchments in the Nepal Middle Hills. Hydrol. Process. 2000, 14, 2559–2574. [Google Scholar] [CrossRef]
- Stubblefield, A.P.; Reuter, J.E.; Goldman, C.R. Sediment budget for subalpine watersheds, Lake Tahoe, California, USA. Catena 2009, 76, 163–172. [Google Scholar] [CrossRef]
- Achite, M.; Ouillon, S. Suspended sediment transport in a semiarid watershed, Wadi Abd, Algeria (1973–1995). J. Hydrol. 2007, 343, 187–202. [Google Scholar] [CrossRef]
- Hunt, J.R. Coupling fine particle and bedload transport in gravel-bedded streams. J. Hydrol. 2017, 552, 532–543. [Google Scholar]
- Park, J.; Hunt, J.R. Modeling fine particle dynamics in gravel-bedded streams: Storage and re-suspension of fine particles. Sci. Total Environ. 2018, 634, 1042–1053. [Google Scholar] [CrossRef]
- Lefrançois, J.; Grimaldi, C.; Gascuel-Odoux, C.; Gilliet, N. Suspended sediment and discharge relationships to identify bank degradation as a main sediment source on small agricultural catchments. Hydrol. Process. 2007, 21, 2923–2933. [Google Scholar] [CrossRef]
- Langlois, J.L.; Johnson, D.W.; Mehuys, G.R. Suspended sediment dynamics associated with snowmelt runoff in a small mountain stream of Lake Tahoe (Nevada). Hydrol. Process. 2005, 19, 3569–3580. [Google Scholar] [CrossRef]
- Navratil, O.; Evrard, O.; Esteves, M.; Legout, C.; Ayrault, S.; Némery, J.; Mate-Marin, A.; Ahmadi, M.; Lefévre, I.; Poirel, A.; Bonté, P. Temporal variability of suspended sediment sources in an alpine catchment combining river/rainfall monitoring and sediment fingerprinting. Earth Surf. Proc. Land. 2012, 37, 828–846. [Google Scholar] [CrossRef]
- Tuset, J.; Vericat, D.; Batalla, R. Rainfall, runoff and sediment transport in a Mediterranean mountainous catchment. Sci. Total Environ. 2016, 540, 114–132. [Google Scholar] [CrossRef] [PubMed]
- López-Tarazón, J.A.; Batalla, R.J. Dominant discharges for suspended sediment transport in a highly active Pyrenean river. J. Soil. Sediment. 2014, 14, 2019–2030. [Google Scholar] [CrossRef]
- Gentile, F.; Bisantino, T.; Corbino, R.; Milillo, F.; Romano, G.; Trisorio Liuzzi, G. Monitoring and analysis of suspended sediment transport dynamics in the Carapelle torrent (southern Italy). Catena 2010, 80, 1–8. [Google Scholar] [CrossRef]
- Ritter, J.R.; Brown, W.M., III. Turbidity and Suspended-Sediment Transport in the Russian River Basin; Open-File Report 72-316; United States Geological Survey: Menlo Park, CA, USA, 1971; pp. 15–29.
- Doomen, A.; Wijma, E.; Zwolsman, J.J.; Middelkoop, H. Predicting suspended sediment concentrations in the Meuse River using a supply-based rating curve. Hydrol. Process. 2008, 22, 1846–1856. [Google Scholar] [CrossRef]
- Birgand, F.; Lefrancois, T.; Grimaldi, C.; Novince, E.; Gilliet, N.; Odoux, C.G. Mesure des flux et échantillonnage des matières en suspension sur de petits cours déau. Ingénieries 2004, 40, 21–35. [Google Scholar]
- Vongvixay, A.; Grimaldi, C.; Dupas, R.; Fovet, O.; Birgand, F.; Gilliet, N.; Gascuel-Odoux, C. Contrasting suspended sediment export in two small agricultural catchments: Cross-influence of hydrological behaviour and landscape degradation or stream bank management. Land Degrad. Dev. 2018, 29, 1385–1396. [Google Scholar] [CrossRef]
- Evrard, O.; Navratil, O.; Ayrault, S.; Ahmadi, M.; Némery, J.; Legout, C.; Lefévre, I.; Poirel, A.; Bonté, P.; Esteves, M. Combining suspended sediment monitoring and fingerprinting to determine the spatial origin of fine sediment in a mountainous river catchment. Earth Surf. Proc. Land. 2011, 36, 1072–1089. [Google Scholar] [CrossRef]
- Navratil, O.; Esteves, M.; Legout, C.; Gratiot, N.; Nemery, J.; Willmore, S.; Grangeon, T. Global uncertainty analysis of suspended sediment monitoring using turbidimeter in a small mountainous river catchment. J. Hydrol. 2011, 398, 246–259. [Google Scholar] [CrossRef]
- Vericat, D.; Batalla, R.J.; Gibbins, C.N. Sediment entrainment and depletion from patches of fine material in a gravel-bed river. Water Resour. Res. 2008, 44, W11415. [Google Scholar] [CrossRef]
- López-Tarazón, J.A.; Batalla, R.; Vericat, D.; Francke, T. Suspended sediment transport in a highly erodible catchment: the River Isábena (Southern Pyrenees). Geomorphology 2009, 109, 210–221. [Google Scholar] [CrossRef]
- Bisantino, T.; Bingner, R.; Chouaib, W.; Gentile, F.; Trisorio Liuzzi, G. Estimation of runoff, peak discharge and sediment load at the event scale in a medium-size Mediterranean watershed using the AnnAGNPS model. Land Degrad. Dev. 2015, 26, 340–355. [Google Scholar] [CrossRef]
- García-Rama, A.; Pagano, S.G.; Gentile, F.; Lenzi, M.A. Suspended sediment transport analysis in two Italian instrumented catchments. J. Mt. Sci. 2016, 13, 957–970. [Google Scholar] [CrossRef]
- Haschenburger, J.K. A probability model of scour and fill depths in gravel-bed channels. Water Resour. Res. 1999, 35, 2857–2869. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Vericat, D.; Batalla, R.J. Sediment transport from continuous monitoring in a perennial Mediterranean stream. Catena 2010, 82, 77–86. [Google Scholar] [CrossRef]
- Collins, A.L.; Walling, D.E. Fine-grained bed sediment storage within the main channel systems of the Frome and Piddle catchments, Dorset, UK. Hydrol. Process. 2007, 21, 1448–1459. [Google Scholar] [CrossRef]
- Walling, D.E.; Owens, P.N.; Leeks, G.J. The role of channel and floodplain storage in the suspended sediment budget of the River Ouse, Yorkshire, UK. Geomorphology 1998, 22, 225–242. [Google Scholar] [CrossRef]
- Walling, D.E.; Collins, A.L.; Jones, P.A.; Leeks, G.J.L.; Old, G. Establishing fine-grained sediment budgets for the Pang and Lambourn LOCAR catchments, UK. J. Hydrol. 2006, 330, 126–141. [Google Scholar] [CrossRef]
- López-Tarazón, J.A.; Batalla, R.J.; Vericat, D.; Balasch, J. Rainfall, runoff and sediment transport relations in a mesoscale mountainous catchment: The River Isábena (Ebro basin). Catena 2010, 82, 23–34. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis and optimization: A review. Comput. Chem. Eng. 2017, 108, 250–267. [Google Scholar] [CrossRef]
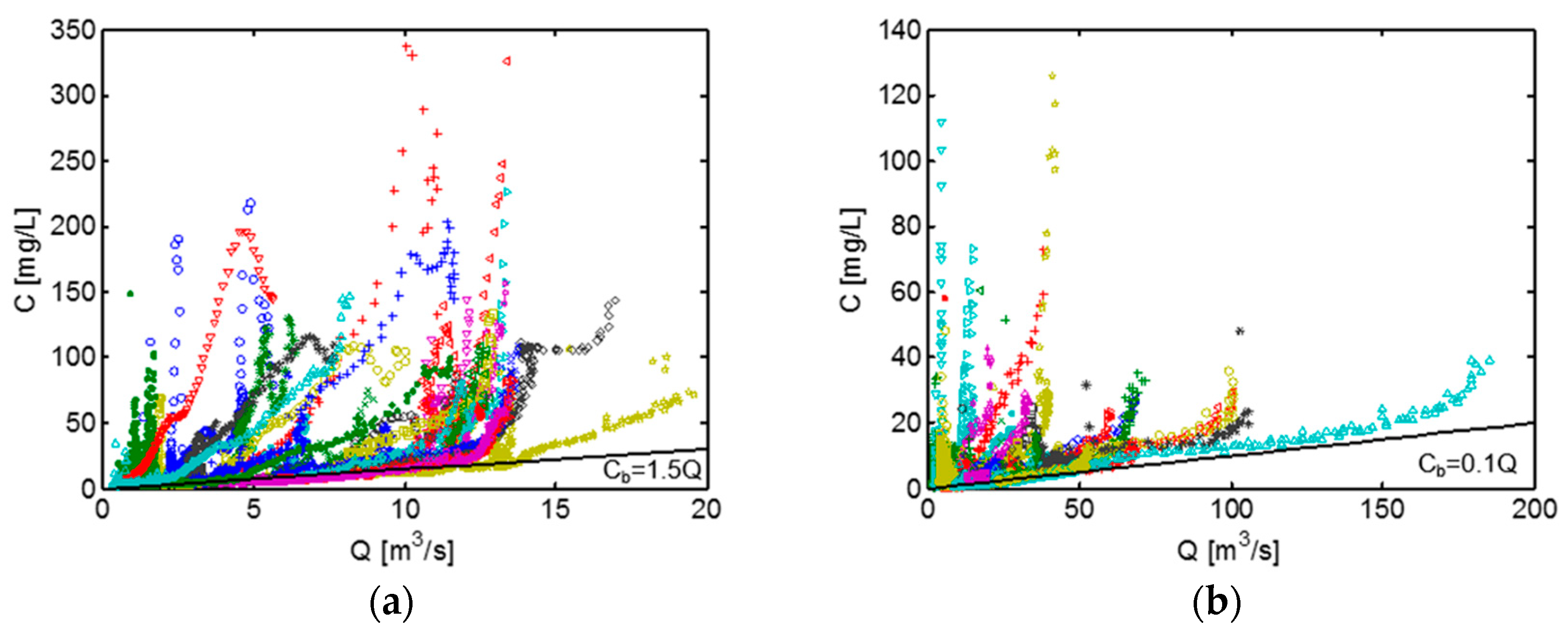

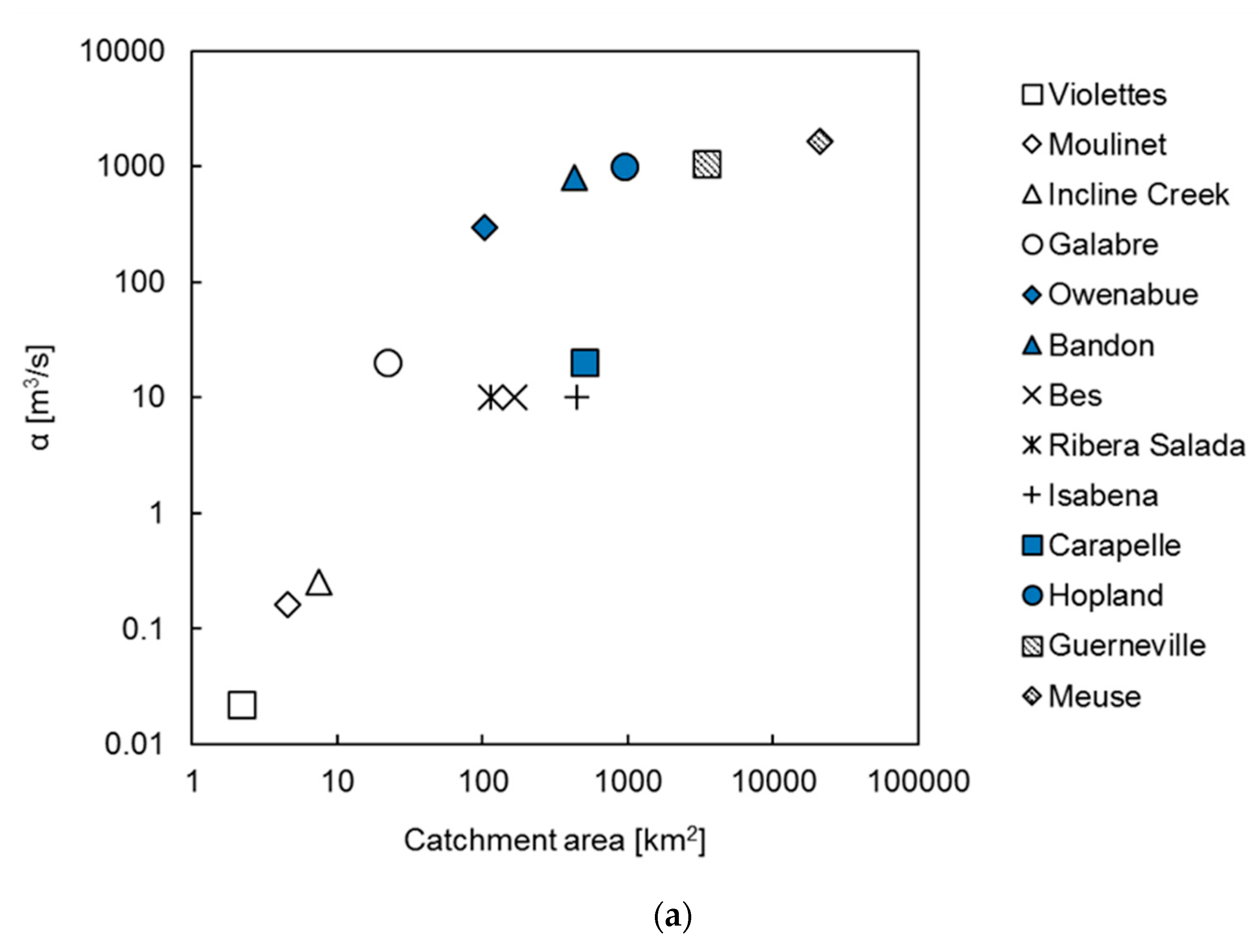
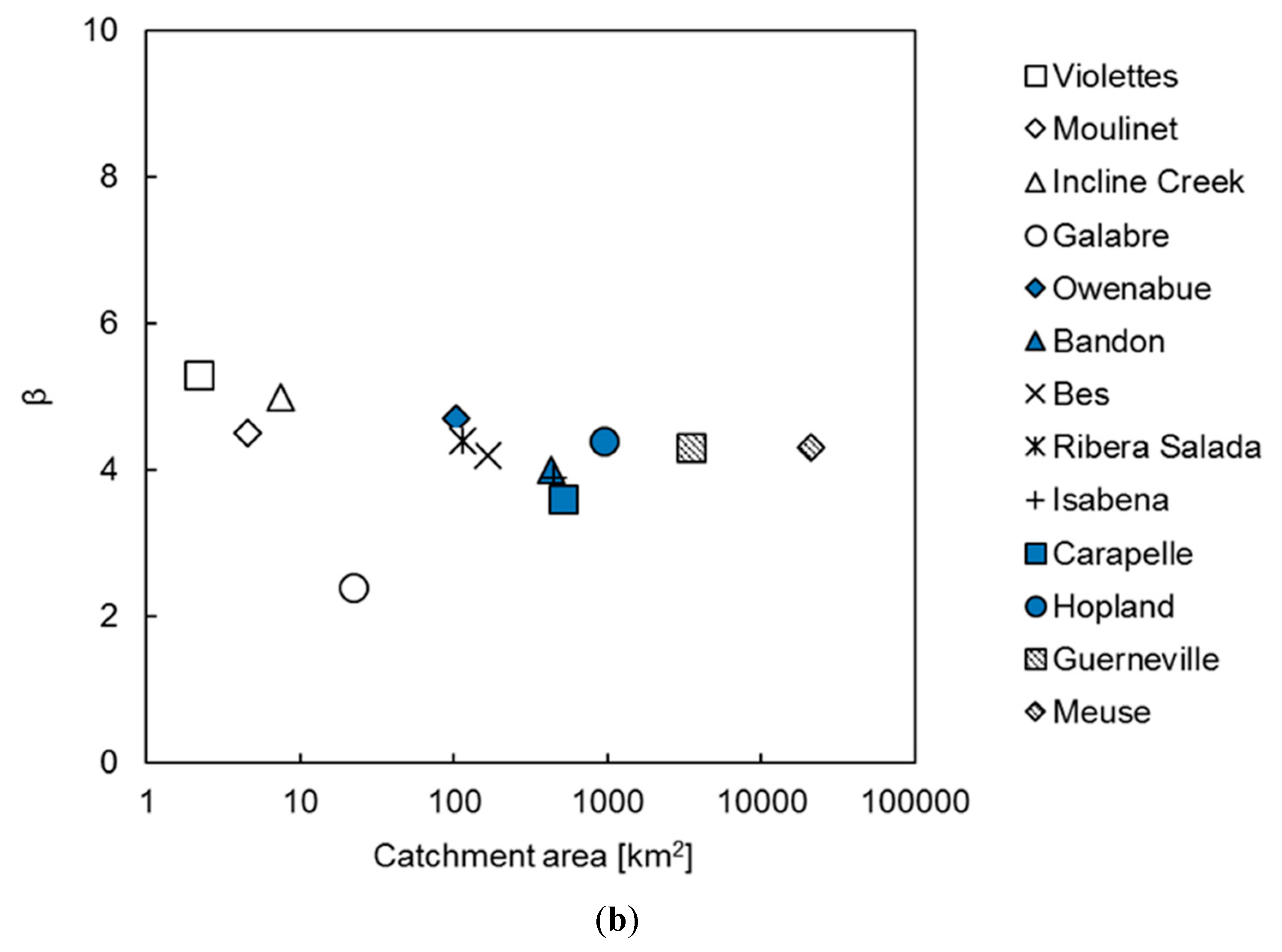
| No | Sites | Catchment Area (km2) | Climate | Mean Annual Precipitation (mm) | Dominant Bed Surface Materials | Observation | Qc (m3/s) | Qmax (m3/s) | Background C (Cb) | Mmax (Mg) | References | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | Frequency (min) | ||||||||||||
| 1 | Violettes | France | 2.2 | Temperate oceanic | 900 | Silty loess | 1 June 2002–31 May 2003 | 10 | 0.05 | 0.15 | 4000Q | 6.7 | [33] |
| 2 | Moulinet | France | 4.5 | Temperate oceanic | 1 June 2002–31 May 2003 | 10 | 0.1 | 0.41 | 300Q | 9.8 | |||
| 3 | Incline Creek | Nevada, USA | 7.4 | Snow melt | 890–1270 | Sandy decomposed granite | 4 April–24 May 2000 | 15 | 0.2 | 0.34 | 100(Q-0.2) | 0.5 | [34] |
| 4 | Galabre | France | 20 | Mediterranean mountainous | 600–1200 | Limestone and marls | 3 October 2007–23December 2009 | 10 | 1 | 22 | 300Q | 2200 | [35] |
| 5 | Owenabue | Ireland | 103 | Temperate oceanic | ~1200 | Mudstone and sandstone | 15 September 2009–15 September 2010 | 15 | 5 | 17 | 1.5Q | 170 | [16] |
| 6 | Bandon | Ireland | 424 | Temperate oceanic | 10 February 2010–9 February 2011 | 15 | 10 | 110 | 0.1Q | 480 | |||
| 7 | Bès | France | 165 | Mediterranean mountainous | 600–1200 | Limestone and marls | 1 April 2008–31 December 2009 | 10 | 10 | 143 | 100Q | 26,600 | [35] |
| 8 | Ribera Salada | Spain | 114 | Mediterranean mountainous | 760 | Limestone and conglomerates | 1 November 2005–30 October 2008 | 5 | 1 | 5.85 | 10Q0.5 + 0.1Q4 | 53.4 | [36] |
| 9 | Isabena | Spain | 445 | Mediterranean mountainous | 770 | Limestone, marls and clay-rocks | 1 November 2007–30 September 2012 | 15 | 10 | 68 | 0.02Q3 + 100 | 100,100 | [37] |
| 10 | Carapelle | Southern Italy | 506 | Mediterranean | 450–800 | clayey-loamy-sandy | 1 January 2007–31 December 2011 | 30 | 8 | 37 | 5Q2 | 23,000 | [38] |
| 11 | Hopland † | California, USA | 938 | Mediterranean | 1000–1200 | Sand-gravel and silty materials | 1 October 2010–31 December 2014 | 15 | 10 | 425 | 2Q | 26,560 | [31,32,39] |
| 12 | Guerneville † | California, USA | 3465 | Mediterranean | 1000–1200 | Sand-gravel and silty materials | 1 October 2009–31 September 2010/ 1 October 2012–31 December 2014 | 15 | 20 | 890 | 0.5Q | 83,960 | |
| 13 | Meuse | Belgian-Dutch border | 21,000 | European-continental | 800– 1000 | Limestone, shales and sandstone | 1 October 1995–30 November 2010 | 1440 | 280 | 1700 | 0.03Q | 187,800 | [40] |
| No | Sites | Optimal Model Parameter | Calibration | Number of Flood Events | Fine Sediment Mass | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| α (m3/s) | β | RSR | R | Period | Released from Sediment Bed (Mg) | Total Mass Transported during Observation Period (Mg) | Released from Sediment Bed as Percent of Total (%) | |||
| 1 | Violettes | 0.022 | 5.3 | 0.68 | 1.23 | 1 June 2002–31 May 2003 | 50 | 33 | 144 | 23 |
| 2 | Moulinet | 0.160 | 4.5 | 0.72 | 1.08 | 1 July 2002–30 June 2003 | 61 | 61 | 116 | 52 |
| 3 | Incline Creek | 0.25 | 5 | 0.73 | 0.94 | 4 April–24 May 2000 | 36 | 3.8 | 11.9 | 32 |
| 4 | Galabre | 20 | 2.4 | 0.64 | 1.05 | 3 October 2007–23 December 2009 | 39 | 14,000 | 26,000 | 54 |
| 5 | Owenabue | 300 | 4.7 | 0.49 | 0.97 | 15 September 2009–15 September 2010 | 32 | 1400 | 2500 | 56 |
| 6 | Bandon | 800 | 4.0 | 0.36 | 0.97 | 10 February 2010–9 February 2011 | 34 | 2580 | 3990 | 65 |
| 7 | Bès | 10 | 4.2 | 0.33 | 1.07 | 1 April 2008–31 December 2009 | 39 | 46,600 | 258,000 | 18 |
| 8 | Ribera Salada | 10 | 4.4 | 0.48 | 1.10 | 1 November 2005–30 October 2007 | 47 | 150 | 510 | 29 |
| 9 | Isabena | 10 | 3.9 | 0.97 | 0.93 | 1 November 2007–30 September 2010 | 79 | 623,000 | 1,063,000 | 58 |
| 10 | Carapelle | 20 | 3.6 | 0.48 | 0.92 | 3 March–23 April 2009 | 22 | 109,400 | 360,300 | 30 |
| 11 | Hopland † | 1000 | 4.4 | 0.36 | 1.02 | 1 October 2010–30 September 2013 | 69 | 137,000 | 330,000 | 42 |
| 12 | Guerneville † | 1050 | 4.3 | 0.35 | 0.83 | 1 October 2009–31 September 2010/ 1 October 2012–30 September 2013 | 25 (18 in 2010 water year, 8 in 2013 water year) | 422,000 | 908,000 | 46 |
| 13 | Meuse | 1650 | 4.3 | 0.47 | 1.06 | 1 October 1995–30 September 2000 | 52 | 1,053,900 | 1,675,600 | 63 |
| Sites | Validation | Number of Flood Events | Fine Sediment Mass | ||||
|---|---|---|---|---|---|---|---|
| RSR | R | Period | Released from Sediment Bed (Mg) | Total Mass Transported during the Observation Period (Mg) | Released from Sediment Bed as Percent of Total (%) | ||
| Ribera Salada | 0.71 | 0.98 | 1 November 2007–30 October 2008 | 52 | 410 | 930 | 44 |
| Isabena | 1.04 | 1.61 | 1 October 2010–30 September 2012 | 42 | 188,500 | 285,000 | 66 |
| Hopland † | 0.35 | 1.22 | Ten flood events between 1 October 2013, and 31 December 2014 | 10 | - | - | - |
| Guerneville † | 0.54 | 0.56 | 1 October 2013–31 December 2014 | 14 | 224,000 | 366,000 | 61 |
| Meuse | 0.62 | 1.20 | 1 October 2000–30 November 2010 | 101 | 1,668,000 | 2,884,000 | 58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Batalla, R.J.; Birgand, F.; Esteves, M.; Gentile, F.; Harrington, J.R.; Navratil, O.; López-Tarazón, J.A.; Vericat, D. Influences of Catchment and River Channel Characteristics on the Magnitude and Dynamics of Storage and Re-Suspension of Fine Sediments in River Beds. Water 2019, 11, 878. https://doi.org/10.3390/w11050878
Park J, Batalla RJ, Birgand F, Esteves M, Gentile F, Harrington JR, Navratil O, López-Tarazón JA, Vericat D. Influences of Catchment and River Channel Characteristics on the Magnitude and Dynamics of Storage and Re-Suspension of Fine Sediments in River Beds. Water. 2019; 11(5):878. https://doi.org/10.3390/w11050878
Chicago/Turabian StylePark, Jungsu, Ramon J. Batalla, Francois Birgand, Michel Esteves, Francesco Gentile, Joseph R. Harrington, Oldrich Navratil, Jose Andres López-Tarazón, and Damià Vericat. 2019. "Influences of Catchment and River Channel Characteristics on the Magnitude and Dynamics of Storage and Re-Suspension of Fine Sediments in River Beds" Water 11, no. 5: 878. https://doi.org/10.3390/w11050878
APA StylePark, J., Batalla, R. J., Birgand, F., Esteves, M., Gentile, F., Harrington, J. R., Navratil, O., López-Tarazón, J. A., & Vericat, D. (2019). Influences of Catchment and River Channel Characteristics on the Magnitude and Dynamics of Storage and Re-Suspension of Fine Sediments in River Beds. Water, 11(5), 878. https://doi.org/10.3390/w11050878





