An Assessment of Groundwater Contamination Risk with Radon Based on Clustering and Structural Models
Abstract
1. Introduction
2. Study Area
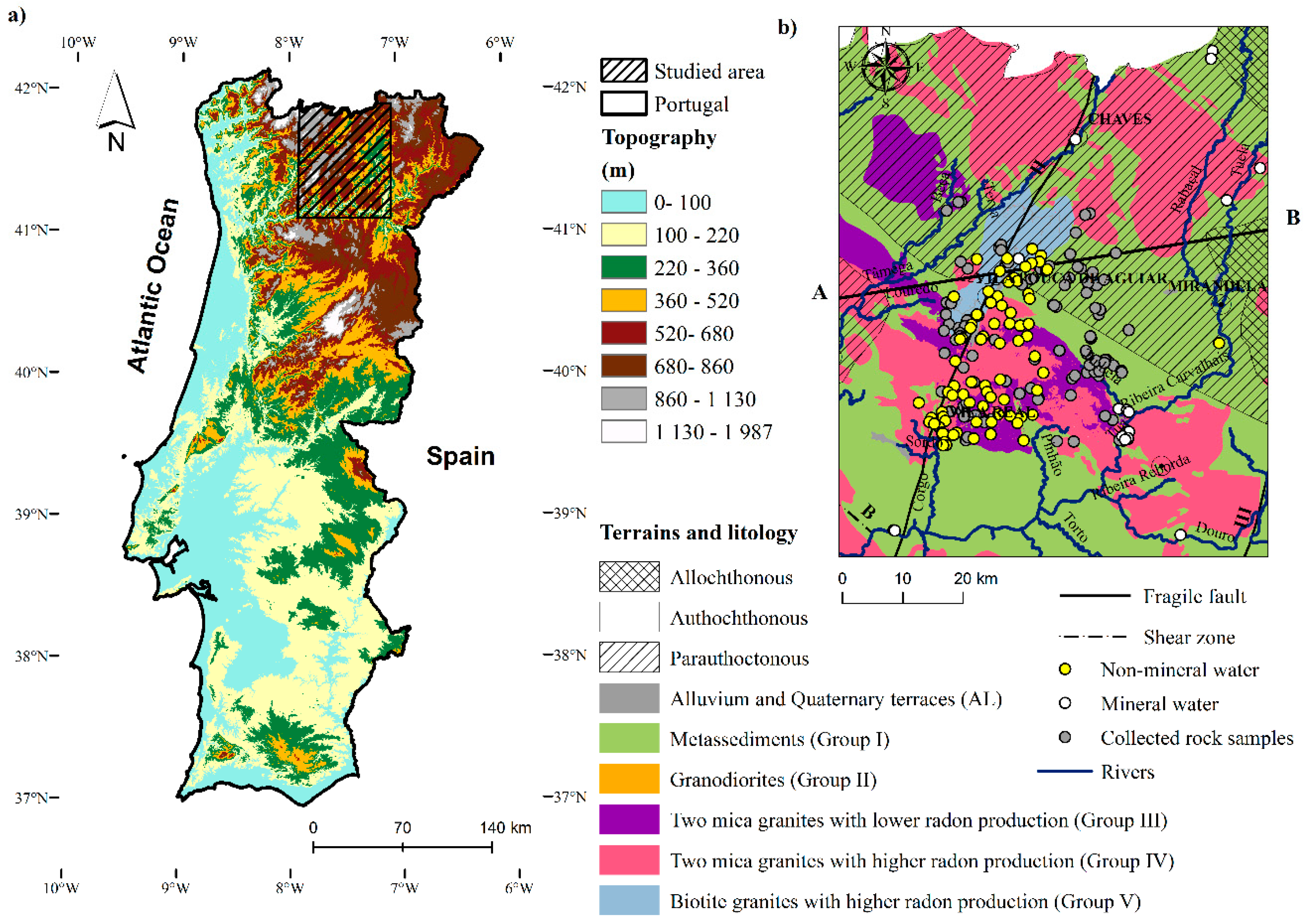
2.1. Location, Geomorphology, and Climate Study Area
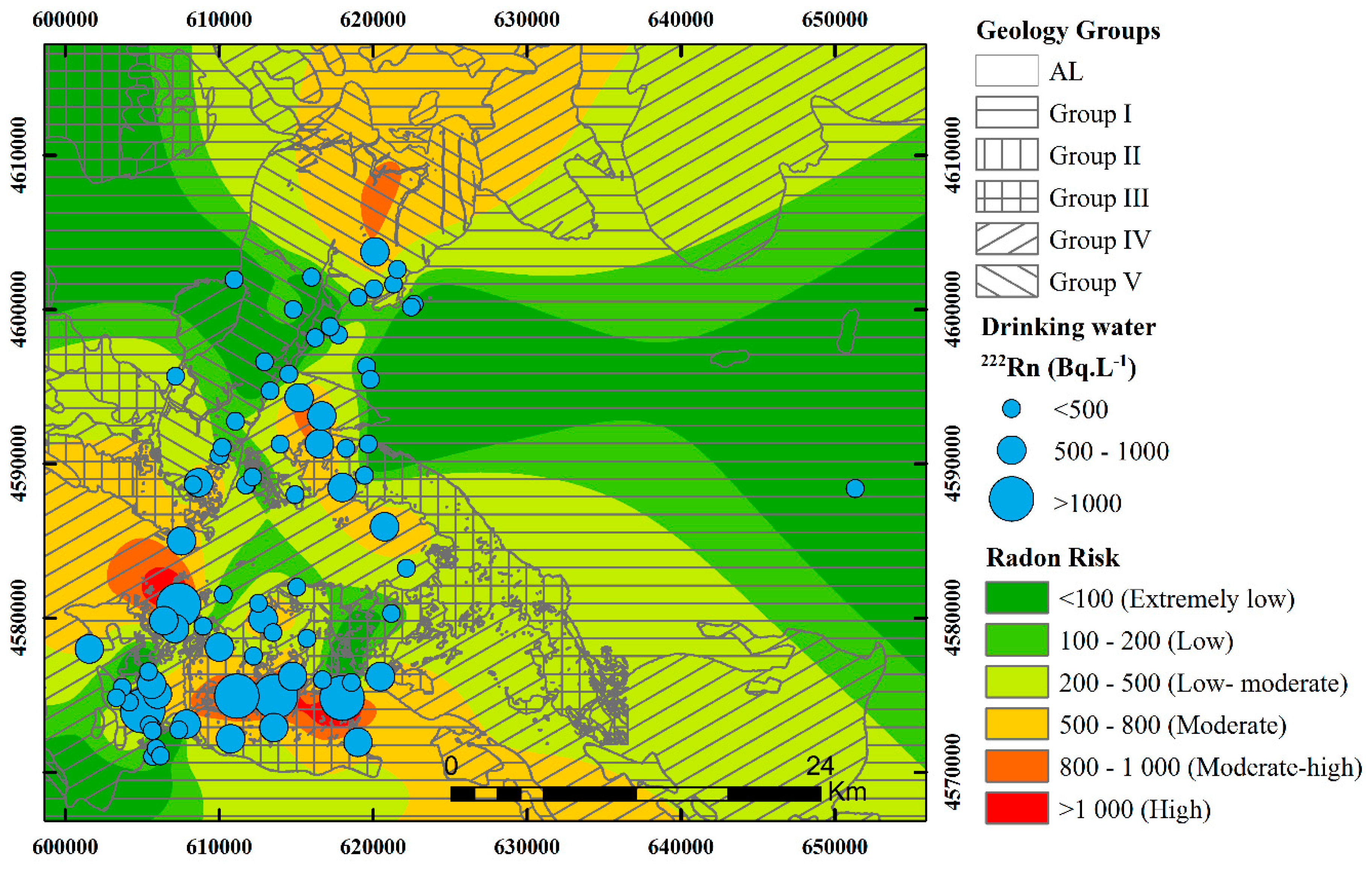
2.2. Geology
3. Materials and Methods
3.1. Analytical Methods
3.1.1. Radiological Profile in Rocks
3.1.2. Groundwater Sampling and Hydraulic Turnover Time Calculation
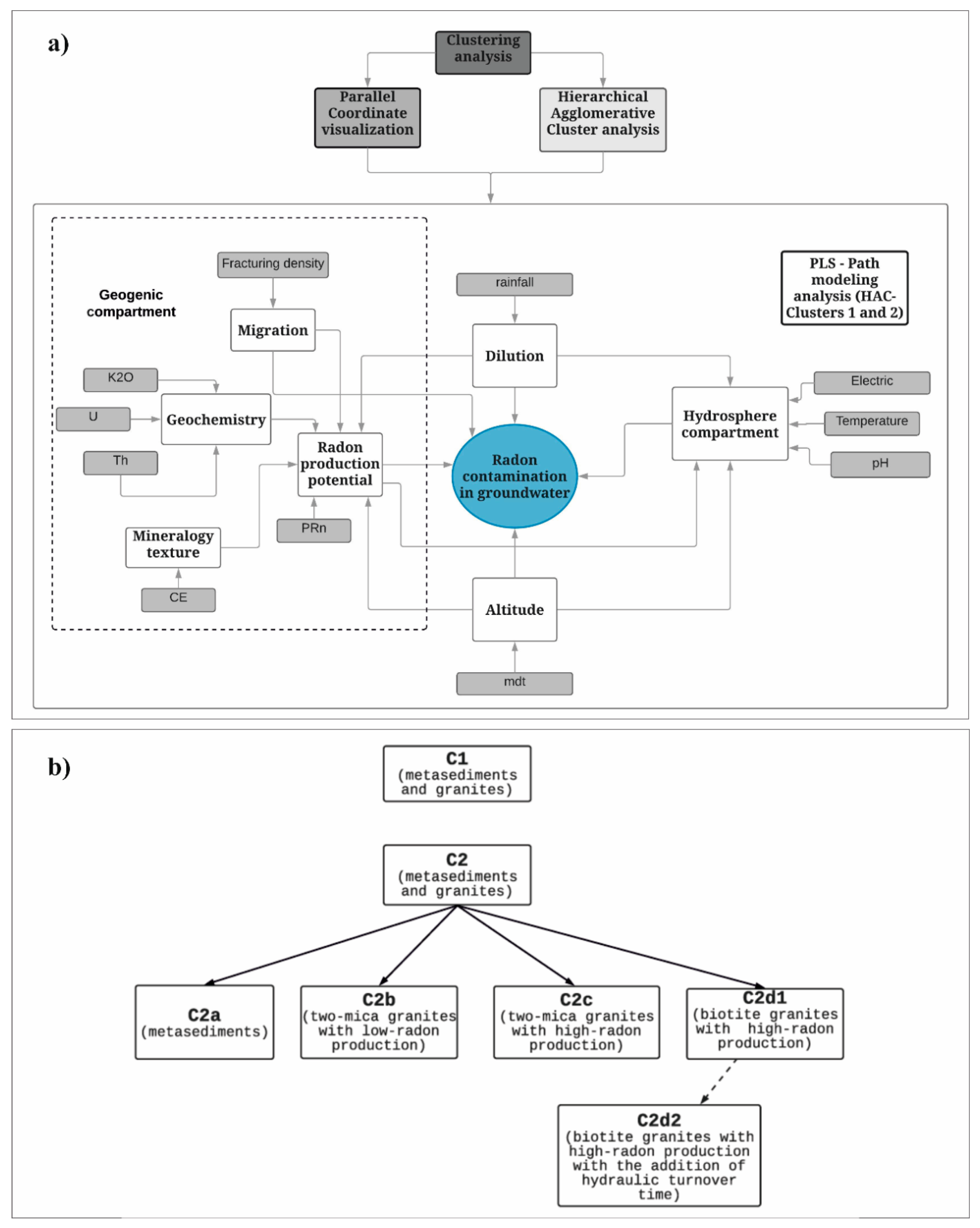
3.2. Hydrogeological Conceptual Model
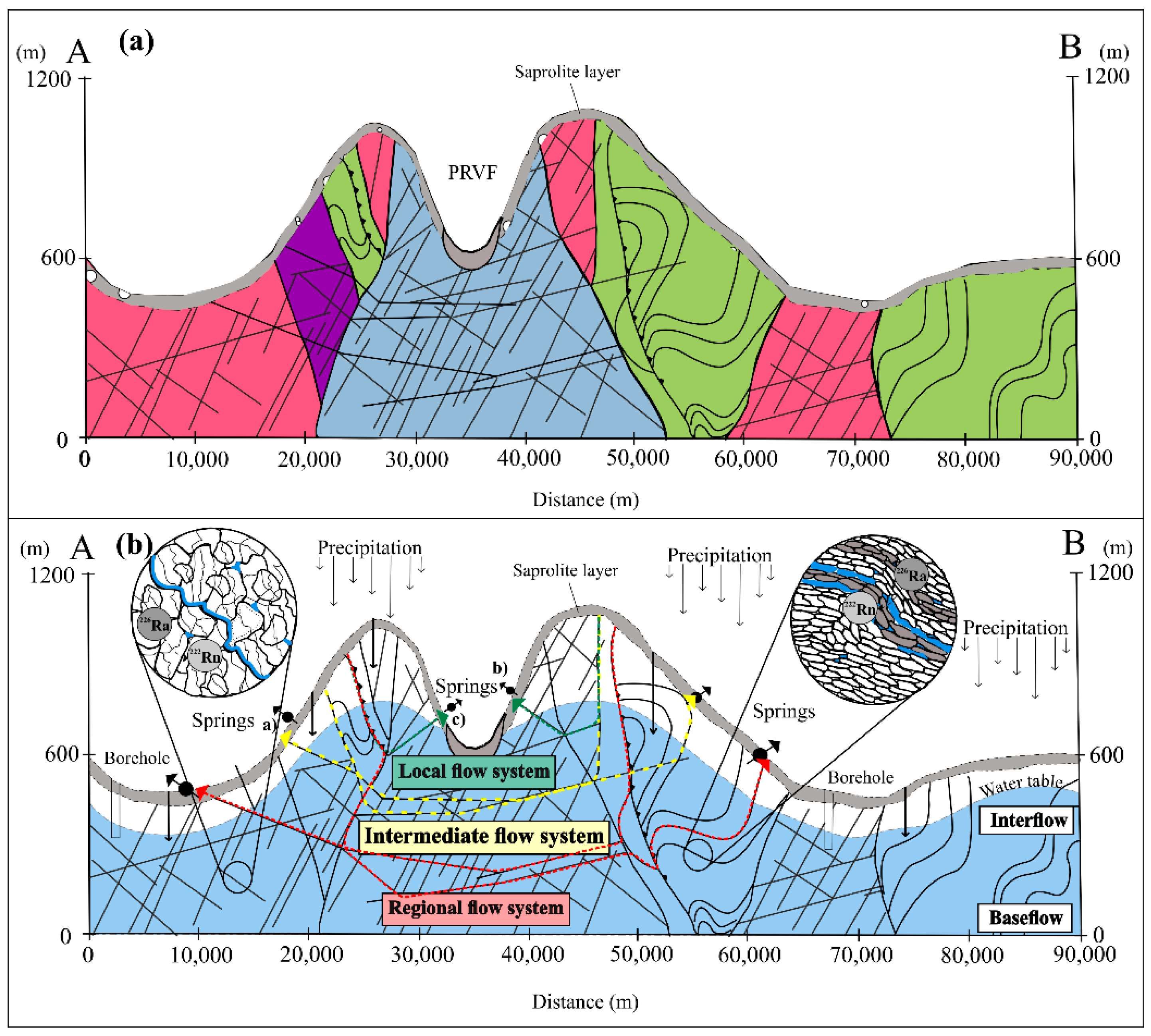
3.3. Technical Workflow
3.3.1. Clustering Analysis (Hierarchical Agglomerative Cluster (HAC) Analysis and Parallel Coordinate Visualization (PCV))
3.3.2. Partial Least Squares-Path Modeling (PLS-PM)
3.4. Dataset Preparation
4. Results
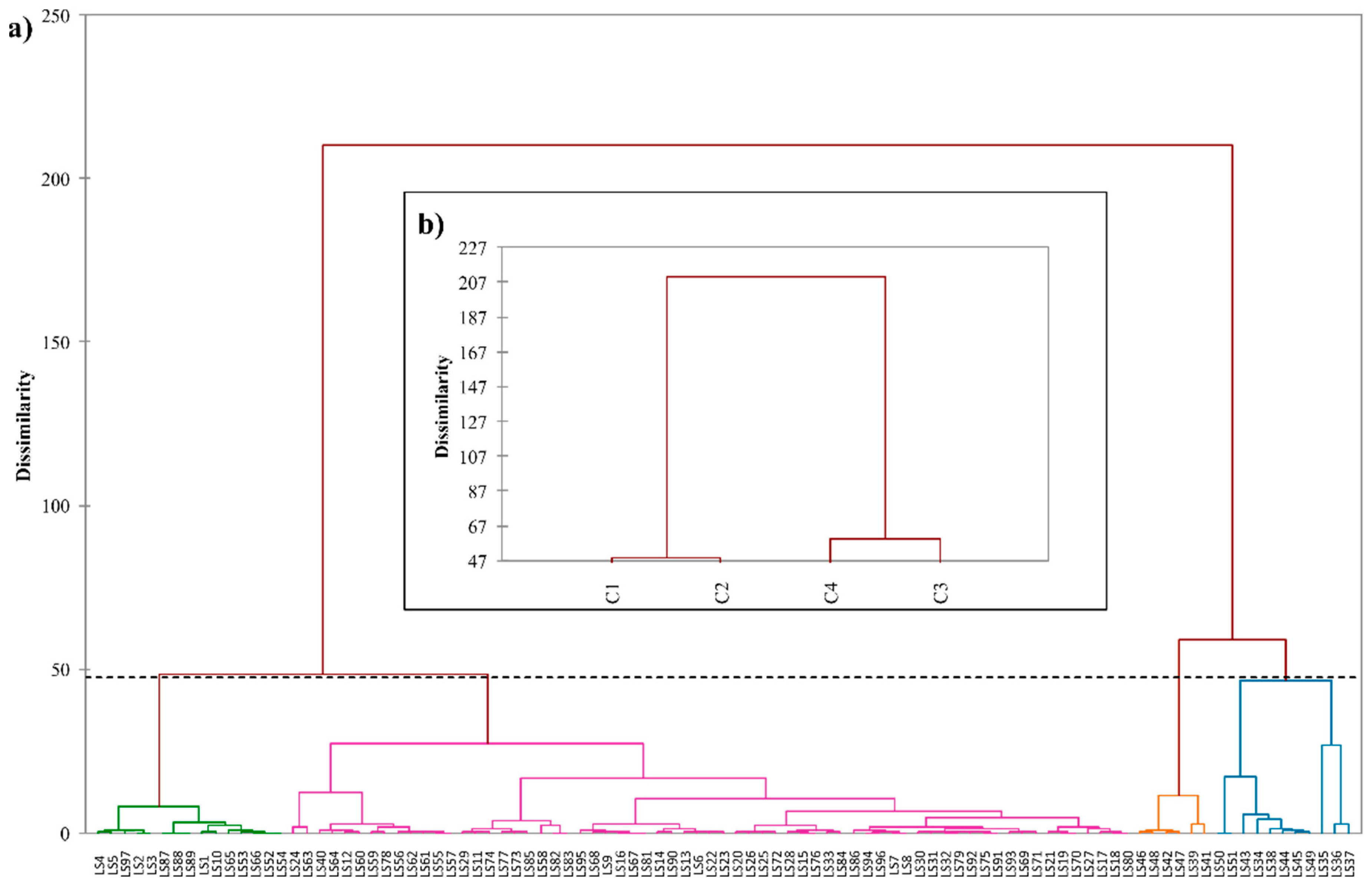
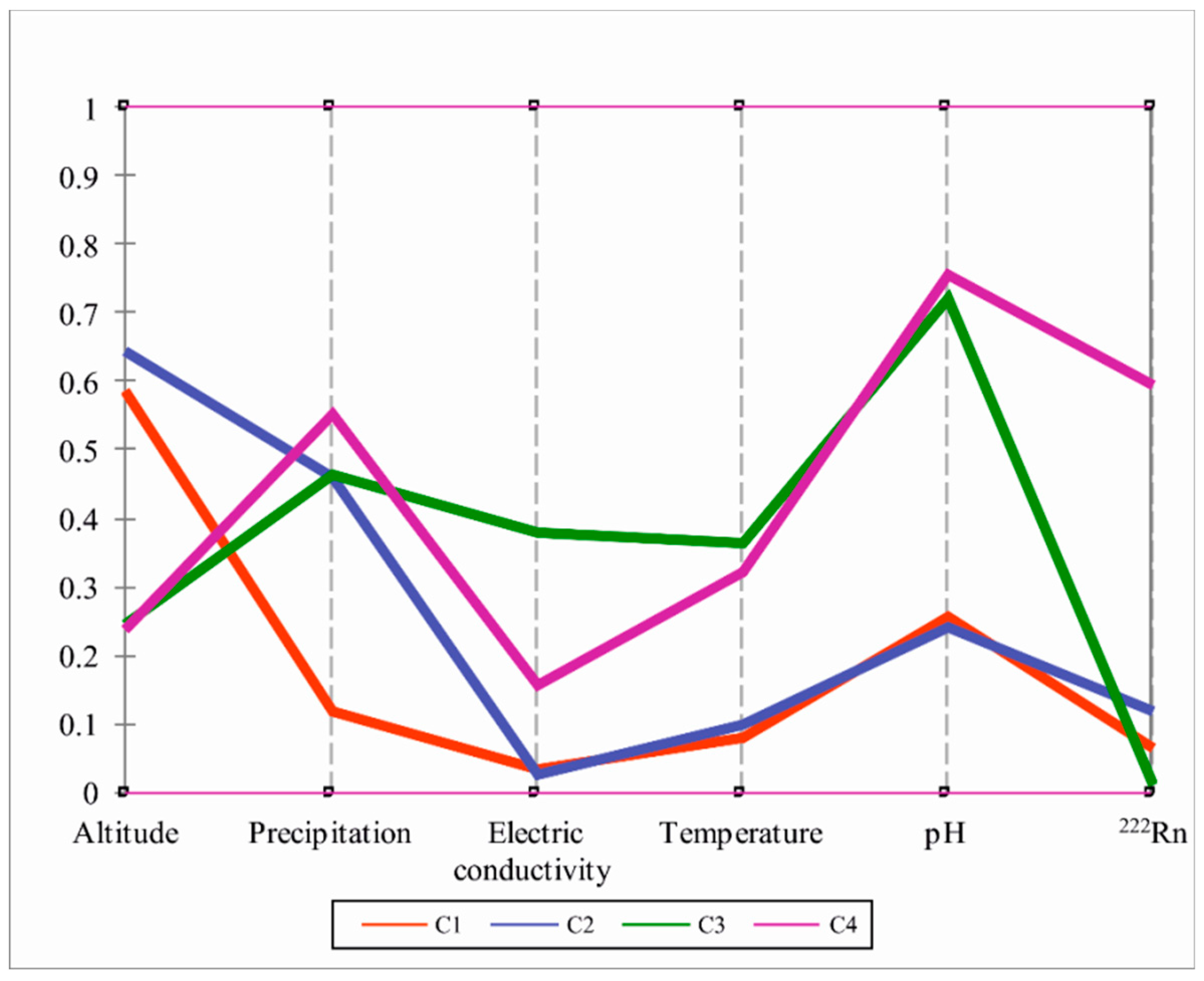
4.1. Clustering Analysis
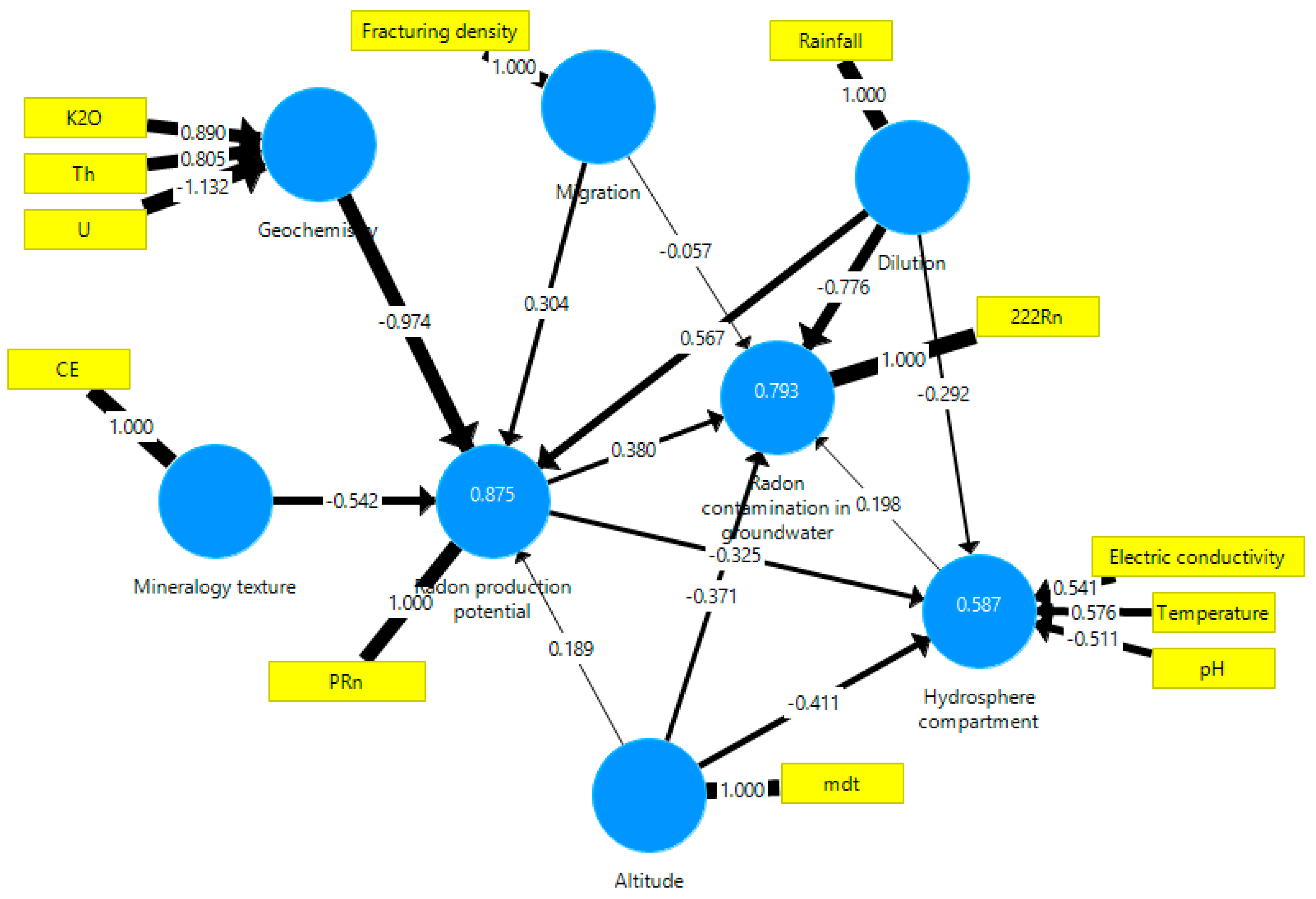
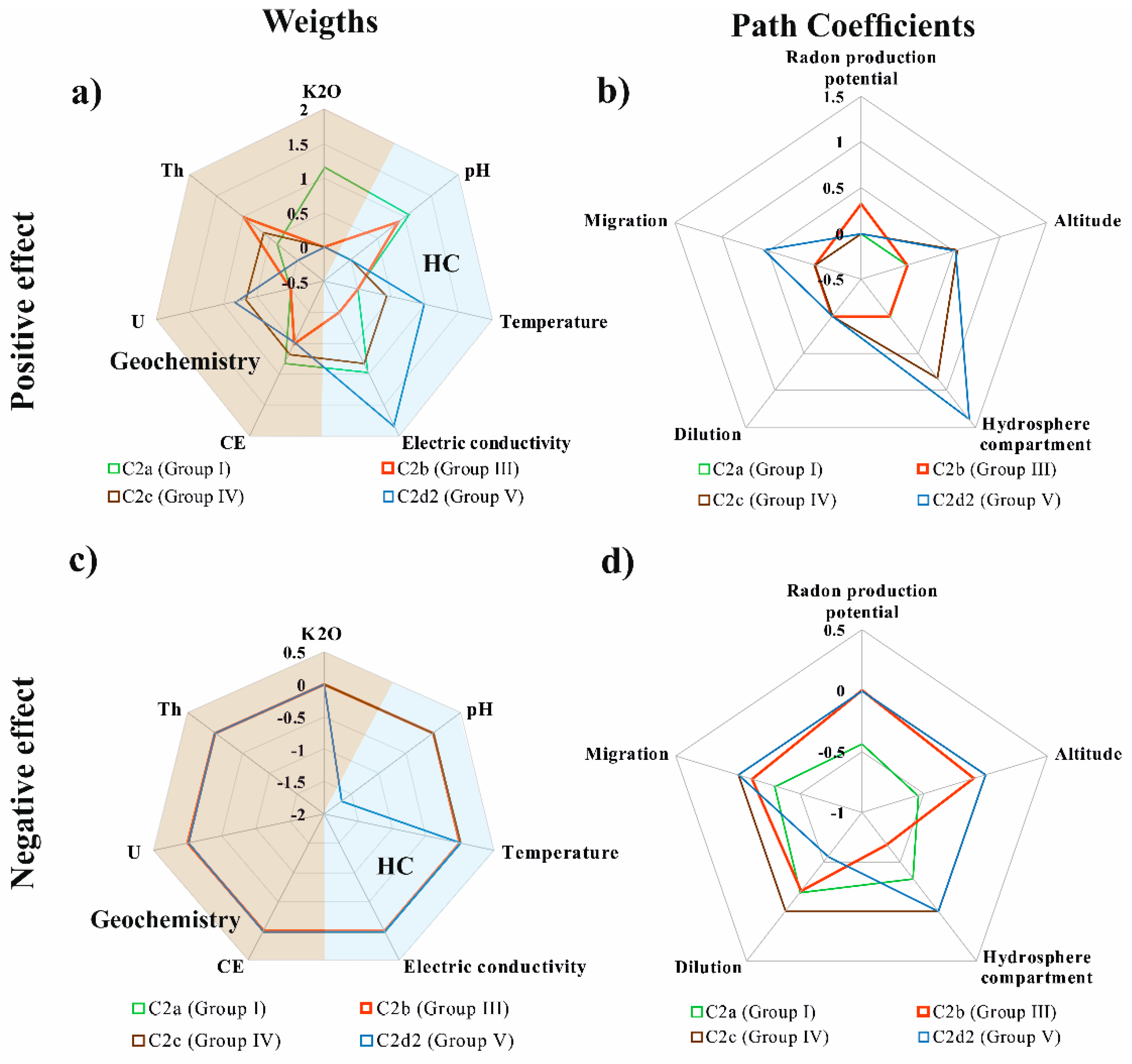
4.2. Partial Least Squares-Path Modeling
4.2.1. Cluster C1 Composed by Metasediments and Granites (n = 12)
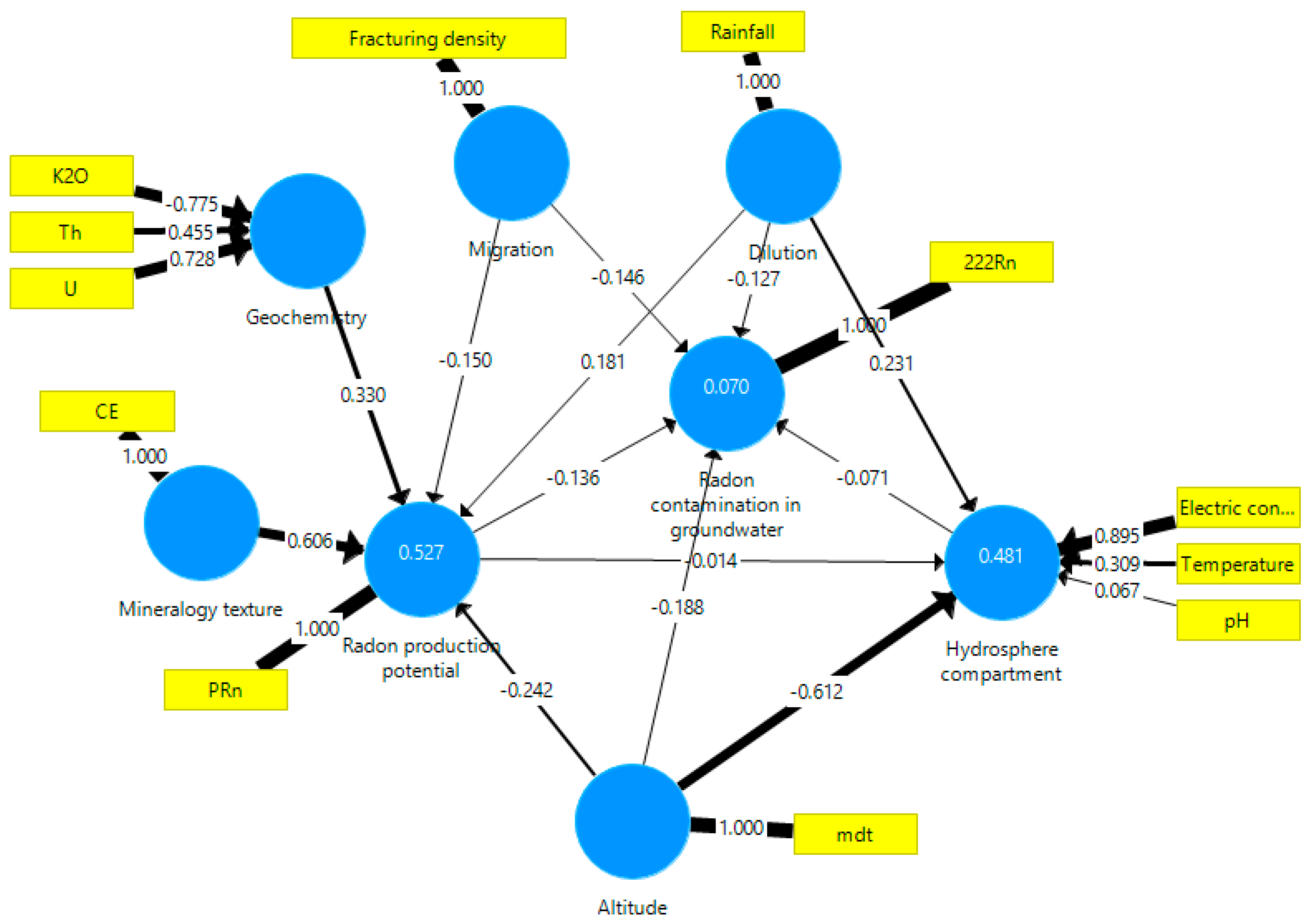
4.2.2. Cluster C2 Composed by Metasediments and Granites (n = 60)
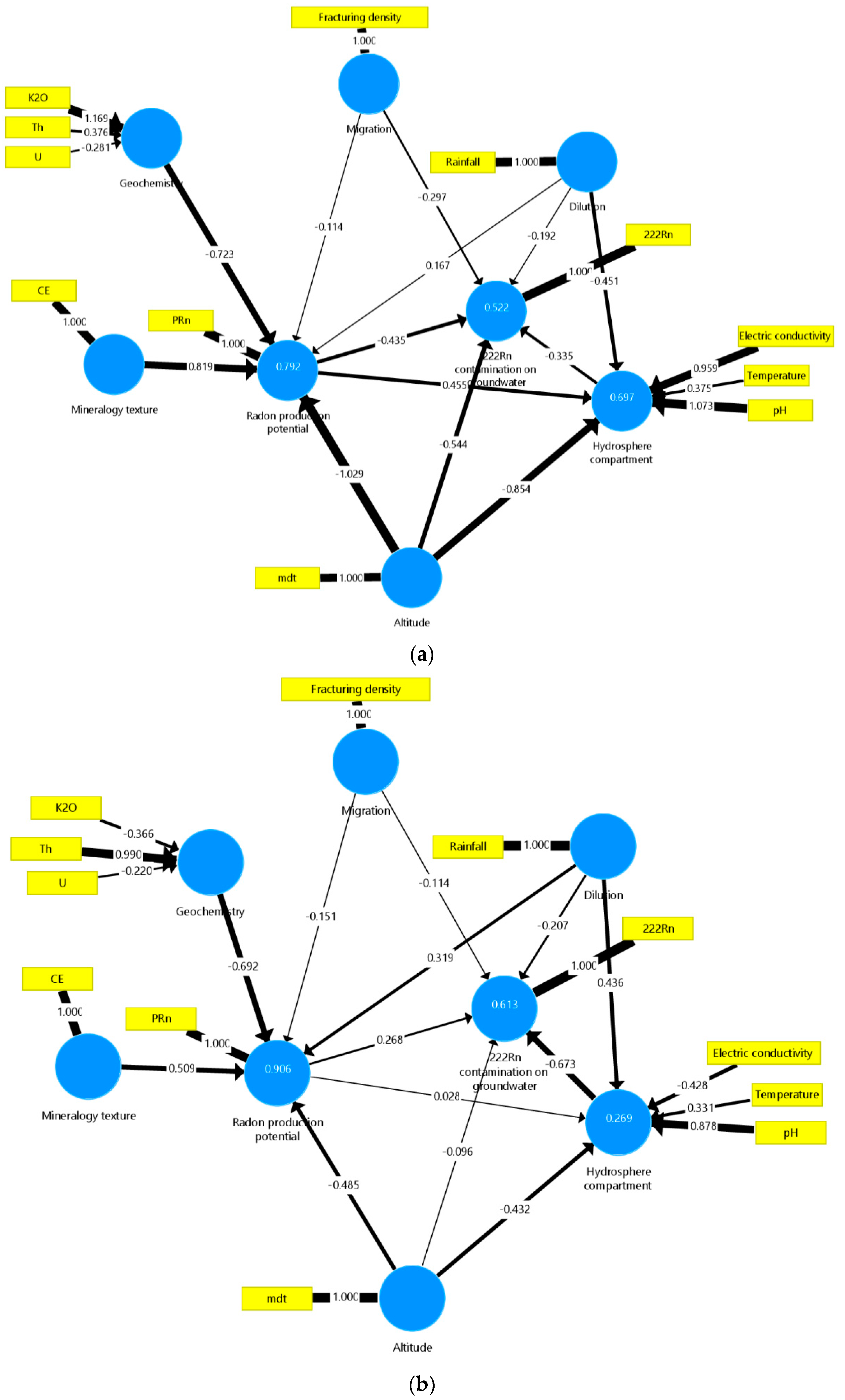
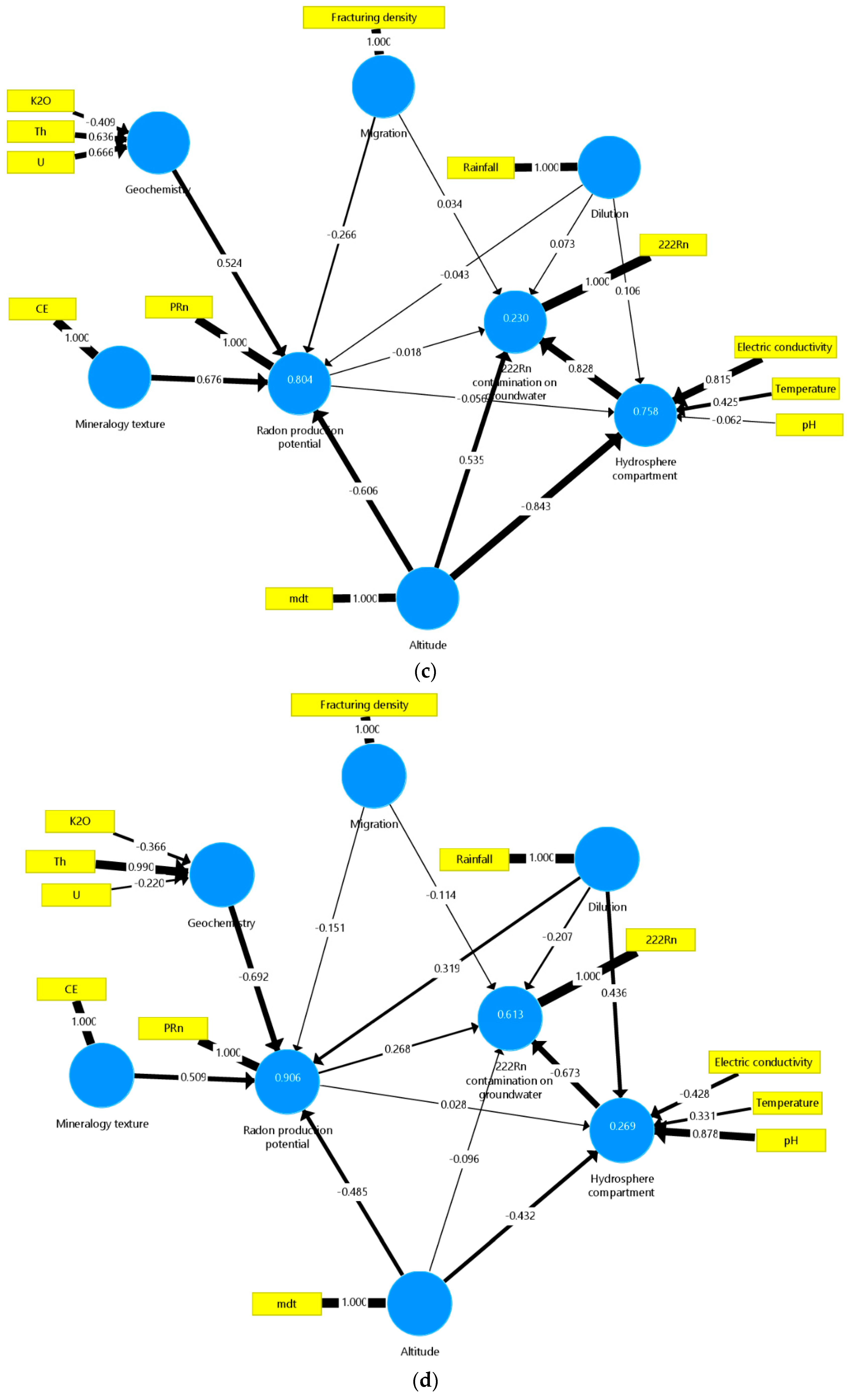
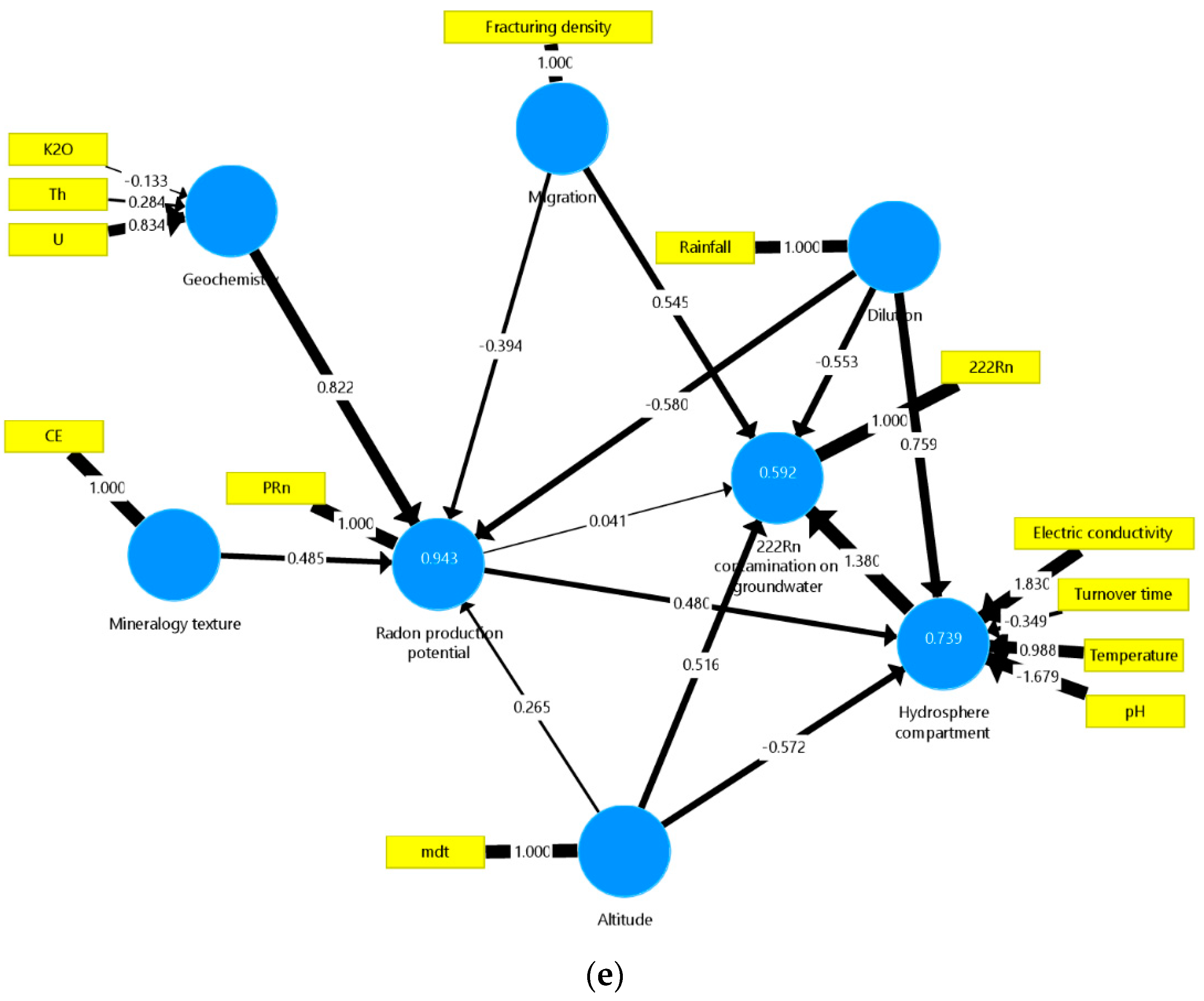
5. Discussion
5.1. General Analysis of HAC and PCV Plot Results
5.2. General Analysis of PLS-PM Results
5.3. Management Guidelines
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Council Directive 2013/51/Euratom. Of 22 October 2013, laying down requirements for the protection of the health of the general public with regard to radioactive substances in water intended for human consumption. Off. J. Eur. Union 2013, 296, 12–21. [Google Scholar]
- Do Ambiente, M.; do Território e Energia, O. Despacho n.o 4859/2015 de 27 de Janeiro de 2015; Direção-Geral de Energia e Geologia: Lisboa, Portugal, 2015; pp. 11477–11478. (In Portuguese) [Google Scholar]
- Kim, S.H.; Hwang, W.J.; Cho, J.S.; Kang, D.R. Attributable risk of lung cancer deaths due to indoor radon exposure. Ann. Occup. Environ. Med. 2016, 28, 8–11. [Google Scholar] [CrossRef] [PubMed]
- Hespanhol, V.; Parente, B.; Araújo, A.; Cunha, J.; Fernandes, A.; Figueiredo, M.M.; Neveda, R.; Soares, M.; João, F.; Queiroga, H. Cancro do pulmão no norte de Portugal: Um estudo de base hospitalar. Rev. Port. Pneumol. 2013, 19, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Choubey, V.M.; Sharma, K.K.; Ramola, R.C. Geology of radon occurrence around Jari in Parvati Valley, Himachal Pradesh, India. J. Environ. Radioact. 1997, 34, 139–147. [Google Scholar] [CrossRef]
- Salih, M.M.I.; Pettersson, H.B.L.; Lund, E. Uranium and Thorium series radionuclides in drinking water from drilled bedrock wells: Correlation to geology and bedrock radioactivity and dose estimation. Radiat. Prot. Dosim. 2002, 102, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Kruger, P.; Stoker, A.; Umaña, A. Radon in geothermal reservoir engineering. Geothermics 1977, 5, 13–19. [Google Scholar] [CrossRef][Green Version]
- Nikolopoulos, D.; Vogiannis, E.; Louizi, A. Radon concentration of waters in Greece and Cyprus. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 19–24 April 2009; Volume 11, p. 3786. [Google Scholar]
- Roba, C.A.; Codrea, V.; Moldovan, M.; Baciu, C.; Cosma, C. Radon and radium content of some cold and thermal aquifers from Bihor County (northwestern Romania). Geofluids 2010, 10, 571–585. [Google Scholar] [CrossRef]
- Sturchio, N.C.; Banner, J.L.; Binz, C.M.; Heraty, L.B.; Musgrove, M. Radium geochemistry of ground waters in Paleozoic carbonate aquifers, midcontinent, USA. Appl. Geochem. 2001, 16, 109–122. [Google Scholar] [CrossRef]
- Vengosh, A.; Hirschfeld, D.; Vinson, D.; Dwyer, G.; Raanan, H.; Rimawi, O.; Al-Zoubi, A.; Akkawi, E.; Marie, A.; Haquin, G.; et al. High naturally occurring radioactivity in fossil groundwater from the middle east. Environ. Sci. Technol. 2009, 43, 1769–1775. [Google Scholar] [CrossRef]
- Vinson, D.S.; Vengosh, A.; Hirschfeld, D.; Dwyer, G.S. Relationships between radium and radon occurrence and hydrochemistry in fresh groundwater from fractured crystalline rocks, North Carolina (USA). Chem. Geol. 2009, 260, 159–171. [Google Scholar] [CrossRef]
- Zukin, J.G.; Hammond, D.E.; Teh-Lung, K.; Elders, W.A. Uranium-thorium series radionuclides in brines and reservoir rocks from two deep geothermal boreholes in the Salton Sea Geothermal Field, southeastern California. Geochim. Cosmochim. Acta 1987, 51, 2719–2731. [Google Scholar] [CrossRef]
- Roba, C.A.; Niţǎ, D.; Cosma, C.; Codrea, V.; Olah, Ş. Correlations between radium and radon occurrence and hydrogeochemical features for various geothermal aquifers in Northwestern Romania. Geothermics 2012, 42, 32–46. [Google Scholar] [CrossRef]
- Ciotoli, G.; Voltaggio, M.; Tuccimei, P.; Soligo, M.; Pasculli, A.; Beaubien, S.E.; Bigi, S. Geographically weighted regression and geostatistical techniques to construct the geogenic radon potential map of the Lazio region: A methodological proposal for the European Atlas of Natural Radiation. J. Environ. Radioact. 2017, 166, 355–375. [Google Scholar] [CrossRef]
- Appleton, J.D.; Miles, J.C.H. A statistical evaluation of the geogenic controls on indoor radon concentrations and radon risk. J. Environ. Radioact. 2010, 101, 799–803. [Google Scholar] [CrossRef] [PubMed]
- Cinelli, G.; Tositti, L.; Capaccioni, B.; Brattich, E.; Mostacci, D. Soil gas radon assessment and development of a radon risk map in Bolsena, Central Italy. Environ. Geochem. Health 2015, 37, 305–319. [Google Scholar] [CrossRef]
- Dubois, G.A.G. An Overview of Radon Surveys in Europe; Office for Official Publications of the European Community: Luxembourg, 2005. [Google Scholar]
- Drolet, J.P.; Martel, R.; Poulin, P.; Dessau, J.C. Methodology developed to make the Quebec indoor radon potential map. Sci. Total Environ. 2014, 473–474, 372–380. [Google Scholar] [CrossRef]
- Friedmann, H.; Gröller, J. An approach to improve the Austrian radon potential map by bayesian statistics. J. Environ. Radioact. 2010, 101, 804–808. [Google Scholar] [CrossRef] [PubMed]
- Gruber, V.; Bossew, P.; De Cort, M.; Tollefsen, T. The European map of the geogenic radon potential. J. Radiol. Prot. 2013, 33, 51–60. [Google Scholar] [CrossRef]
- Hwang, J.; Kim, T.; Kim, H.; Cho, B.; Lee, S. Predictive radon potential mapping in groundwater: A case study in Yongin, Korea. Environ. Earth Sci. 2017, 76, 515. [Google Scholar] [CrossRef]
- Kitto, M.E.; Green, J.G. Mapping the indoor radon potential in New York at the township level. Atmos. Environ. 2008, 42, 8007–8014. [Google Scholar] [CrossRef]
- Kropat, G.; Bochud, F.; Jaboyedoff, M.; Laedermann, J.P.; Murith, C.; Palacios, M.; Baechler, S. Improved predictive mapping of indoor radon concentrations using ensemble regression trees based on automatic clustering of geological units. J. Environ. Radioact. 2015, 147, 51–62. [Google Scholar] [CrossRef]
- Zhukovsky, M.; Yarmoshenko, I.; Kiselev, S. Combination of geological data and radon survey results for radon mapping. J. Environ. Radioact. 2012, 112, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Bossew, P.; Cinelli, G.; Tollefsen, T.; Cort, M.D. The geogenic radon hazard index-another attempt. In Proceedings of the IWEANR 2017, 2nd International Workshop on the European Atlas of Natural Radiation, Verbania, Italy, 6–9 November 2017; p. 22. [Google Scholar]
- Pereira, A.J.S.C.; Neves, L.J.P.F. Geogenic controls of indoor radon in Western Iberia. In Proceedings of the 10th International Workshop on Radon Risk Mapping, Prague, Czech Republic, 22–25 September 2010; pp. 205–210. [Google Scholar]
- Galán López, M.; Martín Sánchez, A. Present status of 222Rn in groundwater in Extremadura. J. Environ. Radioact. 2008, 99, 1539–1543. [Google Scholar] [CrossRef]
- Moreno, V.; Bach, J.; Zarroca, M.; Font, L.; Roqué, C.; Linares, R. Characterization of radon levels in soil and groundwater in the North Maladeta Fault area (Central Pyrenees) and their effects on indoor radon concentration in a thermal spa. J. Environ. Radioact. 2018, 189, 1–13. [Google Scholar] [CrossRef]
- Costa, M.R.; Pereira, A.J.S.C.; Neves, L.J.P.F.; Ferreira, A. Potential human health impact of groundwater in non-exploited uranium ores: The case of Horta da Vilariça (NE Portugal). J. Geochem. Explor. 2017, 183, 191–196. [Google Scholar] [CrossRef]
- Choubey, V.M.; Mukherjee, P.K.; Bajwa, B.S.; Walia, V. Geological and tectonic influence on water-soil-radon relationship in Mandi-Manali area, Himachal Himalaya. Environ. Geol. 2007, 52, 1163–1171. [Google Scholar] [CrossRef]
- Martins, L.M.O.; Gomes, M.E.P.; Neves, L.J.P.F.; Pereira, A.J.S.C. The influence of geological factors on radon risk in groundwater and dwellings in the region of Amarante (Northern Portugal). Environ. Earth Sci. 2013, 68, 733–740. [Google Scholar] [CrossRef]
- Tsunomori, F.; Shimodate, T.; Ide, T.; Tanaka, H. Radon concentration distributions in shallow and deep groundwater around the Tachikawa fault zone. J. Environ. Radioact. 2017, 172, 106–112. [Google Scholar] [CrossRef] [PubMed]
- Yun, U.; Kim, T.S.; Kim, H.K.; Kim, M.S.; Cho, S.Y.; Choo, C.O.; Cho, B.W. Natural radon reduction rate of the community groundwater system in South Korea. Appl. Radiat. Isot. 2017, 126, 23–25. [Google Scholar] [CrossRef]
- Telahigue, F.; Agoubi, B.; Souid, F.; Kharroubi, A. Groundwater chemistry and radon-222 distribution in Jerba Island, Tunisia. J. Environ. Radioact. 2018, 182, 74–84. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Van der Weijden, C.H. Modeling rock weathering in small watersheds. J. Hydrol. 2014, 513, 13–27. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Van der Weijden, C.H. Role of hydraulic diffusivity in the decrease of weathering rates over time. J. Hydrol. 2014, 512, 87–106. [Google Scholar] [CrossRef]
- Alencoão, A.N.A.M.P.; Pacheco, F.A.L. Infiltration in the Corgo River basin (northern Portugal): Coupling water balances with rainfall—Runoff regressions on a monthly basis. Hydrol. Sci. J. 2006, 51, 989–1005. [Google Scholar] [CrossRef][Green Version]
- Pacheco, F.A.L.; Van der Weijden, C.H. Integrating topography, hydrology and rock structure in weathering rate models of spring watersheds. J. Hydrol. 2012, 428–429, 32–50. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Van Der Weijden, C.H. Mineral weathering rates calculated from spring water data: A case study in an area with intensive agriculture, the Morais Massif, northeast Portugal. Appl. Geochem. 2002, 17, 583–603. [Google Scholar] [CrossRef]
- Åkerblom, G.; Mellander, H. Geology and radon. In Radon Measurements by Etched Track Detectors; World Scientific Pub. Co. Pte. Ltd.: Singapore, Singapore, 1997; pp. 21–49. [Google Scholar]
- LNEG Laboratório Nacional de Energia e Geologia. geoPortal do LNEG. A Cartografia ao Serviço do Conhecimento do Território. Available online: http://geoportal.lneg.pt/geoportal/mapas/index.html?lg=pt (accessed on 13 December 2018).
- Ribeiro, A.; Pereira, E.; Dias, R. Structure in the northwest of the Iberian Peninsula. In Pre-Mesozoic Geology of Iberia; Dallmeyer, R.D., Martínez-García, E., Eds.; Springer: Dordrecht, The Netherlands, 1990; pp. 220–246. [Google Scholar]
- Dias, G.; Noronha, F.; Almeida, A.; Simões, P.P.; Martins, H.C.B.; Ferreira, N. Geocronologia e petrogénese do plutonismo tardi-Varisco (NW de Portugal): Síntese e inferências sobre os processos de acreção e reciclagem crustal na Zona Centro-Ibérica. In Ciências Geológicas—Ensino e Investigação e sua História; Associação Portuguesa de Geólogos e Sociedade Geológica de Portugal: Lisboa, Portugal, 2010; pp. 143–160. [Google Scholar]
- Sistema Nacional de Informação de Recursos Hídricos. Available online: http://snirh.apambiente.pt/ (accessed on 16 January 2019).
- Pacheco, F.A.L. Hidrogeologia em Maciços de Rochas Cristalinas (Morais-Chacim-Macedo de Cavaleiros): Bases para a Gestão Integrada dos Recursos Hídricos da Região. Ph.D. Thesis, Trás-os-Montes e Alto Douro University, Vila Real, Portugal, 2000. [Google Scholar]
- Meireles, C. Carta Geológica de Portugal na Escala 1/50 000 e notícia explicativa da Folha 3-D (Espinhosela); Instituto geológico e Mineiro: Lisboa, Portugal, 2000. [Google Scholar]
- Pereira, E. Coord Carta Geológica de Portugal, Escala 1:200 000, Folha 2; Instituto geológico e Mineiro: Lisboa, Portugal, 2000. [Google Scholar]
- Ribeiro, A. Contribuition à l’étude tectonique de Trás-os-Montes Oriental. Mem. 24 Serv. Geol. Port. 1974, 168. [Google Scholar]
- Ribeiro, M.A. Estudo Litogeoquímico das Formações Metassedimentares Encaixantes de Mineralizações em Trás-os-Montes Ocidental. Ph.D. Thesis, Oporto University, Oporto, Portugal, 1998. [Google Scholar]
- Rodrigues, J.F.S. Estrutura do Arco da Serra de Santa Comba-Serra da Garraia: Parautóctone de Trás-os-Montes. Ph.D. Thesis, Lisbon University, Lisbon, Portugal, 2008. [Google Scholar]
- Quesada, C. Geological constraints on the Paleozoic tectonic evolution of tectonostratigraphic terranes in the Iberian Massif. Tectonophysics 1991, 185, 225–245. [Google Scholar] [CrossRef]
- Gomes, M.; Ferreira, N.; Rodrigues, F.; Pires, C.; Matos, A.; Lourenço, J.; Pereira, A.; Teixeira, R.; Ribeiro, A. Carta Geológica de Portugal à escala 1: 50000, folha 10-B Vila Real; Laboratório Nacional de Energia e Geologia: Lisboa, Portugal, 2015. [Google Scholar]
- Dias, R.; Ribeiro, A.; Coke, C.; Pereira, E.; Rodrigues, J.; Castro, P.; Moreira, N.; Rebelo, J. Evolução estrutural dos sectores setentrionais do Autóctone da Zona Centro-Ibérica. In Geologia Pré-Mesozóica de Portugal; Dias, R., Araújo, A., Terrinha, P., Kullberg, J.C., Eds.; Escolar Editora: Lisboa, Portugal, 2013; pp. 403–438. [Google Scholar]
- Pereira, D.I. Características e Evolução do relevo e da drenagem no Norte de Portugal. In Geologia Clássica, Ciências Geológicas. Ensino, Investigação e sua História. Publicação Comemorativa do Ano Internacional do Planeta Terra; Neiva, J.M.C., Ribeiro, A., Victor, L.M., Noronha, F., Ramalho, M.M., Eds.; Associação Portuguesa de Geólogos: Lisboa, Portugal, 2010; pp. 491–500. [Google Scholar]
- Pereira, D.I. Sedimentologia e Estratigrafia do Cenozóico de Trás-os-Montes oriental (NE Portugal). Ph.D. Thesis, Minho University, Minho, Portugal, 1997. [Google Scholar]
- Martins, L.M.O. Controlo geológico e mineralógico da radioatividade natural: Um estudo na região de Trás-os-Montes e Alto Douro. Ph.D. Thesis, Trás-os-Montes e Alto Douro University, Vila Real, Portugal, 2017. [Google Scholar]
- Martins, L.; Pereira, A.; Oliveira, A.; Sanches Fernandes, L.F.; Pacheco, F.A.L.; Martins, L.; Pereira, A.; Oliveira, A.; Sanches Fernandes, L.F.; Pacheco, F.A.L. A new framework for the management and radiological protection of groundwater resources: The implementation of a portuguese action plan for radon in drinking water and impacts on human health. Water 2019, 11, 760. [Google Scholar] [CrossRef]
- Pereira, A.; Lamas, R.; Miranda, M.; Domingos, F.; Neves, L.; Ferreira, N.; Costa, L. Estimation of the radon production rate in granite rocks and evaluation of the implications for geogenic radon potential maps: A case study in Central Portugal. J. Environ. Radioact. 2017, 166, 270–277. [Google Scholar] [CrossRef]
- ASTM D 50721-98. Standard Test Method for Radon in Drinking Water; 1998; Available online: https://www.astm.org/Standards/D5072.htm (accessed on 25 May 2014).
- Pereira, A.J.S.C.; Pereira, M.D.; Neves, L.J.P.F.; Azevedo, J.M.M.; Campos, A.B.A. Evaluation of groundwater quality based on radiological and hydrochemical data from two uraniferous regions of Western Iberia: Nisa (Portugal) and Ciudad Rodrigo (Spain). Environ. Earth Sci. 2015, 73, 2717–2731. [Google Scholar] [CrossRef]
- Belloni, P.; Ingrao, G.; Santaroni, G.P.; Torri, G.; Vasselli, R. Misure di 222Rn in alcune acque potabili mediante scintillazione liquida quale contributo al calcolo della dose. In Proceedings of the Atti del 5° Convegno su Metodologie Radiochimiche e Radiometriche in Radioprotezione, Urbino, Italy, 20–22 June 1995; pp. 181–186. [Google Scholar]
- Pacheco, F.A.L. Regional groundwater flow in hard rocks. Sci. Total Environ. 2015, 506–507, 182–195. [Google Scholar] [CrossRef] [PubMed]
- Shamshirband, S.; Nodoushan, E.J.; Adolf, J.E.; Manaf, A.A.; Mosavi, A.; Chau, K. Ensemble models with uncertainty analysis for multi-day ahead forecasting of chlorophyll a concentration in coastal waters. Eng. Appl. Comput. Fluid Mech. 2019, 13, 91–101. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Chau, K. A review on integration of artificial intelligence into water quality modelling. Mar. Pollut. Bull. 2006, 52, 726–733. [Google Scholar] [CrossRef] [PubMed]
- Gholami, V.; Chau, K.W.; Fadaee, F.; Torkaman, J.; Ghaffari, A. Modeling of groundwater level fluctuations using dendrochronology in alluvial aquifers. J. Hydrol. 2015, 529, 1060–1069. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R.; Danesh, M.; Adolf, J.; Shamshirband, S.; Chau, K.-W. Effect of river flow on the quality of estuarine and coastal waters using machine learning models. Eng. Appl. Comput. Fluid Mech. 2018, 12, 810–823. [Google Scholar] [CrossRef]
- Choubey, V.M.; Ramola, R.C. Correlation between geology and radon levels in groundwater, soil and indoor air in Bhilangana Valley, Garhwal Himalaya, India. Environ. Geol. 1997, 32, 258–262. [Google Scholar] [CrossRef]
- Alonso, H.; Cruz-Fuentes, T.; Rubiano, J.; González-Guerra, J.; Cabrera, M.; Arnedo, M.; Tejera, A.; Rodríguez-Gonzalez, A.; Pérez-Torrado, F.; Martel, P. Radon in groundwater of the northeastern gran canaria aquifer. Water 2015, 7, 2575–2590. [Google Scholar] [CrossRef]
- Hands, S.; Everitt, B. A monte carlo study of the recovery of cluster structure in binary data by hierarchical clustering techniques. Multivar. Behav. Res. 1987, 22, 235–243. [Google Scholar] [CrossRef]
- Blashfield, R.K. Mixture model tests of cluster analysis: Accuracy of four agglomerative hierarchical methods. Psychol. Bull. 1976, 83, 377–388. [Google Scholar] [CrossRef]
- Mooi, E.; Sarstedt, M. A Concise Guide to Market Research the Process, Data, and Methods Using IBM SPSS Statistics Introduction to Market Research; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 9783642125416. [Google Scholar]
- Wold, H. Estimation of Principal Components and Related Models by Iterative Least Squares; Devices, E., Mccumber, D.E., Chynoweth, A.G., Foyt, A.G., Elschner, B., Schlaak, M., Eds.; Acad. Press: New York, NY, USA, 1966; Volume 24, pp. 10–12. [Google Scholar]
- Wold, H. Soft modelling: Intermediate between traditional model building and data analysis. Banach Cent. Publ. 1980, 6, 333–346. [Google Scholar] [CrossRef]
- Ringle, C.M.; Wende, S.; Will, A. Smart PLS. 2015. Available online: http://www.smartpls.deHamburg,Ger (accessed on 3 January 2019).
- Boccuzzo, G.; Fordellone, M. Comments about the use of PLS path modeling in building a job quality composite indicator. Univ. Padua 2015. [Google Scholar] [CrossRef]
- Hair, J.F.; Hult, T.; Ringle, C.; Sarstedt, M. A Primer on Partial Least Squares Structural Equation Modeling; SAGE Publications, Inc.: Newbury Park, CA, USA, 2014; ISBN 1452217440. [Google Scholar]
- Monecke, A.; Leisch, F. semPLS: Structural equation modeling using partial least squares. J. Stat. Softw. 2012, 48, 1–32. [Google Scholar] [CrossRef]
- McIntosh, C.N.; Edwards, J.R.; Antonakis, J. Reflections on partial least squares path modeling. Organ. Res. Methods 2014, 17, 210–251. [Google Scholar] [CrossRef]
- Coltman, T.; Devinney, T.M.; Midgley, D.F.; Venaik, S. Formative versus reflective measurement models: Two applications of formative measurement. J. Bus. Res. 2008, 61, 1250–1262. [Google Scholar] [CrossRef]
- Lohmöller, J.-B. Latent Variable Path Modeling with Partial Least Squares; Physica-Verlag: Heidelberg, Germany, 1989. [Google Scholar]
- Garson, G.D. Partial Least Squares: Regression and Structural Equation Models; Tatistical Associates Publishers: Asheboro, NC, USA, 2016. [Google Scholar]
- ESRI ArcMap (version 10); ESRI Portugal: Lisboa, Portugal, 2010.
- Fernandes, L.F.S.; Terêncio, D.P.S.; Pacheco, F.A.L. Rainwater harvesting systems for low demanding applications. Sci. Total Environ. 2015, 529, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, F.A.L.; Santos, R.M.B.; Fernandes, L.F.S.; Pereira, M.G.; Cortes, R.M.V. Controls and forecasts of nitrate yields in forested watersheds: A view over mainland Portugal. Sci. Total Environ. 2015, 537, 421–440. [Google Scholar] [CrossRef] [PubMed]
- Santos, R.M.B.; Fernandes, L.F.S.; Pereira, M.G.; Cortes, R.M.V.; Pacheco, F.A.L. Water resources planning for a river basin with recurrent wildfires. Sci. Total Environ. 2015, 526, 1–13. [Google Scholar] [CrossRef]
- Santos, R.M.B.; Fernandes, L.F.S.; Cortes, R.M.V.; Varandas, S.G.P.; Jesus, J.J.B.; Pacheco, F.A.L. Integrative assessment of river damming impacts on aquatic fauna in a Portuguese reservoir. Sci. Total Environ. 2017, 601–602, 1108–1118. [Google Scholar] [CrossRef] [PubMed]
- Terêncio, D.P.S.; Fernandes, L.F.S.; Cortes, R.M.V.; Pacheco, F.A.L. Improved framework model to allocate optimal rainwater harvesting sites in small watersheds for agro-forestry uses. J. Hydrol. 2017, 550, 318–330. [Google Scholar] [CrossRef]
- Terêncio, D.P.S.; Fernandes, L.F.S.; Cortes, R.M.V.; Moura, J.P.; Pacheco, F.A.L. Rainwater harvesting in catchments for agro-forestry uses: A study focused on the balance between sustainability values and storage capacity. Sci. Total Environ. 2018, 613–614, 1079–1092. [Google Scholar] [CrossRef]
- Valera, C.A.; Valle Junior, R.F.; Varandas, S.G.P.; Fernandes, L.F.S.; Pacheco, F.A.L. The role of environmental land use conflicts in soil fertility: A study on the Uberaba River basin, Brazil. Sci. Total Environ. 2016, 562, 463–473. [Google Scholar] [CrossRef] [PubMed]
- Valera, C.A.; Pissarra, T.C.T.; Filho, M.V.M.; Junior, R.F.V.; Fernandes, L.F.S.; Pacheco, F.A.L. A legal framework with scientific basis for applying the ‘polluter pays principle’ to soil conservation in rural watersheds in Brazil. Land Use Policy 2017, 66, 61–71. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Fernandes, L.F.S. Environmental land use conflicts in catchments: A major cause of amplified nitrate in river water. Sci. Total Environ. 2016, 548–549, 173–188. [Google Scholar] [CrossRef]
- Bellu, A.; Fernandes, L.F.S.; Cortes, R.M.V.; Pacheco, F.A.L. A framework model for the dimensioning and allocation of a detention basin system: The case of a flood-prone mountainous watershed. J. Hydrol. 2016, 533, 567–580. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Martins, L.M.O.; Quininha, M.; Oliveira, A.S.; Sanches Fernandes, L.F. An approach to validate groundwater contamination risk in rural mountainous catchments: The role of lateral groundwater flows. MethodsX 2018, 5, 1447–1455. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Martins, L.M.O.; Quininha, M.; Oliveira, A.S.; Fernandes, L.F.S. Modification to the DRASTIC framework to assess groundwater contaminant risk in rural mountainous catchments. J. Hydrol. 2018, 566, 175–191. [Google Scholar] [CrossRef]
- Fernandes, L.F.S.; dos Santos, C.M.M.; Pereira, A.P.; Moura, J.P. Model of management and decision support systems in the distribution of water for consumption. Eur. J. Environ. Civ. Eng. 2011, 15, 411–426. [Google Scholar] [CrossRef]
- Fernandes, L.F.S.; Seixas, F.J.; Oliveira, P.C.; Leitão, S.; Moura, J.P. Climate-change impacts on nitrogen in a hydrographical Basin in the northeast of Portugal. Fresenius Environ. Bull. 2012, 21, 3643–3650. [Google Scholar]
- Fernandes, L.F.S.; Marques, M.J.; Oliveira, P.C.; Moura, J.P. Decision support systems in water resources in the demarcated region of Douro—Case study in Pinhão river basin, Portugal. Water Environ. J. 2014, 28, 350–357. [Google Scholar] [CrossRef]
- Santos, R.M.B.; Fernandes, L.F.S.; Pereira, M.G.; Cortes, R.M.V.; Pacheco, F.A.L. A framework model for investigating the export of phosphorus to surface waters in forested watersheds: Implications to management. Sci. Total Environ. 2015, 536, 295–305. [Google Scholar] [CrossRef] [PubMed]
- Prasad, Y.; Prasad, G.; Choubey, V.M.; Ramola, R.C. Geohydrological control on radon availability in groundwater. Radiat. Meas. 2009, 44, 122–126. [Google Scholar] [CrossRef]
- Belgacem, A.; Souid, F.; Telahigue, F.; Kharroubi, A. Temperature and radon-222 as tracer of groundwater flow: Application to El Hamma geothermal aquifer system, southeastern Tunisia. Arab. J. Geosci. 2015, 8, 11161–11174. [Google Scholar] [CrossRef]
- Shende, S.; Chau, K. Forecasting safe distance of a pumping well for effective riverbank filtration. J. Hazard. Toxic Radioact. Waste 2019, 23, 04018040. [Google Scholar] [CrossRef]
- Cothern, C.R.; Smith, J.E.J. Environmental Radon. Environmental Science Research, 35; Springer Science and Business Media: New York, NY, USA, 1987. [Google Scholar]
- Vilaverde, A.L.A. Metodologias para a Delimitação de Áreas Preferenciais de Recarga em Aquíferos Fraturados. Master’s Thesis, Escola de Ciências, Minho University, Minho, Portugal, 2016. [Google Scholar]
- MCTES—Ministério da Ciência Tecnologia e Ensino Superior. Decreto-Lei n.o 23/2016 de 3 de Junho, Diário da República, 1.a série—N.o 107; MCTES—Ministério da Ciência Tecnologia e Ensino Superior: Lisboa, Portugal, 2016; pp. 1744–1751. (In Portuguese)
- EUR-Lex. Directive 2009/54/EC of the European Parliament and of the Council of 18 June 2009 on the Exploitation and Marketing of Natural Mineral Waters; EUR-Lex Home: Brussels, Belgium, 2009. [Google Scholar]
- EUR-Lex. Directive 2001/83/EC of the European Parliament and of the Council of 6 November2011 on the Community Code Relating to Medicinal Products for Human Use; EUR-Lex Home: Brussels, Belgium, 2001. [Google Scholar]
- World Health Organization. WHO Handbook on Indoor Radon: A Public Health Perspective; World Health Organization: Geneva, Switzerland, 2009; ISBN 9789241547673. [Google Scholar]

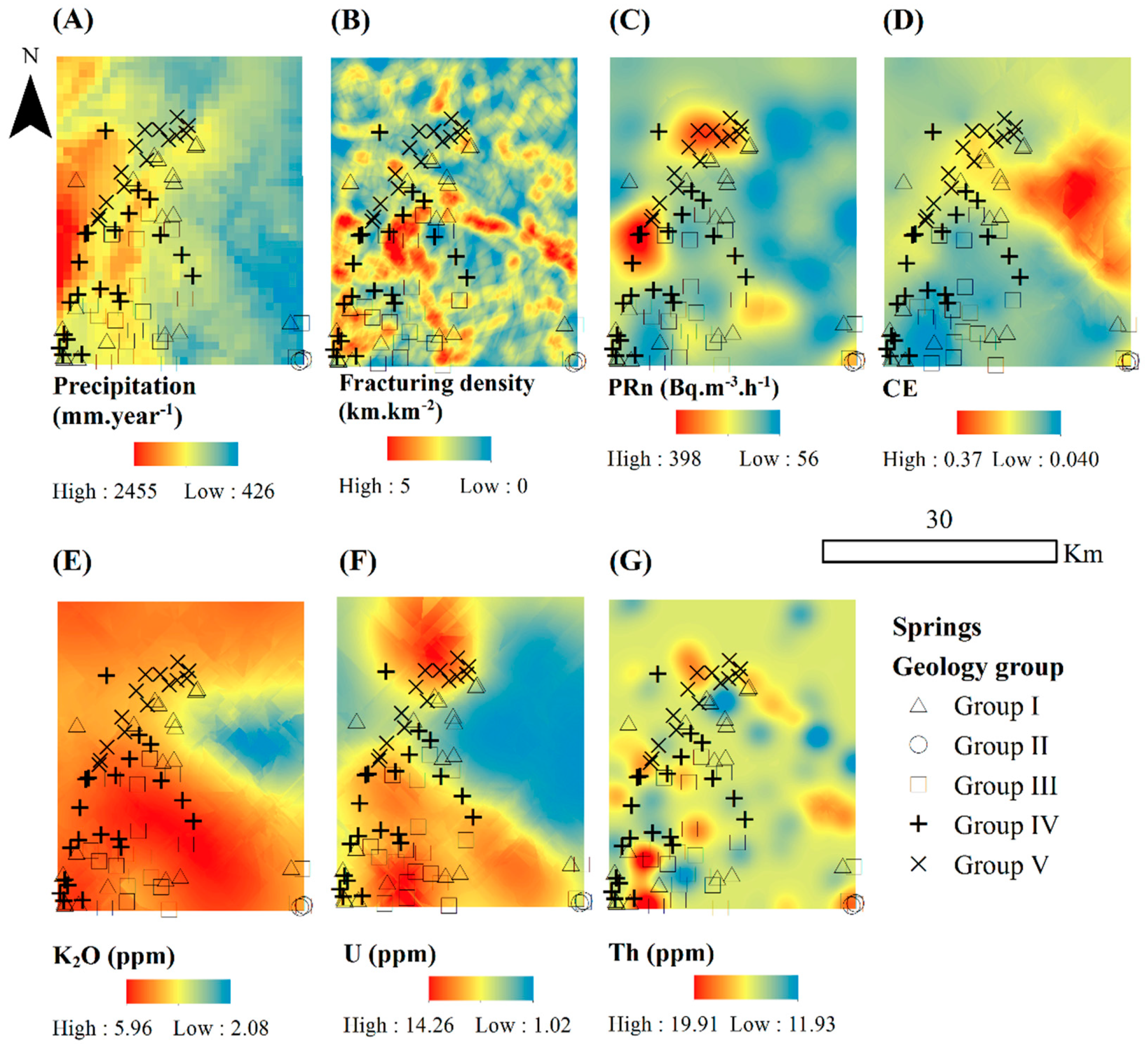
| Compartment Type | Measured Variable | n | HAC Classes | Units | Description | Source | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||||||
| Water 222Rn | 222Rn | 97 | x | x | x | x | Bq·L−1 | Radon potential data in groundwater from 97 monitoring | ||
| Geogenic compartment | Geochemistry | K2O | 119 | x | x | x | x | % | Measured radioactive potassium in 119 samples of rocks and soils of the studied area using a portable spectrometer | |
| U | 119 | x | x | x | x | ppm | Measured radioactive uranium in 119 samples of rocks and soils of the studied area | |||
| Th | 119 | x | x | x | x | ppm | Measured radioactive thorium in 119 samples of rocks and soils of the studied area | |||
| Mineralogy texture | CE | 119 | x | x | x | x | % | Mineralogy texture in 119 samples of rocks (emanation coefficient) | [57] | |
| Radon production potential | PRN | 119 | x | x | x | x | Bq·m−3·h−1 | Radon production potential in 119 samples of rocks of the studied area | [57] | |
| Hydrosphere compartment | Electric conductivity | 97 | x | x | x | x | µS·cm−1 | Electric conductivity data of 97 monitoring stations | ||
| Temperature | 97 | x | x | x | x | °C | Temperature data of 97 monitoring stations | |||
| pH | 97 | x | x | x | x | dimensionless | pH data of 97 monitoring stations | |||
| Altitude | mdt | 97 | x | x | x | x | m | Topography obtained from analysis of a digital elevation model (DEM) | DGT | |
| Migration | Fracturing density | * | x | x | x | x | km·km−2 | Possible migration of radon by fracturing density in rocks from entire studied area | [53] | |
| Dilution | Rainfall | * | x | x | x | x | mm·year−1 | Annual precipitation that may promote some dilution of radon in groundwater | Portuguese information on Water Resources | |
| Id_HAC Classes | Statistics Criteria | Altitude (m) | Precipitation (mm·year−1) | Electric Conductivity (µS·cm−1) | Temperature (°C) | pH | 222Rn (Bq·L−1) |
|---|---|---|---|---|---|---|---|
| Class 1 (n = 15) | µ ± σ | 657.3 ± 176.1 | 670.4 ± 102.4 | 109.8 ± 86.8 | 14.3 ± 1.7 | 5.7± 0.4 | 245.9 ± 230.7 |
| Med | 602.0 | 657.9 | 67.5 | 14.7 | 5.9 | 111.6 | |
| CV | 0.3 | 0.2 | 0.8 | 0.1 | 0.1 | 0.9 | |
| Min.–Max. | 440–1053.0 | 453.6–833.3 | 24.7–274.0 | 11.5–16.8 | 5.0–6.5 | 37.4–642.1 | |
| Class 2 (n = 65) | µ ± σ | 715.4 ± 169.3 | 1291.6 ± 221.1 | 88.8 ± 85.9 | 15.2 ± 2.6 | 5.7± 0.4 | 439.3 ± 380.5 |
| Med | 725.0 | 1286.9 | 51.6 | 15.0 | 5.6 | 342.3 | |
| CV | 0.2 | 0.2 | 1.0 | 0.2 | 0.1 | 0.9 | |
| Min.–Max. | 306.0–1078.0 | 901.9–2275.4 | 18.1–343.0 | 10.3–22.3 | 4.7–6.9 | 9.7–1520.7 | |
| Class 3 (n = 11) | µ ± σ | 305.4 ± 157.5 | 1298.4 ± 316.4 | 973.2 ± 725.6 | 28.0 ± 13.0 | 7.7 ± 1.0 | 49.8 ± 46.7 |
| Med | 284.0 | 1341.8 | 728.0 | 22.4 | 7.9 | 38.9 | |
| CV | 0.5 | 0.2 | 0.7 | 0.5 | 0.1 | 0.9 | |
| Min. –Max. | 54.0–594.0 | 538.0–1803.6 | 335.0–2520.0 | 15.4–58.8 | 6.1–8.9 | 0.6–172.2 | |
| Class 4 (n = 6) | µ ± σ | 297.8 ± 90.4 | 1463.1 ± 122.6 | 413.8 ± 39.0 | 26.0 ± 4.2 | 7.9 ± 0.4 | 2196.4 ± 802.0 |
| Med | 311.5 | 1456.6 | 408.0 | 27.0 | 7.9 | 1949.3 | |
| CV | 0.3 | 0.1 | 0.1 | 0.2 | 0.1 | 0.4 | |
| Min.–Max. | 163.0–396.0 | 1249.6–1642.1 | 364.0–485.0 | 17.8–31.1 | 7.1–8.3 | 1419.1–3687.7 |
| Line | Model | Equation |
|---|---|---|
| 1 | C1 | PRN = −0.542MT − 0.974G + 0.304M + 0.567D + 0.189A |
| 2 | C1 | HC = −0.292D − 0.325PRN − 0.411A |
| 3 | C1 | RN = 0.380PRN − 0.057M − 0.776D + 0.198HC − 0.371A |
| 4 | C2a | PRN = 0.819MT − 0.723G ± 0.114M + 0.167D − 1.029A |
| 5 | C2a | HC = −0.451D + 0.455PRN − 0.854A |
| 6 | C2a | RN = −0.435PRN − 0.297M − 0.192D − 0.335HC − 0.544A |
| 7 | C2b | PRN = 0.509MT − 0.692G − 0.151M + 0.319D − 0.485A |
| 8 | C2b | HC = 0.436D + 0.028PRN − 0.432A |
| 9 | C2b | RN = 0.268 PRN − 0.114M − 0.207D − 0.673HC − 0.096A |
| 10 | C2c | PRN = 0.676MT + 0.524G − 0.266M − 0.043D − 0.606A |
| 11 | C2c | HC = 0.106D − 0.056PRN − 0.843A |
| 12 | C2d1 | PRN = 0.426MT + 1.234G − 0.178M − 0.555D + 0.236A |
| 13 | C2d1 | HC = 0.821D − 0.413PRN − 0.180A |
| 14 | C2d2 | PRN = 0.485MT + 0.822G − 0.394M − 0.580 + 0.265A |
| 15 | C2d2 | HC = 0.759D + 0.480RN − 0.572A |
| 16 | C2d2 | RN = 0.041 PRN + 0.545M − 0.553D + 1.380HC + 0.516A |
| Id_HAC | Statistics Criteria | Altitude (m) | Precipitation (mm·year−1) | Electric Conductivity (µS·cm−1) | Temperature (°C) | pH | 222Rn (Bq·L−1) | PRn (Bq·m−3·h−1) | CE | K2O (%) | Th (ppm) | U (ppm) | Fracturing Density (km·km−2) | Turnover Time (years) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster 1 (n = 12) | µ ± σ | 707.3 ± 162.0 | 689.3 ± 93.9 | 76.4 ± 59.0 | 14.1 ± 1.7 | 5.7± 0.5 | 285.1 ± 242.6 | 165.6 ± 55.6 | 0.14 ± 0.06 | 5.0 ± 0.6 | 15.4 ± 1.4 | 7.4 ± 2.6 | 1.7 ± 0.7 | |
| Med | 670.5 | 677.7 | 53.5 | 14.4 | 5.6 | 216.0 | 152.2 | 0.13 | 5.0 | 15.0 | 8.4 | 1.7 | ||
| CV | 0.2 | 0.1 | 0.8 | 0.1 | 0.1 | 0.9 | 0.3 | 0.39 | 0.1 | 0.1 | 0.3 | 0.4 | ||
| Min.–Max. | 495.0–1053.0 | 581.1–833.3 | 24.7–235 | 11.5–16.8 | 5.0–6.5 | 37.0–642.0 | 100.3–313.2 | 0.06–0.22 | 4.2–5.7 | 13.4–18.4 | 2.7–11.3 | 0.4–2.7 | ||
| Cluster 2 (n = 60) | µ ± σ | 731.7 ± 147.4 | 1291.6 ± 221.1 | 85.4 ± 84.9 | 15.2 ± 2.6 | 5.7± 0.4 | 457.6 ± 387.3 | 189.3 ± 63.5 | 0.13 ± 0.04 | 5.2 ± 0.3 | 15.0 ± 0.9 | 8.3 ± 2.2 | 1.7 ± 0.7 | |
| Med | 734.5 | 1287.6 | 48.8 | 15.0 | 5.6 | 387.0 | 173.7 | 0.13 | 5.3 | 14.9 | 8.5 | 1.7 | ||
| CV | 0.2 | 0.2 | 1.0 | 0.2 | 0.1 | 0.8 | 0.3 | 0.28 | 0.1 | 0.1 | 0.3 | 0.4 | ||
| Min.–Max. | 306.0–1078.0 | 901.9–2275.4 | 18.1–343.0 | 10.3–22.3 | 4.7–6.9 | 14.0–1521.0 | 95.7–397.0 | 0.04–0.21 | 4.4–5.9 | 12.5–18.9 | 2.9–13.6 | 0.1–3.4 | ||
| Cluster 2a (Group I) (n = 11) | µ ± σ | 677.3 ± 183.6 | 1339.5 ± 347.5 | 120.7 ± 113.6 | 15.8 ± 3.0 | 5.6 ± 0.4 | 273.0 ± 298.4 | 159.9 ± 36.2 | 0.13 ± 0.04 | 5.1 ± 0.4 | 14.9 ± 0.5 | 6.9 ± 2.6 | 2.2 ± 0.5 | |
| Med | 701.0 | 1322.8 | 56.0 | 15.3 | 5.6 | 137.0 | 153.2 | 0.12 | 5.3 | 14.9 | 7.7 | 2.1 | ||
| CV | 0.3 | 0.3 | 0.9 | 0.2 | 0.1 | 1.1 | 0.2 | 0.33 | 0.1 | 0.0 | 0.4 | 0.2 | ||
| Min.–Max. | 413.0–970.0 | 933.0–2275.4 | 28.7–330.0 | 12.1–22.3 | 4.7–6.3 | 14–1013.0 | 95.7–234.2 | 0.04–0.21 | 4.4–5.7 | 14.2–16.0 | 2.9–12.2 | 1.5–3.2 | ||
| Cluster 2b (Group III) (n = 17) | µ ± σ | 751.1 ± 74.5 | 1292.3 ± 232.3 | 74.1 ± 67.8 | 15.6 ± 2.6 | 5.6 ± 0.4 | 567.9 ± 444.1 | 165.1 ± 31.9 | 0.11 ± 0.02 | 5.3 ± 0.2 | 15.0 ± 1.4 | 9.8 ± 0.2 | 1.7 ± 0.8 | |
| Med | 732.0 | 1286.9 | 49.8 | 15.1 | 5.5 | 389.9 | 157.3 | 0.11 | 5.3 | 14.9 | 9.8 | 1.5 | ||
| CV | 0.1 | 0.2 | 0.9 | 0.2 | 0.1 | 0.8 | 0.2 | 0.22 | 0.0 | 0.1 | 0.2 | 0.5 | ||
| Min.–Max. | 628.0–879.0 | 901.9–1911.0 | 18.1–250.0 | 12.3–20.8 | 5.1–6.6 | 116.4–1520.7 | 108.6–213.5 | 0.07–0.14 | 4.8–5.9 | 12.5–18.9 | 4.8–13.6 | 0.6–3.4 | ||
| Cluster 2c (Group IV) (n = 20) | µ ± σ | 729.8 ± 171.1 | 1261.9 ± 136 | 86.6 ± 92.2 | 14.7 ± 2.7 | 5.6 ± 0.4 | 594.2 ± 368.2 | 190.8 ± 75.2 | 0.13 ± 0.03 | 5.4 ± 0.2 | 14.8 ± 0.6 | 7.9 ± 1.4 | 1.8 ± 0.8 | |
| Med | 748.0 | 1251.1 | 34.5 | 14.6 | 5.5 | 588.5 | 166.1 | 0.12 | 5.4 | 14.8 | 7.8 | 1.9 | ||
| CV | 0.2 | 0.1 | 1.1 | 0.2 | 0.1 | 0.6 | 0.4 | 0.24 | 0.0 | 0.0 | 0.2 | 0.4 | ||
| Min.–Max. | 434.0–1035.0 | 1037.8–1553.2 | 19.1–343.0 | 10.3–21.3 | 5.0–6.7 | 31.0–1385.0 | 136.1–397.0 | 0.09–0.18 | 4.8–5.8 | 13.7–16.1 | 4.2–9.6 | 0.1–3.3 | ||
| Cluster 2d (Group V) (n = 12) | µ ± σ | 757.2 ± 130.9 | 1280.9 ± 165.9 | 67.1 ± 42.9 | 14.6 ± 1.9 | 6.0 ± 0.3 | 242.9 ± 193.8 | 248.0 ± 54.9 | 0.17 ± 0.02 | 4.8 ± 0.2 | 15.3 ± 0.7 | 8.1 ± 1.6 | 1.3 ± 0.5 | 16.1 ± 21.6 |
| Med | 724.5 | 1286.9 | 54.6 | 14.8 | 6.0 | 189.5 | 240.3 | 0.17 | 4.8 | 15.2 | 8.4 | 1.2 | 7.2 | |
| CV | 0.2 | 0.1 | 0.6 | 0.1 | 0.1 | 0.8 | 0.2 | 0.13 | 0.0 | 0.0 | 0.2 | 0.4 | 1.3 | |
| Min.–Max. | 478.0–1078.0 | 1045.3–1573.9 | 21.2–164.0 | 11.4–17.8 | 5.6–6.9 | 46.0–749.0 | 163.0–344.5 | 0.14–0.21 | 4.6–5.3 | 14.2–16.9 | 5.3–10.7 | 0.8–2.7 | 1.9–71.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martins, L.; Pereira, A.; Oliveira, A.; Fernandes, A.; Sanches Fernandes, L.F.; Pacheco, F.A.L. An Assessment of Groundwater Contamination Risk with Radon Based on Clustering and Structural Models. Water 2019, 11, 1107. https://doi.org/10.3390/w11051107
Martins L, Pereira A, Oliveira A, Fernandes A, Sanches Fernandes LF, Pacheco FAL. An Assessment of Groundwater Contamination Risk with Radon Based on Clustering and Structural Models. Water. 2019; 11(5):1107. https://doi.org/10.3390/w11051107
Chicago/Turabian StyleMartins, Lisa, Alcides Pereira, Alcino Oliveira, António Fernandes, Luís Filipe Sanches Fernandes, and Fernando António Leal Pacheco. 2019. "An Assessment of Groundwater Contamination Risk with Radon Based on Clustering and Structural Models" Water 11, no. 5: 1107. https://doi.org/10.3390/w11051107
APA StyleMartins, L., Pereira, A., Oliveira, A., Fernandes, A., Sanches Fernandes, L. F., & Pacheco, F. A. L. (2019). An Assessment of Groundwater Contamination Risk with Radon Based on Clustering and Structural Models. Water, 11(5), 1107. https://doi.org/10.3390/w11051107








