Optimization of Horseradish Peroxidase Catalytic Degradation for 2-Methyl-6-Ethylaniline Removal Using Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. Experimental Procedure
2.3. Analysis Methods
2.4. Experimental Design and Optimization Method
3. Results and Discussion
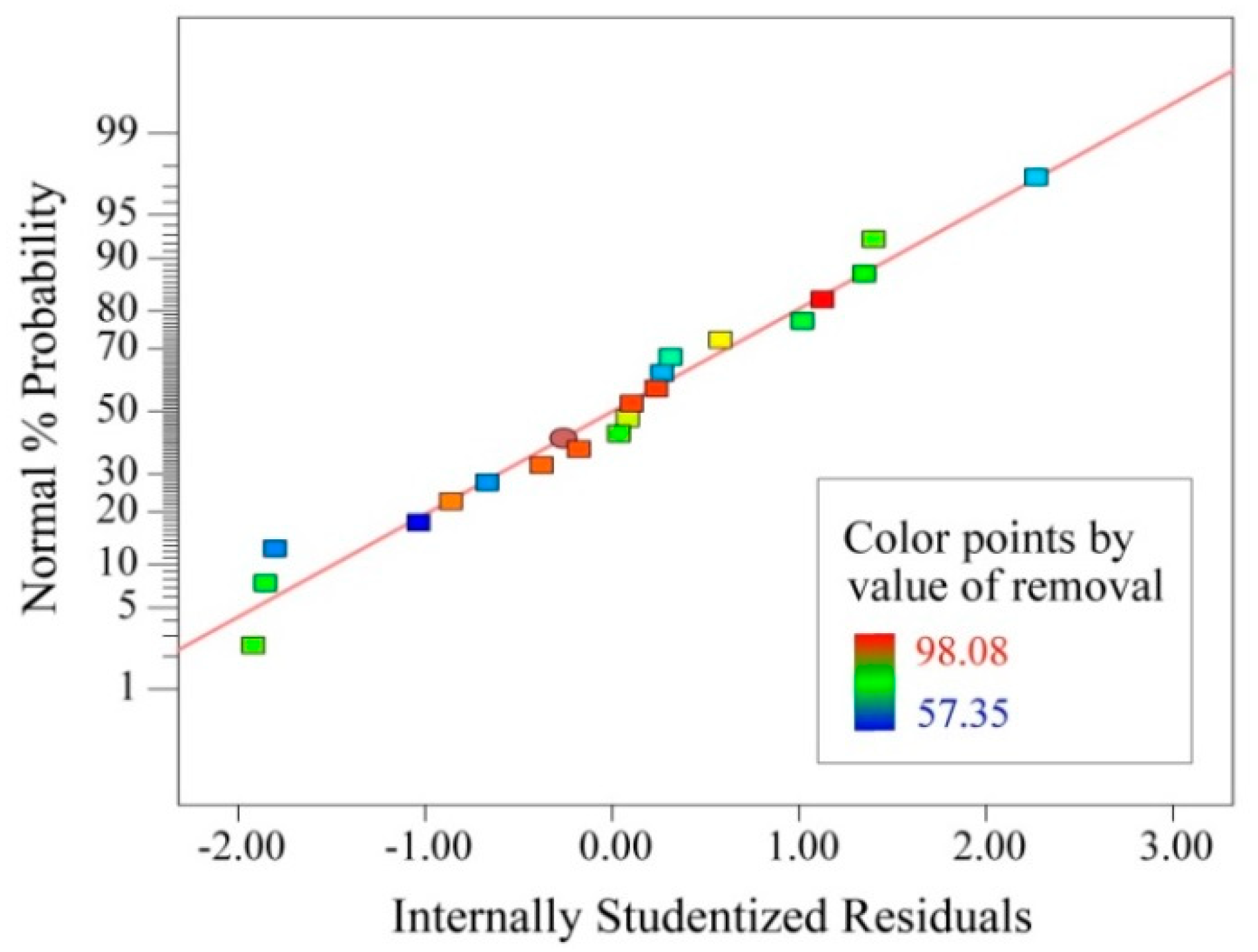
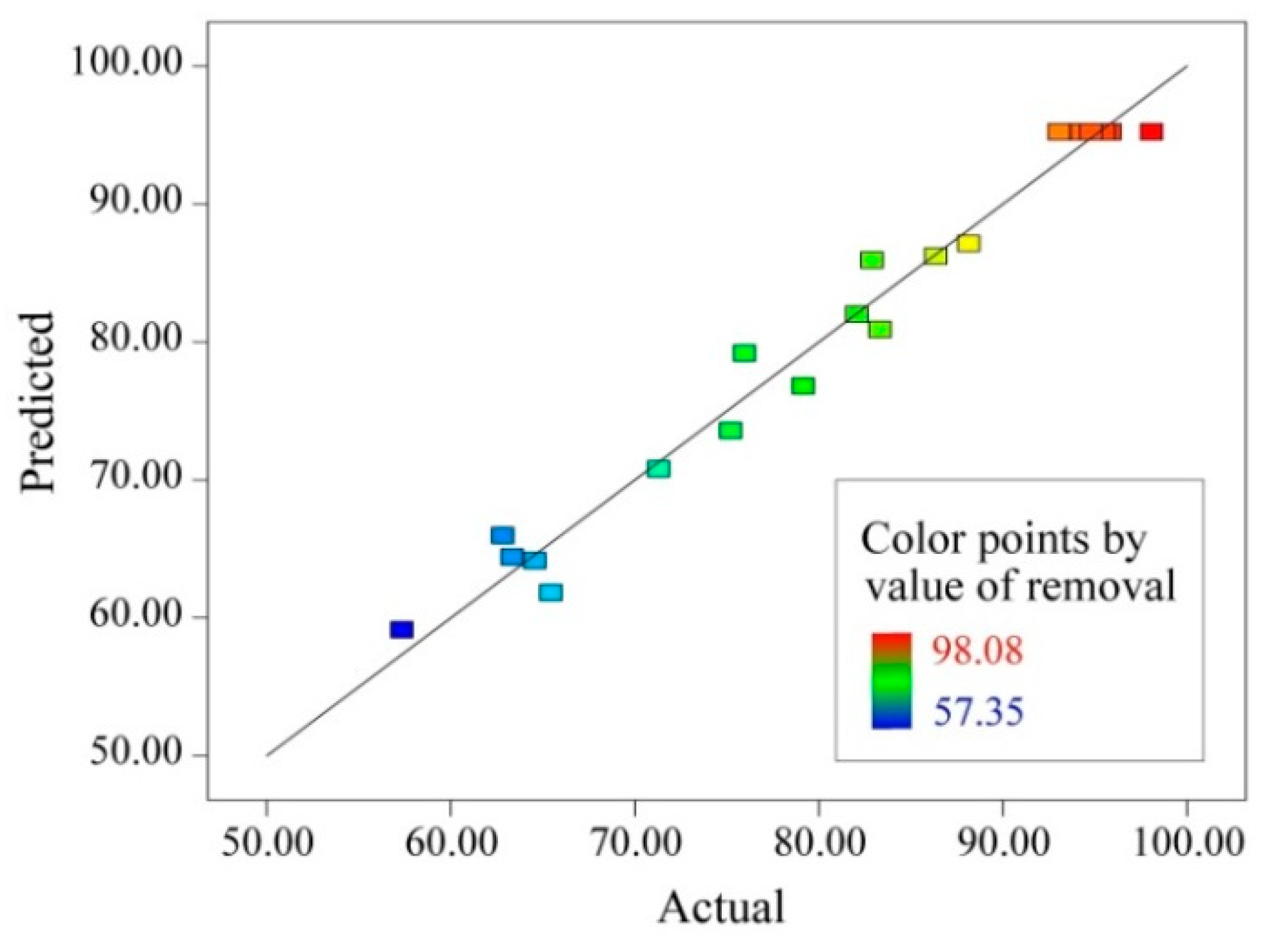
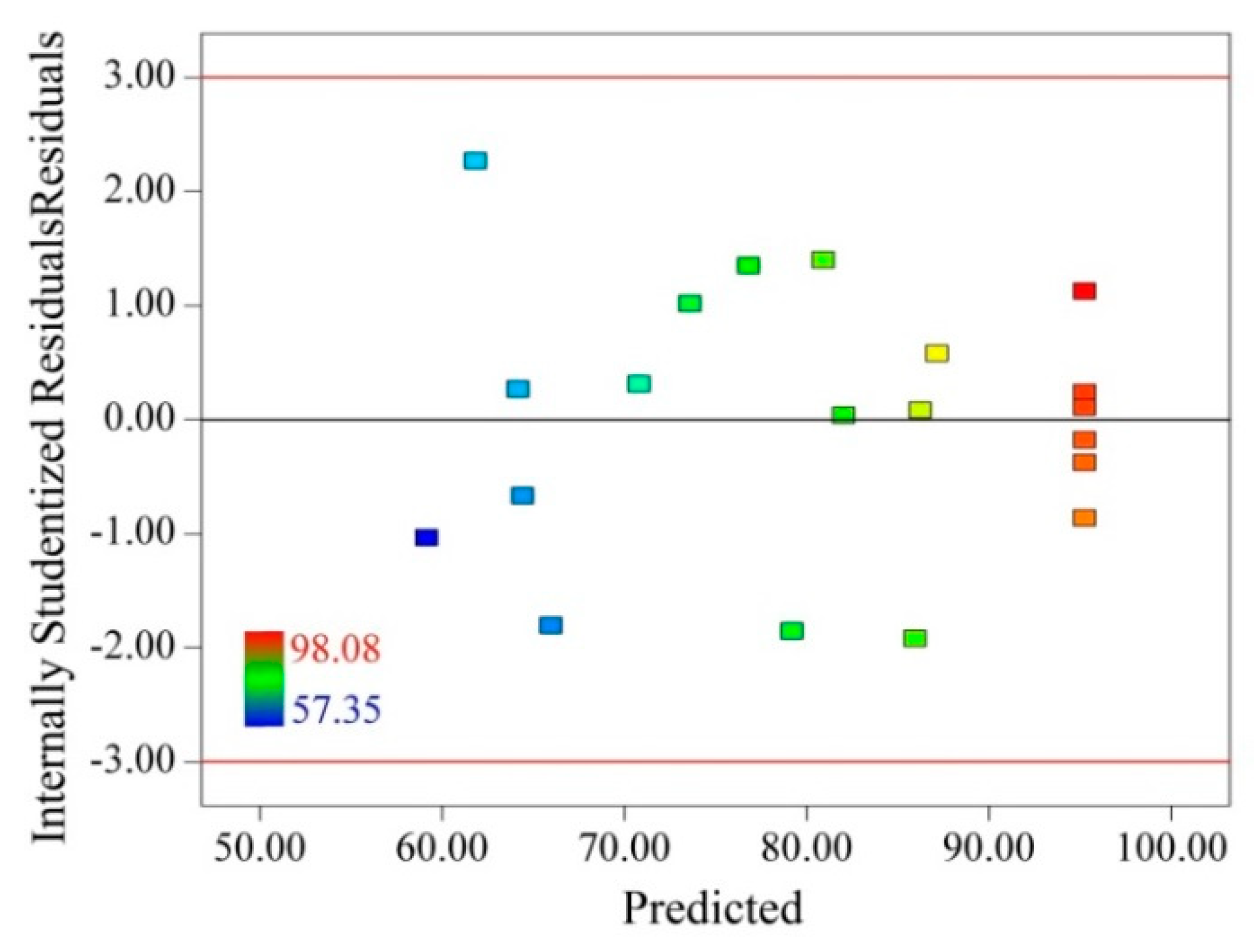
3.1. Model Fitting
4.62X22 − 0.21X32
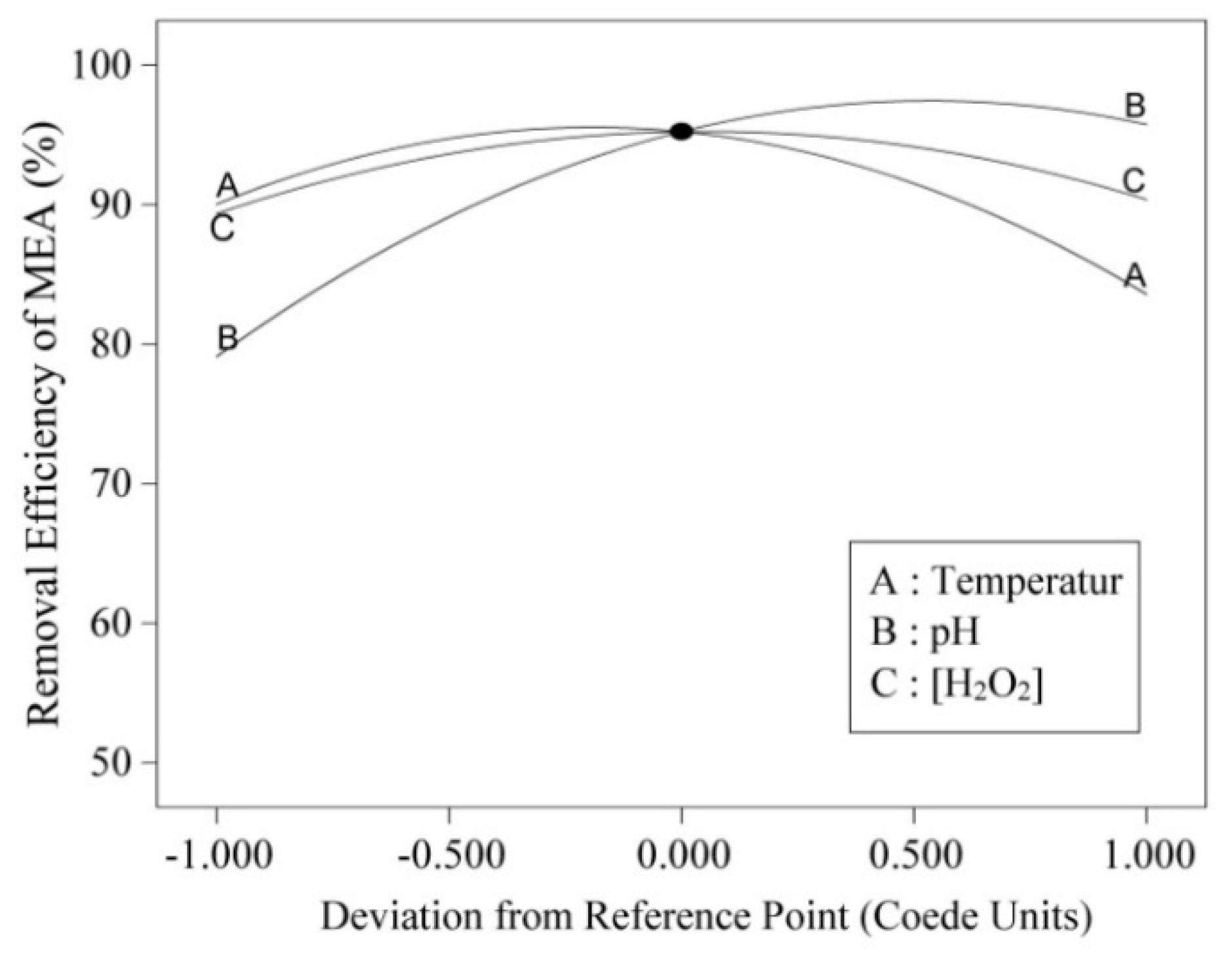
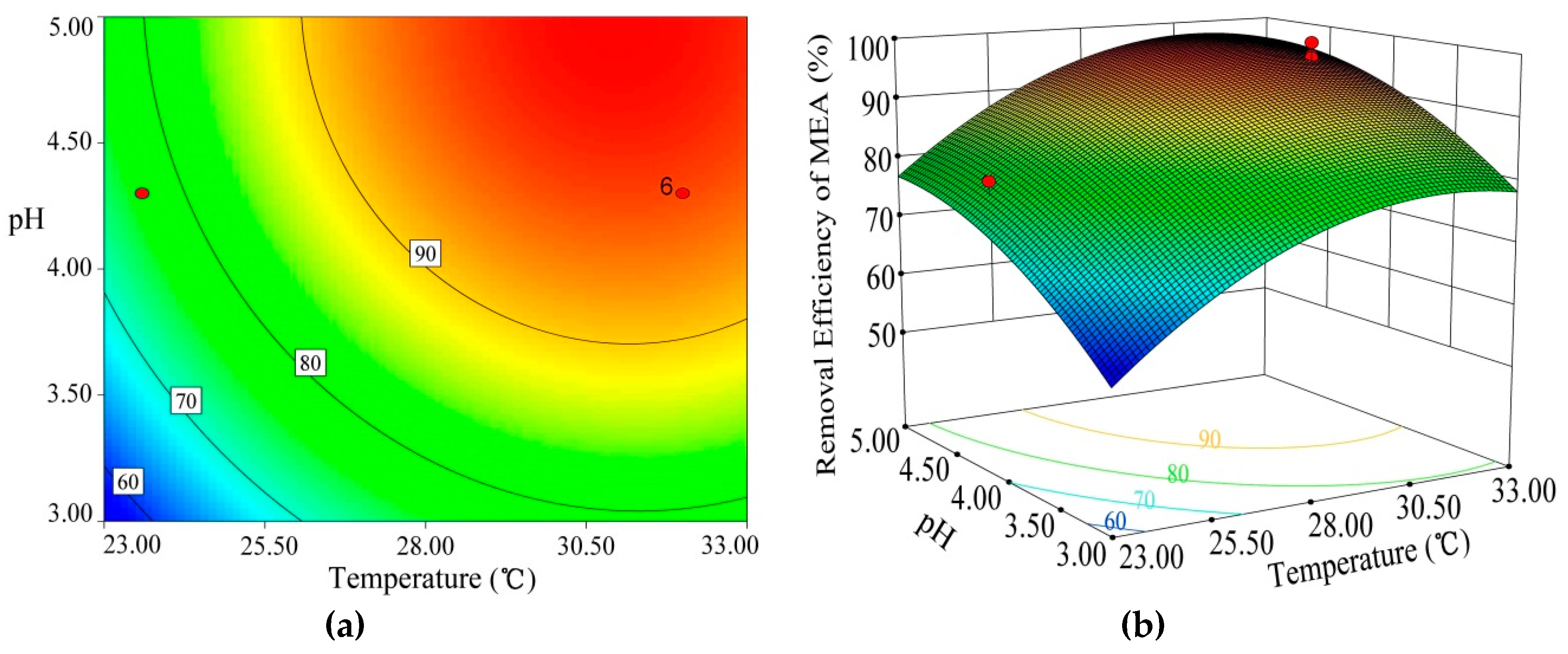
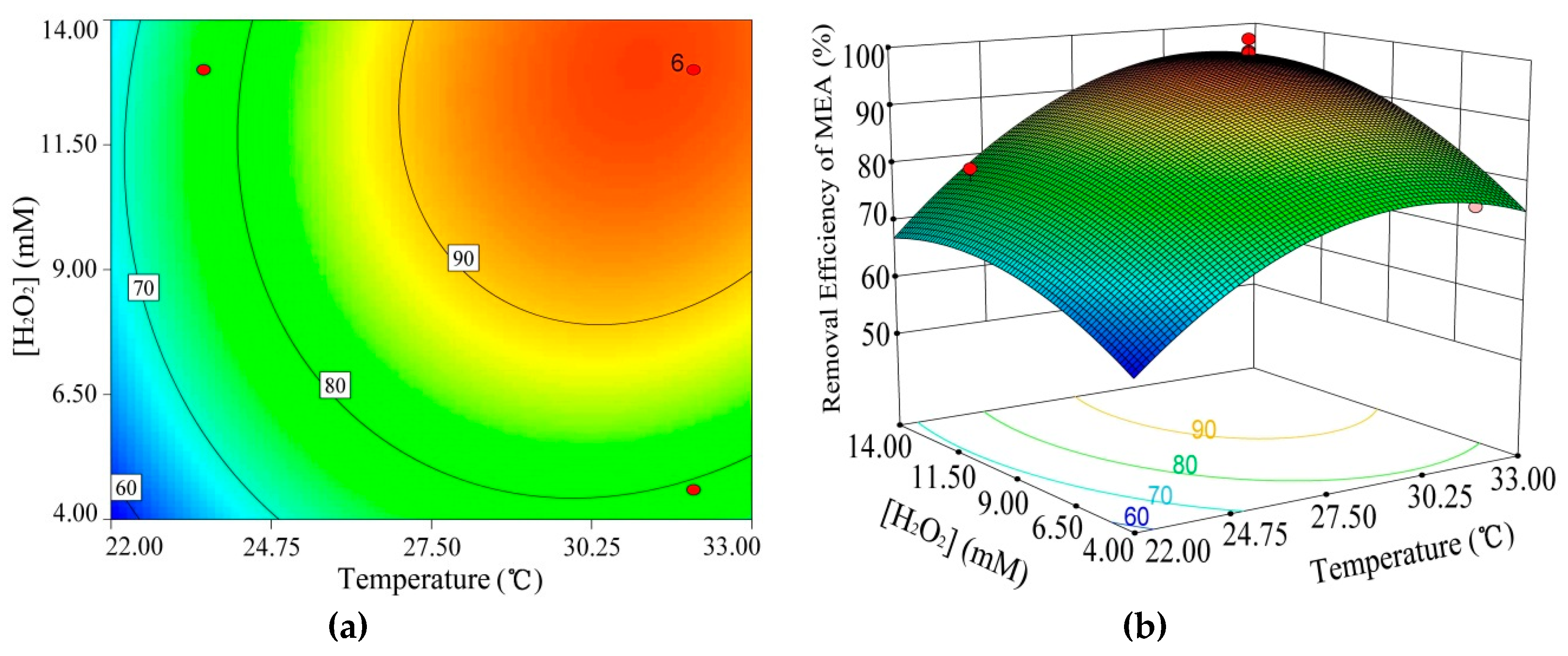
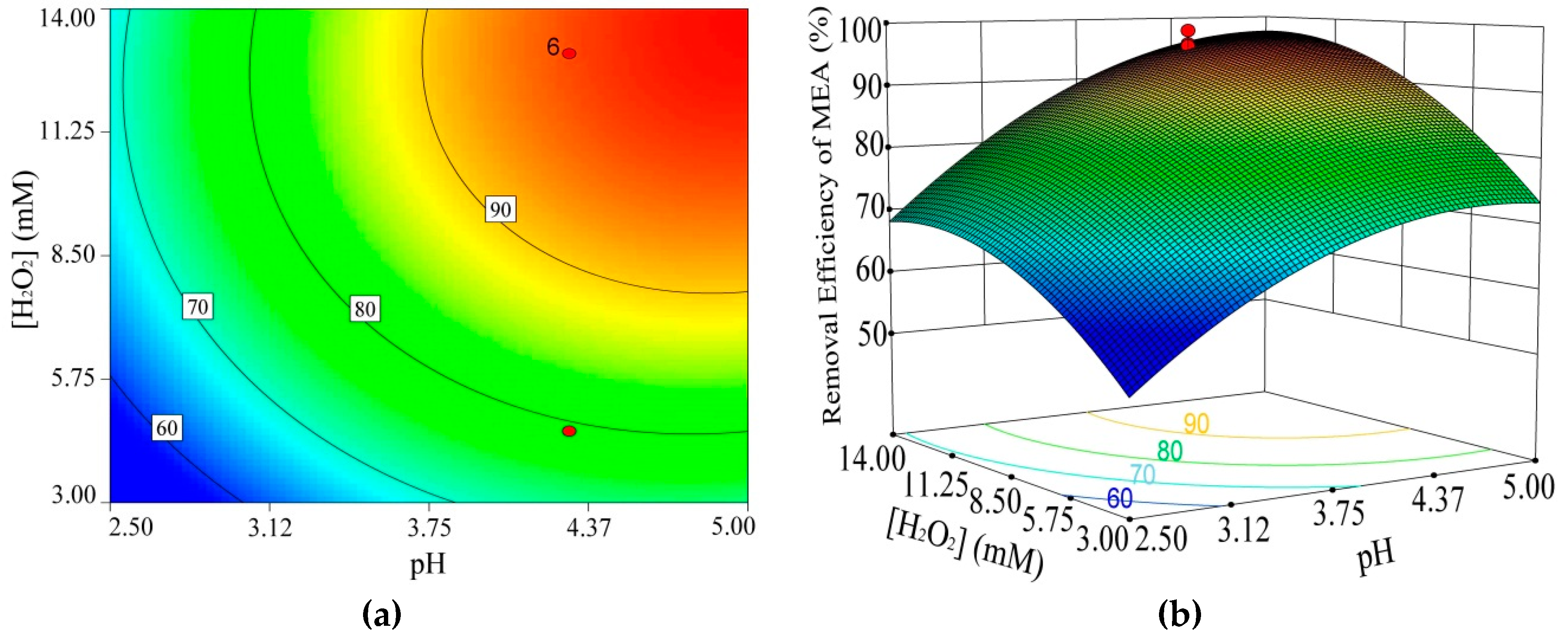
3.2. Influence Factor of 2-Methyl-6-Ethylaniline (MEA) Removal Efficiency
4. Conclusions
- (1)
- A regression model for the removal efficiency of MEA, the ternary quadratic polynomial, was established. The variance analysis showed that the regression model was significant (p < 0.0001), fitted well with experimental data and had a high degree of reliability and accuracy, and the data were reasonable with low errors.
- (2)
- By analyzing interactions and solving the regression model, the maximum MEA removal efficiency was 97.90%, and the optimal conditions were defined as follows: pH 5.02, H2O2 concentration 13.41 mM, and temperature of 30.95 °C. Under the optimal conditions, the average MEA removal efficiency obtained from the experiments was 97.56%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wei, D.; Sun, K.; Han, L. Isolation, identification and analysis of degradation dharacteristics of acetochlor-degrading strain B-2. Genomics and Appl. Biol. 2016, 35, 3069–3075. [Google Scholar]
- Feng, Q.; Wen, S.; Bai, X.; Chang, W.; Cui, C.; Zhao, W. Surface modification of smithsonite with ammonia to enhance the formation of sulfidization products and its response to flotation. Miner. Eng. 2019, 137, 1–9. [Google Scholar] [CrossRef]
- Feng, Q.; Wen, S.; Deng, J.; Zhao, W. Combined DFT and XPS investigation of enhanced adsorption of sulfide species onto cerussite by surface modification with chloride. Appl. Surf. Sci. 2017, 425, 8–15. [Google Scholar]
- Feng, Q.; Zhao, W.; Wen, S. Surface modification of malachite with ethanediamine and its effect on sulfidization flotation. Appl. Surf. Sci. 2018, 436, 823–831. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, J.; Liang, B.; Wang, C.; Cai, S.; Ni, Y.; He, J.; Li, S. Biodegradation of Chloroacetamide Herbicides by Paracoccus sp. FLY-8 in Vitro. J. Agric. Food Chem. 2011, 59, 4614–4621. [Google Scholar] [CrossRef] [PubMed]
- Keith, L.H.; Telliard, W.A. Priority pollutants: I. A perspective view. Enviro. Sci. Technol. 1979, 13, 416–423. [Google Scholar] [CrossRef]
- Tao, H.; Zhou, S.; Gao, T. Experimental research on treatment of aniline-bearing wastewater using 13X molecular sieves. Acta Scientiae Circumstantiae 2002, 22, 408–411. [Google Scholar]
- Enric, B.; Juan, C. Aniline degradation by Electro-Fenton and peroxi-coagulation processes using a flow reactor for wastewater treatment. Chemosphere 2002, 47, 241–248. [Google Scholar]
- Wang, X. New progress in the treatment of aniline wastewater. Ind. Water Treat. 2010, 30, 11–14. [Google Scholar]
- Giardina, P.; Faraco, V.; Pezzella, C.; Piscitelli, A.; Vanhulle, S.; Sannia, G. Laccases: A never-ending story. Cell. Mol. Life Sci. 2010, 67, 369–385. [Google Scholar] [CrossRef]
- Zhong, P.; Peng, H.; Peng, F.; Cai, Q.; He, M. Kinetic Analysis of Laccase catalyze phenolic and aniline compounds and detecting catechol in wastewater. Environ. Sci. 2010, 31, 2673–2677. [Google Scholar]
- Song, W.; Wu, C.; Lin, L.; Ni, J.; Wang, W. Optimization of degradation conditions for degrading bacteria of dianilinodithiophosphoric acid and properties of degrading enzyme. J. Anhui Agric. Sci. 2013, 41, 13486–13488. [Google Scholar]
- Veitch, N.C. Horseradish peroxidase: a modern view of a classic enzyme. Phytochemistry 2004, 65, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Saidman, S.; Rueda, E.H.; Ferreira, M.L. Activity of free peroxidases, hematin, magnetite-supported peroxidases and magnetite-supported hematin in the aniline elimination from water-UV-vis analysis. Biochem. Eng. J. 2006, 28, 177–186. [Google Scholar] [CrossRef]
- Jiang, Y.; Feng, C. The Study on Reaction kinetics based on a new system of the horseradish peroxidase catalyting the oxidation of o-phenylenediamine by H2O2. Spectrosc. Spectral Anal. 2002, 22, 436–440. [Google Scholar]
- Yang, D.; Wu, X.; Chang, Y.; Qiu, X.; Tao, J. Horseradish peroxidase catalyzed polymerization of sulfomethylated alkali Lignin. Acta Polym. Sin. 2014, 4, 473–480. [Google Scholar]
- Reihmann, M.H.; Ritter, H. Oxidative oligomerization of cyclodextrin-complexed bifunctional phenols catalyzed by horseradish peroxidase in water. Macromol. Chem. Phys. 2000, 201, 798–804. [Google Scholar] [CrossRef]
- Zhang, L. Applications of horseradish peroxidase in the phenolic wastewater. J. Shanxi Datong Univ. (Nat. Sci.) 2012, 28, 35–39. [Google Scholar]
- Mayer, R.H.; Montgomery, D.C. Response Surface Methodology; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Hasan, S.D.M.; Melo, D.N.C.; Filho, R.M. Simulation and response surface analysis for the optimization of a three-phase catalytic slurry reactor. Chem. Eng. Process. 2005, 44, 335–343. [Google Scholar] [CrossRef]
- Ma, H.; He, T.; Hong, L.; Wei, D.; Li, J.; Sun, S.; Xu, Z. Optimization of the adsorption of phosphorus by water plant sludge using response surface methodology. Chin. J. Environ. Eng. 2015, 9, 546–552. [Google Scholar]
- Ghasempur, S.; Torabi, S.F.; Ranaei-Siadat, S.O.; Jalali-Heravi, M.; Ghaemi, N.; Khajeh, K. Optimization of peroxidase-catalyzed oxidative coupling process for phenol removal from wastewater using response surface methodology. Environ. Sci. Technol. 2007, 41, 7073–7079. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, T.B.; Shen, X. Market and technical process of acetochlor in China. Chem. Techno-Econ. 2005, 23, 14–16. [Google Scholar]
- Jeffwu, C.F.; Michael, H. Experimental Design and Analysis and Parameter Optimization; China Statistics Press: Beijing, China, 2003; pp. 362–365. [Google Scholar]
- Bhatti, M.S.; Reddy, A.S.; Thukral, A.K. Electrocoagulation removal of Cr(VI) from simulated wastewater using response surface methodology. J. Hazard. Mater. 2009, 172, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Bashir, M.J.K.; Aziz, H.A.; Suffian, Y.M.; Aziz, S.Q.; Mohajeri, S. Stabilized sanitary landfill leachate treatment using anionic resin: treatment optimization by response surface methodology. J. Hazard. Mater. 2010, 182, 115–122. [Google Scholar] [CrossRef]
- Zhang, X.R.; Liu, Z.H.; Fan, X.; Lian, X.; Tao, C.Y. Optimization of reaction conditions for the electroleaching of manganese from low-grade pyrolusite. Int. J. Miner. Metall. Mater. 2015, 22, 1121–1130. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, C.; Zhang, G. Catalytic degradation of benzaldehyde by horseradish peroxidase. J. Taiyuan Normal Univ. (Nat. Sci.) 2017, 16, 78–81. [Google Scholar]
- Ye, P.; Zhang, J.; Chen, S.; Yang, Y.; Wang, W.; Wang, S. Removal of pentachlor ophenol (PCP) by immobilized horseradish peroxidase (HRP). Acta Scientiarum Naturalium Universitatis Pekinensis 2005, 41, 918–925. [Google Scholar]
- Rodriguez-Lopez, J.N.; Hernandez-Ruiz, J.; Garcia-Canovas, F.; Thorneley, R.N.; Acosta, M.; Arnao, M.B. The inactivation and catalytic pathways of horseradish peroxidase with m-chloroperoxybenzoic acid: A spectrophotometric and transient kinetic study. J. Biol. Chem. 1997, 272, 5469–5476. [Google Scholar] [CrossRef]
- Arnao, M.B.; Acosta, M.; del Rio, J.A.; García-Cánovas, F. Inactivation of peroxidase by hydrogen peroxide and its protection by a reductant agent. Biochim. Biophy. Acta 1990, 1038, 85–89. [Google Scholar] [CrossRef]
- Pina, D.G.; Shnyrova, A.V.; Gavilanes, F.; Rodríguez, A.; Leal, F.; Roig, M.G.; Sakharov, I.Y.; Zhadan, G.G.; Villar, E.; Shnyrov, V.L. Thermally induced conformational changes in horseradish peroxidase. Eur. J. Biochem. 2010, 268, 120–126. [Google Scholar] [CrossRef]
- Si, Y.; Xu, R.; Li, F.; Xu, Z. Removal of dyestuff from water catalyzed by horseradish peroxidase. Ind. Water Treat. 2015, 35, 40–43. [Google Scholar]
| Coded Level | Uncoded Level | ||
|---|---|---|---|
| Temperature (°C) | pH | [H2O2] (mM) | |
| −1.68 | 23.59 | 2.11 | 4.59 |
| −1 | 27.00 | 3.00 | 8.00 |
| 0 | 32.00 | 4.30 | 13.00 |
| 1 | 37.00 | 5.60 | 18.00 |
| 1.68 | 40.41 | 6.49 | 21.41 |
| Run | Type | Uncoded Level | Removal Efficiency of MEA (%) | ||
|---|---|---|---|---|---|
| Temperature (°C) X1 | pH X2 | [H2O2] (mM) X3 | |||
| 1 | Star | 27.00 | 3.00 | 8.00 | 71.30 |
| 2 | Star | 37.00 | 3.00 | 8.00 | 64.35 |
| 3 | Star | 27.00 | 5.60 | 8.00 | 86.35 |
| 4 | Star | 37.00 | 5.60 | 8.00 | 75.21 |
| 5 | Star | 27.00 | 3.00 | 18.00 | 63.35 |
| 6 | Star | 37.00 | 3.00 | 18.00 | 64.58 |
| 7 | Star | 27.00 | 5.60 | 18.00 | 82.89 |
| 8 | Star | 37.00 | 5.60 | 18.00 | 82.08 |
| 9 | Axial | 23.59 | 4.30 | 13.00 | 79.15 |
| 10 | Axial | 40.41 | 4.30 | 13.00 | 62.84 |
| 11 | Axial | 32.00 | 2.11 | 13.00 | 57.35 |
| 12 | Axial | 32.00 | 6.49 | 13.00 | 88.15 |
| 13 | Axial | 32.00 | 4.30 | 4.59 | 75.97 |
| 14 | Axial | 32.00 | 4.30 | 21.41 | 83.33 |
| 15 | Center | 32.00 | 4.30 | 13.00 | 93.05 |
| 16 | Center | 32.00 | 4.30 | 13.00 | 95.83 |
| 17 | Center | 32.00 | 4.30 | 13.00 | 95.50 |
| 18 | Center | 32.00 | 4.30 | 13.00 | 98.08 |
| 19 | Center | 32.00 | 4.30 | 13.00 | 94.28 |
| 20 | Center | 32.00 | 4.30 | 13.00 | 94.78 |
| Source | Sum of Squares | DF | Mean Square | F Value | P Value |
|---|---|---|---|---|---|
| Model | 3110.09 | 9 | 345.57 | 45.02 | <0.0001 |
| X1 | 141.9 | 1 | 141.9 | 18.49 | 0.0016 |
| X2 | 945.73 | 1 | 945.73 | 123.2 | <0.0001 |
| X3 | 3.56 | 1 | 3.56 | 0.46 | 0.5112 |
| X1·X2 | 6.72 | 1 | 6.72 | 0.88 | 0.3716 |
| X1·X3 | 37.95 | 1 | 37.95 | 4.94 | 0.0504 |
| X2·X3 | 18.69 | 1 | 18.69 | 2.44 | 0.1497 |
| X12 | 1024.32 | 1 | 1024.32 | 133.44 | <0.0001 |
| X22 | 878.93 | 1 | 878.93 | 114.5 | <0.0001 |
| X32 | 415.7 | 1 | 415.7 | 54.15 | <0.0001 |
| Residual | 76.76 | 10 | 7.68 | ||
| Lack of fit | 62.36 | 5 | 12.47 | 4.33 | 0.0667 |
| Pure error | 14.4 | 5 | 2.88 | ||
| Cor Total | 3186.85 | 19 |
| Optimum Conditions | MEA Removal Efficiency (%) | |||
|---|---|---|---|---|
| pH | H2O2 (mM) | Temperature (°C) | Experimental | Predicted |
| 5.02 | 13.41 | 30.95 | 97.56 | 97.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; Wang, Q.; Shu, J.; Ma, L.; Chen, L.; Xu, Y. Optimization of Horseradish Peroxidase Catalytic Degradation for 2-Methyl-6-Ethylaniline Removal Using Response Surface Methodology. Water 2019, 11, 1093. https://doi.org/10.3390/w11051093
Shen S, Wang Q, Shu J, Ma L, Chen L, Xu Y. Optimization of Horseradish Peroxidase Catalytic Degradation for 2-Methyl-6-Ethylaniline Removal Using Response Surface Methodology. Water. 2019; 11(5):1093. https://doi.org/10.3390/w11051093
Chicago/Turabian StyleShen, Songtao, Qing Wang, Jiancheng Shu, Li Ma, Li Chen, and Yingyi Xu. 2019. "Optimization of Horseradish Peroxidase Catalytic Degradation for 2-Methyl-6-Ethylaniline Removal Using Response Surface Methodology" Water 11, no. 5: 1093. https://doi.org/10.3390/w11051093
APA StyleShen, S., Wang, Q., Shu, J., Ma, L., Chen, L., & Xu, Y. (2019). Optimization of Horseradish Peroxidase Catalytic Degradation for 2-Methyl-6-Ethylaniline Removal Using Response Surface Methodology. Water, 11(5), 1093. https://doi.org/10.3390/w11051093





