Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study
Abstract
1. Introduction
2. Materials and Methods
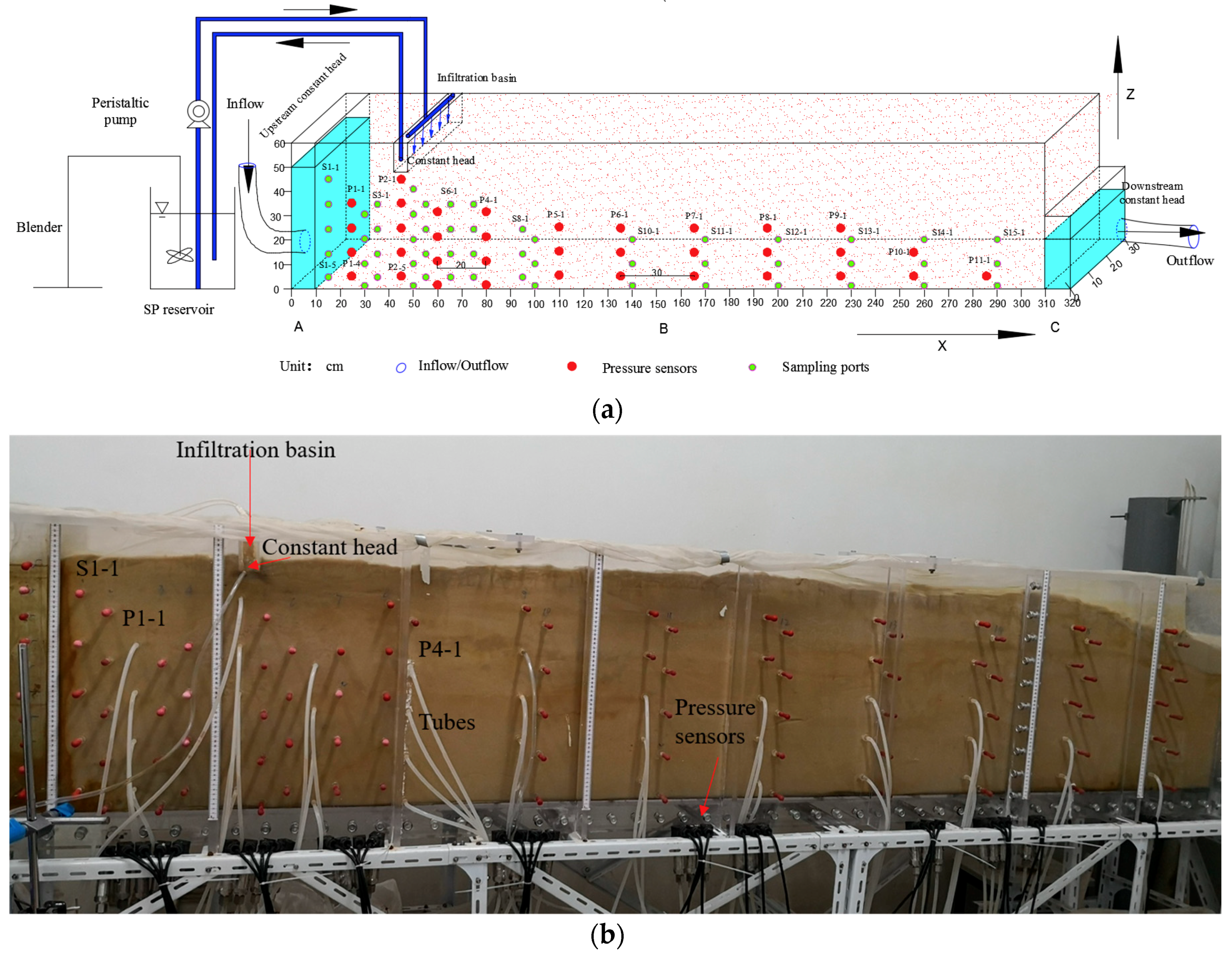
2.1. Design of the Sand Tank
2.2. Properties of Suspended Particles (SP) and Porous Medium
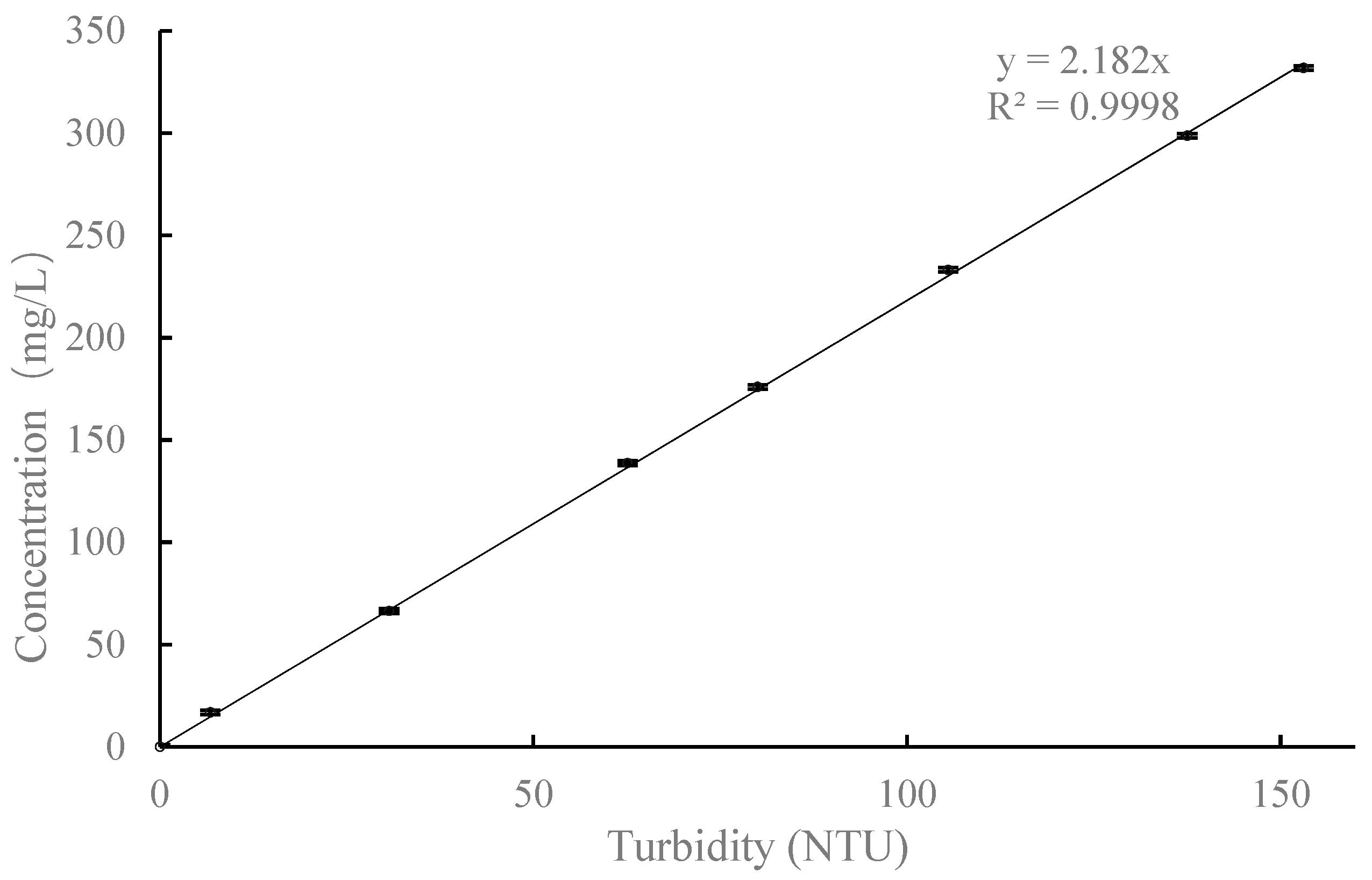
2.2.1. Suspended Particles
2.2.2. Porous Medium
2.3. Experimental Procedures
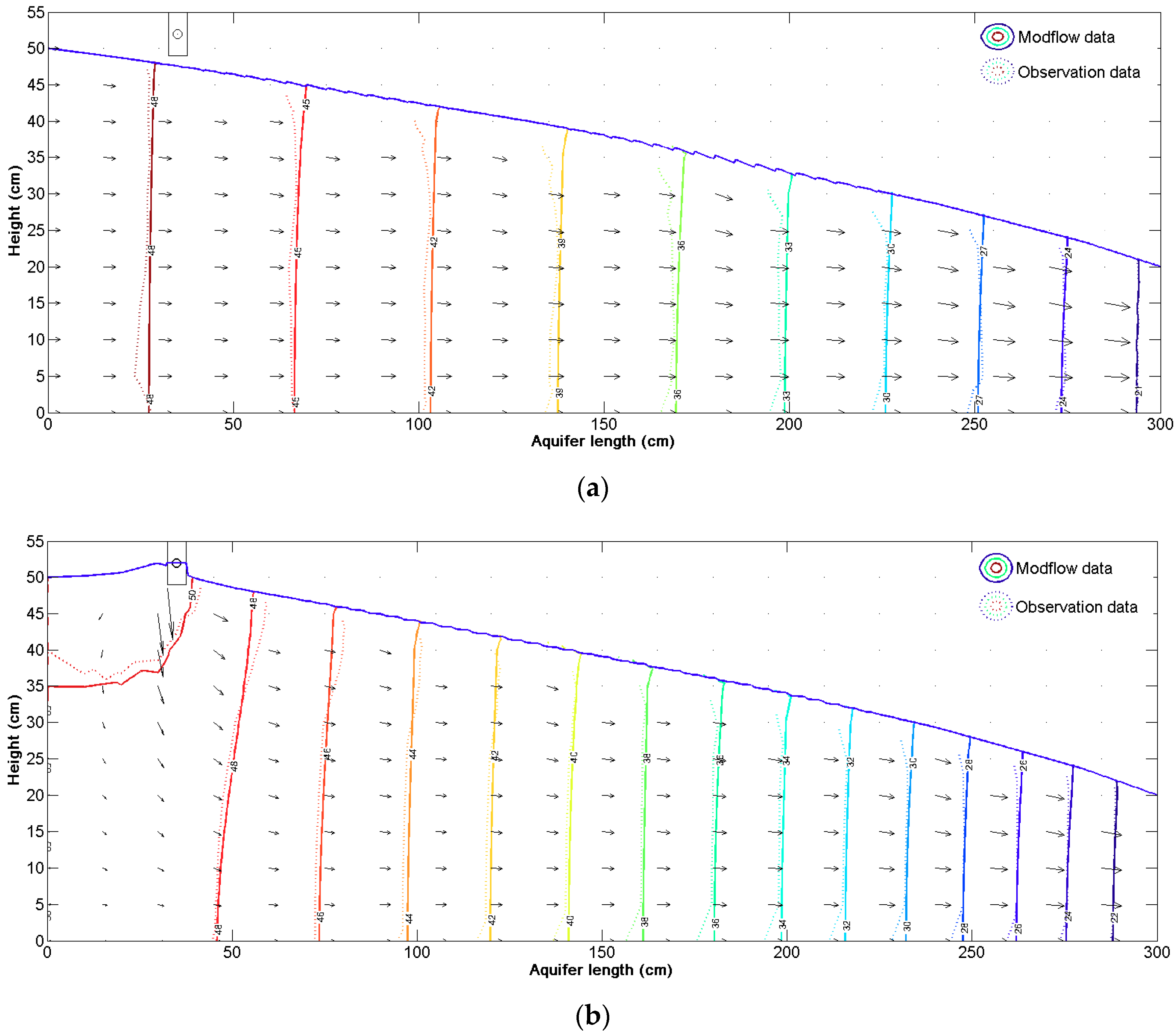
2.4. Mathematical Modeling
3. Results and Discussion
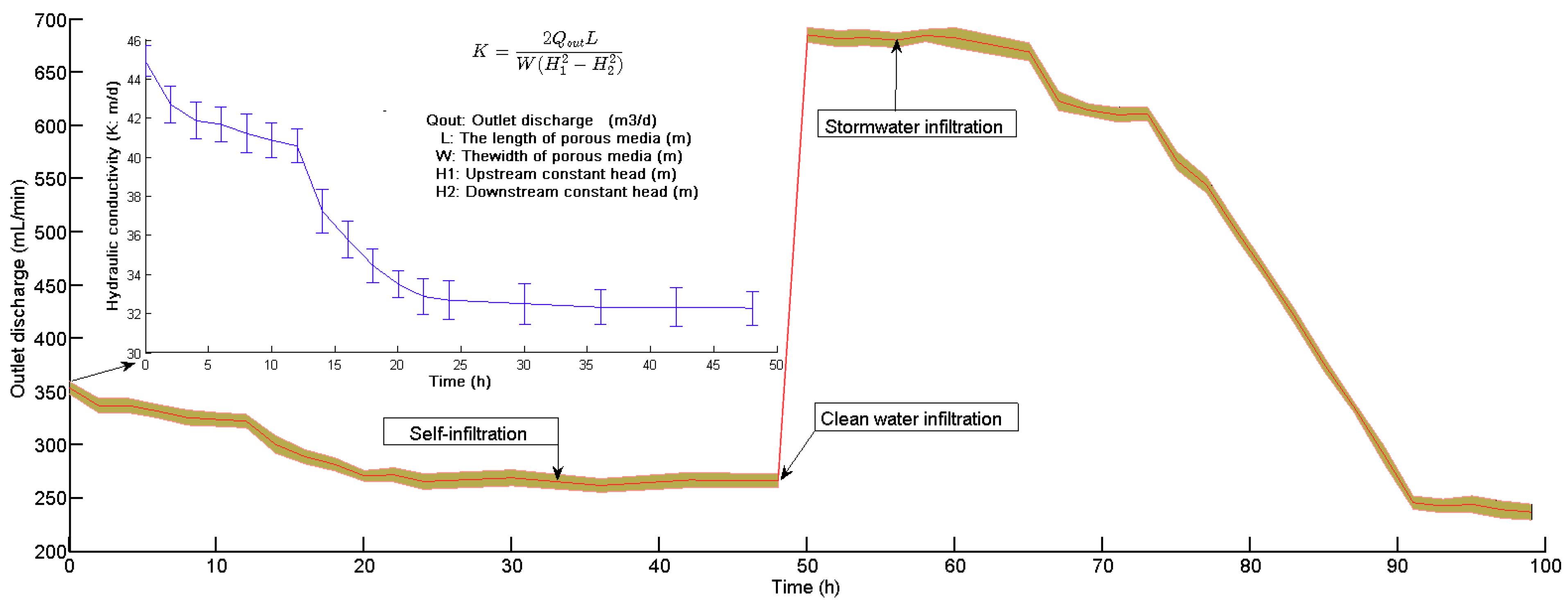
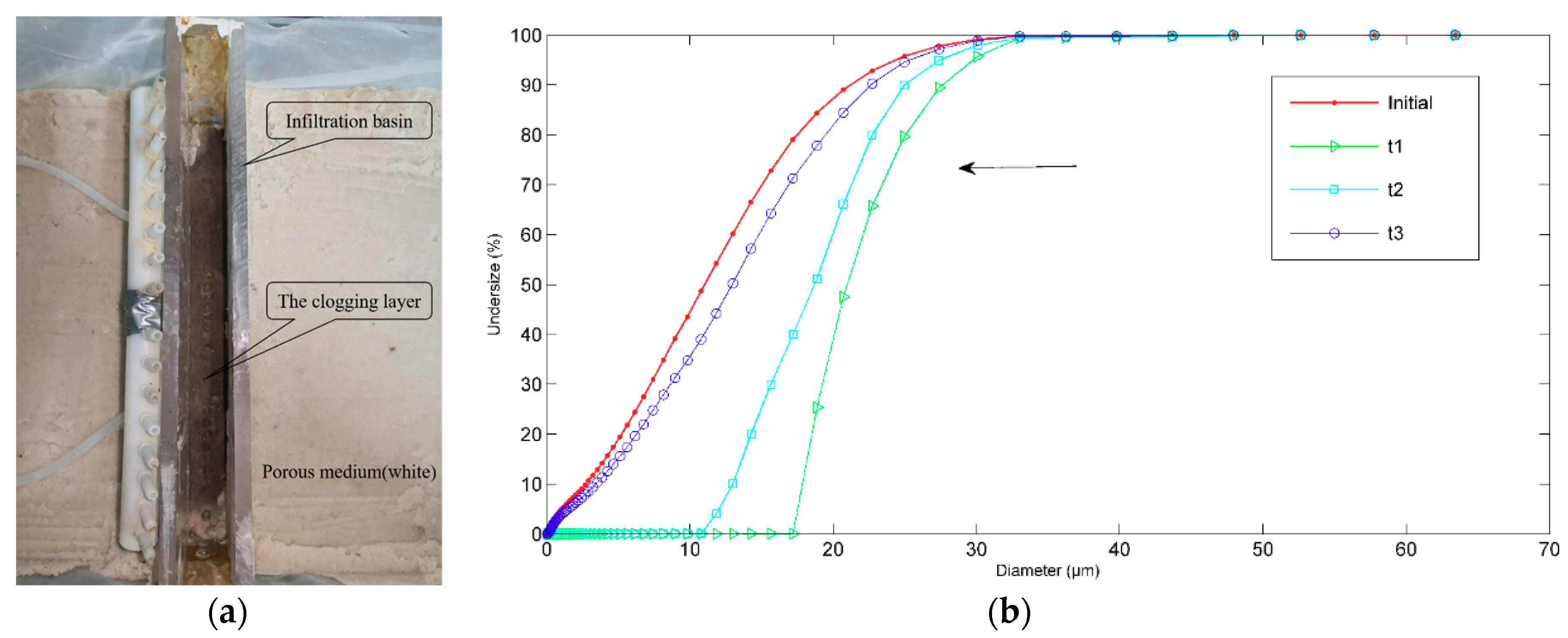
3.1. Self-Filtration of Porous Medium
3.2. Formation of the Clogging Layer due to Straining
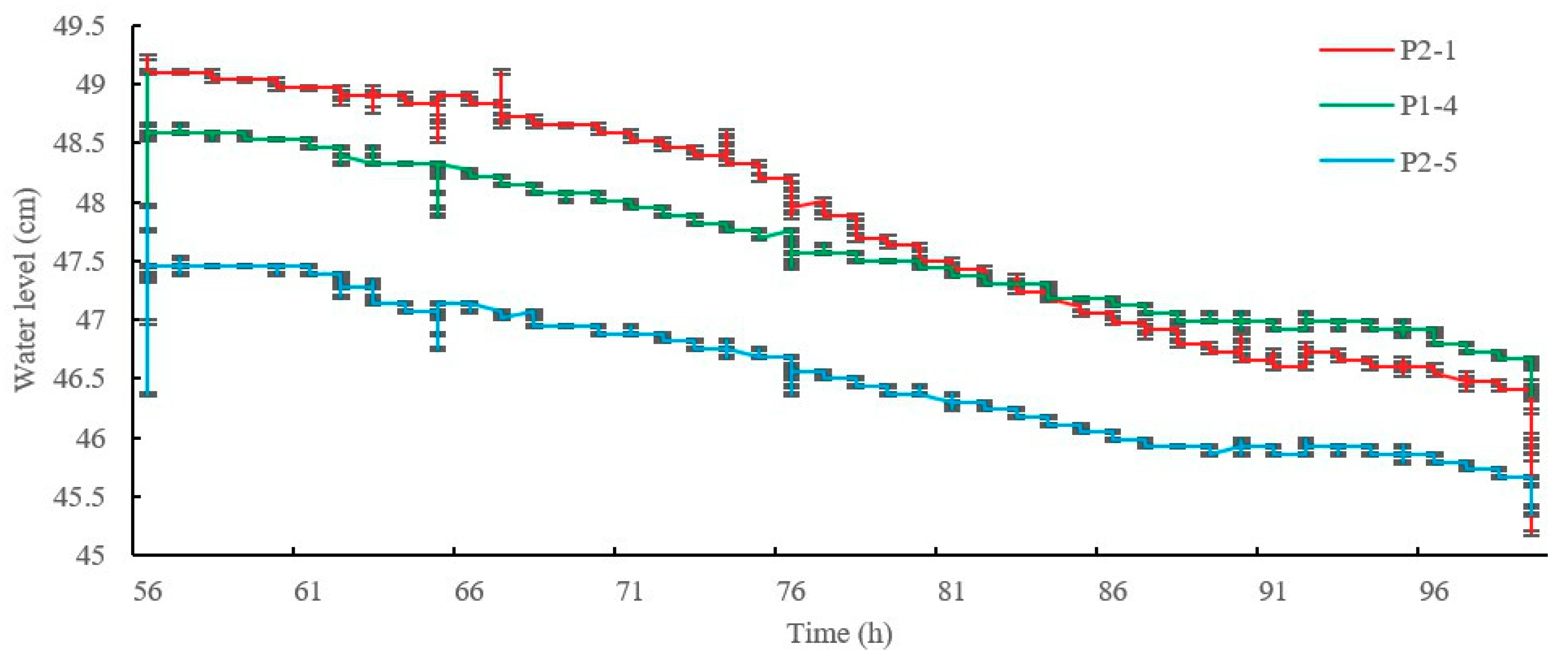
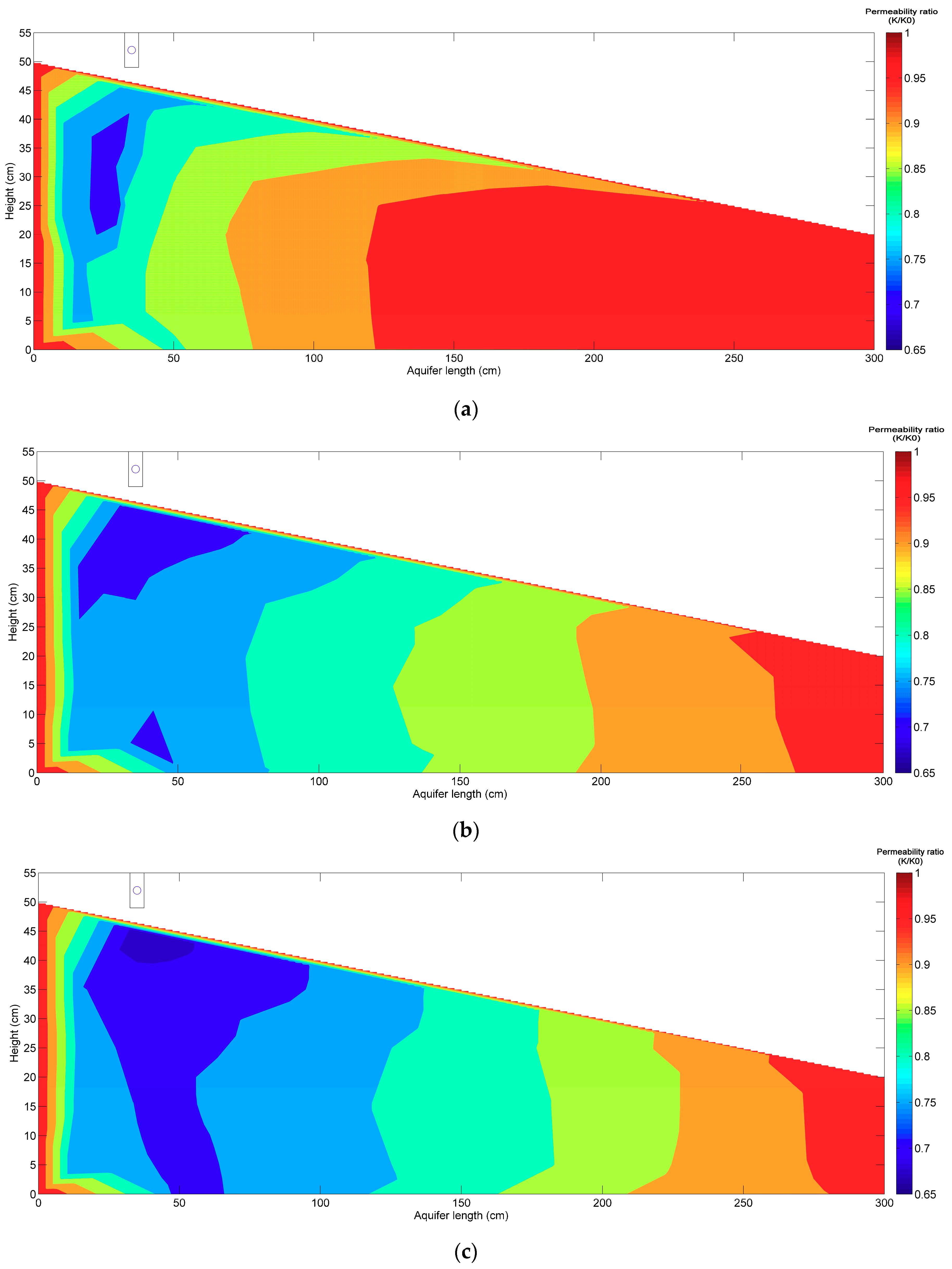
3.3. Permeability Reduction of the Porous Medium
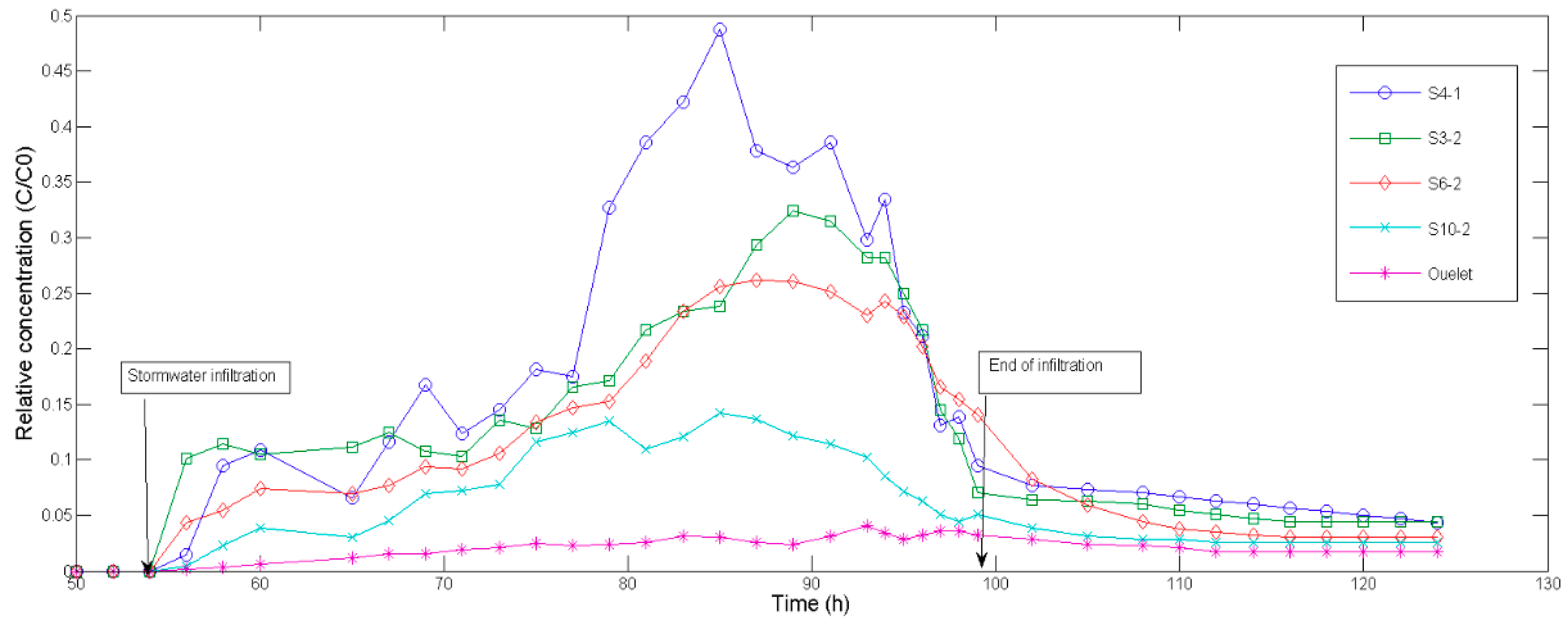
3.4. SP transport and Retention in the Porous Medium
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, N.B.; Lu, J.W.; Chui, T.F.M.; Hartshorn, N. Global policy analysis of low impact development for stormwater management in urban regions. Land Use Policy 2018, 70, 368–383. [Google Scholar] [CrossRef]
- Stéphanie, R.P.; Ragusa, S.; Sztajnbok, P.; Vandevelde, T. Interrelationships between biological, chemical, and physical processes as an analog to clogging in aquifer storage and recovery (ASR) wells. Water Res. 2000, 34, 2110–2118. [Google Scholar]
- Xu, Y.; Shu, L.; Zhang, Y.; Wu, P.; Eshete, C.M. Physical experiment and numerical simulation of the artificial recharge effect on groundwater reservoir. Water 2017, 9, 908. [Google Scholar]
- Liang, X.; Zhan, H.; Zhang, Y.K. Aquifer recharge using a vadose zone infiltration well. Water Resour. Res. 2018, 54, 8847–8863. [Google Scholar] [CrossRef]
- Siriwardene, N.R.; Deletic, A.; Fletcher, T.D. Clogging of stormwater gravel infiltration systems and filters: Insights from a laboratory study. Water Res. 2007, 41, 1433–1440. [Google Scholar] [CrossRef]
- Bouwer, H. Artificial recharge of groundwater: Hydrogeology and engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- Fetzer, J.; Holzner, M.; Plotze, M.; Furrer, G. Clogging of an alpine streambed by silt-sized particles-insights from laboratory and field experiments. Water Res. 2017, 126, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Kandra, H.S.; Mccarthy, D.; Fletcher, T.D.; Deletic, A. Assessment of clogging phenomena in granular filter media used for stormwater treatment. J. Hydrol. 2014, 512, 518–527. [Google Scholar] [CrossRef]
- Ahfir, N.D.; Wang, H.Q.; Benamar, A.; Alem, A.; Massei, N.; Dupont, J.P. Transport and deposition of suspended particles in saturated porous media: Hydrodynamic effect. Hydrogeol. J. 2007, 15, 659–668. [Google Scholar] [CrossRef]
- Lloyd, S.D.; Wong, T.H.F.; Liebig, T.; Becker, M. Sediment characteristics in stormwater pollution control ponds. Aust. J. Water Res. 2002, 5, 137–145. [Google Scholar] [CrossRef]
- Kandra, H.S.; Deletic, A.; Mccarthy, D. Assessment of impact of filter design variables on clogging in stormwater filters. Water Resour. Manag. 2014, 28, 1873–1885. [Google Scholar] [CrossRef]
- Sébastien, L.C.; Fletcher, T.D.; Deletic, A.; Barraud, S.; Poelsma, P. The influence of design parameters on clogging of stormwater biofilters: A large-scale column study. Water Res. 2012, 46, 67743–67752. [Google Scholar]
- Alem, A.; Ahfir, N.D.; Elkawafi, A.; Wang, H.Q. Hydraulic operating conditions and particle concentration effects on physical clogging of a porous medium. Transp. Porous Med. 2015, 106, 303–321. [Google Scholar] [CrossRef]
- Jegatheesan, V.; Vigneswaran, S. The effect of concentration on the early stages of deep bed filtration of submicron particles. Water Res. 1997, 31, 2910–2913. [Google Scholar] [CrossRef]
- Alem, A.; Elkawafi, A.; Ahfir, N.D.; Wang, H.Q. Filtration of kaolinite particles in a saturated porous medium: Hydrodynamic effects. Hydrogeol. J. 2013, 21, 573–586. [Google Scholar] [CrossRef]
- Bradford, S.A.; Bettahar, M.; Simunek, J.; Genuchten, M.T.V. Straining and attachment of colloids in physically heterogeneous porous media. Vadose Zone J. 2003, 3, 384–394. [Google Scholar] [CrossRef]
- Chang, Y.I.; Chen, S.C.; Chern, D.K. Hydrodynamic field effect on Brownian particles deposition in porous media. Sep. Purif. Technol. 2002, 27, 97–109. [Google Scholar] [CrossRef]
- Molnar, I.L.; Johnson, W.P.; Gerhard, J.I.; Willson, C.S.; O’Carroll, D.M. Predicting colloid transport through saturated porous media: A critical review. Water Resour. Res. 2015, 51, 6804–6845. [Google Scholar] [CrossRef]
- Nelson, K.E.; Ginn, T.R. New collector efficiency equation for colloid filtration in both natural and engineered flow conditions. Water Resour. Res. 2011, 47, 143–158. [Google Scholar] [CrossRef]
- Tien, C.; Payatakes, A.C. Advances in deep bed filtration. AIChE J. 1979, 25, 737–759. [Google Scholar] [CrossRef]
- Rege, S.D.; Fogler, H.S. A network model for deep bed filtration of solid particles and emulsion drops. AIChE J. 2010, 34, 1761–1772. [Google Scholar] [CrossRef]
- Mays, D.C.; Hunt, J.R. Hydrodynamic aspects of particle clogging in porous media. Environ. Sci. Technol. 2005, 39, 577–584. [Google Scholar] [CrossRef]
- Mays, D.C.; Hunt, J.R. Hydrodynamic and chemical factors in clogging by montmorillonite in porous media. Environ. Sci. Technol. 2007, 41, 5666–5671. [Google Scholar] [CrossRef]
- Johnson, W.P.; Anna, R.; Eddy, P.; Markus, H. Why variant colloid transport behaviors emerge among identical individuals in porous media when colloid-surface repulsion exists. Environ. Sci. Technol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Davis, A.P. Urban particle capture in bioretention media. II: Theory and model development. J. Environ. Eng. 2008, 134, 419–432. [Google Scholar] [CrossRef]
- Bradford, S.A.; Simunek, J.; Bettahar, M.; Genuchten, M.T.V.; Yates, S.R. Modeling colloid attachment, straining, and exclusion in saturated porous media. Environ. Sci. Technol. 2003, 37, 2242–2250. [Google Scholar] [CrossRef]
- Herzig, J.P.; Leclerc, D.M.; Goff, P.L. Flow of suspensions through porous media-application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- Xu, S.; Gao, B.; Saiers, J.E. Straining of colloidal particles in saturated porous media. Water Resour. Res. 2006, 42, 731–741. [Google Scholar] [CrossRef]
- Vaughan, P.R.; Soares, H.F. Design of filters for clay cores of dams. J. Geotech. Eng. 1982, 108, 17–31. [Google Scholar]
- Reddi, L.N.; Xiao, M.; Hajra, M.G.; Lee, I.M. Physical clogging of soil filters under constant flow rate versus constant head. Can. Geotech. J. 2005, 42, 804–811. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology; Prentice Hall: Upper Saddle River, NJ, USA, 2001; p. 598. [Google Scholar]
- Atlabachew, A.; Shu, L.; Wu, P.; Zhang, Y.; Xu, Y. Numerical modeling of solute transport in a sand tank physical model under varying hydraulic gradient and hydrological stresses. Hydrogeol. J. 2018, 26, 2089–2113. [Google Scholar] [CrossRef]
- Lang, J.S.; Giron, J.J.; Hansen, A.T.; Trussell, R.R.; Hodges, W.E.J. Investigating filter performance as a function of the ratio of filter size to media size. J. Am. Water Works Assoc. 1993, 85, 122–130. [Google Scholar] [CrossRef]
- Zamani, A.; Maini, B. Flow of dispersed particles through porous media-deep bed filtration. J. Petrol. Sci. Eng. 2009, 69, 71–88. [Google Scholar] [CrossRef]
- Boller, M.A.; Kavanaugh, M.C. Particle characteristics and head loss increase in granular media filtration. Water Res. 1995, 29, 1139–1149. [Google Scholar] [CrossRef]
- De Marsily, G. Quantitative Hydrogeology: Groundwater Hydrology for Engineers; Academic Press: Cambridge, MA, USA, 1986; p. 158. [Google Scholar]
- Xu, S.; Saiers, J.E. Colloid straining within water-saturated porous media: Effects of colloid size nonuniformity. Water Resour. Res. 2009, 45, 641–648. [Google Scholar] [CrossRef]
- Mousavi, S.F.; Rezai, V. Evaluation of scraping treatments to restore initial infiltration capacity of three artificial recharge projects in central Iran. Hydrogeol. J. 1999, 7, 490–500. [Google Scholar] [CrossRef]
- Zhang, P.; Johnson, W.P.; Scheibe, T.D.; Choi, K.H.; Mailloux, B.J. Extended tailing of bacteria following breakthrough at the narrow channel focus area, Oyster, Virginia. Water Resour. Res. 2001, 37, 2687–2698. [Google Scholar] [CrossRef]
- Elimelech, M.; Jia, X.; Gregory, J.; Williams, R. Particle deposition and aggregation. Part. Deposition Aggregation 1998, 88, 13–15. [Google Scholar]
- Sen, T.K.; Khilar, K.C. Review on subsurface colloids and colloid-associated contaminant transport in saturated porous media. Adv. Colloid Interface Sci. 2006, 119, 71–96. [Google Scholar]
- Francey, M.; Fletcher, T.D.; Deletic, A.; Duncan, H.P. New insights into water quality of Urban stormwater in South Eastern Australia. J. Environ. Eng. 2010, 136, 381–390. [Google Scholar] [CrossRef]
- Han, Y.H.; Lau, S.L.; Kayhanian, M.; Stenstrom, M.K. Correlation analysis among highway stormwater pollutants and characteristics. Water Sci. Technol. 2006, 53, 235–243. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Z.; Shu, L.; Min, X.; Chifuniro Mabedi, E. Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study. Water 2019, 11, 1083. https://doi.org/10.3390/w11051083
Zou Z, Shu L, Min X, Chifuniro Mabedi E. Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study. Water. 2019; 11(5):1083. https://doi.org/10.3390/w11051083
Chicago/Turabian StyleZou, Zhike, Longcang Shu, Xing Min, and Esther Chifuniro Mabedi. 2019. "Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study" Water 11, no. 5: 1083. https://doi.org/10.3390/w11051083
APA StyleZou, Z., Shu, L., Min, X., & Chifuniro Mabedi, E. (2019). Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study. Water, 11(5), 1083. https://doi.org/10.3390/w11051083




