Simulation of the Surface Energy Flux and Thermal Stratification of Lake Taihu with Three 1-D Models
Abstract
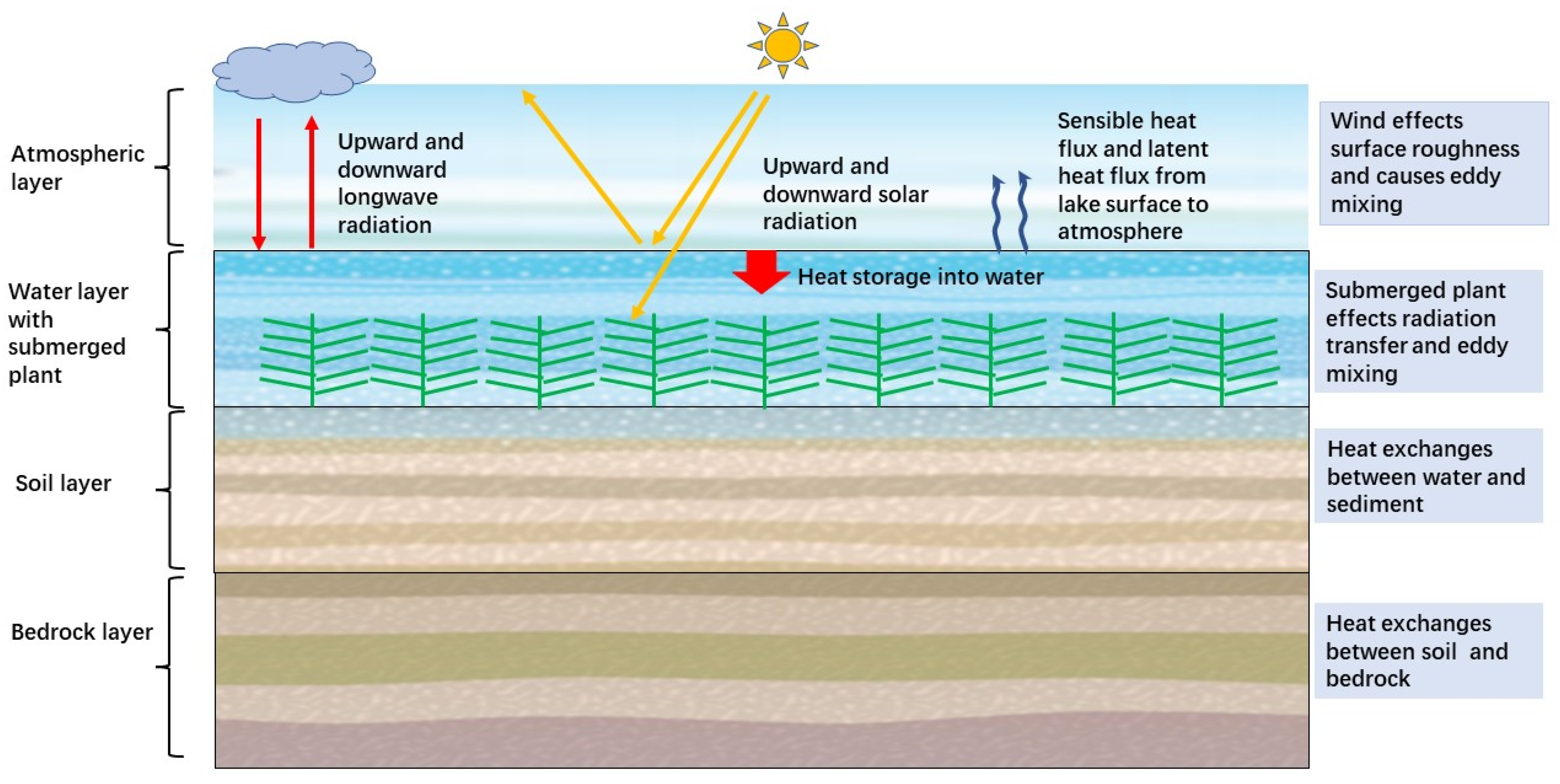
:1. Introduction
2. Materials and Methods
2.1. Three 1-D models for Lake Taihu
2.1.1. CLM4-LISSS Lake Model
2.1.2. E-ε Lake Model
2.1.3. LAKE Model
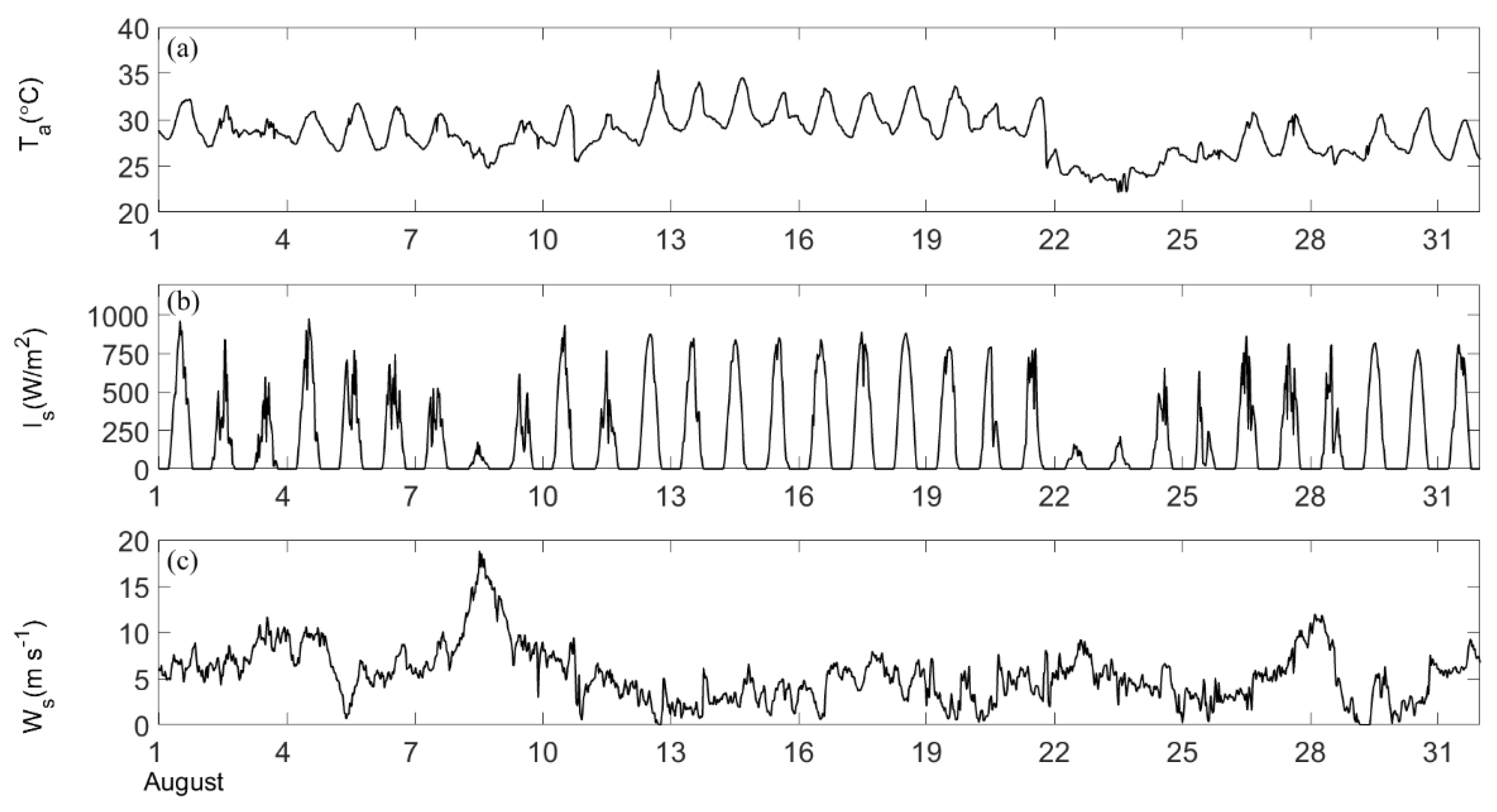
2.2. Observation Data
3. Results and Discussion
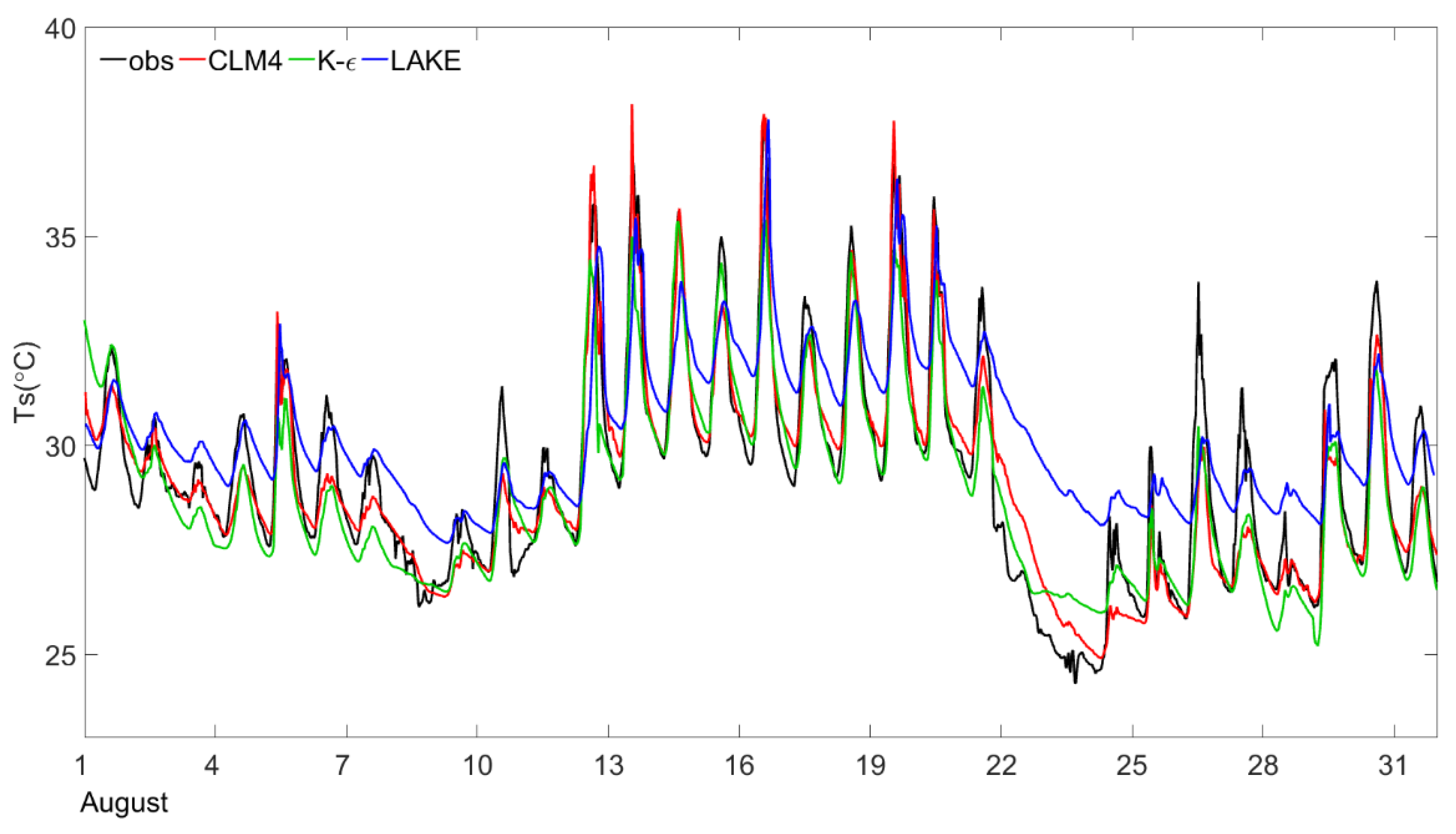
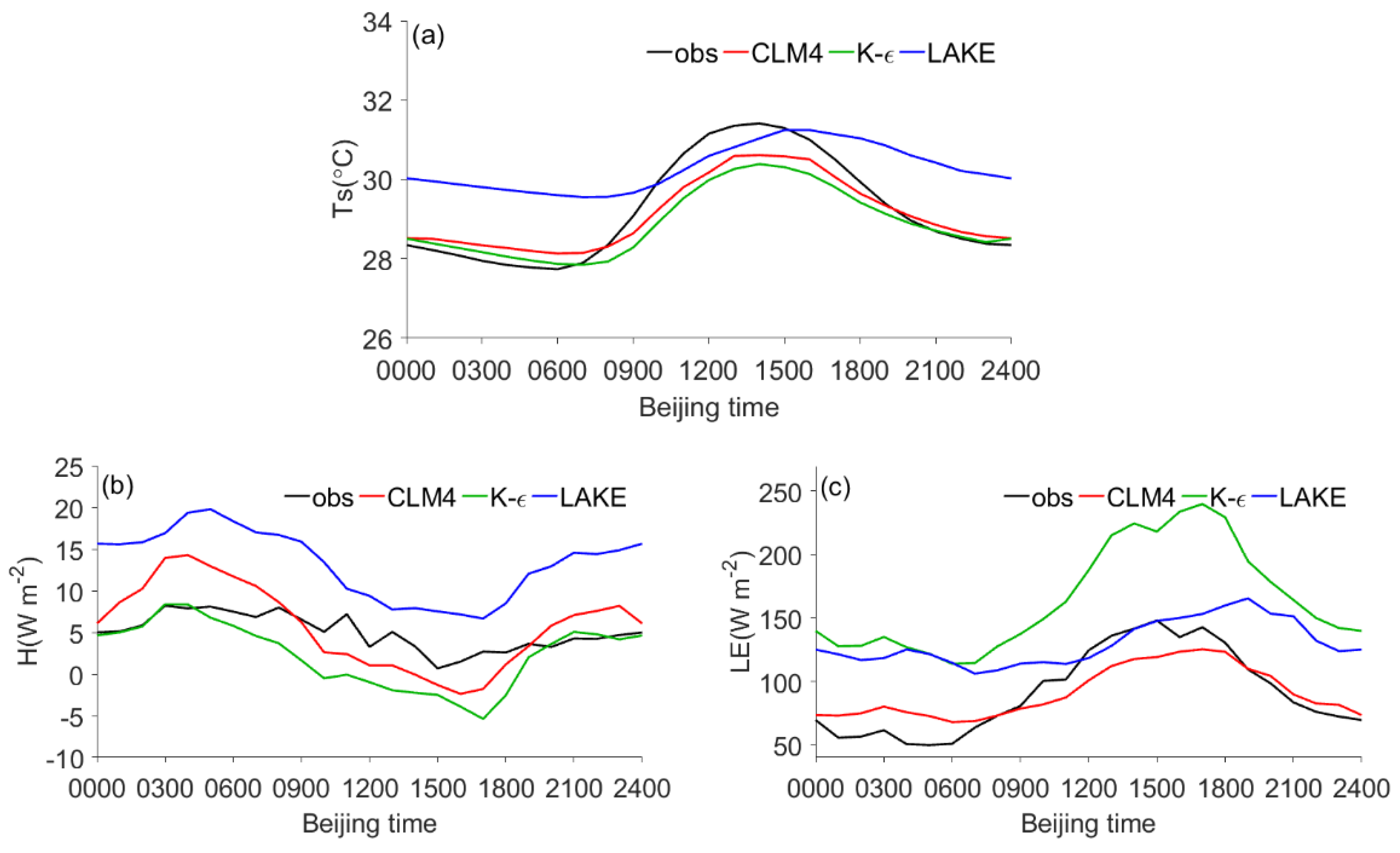
3.1. Lake Surface Temperature
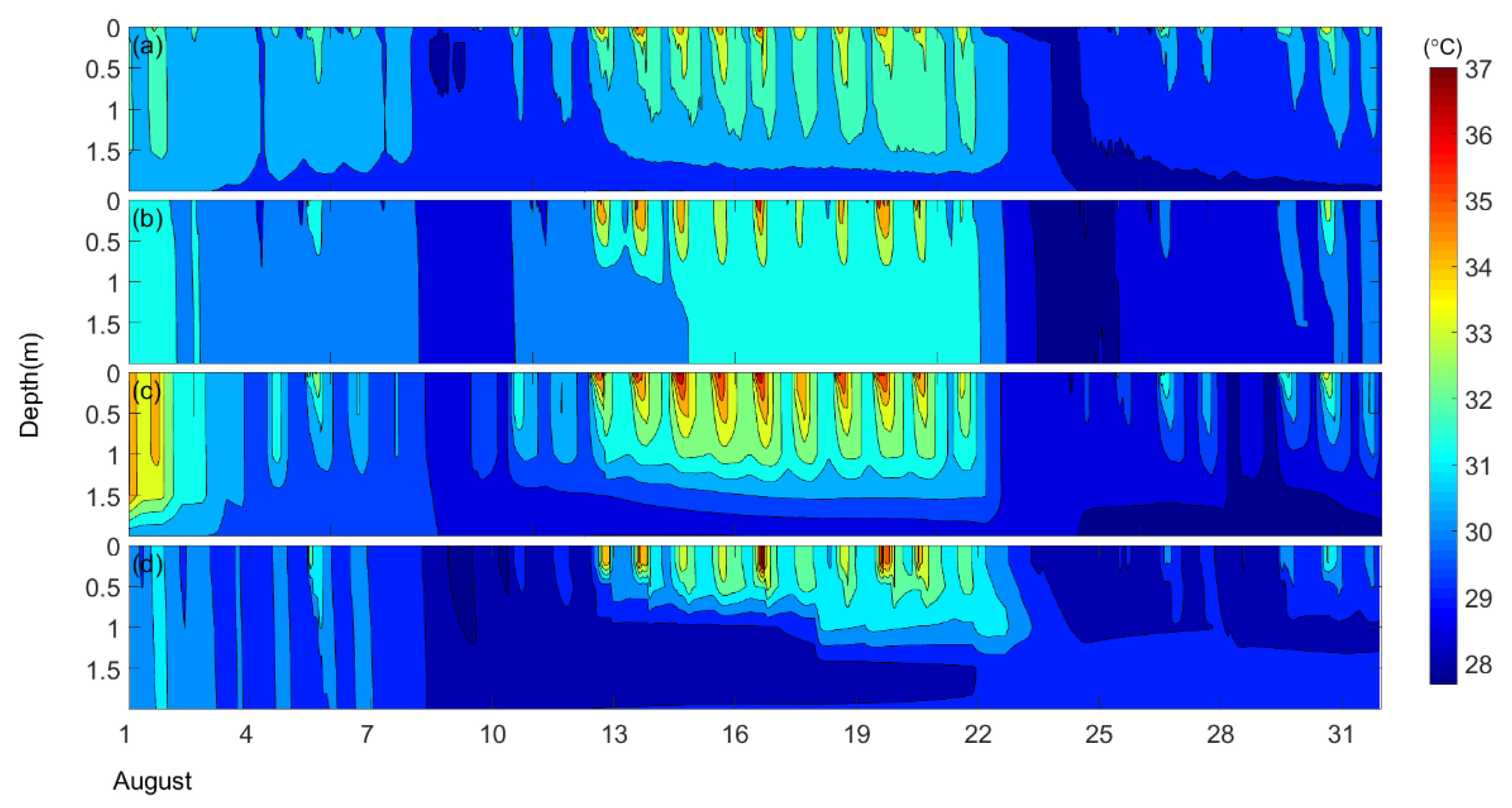
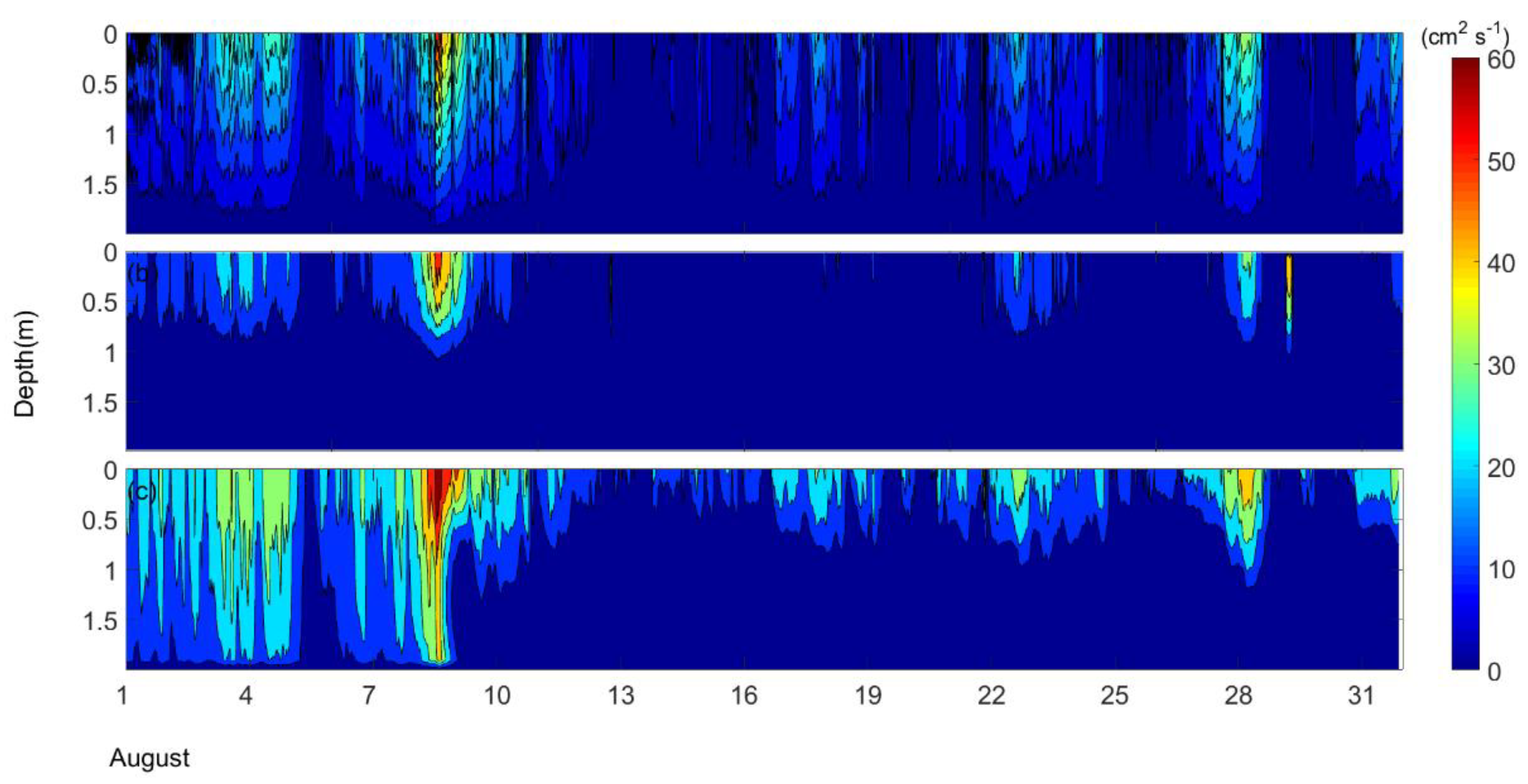
3.2. The Thermal Stratification of Lake
3.3. Differences in EEC and their Effects on Thermal Stratification Simulation
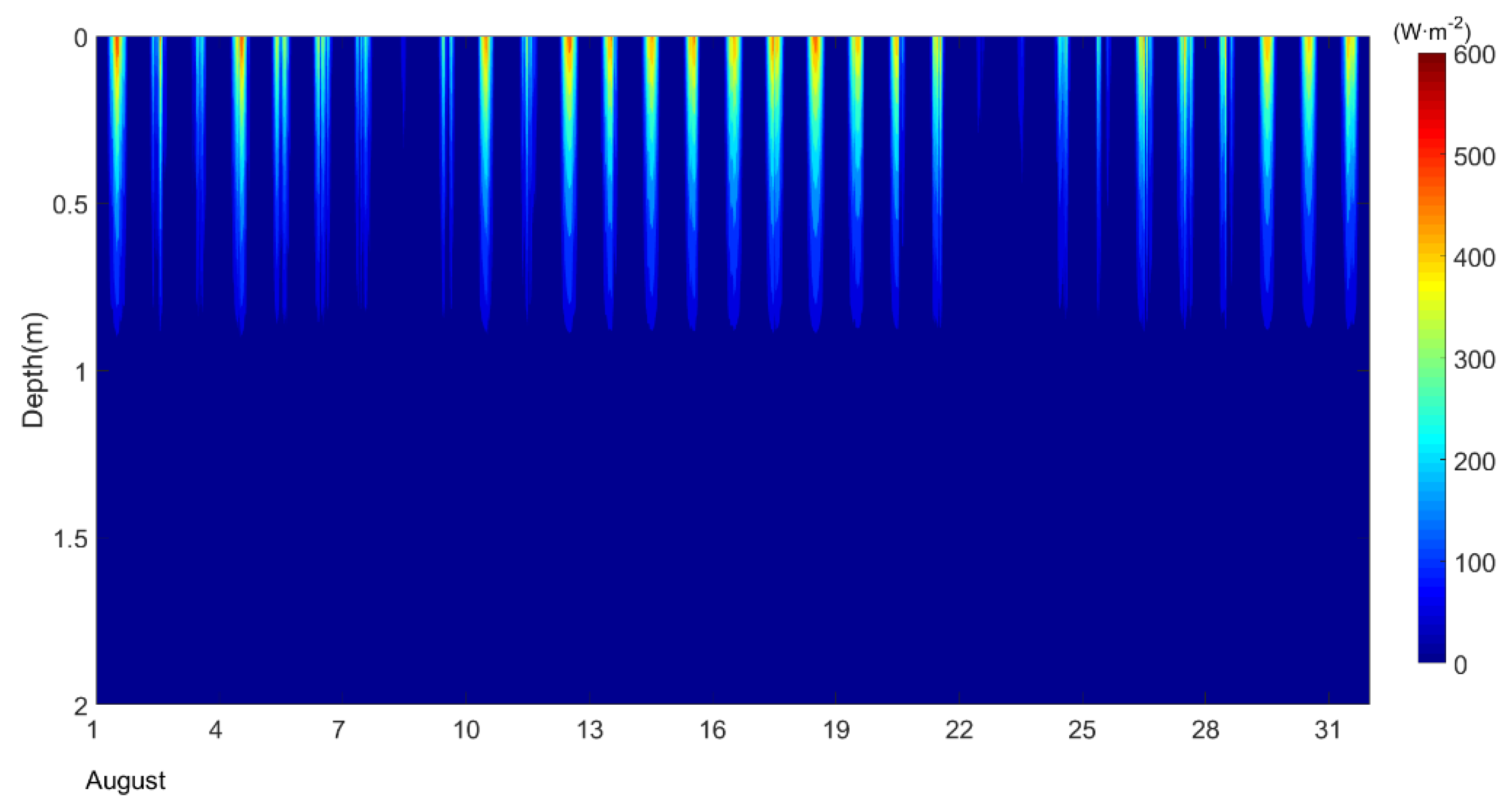
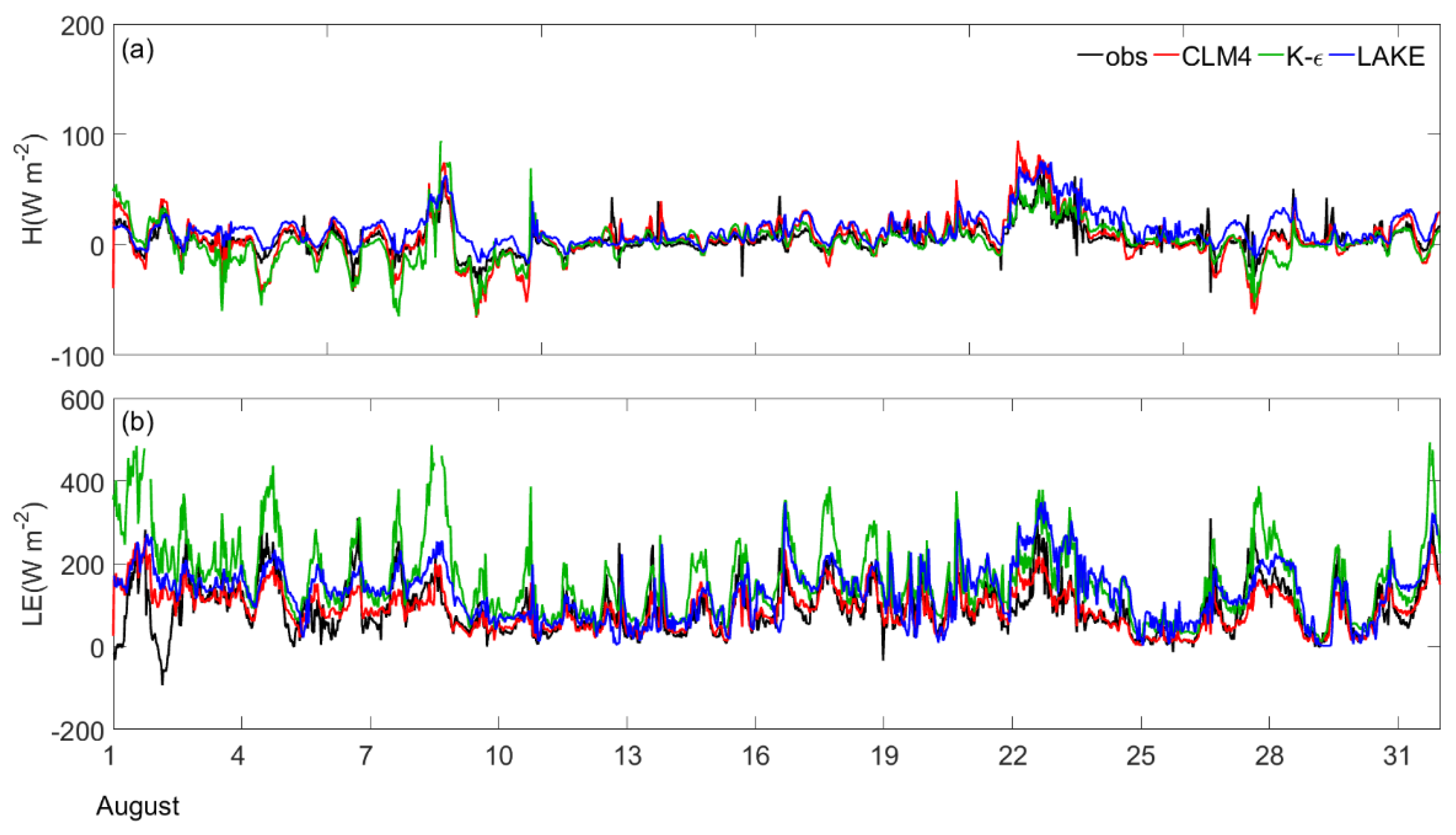
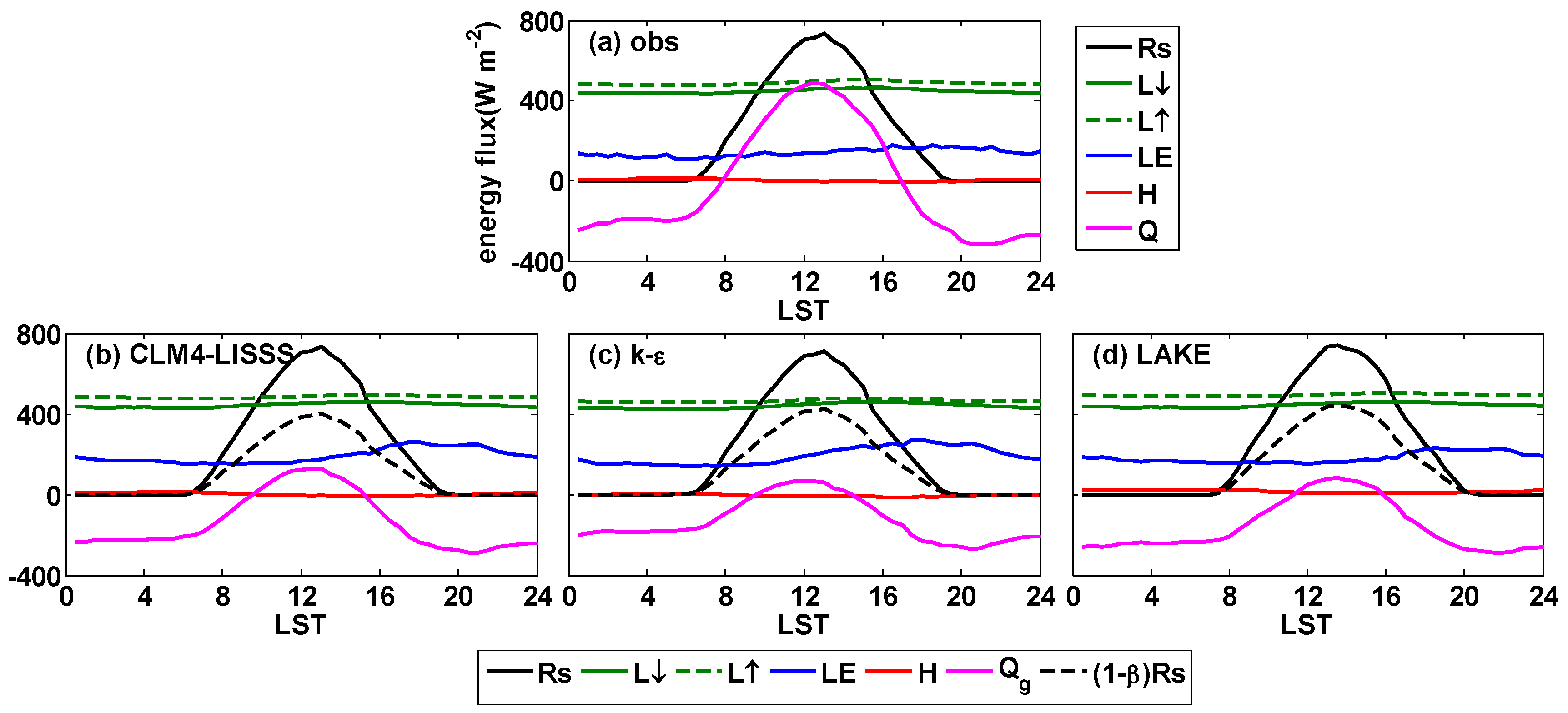
3.4. Lake Surface Energy Flux
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, S.F.; Yan, J.F.; Xia, N.; Li, Q. The model study of water mass and energy exchange between the inland water body and atmosphere. Sci. China Ser. G Phys. Mech. Astron. 2008, 51, 1010–1021. [Google Scholar] [CrossRef]
- Sun, S.F.; Yan, J.F.; Xia, N.; Sun, C.H. Development of a model for water and heat exchange between the atmosphere and a water body. Adv. Atmos. Sci. 2007, 24, 927–938. [Google Scholar] [CrossRef]
- Adrian, R.; Reilly, C.M.O.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van, D.E.; et al. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Long, Z.; Perrie, W.; Gyakum, J.; Caya, D.; Laprise, R. Northern lake impacts on local seasonal climate. J. Hydrometeorol. 2007, 8, 881–896. [Google Scholar] [CrossRef]
- Butcher, J.B.; Nover, D.; Johnson, T.E.; Clark, C.M. Sensitivity of lake thermal and mixing dynamics to climate change. Clim. Chang. 2015, 129, 295–305. [Google Scholar] [CrossRef]
- Goyal, M.K.; Ojha, C.S.P. Evaluation of Rule and Decision Tree Induction Algorithms for Generating Climate Change Scenarios for Temperature and Pan Evaporation on a Lake Basin. J. Hydrol. Eng. 2013, 19, 828–835. [Google Scholar] [CrossRef]
- Lyons, W.A. The climatology and prediction of the Chicago lake breeze. J. Appl. Meteorol. 1972, 11, 1259–1270. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, B.; Gao, J.H.; Kang, H.Q. Impact of Taihu Lake on city ozone in the Yangtze River Delta. Adv. Atmos. Sci. 2017, 34, 226–234. [Google Scholar] [CrossRef]
- Mironov, D.; Heise, E.; Kourzeneva, E. Implementation of the lake parameterisation scheme FLake into the numerical weather prediction model COSMO. Boreal Environ. Res. 2010, 15, 218–230. [Google Scholar]
- Hostetler, S.W.; Bartlein, P.J. Simulation of lake evaporation with application to modeling lake level variations of harney-malheur lake, Oregon. Water Resour. Res. 1990, 26, 2603–2612. [Google Scholar]
- Fang, X.; Stefan, H.G. Long-term lake water temperature and ice cover simulations/measurements. Cold Reg. Sci. Technol. 1996, 24, 289–304. [Google Scholar] [CrossRef]
- Subin, Z.M.; Riley, W.J.; Mironov, D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Modeling Earth Syst. 2012, 4. [Google Scholar] [CrossRef]
- Ren, X.Q.; Li, Q.; Chen, W.; Liu, H.Z. A new lake-gas heat transfer model and its simulation capability evaluation. Adv. Atmos. Sci. 2014, 38, 993–1004. (In Chinese) [Google Scholar]
- Yeates, P.S.; Imberger, J. Pseudo two-dimensional simulations of internal and boundary fluxes in stratified lakes and reservoirs. Int. J. River Basin Manag. 2003, 1, 297–319. [Google Scholar] [CrossRef]
- Goudsmit, G.H.; Burchard, H.; Peeters, F. Application of k-ε turbulence models to enclosed basins: The role of internal seiches. J. Geophys. Res. Ocean. 2002, 107. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Lykossov, V.N. Numerical modeling of heat and moisture transfer processes in a system lake—Soil. J. Russ. Meteorol. Hydrol. 2005, 3, 95–104. [Google Scholar]
- Stepanenko, V.; Joehnk, K.D.; Machulskaya, E.; Perroud, M.; Subin, Z.; Nordbo, A.; Mammarella, I.; Mironov, D. Simulation of surface energy fluxes and stratification of a small boreal lake by a set of one-dimensional models. Tellus 2014, 66, 174–179. [Google Scholar] [CrossRef]
- Thiery, W.; Stepanenko, V.M.; Fang, X.; JӧHnk, K.D.; Li, Z.; Martynov, A.; Perroud, M.; Subin, Z.M.; Darchambeau, F.; Mironov, D.; et al. LakeMIP Kivu: Evaluating the representation of a large, deep tropical lake by a set of one-dimensional lake models. J. Tellus A Dyn. Meteorol. Oceanogr. 2014, 68, 21390. [Google Scholar] [CrossRef]
- Ren, X.Q.; Sun, S.F.; Chen, W.; Liu, H.Z. Summary of current research on numerical simulation of lakes. Adv. Earth Sci. 2013, 28, 347–356. (In Chinese) [Google Scholar]
- Gu, H.P.; Jin, J.M.; Wu, Y.H.; Ek, M.B.; Subin, Z.M. Calibration and validation of lake surface temperature simulations with the coupled wrf-lake model. Clim. Chang. 2015, 129, 471–483. [Google Scholar] [CrossRef]
- Xu, L.J.; Liu, H.Z.; Du, Q.; Wang, L. Evaluation of the WRF-lake model over a highland freshwater lake in southwest China. J. Geophys. Res. Atmos. 2016, 121, 13989–14005. [Google Scholar] [CrossRef]
- Heiskanen, J.J.; Mammarella, I.; Ojala, A.; Stepanenko, V.; Erkkilä, K.M.; Miettinen, H.; Sandstrӧm, H.; Eugster, W.; Leppäranta, M.; Järvinen, H.; et al. Effects of water clarity on lake stratification and lake-atmosphere heat exchange. J. Geophys. Res. Atmos. 2015, 120, 7412–7428. [Google Scholar] [CrossRef]
- Zolfaghari, K.; Duguay, C.R.; Pour, H.K. Satellite-derived light extinction coefficient and its impact on thermal structure simulations in a 1-D lake model. Hydrol. Earth Syst. Sci. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Lee, X.H.; Liu, S.D.; Xiao, W.; Wang, W.; Gao, Z.Q.; Cao, C.; Hu, C.; Hu, Z.H.; Shen, S.H.; Wang, Y.W. The Taihu eddy flux network: an observational program on energy, water, and greenhouse gas fluxes of a large freshwater lake. Bull. Am. Meteorol. Soc. 2014, 95, 1583–1594. [Google Scholar] [CrossRef]
- Yang, Y.C.; Wang, Y.W.; Zhang, Z.; Wang, W.; Ren, X.; Gao, Y.Q.; Liu, S.D.; Lee, X.H. Diurnal and Seasonal Variations of Thermal Stratification and Vertical Mixing in a Shallow Fresh Water Lake. J. Meteorol. Res. 2018, 32, 219–232. [Google Scholar] [CrossRef]
- Horppila, J.; Nurminen, L. Effects of submerged macrophytes on sediment resuspension and internal phosphorus loading in lake hiidenvesi (southern Finland). Water Res. 2003, 37, 4468–4474. [Google Scholar] [CrossRef]
- Dale, H.M.; Gillespie, T.J. The influence of submersed aquatic plants on temperature gradients in shallow water bodies. Botany 1977, 55, 2216–2225. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Dynamics of heat exchange between sediment and water in a lake. Water Resour. Res. 1996, 32, 1719–1727. [Google Scholar] [CrossRef]
- Golosov, S.; Kirillin, G.A. parameterized model of heat storage by lake sediments. Environ. Model. Softw. 2010, 25, 793–801. [Google Scholar] [CrossRef]
- Deng, B.; Liu, S.D.; Xiao, W.; Wang, W.; Jin, J.M.; Lee, X.H. Evaluation of the clm4 lake model at a large and shallow freshwater lake*. J. Hydrometeorol. 2013, 14, 636–649. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, Y.W.; Hu, C.; Wang, W.; Zhang, N.; Xiao, Q.T.; Liu, S.D.; Lee, X.H. The lake-air exchange simulation of a lake model over eastern Taihu Lake based on the E-ε turbulent kinetic energy closure thermodynamic process. Acta Meteorol. Sin. 2016, 74, 633–645. (In Chinese) [Google Scholar]
- Henderson-Sellers, B. New formulation of eddy diffusion thermocline models. J. Appl. Math. Model. 1985, 9, 441–446. [Google Scholar] [CrossRef]
- Herb, W.R.; Stefan, H.G. Dynamics of vertical mixing in a shallow lake with submersed macrophytes. Water Resour. Res. 2005, 41, 293–307. [Google Scholar] [CrossRef]
- Stepanenko, V.M.; Martynov, A.; Jӧhnk, K.D.; Subin, Z.M.; Perroud, M.; Fang, X.; Beyrich, F.; Mironov, D.; Goyette, S. A one-dimensional model intercomparison study of thermal regime of a shallow, turbid midlatitude lake. J. Geosci. Model Dev. 2013, 6, 1337–1352. [Google Scholar] [CrossRef]
- Xiao, W.; Liu, S.D.; Wang, W.; Yang, D.; Xu, J.P.; Cao, C.; Li, H.C.; Lee, X.H. Transfer coefficients of momentum, sensible heat and water vapour in the atmospheric surface layer of a large freshwater lake. Bound-Lay. Meteorol. 2013, 148, 479–494. [Google Scholar] [CrossRef]
- Wang, W.; Xiao, W.; Cao, C.; Gao, Z.Q.; Hu, Z.H.; Liu, S.D.; Shen, S.H.; Wang, L.L.; Xiao, Q.T.; Xu, J.P. Temporal and spatial variations in radiation and energy balance across a large freshwater lake in China. J. Hydrol. 2014, 511, 811–824. [Google Scholar] [CrossRef]
- Shu, Q.A. The human-induced driver on the development of Lake Taihu. In Proceedings of the Conference on the 93rd ESA Annual Meeting, San Jose, CA, USA, 3–8 August 2008. [Google Scholar]

| Lake Type | Vertical Stratification/Layers | Parameterization Scheme of Eddy Flux between Lake and Atmosphere | Parameterization Scheme of EEC | Consideration of Sediment Layers |
|---|---|---|---|---|
| CLM4-LISSS | multilayer/10 layers | Monin-Obukhov Similarity Theory | Henderson–Sellers scheme [32] | Yes |
| E-ε lake model | multilayer/50 layers | Empirical function | Eddy kinetic energy prediction equations | No |
| LAKE | multilayer/10 layers | Monin-Obukhov Similarity Theory | Eddy kinetic energy and dissipation prediction equations | Yes |
| CLM4–LISSS | E–ε Lake Model | LAKE | |
|---|---|---|---|
| Lake surface albedo | 0.055 | 0.055 | 0.055 |
| Extinction coefficient of water turbidity | 5 m−1 | 5 m−1 | 5 m−1 |
| Extinction coefficient of submerged plant | — | 0.02 m2 gdw−1 | — |
| EEC | k: Karman constant : surface friction velocity z: layer depth of lake p0: neutral value of turbulent Prandtl number ri: Richardson number N: Brunt-Vaisala constant | , set to be 0.1 mixing length coefficient turbulent kinetic energy. | λ0: molecular diffusivity V: wind speed V0: wind speed at which eddy diffusivity reaches its maximum λmax = 150 W (m K)−1 |
| Macrophyte height | — | 1.2m | — |
| Macrophyte biomass density | — | 100 gdw m−3 | — |
| CC | Centralized RMSE (°C) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TS | TW (20 cm) | TW (50 cm) | TW (100 cm) | TW (150 cm) | TS | TW (20 cm) | TW (50 cm) | TW (100 cm) | TW (150 cm) | |
| CLM4 | 0.94 | 0.94 | 0.94 | 0.96 | 0.95 | 0.85 | 0.64 | 0.59 | 0.42 | 0.53 |
| E-ε | 0.93 | 0.93 | 0.92 | 0.90 | 0.8 | 0.98 | 0.68 | 0.66 | 0.65 | 1.03 |
| LAKE | 0.82 | 0.93 | 0.89 | 0.58 | 0.06 | 1.45 | 0.64 | 0.78 | 1.20 | 1.49 |
| CC | Centralized RMSE (W m−2) | |||
|---|---|---|---|---|
| H | LE | H | LE | |
| CLM4 | 0.86 | 0.78 | 11.61 | 55.32 |
| E-ε | 0.77 | 0.72 | 11.56 | 64.53 |
| LAKE | 0.71 | 0.55 | 10.96 | 61.96 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ma, Q.; Gao, Y.; Hao, X.; Liu, S. Simulation of the Surface Energy Flux and Thermal Stratification of Lake Taihu with Three 1-D Models. Water 2019, 11, 1026. https://doi.org/10.3390/w11051026
Wang Y, Ma Q, Gao Y, Hao X, Liu S. Simulation of the Surface Energy Flux and Thermal Stratification of Lake Taihu with Three 1-D Models. Water. 2019; 11(5):1026. https://doi.org/10.3390/w11051026
Chicago/Turabian StyleWang, Yongwei, Qian Ma, Yaqi Gao, Xiaolong Hao, and Shoudong Liu. 2019. "Simulation of the Surface Energy Flux and Thermal Stratification of Lake Taihu with Three 1-D Models" Water 11, no. 5: 1026. https://doi.org/10.3390/w11051026
APA StyleWang, Y., Ma, Q., Gao, Y., Hao, X., & Liu, S. (2019). Simulation of the Surface Energy Flux and Thermal Stratification of Lake Taihu with Three 1-D Models. Water, 11(5), 1026. https://doi.org/10.3390/w11051026





