Evaluation of the Effect of Wind Velocity and Soil Moisture Condition on Soil Erosion in Andosol Agricultural Fields (Model Experiment)
Abstract
1. Introduction
2. Methodology
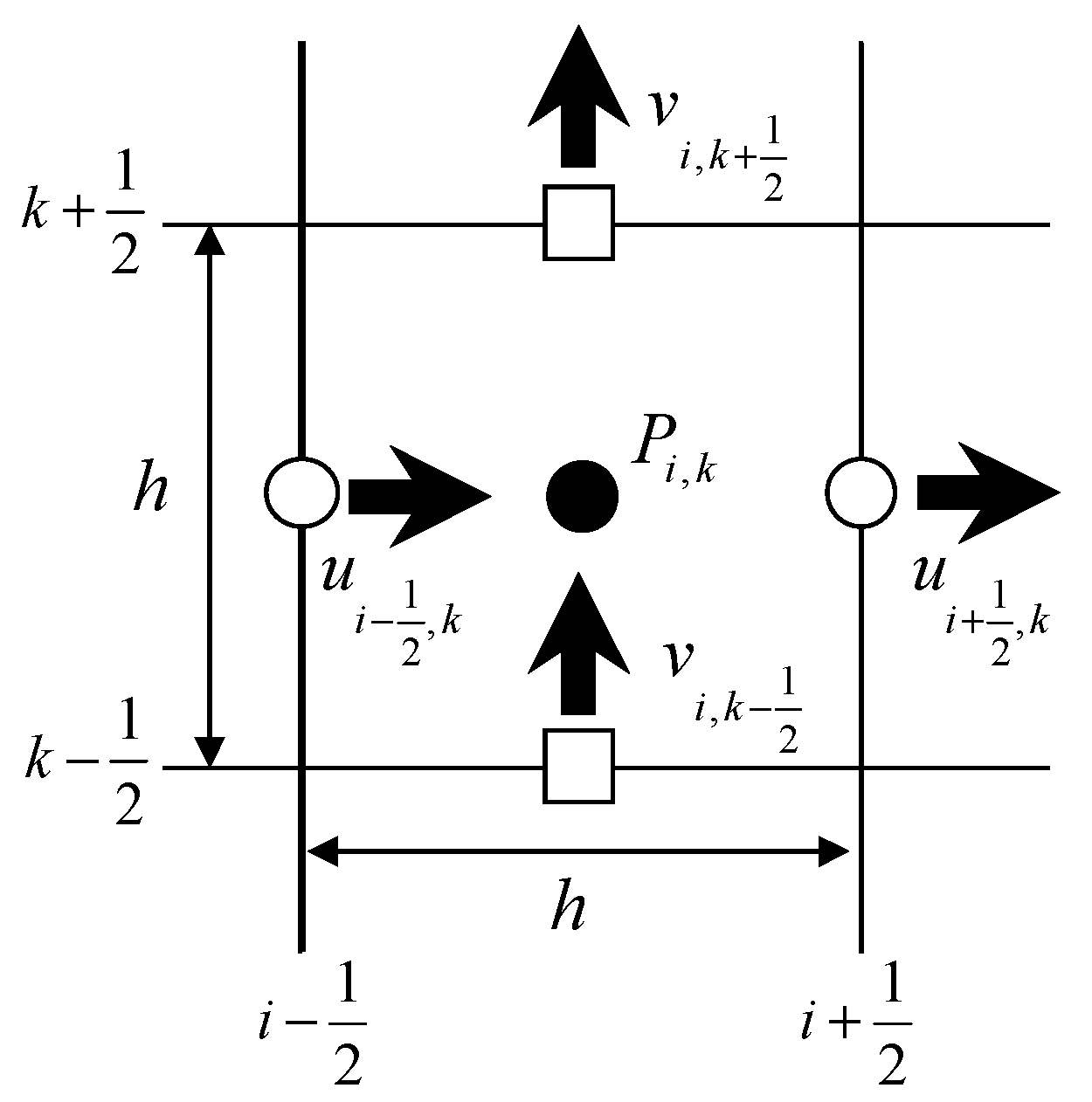
2.1. Numerical Model to Simulate Airflow over a Bare Soil Field
2.2. Eddy Diffusion Coefficient
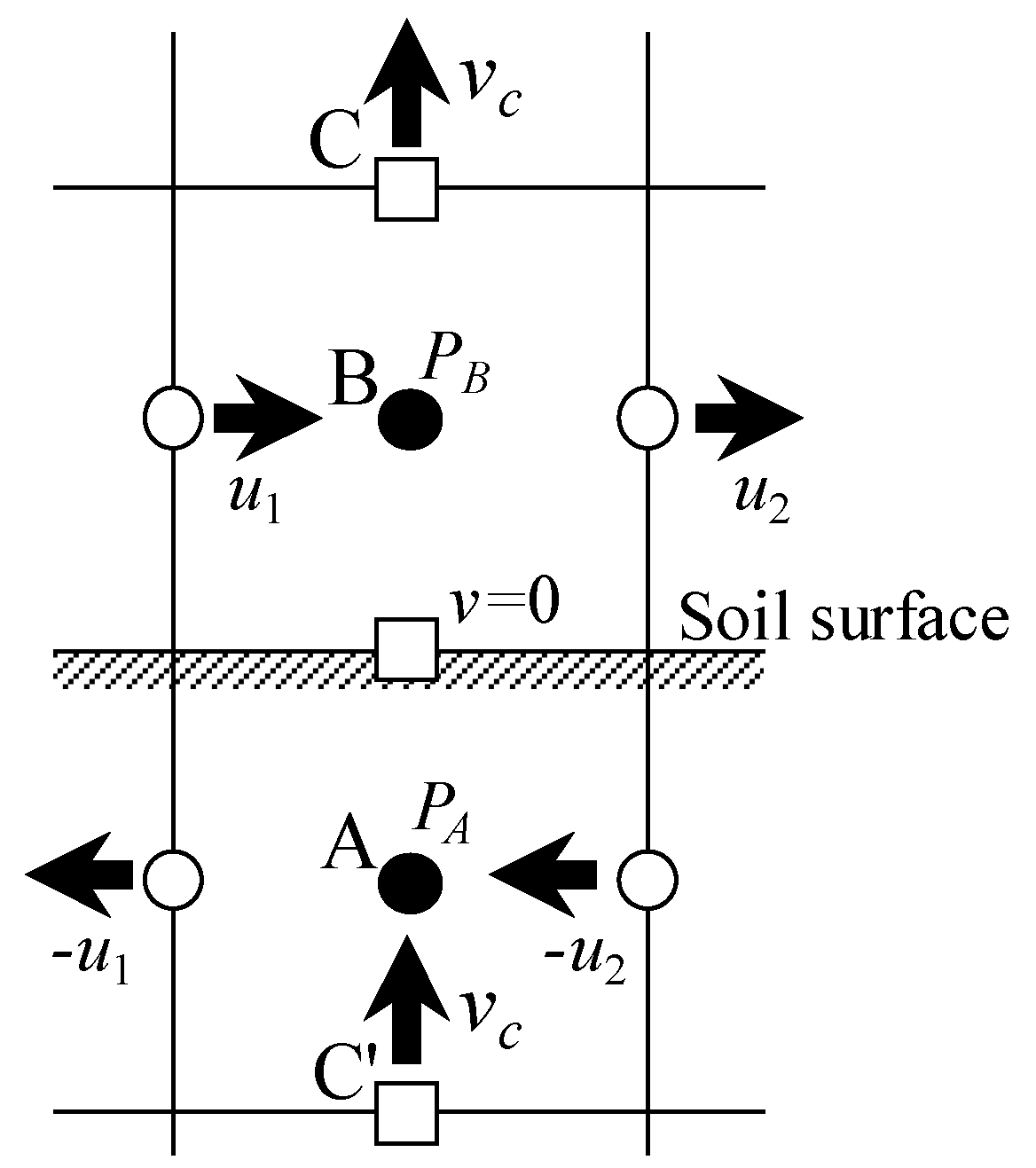
2.3. Boundary Condition
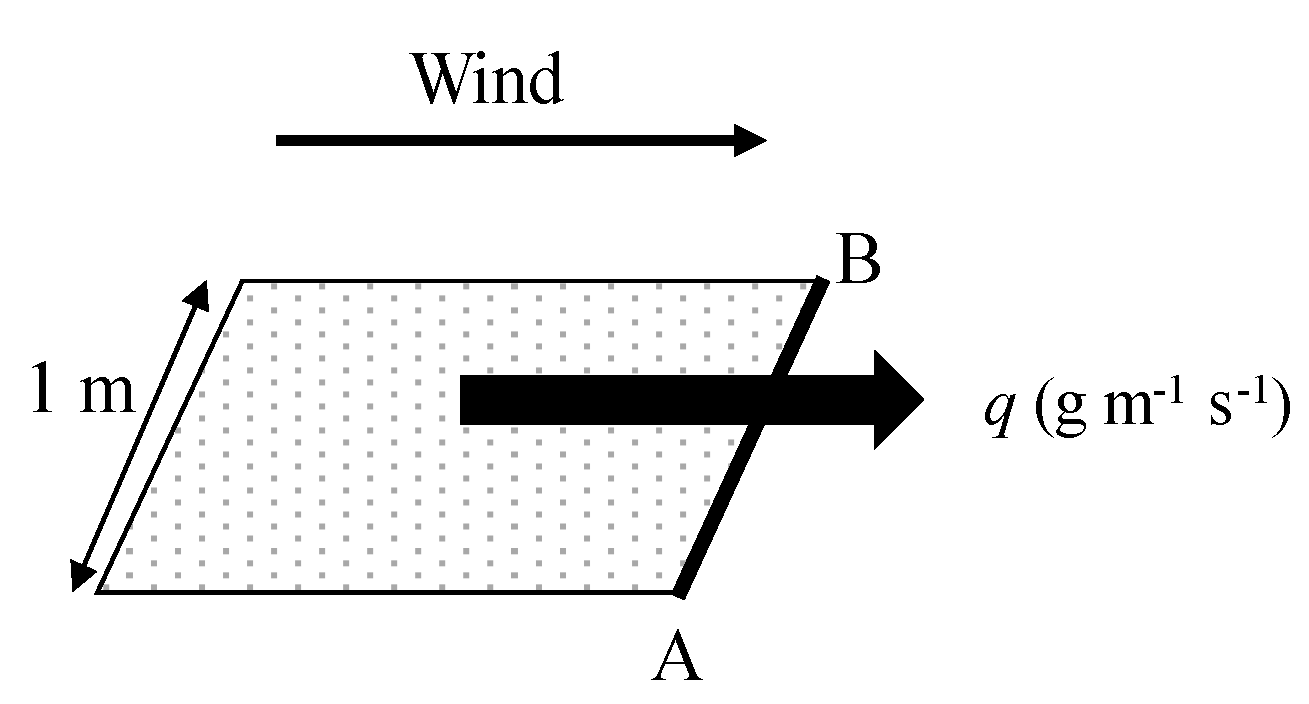
2.4. Quantification of Soil Erosion by the Wind
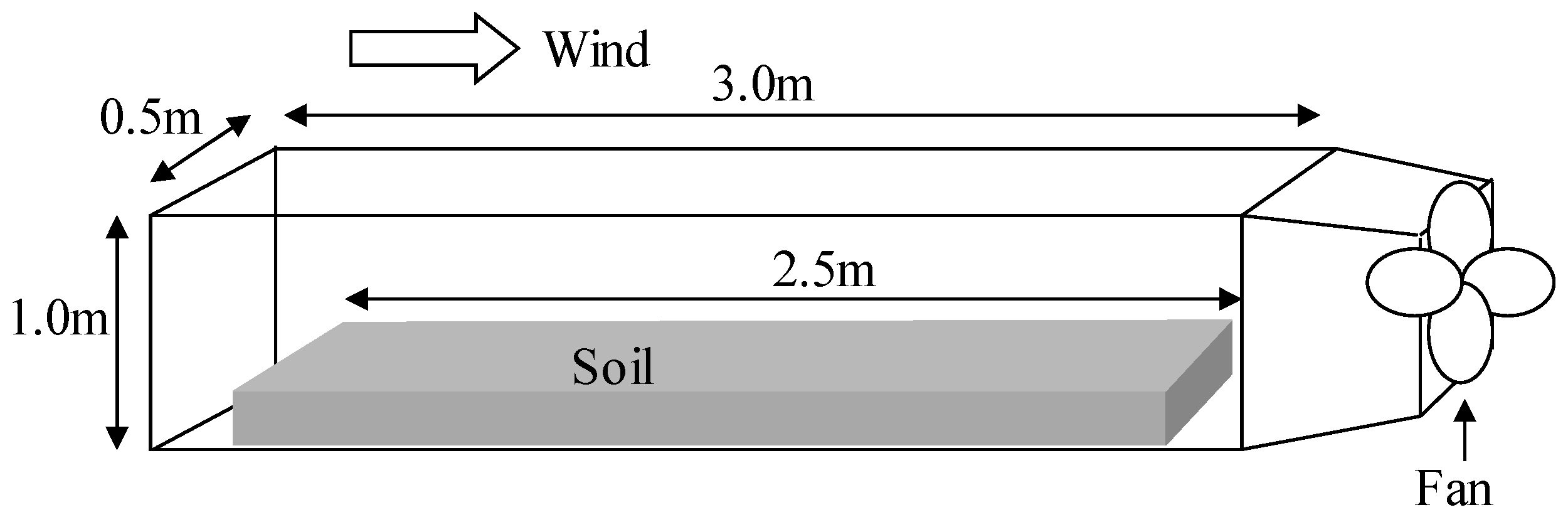
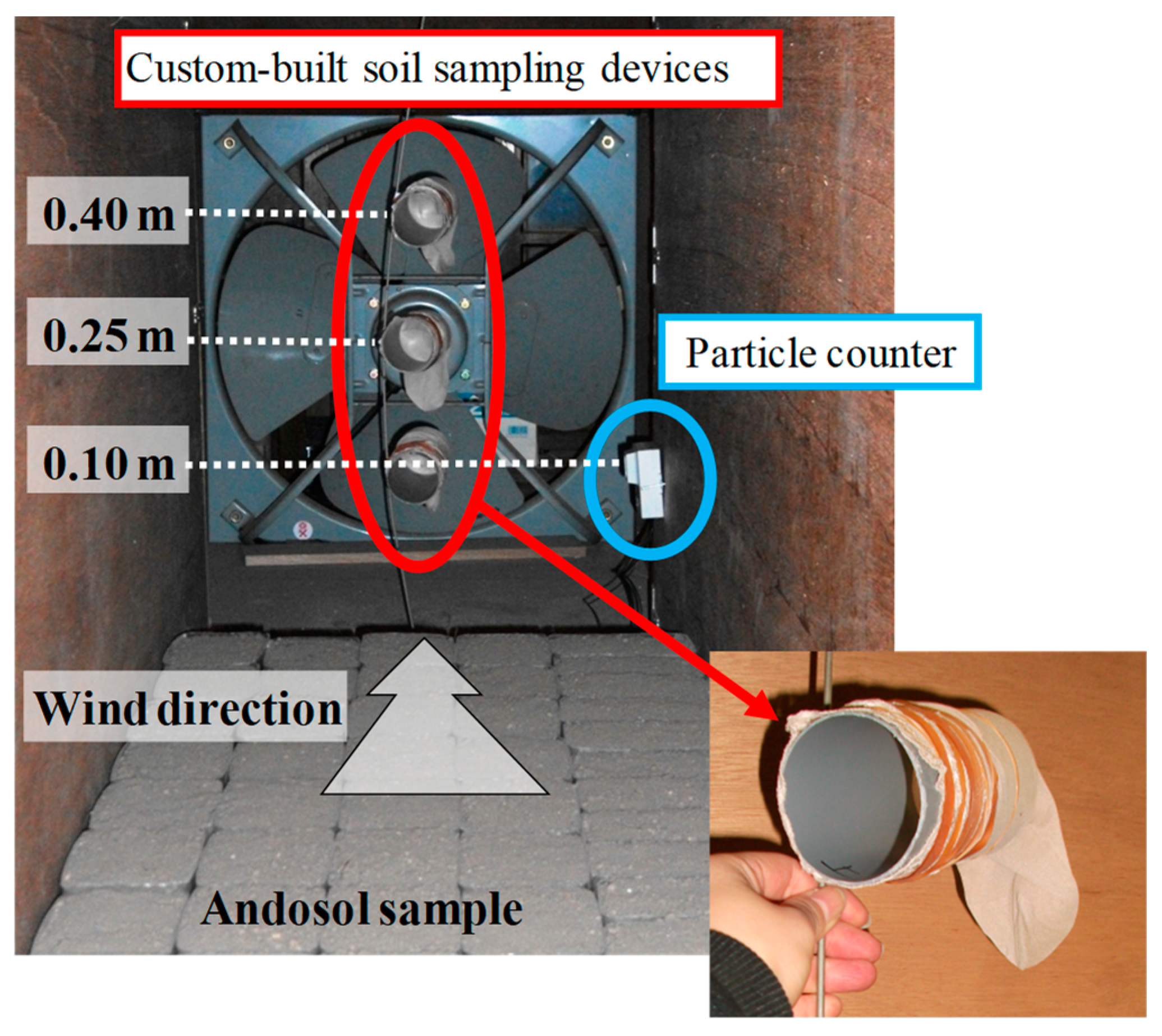
3. Wind Tunnel Experiment
4. Results and Discussion
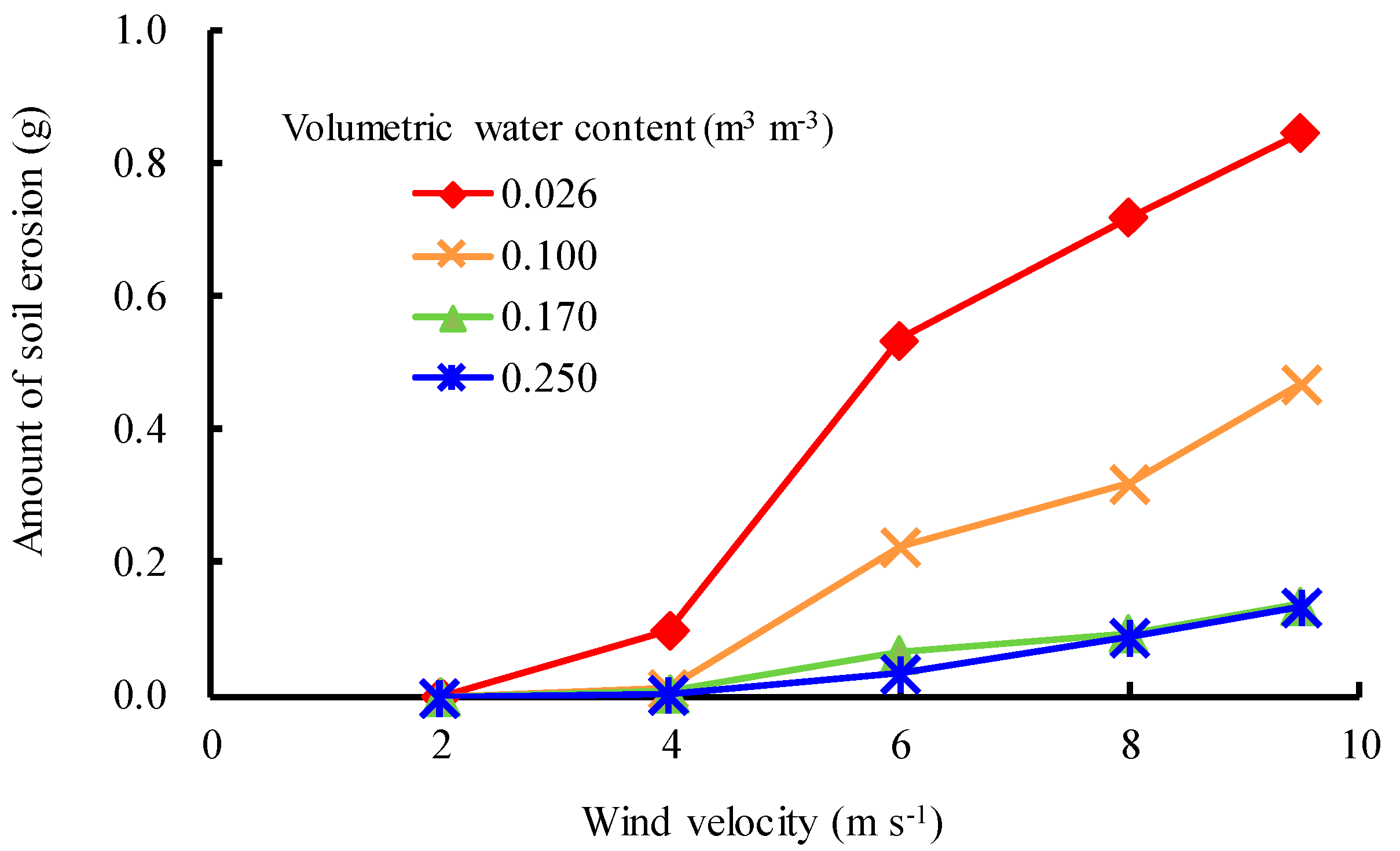
4.1. Relationship between Soil Moisture Condition, wind Velocity, and Amount of Soil Erosion
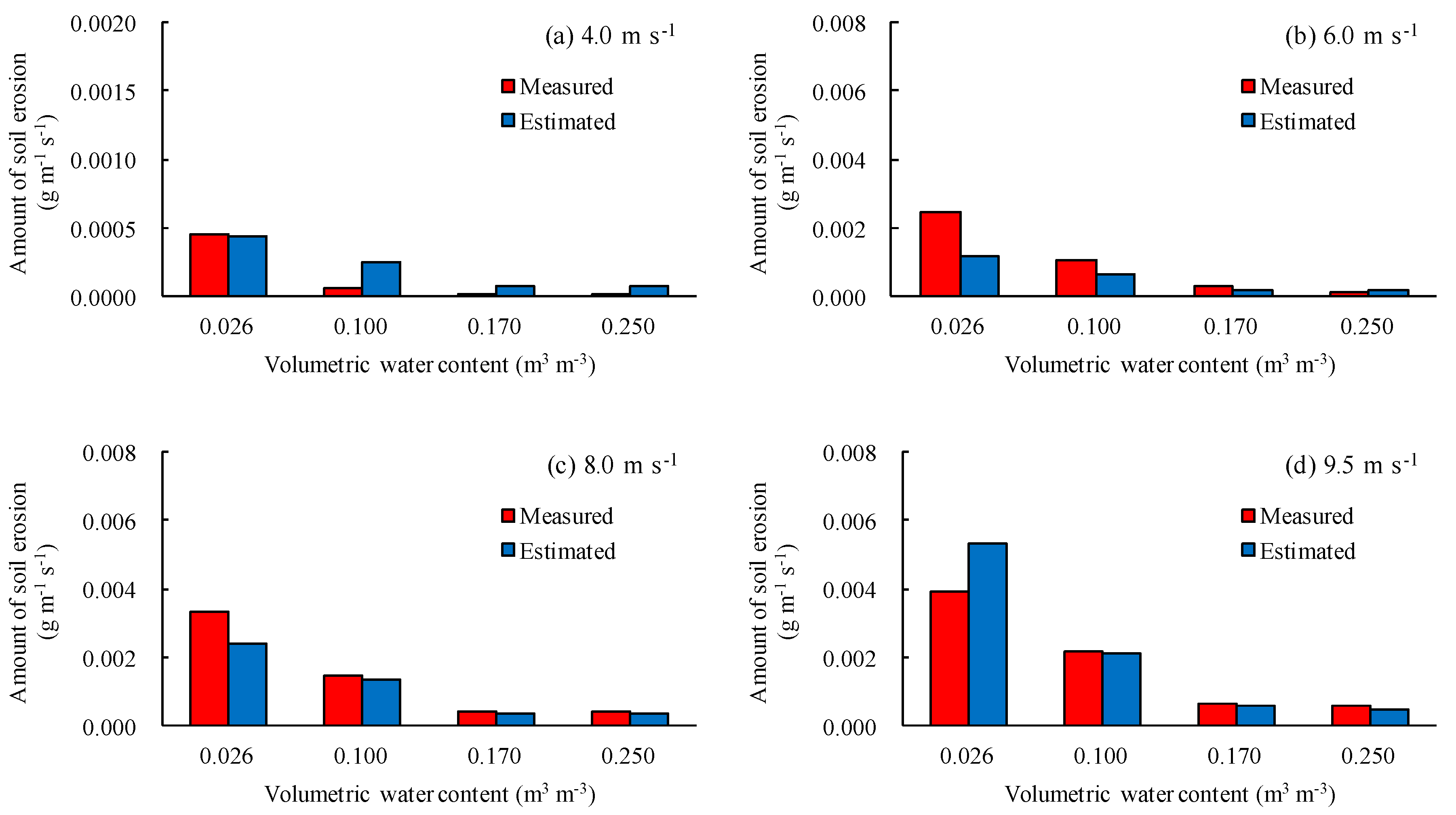
4.2. Parameter Estimation for Quantification of Soil Erosion
4.3. Quantification of Timing and Amount of Irrigation Water to Prevent the Soil Erosion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, L.R. World population growth, soil erosion, and food security. Science 1981, 214, 995–1002. [Google Scholar] [CrossRef] [PubMed]
- Lal, R.; Hall, G.F.; Miller, F.P. Soil degradation: I. Basic processes. Land Degrad. Dev. 1989, 1, 51–69. [Google Scholar] [CrossRef]
- Oldeman, L.R.; Hakkeling, R.T.A.; Sombroeck, W.G. World Map of the Status of Human-Induced Soil Degradation: An Explanatory Note. 1990; ISRIC report; ISRIC: Wageningen, The Netherlands, 1991. [Google Scholar]
- Belnap, J. Surface disturbances: Their role in accelerating desertification. Environ. Monit. Assess. 1995, 37, 39–57. [Google Scholar] [CrossRef] [PubMed]
- Bagnold, R.A. The movement of desert sand. Proc. R. Soc. Lon. Ser-A 1936, 157, 594–620. [Google Scholar] [CrossRef]
- Bagnold, R.A. The size-grading of sand by wind. Proc. R. Soc. Lon. Ser-A 1937, 163, 250–264. [Google Scholar]
- Kawamura, R. Study on sand movement by wind. Rep. Inst. Sci. Tech. Univ. Tokyo 1951, 5, 95–112, (In Japanese with English abstract). [Google Scholar]
- Wang, L.; Shi, Z.H.; Wu, G.L.; Fang, N.F. Freeze/thaw and soil moisture effects on wind erosion. Geomorphology 2014, 207, 141–148. [Google Scholar] [CrossRef]
- Marzen, M.; Iserloh, T.; De Lima, J.L.M.P.; Ries, J.B. The effect of rain, wind-driven rain and wind on particle transport under controlled laboratory conditions. Catena 2016, 145, 47–55. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, K.; Liu, C.; Zou, X.; Kang, L.; Chen, T.; He, W.; Fang, Y. Wind tunnel study of airflow recovery on the lee side of single plants. Agr. Forest Meteorol. 2018, 263, 362–372. [Google Scholar] [CrossRef]
- Shao, Y.; Raypach, M.R.; Leys, J.F. A model for predicting aeolian sand drift and dust entrainment on scales from paddock to region. Aus. J. Soil Res. 1996, 34, 309–342. [Google Scholar] [CrossRef]
- Kuznetsov, M.S.; Abdulkhanova, D.R. Soil loss tolerance in the central chernozemic region of the European part of Russia. Eurasian Soil Sci. 2013, 46, 802–809. [Google Scholar] [CrossRef]
- Lisetskii, F.; Stolba, V.F.; Marininа, O. Indicators of agricultural soil genesis under varying conditions of land use, Steppe Crimea. Geoderma 2015, 239, 304–316. [Google Scholar] [CrossRef]
- Meng, Z.; Dang, X.; Gao, Y.; Ren, X.; Ding, Y.; Wang, M. Interactive effects of wind speed, vegetation coverage and soil moisture in controlling wind erosion in a temperate desert steppe, Inner Mongolia of China. J. Arid Land 2018, 10, 534–547. [Google Scholar] [CrossRef]
- Takahashi, S.; Tanaka, Y. Studies on the wind erosion control by spraying bentonite milk in the Abashiri District. J. Agric. Eng. Soc. Jpn. 1991, 59, 157–162. (In Japanese) [Google Scholar]
- Shingyoji, T.; Watanabe, H. Studies on wind erosion in upland fields in Chiba Prefecture 1. The influence of field length and tillage methods to wind erosion in Andosol area. Bull. Chiba-Ken Agr. Exp. Stn. 1988, 29, 105–114, (In Japanese with English summary). [Google Scholar]
- Watanabe, M. Grazing as a cultural impact on soil formation of andosols. Ann. Ochanomizu Geogr. Soc. 1990, 31, 16–23. (In Japanese) [Google Scholar]
- Kuroda, M.; Kunieda, T. Unsaturated hydraulic conductivity of the Kuroboku soil and its measurement. J. Jpn. Soc. Soil Phys. 1983, 48, 17–25, (In Japanese with English summary). [Google Scholar]
- Maeda, T.; Soma, K.; Ikehata, K. Thermal properties greatly related to water retention of Kuroboku Soils (Organo-volcanic Ash Soils). Trans. Jpn. Soc. Irrig. Drain. Rural Eng. 1983, 103, 13–20, (In Japanese with English abstract). [Google Scholar]
- Hasegawa, S. Field capacity of volcanic ash soil—The real conditions. J. Jpn. Soc. Soil Phys. 2000, 83, 41–46, (In Japanese with English abstract). [Google Scholar]
- Narioka, H.; Komamura, M. Macropore properties of andosols in the Kanto loam formation by physical analysis of soil structure and drainability. Trans. Jpn. Soc. Irrig. Drain. Reclam. Eng. 2000, 210, 735–743, (In Japanese with English abstract). [Google Scholar]
- Tsuji, O.; Matsuda, Y.; Tsuchiya, F. Effect of the windbreak nets on micrometeorological improvement in crop fields. Res. Bull. Obihiro Univ. I 1988, 16, 51–58, (In Japanese with English summary). [Google Scholar]
- Komatsuzaki, M.; Suzuki, K. Influence of cover crop seeding date and their amounts on mitigation of wind erosion. Jpn. J. Farm Work Res. 2009, 44, 189–199, (In Japanese with English summary). [Google Scholar] [CrossRef]
- Hoshikawa, K.; Suzuki, J.; Yoshimura, S. A study of wind erosion in an agricultural area of the southwestern Matsumoto Basin. J. Jpn. Soc. Irrig. Drain. Rural Eng. 2012, 80, 349–352. (In Japanese) [Google Scholar]
- Suzuki, J.; Osawa, K.; Matsuoka, N. Characteristics and restraint measures of the wind erosion in Kanto-Koshin district. J. Agri. Eng. Soc. Jpn. 2017, 85, 649–654. (In Japanese) [Google Scholar]
- Arimori, M.; Endo, Y.; Kobayashi, T. Study on the optimal irrigation method for wind erosion prevention by the simulation. Trans. Jpn. Soc. Irrig. Drain. Rural Eng. 2009, 77, 475–481, (In Japanese with English abstract). [Google Scholar]
- Kawata, Y.; Tsuchiya, Y. Influence of water content on the threshold of sand movement and the rate of sand transport in blown sand. Proc. Jpn. Soc. Civil Eng. 1976, 249, 95–100. (In Japanese) [Google Scholar] [CrossRef]
- Chen, W.; Dong, Z.; Li, Z.; Yang, Z. Wind tunnel test of the influence of moisture on the erodibility of loessial sandy loam soils by wind. J. Arid Environ. 1996, 34, 391–402. [Google Scholar] [CrossRef]
- Fécan, F.; Marticorena, B.; Bergametti, G. Parametrization of the increase of the aeolian erosion threshold wind friction velocity due to soil moisture for arid and semi-arid areas. Ann. Geophys. 1999, 17, 149–157. [Google Scholar] [CrossRef]
- Yuge, K.; Haraguchi, T.; Nakano, Y.; Kuroda, M.; Anan, M. Quantification of soil surface evaporation under micro-scale advection in drip-irrigated fields. Paddy Water Environ. 2005, 3, 5–12. [Google Scholar] [CrossRef]
- Yuge, K.; Anan, M.; Shinogi, Y. Effects of the micro-scale advection on the soil water movement in micro-irrigated fields. Irrig. Sci. 2014, 32, 159–167. [Google Scholar] [CrossRef]
- McKee, S.; Tomé, M.F.; Ferreira, V.G.; Cuminato, J.A.; Castelo, A.; Sousa, F.S.; Mangiavacchi, N. The MAC method. Comput. Fluids 2008, 37, 907–930. [Google Scholar] [CrossRef]
- Young, D.M. Iterative Solution of Large Linear Systems; Academic Press: New York, NY, USA, 1971; ISBN 9781-4832-74133. [Google Scholar]
- Japan Meteorological Agency. Weather, Climate & Earthquake Information. Available online: http://www.jma.go.jp/jma/en/menu.html (accessed on 23 December 2018).
- Arimori, M.; Endo, Y.; Kobayashi, T. Effect of wind and soil moisture on the wind-drift caused by wind erosion: The case of volcanic ash soil fields in Okunakayama Highland, Iwate prefecture. Trans. Jpn. Soc. Irrig. Drain. Rural Eng. 2009, 77, 129–136, (In Japanese with English abstract). [Google Scholar]
- Bergametti, G.; Rajot, J.L.; Pierre, C.; Bouet, C.; Marticorena, B. How long does precipitation inhibit wind erosion in the Sahel? Geophys. Res. Lett. 2016, 43, 6643–6649. [Google Scholar] [CrossRef]


| Volumetric Water Content (m3 m−3) | Parameter b |
|---|---|
| 0.026 | 0.0352 |
| 0.100 | 0.0140 |
| 0.170 | 0.0042 |
| 0.250 | 0.0030 |
| Volumetric Water Content (m3 m−3) | Irrigation Water Amount (mm) | Hourly Amount of Soil Erosion (kg h−1) | ||
|---|---|---|---|---|
| u = 6.0 (m s−1) | u = 8.0 (m s−1) | u = 9.5 (m s−1) | ||
| 0.026 | 0.588 | 1.193 | 1.927 | |
 3.2 3.2 | ||||
| 0.100 | 0.234 | 0.474 | 0.765 | |
 2.6 2.6 | ||||
| 0.170 | 0.069 | 0.141 | 0.227 | |
 2.6 2.6 | ||||
| 0.250 | 0.051 | 0.103 | 0.167 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuge, K.; Anan, M. Evaluation of the Effect of Wind Velocity and Soil Moisture Condition on Soil Erosion in Andosol Agricultural Fields (Model Experiment). Water 2019, 11, 98. https://doi.org/10.3390/w11010098
Yuge K, Anan M. Evaluation of the Effect of Wind Velocity and Soil Moisture Condition on Soil Erosion in Andosol Agricultural Fields (Model Experiment). Water. 2019; 11(1):98. https://doi.org/10.3390/w11010098
Chicago/Turabian StyleYuge, Kozue, and Mitsumasa Anan. 2019. "Evaluation of the Effect of Wind Velocity and Soil Moisture Condition on Soil Erosion in Andosol Agricultural Fields (Model Experiment)" Water 11, no. 1: 98. https://doi.org/10.3390/w11010098
APA StyleYuge, K., & Anan, M. (2019). Evaluation of the Effect of Wind Velocity and Soil Moisture Condition on Soil Erosion in Andosol Agricultural Fields (Model Experiment). Water, 11(1), 98. https://doi.org/10.3390/w11010098




