Abstract
This study applied a soil water balance (SWB) model to simulate groundwater recharge on Catalina Island, California, for the years 2008–2014, a period that coincided with a severe drought. Island-wide average recharge ranged from 0.05 mm/year in 2013 to 82.3 mm/year in 2008, with a 7-year mean of 23.0 mm/year. High recharge is primarily associated with east-facing mountain fronts and the land cover types “developed, open space” and “herbaceous”. This spatial trend is also reflected in recharge estimates for groundwater well locations produced by the Cl mass balance method. Only in 2008 did all areas of the island experience recharge, while the recharge was very low during the drought years 2009 and 2012–2014. Sensitivity analyses indicate an unresolved discrepancy in land cover classification (i.e., herbaceous grass dominated vs. chaparral and coastal sage dominated) to be a significant factor. In a scenario where herbaceous grass dominates, as field studies from the early 1980s imply, recharge estimates nearly double. Nevertheless, the overall low recharge rates presented herein and the fact that drought conditions in Southern California have worsened since 2014 suggest that large parts of the island may not have received any recharge in nearly a decade.
1. Introduction
Groundwater recharge, defined as surface water that reaches the saturated zone via infiltration, is a hydrologic component of remarkable spatial and temporal variability. Recharge rates may range from less than 10 mm to multiple meters per year, depending on influences of climate, geology, land use, and soil type [1]. For low recharge areas, such as semiarid Southern California, proper water management is crucial for sustainable potable water supply. This is especially the case in light of future population growth, increasing water demands for agriculture, and climate change, which may place increasing emphasis upon groundwater use, especially in areas of little precipitation [2,3,4].
The methods that have been devised to quantify groundwater recharge can be broadly classified into two groups: (1) those that yield local or point estimates, and (2) those that provide more spatially distributed estimates. Point estimate methods rely on direct measurements at a specific location (e.g., a groundwater well) over time and include the use of soil lysimeters, water table fluctuations, groundwater age dating tracers, or chemical (i.e., Cl) mass balance [5,6,7,8,9,10]. Methods that provide spatially distributed estimates integrate climatic and hydrological data on various spatial and temporal scales, and include numerical modeling of groundwater flow and soil water balance (SWB) modeling [11,12,13,14,15]. The utility of point estimate methods to produce watershed-wide recharge estimates is somewhat limited because different methods apply to different spatial and temporal scales. Water table fluctuations document current recharge events at the well, whereas Cl mass balance documents mean recharge between where rainfall occurred and the location where the water first entered the aquifer. Age dating tracers allow estimating mean values of recharge between where the sampled water first entered the aquifer and the groundwater discharge point (i.e., the well screen). Given these differences, it becomes clear that recharge extrapolations based on any or any combination of these point scale methods are limited in reliability. Another issue of the point scale method lies in the generally uneven distribution of sampling points, particularly in mountainous watersheds. In such settings, rainfall and recharge rates are typically highest in the undeveloped uplands, for which there are usually only limited groundwater well data available. As a result of this uneven spatial distribution of data points, mean groundwater recharge estimates for these watersheds that are derived solely upon point estimates tend to be biased low [16]. There are also limiting methodological assumptions that need to be accounted for in the point scale methods. For instance, the water table fluctuation method requires specific yield constraints, which may be difficult to obtain for heterogeneous settings [17]. Likewise, the Cl mass balance method requires detailed datasets on Cl contents of groundwater, surface runoff, and rainfall (including dry deposition) [18], which can be scant, particularly in remote settings. The problem of age dating tracers for estimating recharge is the challenge of determining absolute ages of groundwater because a groundwater sample, particularly one derived from a well with a long screen interval, often represents a complex mixture of modern and premodern water proportions [19,20]. Another problem of age dating tracers is often unknown end-members or variations in the input signal [21].
Spatially distributed methods are also not without their limitations. For example, groundwater flow models that solve for recharge as the unknown are reliant on the input of hydraulic conductivity data [14,22], which may vary spatially over orders of magnitude, causing recharge estimates to be inherently uncertain. Water balance modeling has the advantage that it incorporates recharge parameters that are easier to measure (e.g., rainfall or runoff), but it is also subject to uncertainty, particularly because it only provides a potential recharge estimate representative for below the root zone and not the water table. This can result in uncertainties of actual recharge location and timing in more arid watersheds where unsaturated zones can be thick and heterogeneous [23]. It has furthermore been concluded [24] that the accounting order of recharge and evapotranspiration may result in large uncertainty of the recharge estimate if soil moisture storage capacity is small and when water budgets are computed on monthly rather than daily time intervals. Applying monthly over daily time steps also tends to dampen out the effect of extreme precipitation events, which control recharge magnitude [25,26]. Despite these limitations, recent recharge studies in the U.S. southwest have become increasingly dependent on water balance models, particularly because of their ability to accommodate spatial and temporal variability of input factors such as rainfall, runoff, or evapotranspiration to produce spatially and temporally distributed results.
The goal of this study is to apply the soil water balance model [27] to simulate groundwater recharge patterns on Santa Catalina Island in Southern California (hereafter referred to as Catalina or Catalina Island). Although only sparsely populated, about 4000 residents live in and around the town of Avalon, and the island experiences nearly 1 million visitors each year [28]. This, and the fact that Southern California has experienced one of the worst droughts on record from 2012 to 2017 [29,30,31], place a significant stress on groundwater resources. A current critical question is the sustainable yield of the groundwater system that provides almost all of the potable water for the island (a small desalination plant can provide temporary water during shortages). However, little information exists regarding the island’s hydrology and how water supply may change in the face of climate and land use change. For example, it has been observed on Catalina, as well as similar semiarid environments, that there is a “threshold” antecedent moisture content that must be achieved before runoff and groundwater recharge can be observed [32,33]. If storms become more frequent, but smaller in magnitude, groundwater recharge may decrease, while if they become less frequent, but more intense, groundwater recharge may increase. An evaluation of this relationship requires detailed time series data of recharge. Recent studies have also pointed out the importance of land cover (i.e., vegetation) change on groundwater recharge [34,35,36]. This is relevant to Catalina as reports on land cover on the island vary significantly. Field studies [37,38,39] highlight a dominance of herbaceous grassland/weed over chaparral/scrub vegetation, with the former being typically associated with much lower interception values than the latter [40,41]. The most recent, publicly available United States Department of Agriculture (USDA) Natural Resources Conservation Service (NRCS) National Land Cover Dataset (NLCD) reports the opposite trend: a dominance of chaparral and coastal scrub over herbaceous grassland/weed vegetation [42]. Prediction of the effects of various land cover and/or drought scenarios on water resources requires a documentation of groundwater recharge rates island-wide and a sensitivity study that evaluates the relative importance of land cover parameters on modeled recharge [43,44].
The need for meticulous groundwater statistics and management, coupled with the undeveloped nature of the island, makes Catalina a compelling focus area for a soil water balance analysis. The outcome of this study will highlight the ability to utilize publicly available resources as input for a freely available GIS-based model in an effort to constrain groundwater recharge rates in an area where water resources are under stress. Given the lack of reliable island-wide recharge estimates available to date, this study should act as a benchmark for future studies and will illuminate parameters that require further study and/or tools and resources needed for improved recharge assessments.
2. Materials and Methods
2.1. Study Area
Catalina Island is one of the eight Channel Islands, located about 74 km south-southwest of Los Angeles, California (Figure 1a). The island encompasses an area of 194 km2, of which 88% are controlled by the Catalina Island Conservancy, and are completely undeveloped. Elevations reach as high as 639 m above sea level at Mt. Orizaba, with nearly 90% of the elevation drop occurring in the first 1–2 km from the central ridge that bisects the island. The island represents one of several exposed ridge crests of the California Continental Borderland geomorphic province and consists of Mesozoic metamorphic basement (i.e., the Catalina Schist) overlain by Miocene igneous rocks (primarily andesitic lava flows and quartz diorites of the Catalina Island Pluton) and Paleogene to Neogene terrestrial and marine sediments [45].

Figure 1.
Catalina Island topography and locations of climate stations (a) and modified Anderson Level II land cover classification (b).
Catalina Island falls within a Köppen–Geiger climate classification of Mediterranean (Csb) and is marked by warm, dry summers and mild, wet winters. Monthly temperature averages range from 11.9 °C in January to 21.7 °C in August at Avalon Airport for the years 1948 to 2016. The precipitation average for the same period was ~300 mm annually and varies seasonally and spatially depending on orographic factors, with Little Harbor on the southwest side receiving 200 mm and Avalon on the southeast receiving 350 mm per year [38]. There are no perennial streams on the island, although several days of runoff can occur in the larger watersheds, such as Middle Canyon, after intense rainfall events. None of Catalina’s streams are currently instrumented with discharge gauges, which prohibits a more detailed analysis of surface runoff.
According to the NCLD land cover classification, the island is dominated by chaparral shrub/scrub vegetation (82%) with minor proportions of herbaceous grassland (10%; Figure 1b). This classification is not corroborated by field studies [38,39], which highlight a dominance of herbaceous grassland (>80% of cover) with isolated occurrences of chaparral vegetation, coastal sage scrub, and prickly pear.
Despite the recent drought and mandatory water rationing, very little information exists on the island’s hydrogeology. Groundwater elevations roughly follow topography [46], and increased rainfall with elevation implies increased recharge in topographically higher areas. All of the supply wells, which are maintained and operated by an electricity supply company, extract water from the alluvium that is hydraulically connected to the bedrock aquifer; the strength of this connection, however, is undefined [46]. None of these wells were accessible for sampling in this study, but the State Water Board Groundwater Ambient Monitoring and Assessment (GAMA) database reports groundwater geochemistry data for 18 wells and lists well construction data (i.e., screen depth and length) for 11 of those. The wells are generally shallow, with depths to the well screen bottom ranging from 6.1 m to 34.4 m below ground surface. To the authors’ knowledge, data on hydrostratigraphy, hydraulic conductivities, and the water storage capacities of the alluvial aquifers are not yet publicly available. One problem associated with Catalina groundwater is high concentration of total dissolved solids [47]. Many water supply wells installed near Avalon in the early 20th century were abandoned due to salt water intrusion [47], and many wells along the west coast of the island were abandoned in the late 1980s/early 1990s due to high groundwater salinities. The majority of the island’s drinking water is currently derived from supply wells in the immediate vicinity of Thompson Reservoir, a 1.42 × 106 m3 capacity storage reservoir located in Middle Creek Canyon, about 10 km west of Avalon.
2.2. The SWB Model
SWB computes potential groundwater recharge at a daily frequency on a grid-by-grid cell basis. The model follows the approach of Thornthwaite and Mather [48] and quantifies recharge below the root zone as the residual in a mass balance equation (Equation (1)):
where R, P, I. SNmelt, DRin, DRout, ETsm, and ∆S correspond to recharge, gross precipitation, interception, snowmelt, direct runoff into the grid cell from upslope grid cells, direct runoff out of the grid cell, soil moisture evapotranspiration (ET), and change in soil moisture, respectively. The term for soil moisture ET, ETsm, is used to account for soil moisture evaporative losses and plant transpiration [43]. Thus, total ET, ETtot, may be computed as interception, I, plus soil moisture ET (ETtot = I + ETsm).
R = P − I + SNmelt + DRin − DRout − ETsm − ∆S
Recharge from irrigation and/or cloud water interception (i.e., “fog drip”) are not accounted for in the model as these parameters are often difficult to constrain [49,50]. In this study, the grid cell dimension was set to 30 m × 30 m. Gross precipitation was estimated using a natural neighbor algorithm and daily measurements obtained from the Desert Research Institute from 13 climate stations on Catalina and one climate station on nearby San Nicholas Island for the time period 1 January 2008 to 31 December 2014. The lack of concurrent data over the entire island prior to 2008 and from March 2015 onward (Table 1) prevented the analysis of recharge over longer time frames. Natural neighbor was chosen over inverse distance weighting and spline algorithms because it presented a smoother output, gave highest R2 values in linear regression analysis, and produced lower root mean square errors (RMSEs; Figure 2). Geostatistical approaches, such as kriging, were not pursued in this study to eliminate the need for daily variogram. Linear regression analysis was performed to fill in days where climate data was not recorded.

Table 1.
Catalina Climate Stations.
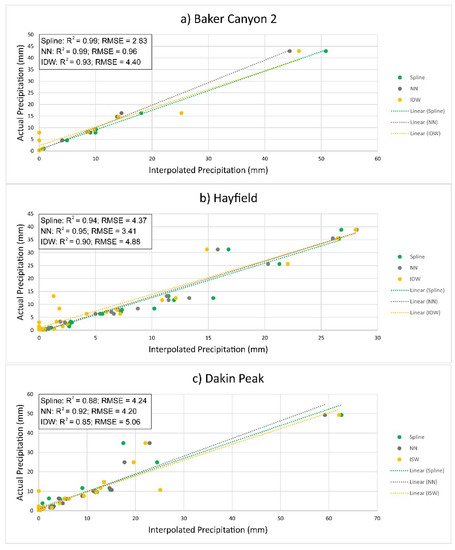
Figure 2.
Linear regression analysis of spline, natural neighbor (NN), and inverse distance weighting (IDW) precipitation interpolation at Baker Canyon 2 (a), Hayfield (b), and Dakin Peak (c) climate stations. Data shown represents rainfall events for 2008. Climate stations were selected for the analysis because they exhibited the least amount of missing data.
In SWB, gross precipitation (P) must exceed maximum assigned interception (I) amounts before the model assumes that net precipitation (Pnet) has reached the soil surface. The authors are not aware of measurements of interception losses on Catalina. Therefore, target interception loss rates for the different types of land cover found on Catalina for both growing season and nongrowing seasons were approximated based on results from comparable settings elsewhere [27,40,51,52,53,54]. These rates are listed in Table 2. This study relied on the NLCD classification of land cover and assumed there is a dominance of chaparral and coastal scrub over herbaceous grassland/weed vegetation. The alternate scenario of grassland dominance, as highlighted in field studies by, e.g., Minnich [38,39], was tested for in the subsequent sensitivity analysis. The assigned growing season lengths (GSLs) of 1 November to 1 June for the chaparral/coastal shrub and from 1 November until 1 May for the herbaceous grasses are based on reported results from studies conducted elsewhere in California [37,55,56].

Table 2.
Interception Storage values (mm).
A flow direction grid was created using the ArcGIS D8 algorithm performed on a digital elevation model (DEM) to simulate runoff. SWB iteratively routes runoff downslope (DRout) to an adjoining cell, where it may be added as a potential infiltration source (DRin), or continues to be redirected until all runoff is infiltrated and/or reaches the boundary of the study area and is removed from the process. This approach is considered an improvement over more traditional water balance approaches where rainfall is considered the sole recharge source [57,58]. Direct runoff was estimated in SWB using the curve number method for the 13 land cover classes and four hydrologic soil groups (HSGs) mapped on Catalina. The HSG input (Figure 3a) stems from the Soil Survey Geographic Database (SSURGO) obtained from the USDA NRCS Geospatial Data Gateway. Assigned curve numbers were based on published values by Hjelmfeld et al. [59] and Westenbroek et al. [27] and are listed in Table 3.
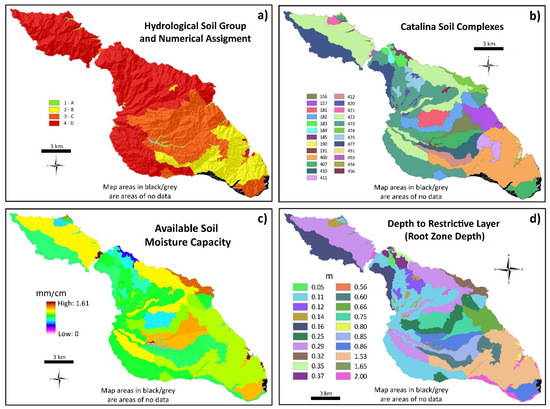
Figure 3.
Spatial distribution of hydrologic soil group assignments (a), available soil moisture capacity (b), soil complex units (c), and depth to restrictive layer (d) for Catalina Island.

Table 3.
Curve Numbers for Hydrologic Soil Groups.
Maximum infiltration rates (MIRs) are used in SWB to specify a maximum daily recharge rate for each of the four HSGs (e.g., [40]). In this study, MIRs were estimated from the range of saturated hydraulic conductivity (Ksat) data reported by the USDA NRCS Soil Survey of Santa Catalina Island (Figure 3b). First, the Ksat of each soil profile of a map unit, such as “Tongva”, “Freeboard”, and “Starbright” (Table 4) found in map unit “156” (see, e.g., Figure 3b), was calculated as the harmonic mean using layer-specific Ksat and depth data (e.g., Table 4). Topsoil layers with Ksat ≥ 42 µm/sec were excluded from this analysis as they were assumed to represent leaf litter associated with interception rather than infiltration in the soil zone. Next, the Ksat values of the map units (e.g., “156”) were averaged based on the profile-percentage makeup within each complex. Map unit Ksat values were then converted to MIRs of HSGs by weight averaging them according to individual HSG areas (Table 5).

Table 4.
Soil Complex Schematic Example.

Table 5.
Maximum Infiltration Rates.
SWB allows for the application of five separate potential evapotranspiration (ETpot) estimation methods [48,60,61,62,63]. In this study, the Hargreaves–Samani (H–S) [61] method was chosen because it was developed with, and tested against, datasets obtained from coastal Californian regions (e.g., the town of Lompoc in Santa Barbara county) that are similar in climate and vegetation to those studied herein. Furthermore, the method is the only available in SWB that is capable of producing spatially distributed output grids rather than just one uniform value to be applied over the entire island. The application of the H–S method requires gridded data of maximum and minimum daily temperature (Tmax, Tmin), which were generated following the approach of Mair et al. [43] and Hagedorn et al. [64] using temperature lapse rates applied to a 30-m DEM. Temperature at any grid cell of the DEM was extrapolated from daily temperature data recorded at the Parsons Landing (PL) climate station. PL was selected as the reference station for T extrapolation because its records contained the least amount of missing data between the years 2008 and 2014.
ETsm was computed from ETpot for each grid cell as follows: (1) when Pnet − ETpot ≥ 0, then ETsm = ETpot; (2) when Pnet − ETpot < 0, then ETsm equates to only the amount of water that can be extracted from the soil via ET, a value computed via the soil moisture retention tables of Thornthwaite and Mather [48] and modified by Westenbroek et al. [27]. Estimates of maximum soil moisture storage capacity needed to use the soil moisture retention tables were computed as the product of the available water soil capacity (AWC) multiplied by the root zone depth. AWC data (Figure 3c) were obtained from the USDA NRCS Web Soil Survey (WSS). Root zone depths (Figure 3d; Table 5) were assigned by accessing “restrictive layer” soil depth data from USDA NRCS WSS and weight-averaging those across both land cover and hydrologic soil types. No depth values were obtained for “Developed, High Intensity Urban” (24) HSG A, “Woody Wetlands” (90) HSG B-D, and for “Emergent Herbaceous Wetlands” (95) HSG B-C. In those instances, reference values reported by Westenbroek et al. [27] were applied.
An initial amount of soil moisture (SM) is needed in SWB to allow for the potential of soil saturation and subsequent infiltration/recharge or evapotranspiration experienced on day 1 of the study period. Two methods may establish the initial SM. The first requires an extra year of data to prime SM for the following (initial) year. This “primer” year may be incorporated into the statistical analysis, albeit at a limited initial accuracy. The second and easier to apply method is to utilize the control file input and assign an estimated initial percentage of AWC. To determine the appropriate initial percentage of AWC, a “phantom” year of 2007 climate data was generated using the National Oceanic and Atmospheric Administration (NOAA)’s Climate at a Glance portal (https://www.ncdc.noaa.gov/cag/). It was determined that the year 2013 was most similar to 2007 for precipitation amounts, while 2009 most resembled maximum and minimum temperature for 2007. Using these datasets and including the phantom year 2007 in the analysis yielded recharge results that closely resemble those obtained from an initial AWC percentage of 80%. Therefore, the assigned initial AWC of 80% was applied, and 2008 was included in the discussion of recharge results.
All the input rasters contained some minor areas of missing data, particularly along the steep and undeveloped southern shoreline of the island (shown in black/grey in Figure 3). The reasons for that lack of data are not clear. All areas of missing data exhibited by any of the input rasters were excluded from the recharge analysis.
2.3. Corroboration of Recharge Estimates
To produce reliable results, it is critical that modeled recharge values are calibrated against independent estimates of recharge and/or measured water balance parameter data. Previous soil water balance studies have relied on various datasets for calibration, including measurements of runoff [43], water table fluctuations [65], or groundwater age tracers [66]. One issue pertaining to Catalina Island, however, is that such datasets are not available. None of the streams on the island are instrumented, and none of the groundwater wells were accessible for sampling for this study. Groundwater level data were also not publicly available, neither from the utility company serving the island nor from resources such as the State Water Board Groundwater Ambient Monitoring and Assessment (GAMA) database, the State Department of Water Resources Groundwater Information Center, or the U.S. Geological Survey (USGS) Groundwater Watch portal. Nevertheless, there were some chemical data available from the GAMA portal that were used to corroborate SWB recharge estimates presented herein.
Groundwater age dating tracer data, specifically concentrations of tritium (3H), were available for only two of Catalina’s wells: well 12 sampled in 2014 and well 30 sampled in 2004 (see Figure 4a for well locations). Both wells exhibited 3H levels below analytical detection limits, although the detection limits for the individual analyses were not explicitly stated. Nevertheless, measurements at or below values of 0.2 tritium units (TUs) should be considered indicative of “old” (i.e., >60 year old) water typically encountered in low-recharge areas [20,67]. The available data on CFC-11 and CFC-12 concentrations from the GAMA database (all below detection limits) cannot be used for groundwater age dating or recharge analysis because they all reflect detection limits (5 μg/L for CFC-11 and 1 μg/L for CFC-12) that are too high for a reliable comparison with atmospheric input since the mid-20th century [68]. Additional age dating data, such as measurements of 14C, 85Kr, SF6, CFC-13, and/or CFC-113, were not available in any of the examined databases. Reasonable estimates of groundwater transit times derived from Darcy’s law could also not be obtained due to the lack of hydraulic head and conductivity data.
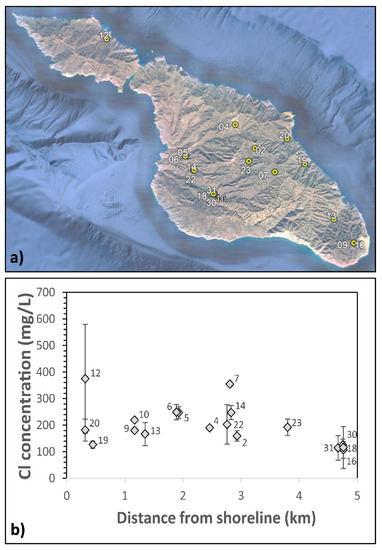
Figure 4.
Location of groundwater wells on Catalina with chemical records (a) and groundwater Cl range on Catalina for the time period 1989–2017 (b). Diamonds indicate geometric means, error bars indicate one standard deviation, and numbers denote well ID.
More extensive data exist on Catalina’s dissolved Cl concentrations of groundwater (Figure 4), which allow for a more in-depth assessment of recharge at wells using the traditional chloride mass balance (CMB) method:
R = PClP/ClGW
Here, P, ClP, and ClGW correspond to mean rainfall, the precipitation weighted mean Cl concentration of precipitation (including dry deposition), and the Cl concentration of groundwater at a particular well, respectively. The method assumes the following: there is no direct runoff; all of the ClGW is derived from evapotranspiration of atmospheric water; Cl is an inert tracer; flow is one-dimensional, vertical downward, piston type; groundwater is well-mixed; and water and tracer mass fluxes are steady. P values for Equation (2) (316–357 mm/year) were estimated for each well from the Parameter–Elevation Relationships on Independent Slopes Model [69] and represent 30-year means (1981–2010). Given that residence times of island groundwater can be on the scale of decades [70], we found this to be a better approach than using the P grids estimated herein that extend back only until 2008. No ClP data were available for Catalina, but for the CA85 Channel Islands National Park station on Anacapa Island for the years 1980 through 1982 [71]. The reported annual Cl deposition for CA85 (located about 120 km NW of Avalon) ranged from 3.48 to 6.90 kg/ha and translates, using measured rainfall rates, to an equivalent ClP range of 3.06 to 13.6 mg/L. These values exceed those estimated for other regions of Southern California, such as 2.33 mg/L in La Conchita Ranch, Ventura County [72], or 2.60 mg/L in the Simi Hills of Ventura County [73], and likely reflect the proximity of the climate station to the ocean, as has been observed in coastal settings elsewhere [74]. To represent uncertainty in the measured data, both ClP end-members for Anacapa Island were applied in Equation (2). Assigning ClGW is more challenging because sample size and value ranges differ greatly among wells (Figure 4b). There are also limited concurrent datasets available because many of the supply wells (i.e., wells 02, 07, 09, 13, 19, and 22) were abandoned in the late 1980s/early 1990s due to high groundwater salinity. Also problematic is the fact that the supply well cluster 16, 18, 30, and 31 is located only about 300–400 m downgradient of Thompson Reservoir dam and, as such, draws primarily from impounded surface water [47]. This scenario violates the assumption of Equation (2) that all groundwater Cl is rainfall and not rainfall + surface water-derived [18]. In the absence of reliable Cl and flow information of the reservoir water that discharges to the wells, data from this well cluster was not included in the analysis. Many previous studies have established ClGW as the arithmetic or geometric mean of measured groundwater data at a well [73,75,76], but this approach was not considered useful for wells with a small sample size and Cl values that varied by more than 100%. As an alternative in this study, ClGW was based on the availability of concurrent datasets. For each of the years 1992, 1995, 1998, 2001, 2004, 2010, 2011, 2012, and 2015, the GAMA database revealed ≥6 concurrent and spatially distributed groundwater Cl data points. Accordingly, these datasets were used for a multiyear CMB analysis.
The mean SWB recharge value for each well for which CMB data was available was calculated following the approach of Johnson and Belitz [77] as the mean of recharge within a 500-m buffer around the well location. Uncertainty in the SWB recharge estimate around each well was represented by the standard deviation of values of all cells within the buffer.
CMB recharge estimates reveal a statistically significant positive correlation (Pearson r ≥ 0.5; P < 0.1) with SWB recharge estimates for all but one of the concurrent datasets (Figure 5). Even though this may be interpreted as some indication for corroboration of spatial recharge patterns obtained by the SWB model, the limiting assumptions inherent in both recharge estimation methods, uncertainty of input data, and the different temporal scales at which these methods apply indicate that a comparison of the different recharge estimates should be treated with caution. It is, however, interesting that the mean SWB recharge values most resemble the upper limit (i.e., high ClP) CMB recharge estimates (Figure 5). Assuming the applied high ClP end-member to reflect a positive outlier, a reasonable assumption based on the lower reported ClP values for other sites in coastal California (e.g., Reference [73]), the depicted trends in Figure 5 suggest either an overestimate of recharge by the SWB model or an underestimate of recharge by the CMB method. A similar discrepancy between CMB and SWB results was also observed for a non-irrigated site elsewhere in Southern California [72] and was attributed to halite dissolution in the subsurface and the resulting potential underestimation of actual chloride inputs to groundwater. Additionally, intrusion by seawater could explain the large Cl range observed in well 12 as this well is located <500 m away from the shoreline (Figure 4b). Leakage of trapped, connate water, a process that has been documented in nearby San Diego County [78], could also explain high Cl and low CMB values. Additional data, particularly concentrations of dissolved Br and B, as well as values of 87Sr/86Sr, 3H/3He, 14C, and δ11B, have shown to be valuable salinity tracers in comparable semiarid settings [78,79,80,81] and are needed to further identify the water Cl sources on Catalina. Still, in the absence of any other potential recharge calibration data, we consider the CMB results, particularly the agreement of spatial trends with SWB estimates, not to contradict but to generally support the SWB model outputs.
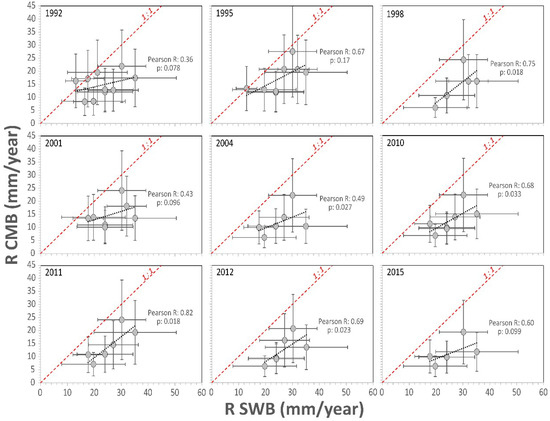
Figure 5.
Comparison of soil water balance (SWB) vs. chloride mass balance (CMB) recharge estimates. Regression coefficients are shown with a 90% confidence interval. Horizontal error bars indicate one standard deviation from the mean of all SWB values within a 500 m well buffer. Vertical error bars represent range of measured ClP values (see text for explanation).
3. Results and Discussion
3.1. SWB Recharge Output
Average yearly recharge for Catalina Island ranged from a low of 0.05 mm/year in 2013 to a high of 82.3 mm/year in 2008 (Table 6), with an average value, for all years combined, of 23.0 mm/year. These estimates agree with those determined for other semiarid regions in southwestern U.S., such as 8.19–43.2 mm/year in the Simi Hills region of Southern California [73], 15.2–21.3 mm/year in the San Gabriel Mountains of Southern California [82], 24.5–30.4 in Eastern California’s Owens Valley [83], and about 20 mm/year in the Basin and Range Carbonate-Rock Aquifer System [84]. The recharge results presented herein also agree with those presented in an in-depth summary of global studies in semiarid areas showing average recharge rates of 0.2–35 mm/year [85]. The ratio of recharge to gross precipitation was calculated to vary between 0.04% in 2012 and 26.3% in 2008, with a ratio for all years combined at 6.55% per year. These ratios reveal high degrees of ET (Table 6) and are also consistent with those determined from other semiarid regions of the world, such as 9% in South Africa [86], 7% in the Basin and Range Carbonate-Rock Aquifer System [84], 4% in San Hollow Basin, Utah [87], and 4% in the Simi Hills region of Southern California [73].

Table 6.
Water Balance Parameters as % of Gross Precipitation.
Spatially, recharge on Catalina tends to be higher along the eastern flanks of the main divide, with greatest values in the north-central portion of the island (Figure 6). Highest recharge occurs in the area east of Whitley’s Peak, the area surrounding Mt. Orizaba trending to the eastern coast, and in the area of Parsons Landing. There are also localized high recharge areas along roadways in the north-central and northern portion of the island and at high elevations around Airport in the Sky. These areas exhibited land cover classifications of “developed, open space” with high MIR soils. Also, clumps of grid cells throughout the island, particularly in the central and north-central portion, had higher recharge relative to neighboring areas, relating to land cover classification “herbaceous”.
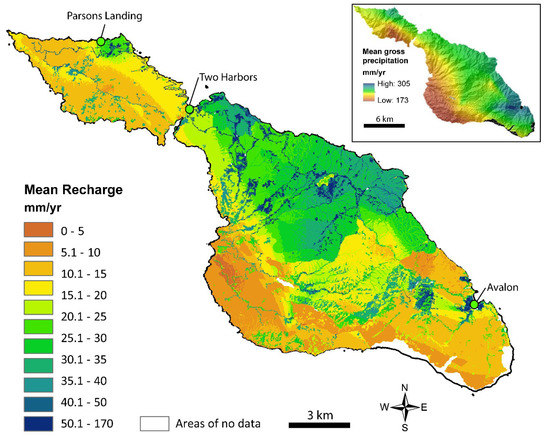
Figure 6.
SWB model results of mean recharge (mm/year).
A year-by-year analysis (Figure 7) displays a trend in recharge with the highest values dominating the north-central portion of the island (to the north of Mt. Orizaba) and the windward (eastern) side. The years 2008 and 2010 had the greatest amount of recharge in response to significant precipitation events. Interestingly, however, the highest recharge year (in terms of percentage of rainfall), 2008, coincided with the second highest rainfall year and vice versa (Table 6). The same is the case at the other end of the spectrum. The lowest recharge year, 2012, coincided with the second lowest rainfall year and vice versa (Table 6). The complex relationship between rainfall and recharge illustrates well the dynamic response of the soil system to decreased rainfall input. Based on the study results, it appears that precipitation rates of >400 mm/year, even if accumulating after a year of drought (2009), favor surface runoff, while rainfall of 313 mm/year, such as observed in 2008, favors groundwater recharge more in the water balance. A time-series comparison between our modeled recharge values at specific locations (for which groundwater level data unfortunately are not yet available) and recharge estimates obtained from water table fluctuations at those locations could provide more information on the lag time between potential recharge below the root zone and the actual recharge pulse at the water table.
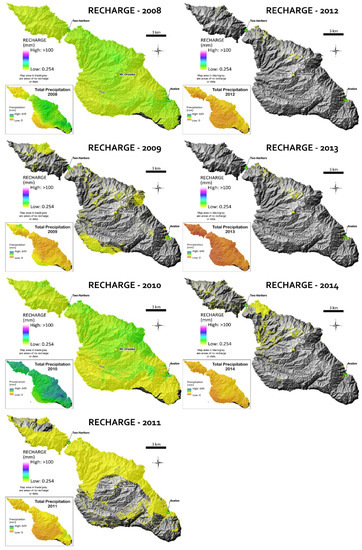
Figure 7.
Year-by-year recharge distribution maps. Insets show yearly gross precipitation.
Only in the relatively wet years, 2008 and 2010, did all areas of the island experience recharge. Recharge in the other years, particularly from 2012–2014, covered significantly smaller portions and occurred primarily along roadways and “bare earth” areas in the north-central parts (Figure 7). The slopes above and around Avalon also experienced greater recharge relative to surrounding areas during the drier years.
3.2. Sensitivity Analysis
Given the dependence of the water balance modeling approach on the numerous climatic and hydrologic input factors, we tested the effect of various parameters on recharge responses in a sensitivity analysis. Due to the potential for misclassification of land cover, an examination of the dominance of land covers “herbaceous” and “shrub/scrub” warranted insight and inclusion in the sensitivity study. To adjust values for the land cover sensitivity analysis, “herbaceous” and “shrub/scrub” shapefile assignments were simply switched. This approach assumes a total misclassification of the 2011 NLCD and follows field study results of, e.g., Minnich [38] that point out a herbaceous grass dominance with >80% of cover. Other parameters considered in the sensitivity analysis were curve number, MIRs, interception, and root zone depth. To determine the relative sensitivity of each of the parameters except for land cover, an across-the-board adjustment of ± 15% was applied to each parameter, separately, while keeping all other parameter values the same, followed by rerunning of the SWB model. For curve number adjustments, all land classes were adjusted with the exception of “open water”, which remained at 98. Also, if curve number adjustments gave values above 100, the values were readjusted to 98.
Results of the sensitivity analysis (Figure 8) show the discrepancy in dominance of land cover (i.e., grass vs. chaparral) to be a significant factor affecting recharge. The scenario in which grassland dominates nearly doubles the total recharge output of the baseline scenario. Care must be taken with this sensitivity study as the inclusion of the land cover comparison was not under the same systematic constraints imposed on the input data (i.e., a change in + 15% or − 15%) but rather based on vegetation mapping in the field. However, it does indicate that fine tuning the spatial distribution of land cover input would be an important step in the refining of recharge estimates. The changes made to curve numbers, MIRs, interception values, and root zone depths suggest that an increase in curve number affects recharge the most with a relative percent sensitivity at -460%. It is interesting to note that an equal percentage decrease in curve number presented only a 3.00% relative sensitivity. Root zone adjustments did display sensitivity in both the increasing and decreasing spectrum with relative percent sensitivities at −76.3% and 92.0% respectively, indicating a need for further root zone depth analyses. Root zone depth was closely followed by sensitivity to interception values, both in the increasing and decreasing spectrum with relative sensitivities of −58.6% and 63.4%, respectively.
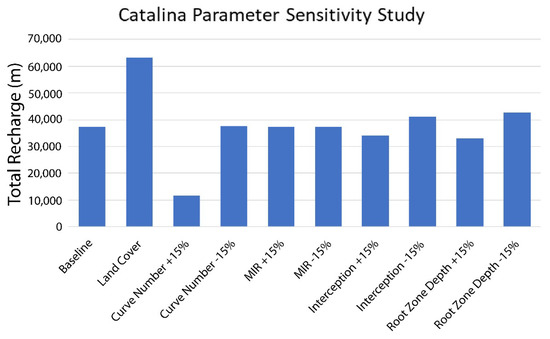
Figure 8.
Recharge results of the baseline model and those obtained from a sensitivity analysis of all parameters, separately altered, including land cover. Total recharge is the sum of all active grid cells for the years 2008–2014, combined, in meters.
3.3. Limitations of Study
While the greatest effort was made to attain high accuracy data, many of the input parameters are uncertain due to a lack of direct measurements. Given this, future work should focus on collection of calibration data, in particular, stream flow point data at selected stream channels, measurement of interception storage values, and root zone depths for various vegetation types as well as point measurements of recharge from, e.g., soil lysimeters, water tables, or groundwater radioactive isotope values. Future research should also address a sensitivity study that specifically focuses on the impact of various interpolation methods of rainfall and temperature on groundwater recharge rates. Moreover, an increase in number and spatial distribution of climate stations would benefit any recharge analysis for both temperature and precipitation events, particularly in light of the topography of the island and associated microclimate changes [49,64].
Uncertainty furthermore stems from the classification of land use/land cover. Field study observations conflict with NLCD classifications when assigning herbaceous grass and shrub/scrub [37,39]. Because NLCD data is derived upon aerial/satellite mapping, only the top-tier land cover is accounted for. NLCD data classifications are generalized toward the entire country; therefore, the spectral signatures acquired by Landsat to identify shrub/scrub and herbaceous grass specific to Catalina may be too broad to adequately identify these vegetation types on Catalina. The possibility also exists that European grasses are a significant part of the understory. The 2011 classification may not necessarily reflect land cover at the time of the study, but, more importantly, when observing grid cell placement, many grid cells were classed inaccurately. For example, “wetlands” grid cells were found in ocean and “developed, open space” in areas of trees. Furthermore, the 28 m2 resolution classification assignment method showed offset of grid cells where the dominant land cover feature was not what was assigned, but was rather appropriate for neighboring grid cells. Future aerial studies specific to Catalina Island, in partnership with field analysis that provides a product with greater resolution, would be beneficial for this study.
The H-S [61] method for evapotranspiration estimation was the chosen method for this study because it accounted for (and provided output to display) the spatial variability of recharge. However, the approach is a very simplistic one that fails to consider any energy balances or meteorological parameters outside of temperature, as more sophisticated methods do [88].
Cloud water interception is not considered within the precipitation parameter or in the SWB algorithm, yet it plays an important role in the water balance [50,89]. Fog would be an indirect source of precipitation via interception through stem flow and canopy drip. While it may provide insignificant amounts of precipitation to allow for percolation into the water table, it does contribute to the soil moisture parameter. Fog also decreases evapotranspiration by reducing solar radiation and temperature, tipping the mass balance equation in favor of recharge. Catalina receives fog (often thick) at all times of the year but most frequently during the dry/hot summer months. A detailed study on Catalina’s fog drip and how it relates to other parameters of the water balance (Equation (1) is warranted for improved recharge estimates.
Another limitation of SWB is that there is no provision for recharge rejection via saturation excess other than by specifying a maximum infiltration rate for a particular soil type. Similarly, because the SWB model does not incorporate the depth to the water table, the model is unable to appropriately handle areas in which the water table rises into the root zone or breaches the land surface. In these areas, such as wetlands or flooded river banks, percolating recharge would thus be refused, and the model may be expected to perform poorly.
The sensitivity study in this research did not mimic those performed in other studies (i.e., inclusion or absence of parameters, range of controlled departures from baseline values, future scenarios of climate, land cover or soil types, etc.) due to the lack of a systematic parameter application across other studies in the literature [12,15,90,91]. Despite the various methods applied to the sensitivity analyses for each study area, it becomes clear that the degree of parameter sensitivity is unique for each study, highlighting the need for sensitivity analyses to be performed individually to illuminate those parameters with the potential for greatest uncertainty.
Lastly and most importantly, the SWB model is simplified, and this simplification can lead to different recharge rates compared to more complex, physically based models. As an illustration, Moeck et al. [92] have shown that physically based models predicted recharge with relatively small uncertainty limits, even when calibration and prediction periods had very different climatic conditions. More simplistic soil water balance models (such as SWB) tend to perform poorer under such conditions and provide uncertain results, particularly for extreme dry or wet events. These biases can have strong implications for water resource management on Catalina should drought conditions worsen. Follow-up investigations collecting more calibration (streamflow, soil moisture, etc.) data and using alternate physically based modeling approaches are therefore warranted.
4. Conclusions and Implications
Catalina Island, located off the coast of Southern California, has suffered from severe droughts that challenge its water supply. Calculated recharge totals for the years 2008–2014 vary over three orders of magnitude and generally follow the distribution of rainfall. Areas of interest for consideration of future water resource assessment projects may be found along the eastern flank of the mountainous divide, particularly in the north-central portion of the island, such as near Airport in the Sky and in the canyon surrounding Avalon.
Average recharge was highest in 2008 with a value of 82.3 mm, followed by 71.7 mm for the year 2010. Most years, however, received recharge below 5 mm. These low rates are comparable to those computed for deserts elsewhere [7,11] and indicate that, for the years 2009, 2011, 2012, 2013, and 2014, significant portions of the island experienced no recharge at all. This attests to the severity of the recent Californian drought and highlights the importance of relating groundwater extraction to short-term changes in recharge for sustainable water supply.
Given the lack of reliable island-wide recharge estimates available to date, the results of this study should act as a benchmark for future recharge studies performed on Catalina. The gridded model output can also be used as input for a groundwater flow model that tests the response of the Catalina Island groundwater system to various scenarios of groundwater usage [93].
Author Contributions
J.H. developed the SWB model. B.H. conducted the CMB analysis. This work was conceptualized by B.H. and J.H. Both authors contributed equally to the writing and editing of the manuscript.
Funding
This research was supported through a RSCA grant by Long Beach State University.
Acknowledgments
The authors thank journal editor T. Elliot and two anonymous reviewers for their insightful comments that significantly improved the quality of the article. S. Westenbroek and A. Mair are acknowledged for their help with the SWB program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McMahon, P.B.; Plummer, L.N.; Boehlke, J.K.; Shapiro, S.D.; Hinkle, S.R. A comparison of recharge rates in aquifers of the United States based on groundwater-age data. Hydrogeol. J. 2011, 19, 779–800. [Google Scholar] [CrossRef]
- Castle, S.L.; Thomas, B.F.; Reager, J.T.; Rodell, M.; Swenson, S.C.; Famiglietti, J.S. Groundwater Depletion during Drought Threatens Future Water Security of the Colorado River Basin. Geophys. Res. Lett. 2014, 41, 5904–5911. [Google Scholar] [CrossRef] [PubMed]
- Service, R.F. California’s Water Crisis: Worse to Come? Science 2009, 323, 1665. [Google Scholar] [CrossRef] [PubMed]
- Thomas, B.F.; Caineta, J.; Nanteza, J. Global Assessment of Groundwater Sustainability Based on Storage Anomalies. Geophys. Res. Lett. 2017, 44. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Z.-C.; Zhang, X.-N.; Chen, Y.-Q.; Qian, M.-K.; Peng, S.-F. Estimation of Groundwater Recharge from Precipitation and Evapotranspiration by Lysimeter Measurement and Soil Moisture Model. J. Hydrol. Eng. 2008, 13, 333–340. [Google Scholar] [CrossRef]
- Crosbie, R.S.; Binning, P.; Kalma, J.D. A time series approach to inferring groundwater recharge using the water table fluctuation method. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Hagedorn, B. Hydrochemical and 14C constraints on groundwater recharge and interbasin flow in an arid watershed: Tule Desert, Nevada. J. Hydol. 2015, 523, 297–308. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Somaratne, N. Characteristics of Point Recharge in Karst Aquifers. Water 2014, 6, 2782–2807. [Google Scholar] [CrossRef]
- Von Freyberg, J.; Moeck, C.; Schirmer, M. Estimation of groundwater recharge and drought severity with varying model complexity. J. Hydrol. 2015, 527, 844–857. [Google Scholar] [CrossRef]
- Izbicki, J.A.; Stamos, C.L.; Nishikawa, T.; Martin, P. Comparison of ground-water flow model particle-tracking results and isotopic data in the Mojave River ground-water basin, southern California, USA. J. Hydrol. 2004, 292, 30–47. [Google Scholar] [CrossRef]
- McCoy, K.J.; Yager, R.M.; Nelms, D.L.; Ladd, D.E.; Monti, J., Jr.; Kozar, M.D. Hydrologic Budget and Conditions of Permian, Pennsylvanian, and Mississippian Aquifers in the Appalachian Plateaus Physiographic Province; U.S. Geological Survey Scientific Investigations Report 2015–5106; U.S. Geological Survey: Reston, VA, USA, 2015; p. 77.
- Moreno, H.A.; Gupta, H.V.; White, D.D.; Sampson, D.A. Modeling the distributed effects of forest thinning on the long-term water balance and streamflow extremes for a semi-arid basin in the southwestern US. Hydrol. Earth Syst. Sci. 2016, 20, 1241–1267. [Google Scholar] [CrossRef]
- Sanford, W. Recharge and groundwater models: An overview. Hydrogeol. J. 2002, 10, 110–120. [Google Scholar] [CrossRef]
- Smith, E.A.; Westenbroek, S.M. Potential Groundwater Recharge for the State of Minnesota Using the Soil-Water-Balance Model, 1996–2010; U.S. Geological Survey Scientific Investigations Report 2015-5038; U.S. Geological Survey: Reston, VA, USA, 2015; p. 85.
- Hagedorn, B.; El-Kadi, A.I.; Mair, A.; Whittier, R.B.; Ha, K. Estimating recharge in fractured aquifers of a temperate humid to semiarid volcanic island (Jeju, Korea) from water table fluctuations, and Cl, CFC-12 and 3H chemistry. J. Hydrol. 2011, 409, 650–662. [Google Scholar] [CrossRef]
- Gehman, C.L.; Harry, D.L.; Sanford, W.E.; Stednick, J.D.; Beckman, N.A. Estimating specific yield and storage change in an unconfined aquifer using temporal gravity surveys. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Somaratne, N. Pitfalls in application of the conventional chloride mass balance (CMB) in karst aquifers and use of the generalised CMB method. Environ. Earth Sci. 2015, 74, 337–349. [Google Scholar] [CrossRef]
- Hagedorn, B.; Clarke, N.; Ruane, M.; Faulkner, K. Assessing aquifer vulnerability from lumped parameter modeling of modern water proportions in groundwater mixtures: Application to California’s South Coast Range. Sci. Total Environ. 2018, 624, 1550–1560. [Google Scholar] [CrossRef] [PubMed]
- Jurgens, B.C.; Boehlke, J.K.; Kauffman, L.J.; Belitz, K.; Esser, B.K. A partial exponential lumped parameter model to evaluate groundwater age distributions and nitrate trends in long screened wells. J. Hydol. 2017, 543, 109–126. [Google Scholar] [CrossRef]
- Koh, D.-C.; Chang, H.-W.; Lee, K.-S.; Ko, K.-S.; Kim, Y.; Park, W.-B. Hydrogeochemistry and environmental isotopes of ground water in Jeju volcanic island, Korea: Implications for nitrate contamination. Hydrol. Process. 2005, 19, 2225–2245. [Google Scholar] [CrossRef]
- Zhu, C. Estimate of recharge from radiocarbon dating of groundwater and numerical flow and transport modeling. Water Resour. Res. 2000, 36, 2607–2620. [Google Scholar] [CrossRef]
- USGS. Documentation of Computer Program INFIL3.0—A Distributed Parameter Watershed Model to Estimate Net Infiltration below the Root Zone; U.S. Geological Survey Scientific Investigations Report 2008-5006; U.S. Geological Survey: Reston, VA, USA, 2008; p. 98.
- Oki, D.S. The Significance of Accounting Order for Evapotranspiration and Recharge in Monthly and Daily Threshold-Type Water Budgets; U.S. Geological Survey Scientific Investigations Report 2008-5163; U.S. Geological Survey: Reston, VA, USA, 2008.
- Jasechko, S.; Taylor, R.G. Intensive rainfall recharges tropical groundwaters. Environ. Res. Lett. 2015, 10, 124015. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healey, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Westenbroek, S.M.; Kelson, V.A.; Dripps, W.R.; Hunt, R.J.; Bradbury, K.R. SWB—A Modified Thornthwaithe-Mather Soil-Water-Balance Code for Estimating Groundwater Recharge; U.S. Geological Survey Techniques and Methods G-A31; U.S. Geological Survey: Reston, VA, USA, 2010; p. 59.
- Lauren-Schlau-Consulting Economic and Fiscal Impacts and Profile of 2016 Catalina Island Visitors Final Report. Available online: https://www.catalinachamber.com/about-avalon-catalina-island/catalina-visitor-statistics/ (accessed on 1 November 2018).
- Macon, D.K.; Barry, S.; Becchetti, T.; Davy, J.S.; Doran, M.P.; Finzel, J.A.; George, H.; Harper, J.M.; Huntsinger, L.; Ingram, R.S.; et al. Coping with Drought on California Rangelands. Rangelands 2016, 38, 222–228. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. Uniqueness and Causes of the California Drought. Procedia Comput. Sci. 2015, 61, 428–435. [Google Scholar] [CrossRef]
- Tortajada, C.; Kastner, M.J.; Buurman, J.; Biswas, A.K. The California drought: Coping responses and resilience building. Environ. Sci. Policy 2017, 78, 97–113. [Google Scholar] [CrossRef]
- Gee, G.W.; Hillel, D. Groundwater recharge in arid regions: Review and critique of estimation methods. Hydrol. Process. 1988, 2, 255–266. [Google Scholar] [CrossRef]
- Milewski, A.; Sultan, M.; Yan, E.; Becker, R.; Abdeldayem, A.; Soliman, F.; Gelil, K.A. A remote sensing solution for estimating runoff and recharge in arid environments. J. Hydrol. 2009, 373, 1–14. [Google Scholar] [CrossRef]
- Brauman, K.A.; Freyberg, D.L.; Daily, G.C. Land cover effects on groundwater recharge in the tropics: Ecohydrologic mechanisms. Ecohydrology 2012, 5, 435–444. [Google Scholar] [CrossRef]
- Zhang, Y.-K.; Schilling, K.E. Effects of land cover on water table, soil moisture, evapotranspiration, and groundwater recharge: A Field observation and analysis. J. Hydrol. 2006, 319, 328–338. [Google Scholar] [CrossRef]
- Fan, J.; Oestergaard, K.T.; Guyot, A.; Lockington, D.A. Estimating groundwater recharge and evapotranspiration from water table fluctuations under three vegetation covers in a coastal sandy aquifer of subtropical Australia. J. Hydrol. 2014, 519, 1120–1129. [Google Scholar] [CrossRef]
- Halsey, R.W.; (Chaparral Institute, Escondido, CA, USA). Personal communication, 2017.
- Minnich, R.A. Vegetation of Santa Cruz and Santa Catalina islands, in the California Islands: Proceedings of a Multidisciplinary Symposium, Santa Barbara, California, USA; Santa Barbara Museum of Natural History: Santa Barbara, CA, USA, 1980; pp. 123–138. [Google Scholar]
- Minnich, R.A. Grazing, Fire, and the Management of Vegetation on Santa Catalina Island, California; Proceedings of the Symposium on Dynamics and Management of Mediterranean-Type Ecosystems; Pacific Southwest Forest and Range Experiment Station, USDA Forest Service: Washington, DC, USA, 1982; pp. 444–449.
- Corbett, E.S.; Crouse, R.P. Rainfall Interception by Annual Grass and Chaparral; Losses Compared; U.S. Department of Agriculture: Berkeley, CA, USA, 1968; p. 11.
- Tate, K.W. Interception on Rangeland Watersheds. Fact Sheet Rangeland Watershed Program; U.S. Department of Agriculture, Natural Resources Conservation Service: Berkeley, CA, USA, 1995; p. 4.
- USGS National Landcover Database. Available online: www.mrlc.gov/nlcd2011.php (accessed on 19 April 2016).
- Mair, A.; Hagedorn, B.; Tillery, S.; El-Kadi, A.I.; Westenbroek, S.M.; Ha, K.; Koh, G.-W. Temporal and spatial variability of groundwater recharge on Jeju Island, Korea. J. Hydrol. 2013, 501, 213–226. [Google Scholar] [CrossRef]
- Engott, J.A.; Vana, T.T. Effects of Agricultural Land-Use Changes and Rainfall on Ground-Water Recharge in Central and West Maui, Hawaii, 1926–2004; U.S. Geological Survey Scientific Investigations Report 2007-5103; U.S. Geological Survey: Reston, VA, USA, 2007; p. 56.
- Rowland, S.M. Geology of Santa Catalina Island. California Geology 1984, 39, 239–251. [Google Scholar]
- Southern California Edison Catalina Island Groundwater Resources; September 2015 Presentation Santa Catalina Island Company, Avalon. Available online: https://www.catalinachamber.com/about-avalon-catalina-island/catalina-visitor-statistics (accessed on 19 April 2018).
- Lozier, W.B. Water Budget Computer Model to Investigate the Effectiveness of Evaporation Control on Thompson Reservoir, Santa Catalina Island, California. Master’s Thesis, University of Arizona, Tucson, AZ, USA, 1984. [Google Scholar]
- Thornthwaite, C.W.; Mather, J.R. Instructions and tables for computing potential evapotranspiration and the water balance. Publ. Climatol. 1957, 10, 185–311. [Google Scholar]
- Engott, J.A. Spatial Distribution of Groundwater Recharge on the Island of Hawaii; U.S. Geological Survey Scientific Investigations Report 2011-5078; U.S. Geological Survey: Reston, VA, USA, 2011; p. 53.
- Juvik, J.O.; DeLay, J.K.; Kinney, K.M.; Hansen, E.W. A 50th anniversary reassessment of the seminal “Lāna‘i fog drip study’ in Hawai’i.’”. Hydrol. Process. 2011, 25, 402–410. [Google Scholar] [CrossRef]
- Llorens, P.; Domingo, F. Rainfall partitioning by vegetation under Mediterranean conditions. A review of studies in Europe. J. Hydrol. 2007, 335, 37–54. [Google Scholar] [CrossRef]
- Mair, A.; Hagedorn, B.; Tillery, S.; Whittier, R.B.; El-Kadi, A.I. Water Budget Analyses and Sustainable Yield Estimation on Jeju Island, Alternative Groundwater Recharge Estimation, Climate Data Analysis, Water Balance Modeling, and Sustainable Yield Assessment, Phase II Report, Prepared for Korea Institute for Geosciences and Mineral Resources (KIGAM), Daejong, Korea; Water Resources Research Center, University of Hawaii at Manoa: Honolulu, HI, USA, 2011. [Google Scholar]
- McLaren, J.R.; Wilson, S.D.; Peltzer, D.A. Plant feedbacks increase the temporal heterogeneity of soil moisture. Oikos 2004, 107, 199–205. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G. Rainfall interception by Santa Monica’s municipal urban forest. Urban Ecosyst. 2002, 6, 291–302. [Google Scholar] [CrossRef]
- Ma, S.; Baldocchi, D.D.; Xu, L.; Hehn, T. Inter-annual variability in carbon dioxide exchange of an oak/grass savanna and open grassland in California. Agric. For. Meteorol. 2007, 147, 157–171. [Google Scholar] [CrossRef]
- Parker, S.S.; Schimel, J.P. Soil nitrogen availability and transformations differ between the summer and the growing season in a California grassland. Appl. Soil Ecol. 2011, 48, 185–192. [Google Scholar] [CrossRef]
- Bradbury, C.G.; Rushton, K.R. Estimating runoff–recharge in the Southern Lincolnshire Limestone catchment, UK. J. Hydrol. 1998, 211, 86–99. [Google Scholar] [CrossRef]
- Seiler, K.P.; Gat, J.R. Groundwater Recharge from Run-Off, Infiltration and Percolation, 1st ed.; Springer: Dortrecht, The Netherlands, 2007. [Google Scholar]
- Hjelmfelt, A.T.; Mockus, V.; Moody, H.F. Estimation of Direct Runoff from Storm Rainfall. In National Engineering Handbook; Hydrology; United States Department of Agriculture—Natural Resources Conservation Service: Washington, DC, USA, 2004. [Google Scholar]
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements; Technical Bulletin No. 1275; U.S. Department of Agriculture: Washington, DC, USA, 1962.
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. Proc. Am. Soc. Civ. Eng. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar]
- Turc, L. Estimation of irrigation water requirements, potential evapotranspiration: A simple climatic formula evolved up to date. Ann Agron 1961, 12, 13–49. (In French) [Google Scholar]
- Hagedorn, B.; Mair, A.; Tillery, S.; El-Kadi, A.I.; Ha, K.; Koh, G.W. Simple equations for temperature simulations on mid-latitude volcanic islands: A case study from Jeju (Republic of Korea). Geosci. J. 2014, 18, 381–396. [Google Scholar] [CrossRef]
- Jie, Z.; van Heyden, J.; Bendel, D.; Barthel, R. Combination of soil-water balance models and water-table fluctuation methods for evaluation and improvement of groundwater recharge calculations. Hydrogeol. J. 2011, 19, 1487–1502. [Google Scholar] [CrossRef]
- Cook, P.G.; Hatton, T.J.; Pidsley, D.; Herczeg, A.L.; Held, A.; O’Grady, A.; Eamus, D. Water balance of a tropical woodland ecosystem, Northern Australia: A combination of micro-meteorological, soil physical and groundwater chemical approaches. J. Hydrol. 1998, 210, 161–177. [Google Scholar] [CrossRef]
- Faulkner, K. A Recharge Analysis of the Indian Well Basin, California Using Geochemical Analysis of Tritium and Radiocarbon. Master’s Thesis, California State University, Long Beach, CA, USA, 2018. [Google Scholar]
- Plummer, L.N.; Busenberg, E. Chlorofluorocarbons in the atmosphere. In Use of Chlorofluorocarbons in Hydrology: A Guidebook; International Atomic Energy Agency: Vienna, Austria, 2006; pp. 9–14. [Google Scholar]
- PRISM Parameter-elevation Relationships on Independent Slopes Model—Precipitation Maps. Northwest Alliance for Computational Science and Engineering. 2010. Available online: http://www.prism.oregonstate.edu (accessed on 20 November 2018).
- Koh, D.C.; Plummer, L.N.; Solomon, D.K.; Busenberg, E.; Kim, Y.-J.; Chang, H.-W. Application of environmental tracers to mixing, evolution, and nitrate contamination of ground water in Jeju Island, Korea. J. Hydrol. 2006, 327, 258–275. [Google Scholar] [CrossRef]
- NADP National Atmospheric Deposition Program. 2017. Available online: http://nadp.sws.uiuc.edu (accessed on 29 November 2018).
- Grismer, M.E.; Bachman, S.; Powers, T. A comparison of groundwater recharge estimation methods in a semi-arid, coastal avocado and citrus orchard (Ventura County, California). Hydrol. Process. 2000, 14, 2527–2543. [Google Scholar] [CrossRef]
- Manna, F.; Cherry, J.A.; McWhorter, D.B.; Parker, B.L. Groundwater recharge assessment in an upland sandstone aquifer of southern California. J. Hydrol. 2016, 541, 787–799. [Google Scholar] [CrossRef]
- Blackburn, G.; McLeod, S. Salinity of atmospheric precipitation in the Murray–Darling Drainage Division, Australia. Aust. J. Soil Res. 1983, 21, 411–434. [Google Scholar] [CrossRef]
- Subyani, A.; Sen, Z. Refined chloride mass-balance method and its application in Saudi Arabia. Hydrol. Process. 2006, 20, 4373–4380. [Google Scholar] [CrossRef]
- Dassi, L. Use of chloride mass balance and tritium data for estimation of groundwater recharge and renewal rate in an unconfined aquifer from North Africa: A case study from Tunisia. Environ. Earth Sci. 2010, 60, 861–871. [Google Scholar] [CrossRef]
- Johnson, T.D.; Belitz, K. Assigning land use to supply wells for the statistical characterization of regional groundwater quality—Correlating urban land use and VOC occurrence. J. Hydrol. 2009, 370, 100–108. [Google Scholar] [CrossRef]
- Anders, R.; Mendez, G.O.; Futa, K.; Danskin, W. A Geochemical Approach to Determine Sources and Movement of Saline Groundwater in a Coastal Aquifer. Ground Water 2013, 52, 1–13. [Google Scholar] [CrossRef]
- Cartwright, I.; Weaver, T.R.; Fulton, S.; Nichol, C.; Reid, M.; Cheng, X. Hydrogeochemical and isotopic constraints on the origins of dryland salinity, Murray Basin, Victoria, Australia. Appl. Geochem. 2004, 19, 1233–1254. [Google Scholar] [CrossRef]
- Vengosh, A.; Spivack, A.J.; Artzi, Y.; Ayalon, A. Geochemical and boron, strontium, and oxygen isotopic constraints on the origin of the salinity in groundwater from the Mediterranean Coast of Israel. Water Resour. Res. 1999, 35, 1877–1894. [Google Scholar] [CrossRef]
- Barbieri, M.; Ricolfi, L.; Vitale, S.; Muteto, P.V.; Nigro, A.; Sappa, G. Assessment of groundwater quality in the buffer zone of Limpopo National Park, Gaza Province, Southern Mozambique. Environ. Sci. Pollut. Res. Int. 2018, 1–16. [Google Scholar] [CrossRef]
- Hendrickx, J.M.H.; Allen, R.G.; Brower, A.; Byrd, A.R.; Hong, S.; Ogden, F.L.; Pradhan, N.R.; Robison, C.W.; Toll, D.; Trezza, R.; et al. Benchmarking Optical/Thermal Satellite Imagery for Estimating Evapotranspiration and Soil Moisture in Decision Support Tools. J. Am. Water Resour. Assoc. 2016, 52, 89–119. [Google Scholar] [CrossRef]
- Hollett, K.J.; Danskin, W.R.; McCaffrey, W.F.; Walti, C.L. Geology and Water Resources of Owens Valley, California; U.S. Geological Survey Scientific Investigation Report 2370-B; U.S. Geological Survey: Reston, VA, USA, 1991; p. 77.
- Flint, A.L.; Flint, L.E. Application of the Basin Characterization Model to Estimate in-Place Recharge and Runoff Potential in the Basin and Range Carbonate-Rock Aquifer System, White Pine County, Nevada, and Adjacent Areas in Nevada and Utah; U.S. Geological Survey Scientific Investigations Report 2007-5099; U.S. Geological Survey: Reston, VA, USA, 2007.
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Sami, K.; Hughes, D.A. A comparison of recharge estimates to a fractured sedimentary aquifer in South Africa from a chloride mass balance and an integrated surface-subsurface model. J. Hydrol. 1996, 179, 111–136. [Google Scholar] [CrossRef]
- Heilweil, V.M.; Solomon, D.K.; Gardner, P.M. Infiltration and Recharge at Sand Hollow, an Upland Bedrock Basin in Southwestern Utah: Chapter I. In Ground-Water Recharge in the Arid and Semiarid Southwestern United States; U.S. Geological Survey Professional Paper 1703; U.S. Geological Survey: Reston, VA, USA, 2007; pp. 221–251. [Google Scholar]
- Giambelluca, T.W.; Martin, R.E.; Asner, G.P.; Huang, S.-H.; Mudd, R.G.; Nullet, M.A.; DeLay, J.K.; Foote, D. Evapotranspiration and energy balance of native wet montane cloud forest in Hawaii. Agric. For. Meteorol. 2009, 149, 230–243. [Google Scholar] [CrossRef]
- Evola, S.; Sandquist, D.R. Quantification of fog input and use by Quercus pacifica on Santa Catalina Island. In Oak Ecosystem Restoration on Santa Catalina Island, California: Proceedings of an On-Island Workshop, Avalon, CA, February 2007; Catalina Island Conservancy: Avalon, CA, USA, 2007. [Google Scholar]
- Stanton, J.S.; Qi, S.L.; Ryter, D.W.; Falk, S.E.; Houston, N.A.; Peterson, S.M.; Westenbroek, S.M.; Christenson, S.C. Selected Approaches to Estimate Water-Budget Components of the High Plains, 1940 through 1949 and 2000 through 2009; U.S. Geological Survey Scientific Investigations Report 2011–5183; US Geological Survey: Reston, VA, USA, 2011; 79p.
- Tillman, F.D. Documentation of Input Datasets for the Soil-Water Balance Groundwater Recharge Model of the Upper Colorado River Basin; U.S. Geological Survey Open-File Report 2015-1160; U.S. Geological Survey: Reston, VA, USA, 2015; p. 17.
- Moeck, C.; von Freyberg, J.; Schirmer, M. Groundwater recharge predictions in contrasted climate: The effect of model complexity and calibration period on recharge rates. Environ. Model. Softw. 2018, 103, 74–89. [Google Scholar] [CrossRef]
- El-Kadi, A.I.; Tillery, S.; Whittier, R.B.; Hagedorn, B.; Mair, A.; Ha, K.; Koh, G.-W. Assessing sustainability of groundwater resources on Jeju Island, South Korea, under climate change, drought, and increased usage. Hydrogeol. J. 2014, 22, 625–642. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).