Characterization of Hydraulic Heterogeneity of Alluvial Aquifer Using Natural Stimuli: A Field Experience of Northern Italy
Abstract
:1. Introduction
2. Materials and Methods
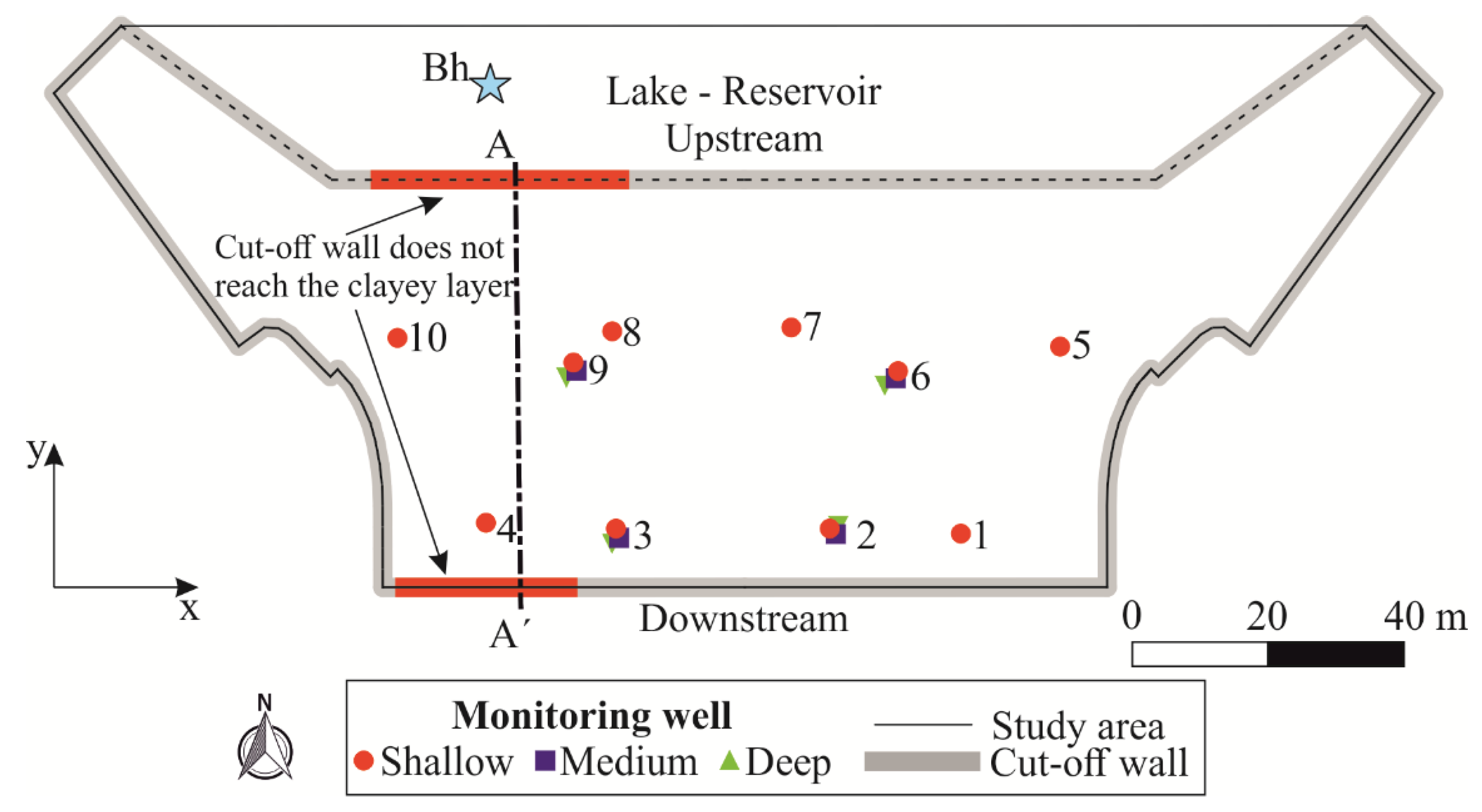
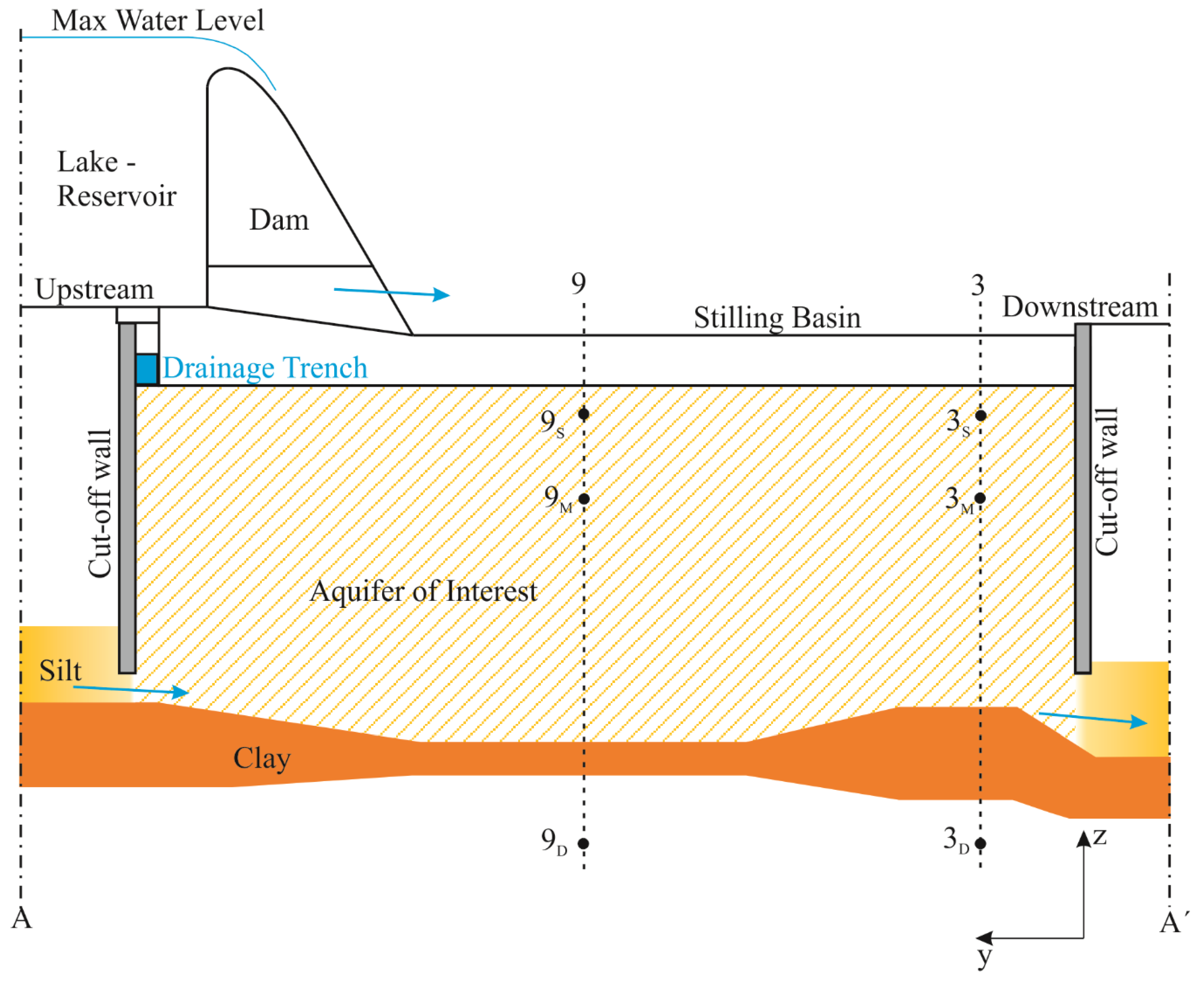
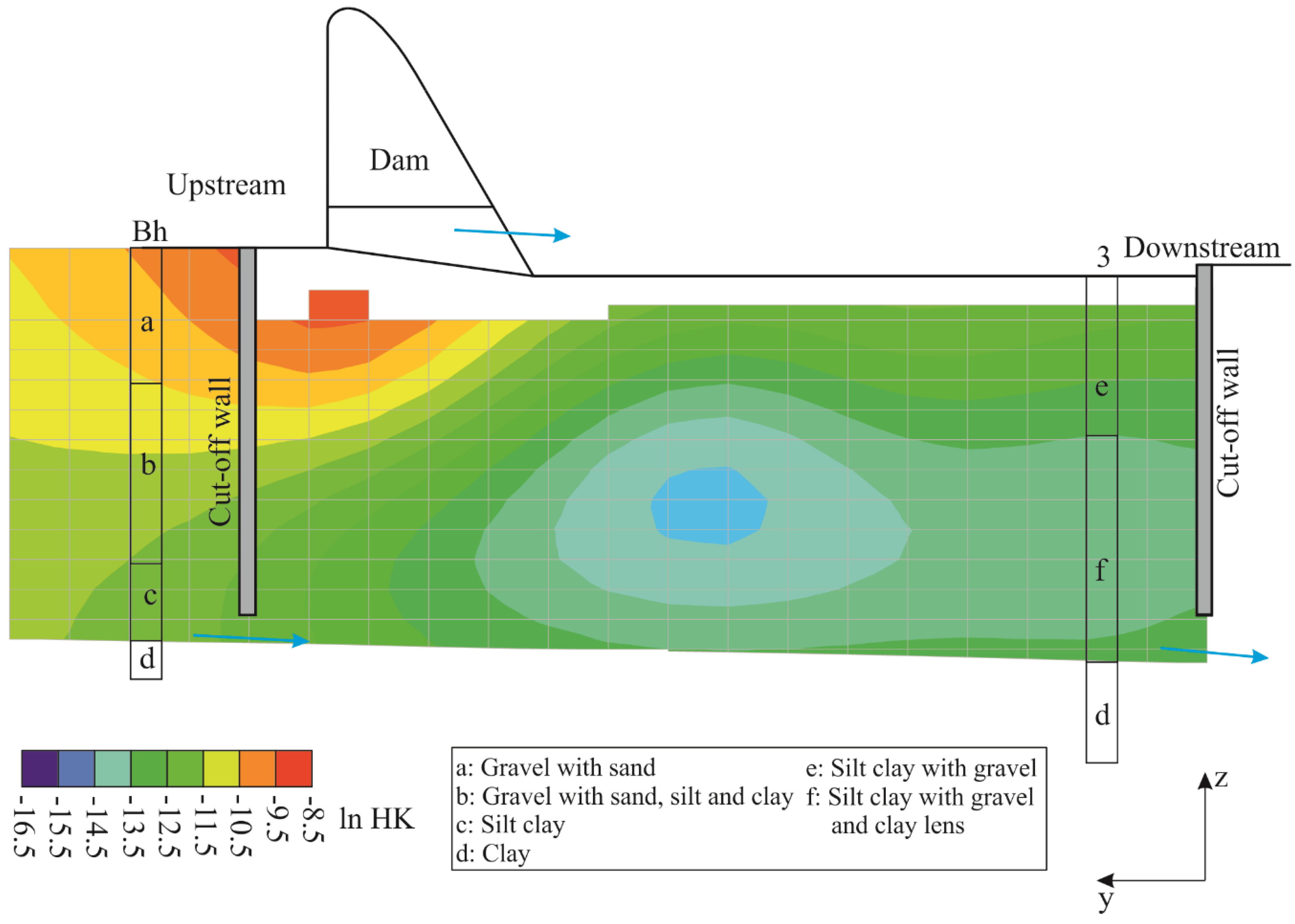
2.1. Case Study and Available Data
2.2. Inverse Approach
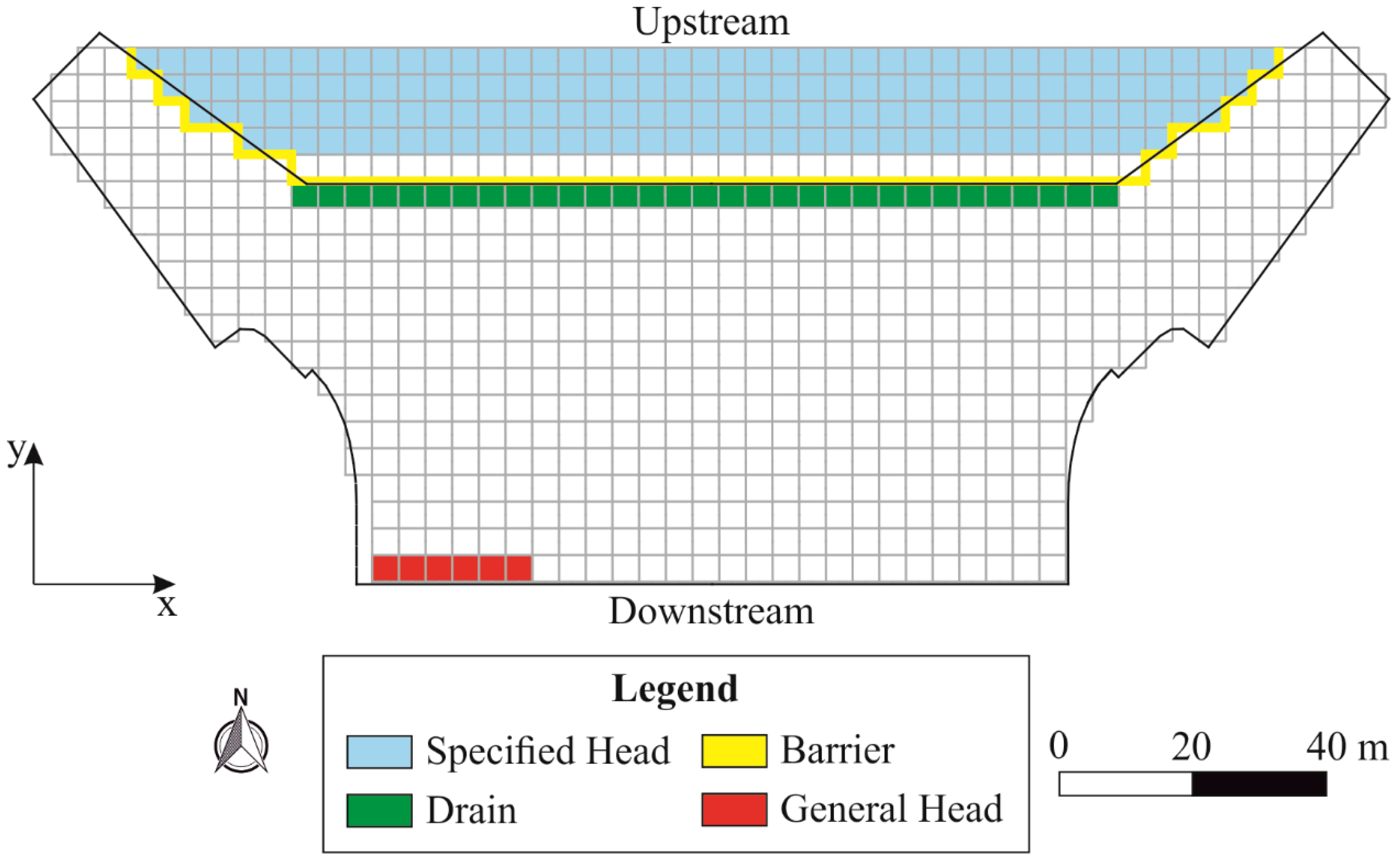
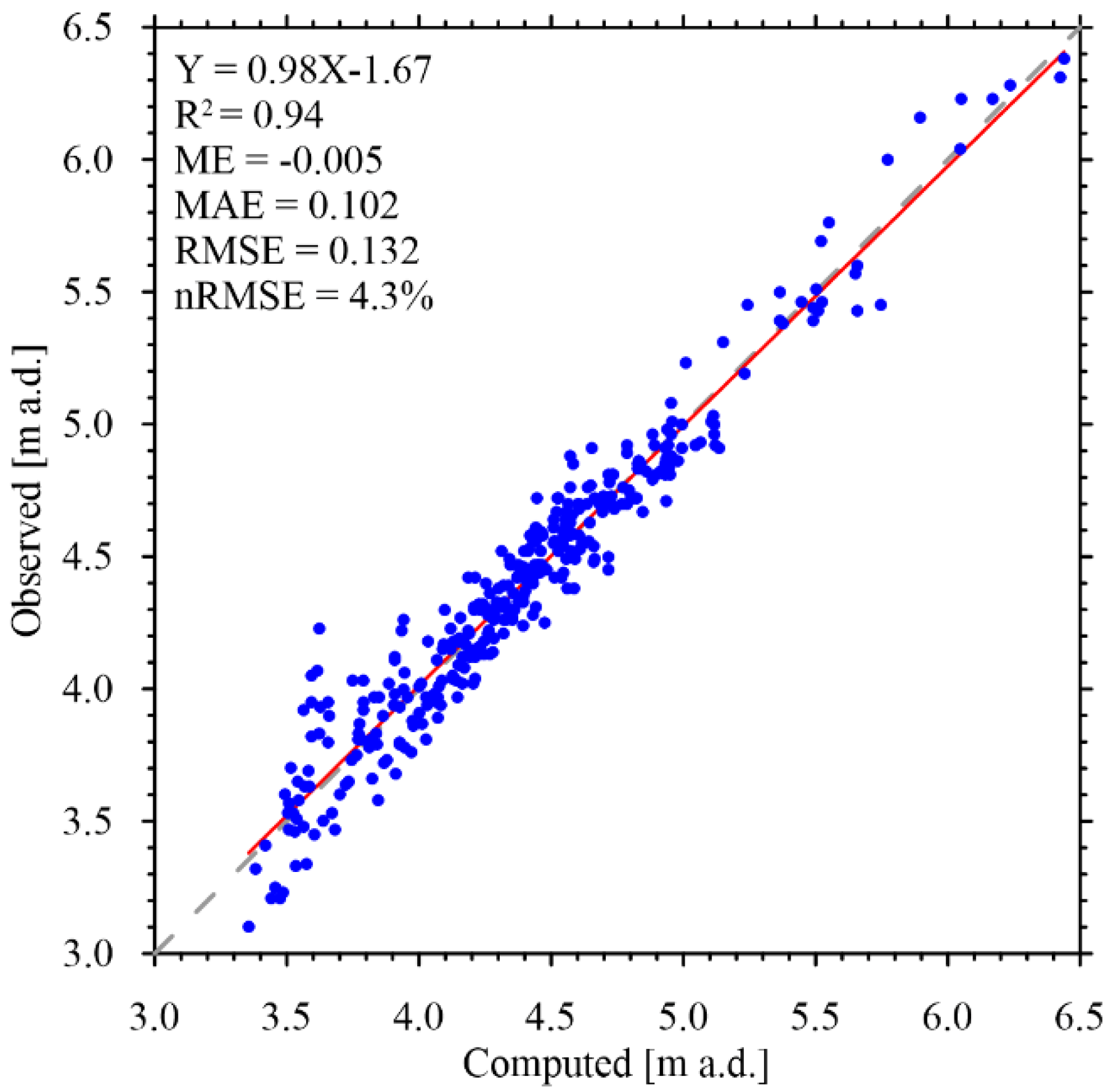
2.3. Flow Model and Calibration
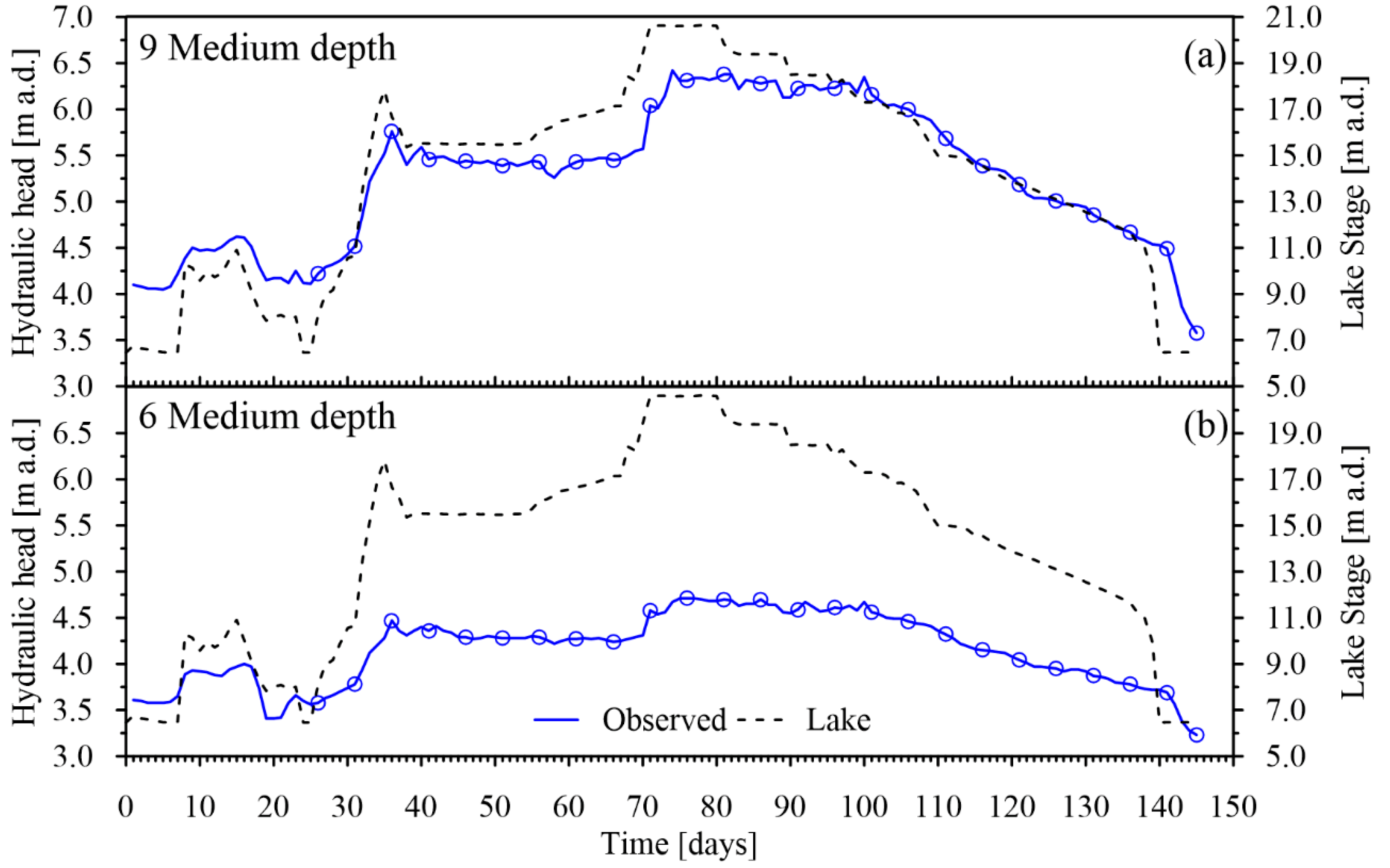
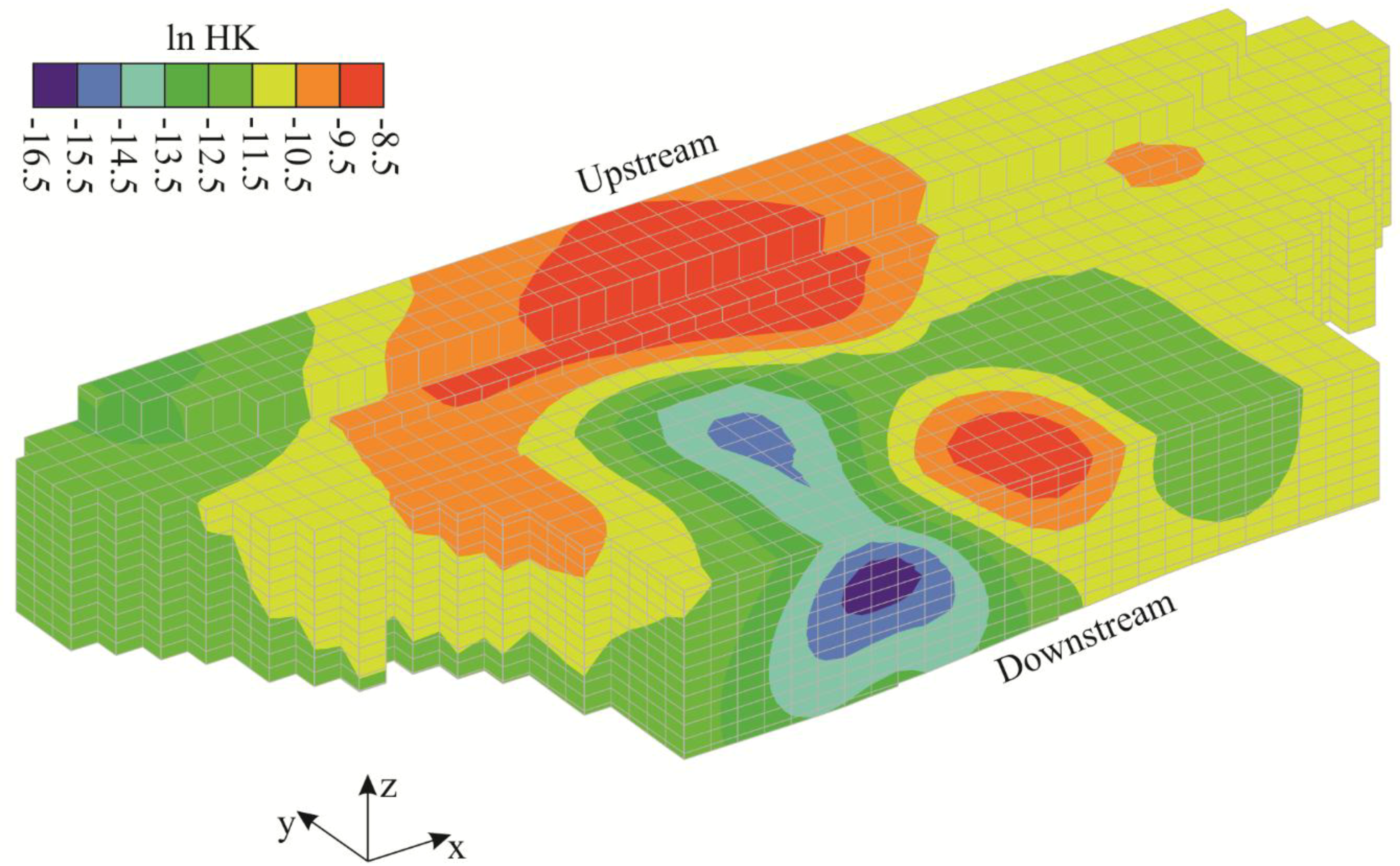
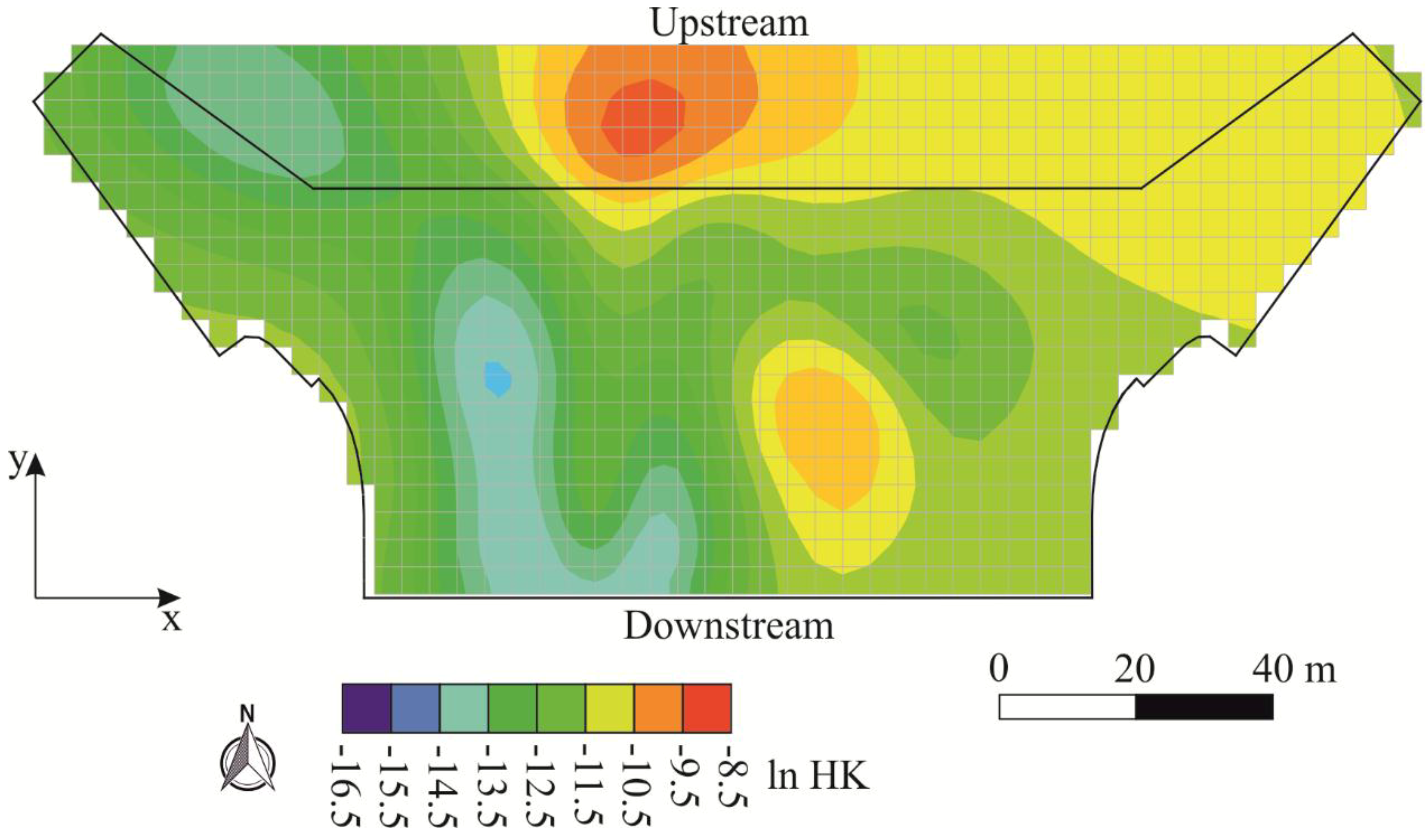
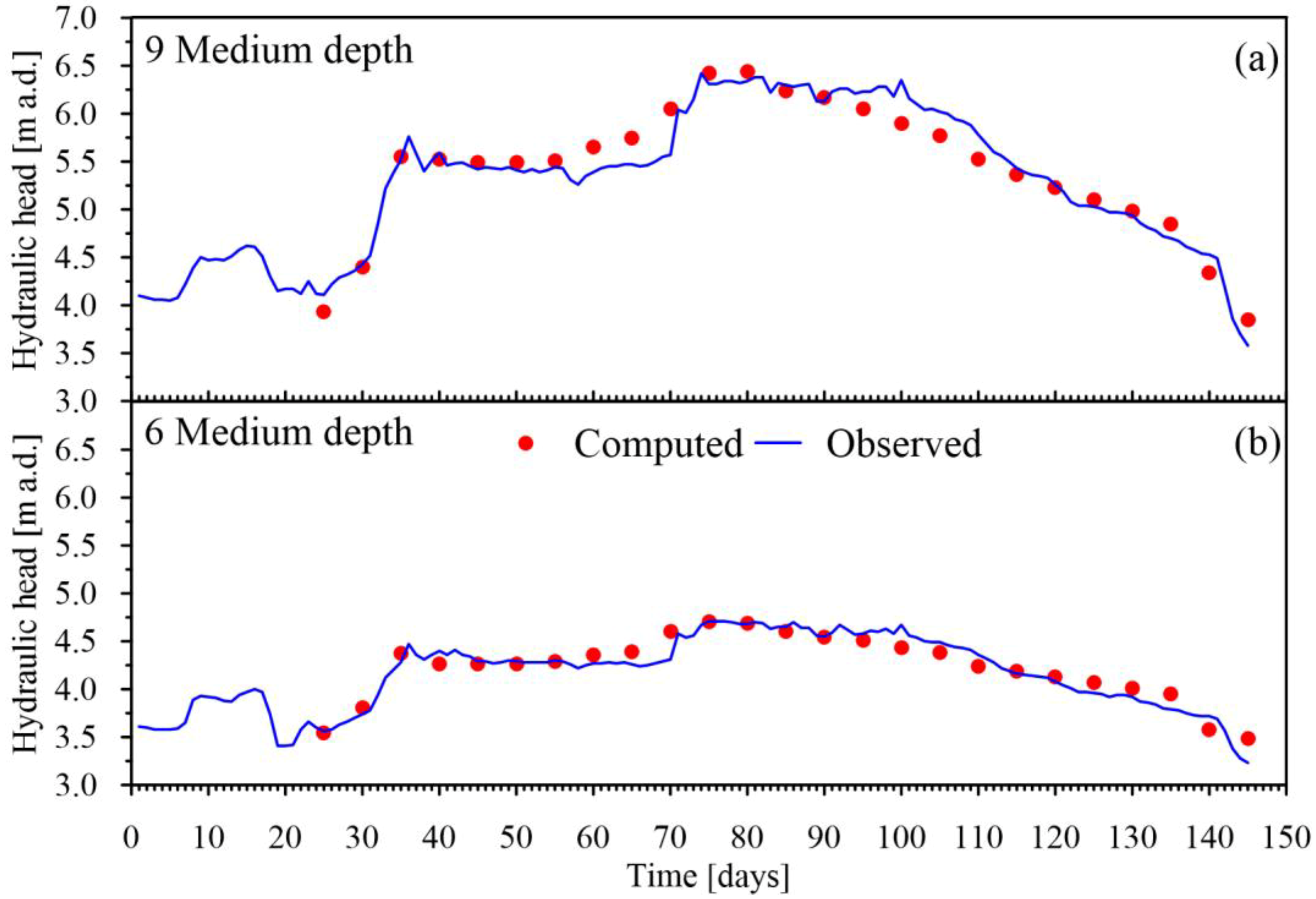
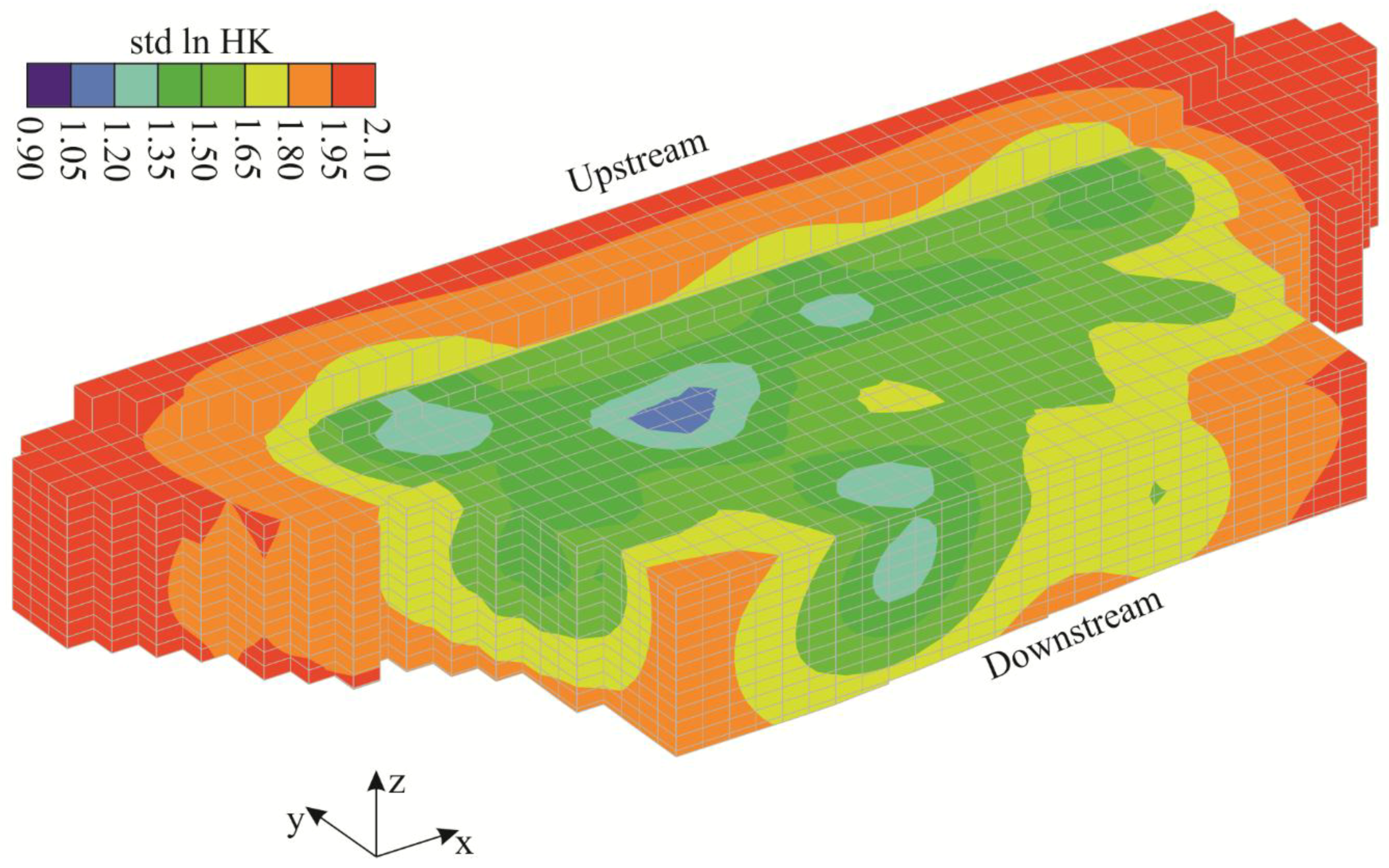
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Petit-Boix, A.; Sevigné-Itoiz, E.; Rojas-Gutierrez, L.A.; Barbassa, A.P.; Josa, A.; Rieradevall, J.; Gabarrell, X. Floods and consequential life cycle assessment: Integrating flood damage into the environmental assessment of stormwater Best Management Practices. J. Clean. Prod. 2017, 162, 601–608. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Sun, W.-J.; Shen, S.-L.; Arulrajah, A. Flood risk assessment in metro systems of mega-cities using a GIS-based modeling approach. Sci. Total Environ. 2018, 626, 1012–1025. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Berg, S.J.; Illman, W.A. Comparison of Hydraulic Tomography with Traditional Methods at a Highly Heterogeneous Site. Groundwater 2015, 53, 71–89. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Gómez-Hernández, J.J. Simultaneous identification of a contaminant source and hydraulic conductivity via the restart normal-score ensemble Kalman filter. Adv. Water Resour. 2018, 112, 106–123. [Google Scholar] [CrossRef]
- Xu, T.; Gómez-Hernández, J.J. Inverse sequential simulation: A new approach for the characterization of hydraulic conductivities demonstrated on a non-Gaussian field. Water Resour. Res. 2015, 51, 2227–2242. [Google Scholar] [CrossRef] [Green Version]
- Marinoni, M.; Delay, F.; Ackerer, P.; Riva, M.; Guadagnini, A. Identification of groundwater flow parameters using reciprocal data from hydraulic interference tests. J. Hydrol. 2016, 539, 88–101. [Google Scholar] [CrossRef]
- Zanini, A.; Tanda, M.G.; Woodbury, A.D. Identification of transmissivity fields using a Bayesian strategy and perturbative approach. Adv. Water Resour. 2017, 108, 69–82. [Google Scholar] [CrossRef]
- Butera, I.; Soffia, C. Cokriging transmissivity, head and trajectory data for transmissivity and solute path estimation. Groundwater 2017, 55, 362–374. [Google Scholar] [CrossRef]
- D’Oria, M.; Zanini, A.; Cupola, F. Oscillatory pumping test to estimate aquifer hydraulic parameters in a Bayesian geostatistical framework. Math. Geosci. 2018, 50, 169–186. [Google Scholar] [CrossRef]
- Chen, Z.; Gómez-Hernández, J.J.; Xu, T.; Zanini, A. Joint identification of contaminant source and aquifer geometry in a sandbox experiment with the restart ensemble Kalman filter. J. Hydrol. 2018, 564, 1074–1084. [Google Scholar] [CrossRef]
- Comunian, A.; Giudici, M. Hybrid inversion method to estimate hydraulic transmissivity by combining multiple-point statistics and a direct inversion method. Math. Geosci. 2018, 50, 147–167. [Google Scholar] [CrossRef]
- Kitanidis, P.K. Quasi-linear geostatistical theory for inversing. Water Resour. Res. 1995, 31, 2411–2419. [Google Scholar] [CrossRef]
- Fienen, M.N.; Clemo, T.; Kitanidis, P.K. An interactive Bayesian geostatistical inverse protocol for hydraulic tomography. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- D’Oria, M.; Lanubile, R.; Zanini, A. Bayesian estimation of a highly parameterized hydraulic conductivity field: A study case. Procedia Environ. Sci. 2015, 25, 82–89. [Google Scholar] [CrossRef]
- Kitanidis, P.K.; Lee, J. Principal component geostatistical approach for large-dimensional inverse problems. Water Resour. Res. 2014, 50, 5428–5443. [Google Scholar] [CrossRef]
- D’Oria, M.; Tanda, M.G. Reverse flow routing in open channels: A Bayesian geostatistical approach. J. Hydrol. 2012, 460–461, 130–135. [Google Scholar] [CrossRef]
- Ferrari, A.; D’Oria, M.; Vacondio, R.; Dal Palù, A.; Mignosa, P.; Tanda, M.G. Discharge hydrograph estimation at upstream-ungauged sections by coupling a Bayesian methodology and a 2-D GPU shallow water model. Hydrol. Earth Syst. Sci. 2018, 22, 5299–5316. [Google Scholar] [CrossRef]
- D’Oria, M.; Mignosa, P.; Tanda, M.G. An inverse method to estimate the flow through a levee breach. Adv. Water Resour. 2015, 82, 166–175. [Google Scholar] [CrossRef]
- Leonhardt, G.; D’Oria, M.; Kleidorfer, M.; Rauch, W. Estimating inflow to a combined sewer overflow structure with storage tank in real time: Evaluation of different approaches. Water Sci. Technol. 2014, 70, 1143–1151. [Google Scholar] [CrossRef]
- Fienen, M.N.; D’Oria, M.; Doherty, J.E.; Hunt, R.J. Approaches in Highly Parameterized Inversion: bgaPEST, a Bayesian Geostatistical Approach Implementation with PEST—Documentation and Instructions; U.S. Geological Survey: Reston, VA, USA, 2013; Volume 7.
- Yeh, T.-C.J.; Xiang, J.; Suribhatla, R.M.; Hsu, K.-C.; Lee, C.-H.; Wen, J.-C. River stage tomography: A new approach for characterizing groundwater basins. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-L.; Yeh, T.-C.J.; Wen, J.-C.; Huang, S.-Y.; Zha, Y.; Tsai, J.-P.; Hao, Y.; Liang, Y. Characterizing subsurface hydraulic heterogeneity of alluvial fan using riverstage fluctuations. J. Hydrol. 2017, 547, 650–663. [Google Scholar] [CrossRef]
- Jardani, A.; Dupont, J.P.; Revil, A.; Massei, N.; Fournier, M.; Laignel, B. Geostatistical inverse modeling of the transmissivity field of a heterogeneous alluvial aquifer under tidal influence. J. Hydrol. 2012, 472–473, 287–300. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; U.S. Geological Survey Techniques and Methods: 6-A16; U.S. Geological Survey: Reston, VA, USA, 2005.
- Grishin, M.M. Hydraulic Structure; Mir Publishers: Moscow, Russia, 1982; Volume 1. [Google Scholar]
- Hoeksema, R.J.; Kitanidis, P.K. An Application of the Geostatistical approach to the inverse problem in two-dimensional groundwater modeling. Water Resour. Res. 1984, 20, 1003–1020. [Google Scholar] [CrossRef]
- Fienen, M.; Hunt, R.; Krabbenhoft, D.; Clemo, T. Obtaining parsimonious hydraulic conductivity fields using head and transport observations: A Bayesian geostatistical parameter estimation approach. Water Resour. Res. 2009, 45, W08405. [Google Scholar] [CrossRef]
- Cardiff, M.; Barrash, W.; Kitanidis, P.K. Hydraulic conductivity imaging from 3-D transient hydraulic tomography at several pumping/observation densities. Water Resour. Res. 2013, 49, 7311–7326. [Google Scholar] [CrossRef] [Green Version]
- Snodgrass, M.F.; Kitanidis, P.K. A geostatistical approach to contaminant source identification. Water Resour. Res. 1997, 33, 537–546. [Google Scholar] [CrossRef] [Green Version]
- Butera, I.; Tanda, M.G. A geostatistical approach to recover the release history of groundwater pollutants. Water Resour Res. 2003, 39, 1372. [Google Scholar] [CrossRef]
- Butera, I.; Tanda, M.G.; Zanini, A. Use of numerical modelling to identify the transfer function and application to the geostatistical procedure in the solution of inverse problems in groundwater. J. Inverse Ill-Posed Probl. 2006, 14, 547–572. [Google Scholar] [CrossRef]
- D’Oria, M.; Mignosa, P.; Tanda, M.G. Bayesian estimation of inflow hydrographs in ungauged sites of multiple reach systems. Adv. Water Resour. 2014, 63, 143–151. [Google Scholar] [CrossRef]
- Cupola, F.; Tanda, M.G.; Zanini, A. Laboratory sandbox validation of pollutant source location methods. Stoch. Environ. Res. Risk Assess. 2015, 29, 169–182. [Google Scholar] [CrossRef]
- Nowak, W.; Cirpka, O.A. A modified Levenberg–Marquardt algorithm for quasi-linear geostatistical inversing. Adv. Water Resour. 2004, 27, 737–750. [Google Scholar] [CrossRef]
- D’Oria, M.; Mignosa, P.; Tanda, M.G. Reverse level pool routing: Comparison between a deterministic and a stochastic approach. J. Hydrol. 2012, 470–471, 28–35. [Google Scholar] [CrossRef]
- Zanini, A.; Kitanidis, P.K. Geostatistical inversing for large-contrast transmissivity fields. Stoch. Environ. Res. Risk Assess. 2009, 23, 565–577. [Google Scholar] [CrossRef]
- Doherty, J. PEST, Model-Independent Parameter Estimation—User Manual. 5th Edition, with Slight Additions; Watermark Numerical Computing: Brisbane, Australia, 2010. [Google Scholar]
- Hsieh, P.A.; Freckleton, J.R. Documentation of a Computer Program to Simulate Horizontal-Flow Barriers Using the U.S. Geological Survey’s Modular Three-Dimensional Finite-Difference Ground-Water Flow Model; U.S. Geological Survey: Reston, VA, USA, 1993.
- Shen, S.-L.; Wu, Y.-X.; Misra, A. Calculation of head difference at two sides of a cut-off barrier during excavation dewatering. Comput. Geotech. 2017, 91, 192–202. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Shen, S.-L.; Yuan, D.-J. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in aquifer. J. Hydrol. 2016, 539, 554–566. [Google Scholar] [CrossRef]
- Clemo, T. MODFLOW-2005 Ground Water Model—User Guide to the Adjoint State Based Sensitivity Process (ADJ); Center for the Geophysical Investigation of the Shallow Subsurface Boise State University: Boise, ID, USA, 2007. [Google Scholar]
- D’Oria, M.; Fienen, M.N. MODFLOW-Style parameters in underdetermined parameter estimation. Ground Water 2012, 50, 149–153. [Google Scholar] [CrossRef]
- Anderson, M.P.; Woessner, W.W. Applied Groundwater Modeling: Simulation of Flow and Advective Transport; Academic Press: San Diego, CA, USA, 1992; ISBN 0-12-059485-4. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Oria, M.; Zanini, A. Characterization of Hydraulic Heterogeneity of Alluvial Aquifer Using Natural Stimuli: A Field Experience of Northern Italy. Water 2019, 11, 176. https://doi.org/10.3390/w11010176
D’Oria M, Zanini A. Characterization of Hydraulic Heterogeneity of Alluvial Aquifer Using Natural Stimuli: A Field Experience of Northern Italy. Water. 2019; 11(1):176. https://doi.org/10.3390/w11010176
Chicago/Turabian StyleD’Oria, Marco, and Andrea Zanini. 2019. "Characterization of Hydraulic Heterogeneity of Alluvial Aquifer Using Natural Stimuli: A Field Experience of Northern Italy" Water 11, no. 1: 176. https://doi.org/10.3390/w11010176
APA StyleD’Oria, M., & Zanini, A. (2019). Characterization of Hydraulic Heterogeneity of Alluvial Aquifer Using Natural Stimuli: A Field Experience of Northern Italy. Water, 11(1), 176. https://doi.org/10.3390/w11010176





