Parameter Estimation and Uncertainty Analysis: A Comparison between Continuous and Event-Based Modeling of Streamflow Based on the Hydrological Simulation Program–Fortran (HSPF) Model
Abstract
1. Introduction
2. Materials and Methods
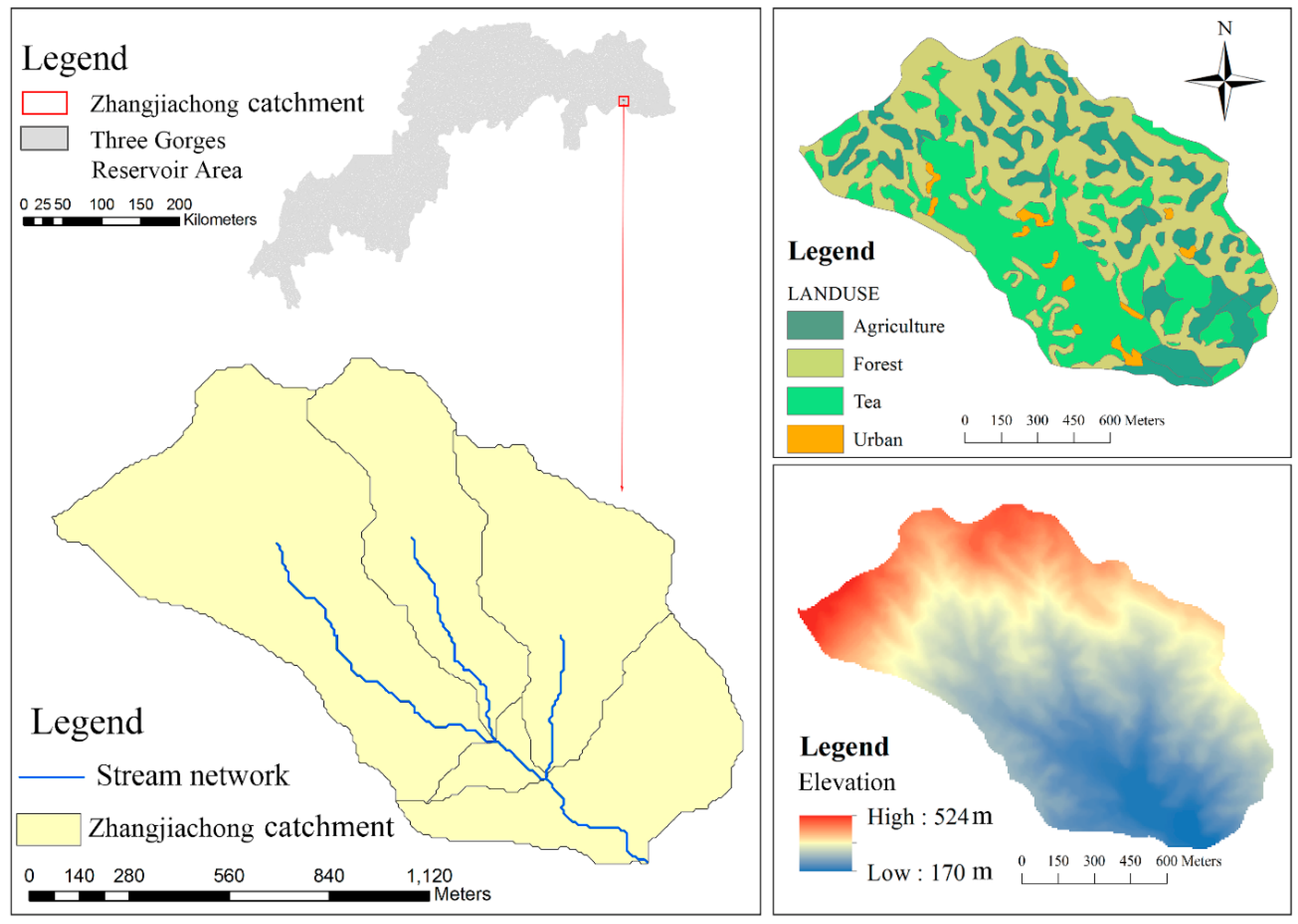
2.1. Study Site and Data Collection
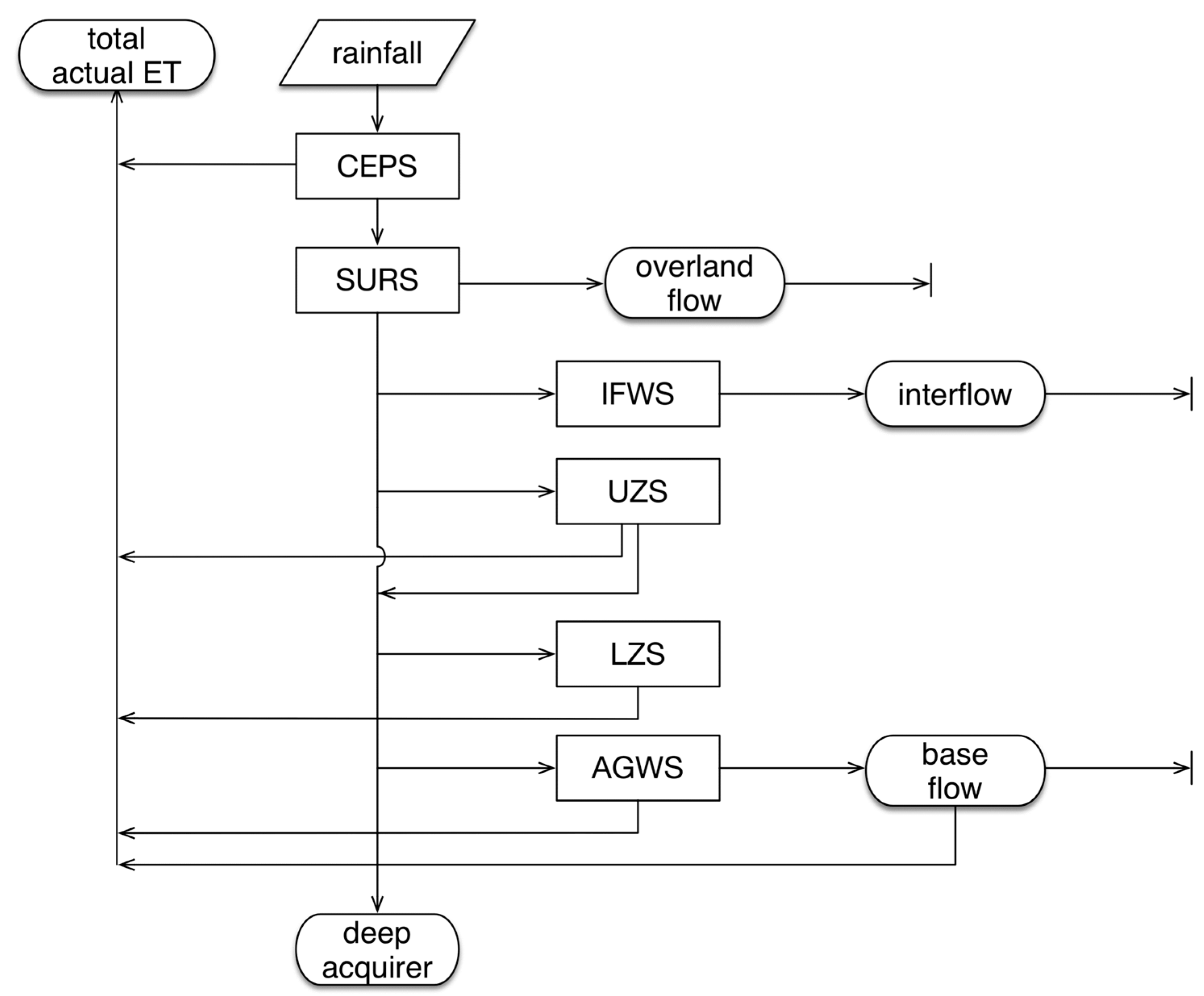
2.2. Description of the HSPF Model
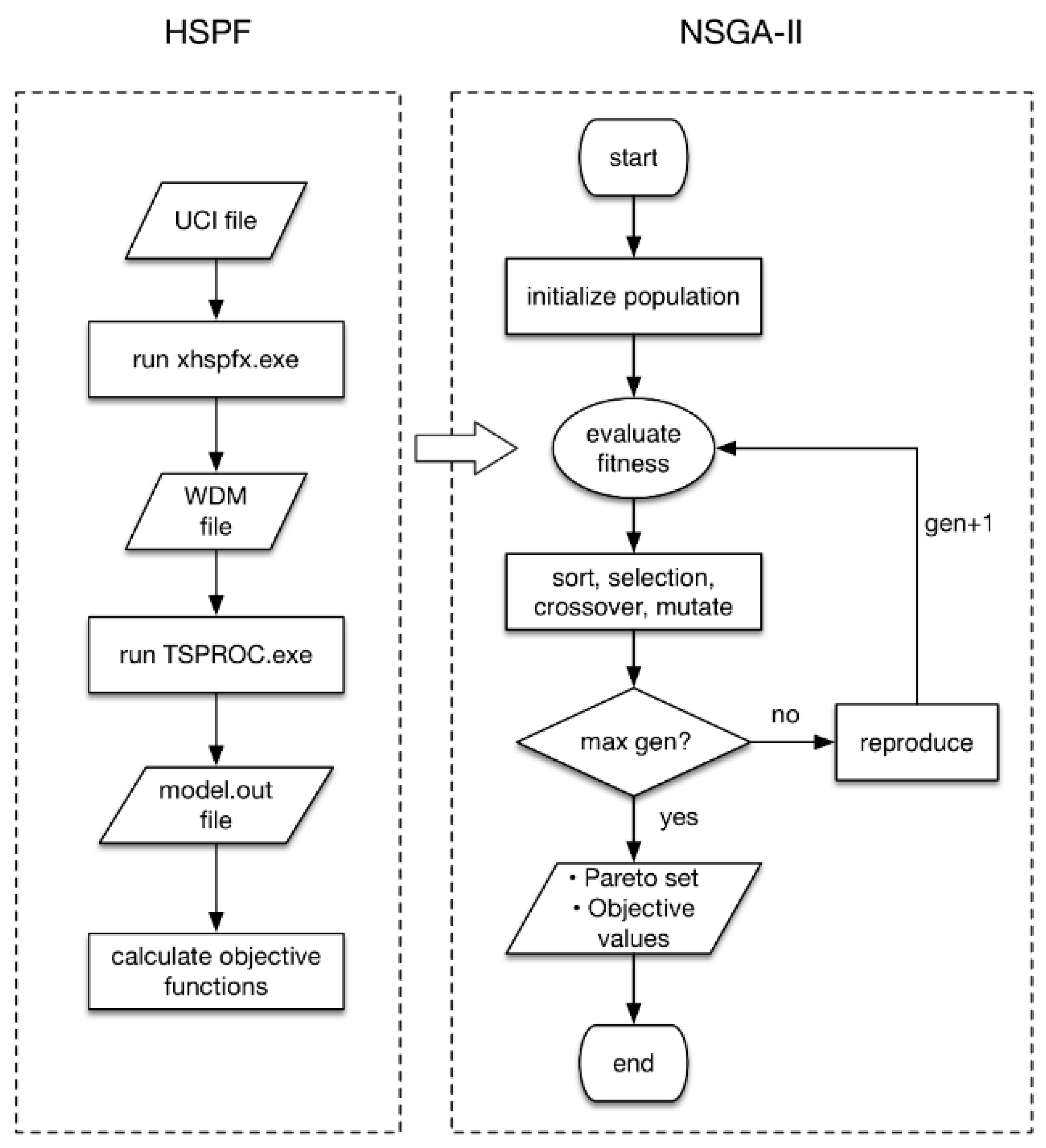
2.3. Multi-Objective Calibration
2.4. Sensitivity and Uncertainty Analysis
2.4.1. Regional Sensitivity Analysis
2.4.2. Generalized Likelihood Uncertainty Estimation
3. Results and Discussion
3.1. Comparison of Parameter Calibration
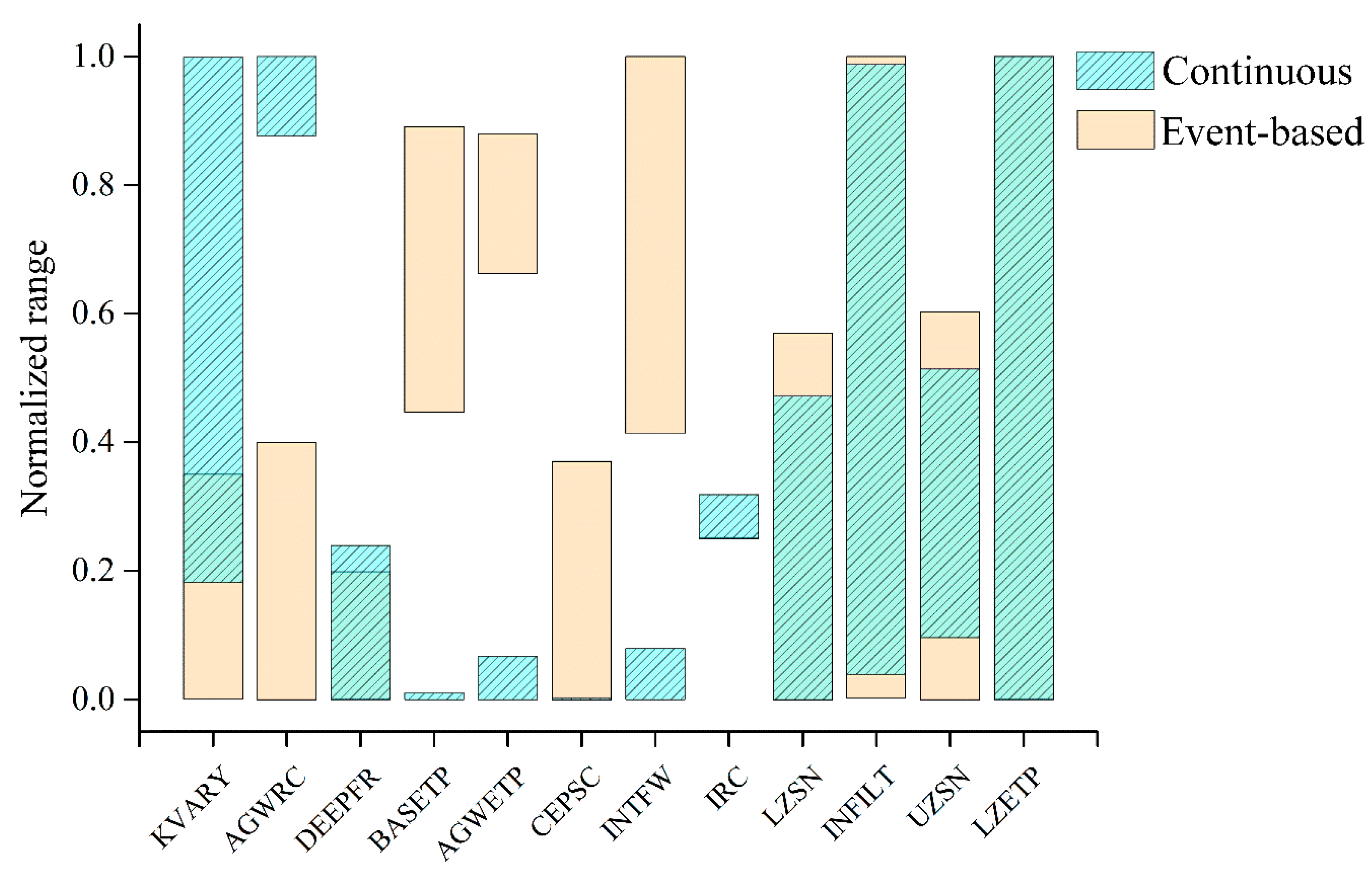
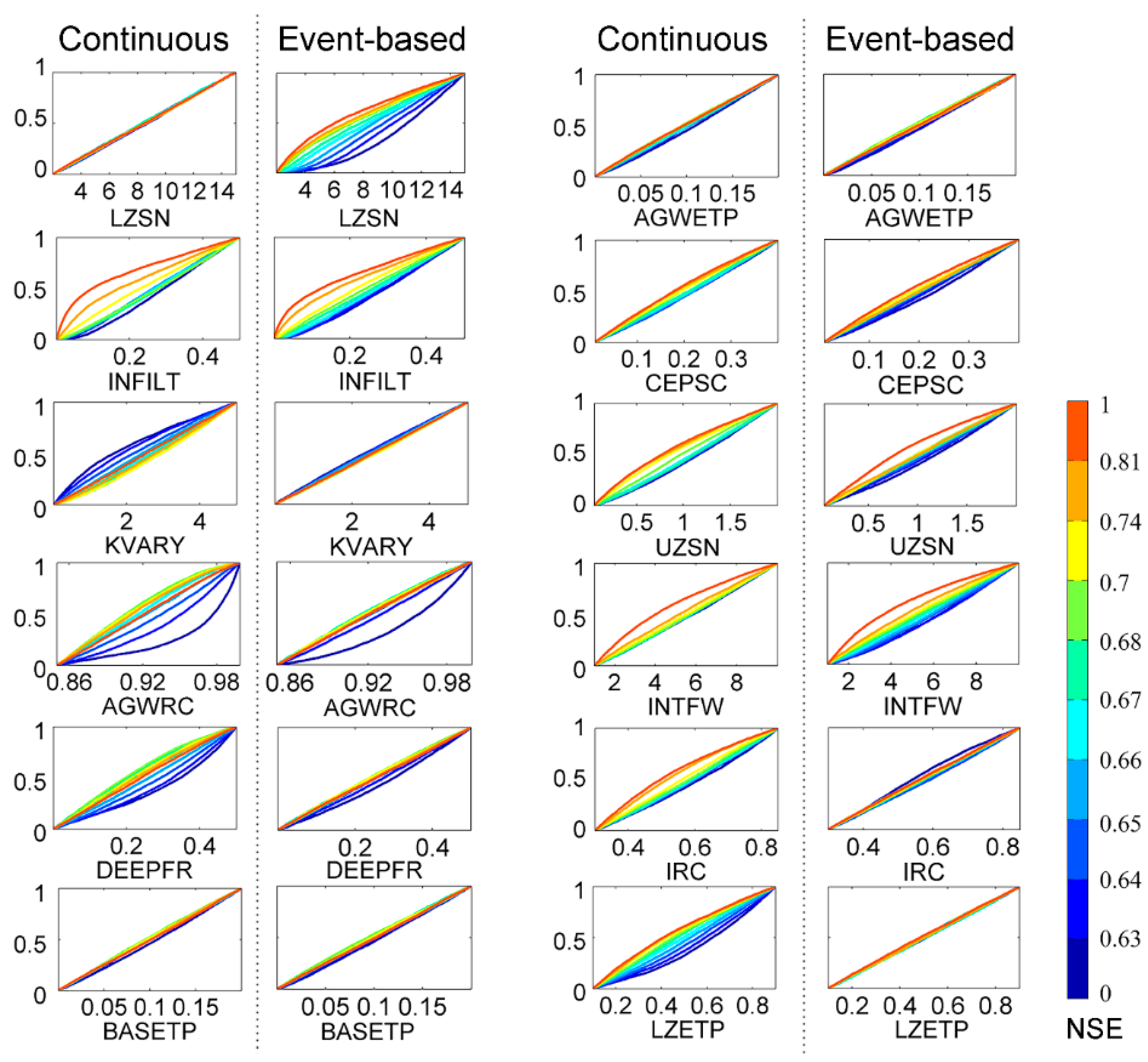
3.2. Comparison of Parameter Sensitivity
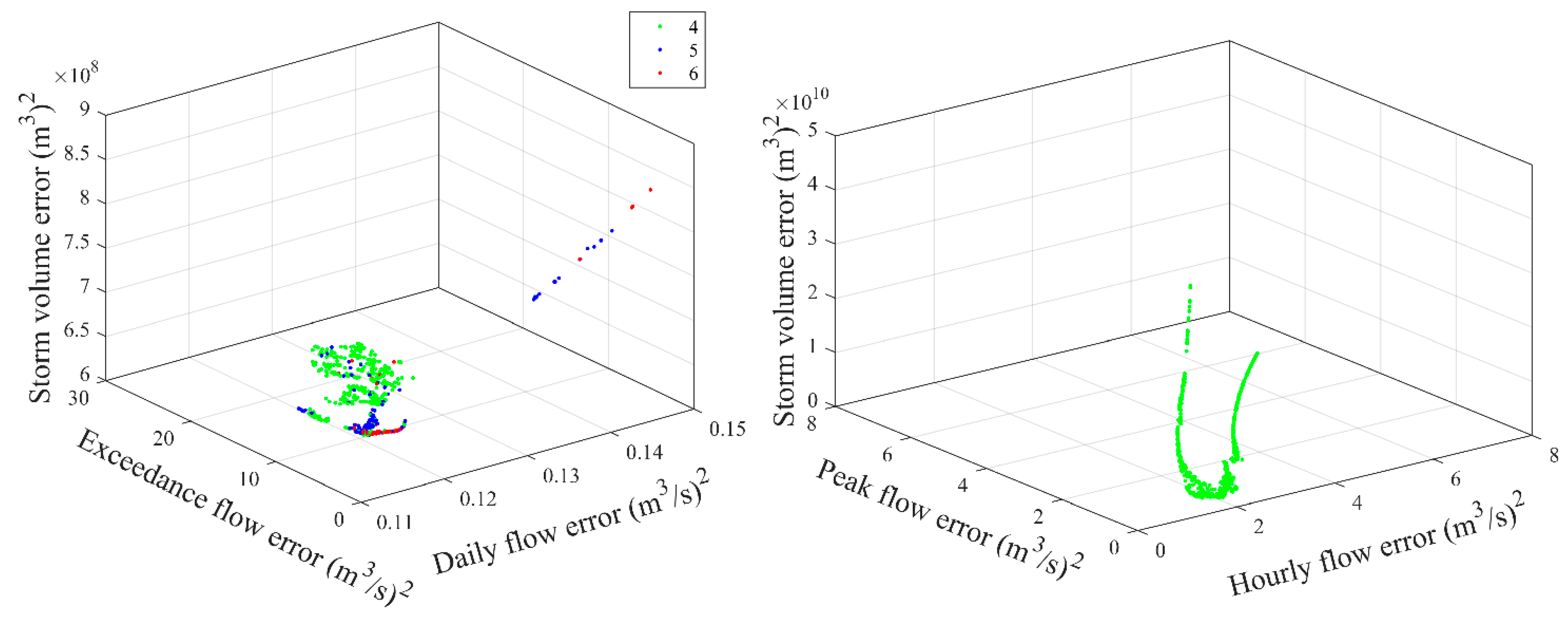
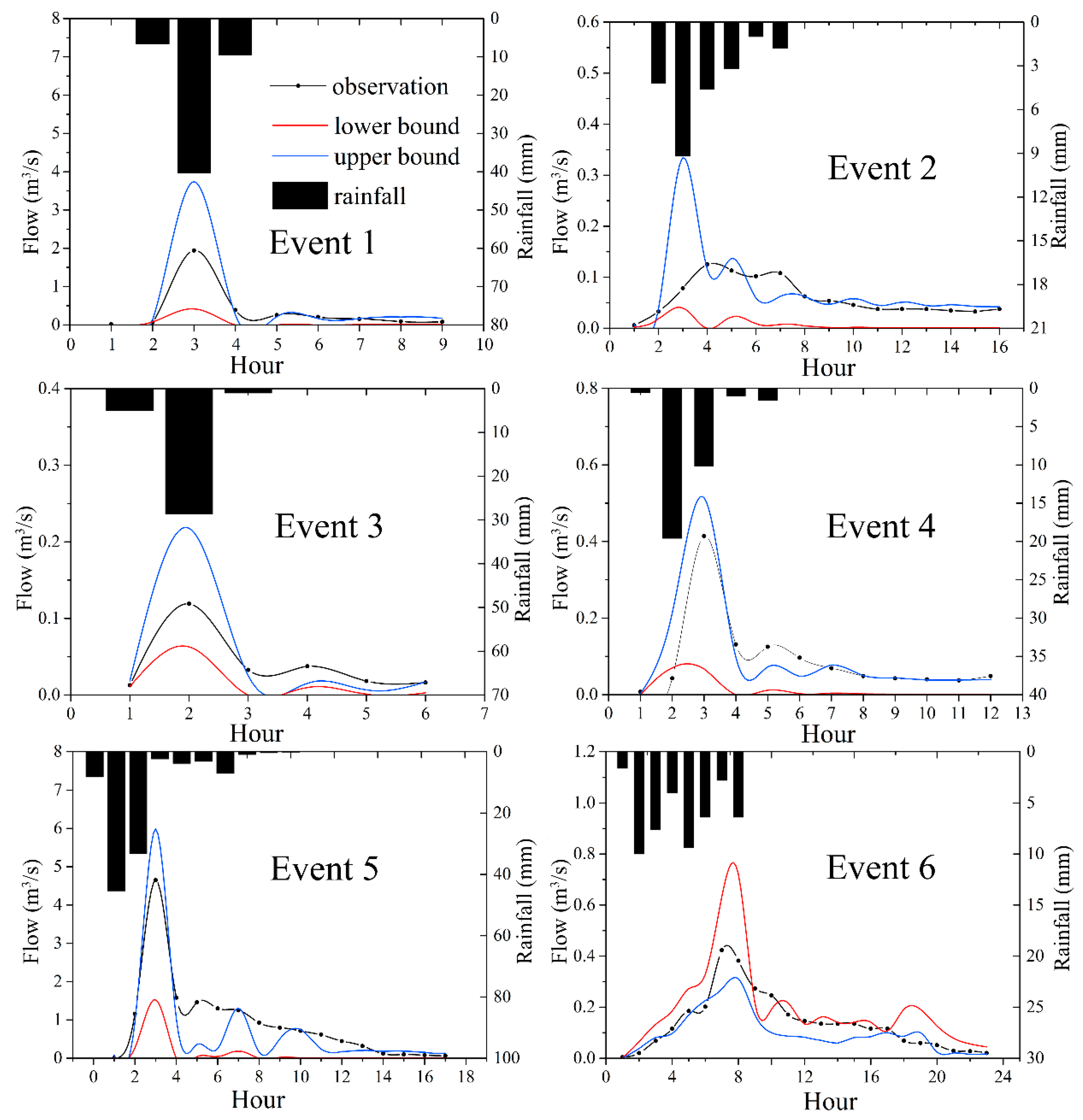
3.3. Comparison of Uncertainty Quantification
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Measure | Criteria (% Error) |
|---|---|
| Total runoff | ±10% |
| Highest 10% flows | ±10% |
| Lowest 50% flows | ±15% |
| Seasonal volume | ±10% |
| Storm peak | ±15% |
| Summer storm volume | ±15% |
References
- Westerberg, I.K.; Guerrero, J.-L.; Younger, P.M.; Beven, K.J.; Seibert, J.; Halldin, S.; Freer, J.E.; Xu, C.-Y. Calibration of hydrological models using flow-duration curves. Hydrol. Earth Syst. Sci. 2011, 15, 2205–2227. [Google Scholar] [CrossRef]
- Amaguchi, H.; Kawamura, A.; Olsson, J.; Takasaki, T. Development and testing of a distributed urban storm runoff event model with a vector-based catchment delineation. J. Hydrol. 2012, 420–421, 205–215. [Google Scholar] [CrossRef]
- Wellen, C.; Arhonditsis, G.B.; Long, T.; Boyd, D. Accommodating environmental thresholds and extreme events in hydrological models: A Bayesian approach. J. Great Lakes Res. 2014, 40, 102–116. [Google Scholar] [CrossRef]
- Wang, L.; van Meerveld, H.J.; Seibert, J. When should stream water be sampled to be most informative for event-based, multi-criteria model calibration? Hydrol. Res. 2017, 48, 1566–1584. [Google Scholar] [CrossRef]
- Stephens, C.M.; Johnson, F.M.; Marshall, L.A. Implications of future climate change for event-based hydrologic models. Adv. Water Resour. 2018, 119, 95–110. [Google Scholar] [CrossRef]
- Yu, D.; Xie, P.; Dong, X.; Hu, X.; Liu, J.; Li, Y.; Peng, T.; Ma, H.; Wang, K.; Xu, S. Improvement of the SWAT model for event-based flood simulation on a sub-daily timescale. Hydrol. Earth Syst. Sci. 2018, 22, 5001–5019. [Google Scholar] [CrossRef]
- Qiu, J.; Shen, Z.; Wei, G.; Wang, G.; Xie, H.; Lv, G. A systematic assessment of watershed-scale nonpoint source pollution during rainfall-runoff events in the Miyun Reservoir watershed. Environ. Sci. Pollut. Res. 2018, 25, 6514–6531. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, K.; Yu, Z.; Li, Z.; Li, Q. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous unit hydrograph. J. Hydrol. 2014, 517, 1035–1048. [Google Scholar] [CrossRef]
- Borah, D.K.; Arnold, J.G.; Bera, M.; Krug, E.C.; Liang, X.-Z. Storm Event and Continuous Hydrologic Modeling for Comprehensive and Efficient Watershed Simulations. J. Hydrol. Eng. 2007, 12, 605–616. [Google Scholar] [CrossRef]
- Ribarova, I.; Ninov, P.; Cooper, D. Modeling nutrient pollution during a first flood event using HSPF software: Iskar River case study, Bulgaria. Ecol. Model. 2008, 211, 241–246. [Google Scholar] [CrossRef]
- Chu, X.; Steinman, A. Event and Continuous Hydrologic Modeling with HEC-HMS. J. Irrig. Drain. Eng. 2009, 135, 119–124. [Google Scholar] [CrossRef]
- De Silva, M.M.G.T.; Weerakoon, S.B.; Herath, S. Modeling of Event and Continuous Flow Hydrographs with HEC–HMS: Case Study in the Kelani River Basin, Sri Lanka. J. Hydrol. Eng. 2014, 19, 800–806. [Google Scholar] [CrossRef]
- Huang, P.; Li, Z.; Yao, C.; Li, Q.; Yan, M. Spatial combination modeling framework of saturation-excess and infiltration-excess runoff for semihumid watersheds. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Reusser, D.; Fohrer, N. Process verification of a hydrological model using a temporal parameter sensitivity analysis. Hydrol. Earth Syst. Sci. 2015, 19, 4365–4376. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Herman, J.D.; Reed, P.M.; Wagener, T. Time-varying sensitivity analysis clarifies the effects of watershed model formulation on model behavior. Water Resour. Res. 2013, 49, 1400–1414. [Google Scholar] [CrossRef]
- Guse, B.; Reusser, D.E.; Fohrer, N. How to improve the representation of hydrological processes in SWAT for a lowland catchment–temporal analysis of parameter sensitivity and model performance. Hydrol. Process. 2014, 28, 2651–2670. [Google Scholar] [CrossRef]
- Xie, H.; Shen, Z.; Chen, L.; Qiu, J.; Dong, J. Time-varying sensitivity analysis of hydrologic and sediment parameters at multiple timescales: Implications for conservation practices. Sci. Total Environ. 2017, 598, 353–364. [Google Scholar] [CrossRef]
- Garambois, P.A.; Roux, H.; Larnier, K.; Castaings, W.; Dartus, D. Characterization of process-oriented hydrologic model behavior with temporal sensitivity analysis for flash floods in Mediterranean catchments. Hydrol. Earth Syst. Sci. 2013, 17, 2305–2322. [Google Scholar] [CrossRef]
- Srivastava, V.; Graham, W.; Muñoz-Carpena, R.; Maxwell, R.M. Insights on geologic and vegetative controls over hydrologic behavior of a large complex basin—Global Sensitivity Analysis of an integrated parallel hydrologic model. J. Hydrol. 2014, 519, 2238–2257. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. From maps to movies: High-resolution time-varying sensitivity analysis for spatially distributed watershed models. Hydrol. Earth Syst. Sci. 2013, 17, 5109–5125. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Zhang, Q.; Werner, A.D.; Wellen, C.; Jomaa, S.; Zhu, Q.D.; Büttner, O.; Meon, G.; Rode, M. Effects of stream nitrate data frequency on watershed model performance and prediction uncertainty. J. Hydrol. 2019, 569, 22–36. [Google Scholar] [CrossRef]
- Wellen, C.; Kamran-Disfani, A.-R.; Arhonditsis, G.B. Evaluation of the Current State of Distributed Watershed Nutrient Water Quality Modeling. Environ. Sci. Technol. 2015, 49, 3278–3290. [Google Scholar] [CrossRef] [PubMed]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L., Jr.; Donigian, A.S., Jr.; Johanson, R.C. Hydrological Simulation Program-FORTRAN. User’s Manual for Release 11; USEPA: Athens, GA, USA, 1997.
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Hydrologic Engieering Center (US). The Hydrologic Modeling System (HEC-HMS); US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2001. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.0; National Risk Management Research Laboratory, Office of Research and Development: Cincinnati, OH, USA, 2009.
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B. Computer Models of Watershed Hydrology; Water Resources Publications: Fort Collins, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Berndt, M.E.; Rutelonis, W.; Regan, C.P. A comparison of results from a hydrologic transport model (HSPF) with distributions of sulfate and mercury in a mine-impacted watershed in northeastern Minnesota. J. Environ. Manag. 2016, 181, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Luo, C.; Jiang, K.; Wan, R.; Li, H. Comprehensive Performance Evaluation for Hydrological and Nutrients Simulation Using the Hydrological Simulation Program–Fortran in a Mesoscale Monsoon Watershed, China. Int. J. Environ. Res. Public. Health 2017, 14, 1599. [Google Scholar] [CrossRef]
- Fonseca, A.; Boaventura, R.A.R.; Vilar, V.J.P. Integrating water quality responses to best management practices in Portugal. Environ. Sci. Pollut. Res. 2018, 25, 1587–1596. [Google Scholar] [CrossRef]
- Ouyang, Y.; Parajuli, P.B.; Feng, G.; Leininger, T.D.; Wan, Y.; Dash, P. Application of Climate Assessment Tool (CAT) to estimate climate variability impacts on nutrient loading from local watersheds. J. Hydrol. 2018, 563, 363–371. [Google Scholar] [CrossRef]
- Ahn, S.-R.; Kim, S.-J. The Effect of Rice Straw Mulching and No-Tillage Practice in Upland Crop Areas on Nonpoint-Source Pollution Loads Based on HSPF. Water 2016, 8, 106. [Google Scholar] [CrossRef]
- Fonseca, A.R.; Santos, M.; Santos, J.A. Hydrological and flood hazard assessment using a coupled modelling approach for a mountainous catchment in Portugal. Stoch. Environ. Res. Risk Assess. 2018, 32, 2165–2177. [Google Scholar] [CrossRef]
- Xie, H.; Wei, G.; Shen, Z.; Dong, J.; Peng, Y.; Chen, X. Event-based uncertainty assessment of sediment modeling in a data-scarce catchment. CATENA 2019, 173, 162–174. [Google Scholar] [CrossRef]
- Lin, S.; Iqbal, J.; Hu, R.; Shaaban, M.; Cai, J.; Chen, X. Nitrous Oxide Emissions from Yellow Brown Soil as Affected by Incorporation of Crop Residues with Different Carbon-to-Nitrogen Ratios: A Case Study in Central China. Arch. Environ. Contam. Toxicol. 2013, 65, 183–192. [Google Scholar] [CrossRef] [PubMed]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Fernandez, R.T.; Xiao, L. Green Roof Stormwater Retention. J. Environ. Qual. 2005, 34, 1036–1044. [Google Scholar] [CrossRef] [PubMed]
- Voyde, E.; Fassman, E.; Simcock, R. Hydrology of an extensive living roof under sub-tropical climate conditions in Auckland, New Zealand. J. Hydrol. 2010, 394, 384–395. [Google Scholar] [CrossRef]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414–415, 148–161. [Google Scholar] [CrossRef]
- Dunnett, N.; Nagase, A.; Booth, R.; Grime, P. Influence of vegetation composition on runoff in two simulated green roof experiments. Urban Ecosyst. 2008, 11, 385–398. [Google Scholar] [CrossRef]
- Whittinghill, L.J.; Rowe, D.B.; Andresen, J.A.; Cregg, B.M. Comparison of stormwater runoff from sedum, native prairie, and vegetable producing green roofs. Urban Ecosyst. 2015, 18, 13–29. [Google Scholar] [CrossRef]
- Chen, L.; Sun, C.; Wang, G.; Xie, H.; Shen, Z. Event-based nonpoint source pollution prediction in a scarce data catchment. J. Hydrol. 2017, 552, 13–27. [Google Scholar] [CrossRef]
- Chen, L.; Sun, C.; Wang, G.; Xie, H.; Shen, Z. Modeling Multi-Event Non-Point Source Pollution in a Data-Scarce Catchment Using ANN and Entropy Analysis. Entropy 2017, 19, 265. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II. In Proceedings of the Parallel Problem Solving from Nature PPSN VI; Schoenauer, M., Deb, K., Rudolph, G., Yao, X., Lutton, E., Merelo, J.J., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Kim, S.M.; Benham, B.L.; Brannan, K.M.; Zeckoski, R.W.; Doherty, J. Comparison of hydrologic calibration of HSPF using automatic and manual methods. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Lumb, A.M.; McCammon, R.B.; Kittle, J.L. Users Manual for an Expert System (HSPEXP) for Calibration of the Hydrological Simulation Program—Fortran; US Geological Survey Reston: Reston, Virginia, 1994.
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hallema, D.W.; Moussa, R.; Andrieux, P.; Voltz, M. Parameterization and multi-criteria calibration of a distributed storm flow model applied to a Mediterranean agricultural catchment. Hydrol. Process. 2013, 27, 1379–1398. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Spear, R.C.; Hornberger, G.M. Eutrophication in peel inlet—II. Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Wagener, T.; Boyle, D.P.; Lees, M.J.; Wheater, H.S.; Gupta, H.V.; Sorooshian, S. A framework for development and application of hydrological models. Hydrol. Earth Syst. Sci. 2001, 5, 13–26. [Google Scholar] [CrossRef]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for Global Sensitivity Analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Abbaspour, K.C. User Manual for SWAT-CUP: SWAT Calibration and Uncertainty Analysis Program; Swiss Federal Institute of Aquatic Science and Technology, Eawag: Duebendorf, Switzerland, 2007. [Google Scholar]
- Fonseca, A.; Ames, D.P.; Yang, P.; Botelho, C.; Boaventura, R.; Vilar, V. Watershed model parameter estimation and uncertainty in data-limited environments. Environ. Model. Softw. 2014, 51, 84–93. [Google Scholar] [CrossRef]
- Chung, E.-S.; Park, K.; Lee, K.S. The relative impacts of climate change and urbanization on the hydrological response of a Korean urban watershed. Hydrol. Process. 2011, 25, 544–560. [Google Scholar] [CrossRef]
- Seong, C.; Her, Y.; Benham, B.L. Automatic calibration tool for Hydrologic Simulation Program-FORTRAN using a shuffled complex evolution algorithm. Water 2015, 7, 503–527. [Google Scholar] [CrossRef]
- Hayashi, S.; Murakami, S.; Xu, K.-Q.; Watanabe, M. Simulation of the reduction of runoff and sediment load resulting from the Gain for Green Program in the Jialingjiang catchment, upper region of the Yangtze River, China. J. Environ. Manag. 2015, 149, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Baloch, M.A.; Ames, D.P.; Tanik, A. Hydrologic impacts of climate and land-use change on Namnam Stream in Koycegiz Watershed, Turkey. Int. J. Environ. Sci. Technol. 2015, 12, 1481–1494. [Google Scholar] [CrossRef]
- Choi, W.; Deal, B.M. Assessing hydrological impact of potential land use change through hydrological and land use change modeling for the Kishwaukee River basin (USA). J. Environ. Manag. 2008, 88, 1119–1130. [Google Scholar] [CrossRef] [PubMed]
- Verhagen, W. Wetland Restoration in an Agricultural Basin. Linking Hydrologic Response, Optimal Location, Ecosystem Services and Stakeholder Opinions. Master’s Thesis, Utrecht University Repository, Utrecht, The Netherlands, 2013. [Google Scholar]
- Lott, D.A.; Stewart, M.T. Base flow separation: A comparison of analytical and mass balance methods. J. Hydrol. 2016, 535, 525–533. [Google Scholar] [CrossRef]
- Risser, D.W.; Gburek, W.J.; Folmar, G.J. Comparison of Methods for Estimating Ground-Water Recharge and Base Flow at a Small Watershed Underlain by Fractured Bedrock in the Eastern United States; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005; Volume 5038.
- Abdulla, F.; Eshtawi, T.; Assaf, H. Assessment of the Impact of Potential Climate Change on the Water Balance of a Semi-arid Watershed. Water Resour. Manag. 2009, 23, 2051–2068. [Google Scholar] [CrossRef]
- Mishra, A.; Kar, S.; Singh, V.P. Determination of runoff and sediment yield from a small watershed in sub-humid subtropics using the HSPF model. Hydrol. Process. 2007, 21, 3035–3045. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, L.; Liao, Q.; Liu, R.; Hong, Q. Impact of spatial rainfall variability on hydrology and nonpoint source pollution modeling. J. Hydrol. 2012, 472–473, 205–215. [Google Scholar] [CrossRef]
- Mohamoud, Y.M.; Parmar, R.; Wolfe, K.; Carleton, J. HSPF toolkit: A tool for stormwater management at the watershed scale. Proc. Water Environ. Fed. 2008, 2008, 421–431. [Google Scholar] [CrossRef]
- Schultz, C.L.; Ahmed, S.N.; Mandel, R.; Moltz, H.L.N. Improvement in HSPF’s Low-Flow Predictions by Implementation of a Power Law Groundwater Storage-Discharge Relationship. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 909–927. [Google Scholar] [CrossRef]
- Sun, N.; Hong, B.; Hall, M. Assessment of the SWMM model uncertainties within the generalized likelihood uncertainty estimation (GLUE) framework for a high-resolution urban sewershed. Hydrol. Process. 2014, 28, 3018–3034. [Google Scholar] [CrossRef]
- Vezzaro, L.; Mikkelsen, P.S. Application of global sensitivity analysis and uncertainty quantification in dynamic modelling of micropollutants in stormwater runoff. Environ. Model. Softw. 2012, 27–28, 40–51. [Google Scholar] [CrossRef]
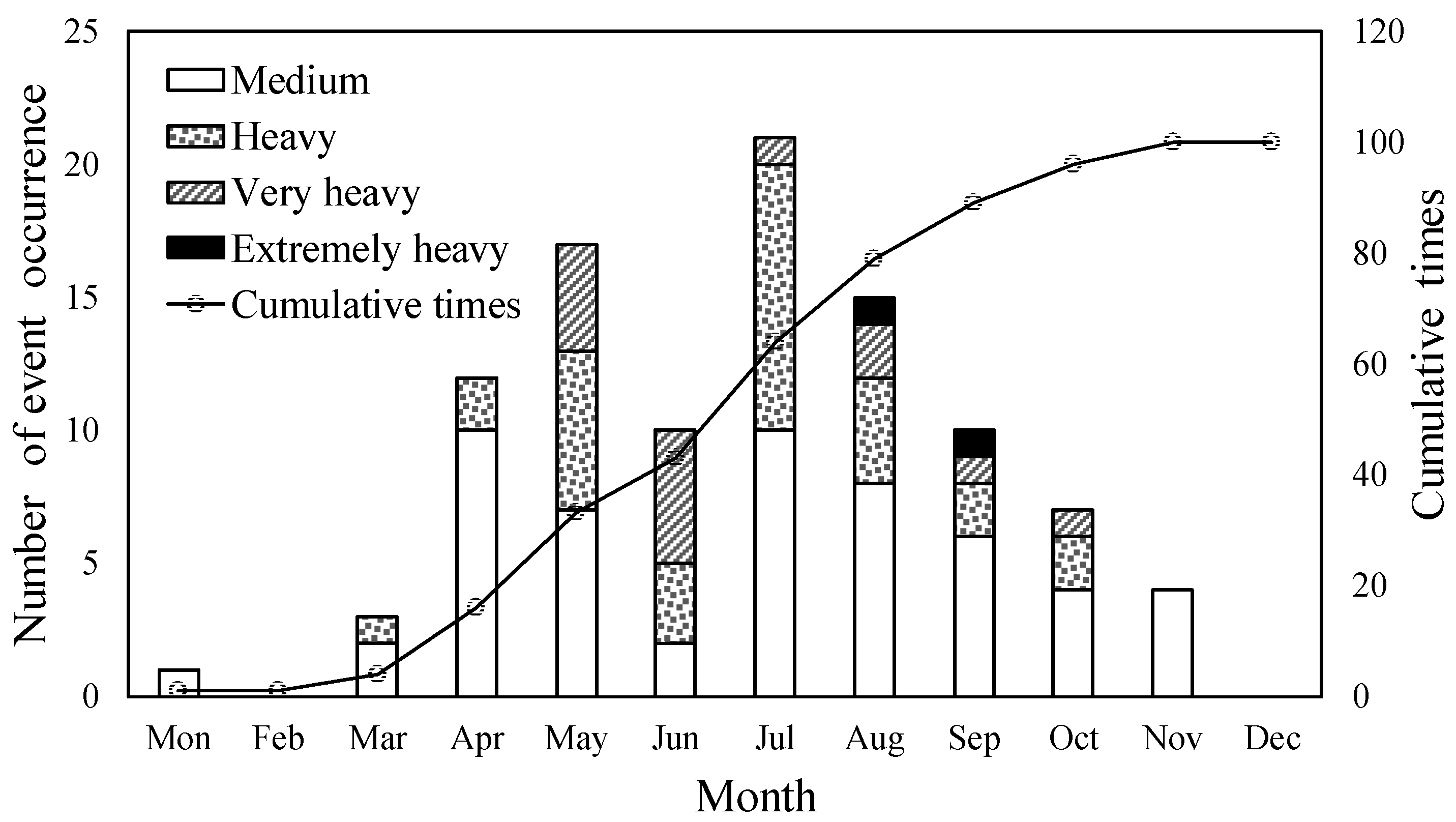


| Event Type | 24-h Cumulative Amount | 12-h Cumulative Amount |
|---|---|---|
| Light | 0.1 mm–9.9 mm | 0.1 mm–4.9 mm |
| Medium | 10 mm–24.9 mm | 5.0 mm–14.9 mm |
| Heavy | 25.0 mm–49.9 mm | 15.0 mm–29.9 mm |
| Very heavy | 50.0 mm–99.9 mm | 30.0 mm–69.9 mm |
| Extremely heavy | 100 mm–249.9 mm | 70.0 mm–139.9 mm |
| Torrential | ≥250 mm | ≥140 mm |
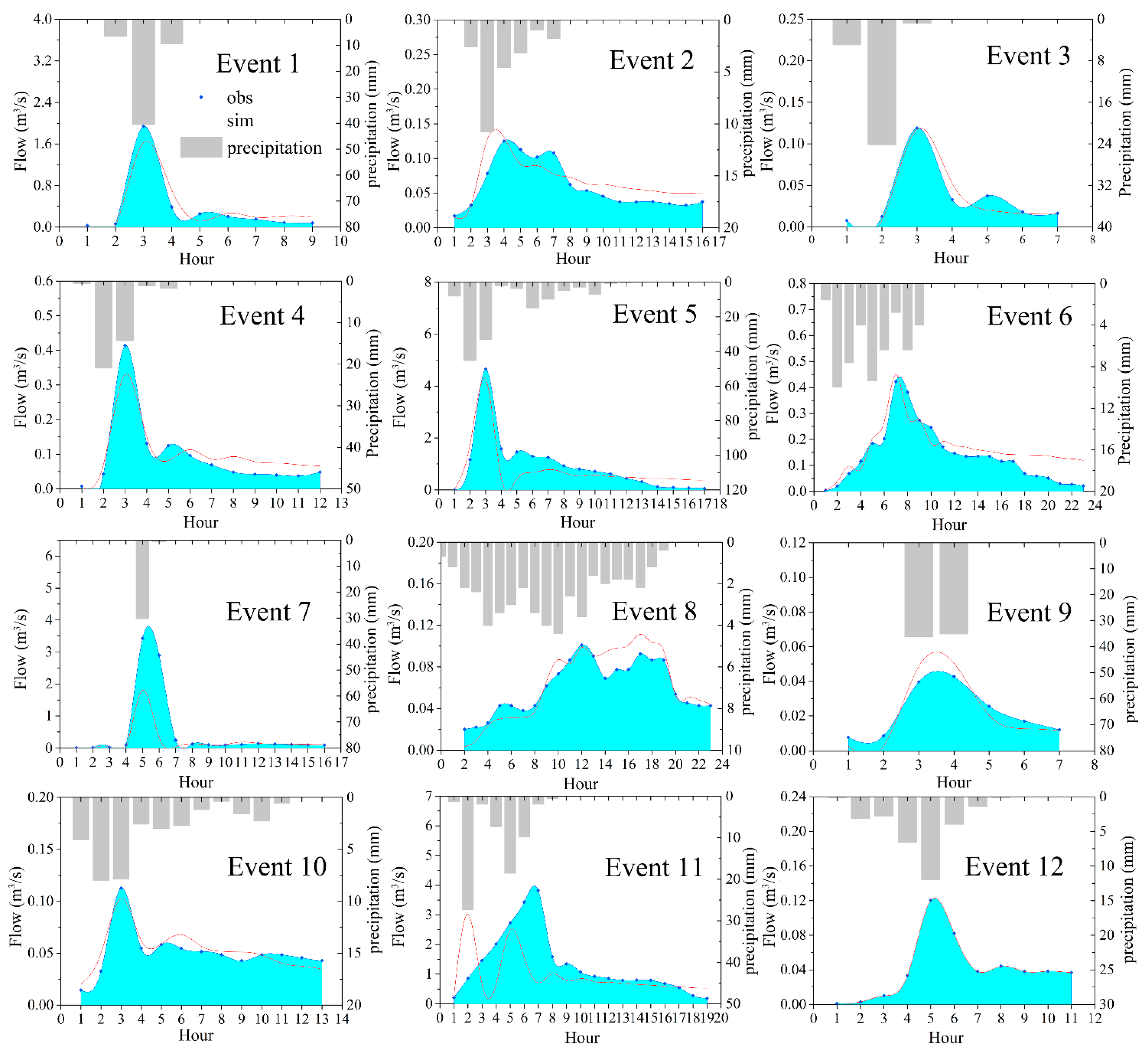
| Event | Start Date | Event Type | Rainfall Amount (mm) | Rainfall Duration (h) | Maximum Intensity (mm/h) |
|---|---|---|---|---|---|
| 1 | 28 August 2013 | Very heavy | 56.5 | 3 | 40.5 |
| 2 | 21 April 2014 | Medium | 24.0 | 6 | 9.2 |
| 3 | 20 July 2014 | Heavy | 34.7 | 3 | 28.7 |
| 4 | 24 July 2014 | Heavy | 33.0 | 5 | 19.6 |
| 5 | 8 May 2014 | Extremely heavy | 104.7 | 10 | 45.4 |
| 6 | 9 February 2014 | Heavy | 48.2 | 8 | 10.0 |
| 8 | 25 June 2013 | Heavy | 31.6 | 6 | 30.3 |
| 11 | 24 September 2013 | Heavy | 48.1 | 20 | 4.4 |
| 7 | 15 April 2014 | Medium | 18.2 | 2 | 14.6 |
| 9 | 25 June 2014 | Heavy | 37.4 | 11 | 7.9 |
| 10 | 7 August 2014 | Very heavy | 69.2 | 8 | 27.4 |
| 12 | 23 August 2014 | Heavy | 30.4 | 7 | 11.2 |
| Parameter | Description | Unit | Possible Range | Calibrated Values for Continuous | Calibrated Values for Event-Based |
|---|---|---|---|---|---|
| LZSN | Low zone nominal soil moisture storage | in. | 2.0–15.0 | 5.502 | 3.703 |
| INFILT | Index to mean soil infiltration rate | in./h | 0.001–0.50 | 0.079 | 0.067 |
| KVARY | Parameter to describe non-linear groundwater recession rate | in−1 | 0.0–5.0 | 3.643 | 0.202 |
| AGWRC | Groundwater recession rate | day−1 | 0.85–0.999 | 0.987 | 0.850 |
| DEEPFR | Fraction of infiltrating water which enters deep aquifers | none | 0.0–0.50 | 0.005 | 0.057 |
| BASETP | Fraction of potential evapotranspiration which fulfilled only as outflow exists | none | 0.0–0.20 | 0.000 | 0.161 |
| AGWETP | Fraction of remaining evapotranspiration that be met from active groundwater storage | none | 0.0–0.20 | 0.000 | 0.166 |
| CEPSC | Interception storage capacity | in. | 0.01–0.40 | 0.010 | 0.123 |
| UZSN | Nominal upper zone soil moisture storage | in. | 0.05–2.0 | 0.668 | 0.415 |
| INTFW | Interflow inflow parameter | none | 1.0–10.0 | 1.000 | 9.999 |
| IRC | Interflow recession parameter | day−1 | 0.3–0.85 | 0.300 | 0.300 |
| LZETP | Index to lower zone evapotranspiration | none | 0.1–0.9 | 0.400 | 0.494 |
| Measures | Observed | Simulated | Percent Error % | HSPEXP Performance Criteria |
|---|---|---|---|---|
| Total runoff (mm) | 543.34 | 534.08 | −1.70 | √ |
| Mean of highest 10% flows (m3) | 0.05692 | 0.0535 | −5.97 | √ |
| Mean of lowest 50% flows (m3) | 0.0062 | 0.0059 | −4.54 | √ |
| Seasonal volume error (mm) | 297.25 | 268.43 | −9.70 | √ |
| Mean of storm peaks (m3) | 0.0960 | 0.0940 | −2.06 | √ |
| Summer storm volume (mm) | 50.13 | 46.24 | −7.76 | √ |
| Coefficient of determination | 0.83 | |||
| Nash–Sutcliffe efficiency | 0.82 | |||
| Root mean square error | 0.76 | |||
| Event | Start date | NSE | RMSE | R2 | PFE a | SVE b | PTO c |
|---|---|---|---|---|---|---|---|
| 1 | 28 August 2013 | 0.91 | 9.72 | 0.92 | 0.16 | 0.05 | 0 |
| 2 | 21 April 2014 | 0.65 | 1.13 | 0.71 | 0.04 | 0.13 | 0 |
| 3 | 20 July 2014 | 0.93 | 0.60 | 0.93 | 0.01 | 0.05 | 0 |
| 4 | 24 July 2014 | 0.90 | 2.11 | 0.93 | 0.20 | 0.10 | 0 |
| 5 | 5 August 2014 | 0.79 | 27.91 | 0.81 | 0.08 | 0.34 | 0 |
| 6 | 2 September 2014 | 0.73 | 3.22 | 0.82 | 0.07 | 0.22 | 0 |
| 7 | 25 June 2013 | 0.83 | 16.17 | 0.98 | 0.38 | 0.29 | 0 |
| 8 | 24 September 2013 | 0.74 | 0.71 | 0.92 | 0.10 | 0.05 | 5 |
| 9 | 15 April 2014 | 0.49 | 0.57 | 0.77 | 0.18 | 0.15 | 0 |
| 10 | 25 June 2014 | 0.83 | 0.48 | 0.84 | 0.07 | 0.04 | 0 |
| 11 | 7 August 2014 | −0.1172 | 60.81 | 0.12 | 0.21 | 0.28 | 5 |
| 12 | 23 August 2014 | 0.82 | 0.60 | 0.95 | 0.25 | 0.02 | 0 |
| Water Balance | Forest | Tea | Agriculture | Urban | ||||
|---|---|---|---|---|---|---|---|---|
| Surface flow | 9.23% | 20.9% | 5.76% | 30.13% | 3.44% | 27.53% | 6.34% | 8.44% |
| Interflow | 2.69% | 63.03% | 4.34% | 54.92% | 6.11% | 65.61% | 2.75% | 64.33% |
| Base flow | 8.45% | 1.31% | 37.6% | 1.95% | 28.46% | 0.03% | 27.44% | 6.06% |
| Deep aquifer | 0.52% | 2.65% | 2.26% | 2.92% | 1.72% | 0.08% | 1.65% | 5.72% |
| Total ET | 79.1% | 12.11% | 50.04% | 10.08% | 60.26% | 6.74% | 61.82% | 15.45% |
| Scenario | Period | p-Factor (%) | r-Factor |
|---|---|---|---|
| Continuous | 2011–2012 (daily) | 40.25 | 2.58 |
| 2011–2012 (monthly) | 70.83 | 0.85 | |
| Event-based | Event 1 (Very heavy) | 44.44 | 1.20 |
| Event 2 (Medium) | 68.75 | 0.52 | |
| Event 3 (Heavy) | 33.3 | 1.13 | |
| Event 4 (Heavy) | 41.67 | 1.21 | |
| Event 5 (Extremely heavy) | 41.17 | 1.79 | |
| Event 6 (Heavy) | 65 | 1.17 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.; Shen, Z.; Chen, L.; Lai, X.; Qiu, J.; Wei, G.; Dong, J.; Peng, Y.; Chen, X. Parameter Estimation and Uncertainty Analysis: A Comparison between Continuous and Event-Based Modeling of Streamflow Based on the Hydrological Simulation Program–Fortran (HSPF) Model. Water 2019, 11, 171. https://doi.org/10.3390/w11010171
Xie H, Shen Z, Chen L, Lai X, Qiu J, Wei G, Dong J, Peng Y, Chen X. Parameter Estimation and Uncertainty Analysis: A Comparison between Continuous and Event-Based Modeling of Streamflow Based on the Hydrological Simulation Program–Fortran (HSPF) Model. Water. 2019; 11(1):171. https://doi.org/10.3390/w11010171
Chicago/Turabian StyleXie, Hui, Zhenyao Shen, Lei Chen, Xijun Lai, Jiali Qiu, Guoyuan Wei, Jianwei Dong, Yexuan Peng, and Xinquan Chen. 2019. "Parameter Estimation and Uncertainty Analysis: A Comparison between Continuous and Event-Based Modeling of Streamflow Based on the Hydrological Simulation Program–Fortran (HSPF) Model" Water 11, no. 1: 171. https://doi.org/10.3390/w11010171
APA StyleXie, H., Shen, Z., Chen, L., Lai, X., Qiu, J., Wei, G., Dong, J., Peng, Y., & Chen, X. (2019). Parameter Estimation and Uncertainty Analysis: A Comparison between Continuous and Event-Based Modeling of Streamflow Based on the Hydrological Simulation Program–Fortran (HSPF) Model. Water, 11(1), 171. https://doi.org/10.3390/w11010171








