Abstract
Numerous Information and Communication Technologies (ICTs) applications have been developed in irrigated agriculture. While there are studies focusing on ICTs impacts at the farm level, no research deals with this issue at the Water Authority (WA) level where ICTs can support strategic decisions on land and water allocation. The present study aims to design a theoretical model to estimate economic benefits from the ICT-informed decision process of water management in agriculture. Specifically, the study analyzes the motivations driving a case study WA using ICTs to support strategic management decisions involving risky choices. Results show that the WA under investigation has potentialities to save water and to implement adaptation strategies to climate change. Higher benefits from ICTs are attainable in areas with limited water availability and where the WA can effectively manage land allocation and control water delivery volumes. The study concludes that ICTs might have a disruptive potential in fulfilling WA’s specific information needs, but there is still a need to improve their accuracy due to the risk surrounding the decisions at stake.
1. Introduction
Climate Change (CC) is an issue of growing importance for irrigated agriculture. It requires new approaches combining adaptation and mitigation strategies to realize the goal of sustainable development. With mitigation, the International Panel on Climate Change refers to “options and strategies for reducing GHG (Green House Gases) emissions and increasing GHG uptakes by the Earth system” [1], whereas adaptation is considered as the “process of adjustment to actual or expected climate and its effects” [1]. Adaptation and mitigation are the two pillars facing CC [1]. In this regard, weather and climate services can help decision-makers in making informed decisions to improve adaptation capacity by assessing and forecasting existing and emerging risk [2]. Since all adaptation actions depend on the availability of adequate information, the rapid diffusion of Information and Communication Technologies (ICTs), such as mobile phones and the Internet, poses new opportunities to face CC by improving accessibility to information and consequently by improving the information environment under which water suppliers and water users operate.
One of the most important problems brought by CC in irrigated agriculture is the increased variability of weather patterns and a higher frequency of extreme weather events. Variability by itself does not necessarily imply losses if this is anticipated and acted upon [3]. Nevertheless, for the management of water resources, Water Authorities (WAs) have to make decisions before knowing the weather conditions they are going to face. The high variability of weather patterns increases the level of uncertainty regarding future weather conditions, causing a moving-target problem. Every year, due to CC, WAs are less able to make decisions consistent with the weather pattern of the following season due to the decreased predictability of events and to the less relevant use of past records to make future decisions. As a consequence, current water management decisions are often a compromise between the outcome determined by all the weather states that could emerge. Such compromise is balanced to the selection of less risky decisions instead of the decision that is best suited for the state that will emerge [4]. As a consequence, WAs make sub-optimal decisions, with negative impacts on profits and water uses [3]. In this respect, the availability of ICTs might contribute to mitigating the moving-target problem by providing timely information on future climate and weather conditions, thereby reducing uncertainty before and during the irrigating season [5]. Overall, the ICT-informed decision process of water management could help irrigated agriculture by reducing losses from climate shocks and taking advantage of favorable years [6,7].
These potentialities of ICTs for the management of water resources in agriculture motivated our study. The objective is to quantitatively estimate economic benefits from the ICT-informed decision process of water management in agriculture at the WA level. In this respect, a theoretical model is designed based on insights from the Bayesian Decision Theory (BDT). It assesses the economic benefits brought by new pieces of information, influencing WA’s perception of uncertain events with direct consequences on its strategic decisions. Specifically, the model investigates the role played by information in supporting WAs to rationalize the management of water resources and the prevention of extreme weather event impacts. Because decisions on land and water allocation are sequential across the season and influenced by one another, the methodology accounts for the passing of time in the decision process to assess how the time of information provision affects its usability. An empirical application is also provided to test the model by comparing current information tools with a new information technology developed in the H2020 European Project Managing crOp water Saving with Enterprise Services (MOSES), http://moses-project.eu/moses_website/.
Developing and applying a method to assess the economic value of ICTs seems to be an interesting topic for agricultural and resource economists [8]. Moreover, considering the growing societal demand for climate services, together with the limited budget availability [2], this topic is of high policy relevance. The novelty of the present paper is two-fold, both in the theoretical model and in its empirical application. To the best of the authors’ knowledge, the former stands out from the existing literature for considering the timing variable in sequential and inter-correlated decision steps. The empirical application of the model is also original: to the best of the authors’ knowledge, no economic research deals with ICTs adoption by WAs for the management of irrigation.
The remainder of the paper is organized as follows: in Section 2, we review the recent literature on the assessment of ICTs; in Section 3, we describe the case study; in Section 4, we define the methodology and the empirical implementation; in Section 5, we show our main results; in Section 6, we discuss the main findings and in Section 7, we draw final remarks.
2. Background
In agriculture, numerous ICTs have been developed and disseminated [9]. Great potential is found for such technologies in contributing to food security and climate change adaptation in the agricultural sector [2,10]. Qualitative studies showed their benefits for both developed and developing countries [11]. Among these, Deichmann, Goyal, and Mishra [6] identified the following: (i) promoting economic performance, (ii) raising efficiency, and (iii) fostering innovation. Nevertheless, Aker, Ghosh, and Burrell [9] suggested that ICTs impacts on decision outcomes are highly variable. One reason for this variability lies in the findings of Nakasone and Torero [10]; according to them, ICTs are successful only when key information needs are addressed. In addition, many ICTs projects do not reach the expected success because developers take useful information for granted [2]. As a consequence, ICTs developers tend to poorly consult end users on their information requirements and the resulting ICTs may turn out to be inapplicable in their decision process. Quantitative analyses come to similar conclusions. Accordingly, Macauley [12] finds that information services are useless if the WAs do not need the information provided. To measure ICTs benefits, Macauley treats information like other production factors, with both a value and a cost [12]. According to him, Keisler et al. [13] defined the Value of Information (VOI) as an increase in the Expected Value (EV) of the decision outcome arising from the introduction of a new piece of information in the decision process. Quantitative analysis determined the VOI not only by accounting for the characteristics of the information provided, but also for the environment in which decisions take place [4]. The elements characterizing information and determining its value are:
- (a)
- content of information: the WA must be able to implement the additional information in the decision process; if the WA is not able to act upon information, it has no value for it;
- (b)
- accuracy of information: the more accurate the information is, the smaller the risk of failures and the higher the VOI; imprecise information is not capable of inducing any change in WA beliefs;
- (c)
- timing of information provision: information must be provided at the right time in the decision process; late messages have no value.
The timing factor (point c) plays a key role in influencing the accuracy of information (point b). Usually, information provided well in advance to the occurrence of an event might condition strategic decisions but it will not be so accurate. If information is provided with a short advance, the decisions influenced by the information will not be so strategic, but the information will be likely more accurate. This is typically the case of emerging information, as weather forecasts. Waiting to get more precise information about the occurrence of events has a cost [14]. The cost of waiting is often identified with losses due to sub-optimal decision performances [15]. Taking into account such a timing element adds complexity to models. Nevertheless, it leads to results more reliable than those coming out from analyses that ignore this important factor [16].
Some parameters of the decision environment are capable of affecting the VOI too; among these, the following can be identified as the most important [15]:
- (a)
- uncertainty in the decision process: the higher the climate variability, the higher the benefits brought by information;
- (b)
- the stake in the decision: the higher the variance of decision outcome, the more the WA will be willing to use information for reducing uncertainty.
As a result, each element characterizing information or the decision environment have the potential to set the VOI to zero [17]. For these reasons, the evaluation of investments in ICTs must go beyond the traditional analysis of costs and revenues by accounting for the peculiarities of the VOI [8]. To do so, Bouma, Woerd, and Kuik [18] applied BDT to model the VOI from imperfect satellite-based technologies. According to them, Hardaker and Lien [19] in their literature analyses found BDT to be a suitable tool to model decision making under uncertainty. Finally, Galioto, Raggi, and Viaggi [20] measured the VOI deriving from sensors adopted in precise irrigation technologies through a model based on the framework of BDT.
3. Case Study
3.1. Description of the Case Study Area
The WA selected as case study is a reclamation and irrigation board named Consorzio di Bonifica della Romagna (CBR), located in northern Italy. It covers 352,456 ha, out of which around 165,000 ha are cultivated (1.2% of the Italian cultivated land). Although the basin includes plain, hilly and mountain areas, the case study region is centered on irrigation districts situated in plain areas (Figure 1). Here the landscape is characterized by a dense irrigation network, where the majority of water delivery infrastructures are made by open-air canals. In the basin, about 4.8% and 1.4% of the Italian fruits and vegetables are respectively produced, generating an estimated revenue of around 700 million euros per year. The climate of the region is continental (summer maximum temperatures above 30 °C), mitigated by the sea influence in the northeastern part. Drought events are frequent in summer with variable intensity. Although the total amount of rainfall appears to be stable (750–850 mm), in the last few years a change of the rainfall distribution was recorded. Specifically, it was observed an increased frequency of heavy rainfall events alternated with longer periods of severe droughts characterizing dry irrigating seasons.
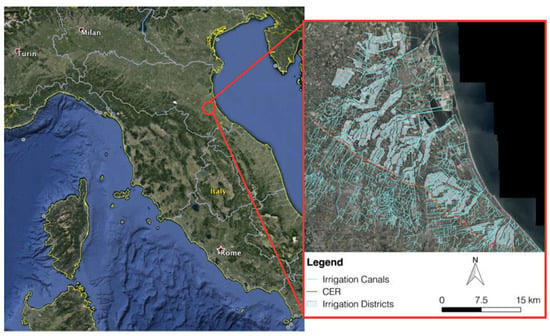
Figure 1.
Case study region (source: own elaboration on data provided by CBR).
The case study region is selected because its decision process for water management is representative of other WAs located in Mediterranean countries where climate uncertainty strongly affects decisions for land and water allocation before and during the irrigating season. Further, the prevalence of open-air canals in the water delivery network enhances both the challenges and the potentialities of ICTs adoption at the WA level. Accordingly, the technical constraints of canals require the WA to anticipate decisions, making forecasts more necessary compared to similar conditions with pressurized pipe networks. Finally, the CBR’s management board is considering adopting a new information service named MOSES, developed in the framework of the MOSES H2020 European project, recently introduced to fulfil WA requirements.
The predominant water source for irrigation is the Canale Emiliano Romagnolo (CER). The CER is an open-air canal which diverts part of the water from the Po river to several irrigation boards. The irrigating season generally takes place from May to September. However, due to yearly variability, it can be anticipated or delayed. Peaks in water delivery are in June and July, when crop water demand is higher. The operational unit at which decisions on water management are taken is the irrigation district. The basin of the CBR includes 81 irrigation districts located in a plain area. The average irrigated area is 68 ha per district and the average length of the water delivery network is 6 km per district. To verify the usability of MOSES services, the WA decided to narrow down the scope of the investigation to a sub-group of its districts. Specifically, the WA selected only 32 of the 81 districts covering an area of 18,845 ha, out of which 6012 ha are cultivated land. Such districts have the common characteristics of a unique water source (represented by the CER) that is managed on demand, and of an irrigation network characterized by open-air canals. On average, the irrigated land is around 2878 ha, 48% of the cultivated land (Figure 2). This area corresponds to the land that can be irrigated in conditions of average operational capacity of the water supply network. However, in regular seasons, the network reaches its maximum operational capacity when it satisfies the demand from irrigated crops for around 3741 ha (130% of the average operational capacity). On the other hand, in dry seasons, the water supply network reaches its minimum operational capacity and the WA is able to satisfy the demand for irrigation for around 2014 ha (70% of the average operational capacity). Despite the fluctuations in rainfall patterns, the land use tends to be constant where winter crops are prevailing (i.e., wheat, barley and meadow), followed by perennial crops (i.e., alfalfa, orchard, vineyard) and summer crops (i.e., maize and sorghum). The irrigation activity is centered around maize, orchard, vineyard and horticulture; winter crops are generally not irrigated, while other crops such as sugar beet and alfalfa are occasionally irrigated.
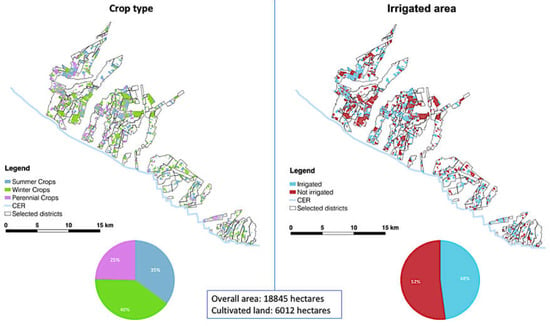
Figure 2.
Land use in the case study region (source: own elaboration on data provided by CBR).
3.2. Management Systems and Information Requirements
Before the irrigating season, the WA decides the amount and allocation of yearly concessions to cultivate annual irrigated crops. Concessions to irrigate permanent crops are granted for the whole lifespan of the plantation. The decision for the amount of yearly concessions to irrigate is taken at the time of seeding/transplanting annual irrigated crops, usually in April. Typically, the WA forbids concessions to the latest applicants if the demand for concessions exceeds the average operational capacity of the supply network (6012 ha). Under conditions of uncertainty regarding the rainfall pattern of the upcoming season, this decision is the best compromise between releasing concessions to the maximum or to the minimum operational capacity of the supply network. During the irrigating season and in each sector of the agricultural region supplied, the WA has to plan with some advance (i.e., one week) whether to deliver water to a sector or not. This is typically the case of surface irrigation networks supplying water to an extended agricultural region. In such conditions, variations in the flow of water downstream of the network occurs with some delay with respect to upstream variations in water flow. Thereby, under uncertain weather conditions, WAs usually decide to supply water on the basis of fixed flow rates varying with the season, consistent with the average climatic condition of the region and with the amount of concessions provided.
Under this framework, the WA is considering the possibility of using the MOSES service to improve its capacity to condition and to satisfy the demand for water to irrigate. Specifically, the WA is interested in knowing the average weather conditions for the upcoming season at the time of seeding/transplanting and short-term forecasts about irrigation requirements in each sector of the region served by the WA during the irrigating season. The first piece of information might influence the WA’s decision on providing concessions to cultivate irrigated crops, reducing the risk of making wrong choices. If a dry season is forecasted, the WA might decide to limit the number of concessions to the minimum operational capacity of the supply network. Otherwise, if a regular season is forecasted, the WA could set the limit of concessions to the maximum capacity of the network. The second piece of information would allow the WA to know whether to deliver water in each sector of the network enough in advance to take timely action, adjusting water flows with the demand. Thus, this additional piece of information might influence the WA’s decisions on changing the management of the supply, improving the efficiency of the supply network. However, because of technical constraints, the WA must guarantee a threshold of minimum flow in the main canal for each district to allow an even water distribution. This condition does not allow the WA to effectively manage water supply volumes and limits its capacity to save water when the demand for water is low.
3.3. Usability of the MOSES Information Service
MOSES provides spatially-detailed information to WAs both before and during the irrigating season. In the first case, the information provided is a seasonal forecast of weather conditions and crop water requirements. In the second case, MOSES delivers a daily seven-day forecast of crop water requirements and weather forecast. To produce such information, MOSES combines crop maps determined with satellite images, crop transpiration models, climate data and weather forecast information as inputs. Specifically, with crop maps, crop water requirements are estimated and forecasted in each plot using crop models with input from climate data and weather forecasts.
As seen in the previous section, MOSES predictions before the irrigating season are likely to be used to manage yearly concessions to irrigate. In the current conditions, the WA fixes concessions to irrigate to the average operational capacity of the supply network. With MOSES services, if a dry season is forecasted, the WA would limit the number of concessions to the minimum operational capacity. Otherwise, in view of a regular season, it will release more concessions up to the maximum operational capacity. Hence, the decision due is binary: to limit concessions to the maximum operational capacity or to the minimum operational capacity of the water supply network. The benefits generated are: avoided drought losses if the dry season occurs or higher agricultural revenues in the case of a regular season. Nevertheless, information is not perfect, and two types of errors can emerge:
- the wrong prediction of a regular season: the WA receives a message specifying a regular season will emerge, but eventually the season will be dry;
- the wrong prediction of a dry season: the WA receives a message specifying a dry season will emerge, but eventually the season will be regular.
The above errors lead to higher or lower concessions than the ones actually possible, causing a sub-optimal use of land. If the number of concessions exceeds the contingent capacity of the WA, as a consequence of error 1, farmers would experience a loss due to the difference between the average income of rain-fed crops and irrigated crops with no irrigation water availability. It can be expected that rain-fed crops have a higher comparative performance in terms of income in the case of low or no irrigation water availability. If the number of concessions is below the capacity of the WA as in the case of error 2, farmers would experience a loss due to the difference between the average income of irrigated crops with fully available water and rain-fed crops.
MOSES forecasts during the irrigation season are likely to be used to support decisions on water allocation too. Due to the fixed water flows and technical thresholds, water allocation decisions are binary: to deliver water to a district or not. Such a decision is repeated daily during the irrigating season for each irrigation district. Compared to the current condition where the WA delivers water to districts disregarding the demand, predictions of crop water requirements could support decisions on water allocation during the irrigating season. The benefits generated by this piece of information are: saving water, lowering supply costs, allocating water efficiently and softening damages in dry periods. Here again, the provided information is not perfect, and two type of errors can emerge:
- the wrong prediction that water requirements are above zero: the WA receives a message specifying that water for irrigation is needed in a specific sector of the network, but eventually water for irrigation is not needed;
- the wrong prediction that water requirements equal zero: the WA receives a message specifying no water demand for irrigation in a specific sector of the network, but eventually water for irrigation is needed.
The above errors lead, respectively, to water flow or no water flow in sectors where no water is needed and water is needed. This causes a sub-optimal use of water, where the first error leads to water waste (measured by the amount of water actually distributed in the sector) with unnecessary supply costs. The second error leads to damaged irrigated crops because of missing water deliveries when water for irrigation is actually needed (difference between the average income of irrigated crops with irrigation and irrigated crops with no irrigation).
The whole decision process is represented in the decision tree of Figure 3. Decision alternatives branch from square nodes; the probabilities of uncertain events branch from round nodes and consequences of actions in state of the world are expressed in terminal nodes with prisms. In the two decision time steps (before and during the irrigating season), information is provided through a message. This might cause a revision of the WA’s beliefs depending on the expected consequences associated with each message content and on the accuracy of the ICT. The whole decision process is divided in two decision time steps (separated in Figure 3 by the horizontal red dashed line) with two sequential binary decisions: to release concessions to the maximum operational capacity or to the minimum operational capacity of the water supply network and to deliver water to a district or not. The decision made in the second step is influenced by the expected consequences of that decision during the irrigating season and by the accuracy of the messages provided before the irrigating season. That implies a strict dominance of the accuracy of the messages provided in previous time steps on subsequent ones.
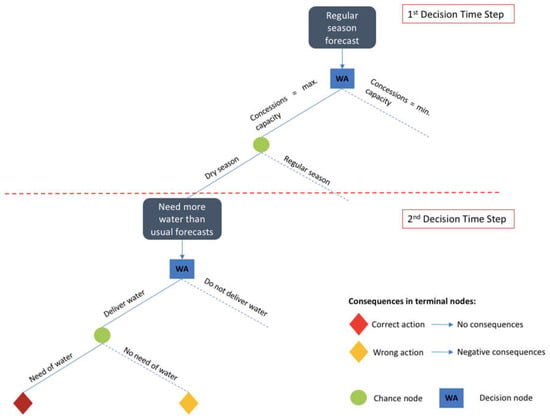
Figure 3.
Decision process of MOSES adoption by the CBR (source: own elaboration).
4. Methodology and Empirical Application
4.1. Definition of the Model
The methodology adopts a simplified decision model to represent the decision-making process of the case study WA to select the best alternative among a set of actions upon receiving new information. The model assumes that a WA is managing water procurement and supply for a given agricultural region and that the WA must plan some actions in advance during two different inter-correlated decision time steps. The first decision step is supposed to be at the time of seeding/transplanting, far in advance to the irrigating season, and involves the decision (action): release concessions to the minimum/maximum operational capacity of the supply network. Such a decision is conditioned by the WA’s expectation about the state of the world (state, from now on): dry/regular season. The second decision step is supposed to be at the time of supplying water for irrigation and involves the decision: deliver/do not deliver water to irrigation districts. Such a decision is conditioned by the WA’s expectation about the state: need/no need water for irrigation. In chronological order, the first decision influences the second. Thus, the usability of such information is then dependent on the accuracy of the messages provided by the information service in both decision steps and on the stakes in the decisions, contributing to determining the expected consequences of using the information. In the following section, we provide an analytical representation of the decision process, both in case of un-informed decisions and ICT-informed decisions. In the latter case, in each decision time step, a new piece of information is provided by a message.
The decision model described before represents a decision process taking place in conditions of uncertainty. In the first place, we assume that the decision process involves a set of actions, X, and a set of states, S. The combination of the possible actions with the possible states determines the associated consequences, , measured in terms of economic payoff of the decision, . The subscript denotes a specific action among the set of possible actions and the subscript s denotes a specific state among the set of possible states, where and . For example, the consequence of not limiting yearly concessions for irrigable areas in a regular season is drought losses, and the associated payoff is the economic estimation of such losses. Thus, the actions taken by the WA have uncertain consequences determined by the probability of occurrence of upcoming states, . In our case, the probability coincides with the climate-relative frequency of the event. Assuming the WA is acting rationally, it will base the choice of an action on the concept of Expected Value (EV) maximization. The EV of an action depends on the probability of the different states and on the payoff of the set of possible actions under the different states of the world [21]. With no information service, the maximization of the EV is obtained by the following Equation (1):
In the case of ICT adoption, the WA can receive a message, , among a set of messages, M (). The probability of receiving message is identified as , which is measured as the frequency of that message relative to all messages delivered by the ICT. Messages provide information regarding the emerging state of the world. For example, a message can specify that a dry season will occur. Messages might modify the WA’s information environment, altering the expectations associated to the upcoming state of the world. The extent to which the WA reviews this prior expectation follows the Bayes Theorem and is measured by the probability of state occurrence conditional to the message received, , also known as posterior probability:
where is the probability of receiving message , conditional to the emergence of state , and is the joint probability of state s and message , also known as the hit rate [18]. This is measured in a likelihood matrix by the frequency of correct messages on all messages delivered by the ICT. As can be noticed, the higher the hit rate of the ICT, the higher the extent to which the WA will revise its prior expectations. This implies that, by means of the accuracy of the ICT, the WA revises its beliefs about a state’s occurrence after receiving a message. This in turn will have an effect on expectations about decision outcomes with direct consequences on the choice of actions, allowing the WA to identify a new optimal action. The EV of this action after receiving a message is determined by the sum of payoffs weighted by the unconditional probability of the message and the respective conditional probability of the states. Considering an ICT delivering multiple messages, the maximization of the EV will be as follows:
Now, consider a simplified version of the model described above, with only two alternative states ( and ), two alternative actions ( and ) and one decision time step. This model can be represented through the diagram in Figure 4. Payoffs in each state are measured vertically and probability is measured horizontally, ranging from zero to one in a bi-directional segment. Since states are alternative, meaning that one excludes the other, probabilities of state occurrence are complementary (). Hence, a point along the segment represents both probabilities. In the diagram, the blue line joining and is the weighed average of payoffs for action . This line expresses the EV for that action as a function of probabilities. Similarly, the pink line, which joins and , represents the EV of action . For a given probability, the EV of the optimal action is displayed by the vertical distance from a point in the horizontal segment of probabilities to the higher EV function between and . Taking into account an information service that can generate two alternative messages ( and ), either message will lead to a vector of posterior probability, . The line joining the EV of the optimal action if is received and if is received, defines the EV of the message service. This is mathematically represented by the probability weighted average of payoffs. So, following Equation (3), the VOI is graphically represented by the vertical distance from the line of the EV of the message service to the EV of the best un-informed action (green segment in Figure 4).
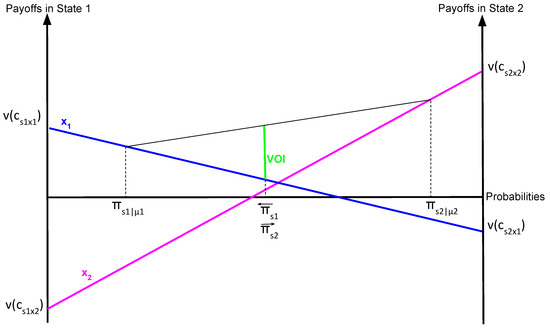
Figure 4.
Graphic representation of the decision model after receiving a new message (source: own elaboration from [16]).
Finally, we take into account a decision problem involving decision time steps. Decision steps are identified as sequential decisions occurring during time (i.e., before and during the irrigating season). For each decision step, t, there are independent actions, , messages, , and states, . The set of possible consequences is obtained with the combination of actions and states in each time step, t, for the subsequent combination until the final decision step. In other words, the combination of actions, states and decision steps allows for the identification of the range of final outcomes of the decision process. Since decision steps, states and messages are independent, the expected value maximization problem can be reformulated as it follows:
Hence, during time in the decision process, the final choice of actions made by the WA depends on the accuracy of the messages received until the final decision step. This way, a lack of accuracy in the first messages has a multiplier effect in determining the expected consequences of sub-sequential actions. Finally, in each decision step and for each message received the WA, the WA seeks the optimal choice of actions among those available. This is done through the identification of the optimal informed action () achieving the highest EV given the states that can emerge and their relative posterior probabilities. The same happens in un-informed conditions, where, given the prior probabilities of states, the WA identifies the optimal un-informed action in each decision step (). After optimizing action choices, the VOI can be estimated as the difference between the EV from the sequence of optimal informed actions given the messages received, and the EV of the optimal un-informed actions given the prior information environment:
As can be seen, the VOI of the ICT is positive only when the expected value of the best informed decision is higher than the EV of the best uninformed decision. This happens when posterior probabilities of the states given messages are higher than their prior. Otherwise, messages would be uninformative, not conditioning any appreciable change in the behavior of the WA.
4.2. Data Collection and Assessment Procedure
The usability of the information service is dependent on the accuracy of the messages provided by the information service itself and on what is at stake in the decisions. These elements contribute to determining the expected consequences of using the information. The sources of information needed to carry out the economic analysis are mainly based on: (1) information obtained by interviewing the WA; (2) information provided by the MOSES service; (3) additional ancillary information.
The first type of information is about the collection of primary data through an ad-hoc questionnaire. The questionnaire includes sections on: (i) WA information requirements; (ii) irrigation infrastructures (including details on water supply costs, efficiency of the supply system and on the amount of water delivered in each sector/district of the network); (iii) land use and cropping patterns (i.e. rain-fed and irrigated crop yields) and (iv) damages caused by extreme weather conditions (probability of a drought, expected damages per crop categories). The questionnaire helped to build the ICT informed decision model and to identify consequences of actions in states. With the joint use of secondary economic data on prices and yields from public databases (RICA–Rete di Informazione Contabile Agricola, 2017: http://rica.crea.gov.it/public/it/index.php) and information on land use, damages, crop prices and costs and on water price and use, it was estimated that the economic payoff associated to consequences of actions in states. To simplify the assessment procedure, impacts of the decisions were estimated with the spatial limitation of the case study area.
The second type of information is about the new data provided by MOSES before and during the 2017 irrigating season. These are mainly crop water demand seasonal and in-season forecasts. Such data were provided with different spatial resolutions, then aggregated in functional management units (sectors of the irrigation network). The collection of such information allowed us to build a complete picture of the information environment which would have characterized the ICT-informed decision process of the WA in 2017.
The third type of information collected was needed to assess the accuracy of MOSES services. These are observed data in the form of: (i) aerial photos (provided by the WA); (ii) weather observation (available from MOSES meteorologists) and (iii) observed crop water requirements. The collection of such information is justified by the fact that the accuracy of the service is mainly dependent on three sources of uncertainty, contributing to the accuracy of the messages provided by MOSES: (1) crop maps; (2) water demand estimates, and; (3) forecasts. The accuracy of information was estimated from the hit rate of the service, coming from the ratio between the number of correct messages of the overall messages received by the WA. This ratio is a rough estimate of the probability of correctly predicting current and upcoming states. Specifically: (1) by comparing MOSES crop maps with aerial photos (provided by the WA), we calculated the probability that an irrigated crop mapped with MOSES satellite images matches with an irrigated crop mapped with aerial photos; (2) by comparing MOSES rainfall forecasts with rainfall observation, we calculated the probability that a forecasted rainfall above the estimated crop water requirements matches with the observed rainfall above the estimated crop water requirements. In addition, due to missing information, we assumed that, by comparing MOSES estimates of irrigation requirements with measured irrigation requirements, the probability that a positive irrigation requirement estimate (greater than zero) matches with a positive irrigation requirement measured with soil moisture sensors. Each of the above comparisons and assumptions contributed to the calculation of the probability of predicting a dry or a regular season before the irrigating season and the probability of predicting water requirements above or below a threshold value of 10 mm. This value is assumed to be the critical level influencing the amount of water to be supplied for each sector of the irrigation network during the irrigating season.
Appendix A provide all the information needed to test the assessment methodology for the estimation of the accuracy of information and the payoffs of the decision process.
5. Results
The estimation of the accuracy of the MOSES information was carried out by comparing MOSES output with observed data, as described in the previous section. Results about the accuracy of the messages provided through MOSES are displayed in the probability matrix of Table 1 and Table 2. The overall accuracy of each message is expressed by the probability to correctly detect the land use multiplied by the probability to correctly predict if water requirements are above the 10 mm threshold. As can be seen from the tables, the accuracy of the messages is not evenly distributed between states and the crop classification appears to be less reliable than the forecast of water requirements.

Table 1.
Probabilities to detect the land use.

Table 2.
Probabilities to predict water requirements.
Water savings brought by the use of the forecast information are determined both in regular and dry seasons. The variability of water savings is measured across time and is calculated by comparing water requirement estimates with the water actually supplied to districts in 2017 (Figure 5). Water savings and water use tend to show a parallel trend. This highlights the fact that higher water savings are more easily achievable in periods with higher water use. In the first weeks of the irrigating season, higher variability of water use can be found, with two peaks at week three and six. Such phenomena are mainly due to the rain distribution in late spring, which is particularly variable in the case study area. Further, at the beginning of the season, peaks in water demand are caused by early concessions to irrigate. These are released to allow the seeding/transplanting of summer crops, which are extremely sensitive to droughts in the first phenological stages. Finally, in dry season with water scarcity, lower water savings are achievable because water demand tends to be equal to the water available.
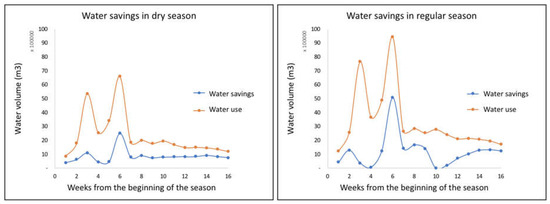
Figure 5.
Estimated water savings during the irrigating season (source: own elaboration).
Table 3 represents the payoff matrix expressing payoffs in each state action combination for both decision steps. In the assessment, the impact of optimal decisions is estimated to be zero, since they stand for the most suited management strategy given the climate conditions. Then, with reference to the optimal decisions, losses are estimated for each sub-optimal state action combination. Great variability in decision outcomes can be found because the same action has extreme consequences with the emergence of a dry season or a regular season. For example, with wrong water allocation decisions, great drought losses can emerge, or wrong land allocation causes sub-optimal use of resources with negative impacts on farmers’ income.

Table 3.
Payoffs of the decision model in the case study region (€).
By applying the model in Section 3, the accuracy of the ICT information is used to compute the EV of each action whose payoffs are represented in Table 3. Then, the VOI is assessed as the difference in expected decision outcome between the best decision process with information and without information. Summing over the VOI assessed in each district, potential benefits of the ICT-informed decision model are estimated to be 156,426 € for the irrigating season of 2017 and for all 32 districts examined (26.02 €/cultivated hectare/year). The spatial distribution of the VOI (Figure 6) is highly variable. Some districts have a null benefit from the implementation of such technologies, others have a very high benefit.
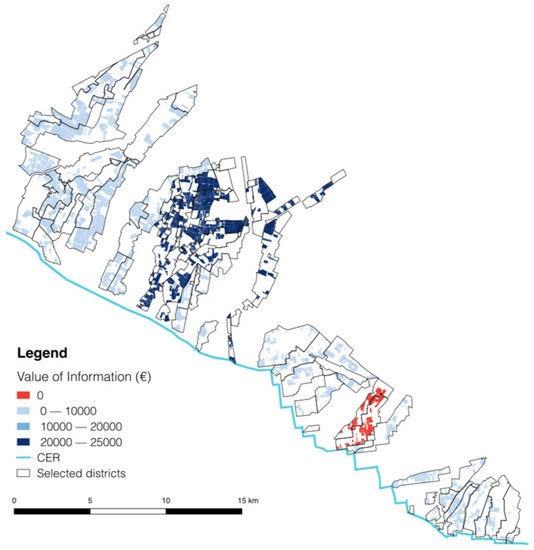
Figure 6.
Distribution of the VOI between irrigation districts (source: own elaboration).
Because the accuracy of information is estimated using inputs from only one irrigating season, it was considered useful to run a sensitivity analysis. This method is frequently adopted in literature for the estimation of ICTs [13]. By varying the accuracy of information in both decision steps, we determined the VOI in each condition of the information environment. In detail, we built an index named Quality of Information (QI), ranging from zero to one, expressing the probability of correctly predicting events. It is determined by the average accuracy of the messages provided to the WA before and during the irrigating season. The QI will be null when the posterior probability to correctly predict events coincides with its prior. The opposite will occur in the case of perfect information; QI will equal one. The graph in Figure 7 shows how the VOI is related to the QI by increasing the accuracy of information of every message in the two subsequent decision time steps. As expected, by raising the QI for both decision steps, we see a non-decreasing linear trend of the VOI. It reaches its minimum in uninformed conditions (QI = zero) and its maximum with perfect information (QI = one), where the WA is sure to make optimal decisions. The trend is linear because of the linear equation used to model the VOI, which it is determined as the difference in EV between informed and uninformed decisions. Kinks can be noticed in the trend of the VOI; these take place when a new piece of information is introduced with the required accuracy to cause a belief revision. Accordingly, for each decision, there will be a threshold in the accuracy of the message provided, under which the WA does not revise its expectations about state occurrence. Above such a threshold, the WA revises its beliefs and perceives benefits of the improved decision. In the second decision step (T2), we determined the VOI both in case of perfect information at the first decision step (T1) (before the season) and no information provision at T1. This choice is motivated by the fact that the overall decision outcome is affected by the accuracy of information at both decision steps. In detail, water allocation decisions are influenced by the expected consequences of that decision during the irrigating season and by the decisions on land allocation made before the irrigating season. This implies that the accuracy of information provided in the first decision step has an effect on the minimum accuracy for information to be usable in the second decision step.
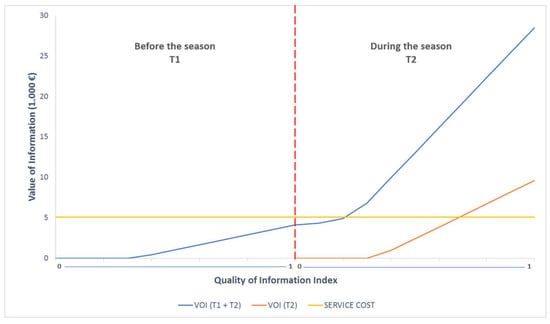
Figure 7.
Sensitivity analysis for the VOI. T1 = first decision step. T2 = second decision step (source: own elaboration).
6. Discussion
Results from the model show positive impacts from ICT adoption, but with a high variability in its spatial and temporal distribution. The former variability is caused by different cropping patterns between districts. Specifically, in districts with high added value crops, the accuracy of information might be too low to cause a change in the WA’s belief. Accordingly, stakes are higher with added value crops in respect to other crops. Thereby, losses caused by wrong information are relatively higher, diminishing the net benefit from following MOSES advice. The latter variability is caused by the fluctuation of water savings during time across the irrigating season. Peaks are mainly due to the combined effect of rainfall patterns and crop water requirements. Considerable water savings can be achieved if consistent rain or no water demands are correctly predicted. When crop water demand is lower than some specific technical threshold in water delivery, no water savings are attainable.
The analyses of the case study showed that in some districts, permanent crops are prevailing, and the VOI is low. This is due to the decisional power of the WA which is not enough to influence land allocation of permanent crops in the medium term. Thereby, the WA cannot act upon the information received. This factor limits the efficiency of land allocation schemes informed by seasonal forecasts and enhances the spatial variability of the VOI. Moreover, due to the characteristics of the supply network, the WA is not able to precisely allocate water according to needs. At this end, decisions are simply on whether to deliver water to a district or not. This, together with the limited decisional power of the WA, limits the potential of MOSES services and highlights how local constraints might have a strong impact on benefits from ICTs adoption.
The complex nature of the decision-making process studied posed limits in the model capabilities to represent the decision problem. The WA selected as a case study has a complex decision environment, with multiple sources of information, stakeholders, and complex decisions. This caused the first modelling limitation which is rooted in the simplification of the decision process of the WA. Further, the model overlooks transaction costs in information processing and implementation, the estimation of which was unfeasible due to lacking data and over-complexity of the model. The analyses showed a decision process that involves high risk prospects with decisions having extreme consequences. As seen in the matrix of payoffs, decision outcomes are extremely variable and wrong decisions bring great losses. Because of this, the model finds its main limitation in neglecting the choice of risky actions by the WA. Accordingly, other behavioral aspects not reflected in the maximization of EV might drive the WA’s decisions. By addressing the risky behavior in perceiving the quality of information, a more reliable estimation of ICT economic benefit would be achieved. In addition, deepening the knowledge regarding the relationship between uncertainty and risk aversion seems a promising topic in the decision analytic literature [13]. Other than risk aversion, more emotional factors may influence the adoption of ICTs, such as fascination with new technologies or aversion to adapt the decision-making process to the same technologies [22]. Nonetheless, we considered the impact of such emotional factors negligible in the medium/long term. Finally, this work, as well as the recent literature on the topic [11], do not consider the potential external benefits of improving the WA’s knowledge. For example, the WA could disseminate the received forecasts between farmers to help them in planning their activities.
A limitation of the exercise carried out in this paper is the data used. Data used as input in the model are just from the 2017 irrigating season. Given the variability of weather data, it would be preferable to have a higher number of years observed. In addition, 2017 was a particularly dry season in respect to the climate average, which implies a likely overestimation of benefits. Even though the results are not representative of the climate average or trends, they can show the VOI in a future climate scenario where drought events are expected to increase in frequency and length. Because the VOI is found to be dependent on agricultural revenues, agricultural prices play a key role in determining the adoption of ICTs. Furthermore, in future scenarios where high price volatility can be expected, this will reflect an increase in the level of uncertainty in the decision environment. This will have a strong effect on the VOI, whose extent is not tackled in the present paper. The sensitivity analysis not only overcame the problem of estimating the accuracy of information with data from only the 2017 irrigating season, but it showed the accuracy threshold levels over which decisions are influenced by a new piece of information. More importantly, it proved that despite the above limitations, the model is able to capture the VOI as a function of the accuracy of the messages provided. Finally, as decision problems are very much location specific, also in relation to existing infrastructures and decision-making flexibility, the results cannot be generalized and would benefit from a wider testing exercise in areas with radically different decision-making conditions.
Despite the limitations described above, the estimation of the VOI is comparable with and confirmed by the results of other studies found in literature. In their review, Meza, Hansen, and Osgood [4] found the value of seasonal forecasts for agricultural decision-making ranging from zero to 700 $/ha. Such values are strongly affected by crop types. Lower bounds can be found in areas predominantly cultivated with cereals and extensive crops, with estimations that are in line with the findings of the present paper. Galioto, Raggi, and Viaggi [20] found higher VOI ranging from 40 €/ha to 200 €/ha depending on water cost, crop price, farmer’s risk attitudes, quality of information and land quality. Particularly, their characterization of the VOI with the quality of information comes to similar conclusions to the sensitivity analysis carried out in this study. Our results are also confirmed by the work of Fernandez et al. [5]. They estimate and characterize a VOI comparable to our findings. Crean et al. [17] also identify a comparable VOI, ranging from 0.20 to 23.18 $/ha. Further, they carry out a sensitivity analysis on the VOI by varying the accuracy of information, which showed a non-decreasing trend of the VOI.
7. Conclusions
The paper quantitatively estimated the potential economic benefits from the ICT-informed decision process of water management in agriculture at the WA level. To do so, a theoretical model was designed, simulating the decision process of a case study WA. The methodology proposed accounted for the combined effect given by: (i) the accuracy of information in a multiple decision step process and (ii) what is at stake in the decision process. This paper has shown that a combination of BDT and EV maximization can offer a suitable approach to deal with complex VOI modelling, such as that for WAs. This approach seems promising, as it links the information with the time it is provided in a sequential decision process made by several decision steps. The implementation of such methodology showed that ICTs can provide useful climate information for improved decision support. Economic benefits are then recognizable, especially when considering adaptation strategies to extreme drought events related to CC. The magnitude of such benefits is conditioned by constraints due to local characteristics of the decision process: (i) site specific conditions (land use and water delivery system); (ii) the decisional power of the WA in affecting land allocation and, most of all, (iii) the quality of information required to make decisions. Notwithstanding the great potential of ICTs for WAs, these constraints strongly affect actual application. Moreover, since many ICTs offer discrete technology components without providing any support to adapt the technology itself to each specific reality, this undermines their usability. VOI is strongly affected by the information environment and ICTs should aim to deliver information tailored to a WA’s specific needs [23]. In detail, requirements in terms of accuracy of information, timing of information provision and constraints in the application of the information have to be considered. This highlights the necessity to develop ICTs jointly with end users. The simple provision of forecast information, even though high-quality, follows the “loading dock approach” [24]. This is described as the production of relevant climate information which has no use in reality because its form or time provision is incompatible with actual decision making [2]. Hence, future ICT development in irrigated agriculture should aim to better answer WAs’ specific needs of information. An approach based this way will foster WAs’ adaptation capacity. Because public institutions have the potential to guide decision making processes through better use of existing knowledge [24], policy intervention is advised. The suggestion is to implement policy tools to help private initiatives facing high transaction costs in ICTs implementation jointly with end users [25]. This is especially necessary in the case of ICTs for WA, given their growing demand for detailed climate information.
Author Contributions
The paper constitutes a collective effort of the four authors. Nevertheless, authors main contribution to each section of the research can be described as follows: Conceptualization, Francesco Galioto, Francesco Cavazza, Meri Raggi and Davide Viaggi; Data curation, Francesco Cavazza and Francesco Galioto; Methodology, Francesco Galioto and Francesco Cavazza; Project administration, Meri Raggi; Supervision, Francesco Galioto and Davide Viaggi; Writing – original draft preparation, Francesco Cavazza.
Acknowledgments
The research has received funding from the European Commission Horizon 2020 Programme under grant agreement No. 642258 – MOSES Project (Managing crOp water Saving with Enterprise Services). However, this work does not necessarily reflect the view of the European Union and in no way anticipates the Commission’s future policy in this area. The authors gratefully acknowledge Consorzio di Bonifica della Romagna, for their provision of data and information, as well as the MOSES Consortium for their support in the development of the research. Finally, we would like to thank the anonymous reviewers for their valuable comments and suggestions. The usual disclaimers apply.
Conflicts of Interest
The authors declare no conflict of interest.
Appendices A1 and A2: Data Used to Estimate Decision Outcomes
In this section, we provide all the information needed to reproduce the payoffs of the decision process. Decision outcomes were estimated in each scenario, given by the combination of a set of actions per set of states of the world. Measures are carried out having the optimal decision in both decision steps as a reference point. All other combinations of actions and states imply economic losses. These are measured in terms of agricultural and water losses. In detail, information about the cultivated land within each irrigation district (Table A1) was combined with technical and economic variables of farm productivity and profitability per group of reference crops. In each district, the agricultural revenue is then determined both in dry and regular seasons, and whether water concessions are given to the maximum or to the minimum operational capacity of the network. Water losses (or savings in Table A2) are measured considering the excessive water distributed to districts in respect to the technically achievable optimal distribution. This is given by optimally allocating water to districts taking into account the rainfall patterns, crop water demand and technical constraints. Then, by multiplying waste by water price (0.0264 €/m3), economic losses are determined.

Table A1.
Cultivated land per main crops per districts.
Table A1.
Cultivated land per main crops per districts.
| District Name | Wheat (ha) | Kiwifruit (ha) | Corn (ha) | Alfalfa (ha) | Apple (ha) | Peach (ha) | Vineyard (ha) | Total (ha) |
|---|---|---|---|---|---|---|---|---|
| Acquara alta | 0.0 | 1.2 | 81.3 | 22.0 | 0.0 | 0.0 | 0.4 | 104.9 |
| Baldone | 0.0 | 0.0 | 35.0 | 9.7 | 0.0 | 0.0 | 0.0 | 44.7 |
| Cannuzzo | 0.4 | 3.1 | 59.8 | 47.7 | 5.6 | 4.2 | 0.6 | 121.4 |
| Cappella | 0.0 | 0.0 | 18.3 | 10.3 | 0.0 | 8.7 | 0.0 | 37.4 |
| Carpena | 3.1 | 2.3 | 69.7 | 350.7 | 10.8 | 20.8 | 80.5 | 537.9 |
| Cavaticcia | 0.0 | 0.0 | 3.3 | 2.0 | 0.0 | 0.2 | 0.2 | 5.7 |
| Cervaro | 0.0 | 0.0 | 14.7 | 10.7 | 0.0 | 0.0 | 0.0 | 25.4 |
| Dismano est | 0.0 | 0.0 | 9.9 | 4.2 | 0.0 | 3.7 | 0.0 | 17.8 |
| Fiumicello superiore | 0.0 | 1.6 | 104.6 | 96.0 | 1.2 | 17.4 | 0.7 | 221.4 |
| Fossatone del bevano | 0.0 | 0.0 | 7.7 | 8.7 | 0.0 | 0.0 | 0.0 | 16.4 |
| Fossatone del rigoncello | 1.7 | 0.0 | 20.0 | 12.6 | 0.0 | 0.0 | 0.0 | 34.3 |
| Lagnano | 0.0 | 0.0 | 0.0 | 0.6 | 0.0 | 0.0 | 0.0 | 0.6 |
| Lama superiore | 0.0 | 0.0 | 13.3 | 83.8 | 0.5 | 3.2 | 6.1 | 106.9 |
| Lupara | 0.0 | 0.0 | 22.4 | 23.1 | 0.0 | 5.8 | 0.0 | 51.3 |
| Masiera | 1.6 | 0.0 | 1.6 | 5.6 | 0.0 | 0.0 | 0.0 | 8.7 |
| Matrice vecchia | 0.0 | 0.0 | 11.1 | 0.0 | 0.0 | 0.0 | 0.0 | 11.1 |
| Mesola del montaletto | 0.0 | 0.0 | 7.8 | 29.9 | 0.0 | 0.0 | 0.0 | 37.7 |
| Olca | 0.0 | 1.8 | 32.4 | 23.3 | 11.0 | 5.0 | 1.2 | 74.7 |
| Pradazzi | 0.0 | 0.0 | 48.1 | 35.1 | 0.0 | 11.5 | 0.0 | 94.7 |
| Re | 0.0 | 0.5 | 27.7 | 21.2 | 2.8 | 0.3 | 20.3 | 72.8 |
| Rigoncello | 0.0 | 0.0 | 8.8 | 18.2 | 0.0 | 0.0 | 0.0 | 27.0 |
| Rio della valle | 0.0 | 0.0 | 28.1 | 22.2 | 0.0 | 0.0 | 0.0 | 50.3 |
| Ronco grosso | 0.0 | 0.0 | 22.4 | 2.0 | 0.0 | 3.4 | 0.0 | 27.8 |
| Salto | 0.0 | 0.0 | 2.4 | 1.7 | 0.0 | 0.0 | 0.0 | 4.1 |
| Saraceta | 0.0 | 0.0 | 5.5 | 21.2 | 0.0 | 0.0 | 0.0 | 26.7 |
| Spadolaro pieve quinta | 0.0 | 0.0 | 0.0 | 8.8 | 0.0 | 0.0 | 1.9 | 10.7 |
| Tratturo fosso ghiaia | 0.0 | 0.0 | 24.0 | 8.5 | 0.5 | 0.9 | 0.4 | 34.3 |
| Vecchio | 0.0 | 0.0 | 4.8 | 12.0 | 0.0 | 0.0 | 0.0 | 16.8 |
| Vena grande | 0.0 | 0.0 | 3.1 | 0.9 | 0.0 | 0.0 | 0.0 | 4.0 |
| Veneziana | 0.0 | 0.0 | 51.7 | 60.8 | 0.0 | 0.0 | 2.5 | 115.0 |
| Via cupa | 0.8 | 0.0 | 42.4 | 103.7 | 0.8 | 26.1 | 58.7 | 232.5 |
| Violone della mesola | 0.0 | 0.0 | 16.8 | 9.8 | 0.0 | 7.4 | 0.0 | 34.0 |
| Total | 9.3 | 10.5 | 818.8 | 1079.4 | 33.2 | 118.6 | 173.5 | 2243.2 |

Table A2.
Potential water savings per district in regular season.
Table A2.
Potential water savings per district in regular season.
| District Name | Water Saving (m3) | |
|---|---|---|
| Regular Season | Dry Season | |
| Acquara alta | 3474330 | 1661437 |
| Baldone | 501248 | 410329 |
| Cannuzzo | 174165 | 214274 |
| Cappella | 329723 | 530877 |
| Carpena | 178205 | 132544 |
| Cavaticcia | 632932 | 544847 |
| Cervaro | 0 | 0 |
| Dismano est | 186174 | 155422 |
| Fiumicello superiore | 3297819 | 1648666 |
| Fossatone del bevano | 495168 | 513337 |
| Fossatone del rigoncello | 937606 | 854854 |
| Lagnano | 276432 | 211418 |
| Lama superiore | 185116 | 65136 |
| Lupara | 492453 | 442914 |
| Masiera | 0 | 0 |
| Matrice vecchia | 873620 | 810796 |
| Mesola del montaletto | 790252 | 661334 |
| Olca | 644390 | 903778 |
| Pradazzi | 0 | 0 |
| Re | 507138 | 406068 |
| Rigoncello | 675181 | 620072 |
| Rio della valle | 0 | 0 |
| Ronco grosso | 283620 | 120797 |
| Salto | 0 | 0 |
| Saraceta | 219990 | 208552 |
| Spadolaro pieve quinta | 403868 | 140262 |
| Tratturo fosso ghiaia | 323829 | 121179 |
| Vecchio | 48992 | 41077 |
| Vena grande | 309933 | 246392 |
| Veneziana | 623470 | 612185 |
| Via cupa | 690420 | 343736 |
| Violone della mesola | 266088 | 251594 |
| Total | 18759766 | 13728732 |
Appendix A3: Land Allocation under Different Management Decisions
In the following table, land allocation per group of crops is shown under different scenarios; it shows the result of land allocation decisions taken under each climatic forecast capable of positively influencing decisions.

Table A3.
Land use under with different scenarios of land allocation decisions.
Table A3.
Land use under with different scenarios of land allocation decisions.
| - | Concessions to the Minimum Operational Capacity | Concessions to the Average Operational Capacity | Concessions to the Maximum Operational Capacity | ||||||
|---|---|---|---|---|---|---|---|---|---|
| District Name | Perennial Crops (ha) | Irr. Seasonal Crops (ha) | Dry Seasonal Crops (ha) | Perennial Crops (ha) | Irr. Seasonal Crops (ha) | Dry Seasonal Crops (ha) | Perennial Crops (ha) | Irr. Seasonal Crops (ha) | Dry Seasonal Crops (ha) |
| Acquara alta | 14.6 | 22.0 | 122.8 | 14.6 | 31.5 | 113.3 | 14.6 | 40.9 | 103.9 |
| Baldone | 3.8 | 23.3 | 16.9 | 3.8 | 33.2 | 6.9 | 3.8 | 43.2 | 0.0 |
| Cannuzzo | 18.7 | 14.8 | 47.4 | 18.7 | 21.2 | 41.0 | 18.7 | 27.5 | 34.6 |
| Cappella | 2.4 | 37.2 | 49.6 | 2.4 | 53.2 | 33.7 | 2.4 | 69.2 | 17.7 |
| Cavaticcia | 3.5 | 3.8 | 29.3 | 3.5 | 5.4 | 27.7 | 3.5 | 7.0 | 26.1 |
| Dismano est | 6.0 | 24.8 | 77.4 | 6.0 | 35.5 | 66.8 | 6.0 | 46.1 | 56.2 |
| Fiumicello superiore | 147.3 | 180.4 | 826.2 | 147.3 | 257.7 | 748.9 | 147.3 | 335.0 | 671.6 |
| Fossatone del bevano | 2.7 | 0.6 | 11.7 | 2.7 | 0.8 | 11.5 | 2.7 | 1.1 | 11.2 |
| Fossatone del rigoncello | 0.0 | 19.2 | 17.2 | 0.0 | 27.4 | 9.0 | 0.0 | 35.6 | 0.8 |
| Lagnano | 0.0 | 0.0 | 1.4 | 0.0 | 0.0 | 1.4 | 0.0 | 0.0 | 1.4 |
| Lama superiore | 73.4 | 25.1 | 211.5 | 73.4 | 35.9 | 200.7 | 73.4 | 46.6 | 189.9 |
| Lupara | 1.6 | 19.6 | 31.1 | 1.6 | 27.9 | 22.7 | 1.6 | 36.3 | 14.4 |
| Masiera | 1.2 | 18.5 | 26.4 | 1.2 | 26.4 | 18.4 | 1.2 | 34.3 | 10.5 |
| Matrice vecchia | 0.1 | 8.9 | 20.9 | 0.1 | 12.7 | 17.1 | 0.1 | 16.5 | 13.3 |
| Mesola del montaletto | 5.0 | 14.5 | 41.4 | 5.0 | 20.7 | 35.2 | 5.0 | 26.9 | 29.0 |
| Olca | 40.6 | 3.9 | 13.1 | 40.6 | 5.6 | 11.4 | 40.6 | 7.2 | 9.7 |
| Pradazzi-rio della valle | 17.5 | 56.7 | 79.5 | 17.5 | 81.0 | 55.3 | 17.5 | 105.2 | 31.0 |
| Re | 13.4 | 8.2 | 22.4 | 13.4 | 11.8 | 18.8 | 13.4 | 15.3 | 15.3 |
| Rigoncello | 2.2 | 8.8 | 26.1 | 2.2 | 12.6 | 22.3 | 2.2 | 16.4 | 18.6 |
| Ronco grosso | 74.9 | 130.0 | 824.3 | 74.9 | 185.8 | 768.6 | 74.9 | 241.5 | 712.9 |
| Salto | 0.0 | 3.3 | 6.7 | 0.0 | 4.7 | 5.3 | 0.0 | 6.1 | 3.9 |
| Spadolaro pieve quinta | 35.1 | 22.7 | 90.1 | 35.1 | 32.4 | 80.4 | 35.1 | 42.1 | 70.7 |
| Tratturo fosso ghiaia | 110.0 | 67.5 | 161.3 | 110.0 | 96.5 | 132.3 | 110.0 | 125.4 | 103.4 |
| Vecchio | 1.5 | 6.7 | 12.7 | 1.5 | 9.5 | 9.9 | 1.5 | 12.4 | 7.0 |
| Vena grande | 0.0 | 2.8 | 1.2 | 0.0 | 4.0 | 0.0 | 0.0 | 5.2 | 0.0 |
| Veneziana | 8.6 | 48.7 | 164.8 | 8.6 | 69.6 | 143.9 | 8.6 | 90.5 | 123.0 |
| Via cupa | 199.8 | 184.6 | 373.6 | 199.8 | 263.7 | 294.5 | 199.8 | 342.8 | 215.4 |
| Violone della mesola | 7.1 | 0.0 | 7.3 | 7.1 | 0.0 | 7.3 | 7.1 | 0.0 | 7.3 |
| Total | 790.8 | 956.6 | 3314.4 | 790.8 | 1366.6 | 2904.4 | 790.8 | 1776.6 | 2494.4 |
References
- Bizikova, L.; Burch, S.; Cohen, S.; Robinson, J. Linking sustainable development with climate change adaptation and mitigation. In Ethics and Human Security; O’Brien, K., Clair, A.St., Kristoffersen, B., Eds.; Cambridge University Press: New York, NY, USA, 2010; pp. 157–179. [Google Scholar]
- Vogel, J.; Letson, D.; Herrick, C. A framework for climate services evaluation and its application to the Caribbean Agrometeorological Initiative. Clim. Serv. 2017, 6, 65–76. [Google Scholar] [CrossRef]
- Hallstrom, D.G. Interannual climate variation, climate prediction, and agricultural trade: The costs of surprise versus variability. Rev. Int. Econ. 2004, 12, 441–455. [Google Scholar] [CrossRef]
- Meza, F.J.; Hansen, J.W.; Osgood, D. Economic value of seasonal climate forecasts for agriculture: Review of ex-ante assessments and recommendations for future research. J. Appl. Meteorol. Clim. 2008, 47, 1269–1286. [Google Scholar] [CrossRef]
- Fernandez, M.A.; Huang, P.; McCarl, B.; Mehta, V. Value of decadal climate variability information for agriculture in the Missouri River basin. Clim. Chang. 2016, 139, 517–533. [Google Scholar] [CrossRef]
- Deichmann, U.; Goyal, A.; Mishra, D. Will Digital technologies transform agriculture in developing countries? 2016. Available online: http://doi.org/10.1596/1813-9450-7669 (accessed on 22 August 2018).
- Guerra, E.; Ventura, F.; Viaggi, D.; Snyder, R.L. Can crop coefficients improve the economics of irrigated crops? Acta Hortic. 2017, 1150, 515–520. [Google Scholar] [CrossRef]
- Tyrychtr, J.; Junek, P.; Vostrovský, V.; Vasilenko, A.; Nouza, J. Towards framework for economic value of analytical systems in agriculture: proposal of research. Agris on-line Pap. Econ. Inform. 2016, VIII, 103–109. [Google Scholar] [CrossRef]
- Aker, J.C.; Ghosh, I.; Burrell, J. The promise (and pitfalls) of ICT for agriculture initiatives. Agric. Econ. 2016, 47, 35–48. [Google Scholar] [CrossRef]
- Nakasone, E.; Torero, M. A text message away: ICTs as a tool to improve food security. Agric. Econ. 2016, 47, 49–59. [Google Scholar] [CrossRef]
- Martin, W. Agriculture in an interconnected world. Agric. Econ. 2016, 47, 3–6. [Google Scholar] [CrossRef]
- Macauley, M.K. The value of information: Measuring the contribution of space-derived earth science data to resource management. Space Policy 2006, 22, 274–282. [Google Scholar] [CrossRef]
- Keisler, J.M.; Collier, Z.A.; Chu, E.; Sinatra, N.; Linkov, I. Value of information analysis: The state of application. Environ. Syst. Decis. 2014, 34, 3–23. [Google Scholar] [CrossRef]
- Smith, J.E.; Ulu, C. Risk aversion, information acquisition, and technology adoption. Oper. Res. 2017, 65, 1011–1028. [Google Scholar] [CrossRef]
- Bikhchandani, S.; Hirshleifer, J.; Riley, J.G. The Analytics of Uncertainty and Information; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Hardaker, J.B.; Huirne, R.B.M.; Anderson, J.R.; Lien, G. Coping with Risk in Agriculture: Applied Decision Analysis; CAB International: Wallingford, UK, 2015. [Google Scholar]
- Crean, J.; Parton, K.; Mullen, J.; Hayman, P. Valuing seasonal climate forecasts in a state-contingent manner. Aust. J. Agric. Resour. Econ. 2015, 59, 61–77. [Google Scholar] [CrossRef]
- Bouma, J.A.; van der Woerd, H.J.; Kuik, O.J. Assessing the value of information for water quality management in the North Sea. J. Environ. Manage. 2009, 90, 1280–1288. [Google Scholar] [CrossRef] [PubMed]
- Hardaker, J.B.; Lien, G. Probabilities for decision analysis in agriculture and rural resource economics: The need for a paradigm change. Agric. Syst. 2010, 103, 345–350. [Google Scholar] [CrossRef]
- Galioto, F.; Raggi, M.; Viaggi, D. Assessing the potential economic viability of precision irrigation: a theoretical analysis and pilot empirical evaluation. Water 2017, 9, 990. [Google Scholar] [CrossRef]
- Kusunose, Y.; Mahmood, R. Imperfect forecasts and decisionmaking in agriculture. Agric. Syst. 2016, 146, 103–110. [Google Scholar] [CrossRef]
- Plant, R.E. Site-specific management: the application of information technology to crop production. Comput. Electron. Agric. 2001, 30, 9–29. [Google Scholar] [CrossRef]
- Furman, C.; Roncoli, C.; Crane, T.; Hoogenboom, G. Beyond the “fit”: Introducing climate forecasts among organic farmers in Georgia (United States). Clim. Chang. 2011, 109, 791–799. [Google Scholar] [CrossRef]
- Cash, D.W.; Borck, J.C.; Patt, A.G. Countering the loading-dock approach to linking science and decision making: comparative analysis of El Niño/Southern Oscillation (ENSO) forecasting systems. Sci. Technol. Hum. Values 2006, 31, 465–494. [Google Scholar] [CrossRef]
- Denton, F.; Wilbanks, T.J.; Abeysinghe, A.C.; Burton, I.; Gao, Q.; Warner, K.; Masui, T.; O’Brien, K.; Lemos, M.C. Climate-resilient pathways: adaptation, mitigation, and sustainable development. Clim. Chang. 2014, 1101–1131. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).