Change and Climatic Linkage for Extreme Flows in Typical Catchments of Middle Tianshan Mountain, Northwest China
Abstract
1. Introduction
2. Study Area and Data
3. Data and Methodology
3.1. Data Collection and Preprocessing
- (1)
- the time length t of the decreasing flank of the first event exceeds a time kp, t > kp;
- (2)
- the discharge drops down—in between the two events—to a fraction lower than f of the peak flow; where qmin, qmax, and qbase would be the minimum discharge, the maximum discharge and the base flow, respectively:
- (3)
- the discharge increment from to has a minimum height , . This procedure for peak flow selection has three parameters: kp, f and . It is based on the concept that a peak flow event can be considered largely independent from the next one, when the interevent discharge drops down to a low flow condition or almost to the baseflow level (see criterion (2)). Under this condition, the quick flow components attributed to the peak flow events are indeed nearly independent.
3.2. Methods
3.2.1. Trends Analysis and Change Point Detect
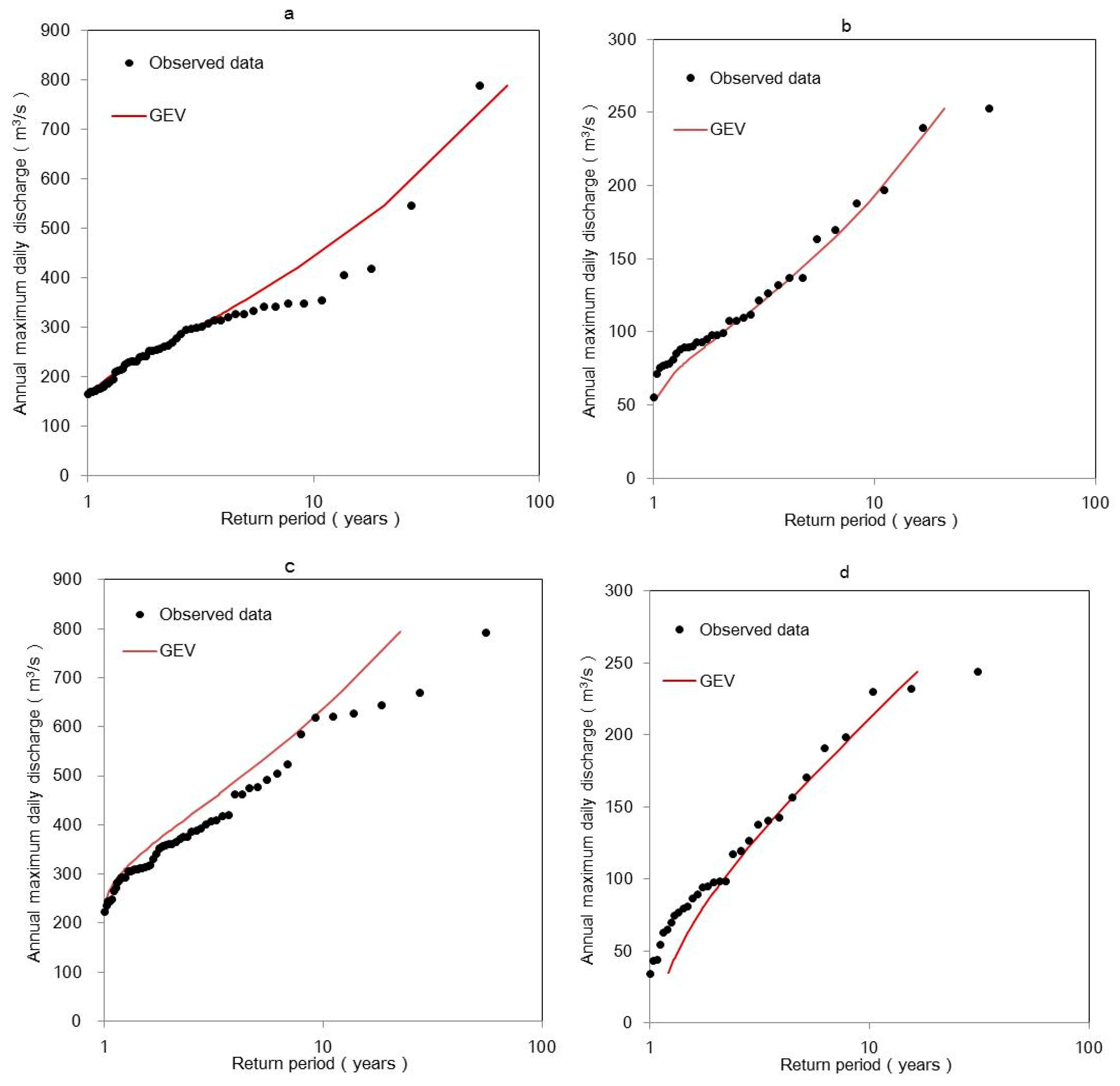
3.2.2. Frequency Analysis
3.2.3. Pearson Correlation Analysis
4. Results and Discussions
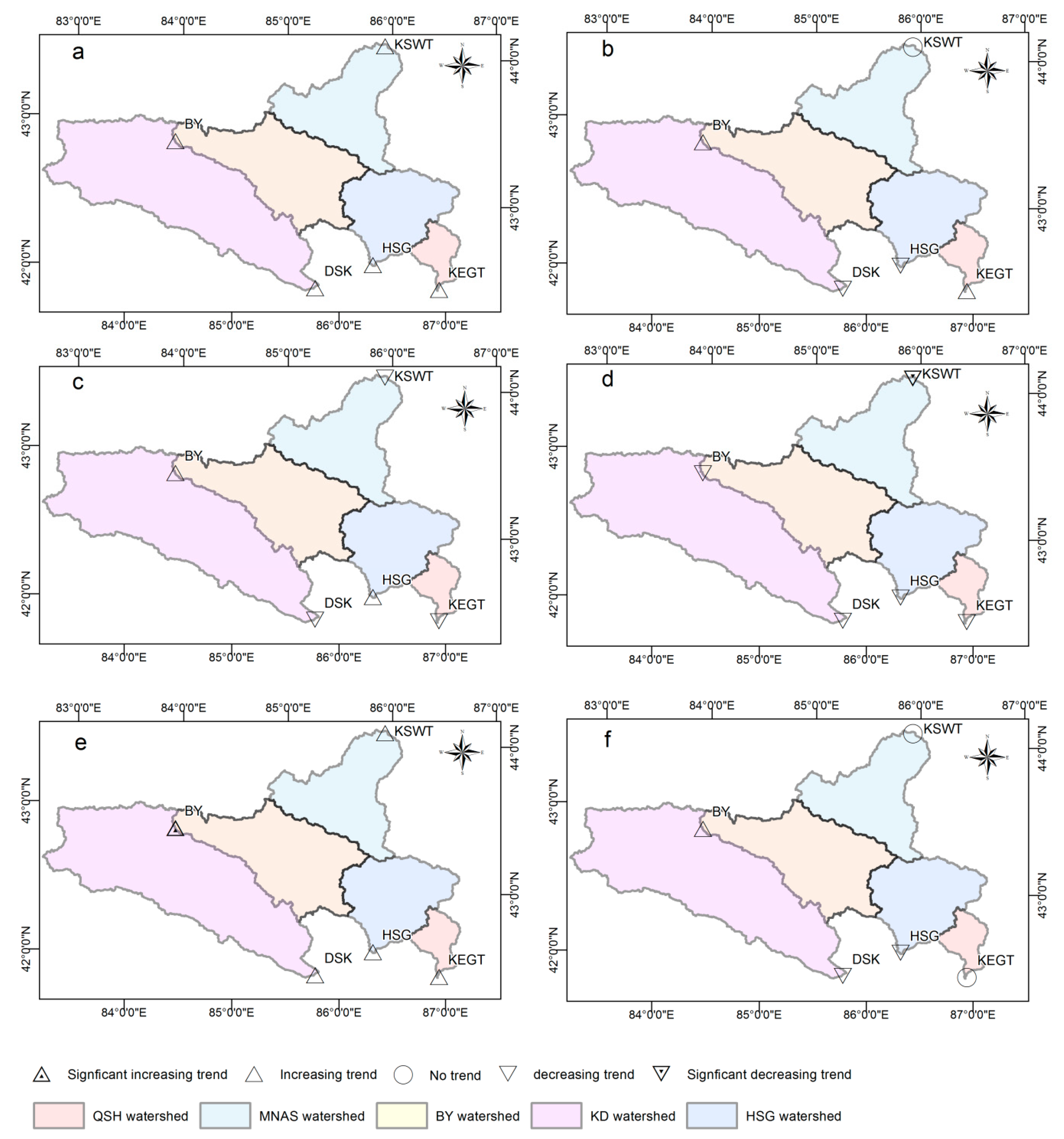
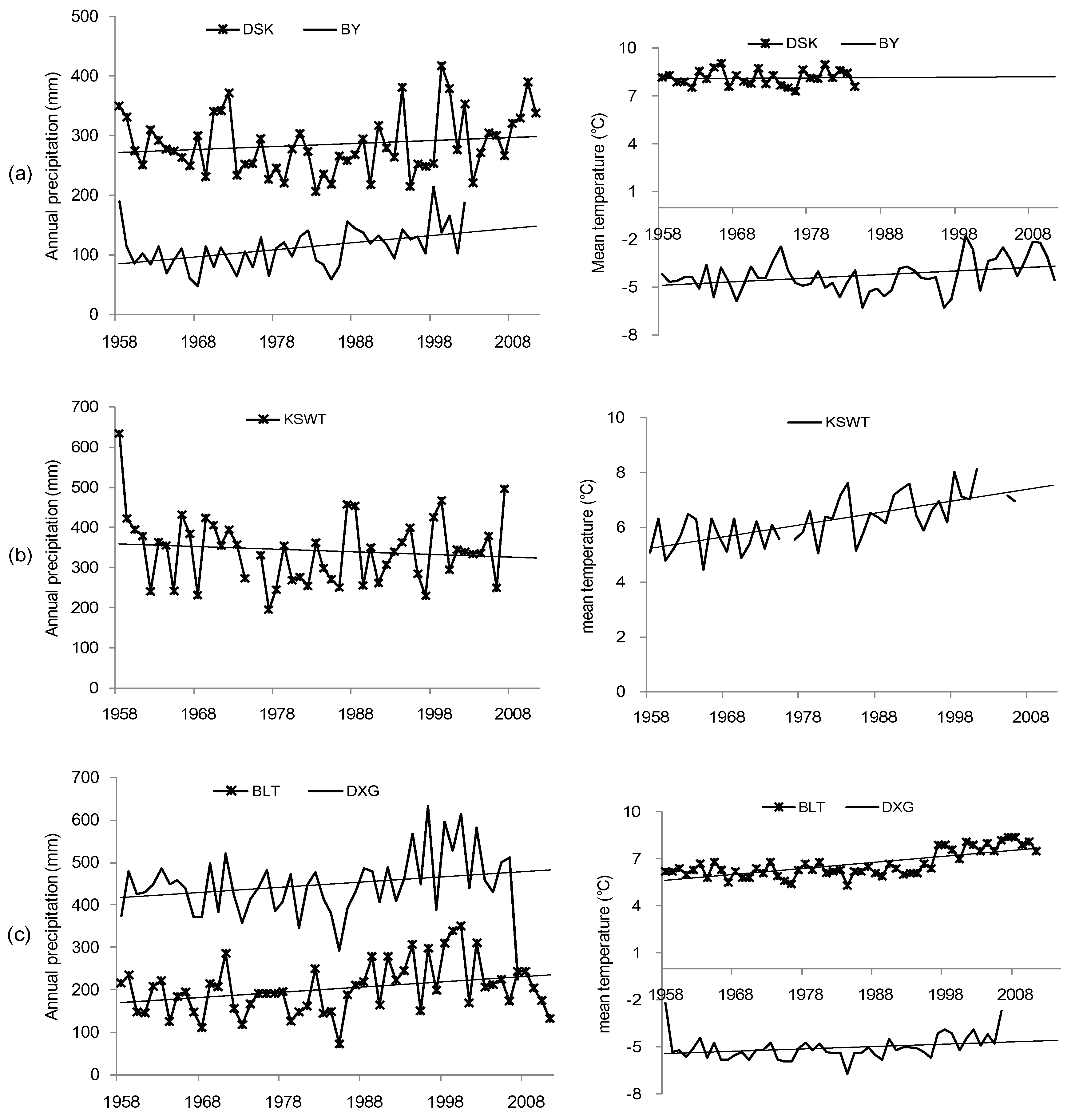
4.1. Trends and Alterations of the Extreme Flow Series
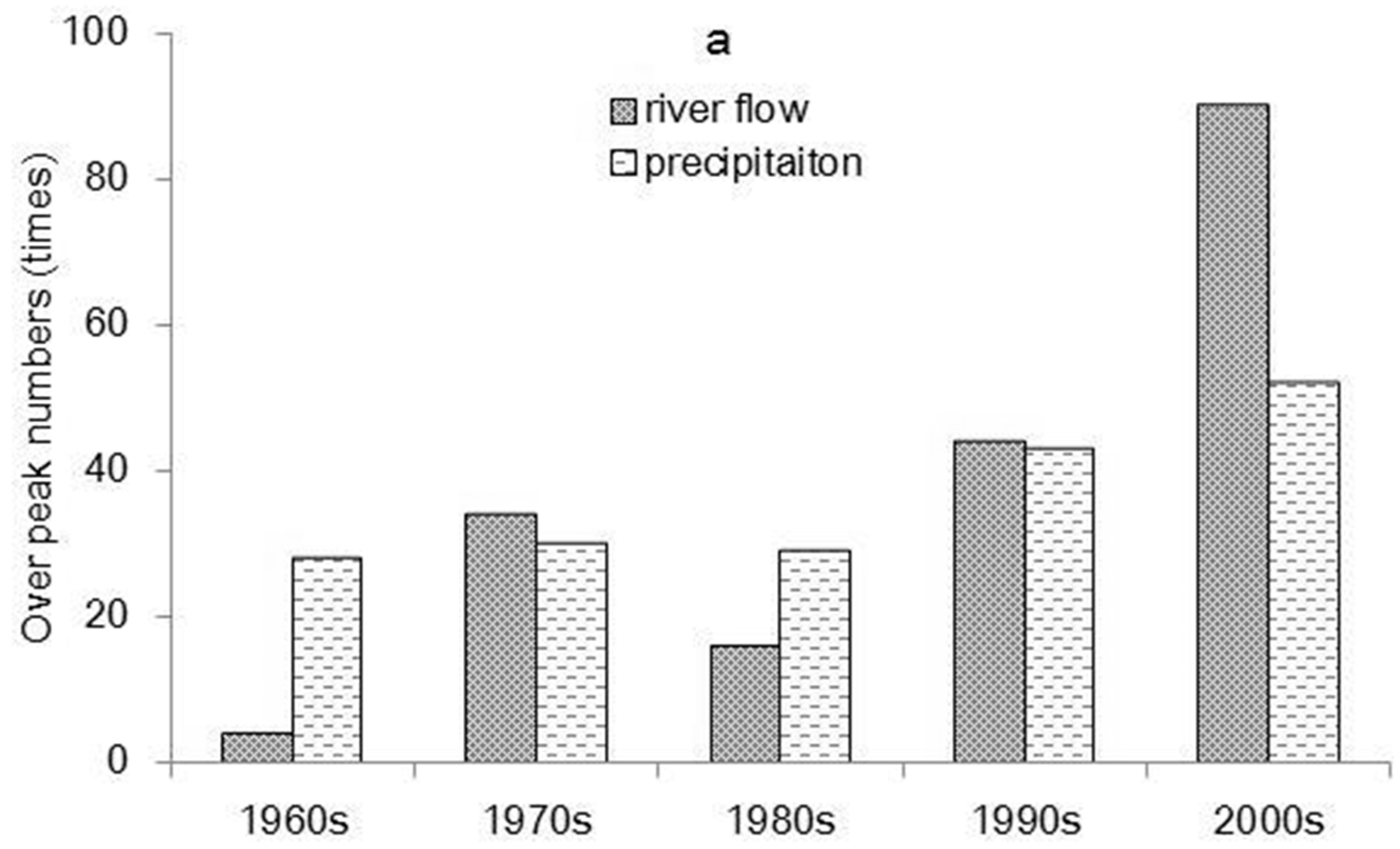
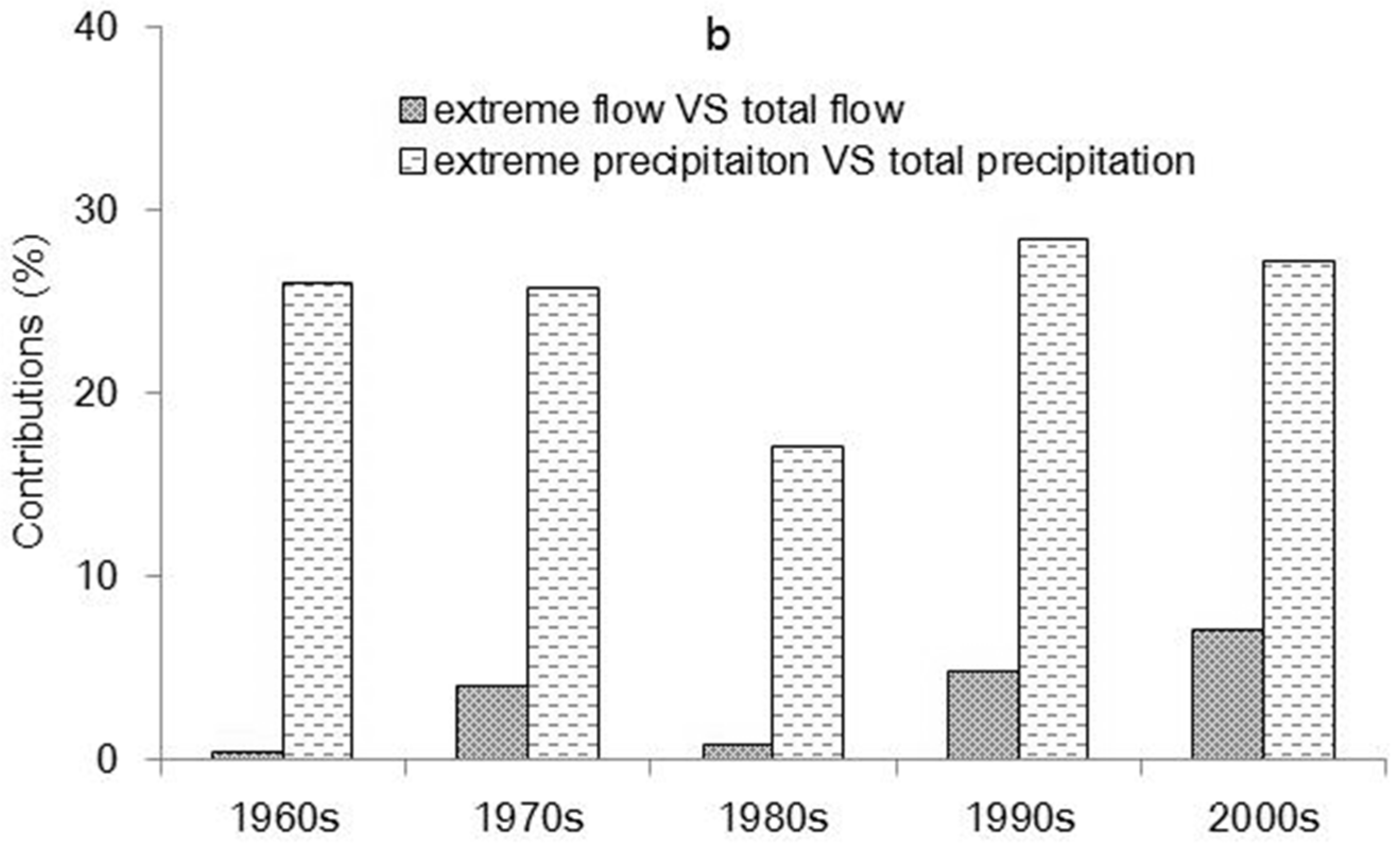
4.2. Extreme Event Analysis
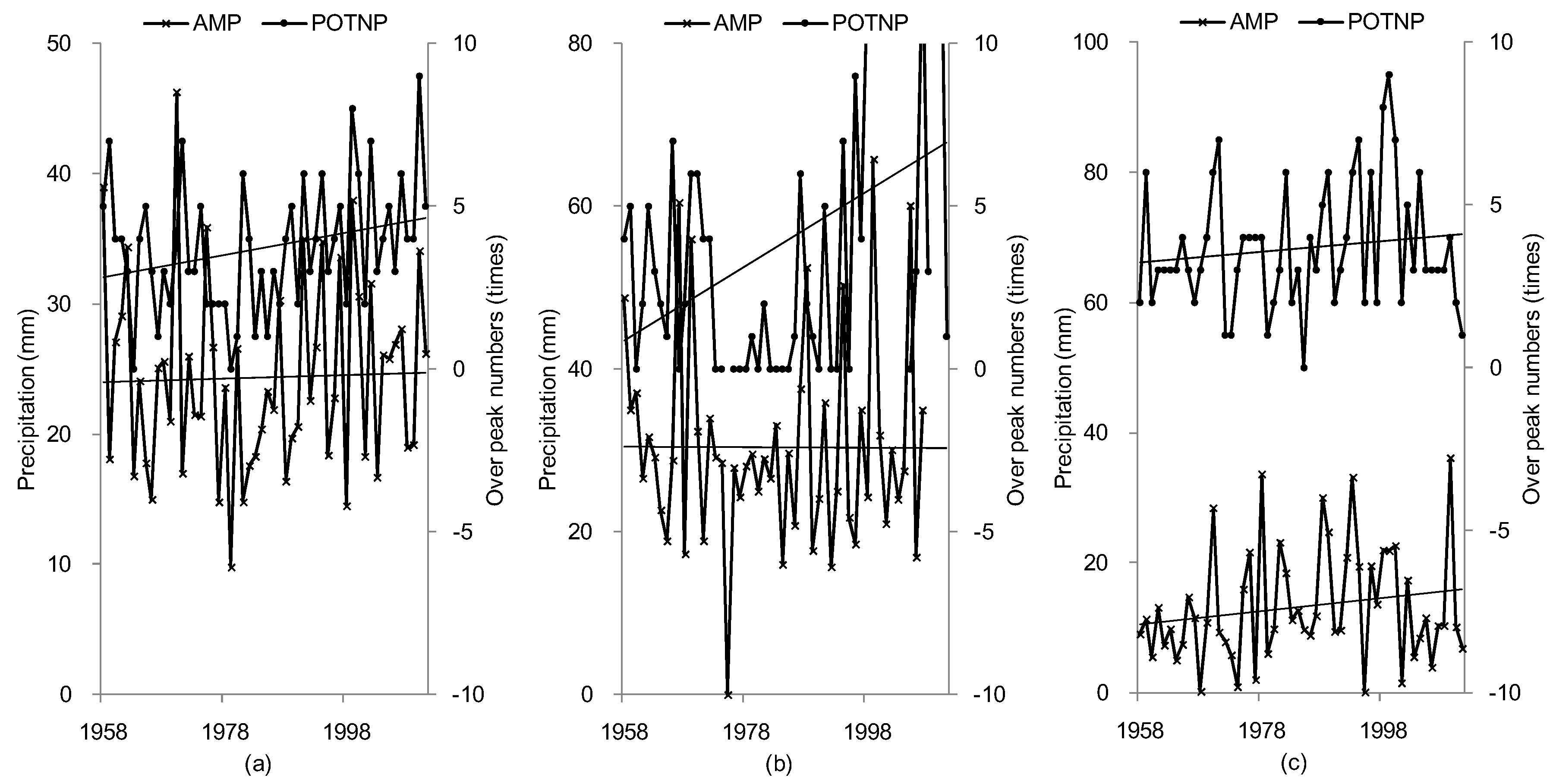
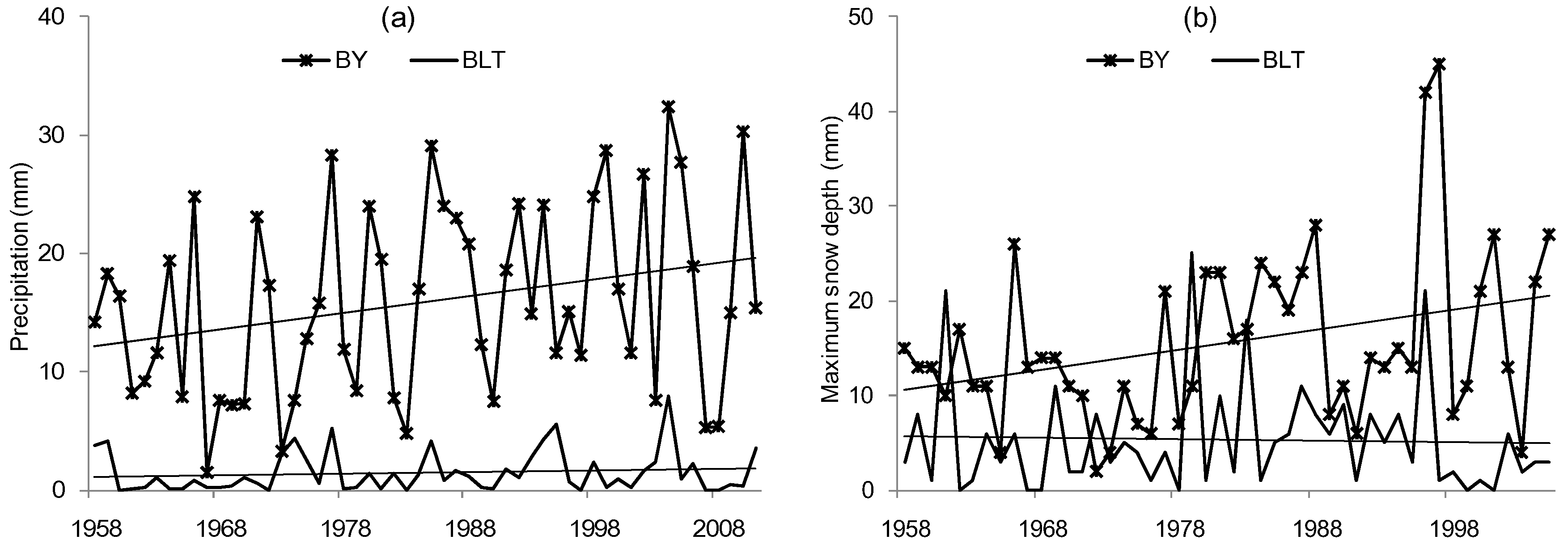
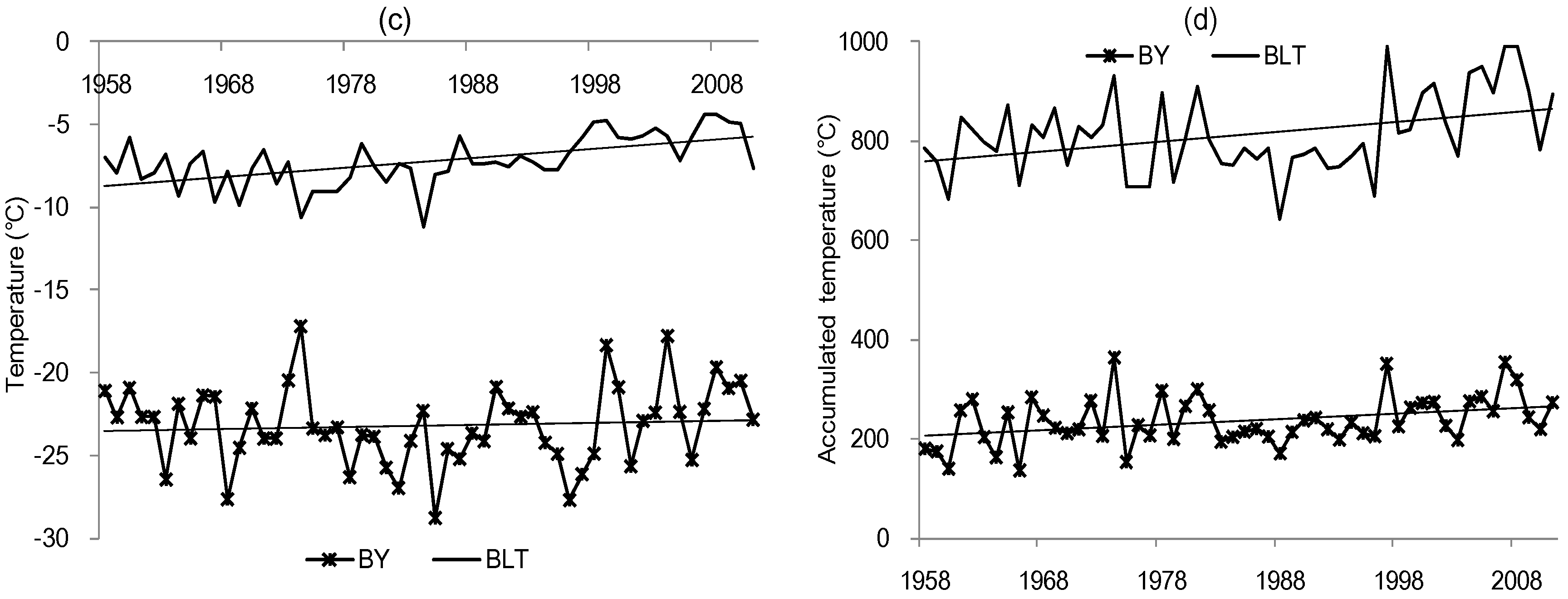
4.3. Discussion of the Linkages between Extreme Flow Change and Climate Factors
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Deng, H.J.; Chen, Y.N.; Wang, H.J.; Zhang, S.H. Climate change with elevation and its potential impact on water resources in Tianshan Mountains, Central Asia. Glob. Planet. Chang. 2015. [Google Scholar] [CrossRef]
- Ogriramoi, P.N.; Willems, P.; Katashaya, G.N. Trend and variability in observed hydrometerological extremes in the Lake Vivtoria basin. J. Hydrol. 2013, 489, 56–73. [Google Scholar] [CrossRef]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Ahmad, B. Snow cover dynamics and hydrological regime of the Hunza River basin, Karakoram Range, Northern Pakistan. Hydrol. Earth Syst. Sci. 2011, 15, 2275–2290. [Google Scholar] [CrossRef]
- Ma, Y.G.; Huang, Y.; Chen, X.; Bao, A.M. Modelling Snowmelt Runoff under Climate Change Scenarios in an Ungauged Mountainous Watershed, Northwest China. Math. Prob. Eng. 2013. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, H.; Li, B.; Li, Z.; Xu, C. Abrupt change of temperature and precipitation extremes in the arid region of northwest China. Quat. Int. 2013, 336, 35–43. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.H.; Vijay, P.S.; Sun, P.; Chen, X.H.; Kong, D.D. Magnitude, frequency and timing of floods in the Tarim River basin, China: Changes, causes and implications. Glob. Planet. Chang. 2016, 139, 44–55. [Google Scholar] [CrossRef]
- Liu, T.; Willems, P.; Pan, X.L.; Bao, A.M.; Chen, X.; Feng, X.W. Climate change impact on water resources extremes in a headwater region of the Tarim basin in China. Hydrol. Earth Syst. Sci. 2011, 15, 3511–3527. [Google Scholar] [CrossRef]
- Luo, Y.; Arnold, J.; Liu, S.; Sun, L. Inclusion of glacier processes for distributed hydrological modeling at basin scale with application to a watershed in Tianshan Mountains, Northwest China. J. Hydrol. 2013, 477, 72–85. [Google Scholar] [CrossRef]
- Wang, S.J.; Zhang, M.J.; Li, Z.Q.; Wang, F.T.; Li, H.L.; Li, Y.J.; Huang, X.Y. Glacier area variation and climate change in the Chinese Tianshan Mountains since 1960. J. Geogr. Sci. 2011, 21, 263–273. [Google Scholar] [CrossRef]
- Zhao, H. Holocene climate changes in westerly-dominated areas of central Asia: Evidence from optical dating of two loess sections in Tianshan Mountain, China. Quat. Geochronol. 2015. [Google Scholar] [CrossRef]
- Sun, C.J.; Yang, J.; Chen, Y.N.; Li, X.G.; Yang, Y.H.; Zhang, Y.Q. Comparative study of streamflow components in two inland rivers in the Tianshan Mountains, Northwest China. Environ. Earth Sci. 2016, 75, 727–738. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, S.Y. Response of glacier mass balance to climate change in the Tianshan Mountains during the second half of the twentieth century. Clim. Dyn. 2015. [Google Scholar] [CrossRef]
- Ding, Y.G.; Jiang, Z.H. Extreme Climate Research Methods; China Meteorological Press: Beijing, China, 2009; Volume 8, pp. 79–80. (In Chinese) [Google Scholar]
- Chen, Y.N.; Takeuchi, K.; Xu, C.C.; Chen, Y.P.; Xu, Z.X. Regional climate change and its effects on river runoff in the Tarim Basin, China. Hydrol. Process. 2006, 20, 2207–2216. [Google Scholar] [CrossRef]
- Chen, Y.N.; Xu, C.C.; Hao, X.M.; Li, W.H.; Chen, Y.P.; Zhu, C.G.; Ye, Z.X. Fifty-year climate change and its effect on annual runoff in the Tarim River Basin, China. Quat. Int. 2009, 208, 53–61. [Google Scholar]
- Xu, H.L.; Zhou, B.; Song, Y.D. Impacts of climate change on headstream runoff in the Tarim River Basin. Hydrol. Res. 2011, 42, 20–29. [Google Scholar] [CrossRef]
- Ling, H.B.; Xu, H.L.; Fu, J.Y. Changes in intra-annual runoff and its response to climate change and human activities in the headstream areas of the Tarim River Basin, China. Quat. Int. 2014, 336, 158–170. [Google Scholar] [CrossRef]
- Kong, Y.L.; Pang, Z.H. Evaluating the sensitivity of glacier rivers to climate change based on hydrograph separation of discharge. J. Hydrol. 2012, 434–435, 121–129. [Google Scholar] [CrossRef]
- Mao, W.F.; Fan, J.; Shen, Y.P. Variations of extreme flood of the rivers in Xinjiang region and some typical watersheds from Tianshan Mountians and their response to climate change in recent 50 years. J. Glaciol. Geocryol. 2012, 34, 1037–1046. (In Chinese) [Google Scholar]
- Zhang, Q.; Xu, C.Y.; Tao, H.; Jiang, T.; Chen, Y.Q. Climate changes and their impacts onwater resources in the arid regions: A case study of the Tarim River basin, China. Stoch. Environ. Res. Risk Assess. 2011, 24, 349–358. [Google Scholar] [CrossRef]
- Huang, W.R.; Xu, S.D.; Nnaji, S. Evaluation of GEV model for frequency analysis of annual maximum water levels in the coast of United States. Ocean Eng. 2008, 35, 1132–1147. [Google Scholar] [CrossRef]
- Nandintsetseg, B.; Greene, J.S.; Goulden, C.E. Trends in extreme daily precipitation and temperature near lake Hövsgöl, Mongolia. Int. J. Climatol. 2007, 27, 341–347. [Google Scholar] [CrossRef]
- Willems, P. A time series tool to support the multi-criteria performance evaluation of rainfall-runoff models. Environ. Model. Softw. 2009, 24, 311–321. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank-Correlation Measures; Charles Griffin: London, UK, 1975; p. 202. [Google Scholar]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the mann-kendall test. Water Resour. Res. 2002, 38, 1–7. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Zhang, Q.; Gu, X.; Singh, V.P.; Chen, X.H. Flood frequency analysis with consideration of hydrological alterations: Changing properties, causes and implications. J. Hydrol. 2014, 519, 803–813. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001; pp. 36–78. [Google Scholar]
- Xia, J.; Liu, C.Z.; Ren, G.Y. Opportunity and challenge of the climate change impact on the water resource of China. Adv. Earth Sci. 2011, 26, 1–12. [Google Scholar]
- Fisher, R.A. Theory of statistical estimation. Proc. Camb. Philos. Soc. 1925, 22, 700–715. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical Contributions to the Theory of Evolution; Dulau and Co.: London, UK, 1904. [Google Scholar]
- Meng, F.H.; Liu, T.; Huang, Y.; Luo, M.; Bao, A.M.; Hou, D.W. Quantitative Detection and Attribution of Runoff Variations in the Aksu River Basin. Water 2016, 8, 338. [Google Scholar] [CrossRef]
- Dowdy, S.; Wearden, S.; Chilko, D. Statistics for Research; John Wiley & Sons Inc.: New York, NY, USA, 1983. [Google Scholar]
- Ling, H.B.; Xu, H.L.; Fu, J.Y. High- and low-flow variations in annual runoff and their response to climate change in the headstreams of the Tarim River, Xinjiang, China. Hydrol. Process. 2013, 27, 975–988. [Google Scholar] [CrossRef]
- Fan, Y.T.; Chen, Y.N.; Li, W.H. Impacts of temperature and precipitation on runoff in the Tarim River during the past 50 years. J. Arid Land 2011, 3, 220–230. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Liu, T.; Ma, Y.G. Flood frequncy analysis for Kaidu watershed in Tianshan Mountauns. Clim. Chang. Res. 2016, 12, 37–44. (In Chinese) [Google Scholar]
- Qian, W.; Lin, X. Regional trends in recent precipitation indices in China. Meteorol. Atmos. Phys. 2005, 90, 193–207. [Google Scholar] [CrossRef]
- Wang, H.J.; Chen, Y.N.; Chen, Z.S. Spatial distribution and temporal trends of mean precipitation and extremes in the arid region, northwest of China, during 1960–2010. Hydrol. Process. 2013, 27, 1807–1818. [Google Scholar] [CrossRef]
- Ling, H.B.; Xu, H.L.; Shi, W.; Zhang, Q.Q. Regional climate change and its effects on the runoff of Manas River, Xinjiang, China. Environ. Earth Sci. 2011, 64, 2203–2213. [Google Scholar] [CrossRef]
- Sidike, A.; Chen, X.; Liu, T.; Durdiev, K.; Huang, Y. Investigating Alternative Climate Data Sources for Hydrological Simulations in the Upstream of the Amu Darya River. Water 2016, 8, 441. [Google Scholar] [CrossRef]
- Tao, H.; Gemmer, M.L.; Bai, Y.G.; Su, B.D.; Mao, W.Y. Trends of streamflow in the Tarim River Basin during the past 50 years: Human impact or climate change? J. Hydrol. 2011, 400, 1–9. [Google Scholar] [CrossRef]
- Valentin, H.; Johann, C.H.; Wolfgan, R. Flood Risk Management in Remote and Impoverished Areas—A Case Study of Onaville, Haiti. Water 2015, 7, 3832–3860. [Google Scholar]
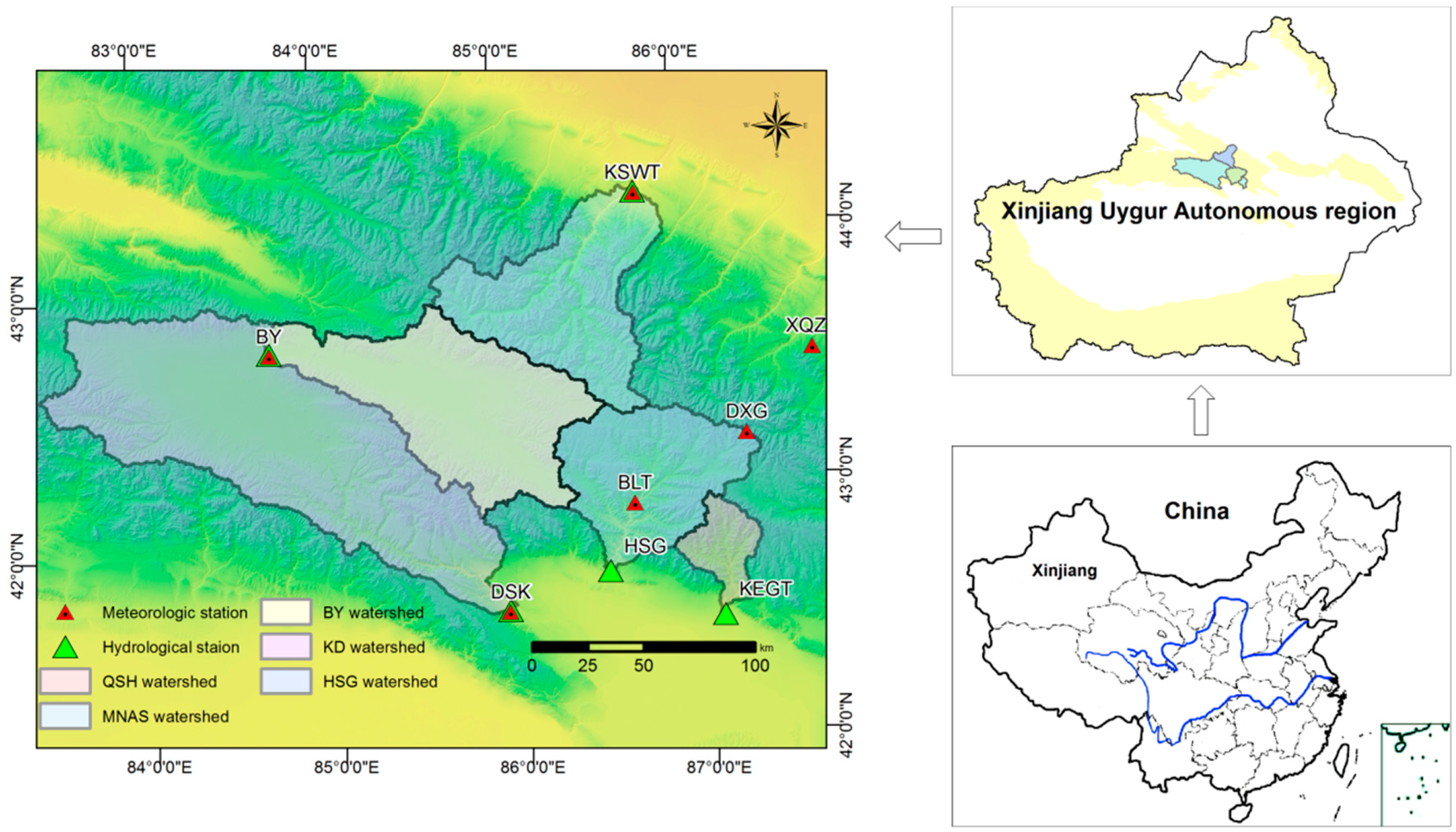
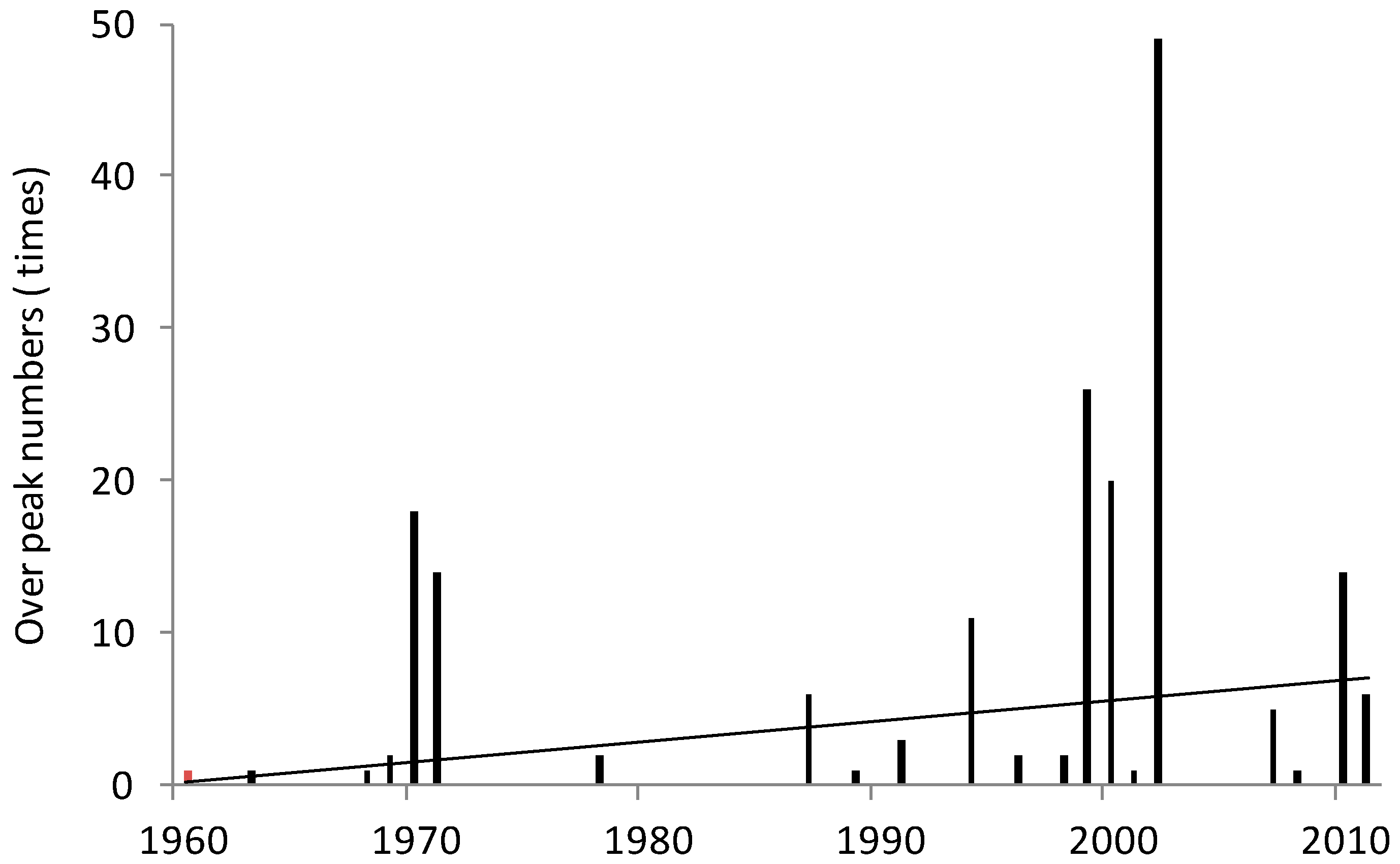

| Stations | Drainage Area (km2) | Time Interval | Longitude | Latitude | |
|---|---|---|---|---|---|
| Manasi River | KSWT | 5167.44 | 1958–2011 | E84.93 | N43.07 |
| Kaidu River | BY | 6645.60 | 1978–2011 | E84.08 | N42.55 |
| DSK | 18653.79 | 1958–2011 | E82.95 | N42.19 | |
| Huangshui River | HSG | 4299.53 | 1958–1989 | E85.79 | N42.44 |
| Qingshui River | KRGT | 1047.66 | 1958–1989 | E86.55 | N42.36 |
| Rivers/Stations | AM | AMT | POT | POTN | |||||||||
| p Value | Change Point | Sig. | p Value | Change Point | Sig. | p Value | Change Point | Sig. Level | p Value | Change Point | Sig. | ||
| Manasi River | KSWT | 0.100 | R | 0.898 | R | 0.047 | 1986 | * | 0.149 | R | |||
| Kaidu River | BY | 0.455 | R | 0.971 | R | 0.488 | R | 0.187 | R | ||||
| DSK | 0.113 | R | 0.470 | R | 0.499 | R | 0.155 | R | |||||
| Huangshui River | HSG | 1.000 | R | 0.282 | R | 0.318 | R | 1.000 | R | ||||
| Qingshui River | KRGT | 0.298 | R | 0.948 | R | 0.059 | R | 0.622 | R | ||||
| AM-SPR | AM-SPRT | AM-SUM | AM-SUMT | ||||||||||
| p Value | Change Point | Sig. | p Value | Change Point | Sig. | p Value | Change Point | Sig. | p Value | Change Point | Sig. | ||
| Manasi River | KSWT | 0.959 | R | 0.004 | 1978 | ** | 0.100 | R | 0.897 | R | |||
| Kaidu River | BY | 0.620 | R | 0.595 | R | 0.282 | R | 0.541 | R | ||||
| DSK | 0.338 | R | 0.441 | R | 0.123 | R | 0.075 | R | |||||
| Huangshui River | HSG | 0.461 | R | 0.511 | R | 0.130 | R | 0.282 | R | ||||
| Qingshui River | KRGT | 0.865 | R | 0.949 | R | 0.228 | R | 0.969 | R | ||||
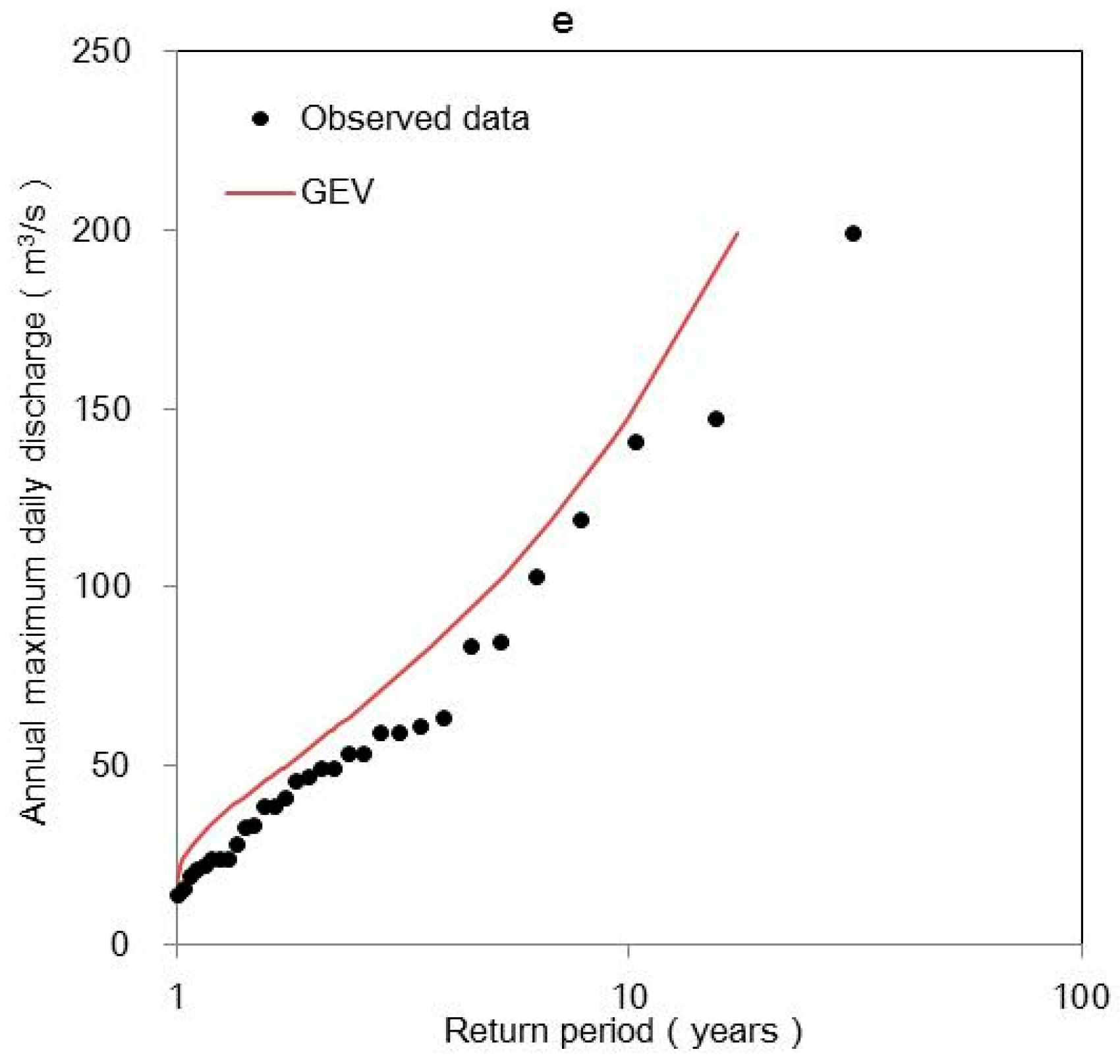
| Rivers | Stations | Time Series | Parameters | Best Fit PDF | K-S Test | Correlation | ||
|---|---|---|---|---|---|---|---|---|
| Manasi River | KSWT | AM | 231 | 66.43 | 0.29 | Frѐchet | 0.109 | 0.994 |
| POT | 226 | 52.39 | 0.23 | Pareto | 0.207 | 0.997 | ||
| Kaidu River | BY | AM | 73.9 | 46.95 | 0 | Gumbel | 0.258 | 0.885 |
| POT | 110 | 32.75 | 0 | Exponential | 0.336 | 0.989 | ||
| DSK | AM | 353 | 92.49 | 0.26 | Frѐchet | 0.148 | 0.991 | |
| POT | 404 | 61.54 | 0.15 | Pareto | 0.223 | 0.998 | ||
| Huangshui River | HSG | AM | 70.1 | 62.74 | 0 | Gumbel | 0.197 | 0.993 |
| POT | 86.3 | 25.80 | 0.30 | Pareto | 0.104 | 0.988 | ||
| Qingshui River | KRGT | AM | 46.2 | 23.88 | 0.52 | Gumbel | 0.196 | 0.986 |
| POT | 28.1 | 14.44 | 0.51 | Pareto | 0.211 | 0.990 | ||
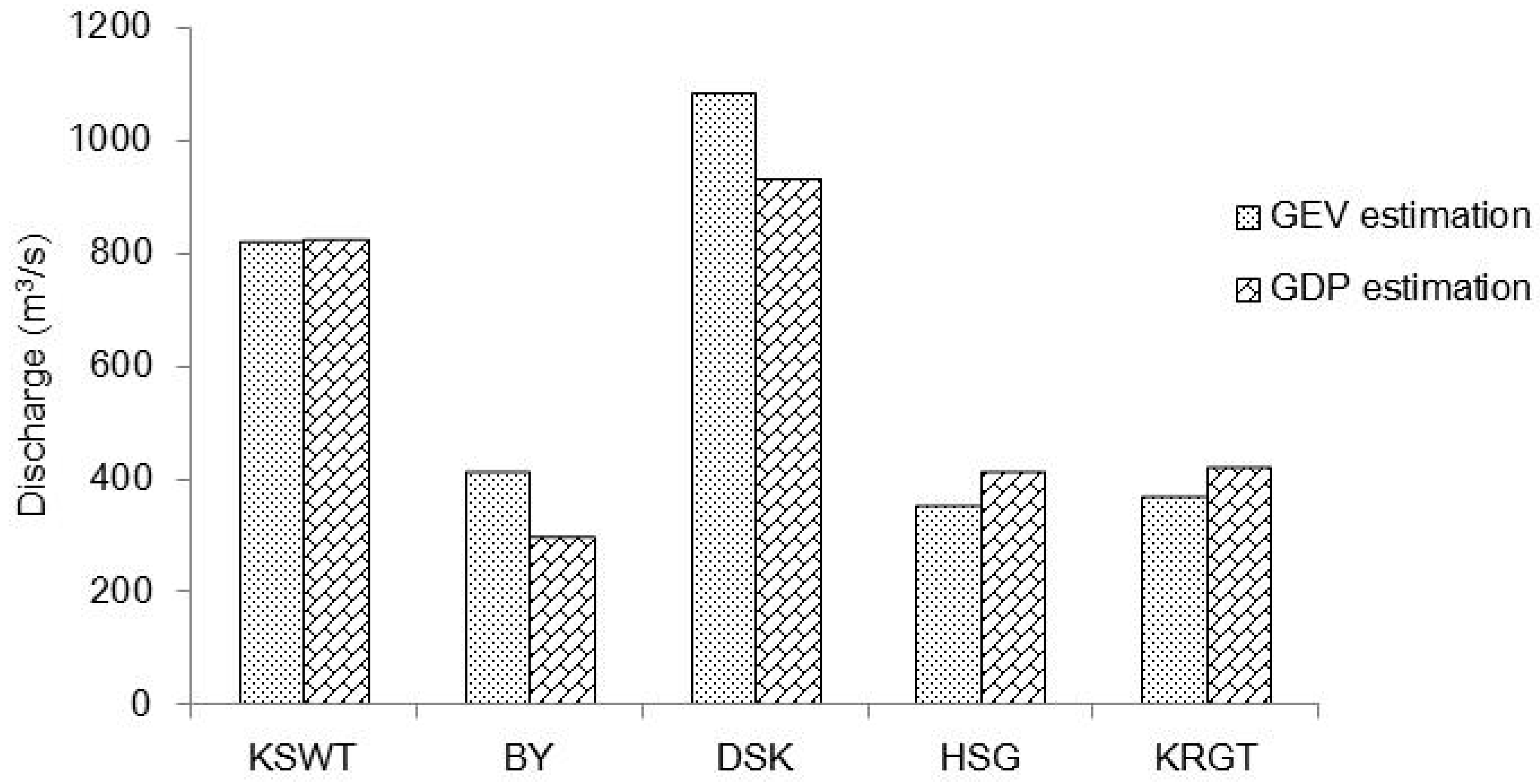
| Stations | Number of Years | Observed | GEV Prediction | Error (%) | |
|---|---|---|---|---|---|
| 5 year | KSWT | - | 330 | 360 | 9.1 |
| BY | - | 137 | 136 | −0.7 | |
| DSK | - | 478 | 488 | 2.1 | |
| HSG | - | 170 | 169 | −0.5 | |
| QSH | - | 85 | 90 | 5.9 | |
| 10 year | KSWT | - | 355 | 428 | 20.6 |
| BY | - | 194 | 186 | −4.1 | |
| DSK | - | 621 | 623 | 0.3 | |
| HSG | - | 230 | 212 | −7.8 | |
| QSH | - | 141 | 150 | 6.4 | |
| 20 year | KSWT | - | 430 | 511 | 18.8 |
| BY | - | 243 | 270 | 11.1 | |
| DSK | - | 652 | 735 | 12.7 | |
| HSG | - | 238 | 241 | 1.3 | |
| QSH | - | 162 | 206 | 27.2 | |
| longest record | KSWT | 54 | 789 | 721 | −8.6 |
| BY | 33 | 253 | 286 | 13.0 | |
| DSK | 54 | 793 | 940 | 18.5 | |
| HSG | 31 | 244 | 280 | 14.8 | |
| QSH | 31 | 199 | 235 | 18.1 |
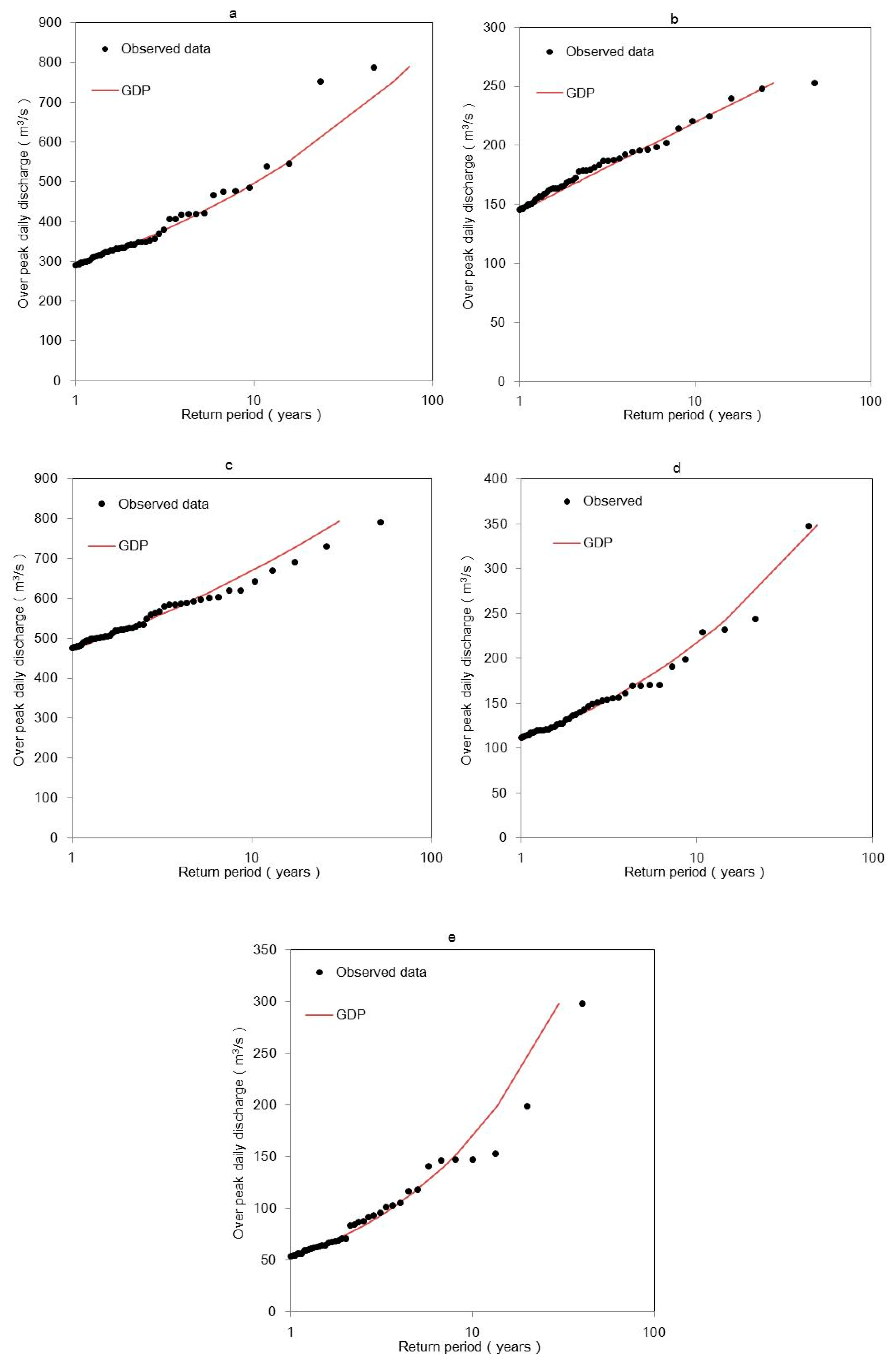
| Stations | Number of Events | Observed | GDP Prediction | Error (%) | |
|---|---|---|---|---|---|
| 5 year | KSWT | - | 421 | 423 | 0.5 |
| BY | - | 197 | 196 | −0.5 | |
| DSK | - | 597 | 600 | 0.5 | |
| HSG | - | 171 | 172 | 0.6 | |
| QSH | - | 139 | 138 | −0.7 | |
| 10 year | KSWT | - | 495 | 496 | 0.2 |
| BY | - | 222 | 221 | −0.4 | |
| DSK | - | 644 | 662 | 2.8 | |
| HSG | - | 230 | 220 | −4.3 | |
| QSH | - | 148 | 161 | 8.8 | |
| 20 year | KSWT | - | 750 | 600 | −14.0 |
| BY | - | 244 | 240 | −1.6 | |
| DSK | - | 702 | 796 | 13.4 | |
| HSG | - | 239 | 265 | 10.9 | |
| QSH | - | 165 | 198 | 20.0 | |
| longest records | KSWT | 172 | 789 | 720 | −8.7 |
| BY | 129 | 253 | 273 | 7.9 | |
| DSK | 176 | 793 | 830 | 4.7 | |
| HSG | 92 | 354 | 338 | −4.5 | |
| QSH | 96 | 199 | 246 | 23.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Huang, Y.; Liu, T. Change and Climatic Linkage for Extreme Flows in Typical Catchments of Middle Tianshan Mountain, Northwest China. Water 2018, 10, 1061. https://doi.org/10.3390/w10081061
Ma Y, Huang Y, Liu T. Change and Climatic Linkage for Extreme Flows in Typical Catchments of Middle Tianshan Mountain, Northwest China. Water. 2018; 10(8):1061. https://doi.org/10.3390/w10081061
Chicago/Turabian StyleMa, Yonggang, Yue Huang, and Tie Liu. 2018. "Change and Climatic Linkage for Extreme Flows in Typical Catchments of Middle Tianshan Mountain, Northwest China" Water 10, no. 8: 1061. https://doi.org/10.3390/w10081061
APA StyleMa, Y., Huang, Y., & Liu, T. (2018). Change and Climatic Linkage for Extreme Flows in Typical Catchments of Middle Tianshan Mountain, Northwest China. Water, 10(8), 1061. https://doi.org/10.3390/w10081061





