1. Introduction
Coastal communities around the world, such as those in the Mississippi River Delta, are vulnerable to natural resource losses and unsustainability due to multiple hazards that interact with climate change [
1]. These communities are vital in providing valuable resources and ecosystem services to the region and the world. Reducing their vulnerability to hazards and impacts from climate change and building a sustainable future for the coastal communities is thus a critical task facing researchers, policy makers, resource managers, and stakeholders.
While many coastal hazards are the product of or are associated with natural processes, their impacts are often exacerbated or compounded by human activities. The literature has recognized the need to consider the coupling effects between the natural and the human components to evaluate the resilience and sustainability of coastal communities [
2,
3,
4,
5,
6] and advantages of using the coupled natural-human (CNH) system approach to studying system complexity and global sustainability have been elaborated [
7]. However, few studies have actually produced numeric models that integrate and quantify the linkages and feedbacks to study the sustainability of coastal deltaic communities under the threat of climate change [
8]. There are many challenges involved in CNH system dynamic research. Kramer et al. (2017) identified top 40 questions in CNH research [
9]. Issues such as how to integrate the two domains—natural and human—when they differ in many aspects, how to determine if the system is resilient or sustainable, and how to link resilience assessment with CNH modeling are some of the major research gaps that need to be addressed by the academic community in the near future.
The objective of this paper is to demonstrate an interdisciplinary approach in studying the Mississippi River Delta (MRD) in southeastern coastal Louisiana, USA as a coupled natural-human system. Like many deltas in the world such as the Nile and Mekong deltas, the MRD has been losing land in the past several decades [
10,
11,
12,
13,
14]. Interaction and co-evolving of natural and human factors over the years have led to a system that suffers persistent land subsidence, coastal erosion, and population decline, especially in the southernmost coastal part of the Delta. With the impending threat of sea-level rise, a pressing question to the region and the nation is: will southern MRD be sustainable? Because of its economic, social, and cultural significance, the MRD has been studied extensively by a number of researchers, agencies, and stakeholders [
15,
16,
17]. However, a system-level study that incorporates both natural and human systems has not been conducted. This paper is an attempt to fill in the gap.
The terms resilience, vulnerability, and sustainability are intricately linked; they are defined differently by researchers in different fields. For ease of discussion, this paper considers vulnerability as part of the broader concept of resilience. Community resilience is the ability of a community to prepare, plan for, absorb, adapt, and recover from adverse events [
18,
19,
20]. Sustainability refers to the capacity of society to meet its current needs while ensuring the well-being of future generations [
21]. Sustainability considers the tradeoffs between environmental (i.e., ecological) services and human outcomes [
22], and long-term resilience is sustainability [
20].
The paper has three parts. We will first describe the major elements and linkages included in our CNH modeling framework. Methods for analyzing the coupled models are outlined. We then describe our major findings from using the framework. The third part of the paper is devoted to lessons learned and suggestions for future directions. Findings from this empirical, complex, system-level study should increase our understanding of coastal resilience. Also, further insights can be gained from the findings that should help inform policies designed to increase resilience and sustainability of the region.
2. Background
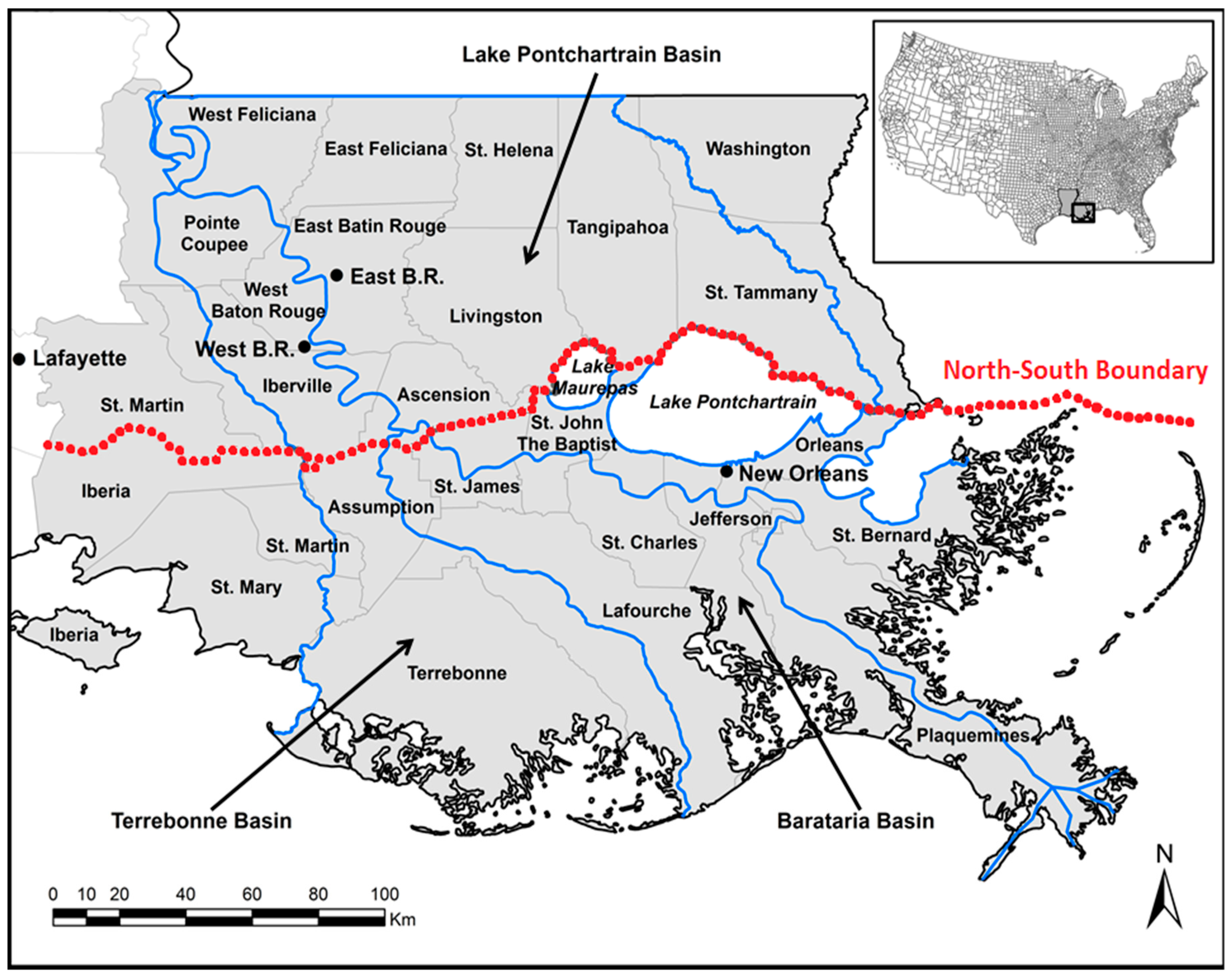
The Mississippi River Delta as a case study is both unique, in terms of its geological history and cultural richness, and common, due to its low-lying environmental setting and exposure to potential threats from hydrological hazards and climate change (
Figure 1). The MRD is a region of plentiful natural resources and economic activities, supporting densely populated cities such as New Orleans (pop 389,617; 2015) and Baton Rouge (pop 228,590; 2015). Like most coastal deltas in other parts of the world (e.g., Nile and Mekong), the region has endured multiple natural and human landscape-level disturbances such as flooding, land loss, subsidence, sea-level rise, hurricanes, and oil spills [
12,
13,
14,
23,
24,
25,
26,
27]. While hurricanes such as Katrina and Rita have been a major cause of coastal erosion and shoreline retreat [
28,
29], hurricane-induced overbank flooding of the Mississippi River and its distributaries could bring much-needed sediments to the fluvial and deltaic wetlands and significantly increase the accretion rates in the region [
30]. Since the early 1900s, humans in this coastal region have significantly modified the landscape by building dams and levees to prevent flooding of populated areas, leading to a significant reduction of river sediment input to replenish the coastal wetlands [
10]. In addition, thousands of miles of canals cut across coastal Louisiana to construct oil and gas pipelines and navigate barges have disrupted natural processes [
31]. As a result, large stretches of land have been lost as this highly engineered deltaic system interacts with other geological, climatic, ecological, and anthropogenic factors. During 1985 to 2010 coastal Louisiana has lost about 42.9 km
2 (16.57 square miles) of wetlands per year [
32]. If this trend persists, it would be equivalent to about losing the size of one football field per hour. Further drowning of the Mississippi River Delta is plausible due to insufficient sediment supply and high rates of regional sea level rise (>9 mm/year) [
10]. Thus, a pressing question is: can the southern MRD be preserved? If so, what strategies are viable for making the region sustainable?
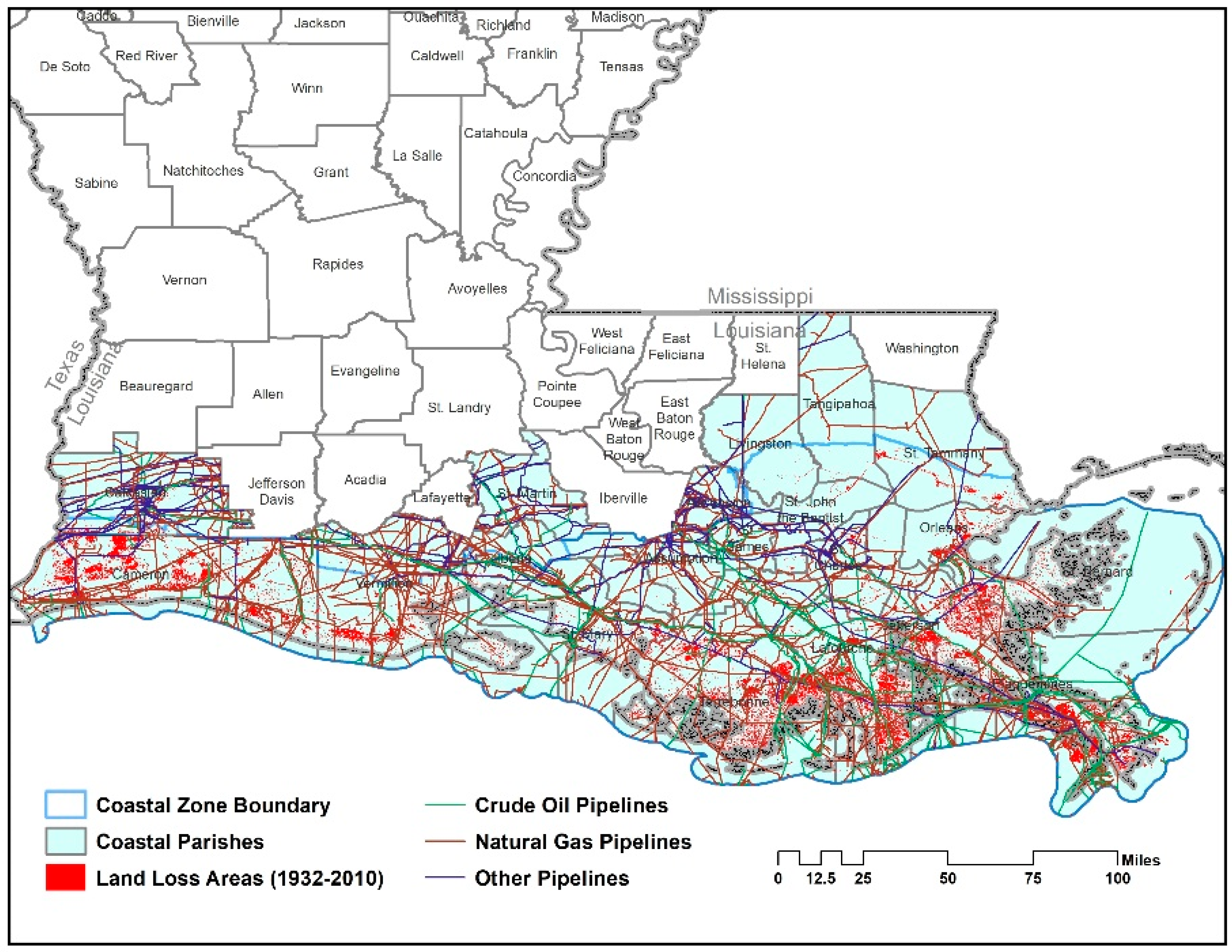
The MRD provides vital economic functions. In 2014, Louisiana was the USA’s No. 1 producer of crude oil, No. 2 in petroleum refining capacity, and No. 3 in natural gas production [
33,
34]. Over the past century, a wide range of critical energy infrastructure has been developed to serve and support the significant oil and gas production along the northwestern Gulf of Mexico. Much of this critical energy infrastructure, such as refineries, petrochemical plants, gas-processing facilities, pipelines, and other support facilities, lie directly in the coastal zone of Louisiana and are at risk to coastal land loss and sea-level rise (
Figure 2) [
34]. In addition, the workforce developing, constructing, operating, upgrading, and servicing this infrastructure on a regular basis live in the same coastal communities where most of this critical energy infrastructure is located. The 2004 and 2005 hurricane activities along the Gulf of Mexico underscored the magnitude of the impact and level of disruption that these natural disturbances have upon economic activities not only in coastal Louisiana, but also in the U.S. and world energy markets [
35].
Because of its economic, social, and cultural significance, the MRD has been widely studied by researchers, stakeholders, and agencies using different approaches to keep the land from disappearing [
15,
16,
17,
36]. However, these previous studies have focused mostly on the natural system, such as developing methods and guidelines for wetland restoration, sediment diversion, and shoreline protection, with little effort paid on examining and quantifying the coupling effect of the human component. A system-level study that incorporates both natural and human systems of the MRD has yet to be conducted. Incorporating the human component literally as part of the equation in the system modeling of coastal sustainability is necessary to better understand the complex dynamics and whether such dynamics will lead to long-term resilience of the region [
7].
Two recent developments in the region demonstrate the importance of incorporating the human factor in coastal protection and resilience. First, at the top-down level, policy makers at state agencies have been developing and updating the State Coastal Master Plan (CMP) every five years since 2007 to help guide coastal restoration efforts. The most recent CMP (2017) outlines a
$50 billion investment designed to build and maintain land, reduce flood risk to communities, and provide habitats to support ecosystems [
17]. A significant shift of emphasis in the 2017 CMP from previous plans is the increased focus on people and communities. In previous CMPs, most of the projects funded have been on “structural” improvements, whereas in the 2017 plan, some 32 non-structural risk reduction projects are planned, including for example residential house elevation where 100-year flood depths are 3 to 14 feet and residential voluntary acquisition where 100-year flood depths exceed 14 feet [
17]. This newly added focus on people and communities and the “non-structural” element is a welcomed and necessary change in coastal protection and restoration, because ultimately it is the citizenry who must be willing to buy in the policies set to protect the coast.
Another development is that during the past two decades there has been considerable population and economic growth in the northern part of the Mississippi River Delta (approximately north of Lake Pontchartrain, hereafter called the “North”), in contrast with significant population decline in the southern part of the MRD including areas surrounding New Orleans (called the “South’) (
Figure 1). During 2000–2010, the population of Louisiana increased by only 3.26%, much lower than the national population increase of 9.7% for the same period (
https://www.census.gov/prod/cen2010/briefs/c2010br-01.pdf). The top two parishes with the largest population increases are located in the North (Ascension Parish with 39.9% and Livingston Parish with 39.4%), whereas the two largest population-decline counties are located in the South (St. Bernard Parish with −46.6% and Orleans Parish with −29.1%).
While extensive “top-down” effort from the state government (the master plans) in coastal restoration has been made in the South, there is an underlying system of people in this part of region making individual decisions on whether to stay or migrate. This voluntary “bottom-up” dynamic phenomenon has not been considered and quantitatively modeled in the planning and management of the region. It is clear from the population decline trend that those restoration projects without taking into account human decisions would not be effective. People could keep moving away despite the coastal restoration effort. The decoupling between policy makers and residents in the decision-making process could result in a steady decline in population, leading to an unsustainable scenario. The outmigration of the entire Indian tribe in Isle de Jean Charles in the “South,” which has been labeled as America’s first climate refugees, epitomizes the seriousness of the land loss and population decline problem in the region [
37]. Relevant questions to address include: Are we restoring land that nobody will want to live in? What are the factors other than land restoration that will affect human decisions to stay or migrate? What are the processes regulating the coupled natural and human dynamics that affect coastal sustainability? Understanding these core questions is crucial to the development of effective strategies for coastal sustainability.
3. The Delta CNH Modeling Framework
Given that land loss is the most critical issue for the existence of the Mississippi River Delta, we formulate “land” (and its associated attributes including elevation, extent of land loss, and land use and land cover changes) as the target variable to integrate natural and human elements throughout the landscape (
Figure 3). Land use systems are considered complex adaptive systems driven by biophysical and socioeconomic processes, and an understanding of the land use dynamics requires detailed analysis of how these processes occur across a wide range of spatiotemporal and socio-political scales [
38,
39]. In the MRD, land loss is partly a result of a lack of natural sediment supply caused by human interventions, such as building dams and levees to divert river flow and suspended sediments directly to the sea [
10]. In turn, humans respond with more coastal protection and restoration measures by building more dams and levees. Industrial infrastructure such as canals and pipelines built to support the energy industry may also increase the land loss probability. The result of these complex feedbacks is a fragmented landscape undergoing accelerated land loss and a decline of population in the South [
40,
41,
42].
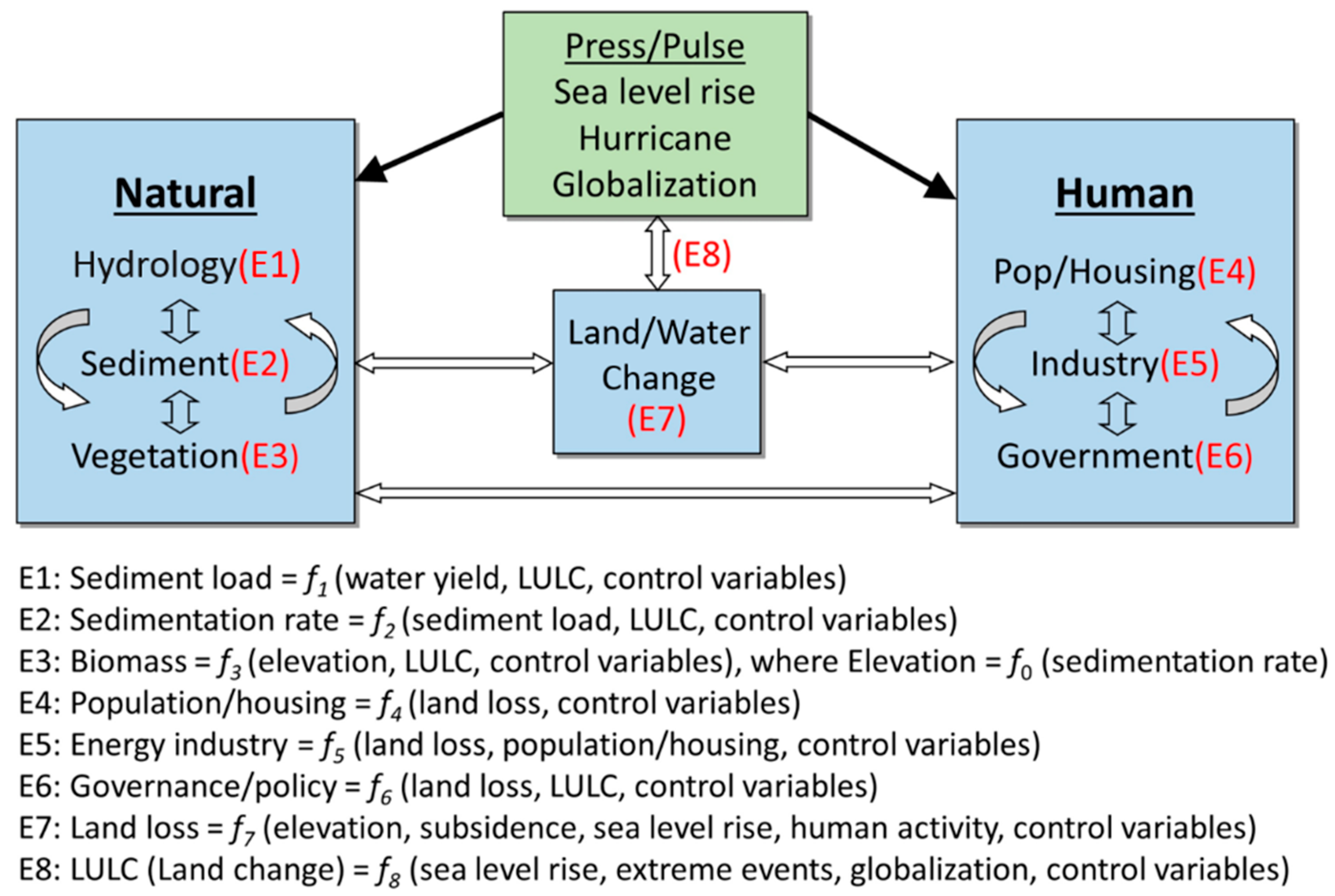
The Delta-CNH framework has six components, linked by a central response variable “land/water change” [
43,
44]. The six components include three from the natural subsystem (hydrology, sediment, and vegetation), and three from the human subsystem (population/housing, industry, and government). In addition, a module representing the presses and pulses to the system is included to signify the effects of external factors to the deltaic system such as sea-level rise, hurricanes, and economic globalization. As shown in
Figure 3, each component has its linkages and feedbacks to all other components, which can then be represented via a system of conceptual equations (Equations (1)–(8)). These equations could be nonlinear functions that quantitatively summarize the main inputs and outputs among subsystems and the main module. In fact, each equation can be regarded as a series of hypotheses describing the linkages between the natural and human subsystems in which common variables are used to ensure the feedbacks are captured and modeled.
The set of linkages among the various components can be briefly described as follows. For Component 1, the main research question is: are the river sediments sufficient, if managed properly, to counteract the sea level rise in the MRD? Thus, research in this component will involve estimating the divertible river flow and sediments from the Mississippi River and its tributaries with or without restrictions from human activities (i.e., dams and levees) and the effects of hurricanes. If the divertible amount of sediments is not used, then how much land could be lost in southeast Louisiana by 2050 due to continuing land subsidence and sea level rise?
Results from Component 1 are linked to Component 2—historical sedimentation rate analysis. The principal output of Component 2 is a set of sedimentation rates (cm/year) measured from various drainage basin sites for different time periods. The sub-hypotheses in this component are: (i) in the South, long-term sedimentation rate has declined during the past century due to the construction of dams and reservoirs along the Mississippi River and its tributaries, which reduces sediment supply to coastal wetlands. (ii) In the North (Lake Pontchartrain basin), long-term sedimentation rate has increased due to increasing human activities that resulted in the conversion of forest to agricultural and urban land uses (LULC changes), thus increasing sediment supply in the form of sediment load. (iii) Hurricanes are a major agent of increased sedimentation rates in the fluvial and deltaic wetlands, especially through the effects of heavy rainfall on overbank flooding of the Mississippi River and other local rivers. Equation 1 and Equation 2 describe the linkages between the first two components, as well as linkages to other components through the inclusion of other control variables from other components.
In turn, sedimentation rate will affect land elevation, which will in turn affect vegetation pattern and biomass (e.g., forest vs. marsh, vs. open water). For example, storm deposition caused by hurricanes can result in increased sedimentation rate and elevation in the region’s wetlands, which will affect vegetation and biomass [
45]. On the other hand, human activities, such as road construction, oil extraction, and timber harvesting, can affect the groundwater table and, consequently, vegetation and biomass, which would in turn affect soil property and sedimentation rate [
46].
Land loss is mainly due to the loss of elevation (e.g., sedimentation rate not catching up with the rate of subsidence, erosion, and sea level rise), which could be exacerbated by human activities such as canal dredging and pipeline construction, leading to fragmentation and saltwater intrusion.
Further, long-term coastal sustainability is a function of the rate of land loss. If the rate of land loss exceeds the rate of land accretion (decrease in elevation), then that land will not be sustainable as reflected by negative population growth or diminished human activity.
The Governance component (Component 6, representing adaptive governance and planning) examines the process of planning among Louisiana parishes in response to land loss and other threats. Several independent variables, provided by the other components, can be used in a multiple-regression analysis to assess the linkages among them, such as land loss, variables concerning population and housing values (Component 4), and variables concerning the presence of the energy industry within a parish (Component 5). Relationships between ruptures on existing pipelines in land loss areas and proximity of other major energy infrastructure facilities to these areas can be examined as potential cases in point.
At the same time, the specific land use ordinances and plans adopted by the Parish governments influence future sediment distribution, sedimentation rates, and land loss for certain protected areas. These ordinances or “rules” can be included in all other components to better predict future physical and ecosystem conditions within the study area.
Finally, once the overall models and linkages are tested and validated, future scenarios under different climate change scenarios and management practices can be simulated with Equation (8) to evaluate their effects on the coupled system and address the question of whether the MRD will be sustainable under different scenarios.
The study area can be subdivided into cells of a specific size, and a spatial dynamic model can be developed to test and simulate the linkages [
47]. Through iterations, these relationships will lead to a trajectory over time. If the trajectory indicates a persistent population decline/land loss trend, then this trajectory indicates an unsustainable state. By comparing the simulation results between the two MRD sub-regions of (the North and the South), we will be able to evaluate the core research question of whether southern coastal Louisiana will be sustainable by 2100 (continuing land loss and population decline). Once the spatial dynamic model is built and validated, simulation of future scenarios under different press and pulse assumptions could be conducted to help inform planning strategies.
4. Modeling Methods and Findings
The framework described above is an idealistic, theoretical construct of a complex deltaic system, synthesizing the various possible relationships and hypotheses. However, many of the relationships may not be amenable to quantitative analysis and testing due to the lack of data and the incompatible data types and scales (both spatial and temporal). There are a number of issues in implementing the Delta-CNH framework into practical models with real data, especially for a large and diverse study area like the MRD. Below, we highlight two key issues commonly faced with modeling complex CNH systems and describe three study methods we used to address these issues in the context of the MRD. The two issues, which are closely interrelated, include (i) how to evaluate and monitor the community or system resilience and (ii) what modeling approaches are most appropriate to model the CNH system dynamics of the deltaic region?
4.1. Resilience Assessment
A critical challenge in CNH research is how to determine if the system is sustainable in the long term. Linking resilience assessment with CNH modeling remains a major research gap. In resilience assessment, despite extensive efforts made in the development of resilience assessment frameworks [
18,
19,
20,
48,
49,
50], there is still no commonly adopted metric in the published literature to assess community or system resilience. Resilience assessment is complicated by three lingering issues [
20]. First of all, disagreements on the terms and definitions among researchers have made the quantification of processes and metrics to measure resilience difficult. Second, resilience indices or scores developed in the literature have seldom been validated with empirical outcome data. Most existing indices were developed by aggregating a number of variables with a subjective weighting scheme. Without an objective, empirical outcome validation (such as by using real recovery or disaster damage data), the resultant index values could be easily manipulated by changing the weights of the variables. Finally, many resilience indices are derived from non-inferential statistical methods (e.g., principal component analysis) for a study area [
50], which means the methods or indices derived cannot be generalized to predict resilience at different time points or in different study areas, making comparison and monitoring of resilience levels across regions and times difficult.
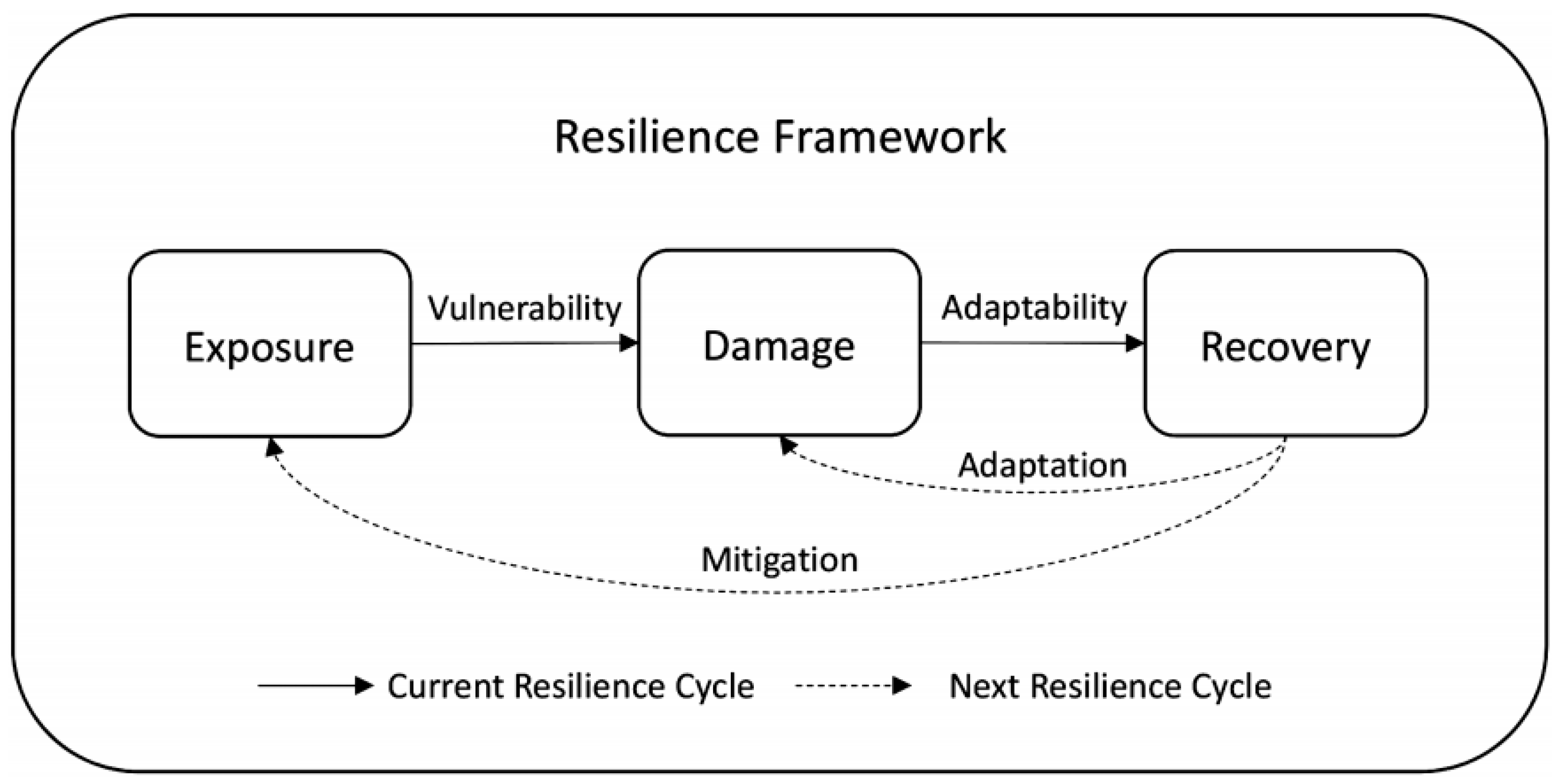
We used the Resilience Inference Measurement (RIM) model to assess the resilience of communities in the MRD [
41]. The RIM model was developed to overcome two main issues in resilience measurement: empirical validation and inferential ability. A detailed description of the RIM model can be found in a number of references [
20,
41,
51,
52,
53]. In brief, the RIM model includes three dimensions and two relationships (
Figure 4). The three dimensions are hazard intensity, damage intensity, and recovery, and the two relationships are vulnerability and adaptability. Vulnerability refers to the latent relationship between hazard intensity and damage, whereas adaptability is the latent relationship between damage and recovery. Resilience is measured according to the two relationships. A high vulnerability/adaptability ratio is considered low resilience, whereas a low vulnerability/adaptability ratio is considered high resilience.
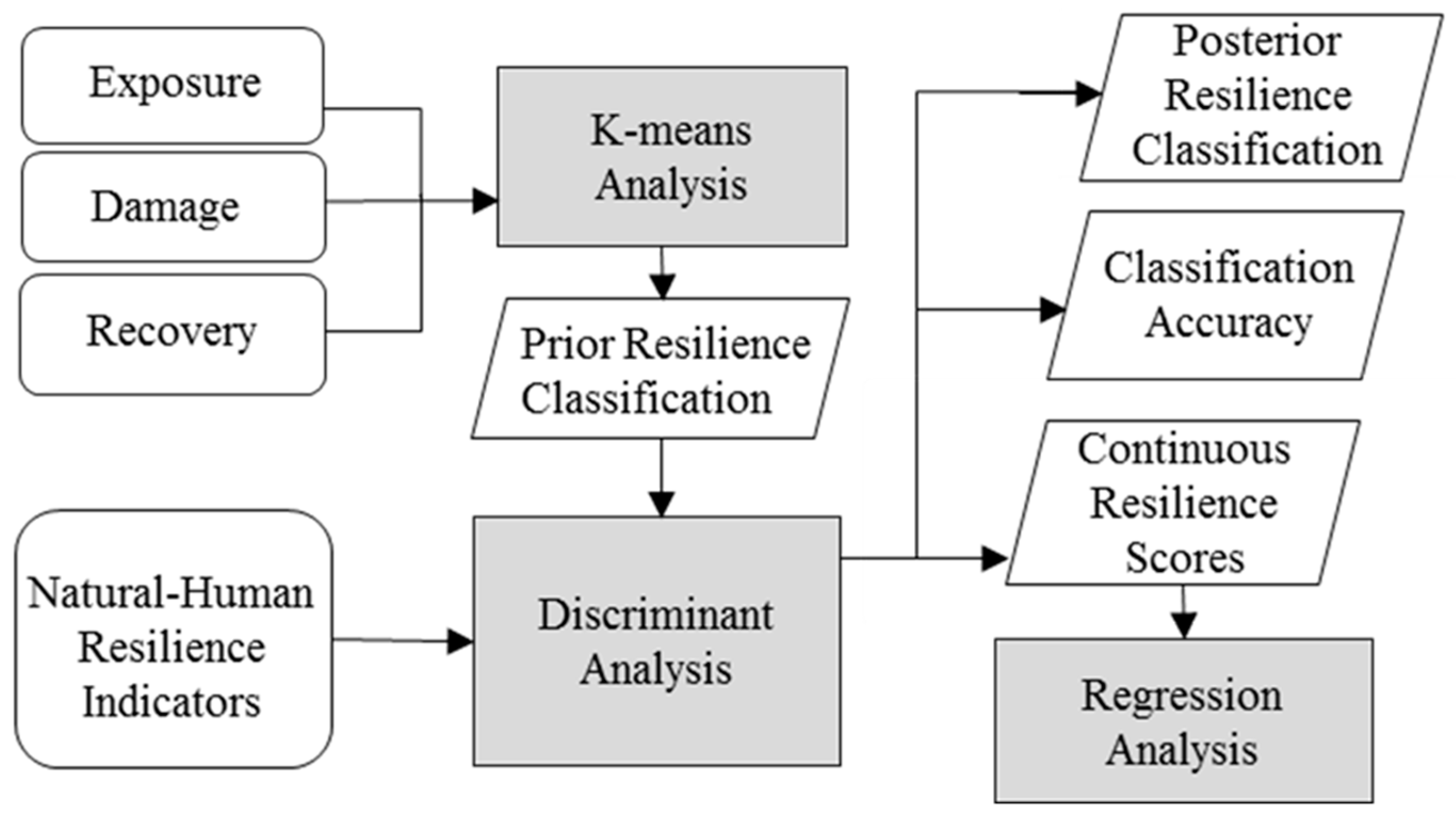
To carry out a RIM analysis, data for the three elements for each community and data describing the resilience capacity of the community are collected (
Figure 5). First, K-means cluster analysis is employed to classify the community into one of the four resilience levels based on the values of the three elements. These four levels from low to high resilience (1–4) are susceptible, recovering, resistant, and usurper. Second, discriminant analysis, an inferential statistical technique, is used to test if the groups are valid and identify the key social, economic, or environmental variables characterizing each group. Third, a continuous RIM score, ranging from 1.0 to 4.0 is constructed for each community based on the probabilities of group membership derived from the discriminant analysis. Fourth, to make the discriminant analysis results easier to use by planners and managers, the discriminant analysis results are translated through a regression analysis between the RIM score and the extracted socioeconomic and environmental variables. If the model is significant with reasonable goodness-of-fit, then the regression results can be used to estimate resilience across different regions and at different time periods.
We applied the RIM model to measure the community resilience of the MRD at the census block-group level using data between 2000 and 2010. Detailed description of the study and the results can be found in Cai et al. (2016) [
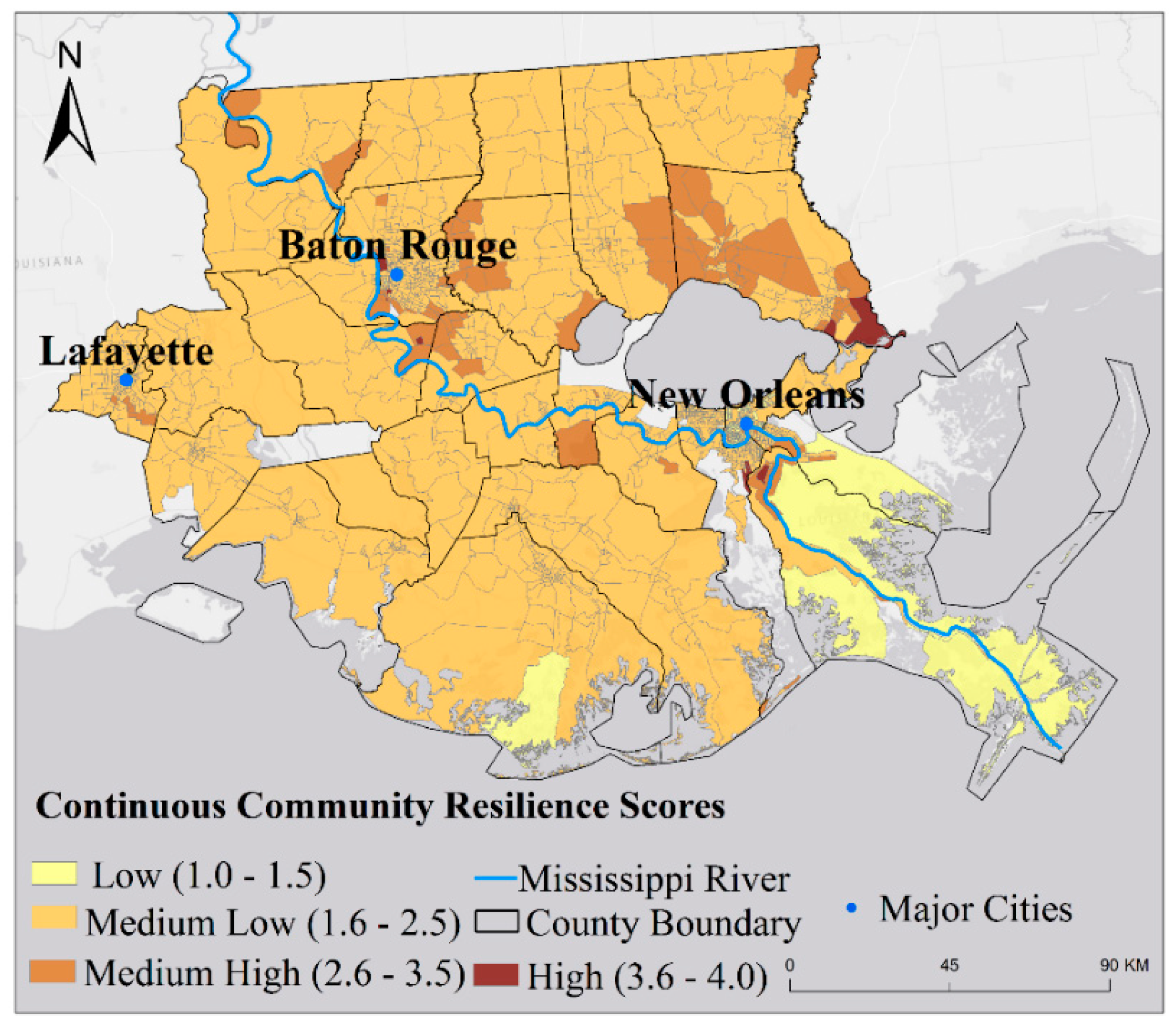
41]. In brief, there were 2086 block groups in the study area. The hazard variable was represented by the number of times a block group hit by coastal hazards, the damage variable was property damage caused by these hazards, and recovery was represented by population change from 2000 to 2010 in each block group. A total of 25 socioeconomic and environmental variables were input to the stepwise discriminant analysis, which selected 11 variables as the best indicators in characterizing the resilience groups. The study results show that during the 10-year period, a total of 420 coastal hazard events hit the region, resulting in over 50 billion dollars of property damage. The final continuous resilience score map indicates that block groups with higher resilience were concentrated in the North, whereas block groups with low resilience were mostly in the South near the mouth of the delta (
Figure 6).
In an effort to translate the results from discriminant analysis into a simpler form to enable the resilience assessment model serve as a useful planning tool in a real-world setting, we developed a regression model between the RIM scores and the selected 11 variables. The regression results led to an R2 of 0.79 with 10 significant variables. These variables serve as indicators of resilience, and they cover all five components of community resilience discussed in the literature (social, economic, infrastructure, community, environmental).
The advantage of the RIM method is that the final resilience score of each community is already validated through the use of real data of hazard threat level, economic damage, and recovery (population return). The method extracts key resilient indicators and their weights (either from discriminant functions or regression function), which can be used to estimate the level of resilience over time or in other similar study areas when the statistical assumptions are met. The resilient variables extracted from the RIM analysis can then be used to guide the selection of variables to be modeled in the master CNH model in the next step (
Table 1).
4.2. A Land Loss Simulation Model
To understand the land loss problem in the MRD through the lens of coupled natural-human system dynamics, we employed a combined artificial neural network (ANN) and cellular automata (CA) approach to model and simulate the land loss in the region. Previous efforts on land loss projections along the Louisiana coast were based on the trends at sample locations without taking into account variables relating to human activities [
32]. This study utilized variables from both the natural and human systems. Detailed description of the study can be found in Qiang and Lam (2015) [
40].
ANN has been used for pattern recognition, classification, and optimization in a variety of applications. An ANN consists of an input layer, one or more hidden layers, and an output layer. Each layer has a number of neurons. Each neuron in the input layer represents an input variable, and through training and iteration, it will generate an output value to the next layer. We used the Matlab neural network toolbox for this study. To train an ANN, the program divides the data set into a training set, a validation set, and a test set. In each iteration, the ANN is updated to fit the training set, and the model is verified using the validation set until an error tolerance or the maximum number of iterations has been reached. The test data set offers an independent evaluation of the performance of the model [
40].
We used Landsat-TM land cover data in 1996 and 2006. The study area was partitioned into 30 × 30 m
2 grid cells to conform to the Landsat-TM data, which resulted in a total of 53,384,656 cells (the North 22,162,275 vs. the South 31,222,381 cells). ANN models for each sub-region, the North and the South, were derived for the period 1996–2006 using 15 variables from both the natural and human components (
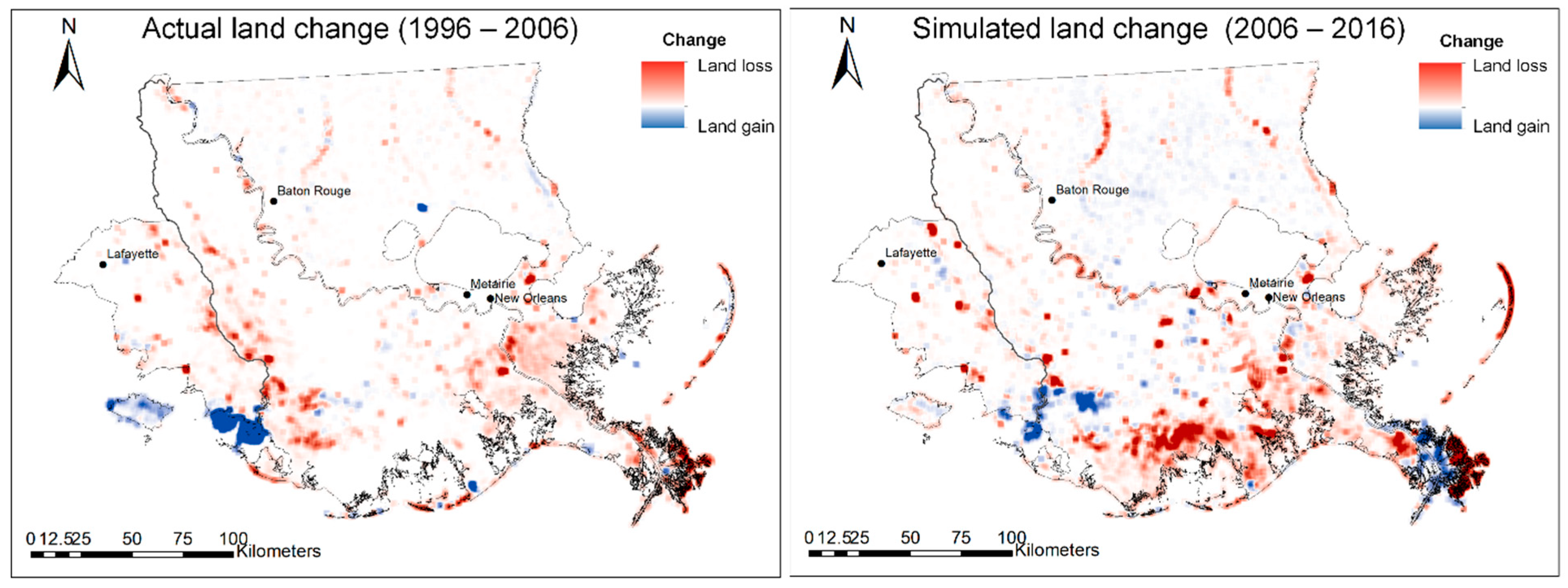
Table 2). The ANN models yielded a degree of accuracy of 91.8% for the North and 97.1% for the South. The derived ANN models were then used as transition rules in a cellular automaton to simulate future land cover changes for the two sub-regions into 2016. Unlike previous land-cover change simulation studies, this study added a stochastic element in the model to represent factors that were not included in the current model. Five land use types were modeled and simulated, including urban, forest, agricultural, wetlands, and water (land loss). Results of the land loss simulation show that land loss would increase 38% in the South from 2006–2016, which is equivalent to an area of 76.8 km
2.
Figure 7 maps the actual land loss from 1996–2006 and the simulated land loss from 2006–2016.
This study has made several contributions. First, conceptually, the study pioneers the incorporation of both natural and human variables for ANN-CA simulation in the region. Second, adding a stochastic element in the model to symbolize the inclusion of unknown factors is considered another conceptual advance. Third, modeling land cover change for a large study area with 53 million cells is technically and computationally challenging, especially that software packages for conducting ANN, CA, and GIS analyses had not been integrated. We implemented the simulation by writing a Python script to loosely couple ArcGIS (version 10.3, ESRI, Redland, CA, USA) and Matlab (2015, MathWorks, Natick, MA, USA). Thus, the study demonstrates a feasible approach to integrate disparate variables and software packages to complete the modeling task. Fourth, the study produces scenarios of land loss pattern with a reasonable degree of accuracy, which will be helpful to the planning and management of the region as it strives to be sustainable.
However, a drawback of modeling using ANN, like many data mining methods, is that it is a black-box approach. This means that the model does not tell which variable is most influential to the output or how the input variables interact with each other that affect the output. Other modeling approaches in which relationships among variables are explicitly quantified (white-box approach), such as using a system of equations derived from regression analysis, will need to be explored.
4.3. A Spatial Dynamic Model of Population Change
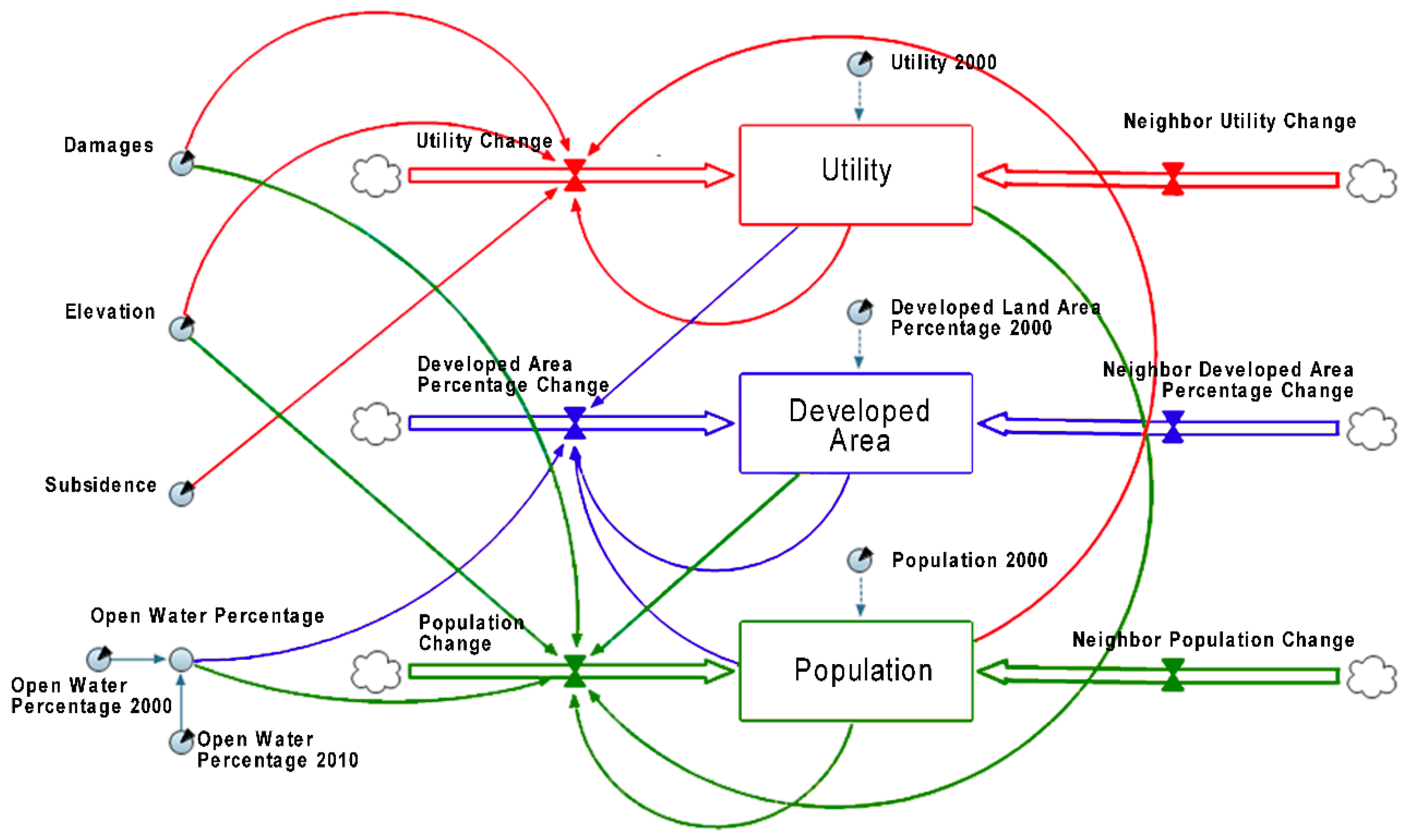
To overcome some of the issues related to using a “black-box” approach, we developed a spatial dynamic model to analyze population changes (and its associated developed land area changes) in the study region using a system dynamic approach [
47]. The system dynamic approach allows systems of equations governing the target variables to be linked and simulated, and the relationships among variables are explicitly quantified, thus constituting a “white-box” approach. In this study, the goal was to identify key socioeconomic variables (combined into a “utility” variable) and environment variables (hazard damage, elevation, and subsidence rate) that affected population changes, and in turn how population changes affected the local utility and the local environment reciprocally.
The study included the following steps. First, the study area was partitioned into a mesh of 3 × 3 km
2 grid cells as the modeling units, and this led to a total of 5890 cells for the analysis. Second, a total of 33 variables, informed by the previous two studies, were selected as model inputs to the analysis. These natural and human variables come in various forms and scales, which need to be transformed into a single platform for analysis. We applied an areal interpolation technique with the volume preserving property to transform all the data at Year 2000 into a unified 3 × 3 km
2 cellular space [
54,
55]. Third, an Elastic Net model was applied which extracted 12 variables from the set of 33 to develop a utility function to capture the major social-environmental variables that have affected population changes [
56]. Fourth, a genetic algorithm was applied to calibrate the neighborhood effects. Finally, a system dynamic model was generated (
Figure 8).
The system dynamic model is governed by three equations, each specifying a state variable (population count, developed area percentage, and utility) in time t + 1 as a function of the same variable in time t plus other influencing variables. Li and Lam (2017) documented the set of equations [
47]. The accuracy assessment shows that the model slightly over-predicts the population count and developed area in 2010. The largest outliers were found to occur mostly in the New Orleans region where population and urban development declined significantly during 2000–2010 after Hurricane Katrina. A Monte Carlo simulation was used to analyze the uncertainty of the model outcome.
Then, population change from 2010 to 2050 was simulated using the spatial dynamic model, and their trajectory was evaluated using the resilience framework. It was projected that areas in the South continue to suffer population loss, whereas areas in the North continue to have steady population growth. In other words, without mitigation and adaptation or any changes in the current condition, the areas in the South will unlikely be sustainable.
The main contribution of this study is that it provides a CNH dynamic model that includes most of the elements in our framework and their feedbacks. Through simulation using a “bottom-up” “white-box” approach, the model uncovers the long-term emergent properties in the region and offers a foundation to compare the different emergent properties between the northern (more inland) part and the southern (more coastal) part of the study region. By utilizing the simulated results, different impact levels of the extracted variables on the more-coastal and more-inland areas can be analyzed in follow-up studies.
4.4. Highlights of Findings
The MRD community resilience assessment study shows that higher-resilience communities were in the northern part of the study area, whereas lower-resilience communities were those located along the coastline and in lower elevation area. More importantly, the study identifies ten statistically significant variables that were associated with the resilience scores. Four of the ten variables contribute positively to resilience, and they include percent of housing units with telephone service available, median household income, percent of population employed in construction, transportation, and material moving, and percent of housing built after 2000. The other six variables contribute negatively to resilience, which include percent female-headed households with children, housing density, road density, percent of native-born population, and percent of inundation zone. These resilient variables identified from this study has guided the selection of variables to be included in the spatial dynamic model.
The land loss modeling using a combined ANN-CA approach shows that the derived ANN models could simulate the land cover changes with a high degree of accuracy (>92% on average). It was projected that between 2006 and 2016 urban growth in both the South and the North would double, the trend of forest loss would cease, and land converted to water (land loss) would increase by 38% in the South, which is equivalent to a land loss of 76.8 km2.
The spatial dynamic modeling study identifies through Elastic Net 12 socioeconomic and four environmental variables to build the model. The four environmental variables are property damage from hazards, elevation, subsidence rate, and percent of open water. The 12 variables include pipeline density, road density, medium housing value, median rent, owner cost as a percentage of household income more than 35%, percent housing units without mortgage, percent housing units with no heating fuel used, percent housing units with no complete kitchen facilities, percent housing units with no complete plumbing facilities, percent units with no telephone, and percent population under five years old. The spatial dynamic model is governed by a set of equations. By varying the values of the variables in the equations, we can predict the system response under different scenarios and evaluate the dynamic feedbacks among all these variables.
5. Lessons Learned
Although the CNH approach has been discussed extensively in the literature, few studies have actually attempted in quantifying the feedback relationships in a real-world setting. Modeling the dynamics of a real CNH system is complex and challenging. We summarize below the challenges and the lessons learned from our research on the MRD and suggest a path forward.
5.1. Data Integration Complexity
First and foremost, incorporating all the major components from both natural and human systems is difficult because of data incompatibility from various disciplines. Modeling the CNH dynamics requires different types of data collected from various sources at multiple spatial and temporal scales. Integrating disparate types of data into a unified platform for CNH modeling is the most fundamental step that requires accurate methods for integration. In our MRD CNH studies, we have demonstrated the use of spatial interpolation methods to harmonize the various types of data. For instance, we used Empirical Bayesian Kriging method to create the land subsidence rate surface in pixel form in the study area [
27,
40], and we used areal interpolation with volume-preserving property to transform socioeconomic data from polygons to pixels so that they can be compatible with the natural data [
47]. These two interpolation methods are considered among the most accurate methods; thus, they could be utilized to integrate the various data needed in CNH analysis.
On a deeper level, there is fundamental incompatibility of the underlying processes and their lagged effects among the various natural and human components. Some processes will take years to observe the difference (e.g., land subsidence and elevation changes), whereas other processes can be measured every day (e.g., water salinity changes). Some processes are global or regional in nature (e.g., policy changes), while others are local (e.g., land loss probabilities). For instance, it is challenging to link riverine sediment dynamics into our current CNH model, because sediment transport and distribution in the Mississippi River are not only affected by natural flow conditions but also by policy making that dictates river engineering practices, such as levee construction, channel dredging, and river diversion [
16,
17]. Our study on the channel morphology of the final 500 km of the Mississippi River found a continuous riverbed aggradation immediately below the Mississippi avulsion node [
57,
58,
59], which poses a risk for the river to be completely captured by the Atchafalaya River. If that happened, the MRD would lose the lifeline of freshwater and sediment and the current deltaic system could experience a complete system change. Capturing and modeling these linked effects remains to be a difficult problem in CNH modeling.
5.2. Scale Issues
It is well known that spatial relationships change with the scale of the data used, thus in modeling coastal resilience we must also consider the scale effects [
60,
61,
62,
63]. One of the scale effects is the neighborhood effect. In other words, when considering the effects of various variables on land loss, we should not be considering only the effects at individual locations, but also the effects from their neighbors. How best to determine the neighborhood effects becomes a critical step for CNH modeling.
For instance, in studying the relationship between landscape fragmentation and land loss probability in the study region, we found that the relationship changed with the neighborhood size used to calculate the fragmentation indices. The fragmentation effects were significant and better observed at the 71 × 71, 51 × 51, and 31 × 31 neighborhood box scales (pixel size was 30 m), but not at the 101 × 101 scale [
42]. The study confirms that scale matters. The neighborhood size, or the spatial context, can also be interpreted as the operational scale of a phenomenon [
61]. In our spatial dynamic model discussed above, we used a genetic algorithm to calibrate the overall neighborhood effect [
47]. A more refined approach would be to explore individual variables’ neighborhood effects, which could be accomplished by examining their variograms. In addition, given the potential errors resulted from data scale, data quality, and data manipulation, uncertainty analysis of the findings should be conducted in CNH modeling research [
47].
5.3. Dynamic Modeling Approaches
The choice of a modeling approach (white-box, black-box, or gray-box) matters, as each approach has its own advantages and disadvantages. In this paper, we show that the black-box data mining approach, such as ANN, can represent non-linear complex relationships which are common in CNH systems, but this approach does not offer a clear structure and linkage among the various variables. On the other hand, the system dynamic approach is often limited to simpler, linear relationships, but the linkages among different components and their feedback mechanisms can be comprehended more easily. For this reason, the white-box approach is preferred whenever possible to reveal the structure and relationships of the natural-human system and extract the rules for building the system dynamics. Its ability to visualize the relationships through numeric formulas and conceptual diagrams helps foster a better understanding of the MRD as a coupled natural-human system for decision makers and stakeholders, which will ultimately benefit policy making on sustainable development in the region.
5.4. Linking Science to Practice
Increasingly, researchers are faced with the challenge of making their scientific findings usable in real-world applications. This is especially true for the study of the MRD when land loss and associated population decline are increasingly threatening the existence of this economically, environmentally, and societally highly relevant river delta. Academic publications and project websites are effective means to disseminate the results, but they are not effective in cultivating bi-directional communication. Toward this end, we conducted a full-day workshop on “Knowledge sharing for a delta resilience community of practice” in 2016, in which coastal managers and community stakeholders in the study area were invited to participate. The workshop format is similar to the one conducted in Reams et al. (2017) [
64], with a goal of cultivating bi-directional communications and sharing information between researchers and stakeholders so that better understanding of the MRD as a coupled natural-human system can be obtained. A detailed description of the workshop will be reported in the future.
To go one step further than communicating research findings to stakeholders and the public, it would be useful, if at all possible, to “translate” theoretical research results into practical tools. This paper has illustrated an effort in translating the RIM resilience measurement results from a less apparent discriminant analysis output (which has three discriminant functions) into a more straightforward regression model while sacrificing a small degree of variance explained (in this case, an R2 of 0.79), so that the relative importance of the variables in the regression model is easily understood and evaluated. In CNH modeling, linking science to practice should be an important goal, and such goal would be best accomplished by bi-directional communication and close collaboration among researchers and stakeholders.
6. Conclusions
A pressing question facing the Mississippi River Delta, like many deltaic communities around the world, is: Will the system be sustainable in the future given the threats of sea level rise, land loss, natural disasters, and depleting resources? Addressing this question requires a thorough understanding of the complex dynamics between natural and human systems and a multi-disciplinary approach using multiple methodologies with analysis of multi-scale and multi-temporal data. This paper describes a CNH modeling framework for analyzing the sustainability problem in the Mississippi River Delta. The framework includes six components from the natural (hydrology, sediment, vegetation) and human (population, industry, government) systems, linked through a target variable land loss, and with press and pulse factors included. These components are common elements in most deltaic systems around the world, and thus the framework should have wide applicability. A distinct feature of the framework is the presence of common variables in the set of equations governing the interrelationships among components, making it possible to model the feedback loops. This feedback loop design implies that any major variables in the system dynamic model can be analyzed and evaluated, thus the framework provides flexibility and allows future additions.
Three interrelated studies using the framework were highlighted to illustrate how the resilience of a coupled natural-human system can be measured, how artificial neural network coupled with cellular automata can be used to estimate future land loss, and how a system dynamic modeling approach can be applied to predict population change in the region. Findings from these studies should help inform decision makers and the general public about key tradeoffs involved in efforts to enhance regional resilience and provide scenarios to support better planning for climate change. The framework, which includes methods of data interpolation and system modeling algorithms, is highly applicable to the study of other deltas. Our approach will shed light on how to study deltas as a coupled natural and human system and gain improved understanding of the regions.
Based on lessons learned from these studies, we conclude that despite the difficulty in harmonizing diverse data and representing both the natural and human subsystems, methods such as those used in the three studies are applicable to investigating complex CNH problems. In addition, we suggest the following. First, although representing and modeling complexity is essential, it is important to have a framework that is feasible for modeling. A simpler model with well-defined elements is likely to offer clarity and better understanding of the underlying processes and findings. Second, due to the issue of data quality, data scale, and data manipulation, uncertainty analysis of the model findings will need to be conducted to help identify where the errors or uncertainties come from. Third, a white-box modeling approach is preferred whenever possible because it provides explicit functions about the interactions and links among various components. Furthermore, future modeling should consider identifying extremes and/or system-changing thresholds in natural and human environments. Last but not the least, an effort should be made to cultivate bi-directional communication between researchers and stakeholders to help improve the relevance and applicability of the findings.