Impacts of Global Circulation Model (GCM) bias and WXGEN on Modeling Hydrologic Variables
Abstract
:1. Introduction
2. Materials and Methods
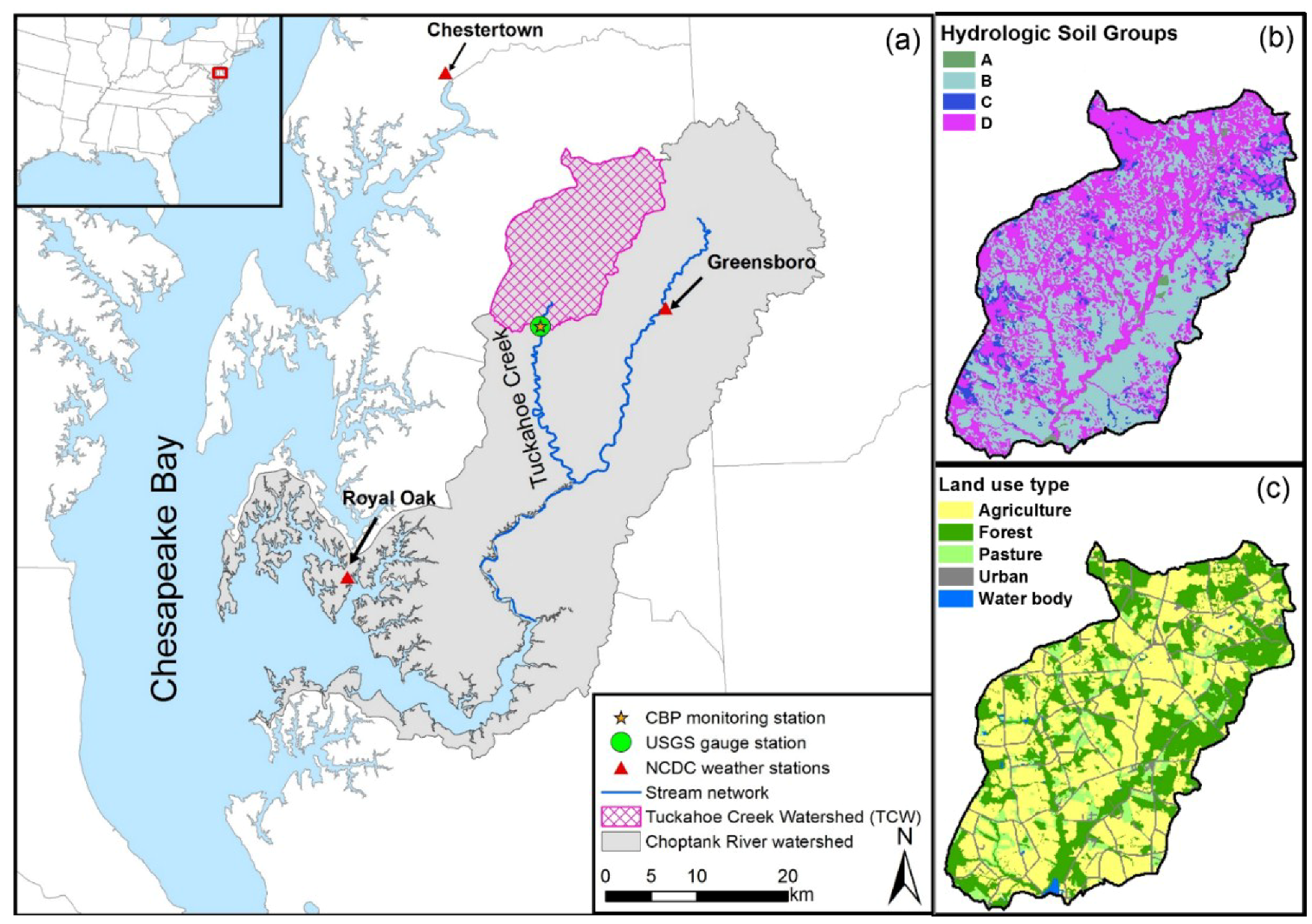
2.1. Study Area
2.2. Soil and Water Assessment Tool (SWAT)
2.3. SWAT Input Data for the Baseline Period
2.4. The SWAT Input Data for the Future Period Indicated by GCM
2.5. Model Calibration and Validation
2.6. Comparison Approach
3. Results and Discussions
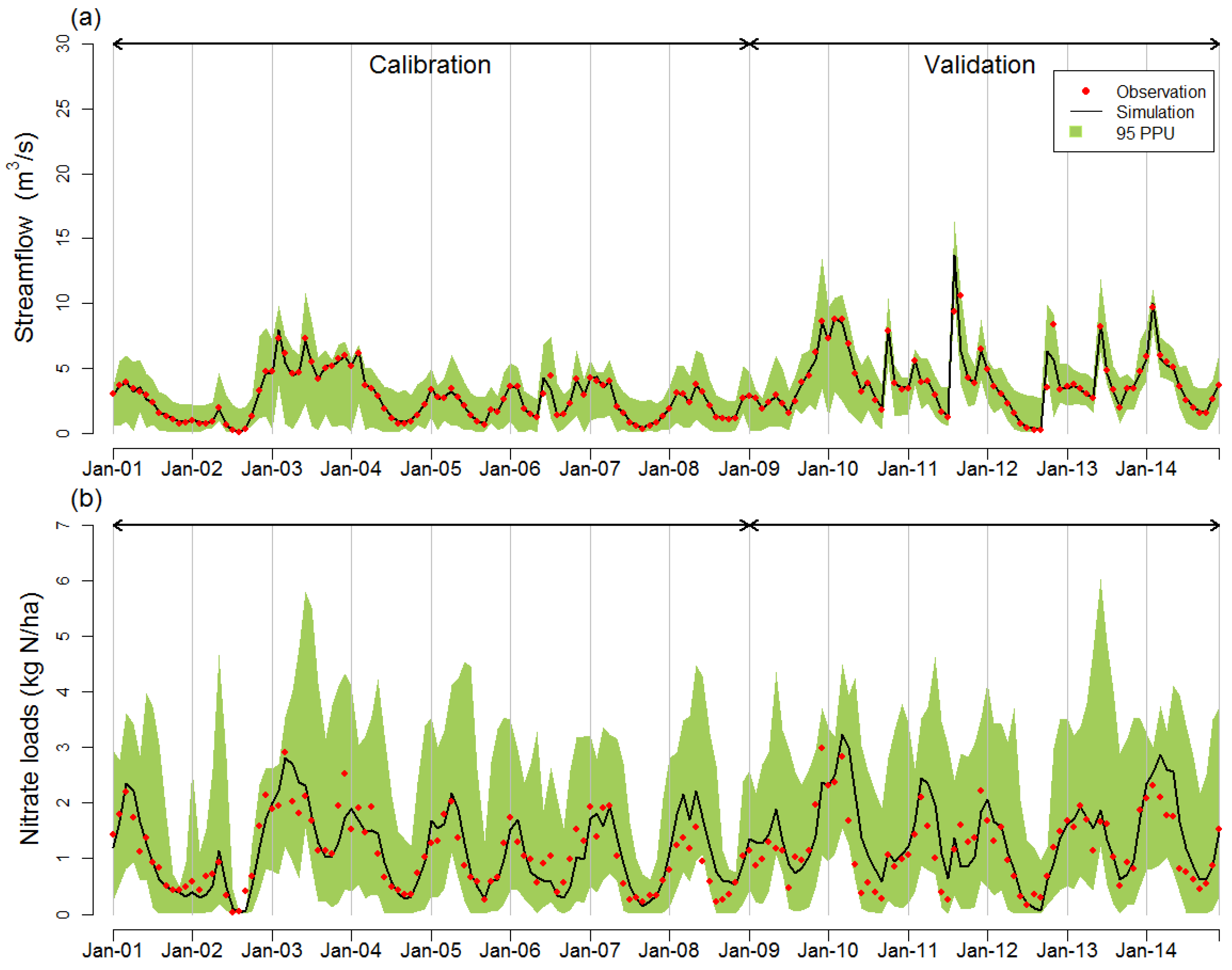
3.1. Model Calibration and Validation
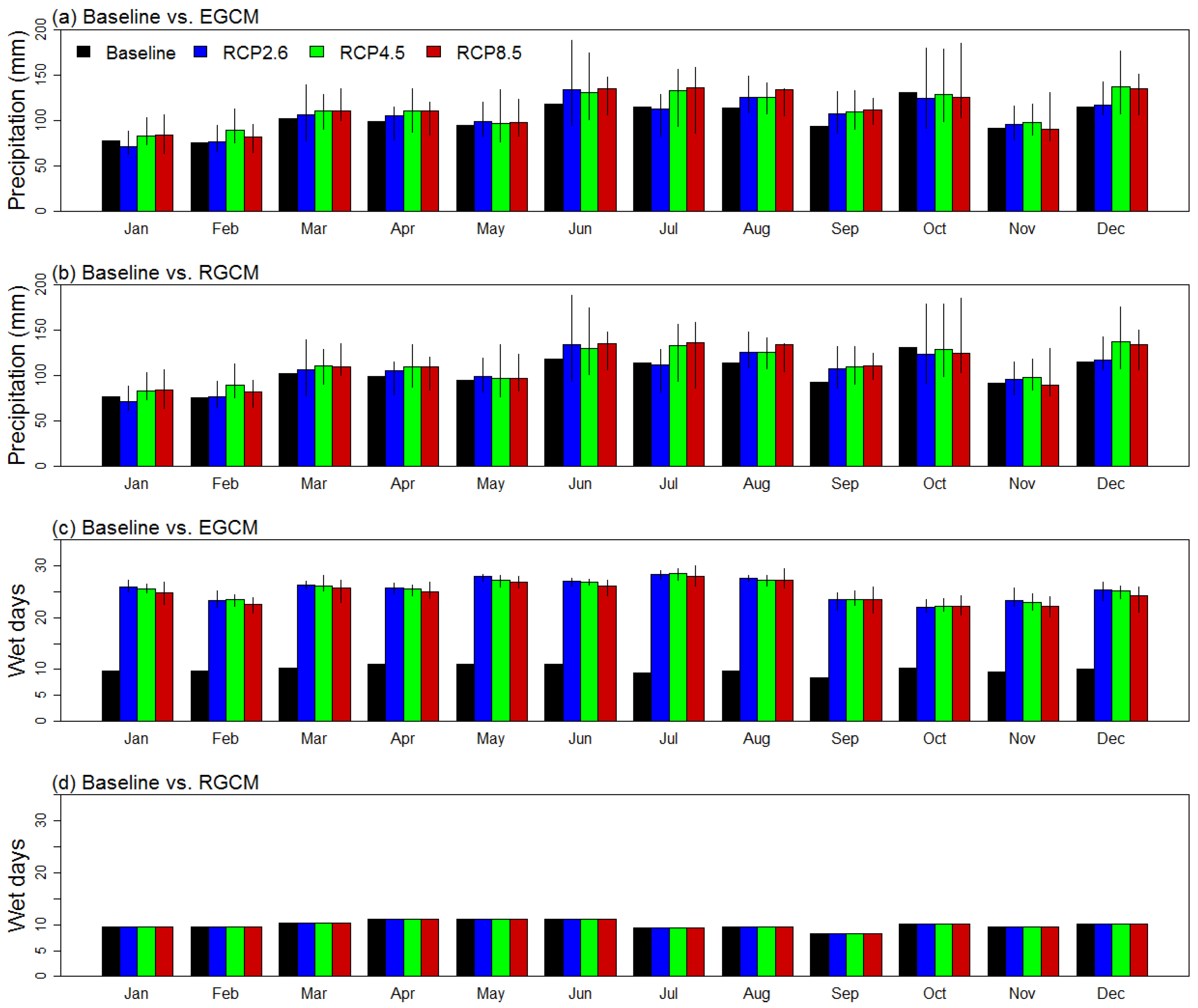
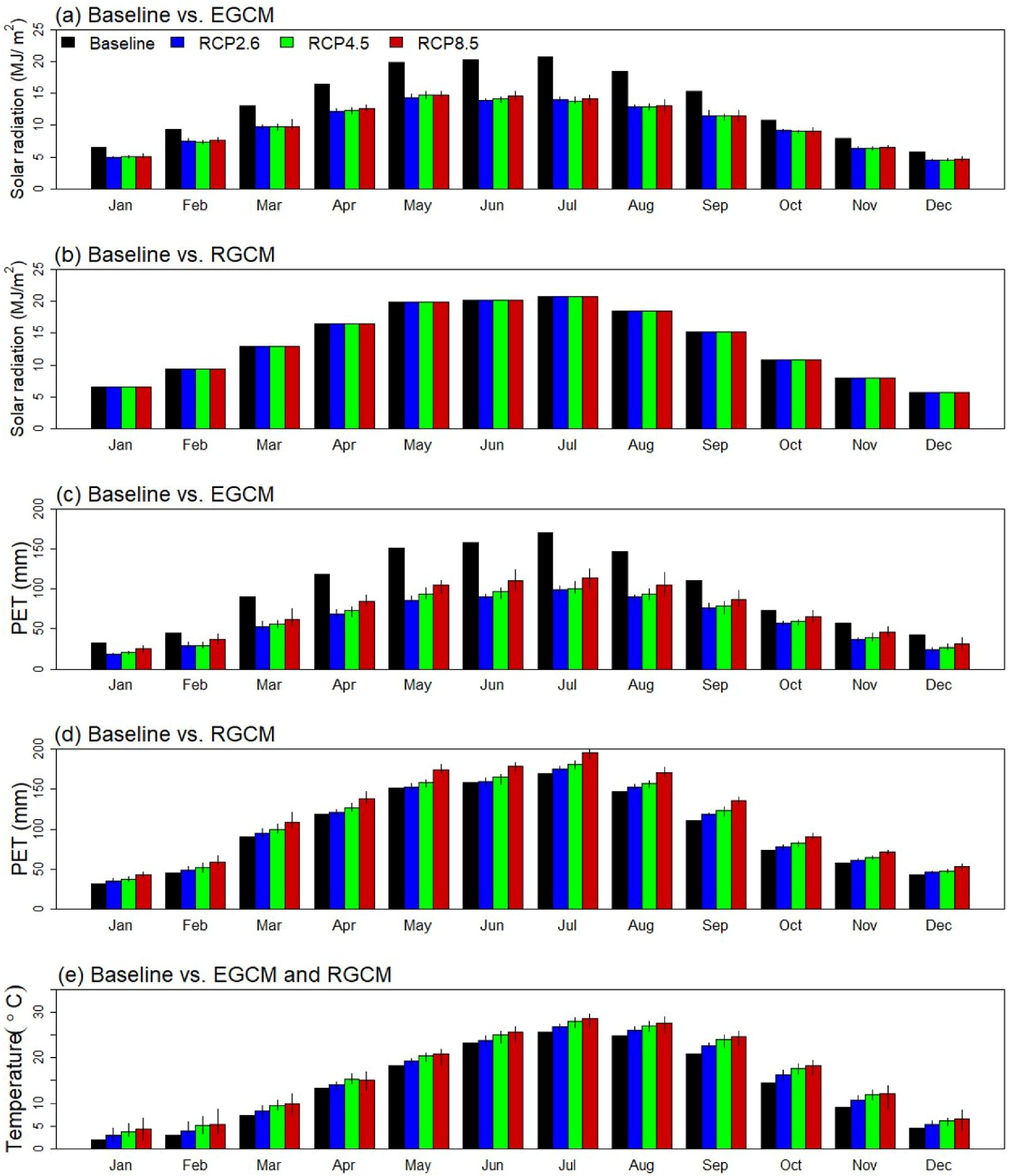
3.2. Climate Variables
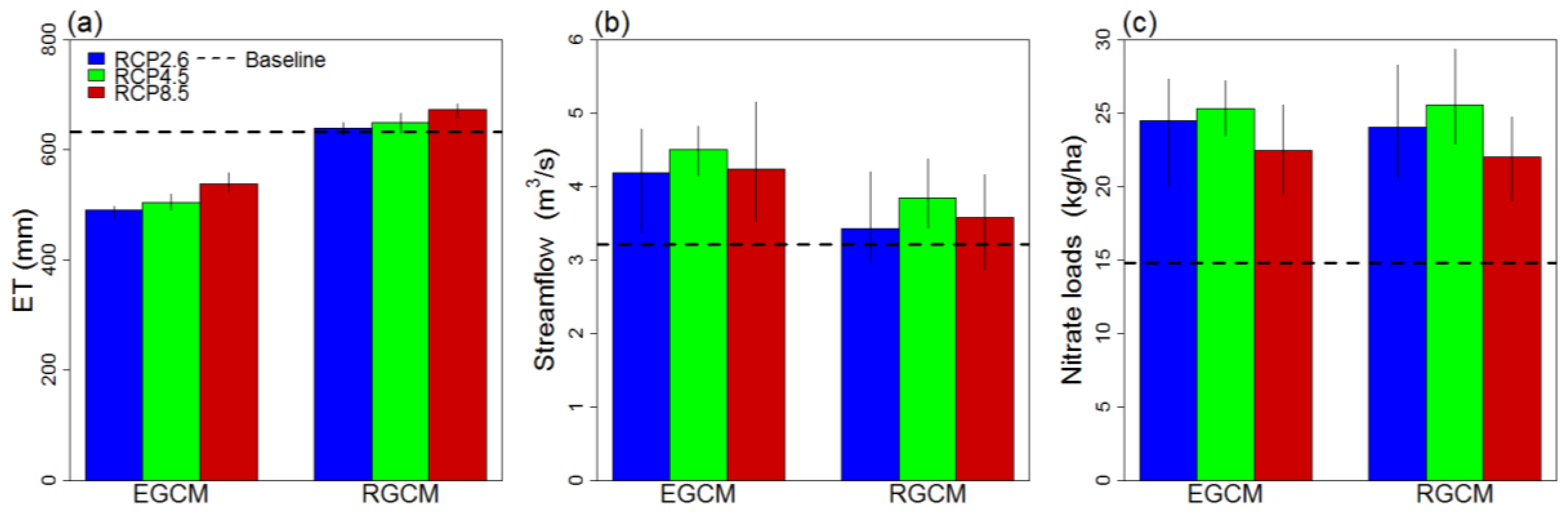
3.3. Hydrologic Variables
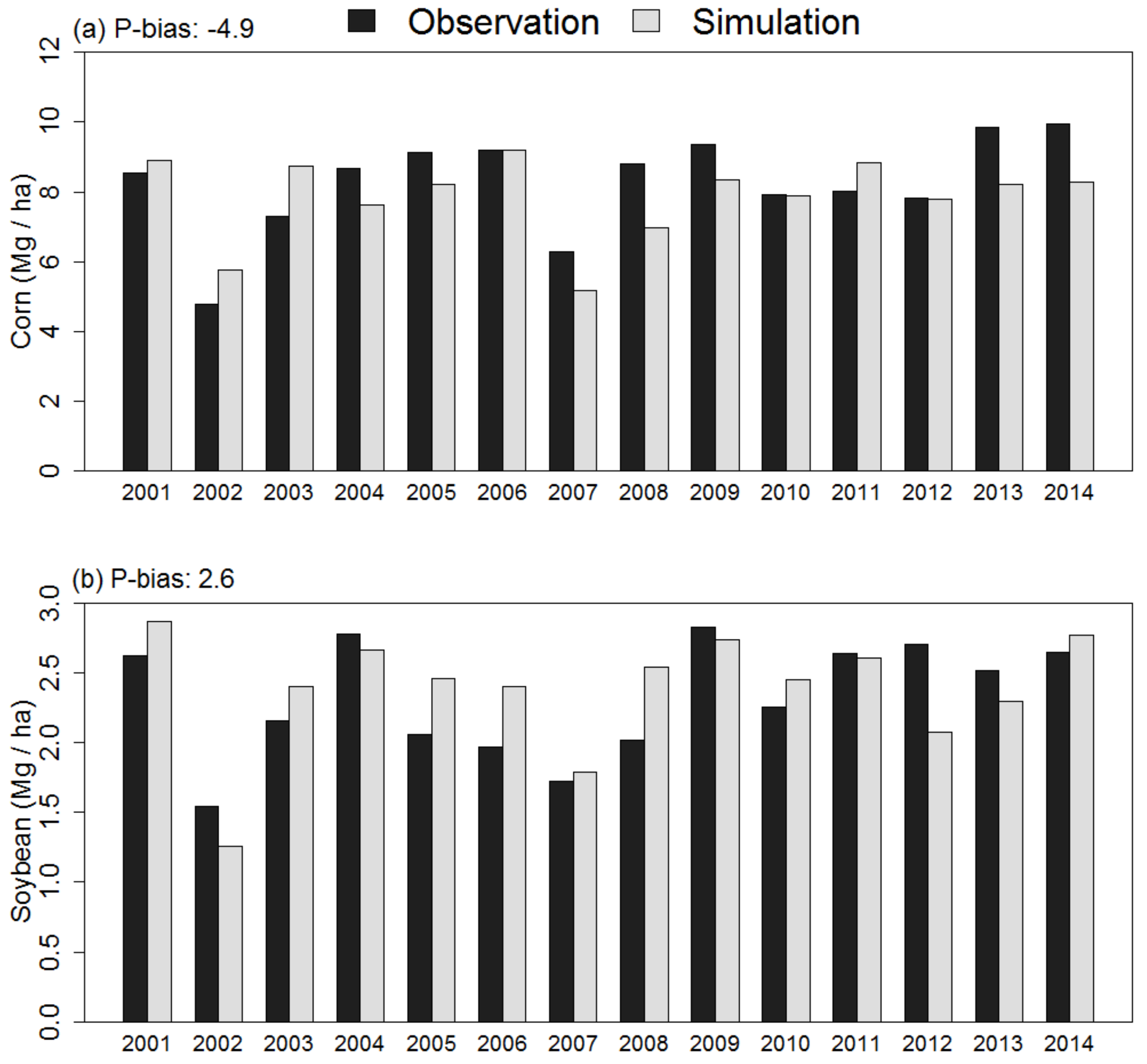
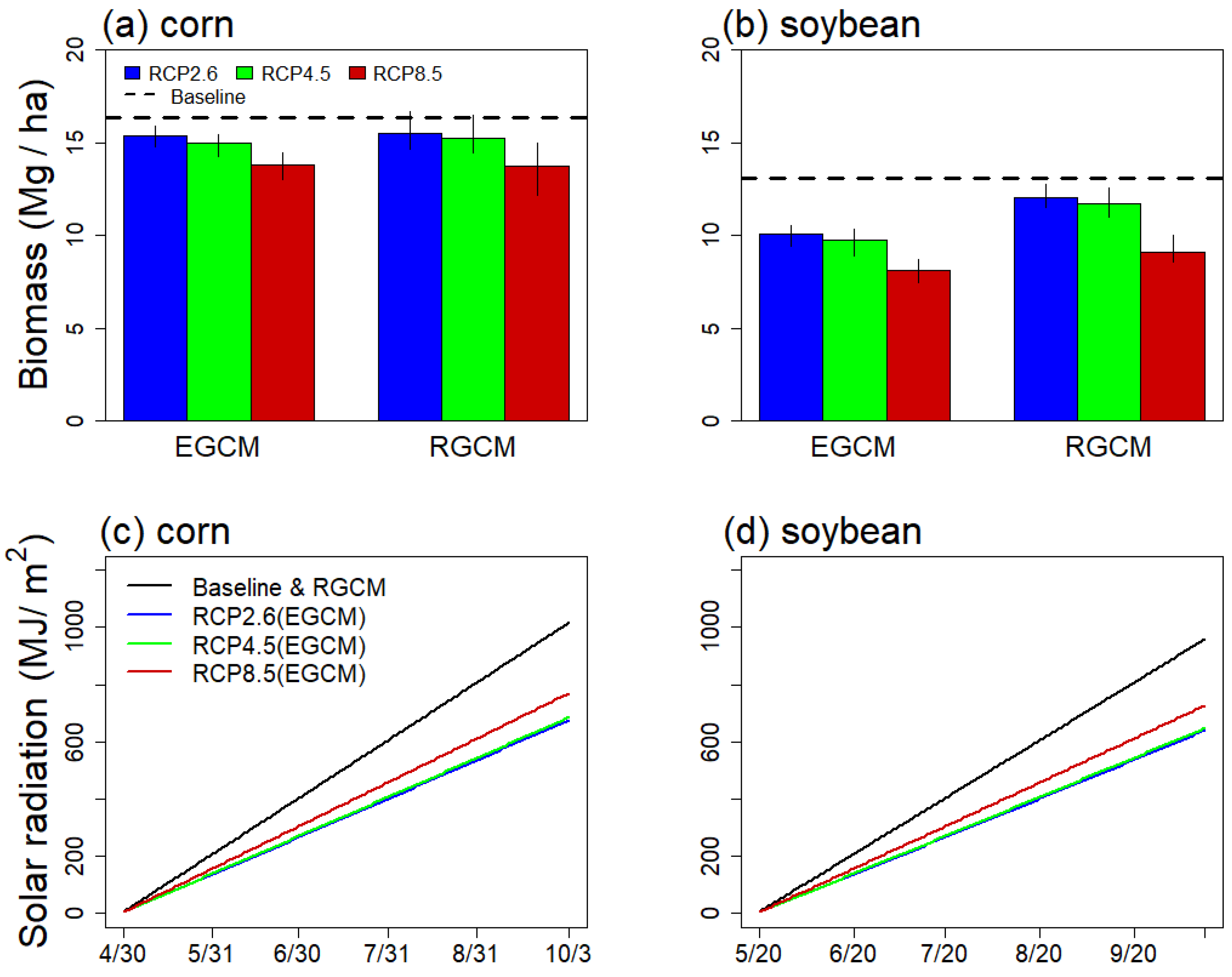
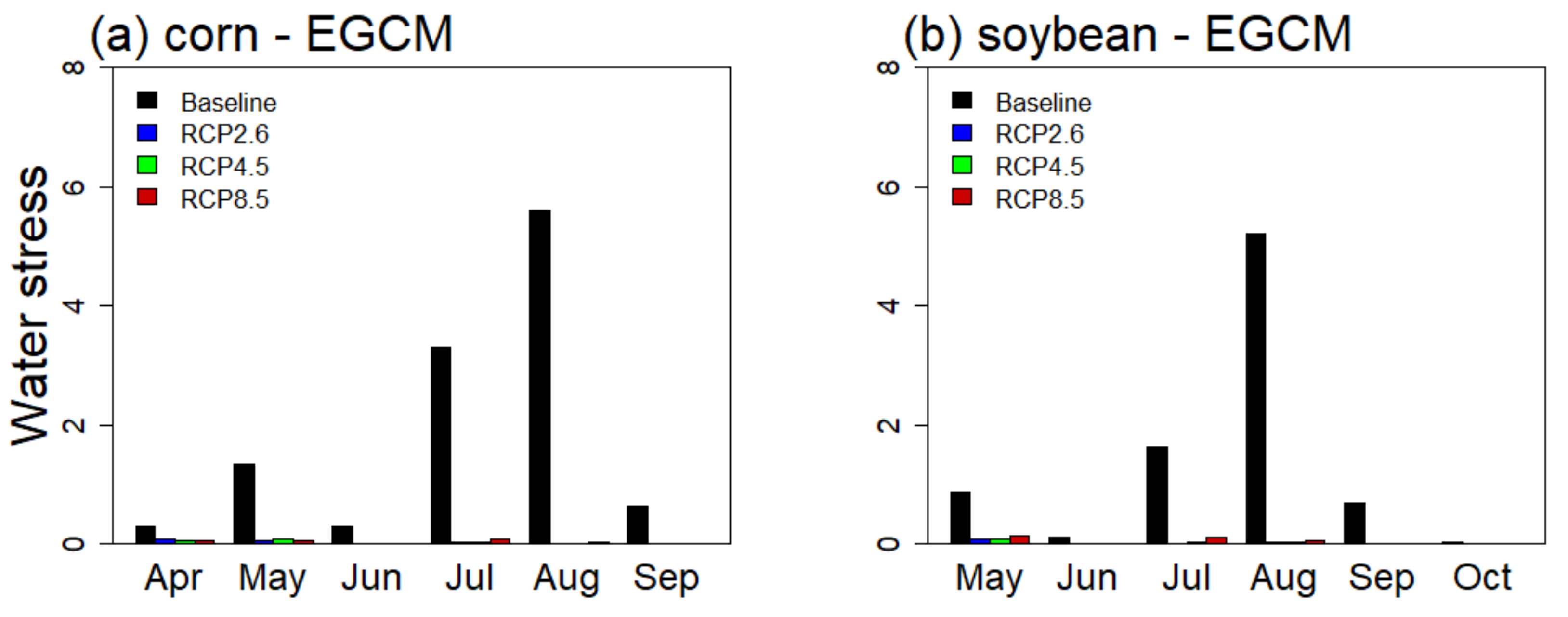
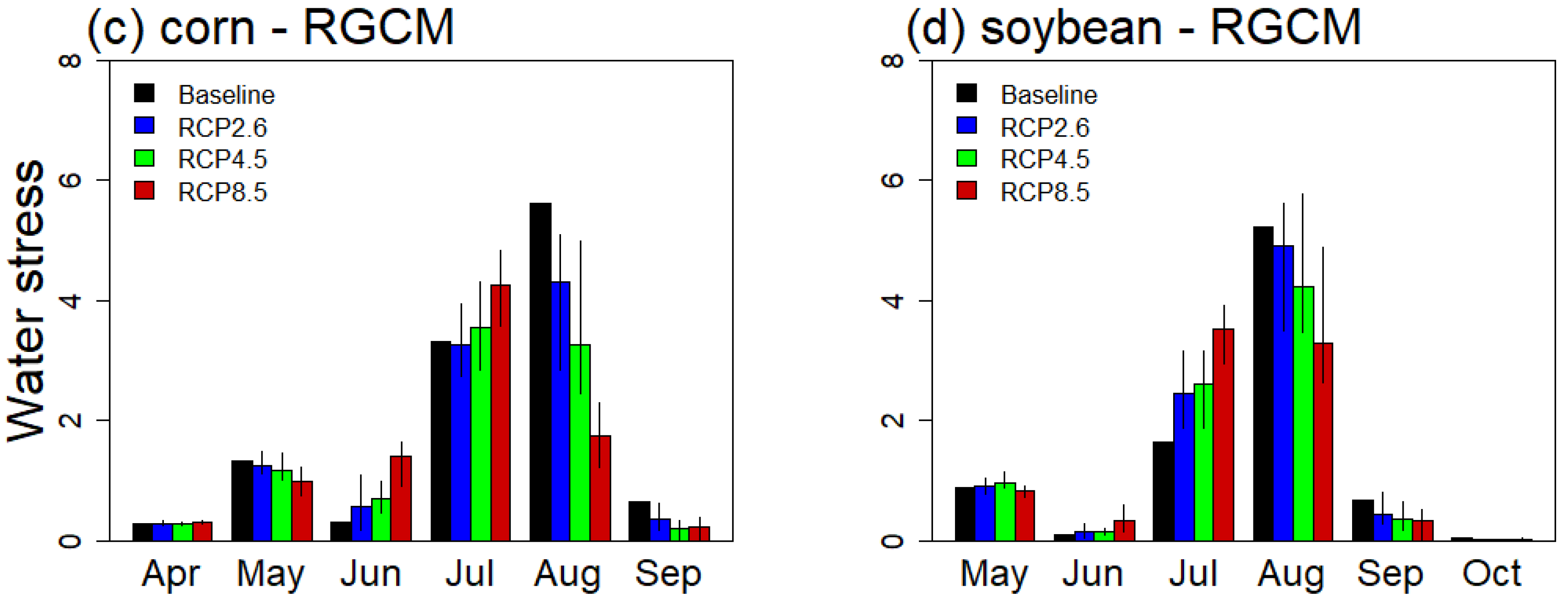
3.4. Crop Biomass
4. Limitations and Implications
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mearns, L.O.; Hulme, M.; Carter, T.R.; Leemans, R.; Lal, M.; Whetton, P. Climate scenario development. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Goddard, L.; Mason, S.J.; Zebiak, S.E.; Ropelewski, C.F.; Basher, R.; Cane, M.A. Current approaches to seasonal to interannual climate predictions. Int. J. Climatol. 2001, 21, 1111–1152. [Google Scholar] [CrossRef] [Green Version]
- Nyunt, C.T.; Koike, T.; Yamamoto, A. Statistical bias correction for climate change impact on the basin scale precipitation in Sri Lanka, Philippines, Japan and Tunisia. Hydrol. Earth Syst. Sci. 2016. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Ines, A.V.; Hansen, J.W.; Robertson, A.W. Enhancing the utility of daily GCM rainfall for crop yield prediction. Int. J. Climatol. 2011, 31, 2168–2182. [Google Scholar] [CrossRef]
- Gassman, P.W.; Sadeghi, A.M.; Srinivasan, R. Applications of the SWAT model special section: Overview and insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Alighalehbabakhani, F.; Miller, C.J.; Selegean, J.P.; Barkach, J.; Abkenar, S.M.S.; Dahl, T.; Baskaran, M. Estimates of sediment trapping rates for two reservoirs in the Lake Erie watershed: Past and present scenarios. J. Hydrol. 2017, 544, 47–155. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Luedeling, E.; Zhang, M. Climate change sensitivity assessment of a highly agricultural watershed using SWAT. J. Hydrol. 2009, 374, 16–29. [Google Scholar] [CrossRef]
- Wallace, C.W.; Flanagan, D.C.; Engel, B.A. Quantifying the Effects of Future Climate Conditions on Runoff, Sediment, and Chemical Losses at Different Watershed Sizes. Trans. ASABE 2017, 60, 915–929. [Google Scholar] [CrossRef]
- Wang, R.; Kalin, L.; Kuang, W.; Tian, H. Individual and combined effects of land use/cover and climate change on Wolf Bay watershed streamflow in southern Alabama. Hydrol. Process. 2014, 28, 5530–5546. [Google Scholar] [CrossRef]
- Yeo, I.Y.; Lee, S.; Sadeghi, A.M.; Beeson, P.C.; Hively, W.D.; McCarty, G.W.; Lang, M.W. Assessing winter cover crop nutrient uptake efficiency using a water quality simulation model. Hydrol. Earth Syst. Sci. 2014, 18, 5239–5253. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Blanco, M.L.; Arias, R.; Taboada-Castro, M.M.; Nunes, J.P.; Keizer, J.J.; Taboada-Castro, M.T. Potential Impact of Climate Change on Suspended Sediment Yield in NW Spain: A Case Study on the Corbeira Catchment. Water 2016, 8, 444. [Google Scholar] [CrossRef]
- Sharpley, A.N.; Williams, J.R.; United States Agricultural Research Service. Erosion/Productivity Impact Calculator, 1. Model Documentation; U.S. Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1990.
- Chen, H.; Sun, J. Projected change in East Asian summer monsoon precipitation under RCP scenario. Meteorol. Atmos. Phys. 2013, 121, 55–77. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Chen, X. Projection and uncertainty analysis of global precipitation-related extremes using CMIP5 models. Int. J. Climatol. 2014, 34, 2730–2748. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute Technical Report; Texas A&M University System: College Station, TX, USA, 2011. [Google Scholar]
- Brekke, L.; Thrasher, B.L.; Maurer, E.P.; Pruitt, T. Downscaled Cmip3 and Cmip5 Climate Projections: Release of Downscaled Cmip5 Climate Projections, Comparison with Preceding Information, and Summary of User Needs; US Department of the Interior, Bureau of Reclamation, Technical Service Center: Denver, CO, USA, 2013.
- McCarty, G.W.; McConnell, L.L.; Hapeman, C.J.; Sadeghi, A.; Graff, C.; Hively, W.D.; Lang, M.W.; Fisher, T.R.; Jordan, T.; Rice, C.P.; et al. Water quality and conservation practice effects in the Choptank River watershed. J. Soil Water Conserv. 2008, 63, 461–474. [Google Scholar] [CrossRef]
- Duriancik, L.F.; Bucks, D.; Dobrowolski, J.P.; Drewes, T.; Eckles, S.D.; Jolley, L.; Kellogg, R.L.; Lund, D.; Makuch, J.R.; O’Neill, M.P.; et al. The first five years of the Conservation Effects Assessment Project. J. Soil Water Conserv. 2008, 63, 185A–188A. [Google Scholar] [CrossRef]
- Lee, S.; Yeo, I.-Y.; Sadeghi, A.M.; Hively, D.W.; McCarty, G.; Lang, M. Impacts of Watershed Characteristics and Crop Rotations on Winter Cover Crop Nitrate Uptake Capacity within Agricultural Watersheds in the Chesapeake Bay Region. PLoS ONE 2016, 11, e0157637. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, A.; Lang, M.W.; McCarty, G.W.; Sadeghi, A.M.; Lee, S.; Yen, H.; Rabenhorst, M.C.; Jeong, J.; Yeo, I.Y. Improving model prediction reliability through enhanced representation of wetland soil processes and constrained model auto calibration—A paired watershed study. J. Hydrol. 2016, 541, 1088–1103. [Google Scholar] [CrossRef]
- Arias, R.; Rodríguez-Blanco, M.L.; Taboada-Castro, M.M.; Nunes, J.P.; Keizer, J.J.; Taboada-Castro, M.T. Water resources response to changes in temperature, rainfall and CO2 concentration: A first approach in NW Spain. Water 2014, 6, 3049–3067. [Google Scholar] [CrossRef]
- Flecher, C.; Naveau, P.; Allard, D.; Brisson, N. A stochastic daily weather generator for skewed data. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Runkel, R.L.; Crawford, C.G.; Cohn, T.A. Load Estimator (LOADEST): A FORTRAN Program for Estimating Constituent Loads in Streams and Rivers; U.S. Geological Survey Paper; U.S. Geological Survey: Reston, VA, USA, 2004.
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Shrestha, R.R.; Dibike, Y.B.; Prowse, T.D. Modelling of climate-induced hydrologic changes in the Lake Winnipeg watershed. J. Great Lakes Res. 2012, 38, 83–94. [Google Scholar] [CrossRef]
- Dlamini, N.S.; Kamal, M.R.; Soom, M.A.B.M.; Mohd, M.S.F.B.; Abdullah, A.F.B.; Hin, L.S. Modeling potential impacts of climate change on streamflow using projections of the 5th assessment report for the Bernam River Basin, Malaysia. Water 2017, 9, 226. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Singh, A.; Imtiyaz, M.; Isaac, R.K.; Denis, D.M. Assessing the performance and uncertainty analysis of the SWAT and RBNN models for simulation of sediment yield in the Nagwa watershed, India. Hydrol. Sci. J. 2014, 59, 351–364. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, R.; Zhang, X.; Arnold, J. SWAT ungauged: Hydrological budget and crop yield predictions in the Upper Mississippi River Basin. Trans. ASABE 2010, 53, 1533–1546. [Google Scholar] [CrossRef]
- Woznicki, S.A.; Nejadhashemi, A.P.; Parsinejad, M. Climate change and irrigation demand: Uncertainty and adaptation. J. Hydrol. Reg. Stud. 2015, 3, 247–264. [Google Scholar] [CrossRef]
- Gitau, M.W.; Chaubey, I. Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds. Water 2010, 2, 849–871. [Google Scholar] [CrossRef] [Green Version]
- Seo, M.; Yen, H.; Kim, M.K.; Jeong, J. Transferability of SWAT Models between SWAT2009 and SWAT2012. J. Environ. Qual. 2014, 43, 869–880. [Google Scholar] [CrossRef] [PubMed]
- Parajuli, P.B.; Jayakody, P.; Sassenrath, G.F.; Ouyang, Y.; Pote, J.W. Assessing the impacts of crop-rotation and tillage on crop yields and sediment yield using a modeling approach. Agric. Water Manag. 2013, 119, 32–42. [Google Scholar] [CrossRef]
- Jha, M.; Arnold, J.G.; Gassman, P.W.; Giorgi, F.; Gu, R.R. Climate change sensitivity assessment on upper Mississippi river basin streamflows using SWAT. J. Am. Water Resour. Assoc. 2006, 42, 997–1015. [Google Scholar] [CrossRef]
- Mengistu, D.T.; Sorteberg, A. Sensitivity of SWAT simulated streamflow to climatic changes within the Eastern Nile River basin. Hydrol. Earth Syst. Sci. 2012, 16, 391–407. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Gallant, A.L. Predicting impacts of increased CO2 and climate change on the water cycle and water quality in the semiarid James River Basin of the Midwestern USA. Sci. Total Environ. 2012, 430, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Praskievicz, S. Impacts of Projected Climate Changes on Streamflow and Sediment Transport for Three Snowmelt-Dominated Rivers in the Interior Pacific Northwest. River Res. Appl. 2016, 32, 4–17. [Google Scholar] [CrossRef]
- Lee, S.; Yeo, I.Y.; Sadeghi, A.M.; McCarty, G.; Hively, D.W.; Lang, M.; Sharifi, A. Comparative analyses of hydrological responses of two adjacent watersheds to climate variability and change scenarios using SWAT model. Hydrol. Earth Syst. Sci. 2018, 22, 689–708. [Google Scholar] [CrossRef]
- Suddick, E.C.; Whitney, P.; Townsend, A.R.; Davidson, E.A. The role of nitrogen in climate change and the impacts of nitrogen–climate interactions in the United States: Foreword to thematic issue. Biogeochemistry 2013, 114, 1–10. [Google Scholar] [CrossRef]
- Döll, P.; Siebert, S. Global modeling of irrigation water requirements. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Räty, O.; Räisänen, J.; Ylhäisi, J.S. Evaluation of delta change and bias correction methods for future daily precipitation: Intermodel cross-validation using ENSEMBLES simulations. Clim. Dyn. 2014, 42, 2287–2303. [Google Scholar] [CrossRef]
| Data | Source | Description | Year |
|---|---|---|---|
| DEM | MD-DNR | LiDAR-based 2-m resolution | 2006 |
| Land use | USDA-NASS | Cropland Data Layer (CDL) | 2008–2012 |
| MRLC | National Land Cover Database (NLCD) | 2006 | |
| USDA-FSA-APFO | National Agricultural Imagery Program digital Orthophoto quad imagery | 1998 | |
| US Census Bureau | TIGER road map | 2010 | |
| Soils | USDA-NRCS | Soil Survey Geographical Database (SSURGO) | 2012 |
| Climate | NCDC | Daily precipitation and temperature | 1999–2014 |
| Streamflow | USGS | Monthly streamflow | 2001–2014 |
| Water quality | USGS and CBP | Daily grab nitrate samples | 2001–2014 |
| Crop yield | USDA-NASS | Corn and soybean yield | 2001–2014 |
| Crop | Planting | Fertilizer | Harvest |
|---|---|---|---|
| Corn (after corn) | 30 April (no-till) | 157 kg N/ha of poultry manure on 20 April | 3 October |
| 45 kg N/ha of sidedress 30% UAN on 7 June | |||
| Corn (after Soybean and Double crop soybean) | 30 April (no-till) | 124 kg N/ha of poultry manure on 20 April | 3 October |
| 34 kg N/ha of sidedress 30% UAN on 7 June | |||
| Soybean | 20 May (no-till) | 15 October | |
| Double crop winter wheat (Dbl WW) | 20 October | 34 kg N/ha of sidedress 30% UAN on 8 October | 27 June |
| 45 kg N/ha of sidedress 30% UAN on 1 March | |||
| 67 kg N/ha of sidedress 30% UAN on 5 April | |||
| Double crop soybean (Dbl Soyb) | 29 June | 1 November |
| Parameter | Variable | Description (Unit) | Range | Value |
|---|---|---|---|---|
| CN2 # | Streamflow | Curve number | −50–50% | −30% |
| ESCO # | Soil evaporation compensation factor | 0–1 | 1 | |
| SURLAG # | Surface runoff lag coefficient | 0.5–24 | 0.5 | |
| SOL_AWC # | Available water capacity of the soil layer (mm H2O·mm soil−1) | −50–50% | −10% | |
| SOL_K # | Saturated hydraulic conductivity (mm·h−1) | −50–50% | 50% | |
| SOL_Z # | Depth from soil surface to bottom of layer (mm) | −50–50% | −20% | |
| ALPHA_BF # | Base flow recession constant (1·days−1) | 0–1 | 0.07 | |
| GW_DELAY # | Groundwater delay time (days) | 0–500 | 130 | |
| GW_REVAP # | Groundwater “revap” coefficient | 0.02–0.2 | 0.10 | |
| RCHRG_DP # | Deep aquifer percolation fraction | 0–1 | 0.01 | |
| GWQMN # | Threshold depth of water in the shallow aquifer required for return flow to occur (mm) | 0–5000 | 1.9 | |
| CH_K2 # | Effective hydraulic conductivity (mm·h−1) | 0–150 | 0 | |
| CH_N2 # | Manning coefficient | 0.01–0.3 | 0.29 | |
| NPERCO † | Nitrate | Nitrogen percolation coefficient | 0.01–1 | 0.5 |
| N_UPDIS † | Nitrogen uptake distribution parameter | 5–50 | 50 | |
| ANION_EXCL † | Fraction of porosity from which anions are excluded | 0.1–0.7 | 0.59 | |
| ERORGN † | Organic N enrichment ratio for loading with sediment | 0–5 | 4.92 | |
| BIOMIX † | Biological mixing efficiency | 0.01–1 | 0.01 | |
| SOL_NO3 § | Initial NO3 concentration in soil layer (mg N·kg−1) | 0–100 | 11.23 | |
| CDN $ | Denitrification exponential rate coefficient | 0–3.0 | 0.7 | |
| SDNCO $ | Denitrification threshold water content | 0.1–1.1 | 1.0 | |
| HVSTI & | Yield | Harvest index for optimal growing conditions | 0.5–0.7 | Corn 0.64 |
| Soyb 0.39 | ||||
| BLAI & | Maximum potential leaf area index | 5–8 | Corn 7.3 | |
| Soyb 4.4 | ||||
| FRGRW1 † | Fraction of the plant growing season of total potential heat units corresponding to the first point on the leaf area development curve | - | Corn 0.05 | |
| Soyb 0.03 | ||||
| FRGRW2 † | Fraction of the plant growing season of total potential heat units corresponding to the second point on the leaf area development curve | - | Corn 0.39 | |
| Soyb 0.39 | ||||
| LAIMX1 † | Fraction of the maximum leaf area index corresponding to the first point on the leaf area development curve | - | Corn 0.80 | |
| Soyb 0.56 | ||||
| LAIMX2 † | Fraction of the maximum leaf area index corresponding to the second point | - | Corn 0.98 | |
| Soyb 0.99 |
| Period | NSE | RSR | P–bias | p-Value | |
|---|---|---|---|---|---|
| Streamflow | Calibration | 0.705 ** | 0.542 ** | 10.5 ** | 0.99 |
| Validation | 0.703 ** | 0.544 ** | −12.6 ** | 0.97 | |
| Nitrate loads | Calibration | 0.738 ** | 0.511 ** | −3.5 *** | 0.99 |
| Validation | 0.515 * | 0.696 * | −14.9 ** | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Wallace, C.W.; Sadeghi, A.M.; McCarty, G.W.; Zhong, H.; Yeo, I.-Y. Impacts of Global Circulation Model (GCM) bias and WXGEN on Modeling Hydrologic Variables. Water 2018, 10, 764. https://doi.org/10.3390/w10060764
Lee S, Wallace CW, Sadeghi AM, McCarty GW, Zhong H, Yeo I-Y. Impacts of Global Circulation Model (GCM) bias and WXGEN on Modeling Hydrologic Variables. Water. 2018; 10(6):764. https://doi.org/10.3390/w10060764
Chicago/Turabian StyleLee, Sangchul, Carlington W. Wallace, Ali M. Sadeghi, Gregory W. McCarty, Honglin Zhong, and In-Young Yeo. 2018. "Impacts of Global Circulation Model (GCM) bias and WXGEN on Modeling Hydrologic Variables" Water 10, no. 6: 764. https://doi.org/10.3390/w10060764
APA StyleLee, S., Wallace, C. W., Sadeghi, A. M., McCarty, G. W., Zhong, H., & Yeo, I.-Y. (2018). Impacts of Global Circulation Model (GCM) bias and WXGEN on Modeling Hydrologic Variables. Water, 10(6), 764. https://doi.org/10.3390/w10060764






