Dynamic Management of Water Storage for Flood Control in a Wetland System: A Case Study in Texas
Abstract
1. Introduction
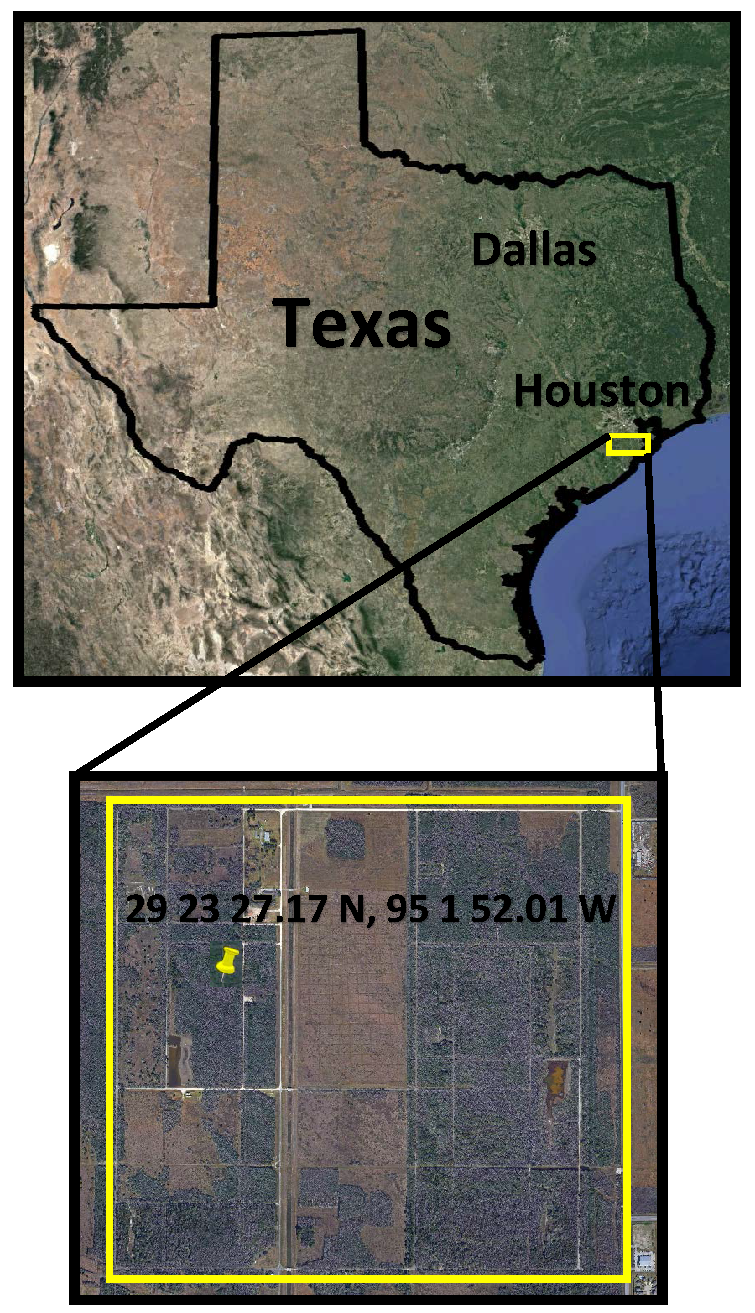
2. Case Study
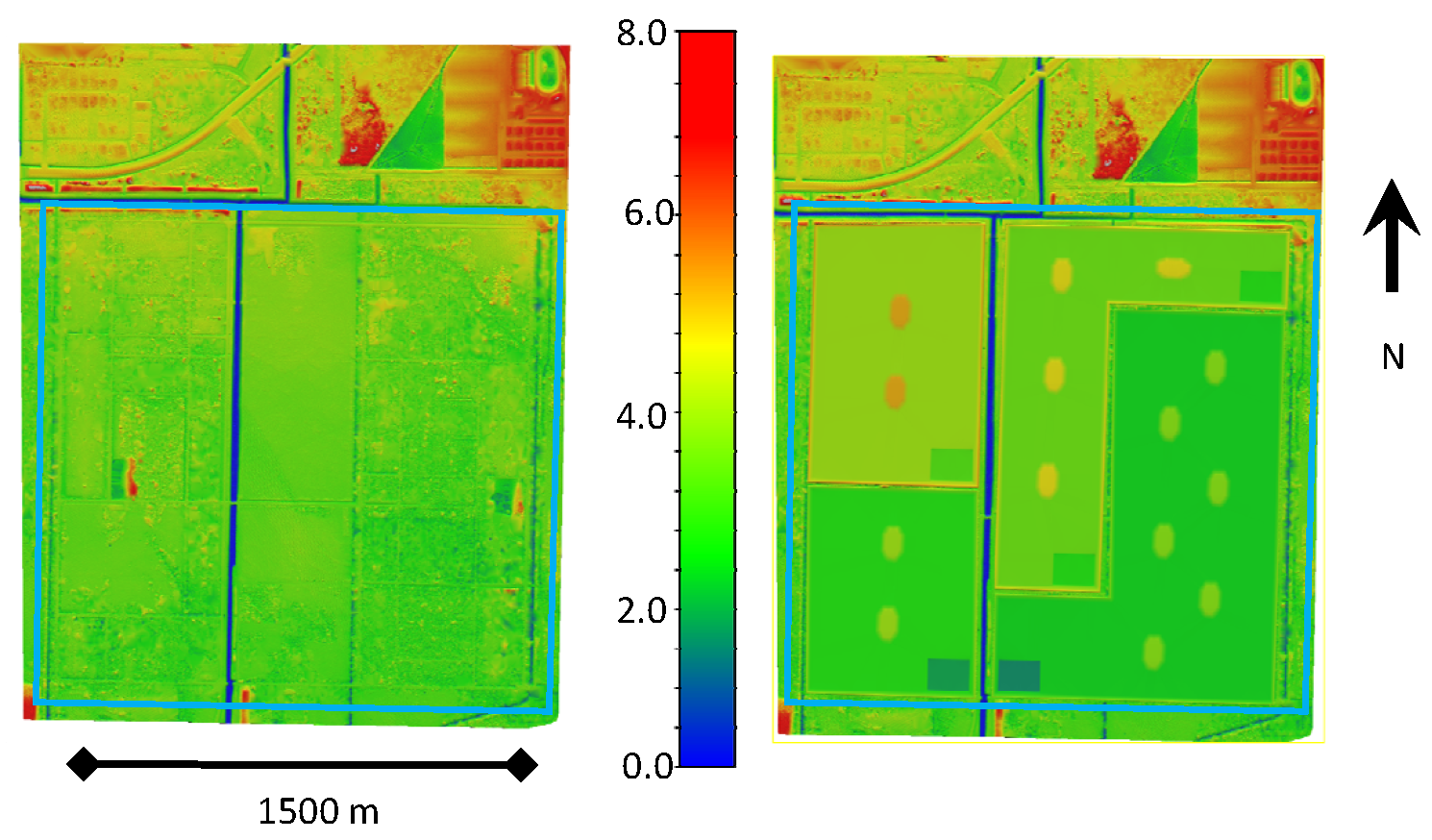
2.1. Geomatic Considerations
2.2. Environmental Considerations
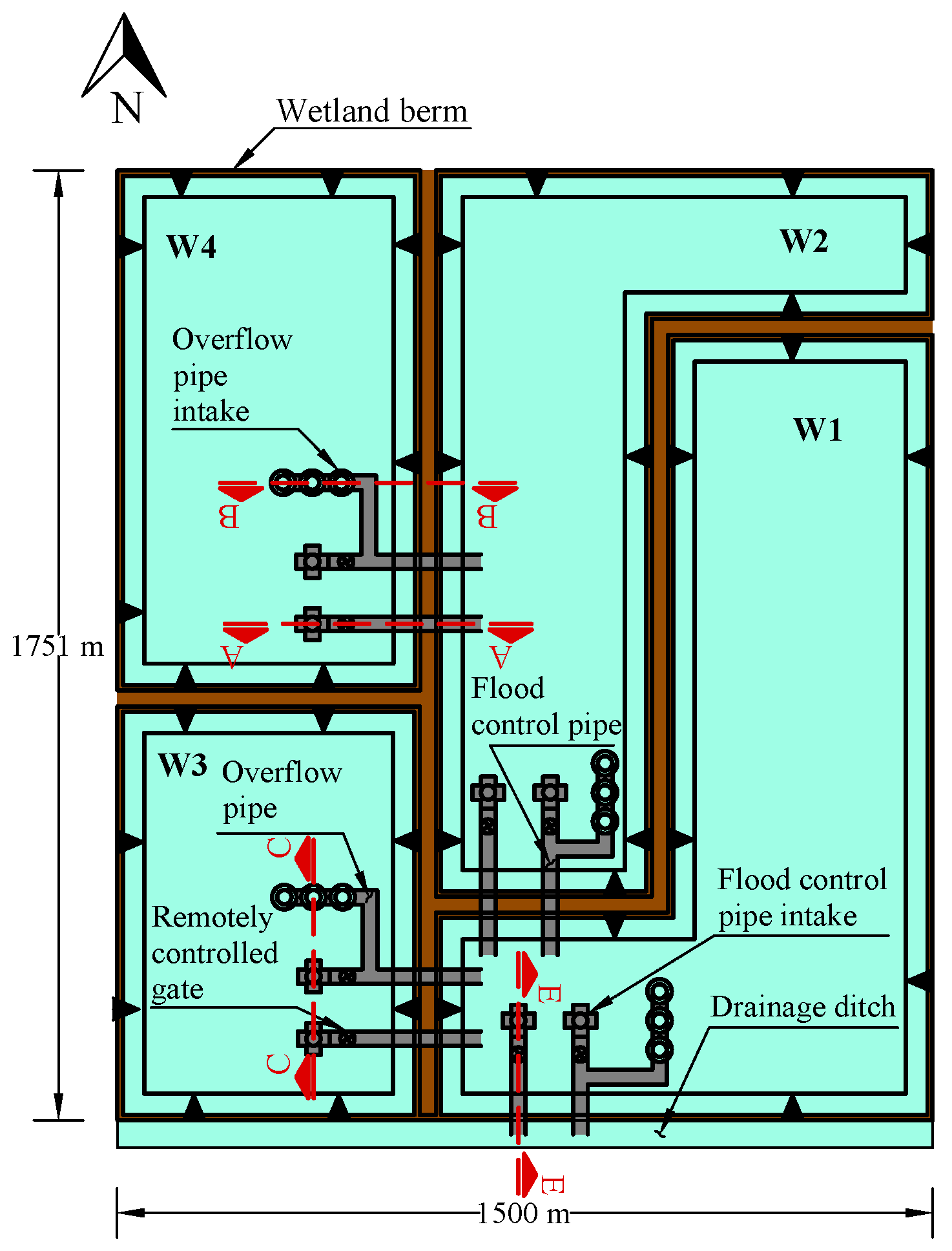
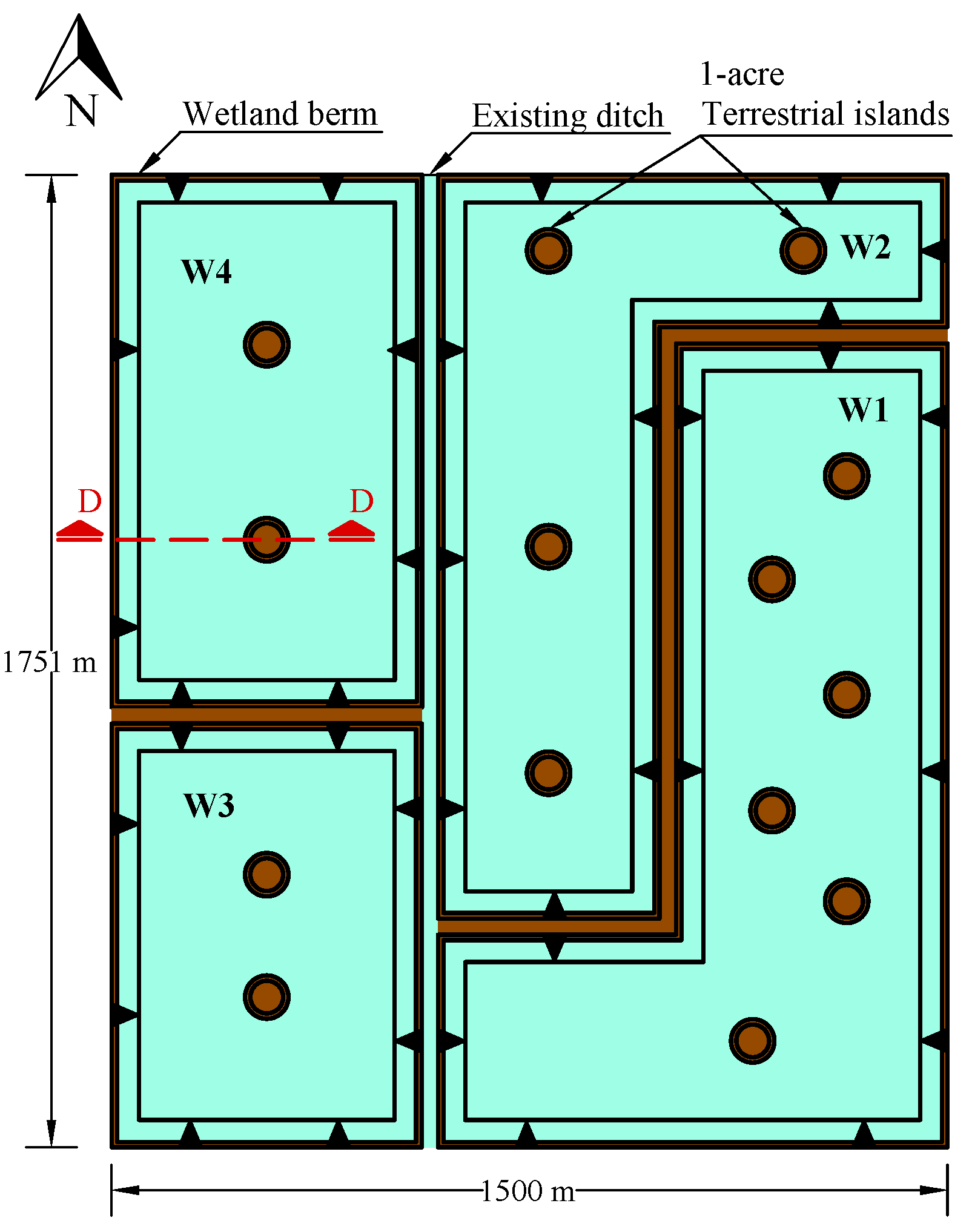
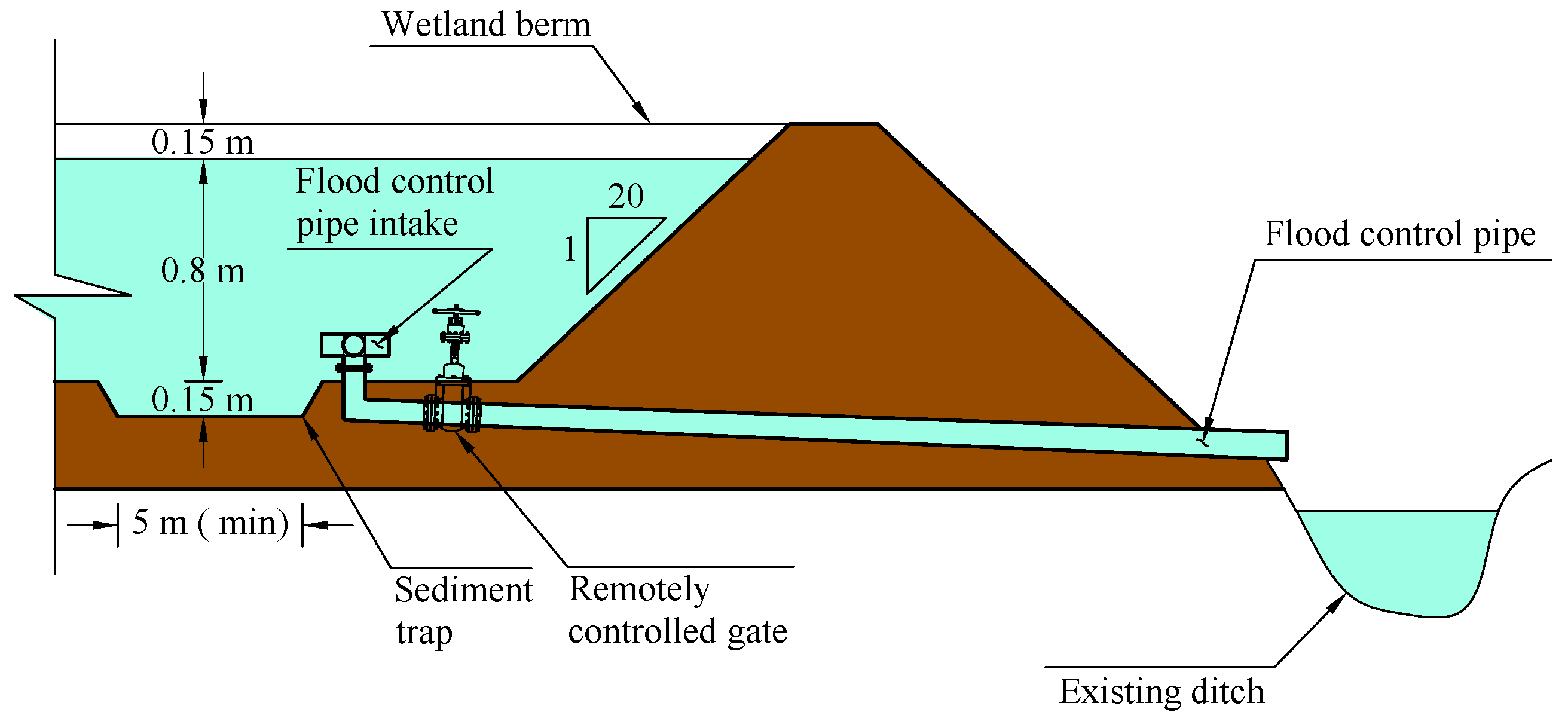
2.3. Simulated Scenario
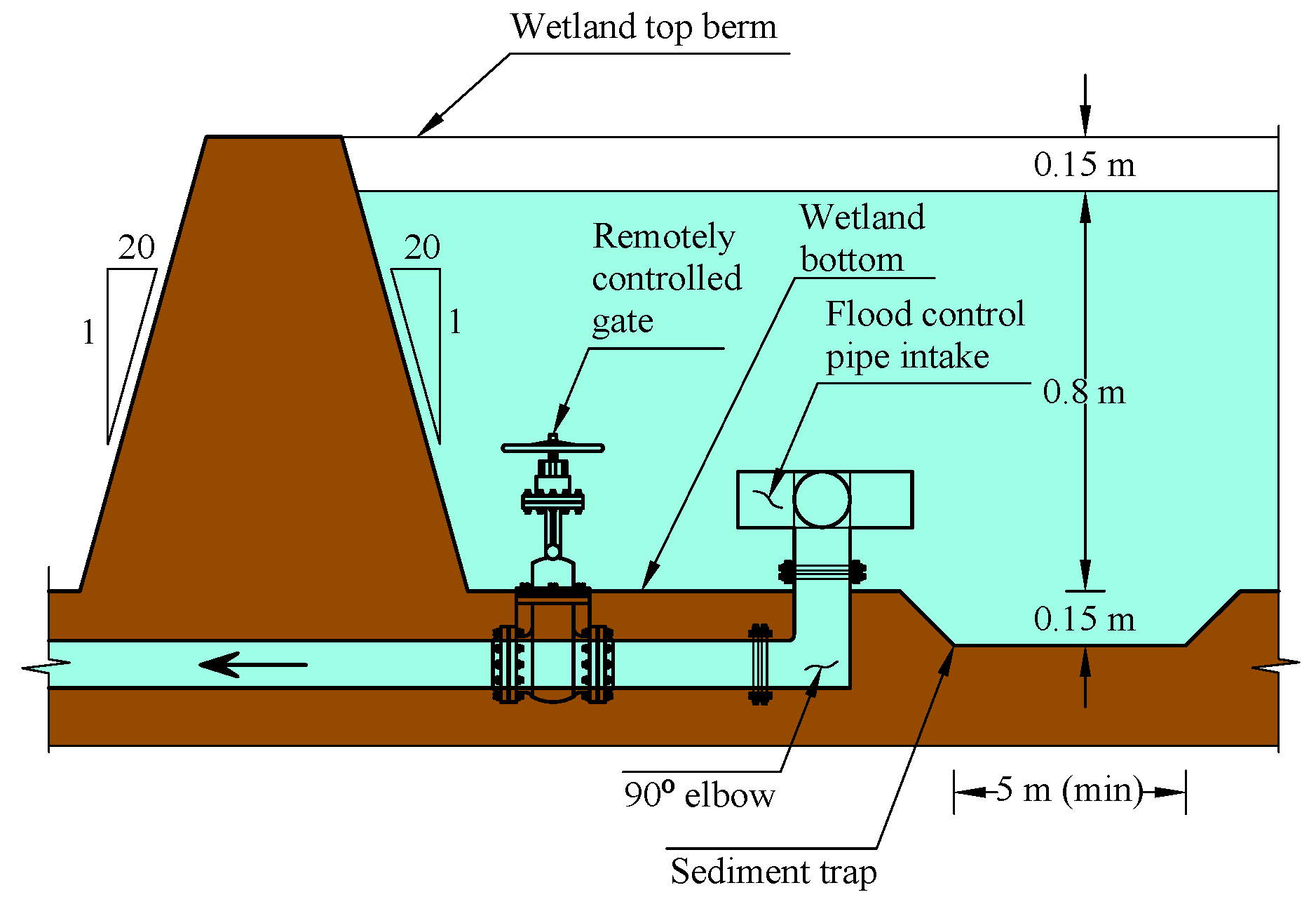
- The tailwater elevation for the flood pipe(s) at wetland 1 is below the outlet invert of the flood pipe(s).
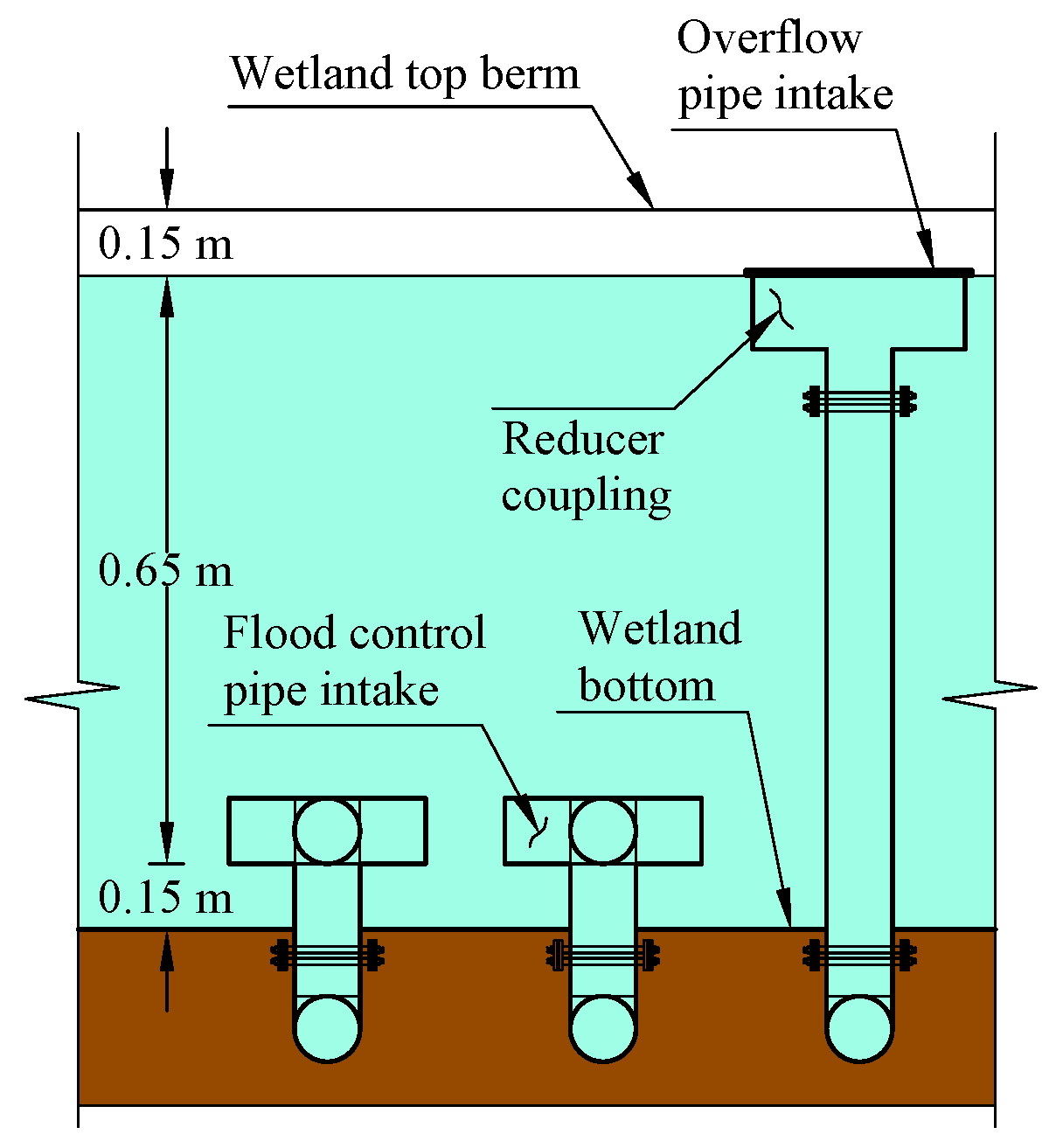
- The drop height between the inlet and outlet inverts () is set to 0.5 ft (0.15 m) for all flood pipes.
- The length (L) for all “flood pipes” is 400 ft (121.9 m).
- The soil cover height over the pipe crown () is set to 1.25D, where D is the pipe diameter.
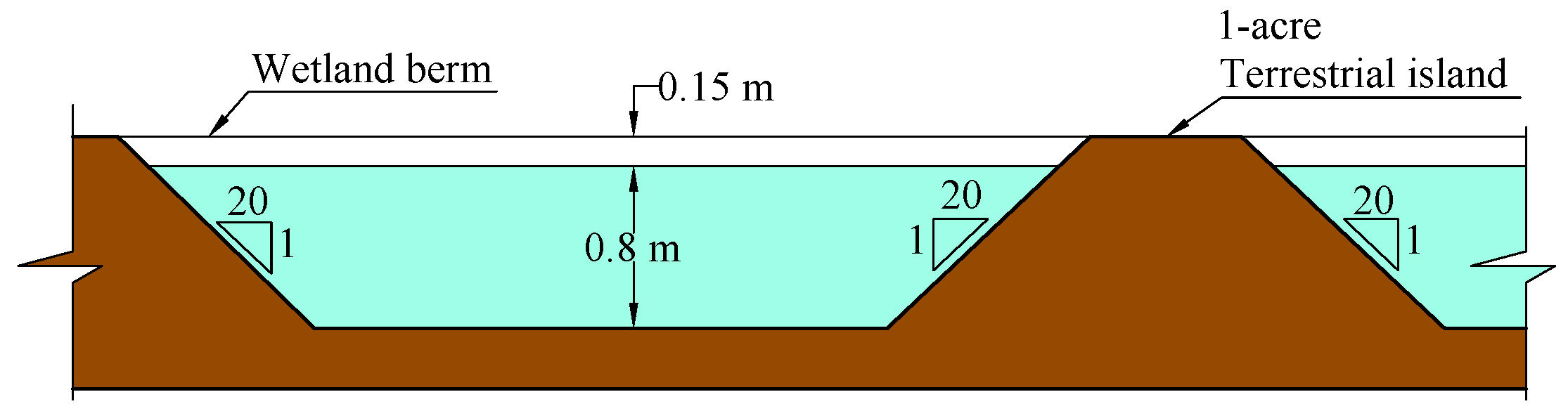
- The surface area () values of wetlands 1 to 4 are 240.31 acres (972,500 m), 161.61 acres (654,000 m), 108.73 acres (440,000 m), and 136.90 acres (554,000 m), respectively.
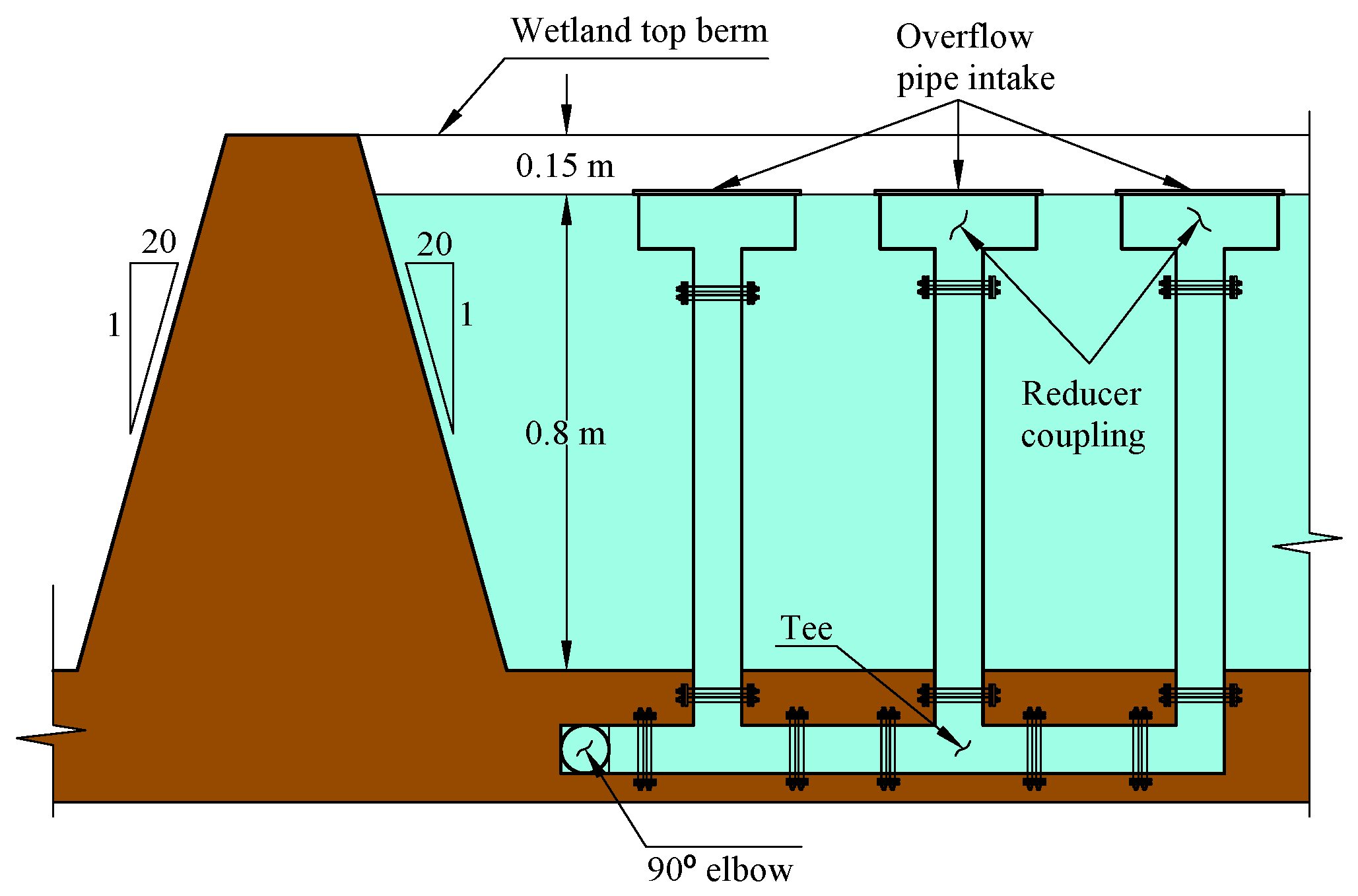
- The vertical distance from the invert of the five-way flood pipe intake to the bottom of the wetland () is set to 0.5 ft (0.15 m).
- The Manning’s roughness (n) for all “flood pipes” is set to 0.009.
- The entrance loss coefficient () for the intake of all “flood pipes” is set to 0.8.
- The initial water depth measured above the invert of the five-way flood pipe intake (h) for all wetlands is set to 2 ft (0.61 m).
2.4. Hydraulics of Simulated Scenarios
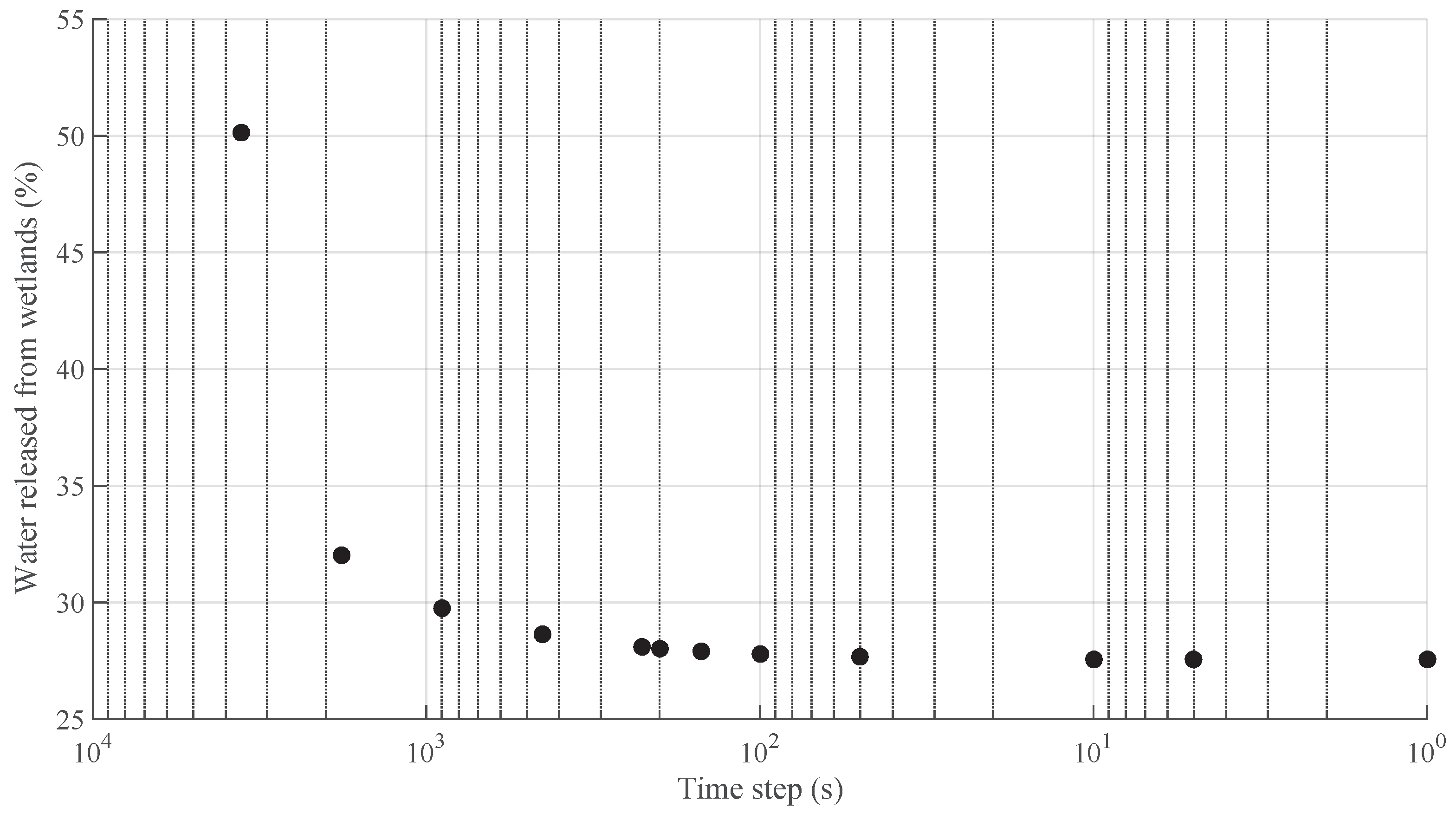
2.5. Time Step Convergence of Wetland Drainage Model
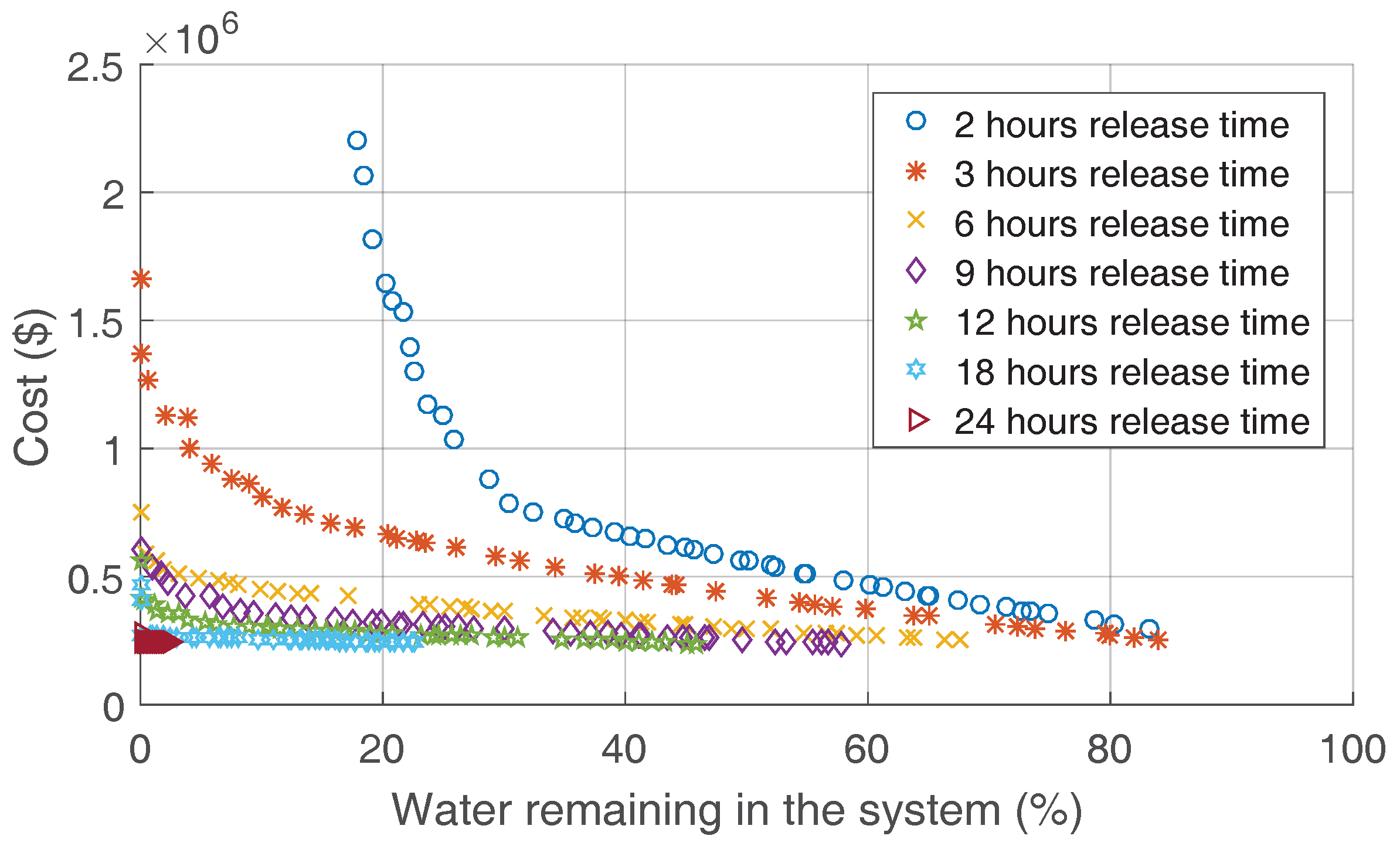
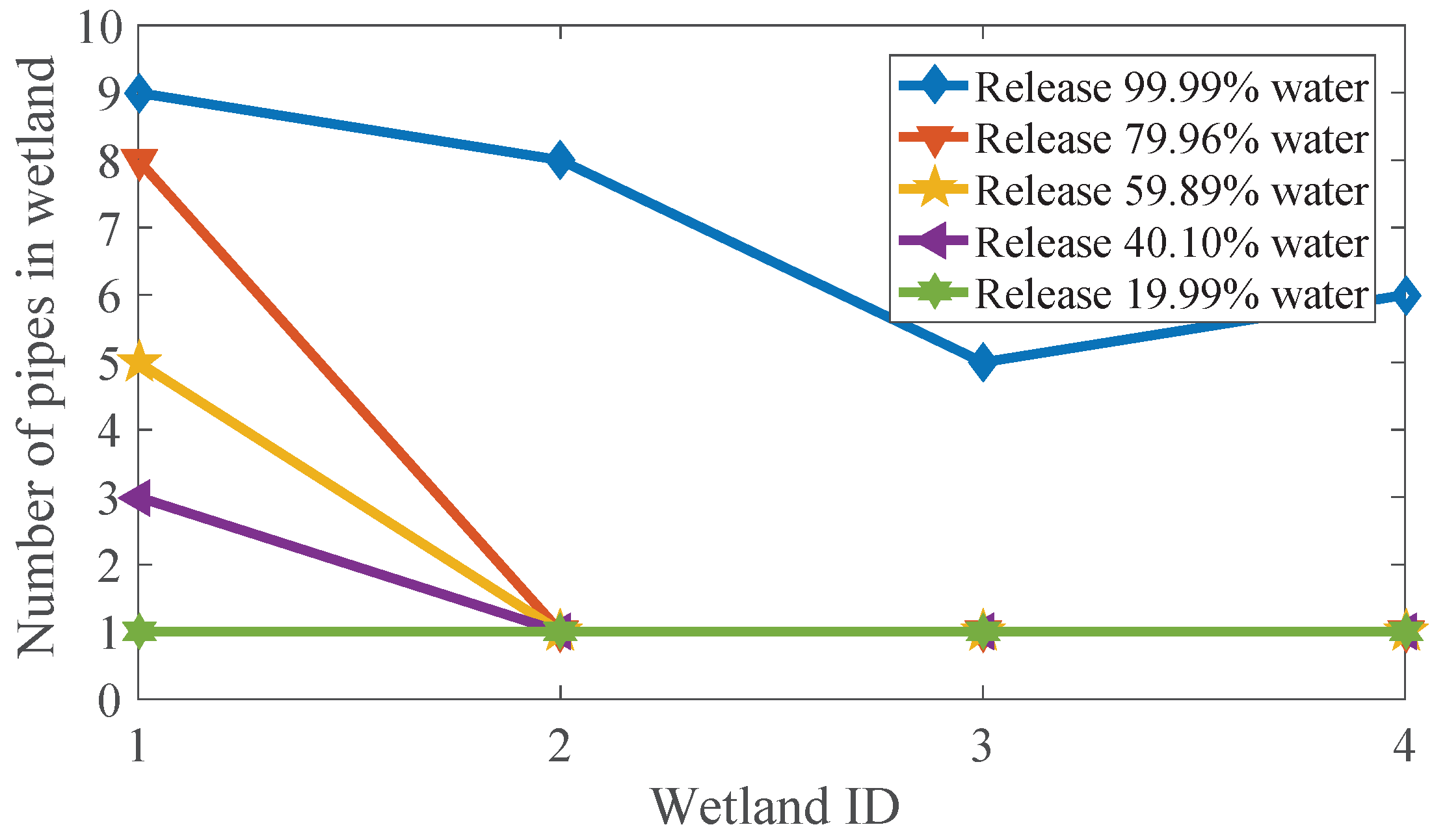
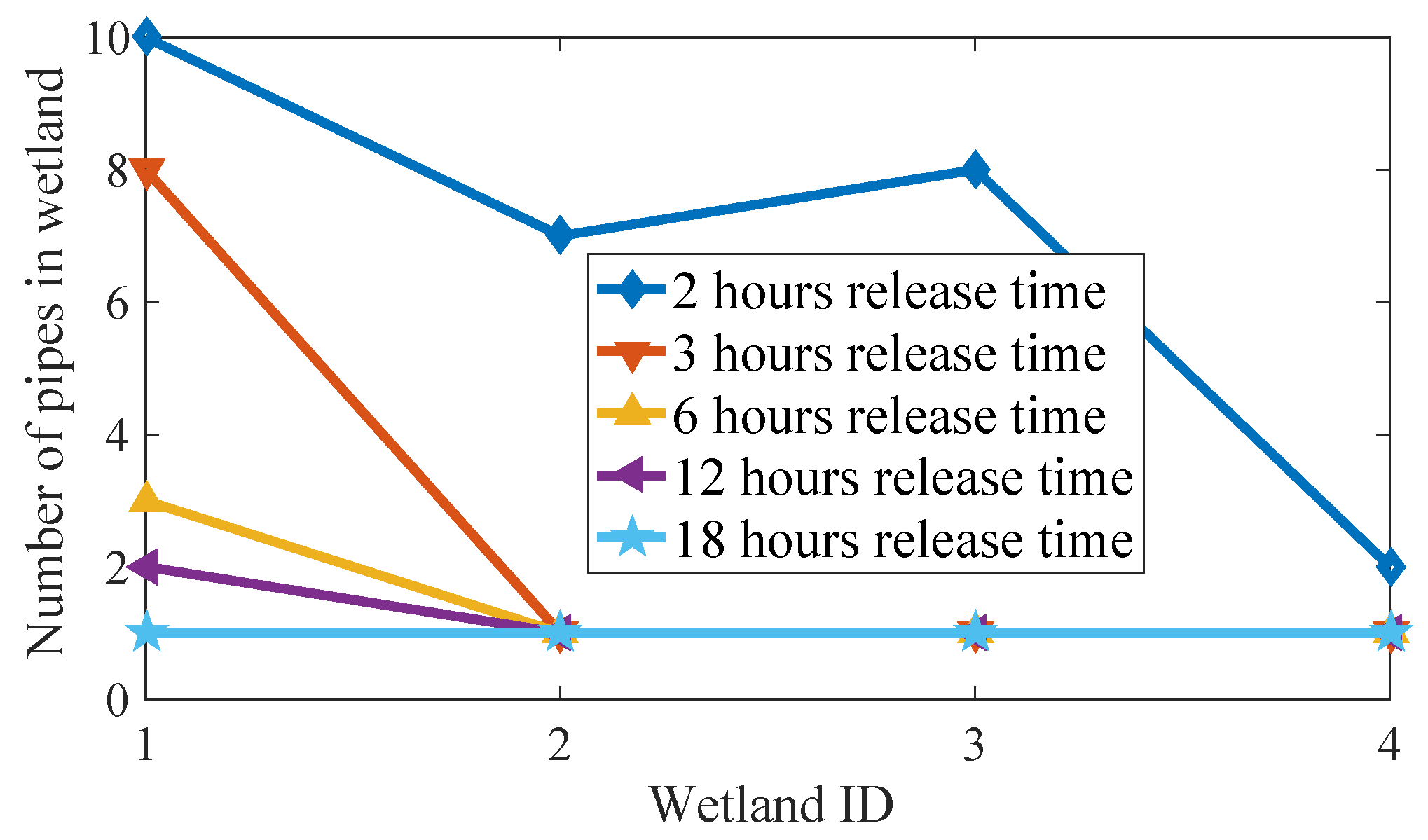
2.6. Optimal Number of Pipes for Each Wetland
2.6.1. Objectives
2.6.2. Constraints
2.7. Discussion of Results
3. Benefit–Cost Analysis
- Water supply (nontidal): $9320/acre/year ($2010). Benefit provided (nontidal): 100,000 gallons/ acre/day (wetlands can provide water at a lower cost than procuring it elsewhere).
- Water quality (nontidal): Median $3500/acre/year ($2010). Benefit provided (nontidal): Can filter 63% of nitrogen, 45% of phosphorous.
- Stormwater regulation/flood protection (nontidal): $7990/acre/year ($2010). Benefit provided (nontidal): Wetlands can typically store one million gallons of floodwater per acre.
- Climate regulation/carbon sequestration: $68–236/acre/year ($2010). Palustrine emergent (100%)—$100.4/acre/year. Because our proposed wetlands are relatively shallow, the wetlands would be mostly palustrine emergent. Benefit provided: Wetlands store between 75,000 and 260,000 lbs of carbon per acre.
- Recreation: $2092/acre/year ($2012). Benefit Provided: Birding/hunting.
4. Conclusions
- In general, the benefit value of wetland services far surpasses the costs of construction and maintenance of the UHCC wetland system for the three considered periods of analysis and the three degrees of dynamic management of wetland storage.
- The benefit/cost ratios increase with the period of analysis.
- Considering flood protection only (e.g., not considering the value of other ecosystem services), as long as dynamic management of wetland storage increases flood protection by about 50% compared to that with no management, the construction of a wetland system would have a benefit/cost ratio of at least 1.9.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kusler, J. Multi-Objective Wetland Restoration in Watershed Contexts; Technical Report; Association of State Wetland Managers: Berne, NY, USA, 2004. [Google Scholar]
- Flotemersch, J.E.; Leibowitz, S.G.; Hill, R.A.; Stoddard, J.L.; Thoms, M.C.; Tharme, R.E. A Watershed Integrity Definition and Assessment Approach to Support Strategic Management of Watersheds. River Res. Appl. 2016, 32, 1654–1671. [Google Scholar] [CrossRef]
- Chescheir, G.M.; Gilliam, J.W.; Skaggs, R.W.; Broadhead, R.G. Nutrient and sediment removal in forested wetlands receiving pumped agricultural drainage water. Wetlands 1991, 11, 87–103. [Google Scholar] [CrossRef]
- Bullock, A.; Acreman, M. The role of wetlands in the hydrological cycle. Hydrol. Earth Syst. Sci. 2003, 7, 358–389. [Google Scholar] [CrossRef]
- Timoney, K. Factors influencing wetland plant communities during a flood-drawdown cycle in the Peace-Athabasca Delta, Northern Alberta, Canada. Wetlands 2008, 28, 450–463. [Google Scholar] [CrossRef]
- Lee, S.Y.; Hamlet, A.F.; Fitzgerald, C.J.; Burges, S.J. Optimized Flood Control in the Columbia River Basin for a Global Warming Scenario. J. Water Resour. Plan. Manag. 2009, 135, 440–450. [Google Scholar] [CrossRef]
- Acreman, M.; Holden, J. How Wetlands Affect Floods. Wetlands 2013, 33, 773–786. [Google Scholar] [CrossRef]
- De Wilde, M.; Puijalon, S.; Vallier, F.; Bornette, G. Physico-Chemical Consequences of Water-Level Decreases in Wetlands. Wetlands 2015, 35, 683–694. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Bernal, B.; Hernandez, M.E. Ecosystem services of wetlands. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2015, 11, 1–4. [Google Scholar] [CrossRef]
- Sterzyńska, M.; Pižl, V.; Tajovský, K.; Stelmaszczyk, M.; Okruszko, T. Soil Fauna of Peat-Forming Wetlands in a Natural River Floodplain. Wetlands 2015, 35, 815–829. [Google Scholar] [CrossRef]
- Kadlec, R.H. Large Constructed Wetlands for Phosphorus Control: A Review. Water 2016, 8, 243. [Google Scholar] [CrossRef]
- Skagen, S.K.; Burris, L.E.; Granfors, D.A. Sediment Accumulation in Prairie Wetlands under a Changing Climate: the Relative Roles of Landscape and Precipitation. Wetlands 2016, 36, 383–395. [Google Scholar] [CrossRef]
- Lee, L.H. Perspectives on Landscape Aesthetics for the Ecological Conservation of Wetlands. Wetlands 2017, 37, 381–389. [Google Scholar] [CrossRef]
- Miller, J.O.; Ducey, T.F.; Brigman, P.W.; Ogg, C.O.; Hunt, P.G. Greenhouse Gas Emissions and Denitrification within Depressional Wetlands of the Southeastern US Coastal Plain in an Agricultural Landscape. Wetlands 2017, 37, 33–43. [Google Scholar] [CrossRef]
- Interagency Floodplain Management Review Committee. Sharing the Challenge: Floodplain Management into the 21st Century: Report of the Interagency Floodplain Management Review Committee to the Administration Floodplain Management Task Force; Executive Office of the President: Washington, DC, USA, 1994.
- McCuskey, S.A.; Conger, A.W.; Hillestad, H.O. Design and implementation of functional wetland mitigation: Case studies in Ohio and South Carolina. Water Air Soil Pollut. 1994, 77, 513–532. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (USEPA). Design Manual, Constructed Wetlands and Aquatic Plant Systems for Municipal Water Treament; Report EPA/625/1-88/022; U.S. Environmental Protection Agency: Washington, DC, USA, 1998.
- United States Environmental Protection Agency (USEPA). General Considerations. In A Handbook of Constructed Wetlands, A Guide to Creating Wetlands for Agricultural Wastewater, Domestic Wastewater, Coal Mine Drainage, Stormwater in the Mid-Atlantic Region; Technical Report; U.S. Environmental Protection Agency: Washington, DC, USA, 2000; Volume 1. [Google Scholar]
- Wooster, R.A.; Reddick, D.C.; McNamee, G.L. Texas. 2018. Available online: https://www.britannica.com/place/Texas-state (accessed on 1 March 2018).
- Glennie, C.L.; Carter, W.E.; Shrestha, R.L.; Dietrich, W.E. Geodetic imaging with airborne LiDAR: the Earth’s surface revealed. Rep. Prog. Phys. 2013, 76, 086801. [Google Scholar] [CrossRef] [PubMed]
- Steele, M.K.; Heffernan, J.B.; Bettez, N.; Cavender-Bares, J.; Groffman, P.M.; Grove, J.M.; Hall, S.; Hobbie, S.E.; Larson, K.; Morse, J.L.; et al. Convergent Surface Water Distributions in U.S. Cities. Ecosystems 2014, 17, 685–697. [Google Scholar] [CrossRef]
- Palta, M.M.; Grimm, N.B.; Groffman, P.M. “Accidental” urban wetlands: ecosystem functions in unexpected places. Front. Ecol. Environ. 2017, 15, 248–256. [Google Scholar] [CrossRef]
- Donohue, I.; Hillebrand, H.; Montoya, J.M.; Petchey, O.L.; Pimm, S.L.; Fowler, M.S.; Healy, K.; Jackson, A.L.; Lurgi, M.; McClean, D.; et al. Navigating the complexity of ecological stability. Ecol. Lett. 2016, 19, 1172–1185. [Google Scholar] [CrossRef] [PubMed]
- Sharitz, R.R.; Batzer, D.P.; Pennings, S.C. Ecology of freshwater and estuarine wetlands: An introduction. In Ecology of Freshwater and Estuarine Wetlands, 2nd ed.; Batzer, D.P., Sharitz, R.R., Eds.; University of California Press: Oakland, CA, USA, 2014. [Google Scholar]
- McPeek, M.A. Trade-Offs, Food Web Structure, and the Coexistence of Habitat Specialists and Generalists. Am. Nat. 1996, 148, S124–S138. [Google Scholar] [CrossRef][Green Version]
- McPeek, M.A. The Consequences of Changing the Top Predator in a Food Web: A Comparative Experimental Approach. Ecol. Monogr. 1998, 68, 1–23. [Google Scholar] [CrossRef]
- Snodgrass, J.W.; Komoroski, M.J.; Bryan, A.L.; Burger, J. Relationships among Isolated Wetland Size, Hydroperiod, and Amphibian Species Richness: Implications for Wetland Regulations. Conserv. Biol. 2000, 14, 414–419. [Google Scholar] [CrossRef]
- Ehrenfeld, J.G. The expression of multiple functions in urban forested wetlands. Wetlands 2004, 24, 719–733. [Google Scholar] [CrossRef]
- Tarr, T.L.; Baber, M.J.; Babbitt, K.J. Macroinvertebrate community structure across a wetland hydroperiod gradient in southern New Hampshire, USA. Wetl. Ecol. Manag. 2005, 13, 321–334. [Google Scholar] [CrossRef]
- Brooks, R.T. Annual and seasonal variation and the effects of hydroperiod on benthic macroinvertebrates of seasonal forest (“vernal”) ponds in central Massachusetts, USA. Wetlands 2000, 20, 707–715. [Google Scholar] [CrossRef]
- Batzer, D.P.; Resh, V.H. Wetland management strategies that enhance waterfowl habitats can also control mosquitoes. Am. Mosq. Control Assoc. 1992, 8, 117–125. [Google Scholar]
- Batzer, D.P.; Wissinger, S.A. Ecology of insect communities in nontidal wetlands. Annu. Rev. Entomol. 1996, 41, 75–100. [Google Scholar] [CrossRef] [PubMed]
- Moulton, D.W.; Jacob, J. Texas Coastal Wetlands Guidebook; Publication TAMU-SG-00-605 (r); Texas Sea Grant: College Station, TX, USA, 2000. [Google Scholar]
- Tiner, R. Geographically isolated wetlands of the United States. Wetlands 2003, 23, 494–516. [Google Scholar] [CrossRef]
- Jacob, J.; Pandian, K.; Lopez, R.; Briggs, H. Houston-Area Freshwater Wetland Loss, 1992–2010; Erpt-002, Tamu-sg-14-303; Texas A&M Agrilife Extension: College Station, TX, USA, 2014.
- Wilcox, B.P.; Dean, D.D.; Jacob, J.S.; Sipocz, A. Evidence of Surface Connectivity for Texas Gulf Coast Depressional Wetlands. Wetlands 2011, 31, 451–458. [Google Scholar] [CrossRef]
- Leon, A.S.; Alnahit, A. A Remotely Controlled Siphon System for Dynamic Water Storage Management. In Proceedings of the 6th IAHR International Symposium on Hydraulic Structures, Portland, OR, USA, 27–30 June 2016; pp. 1–11. [Google Scholar]
- Leon, A.S.; Chen, D.; Yolcu, A. Optimal drainage of interconnected wetlands for flood control. Appl. Water Eng. Res. Under review 2017. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Chen, D.; Leon, A.S.; Gibson, N.L.; Hosseini, P. Dimension reduction of decision variables for multireservoir operation: A spectral optimization model. Water Resour. Res. 2016, 52, 36–51. [Google Scholar] [CrossRef]
- Houston-Wilderness. Ecosystem Services. 2017. Available online: http://houstonwilderness.org/ecosystem-services/ (accessed on 5 July 2017).
- United States Environmental Protection Agency (USEPA). Preliminary Data Summary of Urban Storm Water Best Management Practices; Report EPA-821-R-99-012; U.S. Environmental Protection Agency: Washington, DC, USA, 1999.
- Weiss, P.T.; Gulliver, J.S.; Erickson, A.J. The Cost and Effectiveness of Stormwater Management Practices; Report 2005-23; Minnesota Department of Transportation: Saint Paul, MN, USA, 2005.
- Omnisite. OmniSite Vs. SCADA. 2016. Available online: http://www.omnisite.com/ (accessed on 5 July 2017).
- Texas Coastal Watershed Program. Cost and Maintenance. 2017. Available online: http://tcwp.tamu.edu/stormwater/wetlands/cost-and-maintenance/ (accessed on 5 July 2017).

| Wetland | Bottom Elevation (m) | Water Surf. Elevation (m) | Surface Area (m2) | Storage Volume (m3) | Cut Volume (m3) | Fill Volume (m3) |
|---|---|---|---|---|---|---|
| 1 | 3.6 | 4.4 | 972,500 | 760,000 | 122,000 | 69,000 |
| 2 | 4.4 | 5.2 | 654,000 | 515,000 | 73,400 | 115,400 |
| 3 | 3.8 | 4.6 | 440,000 | 340,000 | 178,200 | 25,500 |
| 4 | 4.8 | 5.6 | 554,000 | 430,000 | 21,500 | 180,500 |
| Ecosystem Services | Unitary Value Ref: Houston-Wilderness | Value in 2018 per Acre | Cum. Value 2018–2037 per Acre | Cum. Value 2018–2047 per Acre | Cum. Value 2018–2067 per Acre |
|---|---|---|---|---|---|
| Water Supply (Nontidal) | $9320/acre/year Year 2010 | $11,049 | $272,508 | $458,920 | $974,779 |
| Water Quality (Nontidal) | $3500/acre/year Year 2010 | $4149 | $102,337 | $172,341 | $366,065 |
| Stormw. Regul./Flood Protect. (Nontidal) | $7990/acre/year Year 2010 | $9472 | $233,620 | $393,430 | $835,674 |
| Climate Regul./Carbon Sequest. Palustrine Emergent (100%) | $100.4/acre/year Year 2010 | $119 | $2936 | $4944 | $10,501 |
| Recreation | $2092/acre/year Year 2012 | $2377 | $58,620 | $98,720 | $209,689 |
| Total | $27,166 | $670,021 | $1,128,355 | $2,396,707 |
| Description | Unitary Value (See References in This Column) | Value per Acre Year 2018 | Value at 2037 or Cum. Value 2018–2037 per Acre | Value at 2047 or Cum. Value 2018–2047 per Acre | Value at 2067 or Cum. Value 2018–2067 per Acre |
|---|---|---|---|---|---|
| Land costs | $50,000/acre (Year 2017) (Estimated) | $51,075 | $76,513 | $94,650 | $144,840 |
| Design and Engineering | $500,000 (entire system) (Year 2017) (Estimated) | $552 | $827 | $1023 | $1566 |
| Earthwork (cut) | $12/cu. yd. (Year 2017) (Aver. of 3 contractors in Houston-Galveston) | $6704 | $10,043 | $12,424 | $19,012 |
| Earthwork (fill) | $12/cu. yd. (Year 2017) (Aver. of 3 contractors in Houston-Galveston) | $6624 | $9924 | $12,276 | $18,785 |
| Drainage pipes and Automated gates | $650,000 (entire system) (Year 2017) (Optimiz. in this paper) | $718 | $1075 | $1330 | $2036 |
| Installing vegetation | $10000/acre (Year 2017) (Texas Coastal Watershed Program 2017) | $10,215 | $15,303 | $18,930 | $28,968 |
| Equipment for remote operation of gates | $11,000,000 (entire system) (Year 2017) (Omnisite) | $12,148 | $18,198 | $22,511 | $34,448 |
| Mainten. of remote operation of gates and cel. annual fees | $575,000/year (Year 2017) (Omnisite 2017) | $635 | $951 | $1177 | $1801 |
| Wetland maintenance (does not include Gate remote operat.) | 9.1% of construction cost per year Weiss et al. (2005) | $2208 | $54,452 | $91,700 | $194,776 |
| Total | $90,879 | $187,286 | $256,021 | $446,232 |
| Description | Total Value 2018–2037 (925 Acres) | Total Value 2018–2047 (925 Acres) | Total Value 2018–2067 (925 Acres) |
|---|---|---|---|
| Construction and maintenance costs | $173,239,346 | $236,819,296 | $412,764,576 |
| Value of benefits of ecosystem services New flood control (FC) = 1 × FC with no storag. manag. | $619,769,648 | $1,043,728,778 | $2,216,954,114 |
| Benefit/cost ratio | 3.58 | 4.41 | 5.37 |
| Value of benefits of ecosystem services New FC = 2 × FC with no storag. manag. | $835,868,379 | $1,407,651,834 | $2,989,952,553 |
| Benefit/cost ratio | 4.82 | 5.94 | 7.24 |
| Value of benefits of ecosystem services New FC = 3 × FC with no storag. manag. | $1,051,967,110 | $1,771,574,890 | $3,762,950,991 |
| Benefit/cost ratio | 6.07 | 7.48 | 9.12 |
| Description | Total Value 2018–2037 (925 Acres) | Total Value 2018–2047 (925 Acres) | Total Value 2018–2067 (925 Acres) |
|---|---|---|---|
| Construction and maintenance costs | 173,239,346 | 236,819,296 | 412,764,576 |
| Value of benefits (New flood control (FC) = 0 × FC with no storag. manag.) | 216,098,731 | 363,923,056 | 772,998,439 |
| Benefit/cost ratio | 1.25 | 1.54 | 1.87 |
| Value of benefits New FC = 0.5 × FC with no storag. manag. | 324,148,096 | 545,884,584 | 1,159,497,658 |
| Benefit/cost ratio | 1.87 | 2.31 | 2.81 |
| Value of benefits New FC = 1 × FC with no storag. manag. | 432,197,462 | 727,846,112 | 1,545,996,878 |
| Benefit/cost ratio | 2.49 | 3.07 | 3.75 |
| Value of benefits New FC = 2 × FC with no storag. manag. | 648,296,193 | 1,091,769,168 | 2,318,995,316 |
| Benefit/cost ratio | 3.74 | 4.61 | 5.62 |
| Value of benefits New FC = 4 × FC with no storag. manag. | 1,080,493,655 | 1,819,615,280 | 3,864,992,194 |
| Benefit/cost ratio | 6.24 | 7.68 | 9.36 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon, A.S.; Tang, Y.; Chen, D.; Yolcu, A.; Glennie, C.; Pennings, S.C. Dynamic Management of Water Storage for Flood Control in a Wetland System: A Case Study in Texas. Water 2018, 10, 325. https://doi.org/10.3390/w10030325
Leon AS, Tang Y, Chen D, Yolcu A, Glennie C, Pennings SC. Dynamic Management of Water Storage for Flood Control in a Wetland System: A Case Study in Texas. Water. 2018; 10(3):325. https://doi.org/10.3390/w10030325
Chicago/Turabian StyleLeon, Arturo S., Yun Tang, Duan Chen, Ahmet Yolcu, Craig Glennie, and Steven C. Pennings. 2018. "Dynamic Management of Water Storage for Flood Control in a Wetland System: A Case Study in Texas" Water 10, no. 3: 325. https://doi.org/10.3390/w10030325
APA StyleLeon, A. S., Tang, Y., Chen, D., Yolcu, A., Glennie, C., & Pennings, S. C. (2018). Dynamic Management of Water Storage for Flood Control in a Wetland System: A Case Study in Texas. Water, 10(3), 325. https://doi.org/10.3390/w10030325






