A 60-Minute Design Rainstorm for the Urban Area of Yangpu District, Shanghai, China

Abstract

Rainfall with varied temporal distribution is an essential input to urban flood models. In this study, a 60-min design rainstorm with different return periods for the urban area of Yangpu District, Shanghai, China was derived. The design of areal rainfall amounts with given return periods was calculated through frequency analysis. The temporal distribution of the hyetograph was derived using the Pilgrim and Cordery method, combined with the fuzzy identification of seven mode hyetographs for single-peak and double-peak rainstorms separately. The derived hyetographs using the Pilgrim and Cordery method were compared with the classic Chicago rainstorm method. The results indicated that: (1) separating single-peak and double-peak rainstorms to derive respective hyetographs is more practical and rational; (2) a design rainstorm using the proposed methodology is superior to the Chicago rainstorm method.

1. Introduction

The inevitable trend of global climate change has brought about considerably frequent occurrences of extreme climate events [1,2,3,4]. Recently, under the influence of typhoons, urban floods caused by rainstorms have exerted great harm on the safety of society. In order to ensure the safety and continued operation of cities under extreme climate conditions, the Chinese government is making every effort to solve the problem of urban flooding by constructing and maintaining drainage pipelines. In order to determine the slope and diameter of the pipeline when designing drainage pipelines, models that simulate urban waterlogging are developed. Rainfall is the input of most kinds of hydrological and hydraulic models, whose accuracy and resolution directly affect the correctness of the model output [5,6]. Usually, a design rainstorm with a given return period is used in such models. The total rainfall amount, with specific duration, can be calculated through frequency analysis. In early studies, a hyetograph was assumed to be uniformly distributed on both spatial and temporal scales [7]. However, this assumption is in conflict with reality because in most rainfall events the rainfall intensity is always variable during the whole process [8]. Therefore, the refinement of the temporal and spatial patterns of hyetographs is more conducive to forecasting urban floods.

The precipitation data obtained by rain gauges only account for observation at one point. In order to study the total rainfall amount in a region, areal rainfall should be calculated. The calculation of areal rainfall is normally carried out through the transformation from “point” to “area” by means of various interpolation methods. Conventional areal rainfall estimation methods are the arithmetic average method, Thiessen polygon techniques, the isohyetal method, and the grid method. Nowadays, the development of remote sensing has brought rainfall data from weather radars and satellites with much higher coverage and finer resolution, which makes the calculation of areal rainfall more accurate and convenient [9,10,11]. Examples of such products are TRMM, 3B42/3B43, CMORPH, PERSIANN, TAMSA, and RFE2.0.

Research into design hyetographs with varying temporal patterns started in the early 20th century. There are several classic and widely used methodologies to derive hyetographs. In 1937, Mo et al. [12] analyzed 800 rainfall events in the former Soviet Union and summarized seven types of hyetographs. They are well-known as “mode hyetographs”. Keifer and Chu [13] proposed a method which is based on an intensity–duration–frequency (IDF) curve and a rainstorm intensity formula. This method is known as the Chicago rainstorm method. Huff [14] divided rainfall events into four classes based on which quarter of the duration the peak falls in. The hyetograph is then derived from quantiles of rainfall events within each class in a different period. Pilgrim and Cordery [15] developed an order-average hyetograph based on the principle of statistics (referred to as the P&C method). It places the peak of the rainfall in the period where it is most likely to happen. For a small drainage area that is below 10 mi², Yen and Chow [16] proposed a triangular-shaped hyetograph. The position of the peak is determined by the dimensionless first-order moment of the rainstorm event. The Natural Resources Conservation Service (NRCS) [17] developed a synthetic hyetograph, utilizing 6 h and 24 h rainstorm data from the US, which is called a “Soil Conservation Service (SCS) hyetograph”. There are four basic types of SCS hyetographs, each of them accounting for a specific region and climate. Besides the above-mentioned classic methods, there are also newly-developed methods to derive hyetographs; refer to Cheng et al. [18], Lin and Wu [19], Powell et al. [20], Lee and Ho [21], and Kottegoda [22] for detailed descriptions.

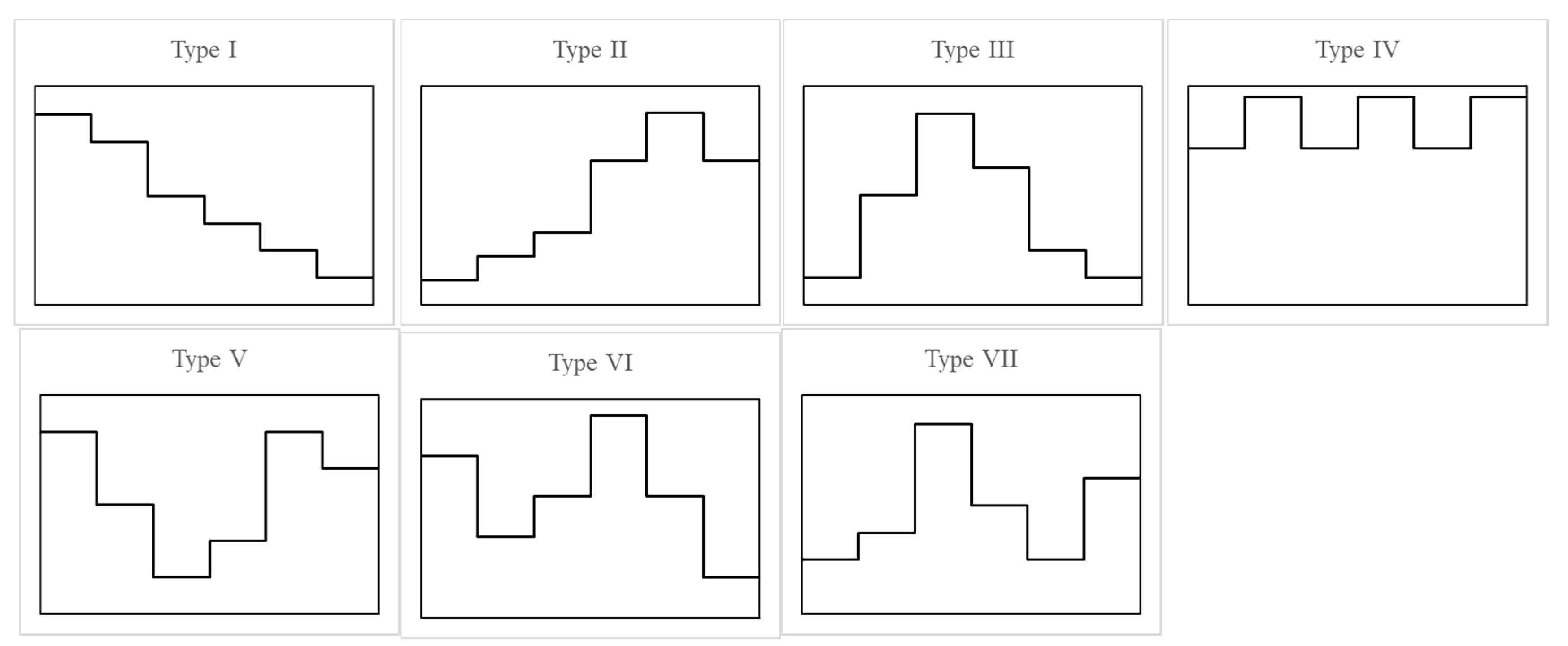
The classification of seven mode hyetographs is simple and distinct. Among them, Types I, II, and III are single-peak hyetographs, with peak falls at the beginning, middle, and end of the event; Type IV is uniformly distributed; V, VI, and VII are double-peak hyetographs with peaks falling at the beginning and end, beginning and middle, middle and end of the event, respectively. Visual estimation and fuzzy identification are often used for classification.

As the representative of statistical hyetographs, the P&C method is based on the statistical analysis of considerable rainfall data, and thus the derived hyetograph approximates the actual rainfall process. The simplicity of its principle and implementation makes it a convenient method. In most cases, all the rainfall events are used to derive one single hyetograph. However, the rainfall events may have a single peak, double-peaks, or multiple peaks. These rainfall events with different numbers of peaks will have different influences on the confluence process. If one mixes single-peak and multiple-peak rainfalls, the derived hyetograph is distorted to some extent. Therefore, in this study, a combination of mode hyetographs and the P&C method is proposed to derive single-peak hyetographs and double-peak hyetographs.

The main objectives of this study are: (1) to derive the design hyetographs for a 60-min rainstorm with different return periods in Yangpu District in order to serve as the input to an urban runoff model; (2) to explore the influences of separating single-peak and double-peak rainstorms in deriving hyetographs; (3) to compare the methodology of combining mode hyetographs and the P&C method with the classic design hyetograph method. The methodology and procedure used to derive hyetographs in this study can also be a reference for other small cities and regions.

2. Materials and Methods

2.1. Study Area

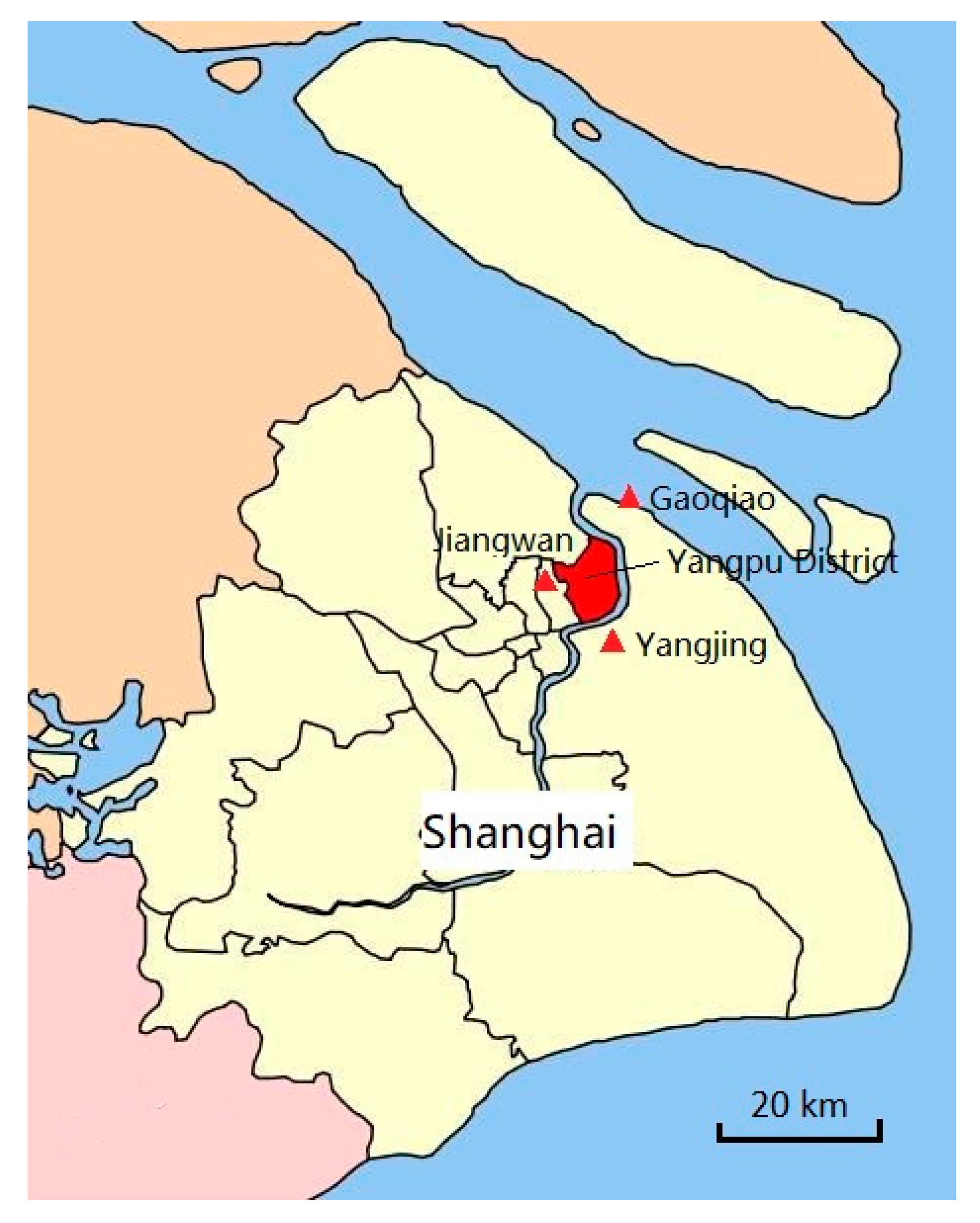
Yangpu District in Shanghai, China, was selected as the study area. Shanghai is located in the Southeast of China. Yangpu District is in the central part of the city, and has an area of about 60 km². The Huangpu River winds along the southeast side of the district. The subtropical monsoon climate results in an average annual precipitation of 1060 mm.

2.2. Process of Precipitation Data

Because Yangpu District is in the downtown area, there are no adequate precipitation data inside the district. Therefore, precipitation data from three nearby stations: Gaoqiao, Yangjing, and Jiangwan (Figure 1) were used for areal rainfall estimation, frequency analysis, and the derivation of hyetographs. Due to the availability of the data, the annual maximum 60-min rainfalls from 1978 to 2015 in Gaoqiao and Yangjing were used for areal rainfall estimation and frequency analysis. The precipitation data from Jiangwan Station with 5 min intervals from 2001 to 2015 were used to derive the hyetographs. The duration for the hyetograph design was 60 min. The individual rainfall events were divided before designing the hyetograph. Different criteria for selecting inter-event times are reported in [23,24,25,26,27,28]. In this study, 120 min was selected as the inter-event time based on the regulations in China [29], by which the successive rainfall processes were divided into independent rainfall events. Rainfall events that exceed 16 mm in 60 min were selected (also based on the regulations in China) to derive the hyetographs, and in total 117 events were selected.

2.3. Overall Procedure

The procedure for deriving the 60-min design hyetographs is as follows:

• Calculation of the areal rainfall in Yangpu District using the arithmetic average method.
• Frequency analysis using Pearson-III distribution in order to derive the maximum 60-min areal rainfall with return periods of 2, 5, 10, and 20 years.
• Classification of rainfall events into seven types of mode hyetographs using the fuzzy identification method.
• Use the P&C method to derive single-peak hyetographs and double-peak hyetographs.

The duration of the design rainstorm was selected based on the following reasons: (1) According to the standard of rainstorm intensity formula and design rainstorm distribution in Shanghai [30], the duration of the design rainstorm should be 5–180 min for drainage system design; (2) The data in the study area are limited, and 60 min is the duration in which the data has the best quality; (3) 60 min is applicable to a large portion of urban drainage work [31].

The design rainstorm using the proposed methodology was compared to the classic design rainstorm to test its superiority. The standard of rainstorm intensity formula and design rainstorm distribution in Shanghai suggest the use of the Chicago rainstorm method for the design rainstorm. Therefore, the design rainstorm using the proposed methodology was compared with the one using Chicago rainstorm method.

2.4. Areal Rainfall Estimation

The arithmetic average method was used to calculate the areal rainfall due to the limited rainfall data in the region. The average value of the rainfall in all stations was used as the areal rainfall. It is expressed as:

$$\overline{x}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{x}_i,$$

(1)

where $\overline{x}$ is the areal rainfall, $x_i$ is the rainfall in each station, and n is the number of stations.

2.5. Frequency Analysis

The maximum 60-min rainstorm amount can be represented by Pearson-III distribution [32]. It is expressed as:

$$f\left(H\right)=\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}{H}^{\alpha -1}{e}^{-\beta H},$$

(2)

where α and β are calculated as:

$$\alpha =\frac{4}{C_s^2},$$

(3)

$$\beta =\frac{2}{\overline{x}{C}_v{C}_s}.$$

(4)

In this study, $\overline{x}$, C_s, and C_v were estimated by the L-moment method [33]. They can be expressed as follows:

If $\left|{\tau }_3\right|<\frac{1}{3},\mathrm{let}z=3\mathsf{\pi }{\tau }_3^2,\alpha$ can be expressed by:

$$\alpha \approx \frac{1+0.2906z}{z+0.1882z^2+0.0442z^3},$$

(5)

If $\frac{1}{3}<|{\tau }_3|<1$, let $z=1-\left|{\tau }_3\right|$, $\alpha$ can be expressed by:

$$\alpha \approx \frac{0.36067z-0.59567z^2+0.25361z^3}{1-2.78861z+2.56096z^2-0.77045z^3}.$$

(6)

Thus x, C_s, and C_v can be expressed by:

$$\overline{x}=l_1,$$

(7)

$$C_v=\frac{l_2{\pi }^{\frac{1}{2}}{\alpha }^{\frac{1}{2}}\mathsf{\Gamma }\left(\alpha \right)}{\mathsf{\Gamma }\left(\alpha +\frac{1}{2}\right)l_1},$$

(8)

$$C_s=2{\alpha }^{-\frac{1}{2}}sign\left({\tau }_3\right).$$

(9)

The concept and computation of l₁, l₂, l₃, and ${\tau }_3$ (${\tau }_3$ = l₂/l₃) can be found in Hosking and Wallis [33].

The exceedance probability was estimated using the Weibull equation:

$$P_m=\frac{m}{n+1},$$

(10)

where m is the rank number for the sequence in descending order, P_m is the empirical probability for the mth term of the sequence, and n is the length of the sequence.

2.6. Fuzzy Identification to Classify Hyetograph

The 117 rainfall events were classified into seven types of mode hyetographs. Figure 2 shows the hyetographs of each type.

Fuzzy identification was used for classification. The basic concept of fuzzy identification is to compare mode matrices with actual indices of rainfall events and classify the hyetograph into the one with the least differences. The steps for the method are as follows:

Each rainfall event is divided into n periods, and the percentage of the rainfall in each period is expressed as:

$$x_i=\frac{H_i}{H}\left(i=1,2,\dots n\right),$$

(11)

where i is the ith period of the rainfall process, H_i is the rainfall in the ith period, and H is the total rainfall.

This group of x_i is defined as the actual rainfall indices, denoted as vector X:

$$X=\left(x_1,x_2,\dots ,x_n\right).$$

(12)

The mode matrices of the seven hyetographs are defined in a similar way, denoted as V_k:

$$V_k=\left(v_{k1},v_{k2},\dots ,v_{kn}\right)\left(k=1,2,\dots ,7\right),$$

(13)

where k is the kth type of hyetograph and v_ki is computed in the same way as x_i.

The nearness degree (${\sigma }_k$) of actual rainfall indices and mode matrices is computed as:

$${\sigma }_k=1-\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(v_{ki}-x_i\right)}^2}\left(k=1,2,\dots ,7\right).$$

(14)

The larger ${\sigma }_k$ indicates that the rainfall event is closer to a kth type of hyetograph, and thus can be classified into it.

In this study, rainfall events were divided into six equal periods, and the mode matrices of the seven hyetographs are defined as:

$$V=\left[\begin{array}{cccccc}7/23& 6/23& 4/23& 3/23& 2/23& 1/23\\ 1/26& 2/26& 3/26& 6/26& 8/26& 6/26\\ 1/20& 4/20& 7/20& 5/20& 2/20& 1/20\\ 3/21& 4/21& 3/21& 4/21& 3/21& 4/21\\ 5/20& 3/20& 1/20& 2/20& 5/20& 4/20\\ 4/18& 2/18& 3/18& 5/18& 3/18& 1/18\\ 2/23& 3/23& 7/23& 4/23& 2/23& 5/23\end{array}\right].$$

(15)

In the matrix, the seven rows indicate seven types of hyetographs. The six columns indicate the rainfall events divided into six periods. Each term in the matrix indicates that the percentage of the rainfall amount in the ith period of the event should be v_ki.

2.7. Pilgrim and Cordery Method

The steps of t P&C method [15] are as follows:

• Each rainfall event is divided into n periods by certain time intervals, and the percentage of the rainfall in each period is computed.
• The periods are sorted in descending order according to the percentage of the rainfall, and for each period, the average rank of all the rainfall events is computed as the rank for this period.
• For all the rainfall events, the average percentage of the rainfall in the periods of the same rank is computed.
• For each period, the rank and the percentage of the rainfall are paired to obtain the temporal distribution of the rainfall process.
• The hyetograph can be obtained by multiplying the percentage of the rainfall in each period by the design rainstorm amount with a given return period.

In this study, the time interval was selected as 5 min. Three scenarios were established in which hyetographs were derived:

• Scenario 1: Single-peak hyetograph (Type I, II, III);
• Scenario 2: Double-peak hyetograph (Type V, VI, VII);
• Scenario 3: General hyetograph (excluding Type IV).

2.8. The Chicago Rainstorm Method

The Chicago rainstorm method [13] is based on an intensity–duration–frequency (IDF) curve and the rainstorm intensity formula. According to the standard of rainstorm intensity formula and design rainstorm distribution in Shanghai, the rainfall intensity is calculated as:

$$i\left(t_b\right)=\frac{9.581\left(1+0.846logP\right)\left[\frac{\left(1-0.656\right)t_b}{r}+7.0\right]}{{\left(\frac{t_b}{r}+7\right)}^{0.656+1}},$$

(16)

$$i\left(t_a\right)=\frac{9.581\left(1+0.846logP\right)\left[\frac{\left(1-0.656\right)t_a}{1-r}+7.0\right]}{{\left(\frac{t_b}{1-r}+7\right)}^{0.656+1}},$$

(17)

where $t_a$ is the duration after the peak, $t_b$ is the duration before the peak, $i\left(t_a\right)$ is the rainfall intensity after the peak (mm/min), $i\left(t_b\right)$ is the rainfall intensity before the peak (mm/min), P is the return period, and r is the position coefficient of rainstorm peak (adopt 0.405 according to the standard of rainstorm intensity formula and design rainstorm distribution in Shanghai [30]).

3. Results and Discussion

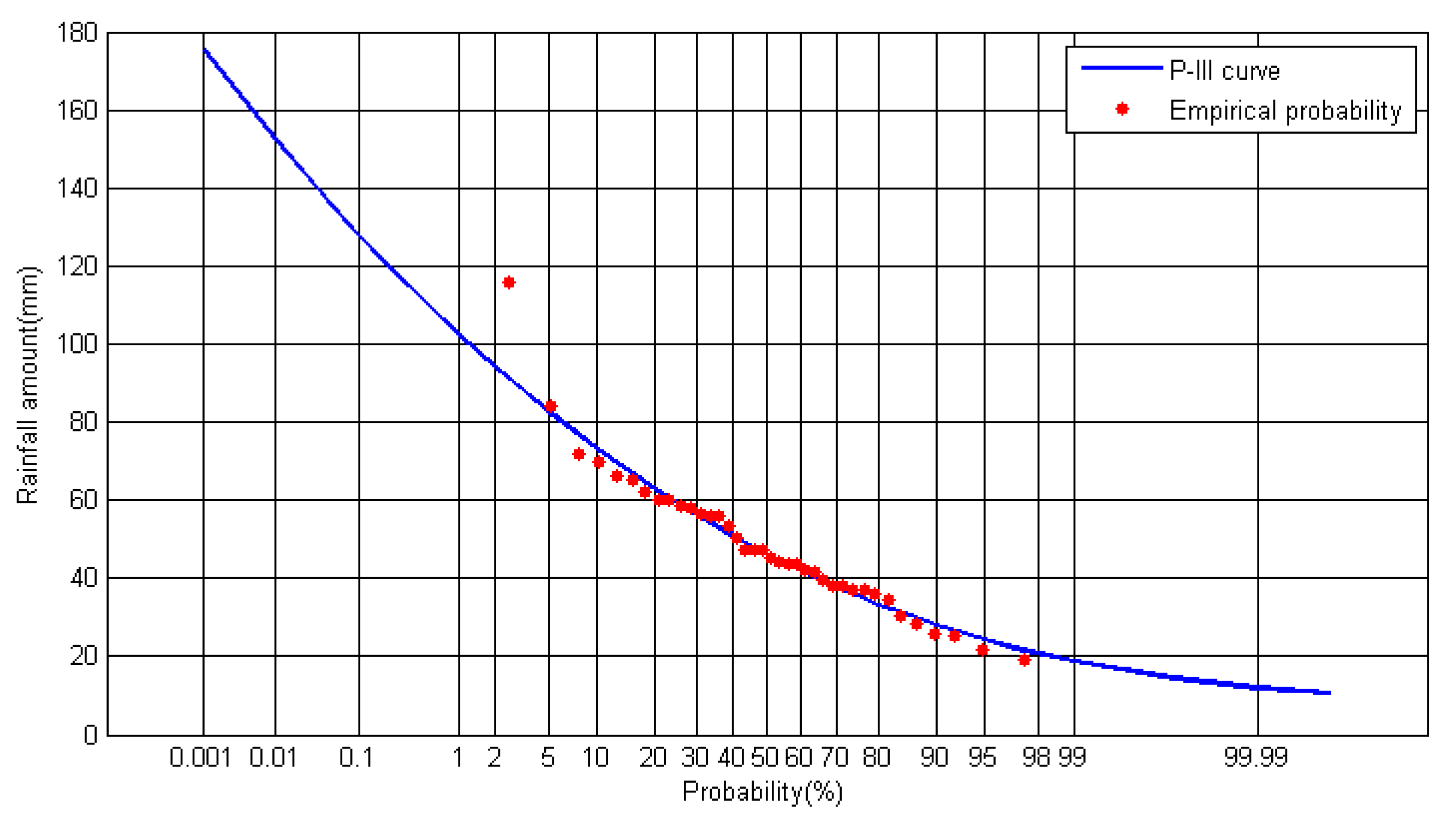
The P-III distribution curve and empirical probability points are shown in Figure 3. The maximum value occurred in 1985 and amounted to 116 mm. It can be seen that the P-III distribution curve fits the empirical probability points well, except for the maximum value of the sequence, which seems to be abnormal. The exceedance probability computed using Equation (10) for the point was 1/39. However, one assumes the actual exceedance probability for it should be smaller than 1/39, although there is not concrete evidence for this assumption due to limited data and records in the region. Considering this aspect, the fitted P-III curve should be rational. The Nash–Sutcliffe efficiency coefficient (NSE) between observation and theoretical values was 0.94. The maximum 60-min areal rainfall values with different return periods computed from the fitted P-III distribution are shown in

Table 1. Design areal rainfall amount with different return periods.

Return Period/a	Design Areal Rainfall Amount/mm
2	46
5	63
10	73
20	83

.

The classification of the 117 rainfall events is presented in

Table 2. Summary of mode hyetograph types in Yangpu District.

Type	Events	Percentage/%
I	19	16.24
II	20	17.09
III	30	25.64
IV	14	11.97
V	17	14.53
VI	11	9.40
VII	6	5.13

. It can be seen that single-peak hyetographs make up most of the rainfall events, taking up about 60%. Double-peak hyetographs account for approximately 30% of the rainfall events, the rest (about 10%) are uniformly distributed hyetographs. Among single-peak hyetographs, the ones with peak falling at the end of the process (Type III) slightly outnumber the other two types. For double-peak hyetographs, the number of Type V hyetographs—whose peaks fall at the beginning and end—are slightly larger than the number of Type VI and Type VII. Although the number of single-peak hyetographs is two times that of double-peak hyetographs, the latter still makes up a considerable portion of all the hyetographs. Therefore, it is worth exploring the influences of separating and combining these two kinds of hyetographs.

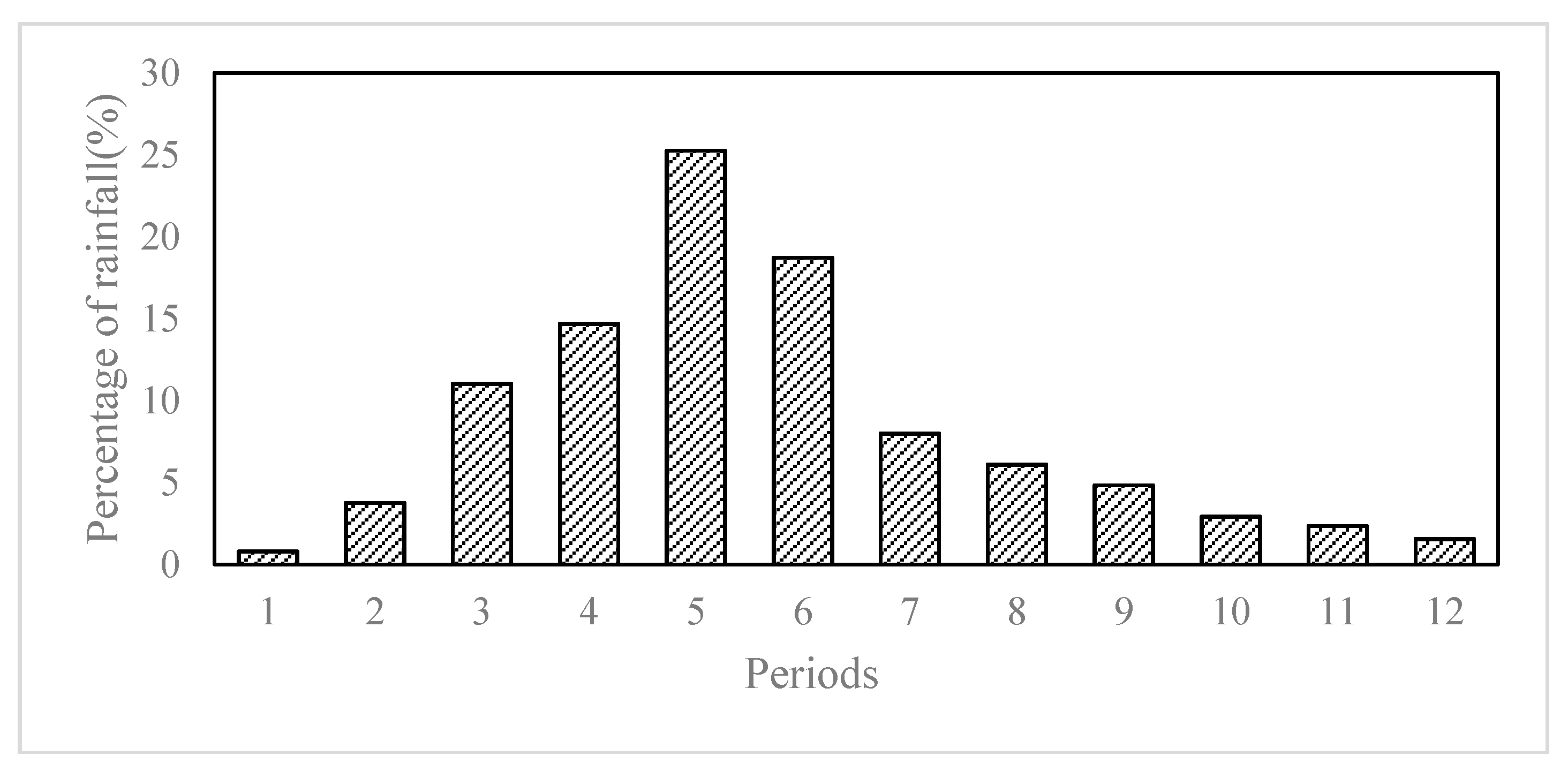
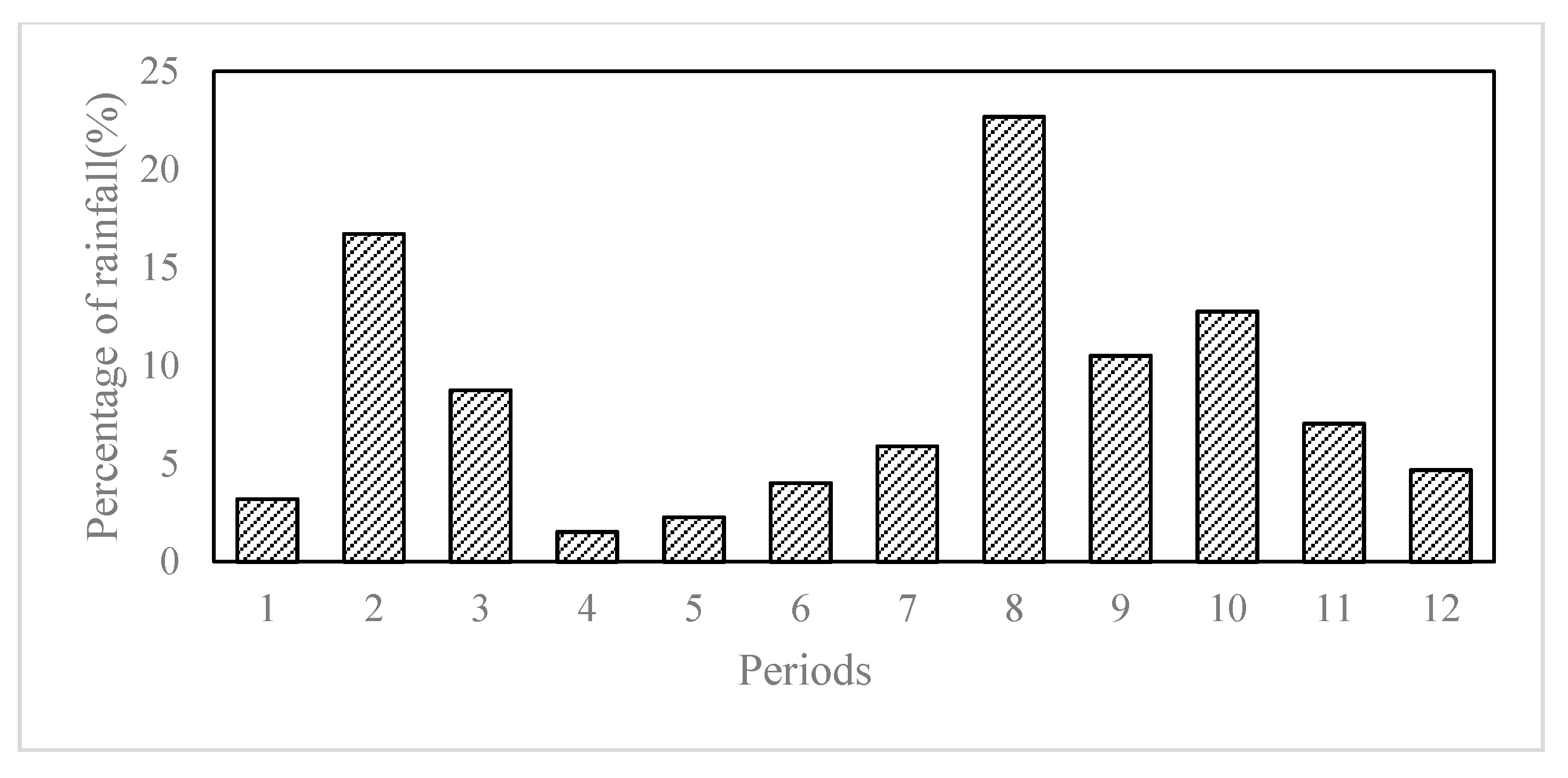
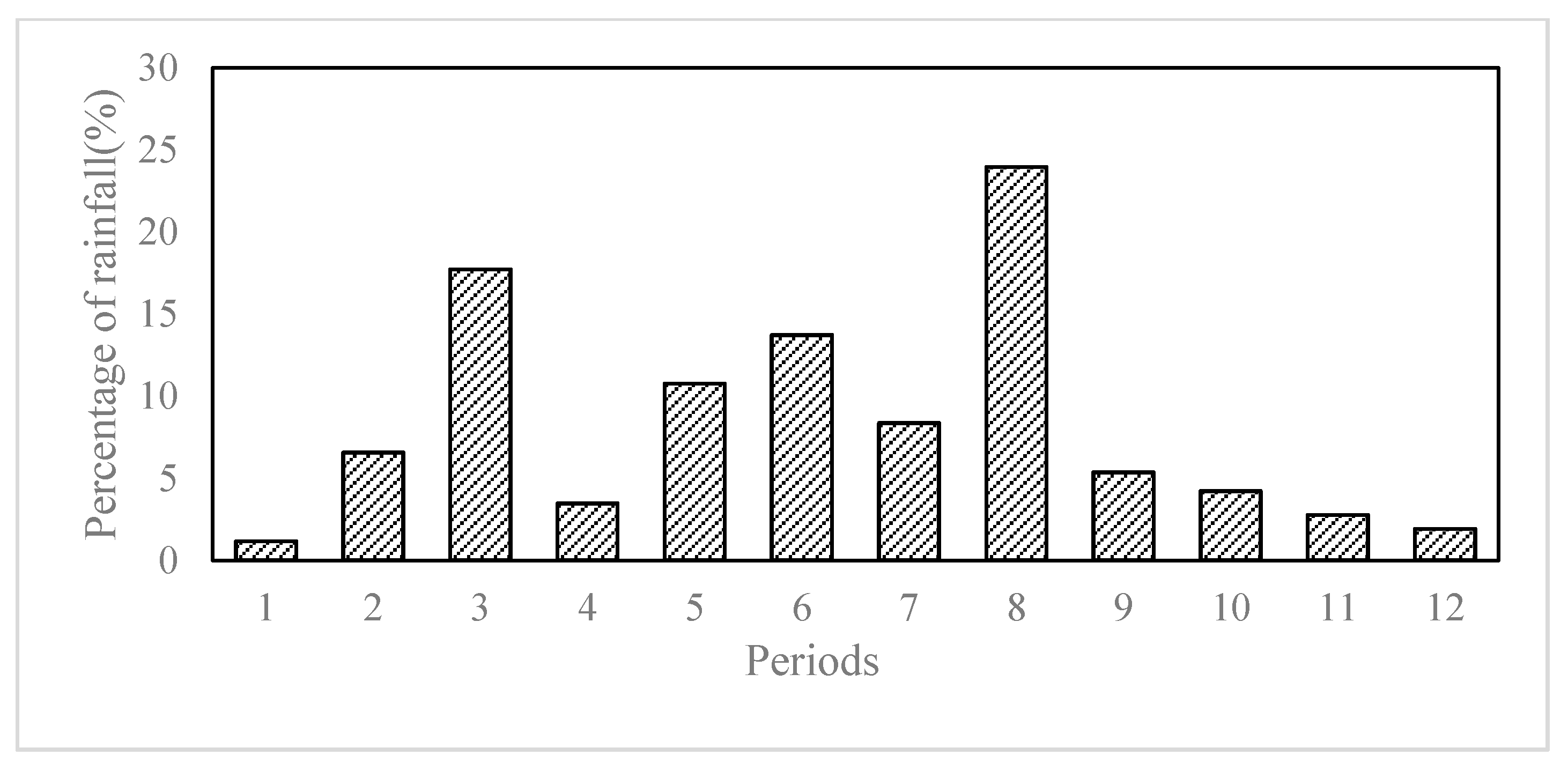
Figure 4, Figure 5 and Figure 6 demonstrate the hyetographs for the three scenarios. For the single-peak hyetograph of scenario 1 (Figure 4), the peak falls in the 5th period, which is in the middle of the event. Most of the rainfall concentrates in the 3rd to 6th periods, which take up 69.69% of the total rainfall amount. The single-peak hyetograph seems to be quite smooth and rational. For the double-peak hyetograph of scenario 2 (Figure 5), the peaks fall in the 2nd and 8th periods, which are at the beginning and end of the event. The rainfall concentrates in the 8th to 10th period, which account for 45.95% of the total rainfall amount. In general, the double-peak hyetograph is rational and smooth, except after the second peak, the rainfall in the 10th period exceeds that in the 9th period. However, the rainfall in the two periods does not have much difference in quantity, and thus it is acceptable. The general hyetograph of scenario 3 (Figure 6) seems to have three peaks, in the 3rd, 6th, and 8th periods. The peaks are not as obvious, and the rainfall is not as concentrated when compared with other two scenarios. Therefore, it demonstrates that when combining single-peak and double-peak rainfall events, the derived hyetograph will lose important features, and thus is not rational in some senses.

Generally speaking, single-peak rainstorms have more concentrated rainfall, and especially those peaks that appear in the early part of the event are more liable to cause urban flood issues. Therefore, more attention should be paid to single-peak hyetographs. Double-peak rainstorms are less prone to cause waterlogging issues. Nevertheless, if the rainfall is highly concentrated on one of the peaks, it may still cause flood issues. To explore the influences of different hyetographs on urban floods, one can compare the outputs of the waterlogging model when using different hyetographs as an input for the model.

The final hyetograph can be obtained by multiplying the percentage of the rainfall in each period by the design areal rainfall amount with a given return period. For example, a 20-year 60-min design hyetograph with a single peak is presented in

Table 3. Rainfall allocation of a single-peak rainstorm with a 60-min duration and a 20-year return period in Yangpu District.

Time/min	Percentage of Rainfall/%	Rainfall Amount/mm	Cumulative Rainfall Amount/mm
5	0.81	0.67	0.67
10	3.76	3.10	3.77
15	11.03	9.10	12.87
20	14.69	12.12	24.99
25	25.25	20.83	45.83
30	18.72	15.45	61.27
35	7.99	6.59	67.86
40	6.10	5.03	72.90
45	4.84	3.99	76.89
50	2.93	2.42	79.31
55	2.35	1.94	81.25
60	1.55	1.28	82.51

, whereas the double-peak hyetograph is shown in

Table 4. Rainfall allocation of double-peak rainstorm with a 60-min duration and a 20-year return period in Yangpu District.

Time/min	Percentage of Rainfall/%	Rainfall Amount/mm	Cumulative Rainfall Amount/mm
5	3.19	2.63	2.63
10	16.71	13.79	16.42
15	8.74	7.21	23.63
20	1.52	1.25	24.89
25	2.27	1.87	26.76
30	4.02	3.32	30.07
35	5.89	4.86	34.93
40	22.68	18.71	53.65
45	10.51	8.67	62.32
50	12.76	10.53	72.85
55	7.05	5.82	78.67
60	4.68	3.86	82.51

.

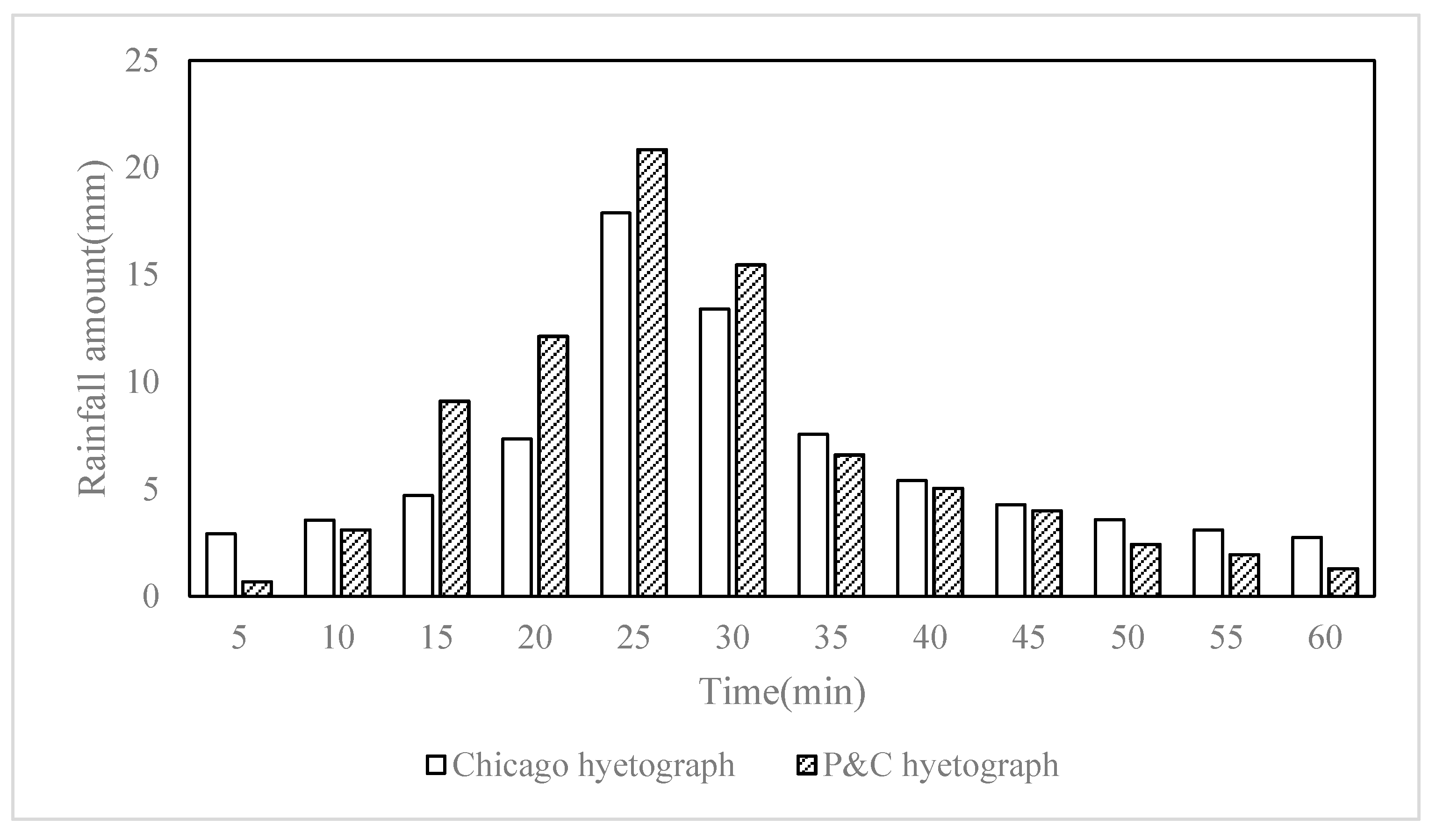
Because the design rainstorm derived by the Chicago rainstorm method (denoted as Chicago hyetograph) can only be a single-peak rainstorm, it is only compared with the single-peak rainstorm hyetograph derived by the P&C method (denoted as P&C hyetograph). The 60-min design hyetographs with 20-year return periods are shown in Figure 7. The total rainfall amount of the Chicago hyetograph (76.46 mm) is smaller than that of the P&C method (82.51 mm), due to the different data used in both methods. The parameter of the intensity rainstorm formula in the standard of rainstorm intensity formula and design rainstorm distribution in Shanghai was estimated using rainfall data from the rain-gauge stations in the range of the whole city of Shanghai, while the P&C hyetograph only used rainfall data of two rain-gauge stations near Yangpu District. The P&C hyetograph is more typical for the study area in this aspect. Both of the peaks fall in the 5th period (20–25 min). In the rising part of the hyetograph, the P&C hyetograph has a higher rainfall amount (45.82 mm, 55.53%) than the Chicago hyetograph (36.39 mm, 47.59%). In general, the P&C hyetograph is similar to the Chicago hyetograph, which proves the rationality of separating single-peak and double-peak rainstorms while applying the P&C method. Furthermore, the P&C hyetograph has a higher rainfall amount before reaching peak, which is less favorable in terms of runoff model results. In addition, the Chicago rainstorm method can only derive single-peak hyetographs, while the P&C method can derive both single-peak and double-peak hyetographs. Therefore, the design rainstorm using the proposed methodology is superior to the classic Chicago rainstorm method.

4. Conclusions and Recommendations

With the change of climate, rainstorms caused by extreme weather events are becoming increasingly frequent. The time distribution of hyetographs, as the input to various hydrological models, exerts a critical influence on the output of the model. In this study, 60-min design rainstorms with return periods of 2, 5, 10, 20 years were derived for the urban area of Yangpu District. The design areal rainfall of different return periods was calculated based on frequency analysis using the method of L-moments. The rainfall events were initially classified into seven types of mode hyetographs and then used to derive the 60-min duration hyetograph by using the P&C method with respect to three scenarios: single-peak, double-peak, and general hyetographs. The derived hyetograph using the P&C method was compared with the classic Chicago rainstorm method. Based on the results, the following conclusions can be drawn:

• The result of the classification of the 117 rainstorm events indicates that single-peak hyetographs account for about 60% of these events, compared to double-peak hyetographs which account for about 30%. The rest are uniformly distributed hyetographs.
• Both the single-peak and double-peak hyetographs are smooth and rational. The general hyetograph is irrational due to its relatively even and disordered distribution of rainfall amount.
• The design rainstorm using the proposed methodology in this study shows superiority to the classic Chicago rainstorm method. On one hand, it can derive both single-peak and double-peak hyetographs. On the other hand, it is more disadvantageous as input to runoff models.

In conclusion, rainstorms of different types have different distributions and thus have different influences on urban runoff models. It is recommended to derive hyetographs for each type of rainstorm separately, and then choose the most disadvantageous one as the input for waterlogging model (or other hydrological models).