Abstract
This paper presents a comparison between C-band and X-band radar data over an instrumented and regulated catchment of the Paris region. We study the benefits of polarimetry and the respective hydrological impacts with the help of rain gauge and flow measurements using a semi-distributed hydrological model. Both types of radar confirm the high spatial variability of the rainfall down to their space resolution (1 km and 250 m, respectively). Therefore, X-band radar data underscore the limitations of simulations using a semi-distributed model with sub-catchments of an average size of 2 km. The use of the polarimetric capacity of the Météo-France C-band radar was limited to corrections of the horizontal reflectivity, and its rainfall estimates are adjusted with the help of a rain gauge network. On the contrary, no absolute calibration and scanning optimisation were performed for the polarimetric X-band radar of the Ecole des Ponts ParisTech (hereafter referred to as the ENPC X-band radar). In spite of this and the fact that the catchment is much closer to the C-band radar than to the X-band radar (average distance of 15 km vs. 35 km, respectively), the latter seems to perform at least as well as the former, but with a higher spatial resolution. This was best highlighted with the help of a multifractal analysis, which also shows that the X-band radar was able to pick up a few rainfall extremes that were smoothed out by the C-band radar.
1. Introduction
Management of weather extremes—particularly intense precipitation events and heat waves—in the Paris area (Île-de-France) is a big challenge for the future. The ongoing urbanisation and rising population density increase the vulnerability of the region. The adaptation to climate change is a necessity and is now a critical societal issue [1]. The risks and their large associated uncertainties are at odds with people’s request for a higher quality of life, as testified by “Grenelle de l’Environnement”, COP21 (also known as the 2015 Paris Climate Conference) and several European directives. Such life standards require refined management and control of floods, water and air quality. This could be achieved by our improved abilities to measure, understand, model and predict the hydro-meteorological processes in urban and peri-urban environments. This should be organised over the relevant range of space–time scales and with much better accuracy and reliability. Conventional local measurements in urban areas often do not satisfy the World Meteorological Organization (WMO) criteria for measurement of precipitation [2]. Remote sensing is becoming more important in elucidating complex structures of urban environment, and the hydro-meteorological challenges become broader and broader [3]. This paper focuses on rainfall and its hydrological consequences on the Bièvre River catchment, approximately 20 km from the Paris city centre. Historically, this catchment is not only known for the severe floods that impact its urban areas, but also for its contribution to Paris floods [4].
Weather radars provide spatiotemporal measurements of rainfall fields. However, as they do not measure rainfall directly, radar-based rainfall estimates may have substantial uncertainties. To quantify the uncertainty on accumulated rainfall, the authors usually perform either a comparison of different radar products, or compare ground measurements and precipitation estimates on radar pixels where rain gauges are located [5,6,7,8,9]. Tabary [10] shows that, in spite of the greatly improved quality of the operational C-band radar estimates, the average differences between the radar estimates (without calibration with gauges) and ground observations vary between 28% and 54%, increasing with distance. Polarimetric radars have opened a new perspective to improve estimates for stronger rainfall by using the specific differential phase (KDP) values to directly estimate the rainfall intensity [8]. However, in the French context, this option remains yet a perspective for the reference operational products of the French meteorological institute, Météo-France. Up to now, Météo-France only used the double polarisation for attenuation and clear air corrections. This underlines that the optimal choice of radar algorithms remains an open question in the community and therefore a research topic.
The differences of observation scales, and in fact of dimensionality, between radars (typically 1 km) and rain gauges (few tens of cm) add a fundamental complexity to this comparison [7,11,12]. This intrinsic issue of volumetric measurements (radars) vs. point measurement (rain gauges) comparison led to the development of other ways of validation of radar products, notably hydrological validation. It basically consists of inputting various rainfall fields into hydrological models and checking how they affect their ability to reproduce observed hydrographs. This has been done either in rural [13,14,15,16] or urban environment [17,18,19,20,21,22,23]. Obviously, it has the drawback of relying on imperfect rainfall–runoff models. For instance, numerous studies showed a strong influence of rainfall spatiotemporal variability on model response, especially in urban areas, where response times are shorter due to high levels of imperviousness and smaller catchments [24,25,26,27,28,29,30,31]. This calls for hydrological models with sufficiently high resolution to properly account for rainfall variability [32]. This is one of the drivers of the development of fully distributed models [22,33,34,35].
There is also growing interest in developing operational hydrological models that incorporate higher space resolution of the rainfall data. A step in this direction has been made by SCHAPI (“Service Central d’Hydrométéorologie et d’Appui à la Prévision des Inondations”, a national service in charge of flood forecasting in France) in the study of Tramblay et al. [36], which compares different Météo-France radar products. Another example can be found in Ochoa-Rodrigues et al. [30], who used nine storm events (with a total duration of approximately 24 h) measured by a dual-polarimetric X-band weather radar at the Cabauw experimental site (Netherlands), to investigate the impact of rainfall input resolution on the outputs of semi-distributed operational hydrodynamic models of seven urban catchments of similar size (between 3 and 8 km2). The study was carried out in the framework of the RainGain project [37].
The goal of the present study is therefore threefold: (i) a comparison across scales of both C- and X-band radar data using multifractal theory and furthermore enabling the selection of the best X-band radar product for this study; (ii) a hydrological comparison of the rainfall data resulting from C-band radar, X-band radar and rain gauges measurements; and (iii) a study of the impact of increased radar data resolution that enables a better assessment of small-scale rainfall variability. It is carried out over the 110 km2 upstream catchment of the Bièvre River in the Ile-de-France region. This catchment is an example of a peri-urban area, some parts of which are highly urbanised. Veolia is the company chosen since 1991 by the local authority SIAVB (“Syndicat Intercommunal pour l’Assainissement de la Vallée de la Bièvre”—Bièvre Valley Intermunicipal Sanitation Office) to design, install and operate a real-time control system of the river over the area. Hence, the study is performed with Veolia’s operational model, Optim Sim. Instead of suffering limitations, the aforementioned methodological goal and the present study benefit from cross-fertilisation of research and operational hydrology, whereas they have both suffered from a long-lasting divorce [38]. Furthermore, the potential decentralisation of meteorological and hydrological data collection, processing and distribution should enable most of businesses to optimise their operational management, because often more than 60% of their activities are weather-sensitive.
2. Materials and Methods
This section first presents the experimental catchment in the Paris region that is studied in this paper. It was chosen because of its capacity to generate flash floods upstream to a densely-populated area, especially during strong rainfall. Obviously, due to these features, strong and efficient regulation (which means the implementation of drainage control devices, such as weirs, gates, and others) had to be employed throughout the river path. Although this enables us to study an operationally challenging area, it makes comparison between simulated and observed hydrography trickier but not impossible. Limitations will be clearly pointed out, as well as possible ways of overcoming them. The catchment description is linked with the description of the operational platform and its integrated hydrological model calibrated over the catchment, by explaining their features and the employed methodologies.
Afterward, the details of the selected rainfall events and the available rainfall data of three different types, all of them being used as inputs to the hydrological models, are described. Then, the differences among the rainfall measuring devices in relation to their geographical locations w.r.t. the catchment, as well as the differences in data processing, and the role of dual-polarisation in the rainfall retrieval algorithms are also discussed. Finally, a short recap of multifractals and the error metrics used in this study is presented.
2.1. Case Study Site
The upstream catchment of the Bièvre River is a peri-urban area with a very complex topography in the southwest region of Paris. Two local authorities are in charge of the river system management in the area: the CASQY (“Communauté d’Agglomération de Saint-Quentin-en-Yvelines”—Saint-Quentin-en-Yvelines Agglomeration Community) in the upstream portion and the SIAVB in the downstream portion. Veolia has been given the responsibility of operating the system in this area. A map of the Bièvre River can be found in Figure 1. The river network was plotted with the help of data available for the Ile-de-France region [39]. There are some gaps in this network due to missing data on the storage basins along the Bièvre River and covered parts of the river. The level of urbanisation of the catchment increases going downstream (from West to East). The Bièvre River flows in a valley with steep slopes on each side, especially in the northern part.
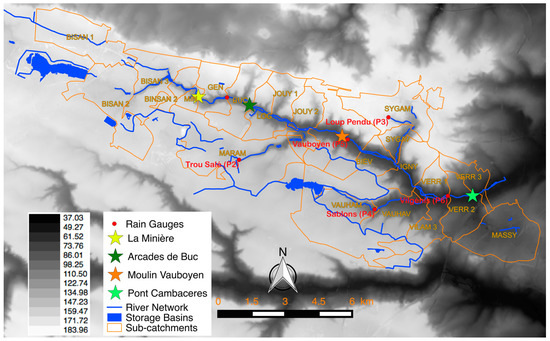
Figure 1.
Illustration of the Bièvre catchment area with its representation in 27 sub-catchments used in InfoWorks CS. Five of them—BISAN 1, BISAN 2, BISAN 3, BINSAN 2 and VAL D’OR—belong to the CASQY-Bièvre catchment while the others belong to the SIAVB-Bièvre catchment. Locations of six rain gauges over the SIAVB-Bièvre catchment and four measurement points are shown. The altitude scale is also represented, in meters.
Following severe flood events in 1973 and 1982, local authorities started the construction of storage basins (integrated in the landscape) to limit the consequences of extreme events. Four of these basins along the Bièvre River can be remotely regulated. In standard situations, basins are locally regulated according to downstream measured water levels, while in extreme situations an optimisation of flows and storage capacity is done at the catchment scale using water levels in the river and in storage basins, along with rainfall data provided by six rain gauges (see Figure 1). The catchment scale regulation is automated, although under permanent human supervision.
2.2. Selected Rainfall Events and Three Data Types
Three rainfall events that occurred in 2015 were studied in this paper: 12–13 September 2015 (44 h: 04:05–00:00), 16 September 2015 (16.8 h: 00:05–16:50), and 5–6 October 2015 (31 h: 09:10–16:05). These rainfall events last in total more than 90 h, and were purposefully not split into many successive rainy periods as commonly done, which would have somehow artificially increased their number. In term of rainfall properties, it could have been justified to do so, but from a hydrological point of view, it was more relevant to carry out single simulations to limit the impact of improper initial conditions. Additionally, they were selected taking into account the hydrologic impacts on the Bièvre catchment as well as to cover the most common meteorological situations of the area. More precisely the rainfall of 12–13 September is due to two successive depressions coming from the British Islands (North-West) combined with the influence of Cevenol events from the South. The event of 16 September is associated with a storm Henry, generated by a former tropical depression coming from the South. It resulted in high winds. The 5–6 October event is associated with a depression coming from the West. A combination of stratiform and convective rainfall was observed during these events. It means that these events are altogether sufficiently representative for the purpose of this study. The first two events triggered an optimisation of the river management at the catchment scale, while only local regulations (with no optimisation at all) were used for the third one.
Over the Bièvre catchment (see Figure 2), the rainfall data could be provided from three different sources:
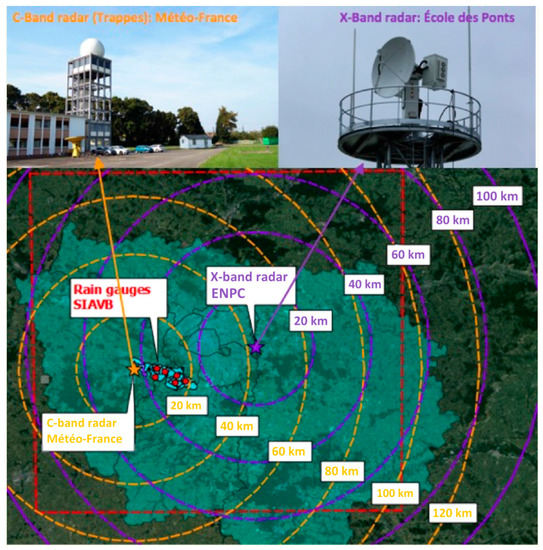
Figure 2.
Illustration of rainfall measurement devices available over the Bièvre catchment. The square area (red dashed line) is the 128 × 128 km2 area, covered by the two radars.
- The SIAVB network of six tipping bucket rain gauges, being distributed over the catchment;
- The Météo-France polarimetric C-band radar of Trappes, being located in a direct proximity (~0–20 km) of the catchment;
- The ENPC polarimetric X-band radar of Champs-sur-Marne, with distances ranging between 25 to 45 km.
Finally, we use data from a OTT Parsivel2 disdrometer installed near the ENPC X-band radar [40] to illustrate that the 16 September event could have been split into four sub-events having quite different parameters a and b of Marshall–Palmer Z–R relation [41] to convert the corrected reflectivity factor () to rain rate :
where the standard parameter values are a = 200 and b = 1.6.
As illustrated by Figure 3a,b, four periods are identified, corresponding to different levels of rain rates and drop size distribution (DSD, in ) features, and could be used to compute . Figure 3c displays four distinct classes of parameters a and b. For instance, no large drops (with an equivolumic diameter greater than 2 mm) are observed during the first portion of the event (in blue in Figure 3a). This points out that the three selected rainfall events represent a larger number of sub-events, and therefore a given spectrum of rainfall variability in the Ile-de-France region.
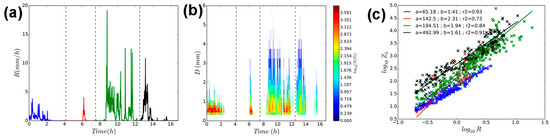
Figure 3.
Disdrometer data output for the 16 September event. (a) Temporal evolution of the rain rate with 30 s time steps; (b) temporal evolution of the drop size distribution with 30 s time steps; (c) scatter plot of the Marshall–Palmer relation (Equation (1)) and corresponding orthogonal regression for the four selected periods.
2.3. Radar Data Processing
2.3.1. From Météo-France
For its C-band radar products, Météo-France uses the standard a–b values of the Z–R relation (Equation (1)). The data provided by Météo-France is the radar mosaic for precipitation amount over the whole territory generated with the help of its radar network, initially called Aramis [42]. Within the PANTHER project (Aramis New Technologies Hydrometeorology Extension and Renewal), this network includes 29 radars. Being spread over the entire territory, the radars have a range of about 100 km to measure the amount of precipitation and about 200 km to detect them. A number of “individual radar” products are transmitted every 5 min to the Météo-France centre in Toulouse. Mosaics are then constructed from these products by selecting for each pixel the individual radar information with best quality. Given that the Bièvre catchment is located very close to the polarimetric C-band radar of Trappes (~25 km maximum), the mosaic data basically come only from the Trappes radar.
In the PANTHER products, the incremental rainfall accumulation is calculated at time steps of 5 min. It results from many post-treatments that manage the common radar issues of partial masks, bright band, fixed echoes and signal attenuation. For example, Gourley et al. [43] suggested that the specific attenuation is related to the specific differential phase with the help of a simple linear relation and calibrated it for the Trappes radar. Since February 2012, the double polarisation is used, but exclusively for the attenuation and clear air corrections, it does not take into account the biases introduced by large drops and therefore the different rainfall regimes. The ratio of reflectivity and incremental accumulation therefore requires calibration in real time, which is evenly performed over the entire area of the radar (radius of about 100 km) and according to a quality code based on the last 12 hours’ rain gauge radar comparison. This ratio is calculated in particular for correcting a slow drift of the measurement and is used to trigger the appropriate intervention for radar maintenance.
2.3.2. From ENPC
The ENPC X-band radar rainfall data were processed with the standard Rainbow software [44]. Due to the initial choice of the pulse width and angle step, the highest resolution of pixel in the radial direction is 250 m and 3.4 min. Hence, a more appropriate choice of scan/scheduler parameters could further improve the space–time resolution of the rainfall products for the Bièvre catchment.
In this study we use the Dual Polarisation Surface Rainfall Intensity (DPSRI) product. Contrary to the Surface Rainfall Intensity (SRI) product, it is not generated only with the help of the horizontal reflectivity data, but also uses the vertical one with the help of the differential reflectivity, ZDR, and the specific differential phase, KDP. The signal of the differential phase shift () is quite noisy and, in practice, it is smoothed before computing the specific differential phase. The Rainbow software proposes a choice of several sophisticated smoothing methods, starting from the classical filter that is based on a (weighted or non-weighted) moving average, a median filter (which produces the simply filtered KDP) up to the Finite Impulse Response (FIR) filter. The resulting specific differential phase is almost independent of attenuation and partial beam blocking by attenuation. The DPSRI Selex product uses a hybrid radar algorithm with a Z–R relation used at only for very low intensities and R–KDP for higher intensities:
To illustrate the influence of the choice of either Selex data filtering procedures or parameters for the DPSRI at 1.5 km, the time evolution of ENPC X-band radar rainfall accumulations over the six sub-catchments containing the rain gauges is considered here, for the event of 12–13 September 2015. Firstly, we use the FIR filtered KDP with the Z–R parameters a = 200 and b = 1.6, those applied by Météo-France for the C-band radar in Trappes. Then, we change the Z–R parameters to a = 150 and b = 1.3, using either FIR or simply filtered KDP. Figure 4 displays the obtained results that suggest two intermediate conclusions. By comparing the left and middle graphs, the first observation is that, in spite of the fact that the change of Z–R parameters for DPSRI modifies only very low rainfall intensities (lower than typically 7 mm·h−1), this change increases the rainfall totals by about 40%. This simple analysis highlights how critical the choice of a and b parameters is, furthermore considering the wide range of possible values discussed in the literature (examples: [41,45,46]). By comparing the middle and right graphs, the second observation is that simply filtered KDP results in a slight increase in the rainfall estimates. Similar behaviour was observed for two other events. Selecting the appropriate radar algorithms remains a challenging, methodological, observational question that has far-reaching implications on water management. In Section 3.1.1, we innovatively use multifractal analysis to help to choose which X-band radar product will be used for the hydrological modelling. To the knowledge of the authors, this is the first time that such methodology has been developed.
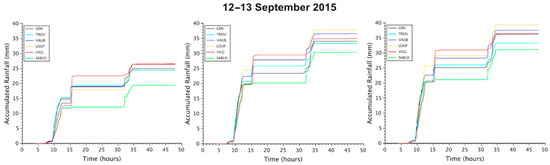
Figure 4.
Time evolution of accumulated X-band rainfall during the event of 12–13 September 2015 over six catchments containing the rain gauge: GEN (P1 Geneste/GEN), MARAM (P2 Trou Salé/TROU), SYGAM (P3 Loup Pendu/LOUP), VAUHAM (P4 Sablons/SABLO), JOUY3 (P5 Vauboyen/VAUB) and VERR2 (P6 Vilgénis/VILG). The three DPSRI rainfall products at 1.5 km were obtained with: FIR filter and Z–R parameters a = 200 and b = 1.6 (left); FIR filter and Z–R parameters a = 150 and b = 1.3 (centre); and simple filter and Z–R parameters a = 150 and b = 1.3 (right).
The ENPC X-band radar had only a one-point calibration, i.e., to test the equivalence of the vertical and horizontal reflectivity’s for an isotropic scattering (such as the solar radiation, which is used for this test), but no absolute calibration was used up to now.
2.4. Hydrological Model
The catchment is modelled with InfoWorks CS (Collection Systems), widely-used, semi-distributed modelling software [47]. The area is divided into 27 sub-catchments, as displayed in Figure 1. Their sizes range from 0.3 to 11 km2. This model is integrated in the Optim Sim platform, an offline tool developed by Veolia that imitates the actual regulation of the storage basins either at the local or catchment scale. It should be mentioned that the settings of neither InfoWorks CS model nor Optim Sim are fully up to date. For instance, a recent modification of the networks that consisted in the removal of the Vilgénis basin to restore the natural flow of the river (near “Vilgénis” rain gauge P6 on Figure 1) is not yet taken into account in the models. This difficulty pushes us in this study to focus on events without active regulation, i.e., when gates positions remain unchanged and therefore to focus on the differences associated with rainfall. There are two simulation modes in Optim Sim: the “replay mode” and the “forecasting mode”. The first one enables to replay past events by extracting data from the linked database of the six rain gauges of the SIAVB. The rain rates for each sub-catchment are obtained using the Thiessen polygons technique. Then the simulations and observations (flood depth or flow at the measuring points) can be compared and analysed. It should be noted that, during Optim Sim simulations in “replay mode”, the positions of gates are not necessarily the same as the ones resulting from the regulation during the real events. Since no other source of rainfall data can be used with this mode, we used the “forecasting mode”. This second mode simulates the behaviour of the river by introducing rainfall data from different possible sources, notably from (fully distributed) C-band radar measurements, although being converted in semi-distributed ones (i.e., a unique rainfall time series per catchment). It is also possible to use the forecasting mode for replays by merely setting past dates, thereby making it possible to compare the simulations with measured flow observations. Rainfall data can be input in three ways: an average intensity (mm/h) over all sub-catchments; a single average intensity time series over all sub-catchments; and an average intensity time series over each sub-catchment. In the last case, which we chose, a text file with a column containing rainfall intensity in mm/h with 5-min time steps has to be generated for each sub-catchment.
Practically, in order to generate the rain over each sub-catchment, we used the Bièvre catchment map with sub-catchment boundaries in GIS format along with the radar data ones (C-band and X-band). Then, we calculated the weighted average of the radar pixel rainfall rate values by the intersection area of the radar pixels with the sub-catchment areas :
where the sum is made over all radar pixels . For the rain gauges, the input rainfall data were generated using the Thiessen polygon method [48].
In spite of the subdivision of the catchment for the InfoWorks CS model into 27 sub-catchments, as displayed in Figure 1, we used a version of the Optim Sim model with 26 sub-catchments, where the sub-catchment BINSAN2 is modelled as part of the sub-catchment BISAN3.
2.5. Short Recap of Multifractals and Classical Error Metrics
Multifractals have been developed and applied to analyse and simulate geophysical fields exhibiting extreme variability over a wide range of scales such as rainfall [29,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]. For such fields the statistical moment of order of a field at the resolution (, where is the outer scale of the phenomenon and the observation scale) is a power-law behaviour related to the resolution:
where K(q) is the scaling moment function. It fully characterises the variability across scales of the studied process.
The trace moment (TM) analysis [49], which consists in checking the validity of Equation (5), enables to confirm the scaling behaviour of the field. More precisely, moments for various resolution are computed by upscaling the field from its maximum resolution, then Equation (5) is plotted in a log–log scale for various , and straight lines of slope K(q) are retrieved for multifractal fields.
Universal multifractals (UM) are a multifractal framework toward which multifractal processes converge under rather wide conditions [49,68,69]. In UM, conservative multifractal fields, whose mean is conserved through scales, are characterised with the help of only two parameters: > 0, the mean intermittency co-dimension, measuring the sparseness of the average intensity of the field ( for a homogeneous field) and , the multifractality index, which measures the variability of the intermittency when considering intensities different from the average. In this case, the statistical moment scaling function is then given by:
Lavallée et al. [70] developed a robust technique to directly estimate the UM parameters and , without having to rely on a fitting of the scaling moment function . It is called the Double Trace Moment (DTM) method and is in fact a generalisation of the TM method, which is applied to a renormalised -power of the field , defined by:
Then the -order moments of the renormalised field remain scale-invariant:
Furthermore, in the UM framework, one may obtain:
which enables the estimation of , as the slope of the linear part of vs. in a log–log plot, for a given . is estimated from the intercept of this same linear part (see Hoang [71] for more details).
In this paper, these estimates were performed in three different ways. The first method is based on the estimate of the slope over a fixed interval of (here: [71], while the second is obtained around the inflection point [72,73] (the second derivative of is equal to 0). The third one (hereinafter called “best fit”) determines the interval of containing the point that yields the best linear behaviour.
Finally, to quantitatively compare the rainfall estimates and the hydrological simulations, three standard metrics parameters were used in this paper (see further results in Section 3.1.2 and Section 3.2). Considering the time series and , with same number N of time steps:
- The correlation coefficient () measures the strength and the direction of the linear relationship between the both time series:where a positive value indicates that the two time series possess the same dynamic (increasing and decreasing at the same moment).
- The Nash–Sutcliffe Efficiency () is the most commonly used indicator to quantify performance of models in urban hydrology. It measures how well the model outputs () reproduce the observations ( in comparison to a model that only uses the mean of the observed data. It is calculated as:where a value of 1 indicates a perfect model (both time series are equal), a value of zero indicates performance no better than simply using the mean ( is equal to the mean of ), and a negative value corresponds to a performance worse than just using the mean.
- The Root-Mean-Square Error (RMSE) is used in urban hydrology to quantify errors between two time series. It measures the deviation of predictions from observed value (calculated as the square root of average square deviation):
3. Results
In this section, we study the space–time rainfall variability detected by different types of radar. The multifractal framework is particularly appropriate for analysis of such highly intermittent fields and is expected to better differentiate the rainfall products than standard scores. Indeed, it enables a comparison across scales and not only at a given scale, as is classically done. This yields more robust conclusions, notably when the observation scales of the two measuring devices are not the same, as is the case here. Then we discuss the results of a hydrological comparison performed with the best rainfall products available for each type of radar. The present results presumably have significant implications for the rainfall physics that would need to be further explored elsewhere.
3.1. Direct Comparison of Rainfall
3.1.1. Multifractal Analysis
In this paper, we study 2D rainfall fields. The rainfall maps for each time step are upscaled independently and the average of Equation (5) is computed over the ensemble of time steps. Figure 5 displays the TM curves obtained over the full duration of the 12 September 2015 rainfall event for three DPSRI X-band radar rainfall products at 1.5 km height and C-band radar data. Maps of the size 64 km × 64 km are analysed up to the resolution . In all cases a single scaling behaviour is considered. Figure 5a displays the result of trace moment analysis for the FIR filtered DPSRI product with Z–R parameters a = 200 and b = 1.6. One may note that there is a strong curvature of the TM curves, and hence this product is not really in agreement with the expected and widely reported in the literature scaling behaviour of the rainfall fields. The multifractal scaling behaviour of the DPSRI products with Z–R parameters a = 150 and b = 1.3 is much more evident (Figure 5b,c, for FIR and simple filter, respectively). It confirms that this change of parameters improves the scaling, while it increases the rainfall intensity maxima. Based on these analyses and on the fact that the choice between FIR and simple filter does not make a significant difference, the X-band product chosen to be used hereafter was the DPSRI with FIR filter, and a = 150 and b = 1.3 for low intensities. Refining this analysis using this methodology is outside the scope of this paper and will be done in future studies. Finally, Figure 5d displays the TM analysis result for the C-band radar data. This figure shows that it also has a great scaling behaviour, not to mention the fact that there are fewer points than in the X-band radar because of the small spatial resolution difference (250 m for X-band, and 1 km for C-band).
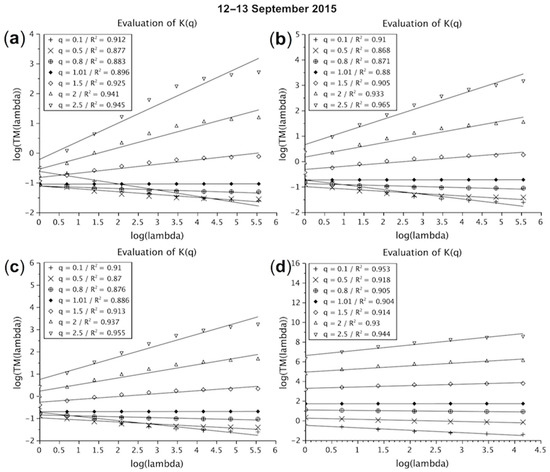
Figure 5.
TM (Equation (5) in log–log plot) analysis for the 12–13 September 2015 event: X-band DPSRI rainfall products at 1.5 km obtained with (a) FIR filter and Z–R parameters a = 200 and b = 1.6 for low intensities; (b) FIR filter and Z–R parameters a = 150 and b = 1.3 for low intensities; (c) simple filter and Z–R parameters a = 150 and b = 1.3 for low intensities; and (d) C-band rainfall fields.
It is important to note that for the X-band DPSRI products, a change of scaling regime may also occur for scales smaller than 1 km, but given the limited number of points, it is not possible either to confirm or refute this consideration. Should the break indeed be real, it would mean that rainfall structures and extremes could not be extrapolated from measurements at larger scales. The overall estimates of the coefficient of determination R2, being used as a metrics of scaling behaviour, are lower for X-band radar data. Somewhat similar scaling behaviour is found for the other two rainfall events.
We first assessed the UM parameters of the three selected events by using the DTM method [70], for both C-band and X-band (DPSRI; FIR filter; a = 150 and b = 1.3 for low intensities) radar data, on ensemble average over each whole event. Table 1 summarises the UM parameter estimates obtained by using the “best fit” technique. It is important to note that the estimates summarised in the table are computed over the full range of considered space scales, i.e., 1–64 km for the C-band radar and 0.25–64 km for the X-band radar. At the same time, it will be fruitful to mention that the overall estimates of R2 (see Figure 5b,d, for the event of 12–13 September 2015), being used as a metrics of the scaling behaviour, are lower for the X-band radar data, mainly because changes in scaling may occur over smaller scales that are not available with the C-band measurements. We tested that two scaling regimes with distinct linear fits in a log–log plot yield two distinct pairs of UM parameters for the X-band spatial rainfall. While the multifractality parameter estimated over large scales (1–64 km) becomes closer to that obtained for the C-band radar data (on the same range), the DTM estimator gives spurious multifractality parameter (>2) over the small scales (0.25–1 km, unknown for the C-band radar). This could be due to the emergent properties of rainfall extremes at small scales. Indeed, a well-known basic property of precipitation is that small-scale extremes (short duration or/and size, e.g., heavy rainfall episodes) can drastically influence much larger scales (e.g., yearly statistics and even climate) to the point of creating heavy tails for the probability of larger scale extremes. This basic feature remains out of reach from (quasi-) linear models (e.g., the still used Scott–Newman model and variants), whereas it is generic in multifractal cascade models.

Table 1.
UM parameters of the three events.
In Table 1, one can verify that, for each of three rainfall events, the parameters are greater for the X-band radar data than for the corresponding C-band ones, though the parameters remain almost the same for both radar data types (especially for the second and third events). These results mean that the X-band radar data have stronger extremes (having more spikes), while a similar intermittency of the average intensity. This result needs to be confirmed on a wider sample, but emphasises the importance of having high-resolution precipitation data so as not to miss local rainfall extremes. It is important to note that such pronounced variability being found on X-band data does not necessarily imply that the X-band rainfall rates are higher than the C-band ones.
Then, to estimate the uncertainties, we performed a DTM analysis over each time step (without considering those with less than 1% of rainy pixels over the 64 km × 64 km area, which are classified as “no-rain steps”) for the three rainfall events using both X-band and C-band radar data. Figure 6 presents the distributions of the parameter estimates obtained in two different ways: using the fixed interval of (red dashed lines) and the inflection point (green lines) methods. For comparison, the “best fit” ensemble average estimates, presented in Table 1, are indicated by vertical black lines. It is well known that a high percentage of zeros (or a small percentage of rainfall occurrence) biases the DTM analyses, by overestimating and underestimating (e.g., [74]). These biases are obvious in Figure 6, with individual estimates far from the ensemble estimates. Additionally, some spurious statistics () were retrieved, especially with the inflection point method. Fortunately, these biases are statistically smoothed by the ensemble average. This is due to the fact that the ensemble averaging is performed over the double trace moments (see Equation (8)) and not over the individual exponents estimated on each sample.
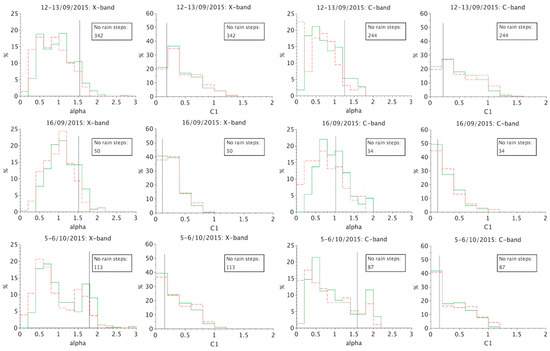
Figure 6.
UM parameter estimates for three rainfall events (12–13 September 2015, 16 September 2015 and 5–6 October 2015 from top to bottom) using X-band and C-band radar rainfall (from left to right). Distributions (%) of parameter estimates (0.2-length bins) over individual time steps using the fixed interval of method (red dashed lines) and the inflection point method (continuous green lines) are displayed. The vertical black lines indicate the “best fit” estimates obtained on the ensemble averaged DTM curves.
Furthermore, X-band and C-band data yield similar patterns of parameter distributions, but with a shift for the multifractality index and not for , in agreement with the ensemble average results displayed in Table 1 (higher for the X-band radar). These results confirm the ability of the X-band radar to observe singularities (spikes) that the C-band radar cannot detect, while both have a similar ability to observe lower intensity events.
3.1.2. Rainfall Estimates over the Catchment
Before analysing the impact of the rainfall multifractality on the flow, this subsection gives a classical statistical analysis of the rainfall data adding the SIAVB rain gauge records during each of three events and reducing the radar data grid to the catchment area. Whereas all measuring techniques overall agree on the dynamics of the total rainfall during the events studied, there are some significant differences among the rainfall estimates. It seems that they are primarily occurring during low rainfall periods, for which the choice of parameters in the Marshall–Palmer relation is crucial, as previously discussed.
Figure 7 displays maps of the total accumulated rainfall depth, for X-band and C-band rainfall measurements along with the SIAVB rain gauges’ estimates (circle) for the rainfall events studied. The colour palette remains the same for all maps. It appears that C-band data yield greater estimates than those of the X-band and rain gauges. This figure illustrates well the loss of information with regards to rainfall when considering only a limited number of sub-catchments. Comparing the C-band and X-band rainfall totals to those resulting from the SIAVB tipping bucket rain gauges, one may note that the X-band radar tends to underestimate, while C-band radar mostly overestimates them. However, these observations remain non-conclusive due to the fact that the rainfall is strongly variable at small scales, and totals measured by a single rain gauge are not necessary representative at the scale of whole catchment.
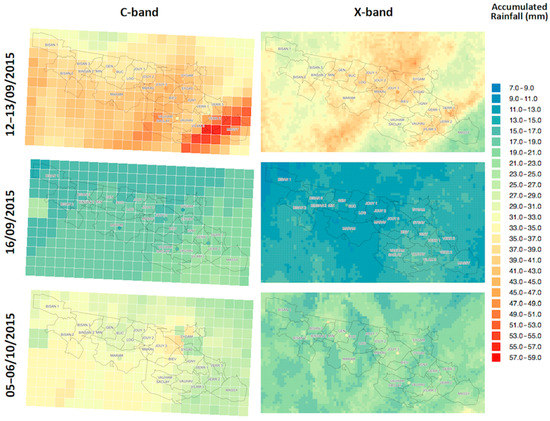
Figure 7.
C-band (left) and X-band (right) pixel maps of the rainfall totals for the three events studied: 12–13 September 2015 (top); 16 September 2015 (centre) and 5–6 October 2015 (bottom). Six circles indicate the rain-gauged values.
Additionally, Figure 8 summarises results of quantitative comparison between several rainfall products time series. These series were obtained either by computing the mean rainfall over the six sub-catchments containing a SIAVB rain gauge (as explained in Section 2.4) or by taking the corresponding radar pixels, during the three events. The rain gauge rainfall time series were taken as the basis of comparison for the three events. The differences between the rainfall series estimated per pixel or per sub-catchment for the same rainfall type (C-band, X-band or rain gauge) highlight the misrepresentation of whole catchment with the help of a single point as discussed earlier. These differences remain inferior to the uncertainties induced by the unmeasured (below the radar observation scale) rainfall variability [12]; making it difficult to compare directly the rainfall estimates. This illustrates well the contribution of the multifractal analysis carried out in this paper, which proposes a comparison framework independent of an observation scale, as well as the need for further hydrological modelling that would reduce the uncertainties in multifractal parameters estimation.
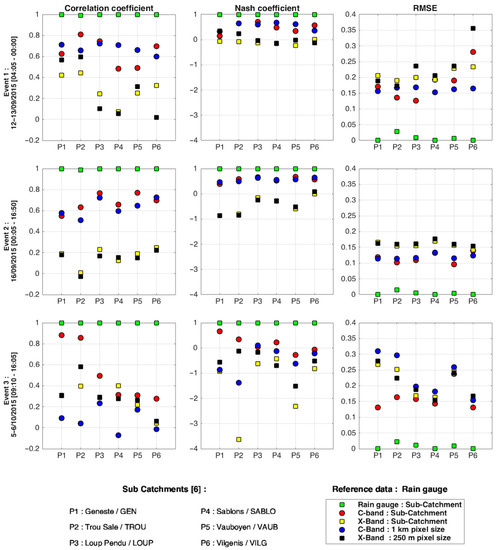
Figure 8.
Statistical comparison of the temporal rainfall series over the six sub-catchments for which rain gauge measurements were available. For all quantitative parameters, the rain gauge information was used as the reference data.
From Figure 8, one may notice that the C-band radar product is closer to the rain gauge measurement than the X-band radar at all six SIAVB rain gauges’ locations for the first two events. Indeed, RMSEs are greater and correlations are smaller, as are the Nash–Sutcliffe values for the X-band radar. These discrepancies vary according to the rain gauge. For instance for event 1, X-band and C-band exhibit much closer performances for P1 and P2 than for P3 and P4. Results are less straightforward for the third event, for which there is greater variability between the pixel and catchment scale measurements. For event 3, C-band radar data at catchment scale exhibit better performances than for the corresponding pixels. This unintuitive behaviour illustrates well the previously mentioned small scale unmeasured rainfall variability that introduces an intrinsic bias in the computation of these metrics due to the differences of observation scale between the devices. Finally, it should be reminded here that the C-band product was adjusted in real time to a rain gauge network whereas no adjustment—calibration—was performed for the ENPC X-band radar.
The small errors estimated (especially at P2, P3 and P5) for the cumulative rainfall time series obtained with rain gauges per sub-catchment are result of the Thiessen polygons’ method.
Finally, as already mentioned, these results have to be analysed cautiously, since the tipping-bucket rain gauges do not necessarily give the “truth”, even at their observation scale, which is different from that of radar. There are several studies in the literature pointing out the many sources of errors that affect the quality and reliability of rain gauge information, like wind, local turbulence and sampling error [7,75,76,77,78].
3.2. Hydrological Comparison
As already indicated, the goal of this study is a hydrological comparison of the rainfall data resulting from C-band and X-band radar measurements notably to study the impact of small-scale rainfall variability over the Bièvre catchment. We use in this work the Optim Sim model (coupled with InfoWorks CS), as described in Section 2.4.
Simulated flows are compared with observations at four locations from upstream to downstream (see Figure 1): “La Minière”, “Arcades de Buc”; “Moulin Vauboyen” and “Pont Cambaceres”. “La Minière” is actually the point where the portion of the Bièvre River managed by the SIAVB starts, while the upstream area is modelled to simulate the flow entering the SIAVB territory. “Pont Cambaceres” is the only point located downstream the Vilgénis basin (not existing anymore, but still remaining in the model). However, this situation could have only a limited impact on simulation outputs because the unregulated flow should remain similar whether the basin is removed or not.
These four locations correspond to an increasing number of regulated storage basins: none for “La Minière”, while two for “Arcades de Buc”, three for “Moulin Vauboyen” and seven for “Pont Cambaceres”. This implies that the simulated outputs downstream will potentially be more affected by a regulation at the whole catchment scale, i.e., at “Pont de Cambaceres” than at “La Minière”.
Figure 9, Figure 10 and Figure 11 display the simulated flows at the four selected points for the 12–13 September event, the 16 September event and the 5–6 October event. The tool simulating the optimisation of the regulation at the basin scale was not used. All C-band data, X-band data and SIAVB rain gauge network were tested and compared. In addition, Figure 12 presents the error metrics related to these hydrological results for the three events studied, taking the local observations as the basis of comparison.
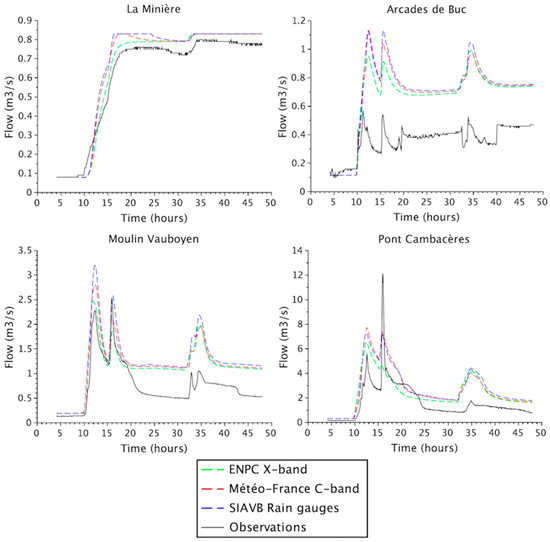
Figure 9.
Flow simulated at the four studied locations with X-band, C-band and rain gauged data for the 12–13 September event, along with observations. Simulations are carried out without the implementation of the tool mimicking regulation at the basin scale.
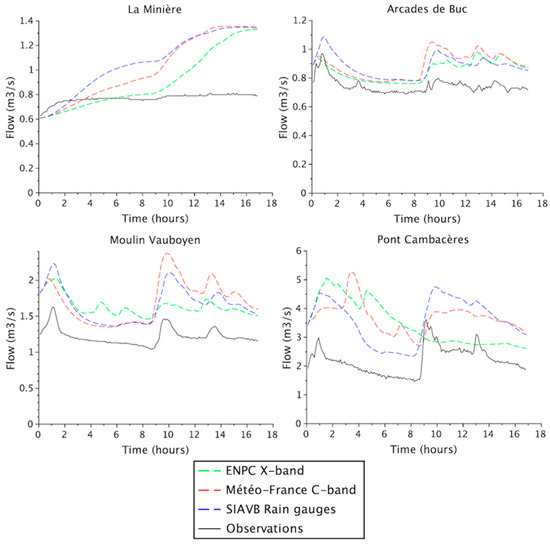
Figure 10.
Flow simulated at the four studied locations with X-band, C-band and rain gauged data for the 16 September event, along with observations. Simulations are carried out without the implementation of the tool mimicking regulation at the basin scale.
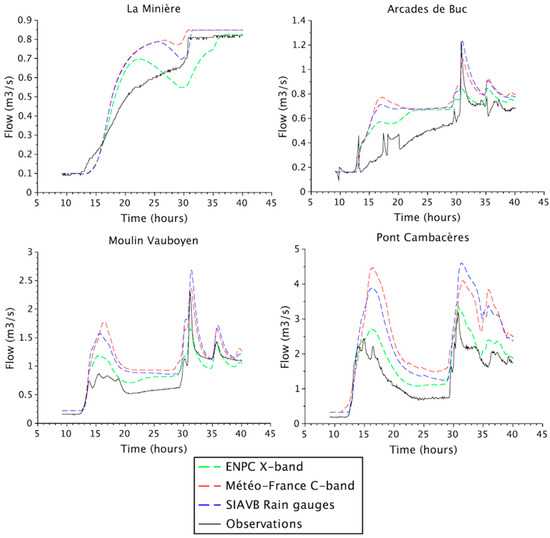
Figure 11.
Flow simulated at the four studied locations with X-band, C-band and rain gauged data for the 5–6 October event, along with observations. Simulations are carried out without the implementation of the tool mimicking regulation at the basin scale.
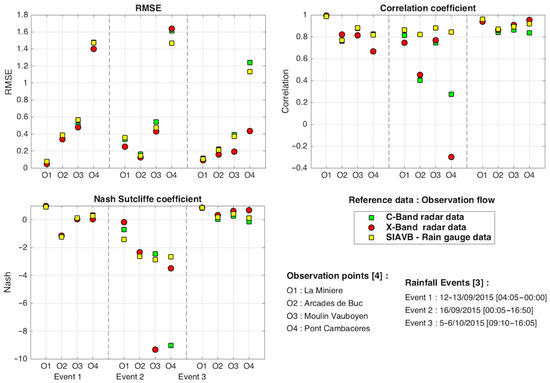
Figure 12.
Statistical comparison of all hydrological modelling results, with respect to the local flow measurements.
For the 12–13 September event (Figure 9), the increase of flow at “La Minière” reaches its regulated target value of 0.8 m3/s, being well reproduced with the three rainfall products, which is confirmed by the error metrics (Figure 12): , and . For the other observation points, the three rainfall products reproduce the observed flow dynamic (correlation values are approximately 0.8), with important differences in the obtained volumes (RMSE errors are between 0.35 and 0.6 for “Arcades de Buc” and “Moulin Vauboyen” and around 1.4 for “Pont Cambaceres”; Nash values are between −1.5 and 0.2). The fact that regulation at the catchment scale is not mimicked makes comparison with observations not relevant, as discussed above. For this event, there is a tendency of the X-band data to generate slightly smaller flows than the other two products, well visible on all curves of the figure. This tendency is more pronounced for the first half of the event (until 13 September 2015 at 07:00) than for the second one.
For the 16 September event (Figure 10) the simulated flows are much greater than observed ones, for which the optimisation of the outflow regulations of the catchment was deployed, again highlighting the issue with the simulation of local regulation for this event. This is confirmed by the metrics: correlations are under 0.9 for all rainfall products, and even under 0.3 for both radar products at “Pont Cambaceres”; all Nash values are under 0, confirming worse performances even for rain gauge data; and RMSE errors are higher than 0.13, especially at “Pont Cambaceres”; as displayed in Figure 12. It is important to mention here that the values observed at “La Minière” are greater than the 0.8 m3/s regulated target value because additional water coming from an overflow at Val d’Or is input in the model for this event. This should be investigated more precisely in future work. The differences between the three rainfall products on the simulated flows are more pronounced for this event than for the other two, as it can be noticed in Figure 12 (with bigger gaps between the three points for this event). It should also be noted that there are some changes according to the observation point and time. For instance, at the beginning of the event (before 16 September 2015 at ~ 05:00), rain gauges yield a greater flow at “Arcades de Buc” and “Moulin Vauboyen” whereas it is at “Pont Cambaceres” for the X-band radar. At this location, the C-band rainfall data generate a peak that is found neither with other rainfall data nor on observations. In the period between 08:00 and 16:50 on 16 September 2015, C-band data yield greater flows at “Arcades de Buc” and “Moulin Vauboyen” (more pronounced for the beginning of this period) whereas it is the rain gauges at “Pont Cambaceres”. Here the simulated flows are much smaller with X-band data. As for the 12–13 September event, it is not relevant to compare with actual measurements due to the problematic simulation of regulation at the catchment scale that was actually deployed.
As previously mentioned, for the 5–6 October event, the regulation at the basin scale was only implemented at the end of the event, meaning that comparison with observations is more relevant (see Figure 11). As displayed in Figure 12, there is a high overall correlation () for this event, suggesting a better reproduction of the observed flow dynamic. Although Nash values are between −0.3 and 1, those for X-band are considerably better than those for C-band and rain gauges. At “Arcades de Buc”, there is overall less overestimation of flows, but it should be noted that the peak at about 12:00 on 6 October 2015 is underestimated with the X-band radar data. Similar patterns are found at “Moulin Vauboyen” with a lower underestimation for the peak. For these two observation points, all RMSE values are under 0.4, indicating lower differences between modelled and observed flows. At “Pont Cambaceres”, simulations with X-band data reproduce well observations (lower RMSE values than C-band and rain gauge), whereas there is an overestimation with C-band data and rain gauges. It is interesting to note that despite the rather higher level of processing—calibration (performed for many years) and real-time adjustment to rain gauges—of the C-band radar is not so successful with respect to the (unadjusted, uncalibrated) dual-polarimetric data of the X-band radar. This finding is all the more interesting given that, as pointed out before, the C-band radar has the advantage to be closer to the test site than the X-band radar (15 km vs. 35 km) putting it a better position from the beginning.
Finally, an additional simulation with the optimising tool using X-band data was made for the 16 September event. Figure 13 displays the results at the four locations studied (thick violet for the additional curve). While all simulations presented up to now were performed at a 5 min time step, the time step of update of gate positions remains of 15 min. It is possible to reduce it to 5 min as well, but it would multiply by three the computation time. Although it could affect the results, it is likely that it does not really in this case because the model’s sensitivity to the time step is rather low due to the size of the sub-catchments. As it can be seen from this figure, at “La Minière”, since there is no regulated basin upstream this location, the flows simulated using X-band radar data with and without optimisation are the same. At “Arcades de Buc”, the observations are situated right in between the two simulations using the X-band radar data, with and without the implementation of the Optim Sim tool. Here, the differences are very significant, showing that the optimisation of the regulation has strong consequences. It illustrates well the difficulty to accurately compare simulations with observations given the previously mentioned limitations of this tool. The last two locations also present some differences between both simulated flows using X-band radar data. However, at “Moulin Vauboyen”, both X-band simulated flows reproduce relatively well the observations behaviour, getting even closer to the latter when using the optimisation tool. The impacts of optimisation are stronger at “Pont Cambaceres”, since it is located downstream seven regulated storage basins. It is possible to identify that the use of the optimisation tool even anticipates the second X-band peak, in relation to that without optimisation.
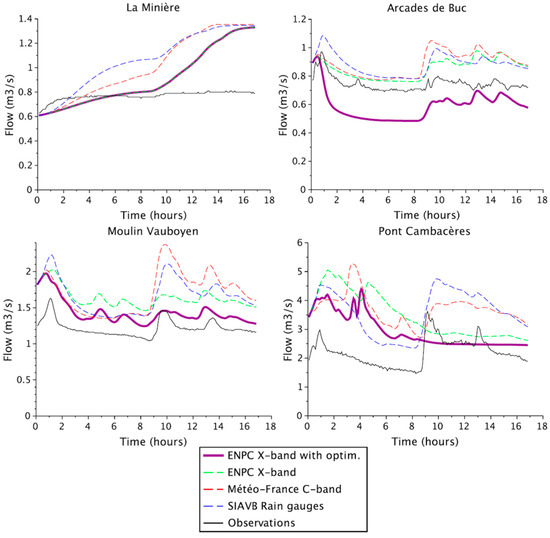
Figure 13.
Flow simulated at the four locations studied for the 16 September event: without the implementation of the tool optimising regulation at the catchment scale using X-band, C-band and rain gauge data; and with the optimising tool using X-band data.
4. Discussion
First, it is worthwhile to recall in what conditions the present results were obtained. The Bièvre catchment, which is much closer to the Météo-France C-band radar than to the ENPC X-band radar, has a very complex topography, e.g., with very steep slopes (see Figure 1), that has various influences on the rainfall (micro orographic effects), its detection (ground clutter) and the runoff. The ENPC X-band radar rain rate estimates were obtained by the product DPSRI (Double Polarisation Surface Rainfall Intensity) at 1.5 km height over the ground, with a spatial resolution of 250 m × 250 m, without any adjustments using rain gauges; whereas the Météo-France C-band estimates correspond to the data, with a 1 km2 spatial resolution, having the highest quality indicator over the pixel’s vertical and are adjusted to rain gauges. In addition, the SIAVB rain gauge network provided the third set of rainfall data studied. Furthermore, the semi-distributed model InfoWorks CS was used with sub-catchments of average size of 2 km, which highlights its limitations to take into account the high spatial variability of the rainfall.
It is therefore interesting to note that in such conditions a semi-quantitative agreement was obtained by the X-band radar estimates with respect to the in-situ observations and those of the Météo-France C-band radar (with a higher level of processing: calibration performed for many years and real time adjustment to rain gauges) and of the SIAVB rain gauge network. It turned out that comparison with distributed data in “replay mode” was more difficult than expected due to the necessary update for the tool mimicking actual real-time control of the river network. In general, for the first two events, the X-band radar data yields slightly lower simulated flows. It is also the case for the last rainfall event, where observations tend to validate the use of X-band radar data, although there are some discrepancies on a peak.
Two differences are also worthwhile to note and to discuss. First, as expected, the X-band radar was able to pick up a few extremes that were smoothed out by the C-band radar. This was quantified with the help of a multifractal analysis, in which higher multifractality indexes () were estimated for the X-band radar data, for the three studied events. Indeed, higher corresponds to higher intermittency of the extremes and therefore to a higher frequency of them. We developed a specific analysis of DTM sample fluctuations vs. their ensemble estimates to demonstrate that the difference of alpha between C- and X-band data was statistically significant. We also showed that this was not the case for , especially for the two last events. On the contrary, the DPSRI product of the X-band radar seems to have underestimated low-intensity episodes of the chosen events, which might be explained by both the chosen data processing and acquisition strategies. However, this requires further investigation, as discussed below.
Furthermore, it is important to distinguish polarimetric from non-polarimetric X-band radar. Although there are many studies about X-band radar adjusted by using rain gauge networks [79,80,81,82], most of them do not consider polarimetric X-band radar. Additionally, there are many other studies demonstrating that the use of polarimetric X-band radar does not require any absolute calibration, including rain gauge adjustments [5,83,84,85,86,87]. This discussion, which is not the purpose of this study, therefore remains widely open. In addition, the pitfalls of the spatial sparseness of rain gauge network, highlighted with the help of the ENPC X-band radar, and its implications to hydrological modelling [88] will be issue of a future work.
This study should be therefore considered as a very first attempt to compare the rain gauge network, the X-band and C-band radar rainfall products using hydrological models. As already mentioned, further investigations are required. They are of two types: those that can be achieved with the past data (without changing the data acquisition), and those that cannot (changing the data acquisition). The first ones correspond to modify given stages of the data processing chain leading to a given type of rainfall estimate. Main options include at least two different methodologies to estimate the specific differential phase shift (KDP), using differently the double polarisation (e.g., the R–KDP relation including for low reflectivity’s), attenuation correction, different heights for the product DPSRI, defining other products (e.g., closer to those used by Météo-France). The second set of investigations includes modifying the scan strategy, the pulse repetition frequency and the pulse length itself. Both approaches show a large choice of possible settings for data processing or data acquisition. The former was slightly investigated, although not presented in this work. Further X-band radar tests and comparative studies are necessary in order to ensure the optimal measurement capability.
The last, but not least, remarks correspond to the manifest requirement of hydrological models able to take into account the spatiotemporal variability of rainfall fields, with sufficiently high resolution, and the necessity to proceed to similar studies on other test sites, in particular those being located at a similar distance from both types of radar.
Supplementary Materials
Data can be accessed at http://doi.org/10.5281/zenodo.1069034.
Acknowledgments
The authors greatly acknowledge partial financial supports of the Chair “Hydrology for resilient cities” endowed by Veolia, and of the Department of Science and Technology of the Brazilian Army. The authors are thankful to M Bernard Urban (Météo-France) for providing access to the C-band radar data and documentation in the framework of the INTERREG NWE RainGain project.
Author Contributions
Igor Paz wrote the paper; Ioulia Tchiguirinskaia, Daniel Schertzer and Bruno Tisserand conceived and designed the study; Ioulia Tchiguirinskaia and Daniel Schertzer collected the ENPC X-band radar data; Bernard Willinger gave access to the hydrological model; Igor Paz prepared the input data for the simulations; Bernard Willinger, Igor Paz, Auguste Gires and Laurent Monier performed the hydrological simulations; Igor Paz performed the multifractal analyses; Abdellah Ichiba, Igor Paz and Auguste Gires performed the metrics analyses; Igor Paz, Auguste Gires, Ioulia Tchiguirinskaia and Daniel Schertzer analysed all the results; Auguste Gires, Laurent Monier, Christophe Zobrist, Bruno Tisserand, Ioulia Tchiguirinskaia and Daniel Schertzer revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Loukas, A.; Llasat, M.-C.; Ulbrich, U. Preface: “Extreme events induced by weather and climate change: Evaluation, forecasting and proactive planning”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1895–1897. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guide to Meteorological Instruments and Methods of Observation WMO-No. 8. 2014. Available online: http://www.wmo.int/pages/prog/www/IMOP/CIMO-Guide.html (accessed on 14 February 2017).
- National Research Council of the National Academies. Urban Meteorology: Forecasting, Monitoring, and Meeting Users’ Need; National Academy Press: Washington, WA, USA, 2012. [Google Scholar]
- SIAVB. Available online: http://www.siavb.fr/riviere.aspx (accessed on 4 November 2016).
- Diss, S.; Testud, J.; Lavabre, J.; Ribstein, P.; Moreau, E.; Parent du Chatelet, J. Ability of a dual polarized X-band radar to estimate rainfall. Adv. Water Resour. 2009, 32, 975–985. [Google Scholar] [CrossRef]
- Tabary, P.; Boumahmoud, A.-A.; Andrieu, H.; Thompson, R.J.; Illingworth, A.J.; Le Bouar, E.; Testud, J. Evaluation of two “integrated” polarimetric Quantitative Precipitation Estimation (QPE) algorithms at C-band. J. Hydrol. 2011, 405, 248–260. [Google Scholar] [CrossRef]
- Emmanuel, I.; Andrieu, H.; Tabary, P. Evaluation of the new French operational weather radar product for the field of urban hydrology. Atmos. Res. 2012, 103, 20–32. [Google Scholar] [CrossRef]
- Figueras i Ventura, J.; Boumahmoud, A.-A.; Fradon, B.; Dupuy, P.; Tabary, P. Long-term monitoring of French polarimetric radar data quality and evaluation of several polarimetric quantitative precipitation estimators in ideal conditions for operational implementation at C-band. Q. J. R. Meteorol. Soc. 2012, 138, 2212–2228. [Google Scholar] [CrossRef]
- Figueras i Ventura, J.; Tabary, P. The New French Operational Polarimetric Radar Rainfall Rate Product. J. Appl. Meteorol. Climatol. 2013, 52, 1817–1835. [Google Scholar] [CrossRef]
- Tabary, P. The new French operational radar rainfall product, Part I: Methodology. Weather Forecast. 2007, 22, 393–408. [Google Scholar] [CrossRef]
- Ciach, G.J.; Habib, E.; Krajewski, W.F. Zero-covariance hypothesis in the error variance separation method of radar rainfall verification. Adv. Water Resour. 2003, 26, 573–580. [Google Scholar] [CrossRef]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Schellart, A.; Berne, A.; Lovejoy, S. Influence of small scale rainfall variability on standard comparison tools between radar and rain gauge data. Atmos. Res. 2014, 138, 125–138. [Google Scholar] [CrossRef]
- Wyss, J.; Williams, E.R.; Bras, R.L. Hydrologic modeling of New England river basins using radar rainfall data. J. Geophys. Res. 1990, 95, 2143–2152. [Google Scholar] [CrossRef]
- Sun, X.; Mein, R.G.; Keenan, T.D.; Elliot, J.F. Flood estimation using radar and raingauge data. J. Hydrol. 2000, 239, 4–18. [Google Scholar] [CrossRef]
- Germann, U.; Berenguer, M.; Sempere-Torres, D.; Zappa, M. REAL—Ensemble radar precipitation estimation for hydrology in a mountainous region. Q. J. R. Meteorol. Soc. 2009, 135, 445–456. [Google Scholar] [CrossRef]
- Lobligeois, F. Mieux Connaître la Distribution Spatiale des Pluies Améliore-t-il la Modélisation des Crues? Diagnostic sur 181 Bassins Versants Français. Ph.D. Thesis, Agro ParisTech, Paris, France, 2014. [Google Scholar]
- Einfalt, T.; Denoeux, T.; Jacquet, G. A radar rainfall forecasting method designed for hydrological purposes. J. Hydrol. 1990, 114, 229–244. [Google Scholar] [CrossRef]
- Vieux, B.E.; Bedient, P.B. Assessing urban hydrologic prediction accuracy through event reconstruction. J. Hydrol. 2004, 299, 217–236. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.-E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Berenguer, M.; Corral, C.; Sánchez-Diezma, R.; Sempere-Torres, D. Hydrological Validation of a Radar-Based Nowcasting Technique. J. Hydrometeorol. 2005, 6, 532–549. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A.; Schellart, A.N.A.; Saul, A.J. Using probabilistic radar rainfall nowcasts and NWP forecasts for flow prediction in urban catchments. Atmos. Res. 2012, 103, 80–95. [Google Scholar] [CrossRef]
- Ichiba, A. X-band Radar Data and Predictive Management in Urban Hydrology. Ph.D. Thesis, Université Paris-Est, Paris, France, 2016. [Google Scholar]
- Peleg, N.; Blumensaat, F.; Molnar, P.; Fatichi, S.; Burlando, P. Partitioning the impacts of spatial and climatological rainfall variability in urban drainage modeling. Hydrol. Earth Syst. Sci. 2017, 21, 1559–1572. [Google Scholar] [CrossRef]
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Aronica, G.; Cannarozzo, M. Studying the hydrological response of urban catchments using a semi-distributed linear non-linear model. J. Hydrol. 2000, 238, 35–43. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.-D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Segond, M.L.; Neokleous, N.; Makropoulos, C.; Onof, C.; Maksimović, Č. Simulation and spatio-temporal disaggregation of multi-site rainfall data for urban drainage applications. Hydrol. Sci. J. 2007, 52, 917–935. [Google Scholar] [CrossRef]
- Schellart, A.N.A.; Shepherd, W.J.; Saul, A.J. Influence of rainfall estimation error and spatial variability on sewer flow prediction at a small urban scale. Adv. Water Resour. 2012, 45, 65–75. [Google Scholar] [CrossRef]
- Gires, A.; Onof, C.; Maksimović, Č.; Schertzer, D.; Tchiguirinskaia, I.; Simoes, N. Quantifying the impact of small scale unmeasured rainfall variability on urban runoff through multifractal downscaling: A case study. J. Hydrol. 2012, 442, 117–128. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Gires, A.; Pina, R.D.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modeling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Simões, N.E.; Ochoa-Rodriguez, S.; Wang, L.-P.; Pina, R.D.; Marques, A.S.; Onof, C.; Leitão, J.P. Stochastic Urban Pluvial Flood Hazard Maps Based upon a Spatial-Temporal Rainfall Generator. Water 2015, 7, 3396–3406. [Google Scholar] [CrossRef]
- Gires, A.; Giangola-Murzyn, A.; Abbes, J.-B.; Tchiguirinskaia, I.; Schertzer, D.; Lovejoy, S. Impacts of small scale rainfall variability in urban areas: A case study with 1D and 1D/2D hydrological models in a multifractal framework. Urban Water J. 2014, 12, 607–617. [Google Scholar] [CrossRef]
- El-Tabach, E.; Tchiguirinskaia, I.; Mahmood, O.; Schertzer, D. Multi-Hydro: A spatially distributed numerical model to assess and manage runoff processes in peri-urban watersheds. In Proceedings of the Final Conference of the COST Action C22, Road map towards a flood resilient urban environment, Paris, France, 26–27 November 2009; Pascheet, E., Evelpidou, N., Zevenbergen, C., Ashley, R., Garvin, S., Eds.; Hamburger Wasserbau-Schriftien: Hamburg, Germany, 2009. [Google Scholar]
- Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking urban flood models of varying complexity and scale using high resolution terrestrial LiDAR data. Phys. Chem. Earth 2011, 36 Pt A/B/C, 281–291. [Google Scholar] [CrossRef]
- Giangola-Murzyn, A.; Gires, A.; Hoang, C.T.; Tchiguirinskaia, I.; Schertzer, D. Multi-Hydro modelling to assess flood resilience across scales, case study in the Paris region. In Proceedings of the 9th International Conference on Urban Drainage Modelling, Belgrade, Serbia, 4–7 September 2012. [Google Scholar]
- Tramblay, Y.; Bouvier, C.; Crespy, A.; Marchandise, A. Improvement of flash flood modelling using spatial patterns of rainfall: A case study in southern France. In Proceedings of the Sixth World FRIEND Conference, Montpellier, France, 7–10 October 2014; IAHS Publ.: Fez, Morocco, 2010; p. 340. [Google Scholar]
- RainGain Project. Available online: www.raingain.eu (accessed on 21 July 2016).
- Schertzer, D.; Tchiguirinskaia, I.; Lovejoy, S.; Hubert, P. No monsters, no miracles: In nonlinear sciences hydrology is not an outlier! Hydrol. Sci. J. 2010, 55, 965–979. [Google Scholar] [CrossRef]
- Réseau Hydrographique. Available online: Https://www.data.gouv.fr/fr/datasets/reseau-hydrographique-idf/ (accessed on 14 December 2015).
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D. Multifractal comparison of the outputs of two optical disdrometers. Hydrol. Sci. J. 2016, 61, 1641–1651. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrop with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Parent du Châtelet, J. ARAMIS, le réseau Français de radars pour la surveillance des précipitations. La Météorologie 2003, 40, 44–52. [Google Scholar] [CrossRef][Green Version]
- Gourley, J.J.; Tabary, P.; Parent du Chatelet, J. A fuzzy logic algorithm for the separation of precipitating from nonprecipitating echoes using polarimetric radar observations. J. Atmos. Ocean. Technol. 2007, 24, 1439–1451. [Google Scholar] [CrossRef]
- Selex. Selex METEOR manual; Selex ES GmbH: Neuss, Germany, 2015. [Google Scholar]
- Fulton, R.A.; Bredienbach, J.P.; Seo, D.-J.; Miller, D.A.; O’Bannon, T. The WSR-88 rainfall algorithm. Weather Forecast. 1998, 13, 377–395. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Clark, K.A.; Martner, B.E.; Tokay, A. X-Band Polarimetric Radar Measurements of Rainfall. J. Appl. Meteorol. 2002, 41, 941–952. [Google Scholar] [CrossRef]
- Wallingford Software. InfoWorks CS Help Documentation; HR Wallingford Group: Wallingford, UK, 2009. [Google Scholar]
- Clarke, D.L. Analytical Archaeology; Methuen: London, UK, 1968. [Google Scholar]
- Schertzer, D.; Lovejoy, S. Physical modeling and Analysis of Rain and Clouds by Anisotropic Scaling Multiplicative Processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. A Statistical Analysis of Mesoscale Rainfall as a Random Cascade. J. Appl. Meteorol. 1993, 32, 251–267. [Google Scholar] [CrossRef]
- Harris, D.; Menabde, M.; Seed, A.; Austin, G. Multifractal characterization of rain fields with a strong orographic influence. J. Geophys. Res. 1996, 101, 26405–26414. [Google Scholar] [CrossRef]
- Marsan, D.; Schertzer, D.; Lovejoy, S. Causal space-time multifractal processes: Predictability and forecasting of rain fields. J. Geophys. Res. 1996, 101, 26333–26346. [Google Scholar] [CrossRef]
- Olsson, J.; Niemczynowicz, J. Multifractal analysis of daily spatial rainfall distributions. J. Hydrol. 1996, 187, 29–43. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Grasman, J. Multifractal analysis of 15-min and daily rainfall from a semi-arid region in Portugal. J. Hydrol. 1999, 220, 1–11. [Google Scholar] [CrossRef]
- Deidda, R. Rainfall downscaling in a space-time multifractal framework. Water Resour. Res. 2000, 36, 1779–1794. [Google Scholar] [CrossRef]
- Pathirana, A.; Herath, S. Multifractal modeling and simulation of rain fields exhibiting spatial heterogeneity. Hydrol. Earth Syst. Sci. 2002, 6, 695–708. [Google Scholar] [CrossRef]
- Biaou, A.; Hubert, P.; Schertzer, D.; Tchiguirinskaia, I.; Bendjoudi, H. Fractals, multifractals et prévision des précipitations. Sud Sci. Technol. 2003, 10, 10–15. [Google Scholar]
- Pathirana, A.; Herath, S.; Yamada, T. On the modeling of temporal correlations in spatial-cascade rainfall downscaling. In Weather Radar Information and Distributed Hydrological Modeling; Tachikawa, Y., Vieux, B.E., Georgakakos, K.P., Nakakita, E., Eds.; IAHS Publication: Sapporo, Japan, 2003; Volume 282, pp. 74–82. [Google Scholar]
- Ferraris, L.; Gabellani, S.; Parodi, U.; Rebora, N.; von Hardenberg, J.; Provenzale, A. Revisiting multifractality in rainfall fields. J. Hydrometeorol. 2003, 4, 544–551. [Google Scholar] [CrossRef]
- Ferraris, L.; Gabellani, S.; Rebora, N.; Provenzale, A. A comparison of stochastic models for spatial rainfall downscaling. Water Resour. Res. 2003, 39, 1368–1384. [Google Scholar] [CrossRef]
- Macor, J.; Schertzer, D.; Lovejoy, S. Multifractal Methods Applied to Rain Forecast Using Radar Data. La Houille Blanche 2007, 4, 92–98. [Google Scholar] [CrossRef]
- Royer, J.F.; Biaou, A.; Chauvin, F.; Schertzer, D.; Lovejoy, S. Multifractal analysis of the evolution of simulated precipitation over France in a climate scenario. C. R. Geosci. 2008, 340, 431–440. [Google Scholar] [CrossRef]
- Nykanen, D.K. Linkages between Orographic Forcing and the Scaling Properties of Convective Rainfall in Mountainous Regions. J. Hydrometeorol. 2008, 9, 327–347. [Google Scholar] [CrossRef]
- De Montera, L.; Barthes, L.; Mallet, C.; Gole, P. The effect of rain-no rain intermittency on the estimation of the universal multifractals model parameters. J. Hydrometeorol. 2009, 10, 493–506. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D.; Furcolo, P.; Lepore, C. Multifractal rainfall extremes: Theoretical analysis and practical estimation. Chaos Solitons Fractals 2009, 39, 1182–1194. [Google Scholar] [CrossRef]
- Tchiguirinskaia, I.; Schertzer, D.; Hoang, C.-T.; Lovejoy, S. Multifractal study of three storms with different dynamics over the Paris region. In Proceedings of the Weather Radar and Hydrology, Exeter, UK, 18–21 April 2011; Moore, J., Cole, S., Illingworth, A., Eds.; IAHS Publ.: Exeter, UK, 2011; 351, pp. 421–426. [Google Scholar]
- Hoang, C.-T.; Tchiguirinskaia, I.; Schertzer, D.; Lovejoy, S. Caractéristiques multifractales et extrêmes de la précipitation à haute resolution, application à la détection du changement climatique. J. Water Sci. 2014, 27, 205–216. [Google Scholar] [CrossRef][Green Version]
- Schertzer, D.; Lovejoy, S. Universal Multifractals do Exist! J. Appl. Meteorol. 1997, 36, 1296–1303. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Multifractals, generalized scale invariance and complexity in geophysics. Int. J. Bifurcat. Chaos 2011, 21, 3417–3456. [Google Scholar] [CrossRef]
- Lavallée, D.; Lovejoy, S.; Ladoy, P. Nonlinear variability and landscape topography: Analysis and simulation. In Fractals in Geography; De Cola, L., Lam, N., Eds.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993; pp. 171–205. [Google Scholar]
- Hoang, C.T. Prise en Compte des Fluctuations Spatio-Temporelles Pluies-Débits Pour une Meilleure Gestion de la Ressource en eau et une Meilleure Évaluation des Risques. Ph.D. Thesis, Université Paris-Est, France, 2011. [Google Scholar]
- Hittinger, F. Intercomparaison des incertitudes dans l’Analyse de Fréquence de Crues classique et l’Analyse Multifractale de Fréquence de Crues. Master’s Thesis, Ecole Nationale Supérieure d’Hydraulique et de Mécanique de Grenoble, Grenoble, France, 2008. [Google Scholar]
- Hoang, C.T. Analyse fréquentielle classique et multifractale des 10 séries pluviométriques à haute résolution. Master’s Thesis, Université P. & M. Curie, Paris, France, 2008. [Google Scholar]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Lovejoy, S. Influence of the zero-rainfall on the assessment of the multifractal parameters. Adv. Water Resour. 2012, 45, 13–25. [Google Scholar] [CrossRef]
- Sevruk, B.; Hamon, W.R. International Comparison of National Precipitation Gauges with a Reference Pit Gauge; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1984. [Google Scholar]
- Fankhauser, R. Influence of systematic errors from tipping bucket rain gauges on recorded rainfall data. Water Sci. Technol. 1998, 37, 121–129. [Google Scholar] [CrossRef]
- Habib, E.; Krajewski, W.; Kruger, A. Sampling errors of Tipping-Bucket rain gauge measurements. J. Hydrol. Eng. 2001, 6, 159–166. [Google Scholar] [CrossRef]
- Ciach, G.J. Local random errors in Tipping-Bucket rain gauge measurements. J. Atmos. Ocean. Technol. 2003, 20, 752–759. [Google Scholar] [CrossRef]
- Einfalt, T.; Jessen, M.; Mehlig, B. Comparison of radar and raingauge measurements during heavy rainfall. Water Sci. Technol. 2005, 51, 195–201. [Google Scholar] [PubMed]
- Gabella, M.; Orione, F.; Zambotto, M.; Turso, S.; Fabbo, R.; Pillon, A. A Portable Low Cost X-band RADAR for Rainfall Estimation in Alpine Valleys; FORALPS Technical Report; Universita degli Studi di Trento: Trento, Italy, 2008; pp. 1–52. [Google Scholar]
- Allegretti, M.; Bertoldo, S.; Prato, A.; Lucianaz, C.; Rorato, O.; Notarpietro, R.; Gabella, M. X-Band Mini Radar for Observing and Monitoring Rainfall Events. Atmos. Clim. Sci. 2012, 2, 290–297. [Google Scholar] [CrossRef]
- Borup, M.; Grum, M.; Linde, J.J.; Mikkelsen, P.S. Dynamic gauge adjustment of high-resolution X-band radar data for convective rain storms: Model-based evaluation against measured combined sewer overflow. J. Hydrol. 2016, 539, 687–699. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Anagnostou, M.N.; Kalogiros, J.; Anagnostou, E.N.; Tarolli, M.; Papadopoulos, A.; Borga, M. Performance evaluation of high resolution rainfall estimation by X-band dual-polarization radar for flash flood applications in mountainous basins. J. Hydrol. 2010, 394, 4–16. [Google Scholar] [CrossRef]
- Otto, T.; Russchenberg, H.W.J.; Leijnse, H. Advances in polarimetric X-band weather radar. In Proceedings of the 9th European Radar Conference, Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 174–177, ISBN 978-2-87487-029-3. [Google Scholar]
- Otto, T.; Russchenberg, H.W.J. High-resolution polarimetric X-band weather radar observations at the Cabauw Experimental Site for Atmospheric Research. Geosci. Data J. 2014, 1, 7–12. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Baldini, L.; Bharadwaj, N.; Smith, P.L. Calibration procedures for global precipitation-measurement ground-validation radars. URSI Radio Sci. Bull. 2015, 88, 45–73. [Google Scholar] [CrossRef]
- Da Silva Rocha Paz, I.; Ichiba, A.; Skouri-Plakali, I.; Lee, J.; Gires, A.; Tchiguirinskaia, I.; Schertzer, D. Challenges with space-time rainfall in urban hydrology highlighted with a semi-distributed model using C-band and X-band radar data. In EGU General Assembly 2017, Vienna, Austria, 23–28 April 2017; Geophysical Research Abstracts: Vienna, Austria, 2017; p. 19, EGU2017-327. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).