1. Introduction
Exposure to urban pluvial flooding may pose a health risk to humans, since the floodwater may contain a variety of contaminants depending on its origin. During the past years, there has been an increased interest in microbial impacts through pluvial flooding, see, e.g., [
1,
2,
3,
4,
5,
6,
7,
8,
9] and combined sewer overflow (CSO) spills [
10], as well as economic, social, and psychological impacts of urban flooding [
11]. The latter are expressed as stressors on communities due to repeated flood events.
Originating from rainfall-generated surface runoff, pluvial flooding may be contaminated by dirt from paved surfaces (e.g., dog faeces and bird droppings). From combined sewer systems, it will be contaminated with wastewater and from storm sewers due to illicit connections. The contaminations include human enteric pathogens (e.g., norovirus and enterovirus) from urban wastewater [
12], and
Campylobacter,
Giardia, and
Cryptosporidium from both animal faeces and human wastewater [
13,
14]. According to De Wit et al. [
15] and Mead et al. [
16], these pathogens account for the majority of gastrointestinal illnesses in The Netherlands and the US. Harder-Lauridsen et al. [
10] demonstrated that the risk of illness from water intake by physically fit, long distance swimmers when swimming in sea water shortly after an extreme rainfall event is considerably larger than from non-polluted water.
In-sewer defects affect the hydraulic performance of a sewer system and may cause increased pluvial flooding. Possible defects include sedimentation, root intrusion, surface damage, attached/settled deposits, corrosion, protruding objects, joint eccentricity, and subsidence, see, e.g., [
17,
18]. Van Bijnen et al. [
19] demonstrated the impact of defects on flooding using data from visual inspections and Monte Carlo simulations for a full hydrodynamic model. The studied defects are sedimentation, root intrusion, surface damage, and attached/settled deposits. The results show that in-sewer defects significantly affect flooding with sedimentation as the predominant factor.
Health risks of exposure to pluvial flooding from urban drainage, including combined sewers, were quantified by De Man et al. [
5] using Quantitative Microbial Risk Assessment (QMRA). This requires information on the concentration of pathogens in the water or on the correlation between indicator bacteria and pathogens in the water, the exposure of people to these pathogens, and dose-response relations for different pathogens.
This paper addresses the impact of in-sewer defects on urban pluvial flooding and, subsequently, on health risks to humans. The analysis is based on flooding frequencies from Monte Carlo simulations as presented by Van Bijnen et al. [
19] and infection probabilities due to the ingestion of urban floodwater as presented by De Man et al. [
5]. The average infection probability for the whole catchment per year is based on a weighted average accounting for the number of inhabitants per manhole. The results show that the occurrence of flooding, and therefore the infection probability, are substantially enlarged by in-sewer defects.
2. Materials and Methods
An overview of the data utilised and analysed in this study is shown in
Figure 1. The catchments of ‘Tuindorp’ and ‘Loenen’ have been analysed accordingly. A detailed description is given in
Section 2.1,
Section 2.2,
Section 2.3,
Section 2.4,
Section 2.5,
Section 2.6 and
Section 2.7. The impact of sewer condition on urban flooding has been quantified using Monte Carlo simulations accounting for in-sewer defects, in particular sedimentation. Based on the simulation results, the summed frequency of threshold exceedances has been calculated for each manhole. From this result, the catchment-wide average infection probability per year has been calculated using infection probabilities from De Man et al. [
5].
2.1. Research Catchments
Two combined sewer systems with different characteristics are studied: ‘Tuindorp’ (Utrecht, The Netherlands) and ‘Loenen’ (Apeldoorn, The Netherlands).
The ‘Tuindorp’ catchment area is a combined sewer system constructed in the 1970s as a looped gravity flow system. The catchment is relatively flat. It comprises a range of contributing areas in terms of types of roofs and types of pavement. The collected sewage is transported to the pumping station in the southern part of the catchment. The sewer system contains five combined sewer overflow (CSO) structures (see
Figure 2). One of the CSOs discharges into a storage-settling tank. There are no discharges and inflows from adjacent systems into the catchment. The characteristics of this catchment are summarized in
Table 1. The layout of the sewer system is presented in
Figure 2.
The ‘Loenen’ catchment is also a combined sewer system. It has been constructed as a partly branched gravity system and the catchment is mildly sloping. The sewer system is equipped with one pumping station and two CSO structures. One of these CSO structures discharges into a large pond. There is a relatively large average dry weather flow per inhabitant because of several industrial discharges and an inflow from an adjacent catchment. The characteristics of this catchment are summarized in
Table 1. The layout of the sewer system is presented in
Figure 2.
2.2. Description of In-Sewer Defects
Observed sediment depths [
19] were used to include sediment deposition in the hydrodynamic model. Crabtree [
21] describes five categories of sediment deposits, based on observations of the provenance, nature, and location of the deposits within the sewer system. Sediment deposits in The Netherlands can typically be classified as type C: mobile, fine grained deposits found in slack flow zones. In this study, sediments are defined as type C deposits, which can be removed from a pipe by means of jetting. In Utrecht, sediment depths are registered by cleaning engineers before jetting individual pipes while carrying out the annual cleaning program. Attached deposits that have to be removed by other techniques can only be detected by detailed visual inspection of sewer pipes. Sediment depths are classified according to the percentage of obstructed pipe height. The accuracy of observed sediment depths depends on cleaning engineers’ experience and opinion [
22,
23]. Before jetting an individual pipe, the cleaning engineer makes an estimation of the sediment depth as can be seen from ground level after opening the manhole. After jetting the pipe, the removed amount of sediment for each pipe is also estimated. Sediment depths are registered as a relative depth (ratio of observed sediment depth and conduit height).
Observed depths were translated into model parameters accounting for pipe shape (circular, egg) and pipe height (250–1250 mm). For that purpose, a beta distribution function was fitted on observed sediment depths [
19] in order to statistically describe the sediment depth for each pipe category (combinations of shape and height). In the hydrodynamic model simulations, the relative sediment depths in the pipes were randomly drawn from the corresponding distribution.
2.3. Model Set-Up
InfoWorks was used for the hydraulic calculations. The InfoWorks models of both sewer systems have been validated but not calibrated. The validation aims at the removal of systematic errors from the model. This is done according to the method described in Van Mameren and Clemens [
24], Clemens [
25], and Stichting Rioned [
26]. This implies that system data on structural and geometrical data, ground levels, pumping capacities, etc., are verified in the field and that a comparison is made between call data on flooding events and locations where the model predicts flooding (see
Section 2.4).
Van Bijnen et al. [
20] showed for the ‘Tuindorp’ system that calibrated model parameters based on different storm events vary considerably. Since the calibration parameter set predominantly contains runoff parameters, which change between different rainfall events because the values also incorporate the antecedent condition of the catchment area, it is impossible to find one single parameter value set which can be used for a long time series. In addition, the values of calibrated model parameters and their correlations are affected by the presence of the in-sewer defects because these defects are local obstructions to the flow and cannot be included as uniquely identifiable calibration parameters. As a result, the presence of defects will affect the values of the calibrated parameters values which are mainly related to runoff. Considering that the characteristics of the network (i.e., the system state) in the Monte Carlo simulations change each run due to defects at randomly chosen locations, it is nearly impossible to use a set of calibrated parameters derived from a single model state with defects at different locations.
An integrated 1D/1D model has been applied to describe the interaction between the underground sewer network and surface flooding. This modelling approach is sufficient for flat catchments. Leandro et al. [
27] showed, for a relatively flat catchment, that a validated 1D/1D model is able to replicate the 1D/2D maximum flood extent. This is a safe assumption, as the gradient of the catchment presented in [
27] as a case study, is larger than in the ‘Tuindorp’ and ‘Loenen’ catchments (‘Tuindorp’ factor 10 and ‘Loenen’ factor 2). Furthermore, the calculation time in the case of a 1D/2D model in combination with long-term rainfall series would not be within acceptable limits.
2.4. Model Validation
For the model validation, a comparison between call data on flooded streets and simulated flood locations was made for the rainfall event on 4 November 2013. This event was chosen because in 2012, the whole ‘Tuindorp’ sewer system was cleaned, and between January and July 2013, observed defects were removed, except for root intrusions in the central part of the sewer system. Following these actions, the sewer system was considered “clean” and suitable for validating the InfoWorks model.
Reported incidents from the call data of the municipality supplemented with interviews with residents were compared with model results. For the storm event on 4 November 2013, this comparison is shown in
Figure 3. Most of the locations that suffered from flooding in reality coincide with the model results, although some reported incidents in the northern part of the catchment are not present in the simulations. This may be caused by call data systematically underestimating the extent of flooding due to underreporting [
28].
2.5. Monte Carlo Simulations
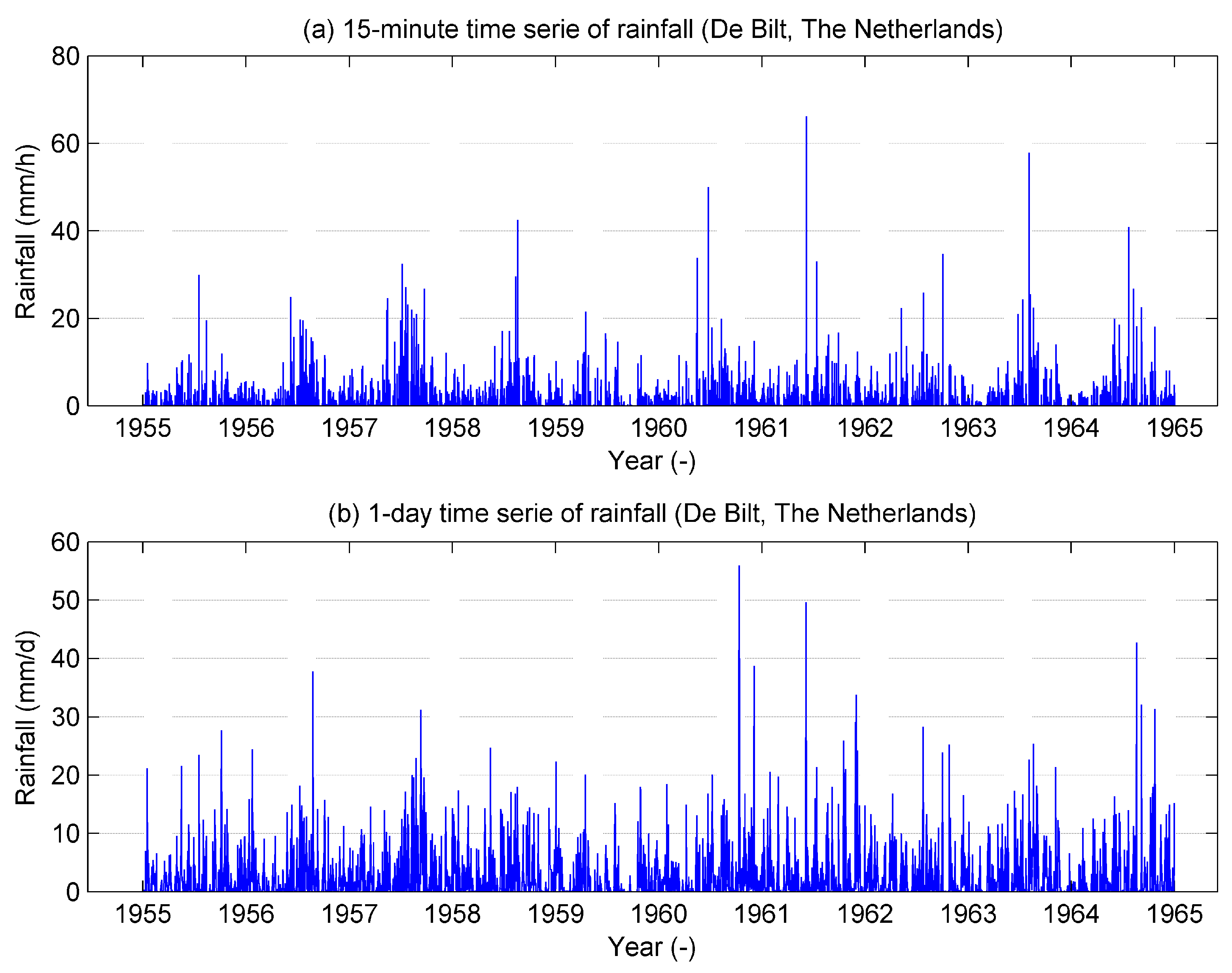
Monte Carlo simulations were used to evaluate the impact of in-sewer defects on flooding frequencies at each manhole. Detailed InfoWorks models were used for the simulations. Because of the random changes in the characteristics of the network (i.e., the system state) in each run during the Monte Carlo procedure, it is impossible to predict beforehand which storm events will cause flooding. Therefore, in the Monte Carlo simulations, long-term rainfall series were used. This series was observed by the Royal Dutch Meteorological Institute in De Bilt (The Netherlands) during the period 1955–1964. This series comprises continuous series of rainfall volumes in De Bilt, as observed with an interval of 15 min (
Figure 4). This time series is generally used in The Netherlands to evaluate the design performance of sewer systems [
29]. In the case of the ‘Tuindorp’ catchment, 322 independent storm events were filtered from the 10-year time series. This filter is based on in-sewer storage volume, pumping capacity, and required length of dry periods between storm events. For the ‘Loenen’ catchment, 572 events remained after filtering. The rain volume and the time in between storms are such that the system has returned to a stable dry weather flow configuration. As a result, the initial conditions are the same for each storm so as to prevent interdependence between storm events.
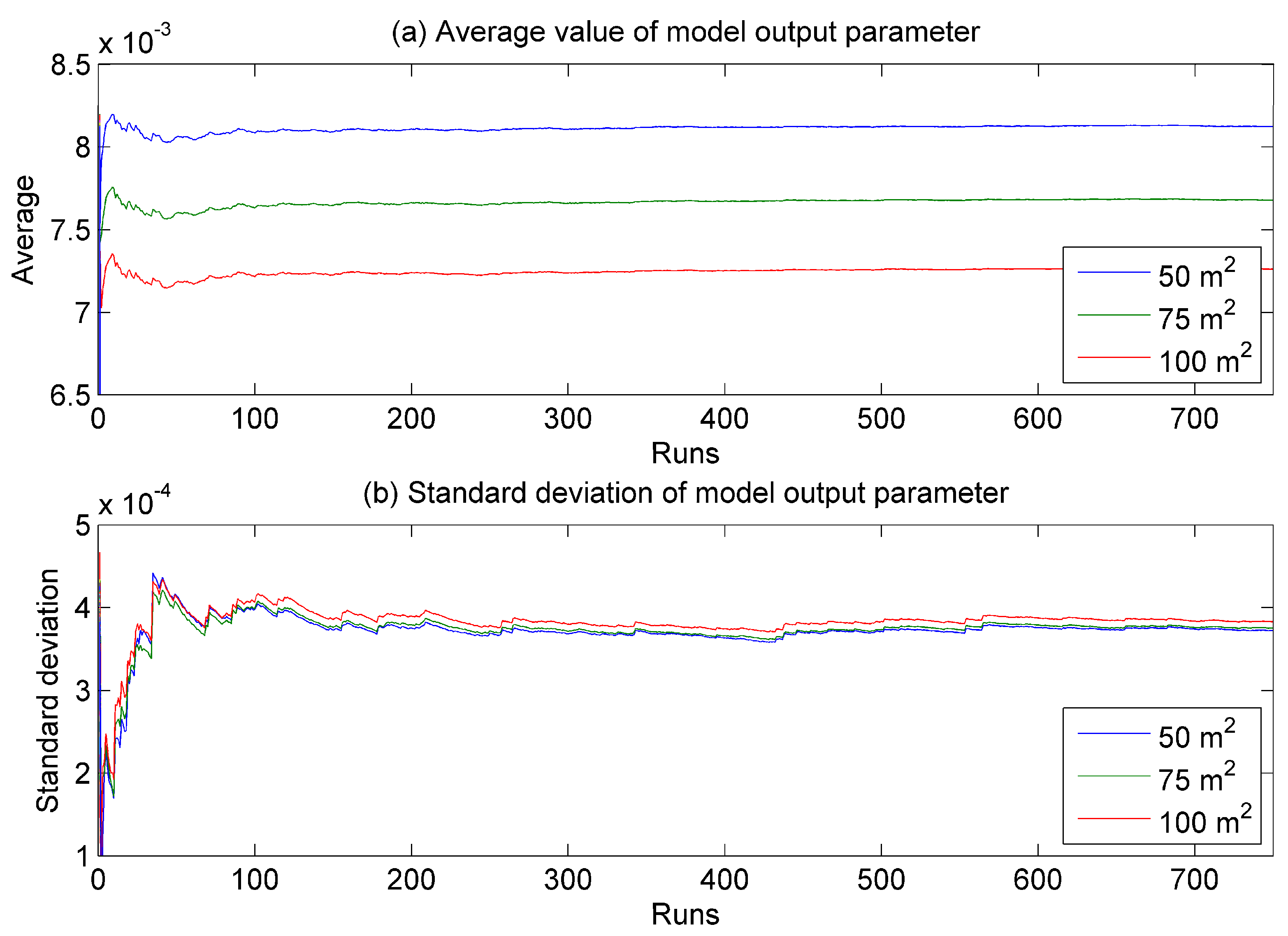
A single run in the Monte Carlo procedure is defined as the hydrodynamic simulation of the complete collection of the selected (and independent) storm events for a single system state. In each Monte Carlo run, the relative sediment depth of each pipe was randomly drawn from the beta distributions describing the presence of sediments. As a result, the network will have a different configuration in each Monte Carlo run. For reliable estimates of flooding frequencies, 750 Monte Carlo runs were performed. This number of runs is sufficient because the mean and standard deviation of the average infection probability per year become stable after approximately 600 runs (
Figure 5).
The sediment depth at the pipe bottom reduces the hydraulic capacity of the pipe. The sediment is modelled as permanent sediment deposits in the InfoWorks model. Erosion or deposition of sediment and transport of sediment through the system are not accounted for in the applied model approach.
2.6. Quantification Flooding Frequencies
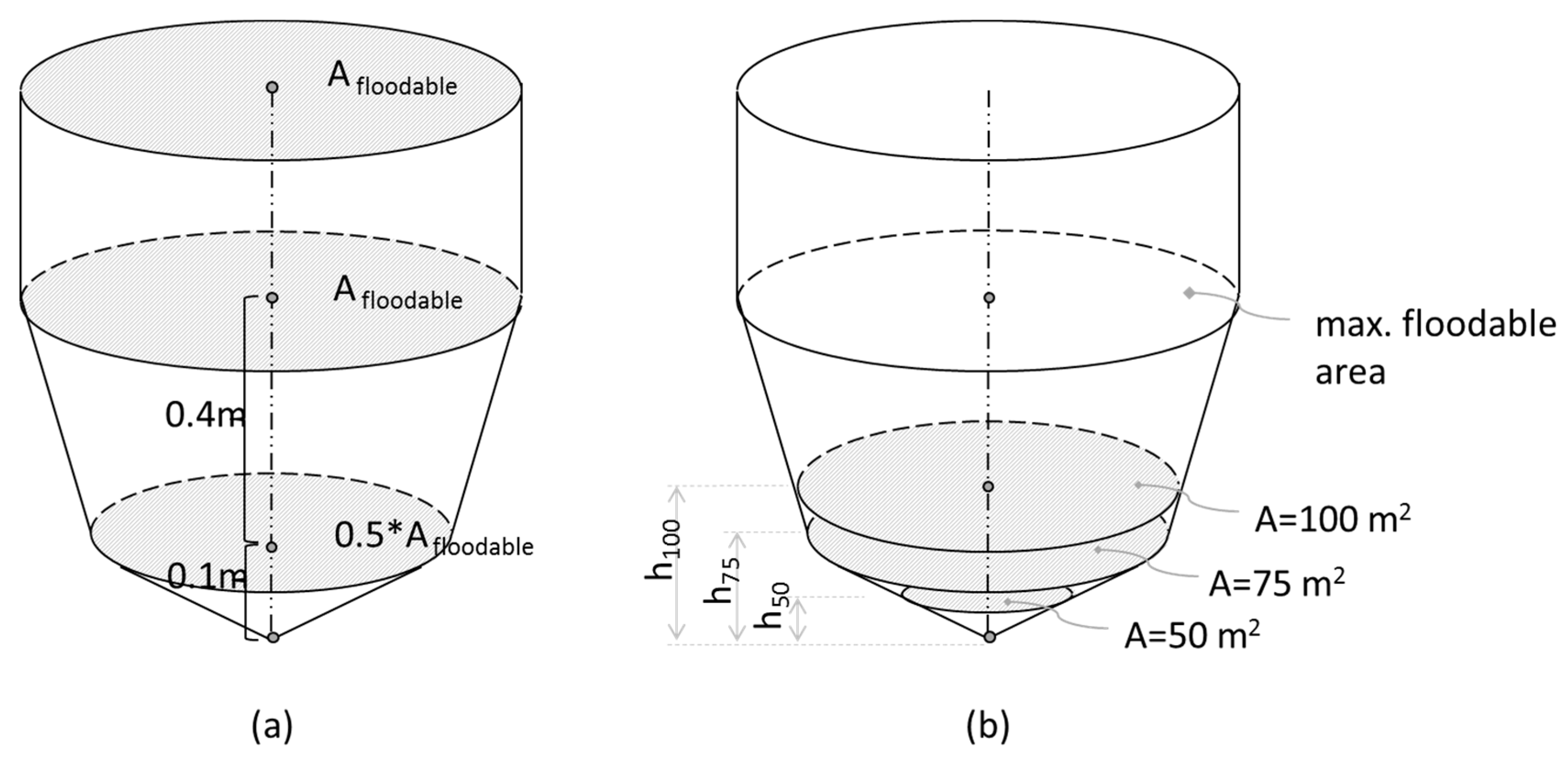
Calculated water levels exceeding manhole cover levels are considered as flooding. Since overland flow is not considered in the 1D/1D approach chosen for this study, the storage of floodwater is included in the model by adding a ‘cone’ on top of the manhole. In modeling terms, this floodwater is stored above ground in a flood cone. The volume of water held by the cone will be discharged into the sewer system as the water level drops again. The shape of the flood cone is sketched in
Figure 6. The floodable area (A
floodable) is the total area available for the storage of floodwater at a specific node. As a result, it is the sum of the contributing areas draining to this node.
The shape of the flood cone (
Figure 6) determines the relationship between flood volume and water level above street. Flood volume is defined as the calculated water volume on street level due to a flooding event at a specific manhole. The part of the flood cone below 0.1 m represents the contributing areas of streets and adjacent pavements (
Figure 6). This equals approximately 50% of the total floodable area at each node, which corresponds to the average value of contributing impervious and semi-pervious areas of all nodes. The second part runs from 0.1 m to 0.5 m, with a linear increase in floodable area from 50% to 100%. Above 0.5 m, the floodable area remains 100% (
Figure 6). This implies that, with flood depths below 0.1 m, the flooded area stays between the sidewalks, whereas for larger depths, the flooded area spreads across the entire contributing area of a node.
The severity of exposure to floodwater depends on the amount of floodwater and the duration of the flooding event. De Man et al. [
5] took samples of pluvial flooding if the flooded area was larger than 100 m
2. In order to assess the sensitivity of the results for the flooded area, next to this value, threshold values for the flooded area of 50 and 75 m
2 are applied as well. For each threshold area, a corresponding threshold water level is calculated given the shape of the flood cone (
Figure 6). The maximum threshold level for the flood depth is limited to 0.15 m in order to avoid levels above the sidewalks and to exclude the part of the flood cone representing flat and inclining roofs. This limitation is only necessary at locations with very small contributing areas.
For each manhole, the number of exceedances of threshold water levels is calculated from the 10-year rainfall series. An exceedance is defined as an event in which the calculated flood depth in the sewer system exceeds the threshold water levels corresponding with a specific threshold value of the flooded area at an individual manhole. Consequently, exceedance of a threshold at two different manholes during the same time step is counted as two separate threshold exceedances. Finally, the summed frequency of exceedances at each manhole per system state per year is calculated.
2.7. Quantification of Health Risks
Due to backflow from combined sewer systems, pluvial flooding may contain high amounts of pathogenic micro-organisms [
30]. Consequently, exposure to this floodwater entails a risk for public health. In De Man et al. [
5], infection risks from exposure to urban pluvial flooding were assessed using QMRA. Urban floodwater was sampled to quantify the presence of waterborne pathogens
Campylobacter,
Cryptosporidium,
Giardia, norovirus, and enterovirus. Samples of approximately 20 L were taken during flood incidents in The Netherlands and the concentrations of the pathogens were analysed according to ISO standards [
5]. Questionnaires were used for an estimation of the volume of floodwater ingested by people during exposure. Based on pathogen data and exposure data, the probability of infection due to flooding from combined sewers, storm sewers, and rainfall generated surface runoff was quantified.
A distinction was made between children and adults in terms of infection probabilities because of the higher ingestion probability for children. For adults, the average probability of infection equals 3.9% per event. For children, this probability is almost ten times higher and amounts to 33%.
De Man et al. [
5] applied dose-response relationships for the quantification of the probability of infection per exposure event (P
event) for the different pathogens
Campylobacter,
Cryptosporidium,
Giardia, norovirus, and enterovirus. It is assumed that, except for enteroviruses, all waterborne pathogens are infectious. This can be justified by the fact that the different pathogens lead to similar complaints concerning public health and that one pathogen was likely to prevail to cause a gastrointestinal infection. As a result, the overall probability of infection per exposure event (P
infection/event) is quantified by summation of the values for each pathogen.
The infection probability per year is calculated from the overall probability of infection per exposure event and the frequency of flooding events (i.e., exceedances of defined thresholds values of floodable area), as follows:
where n is the frequency of exposure events to flooding per year. Using equation (1), the infection probability per year at each manhole is calculated. Based on these probabilities, the average infection probability per year was determined as a weighted average based on the number of inhabitants per manhole.
3. Results
3.1. Results ‘Tuindorp’ Catchment
3.1.1. Frequency of Flooding
Exposure to floodwater is influenced by the frequency of flooding [
31,
32]. De Man et al. [
31] showed that floodwater-associated diseases occur in urban areas after flood events due to extreme rainfall. The total number of people visiting the general practitioner for gastrointestinal, influenza-like illness, and dermatological complaints increased by 13% compared to a situation without flooding.
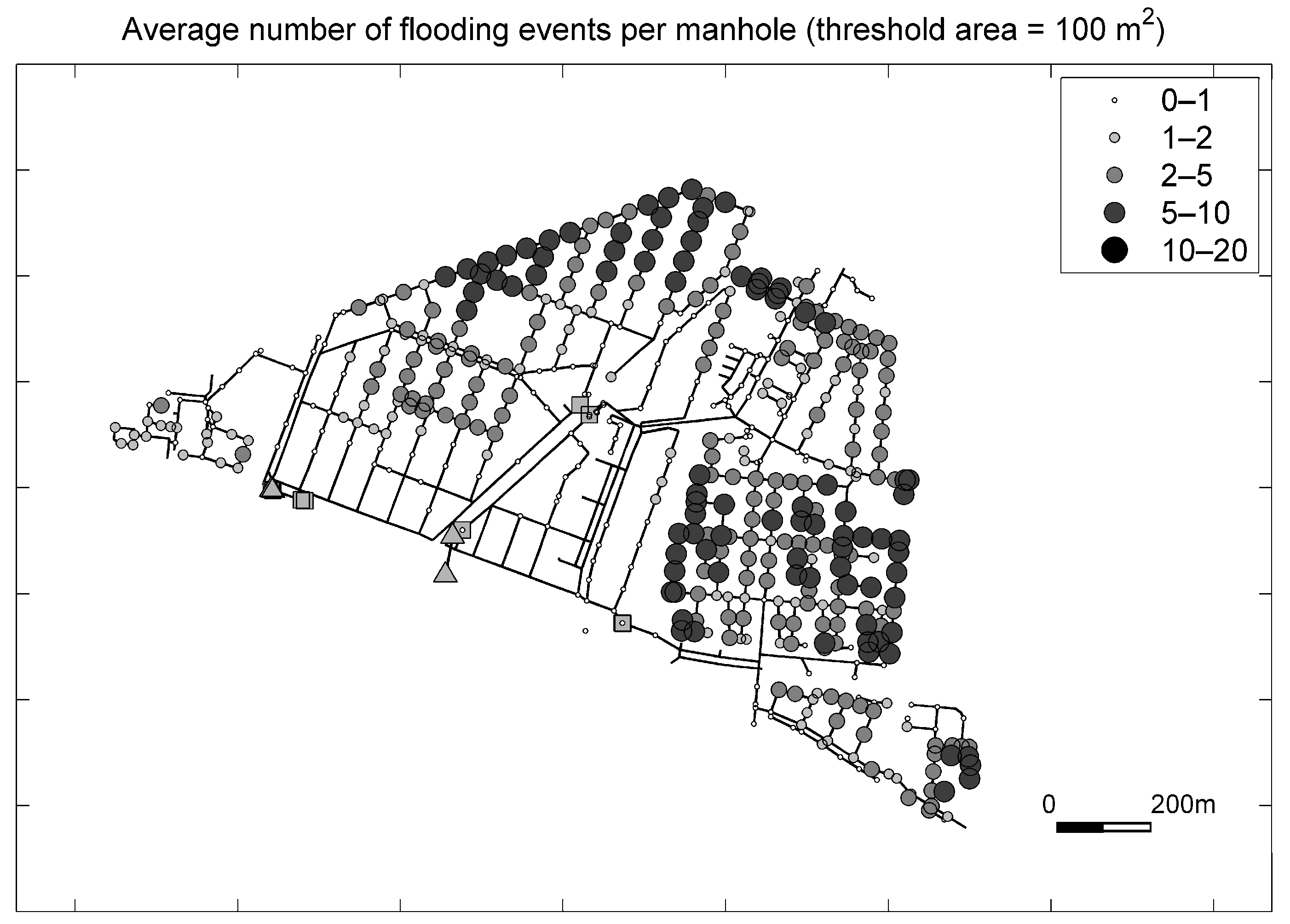
Flooding frequency varies across the ‘Tuindorp’ catchment (
Figure 7). This Figure shows the average number of flooding events per manhole in the catchment, which is calculated from the results of the 750 Monte Carlo runs. Spatial differences indicate the sensitivity to flooding of a location or area. The eastern and north-western parts of the catchment are more sensitive to flooding. The eastern part is more sensitive because it is a sub-catchment with a very limited number of direct connections to CSO structures.
3.1.2. Duration of Flooding
Next to frequency, the impact of exposure to floodwater depends on the duration of flooding. This also varies across the catchment (
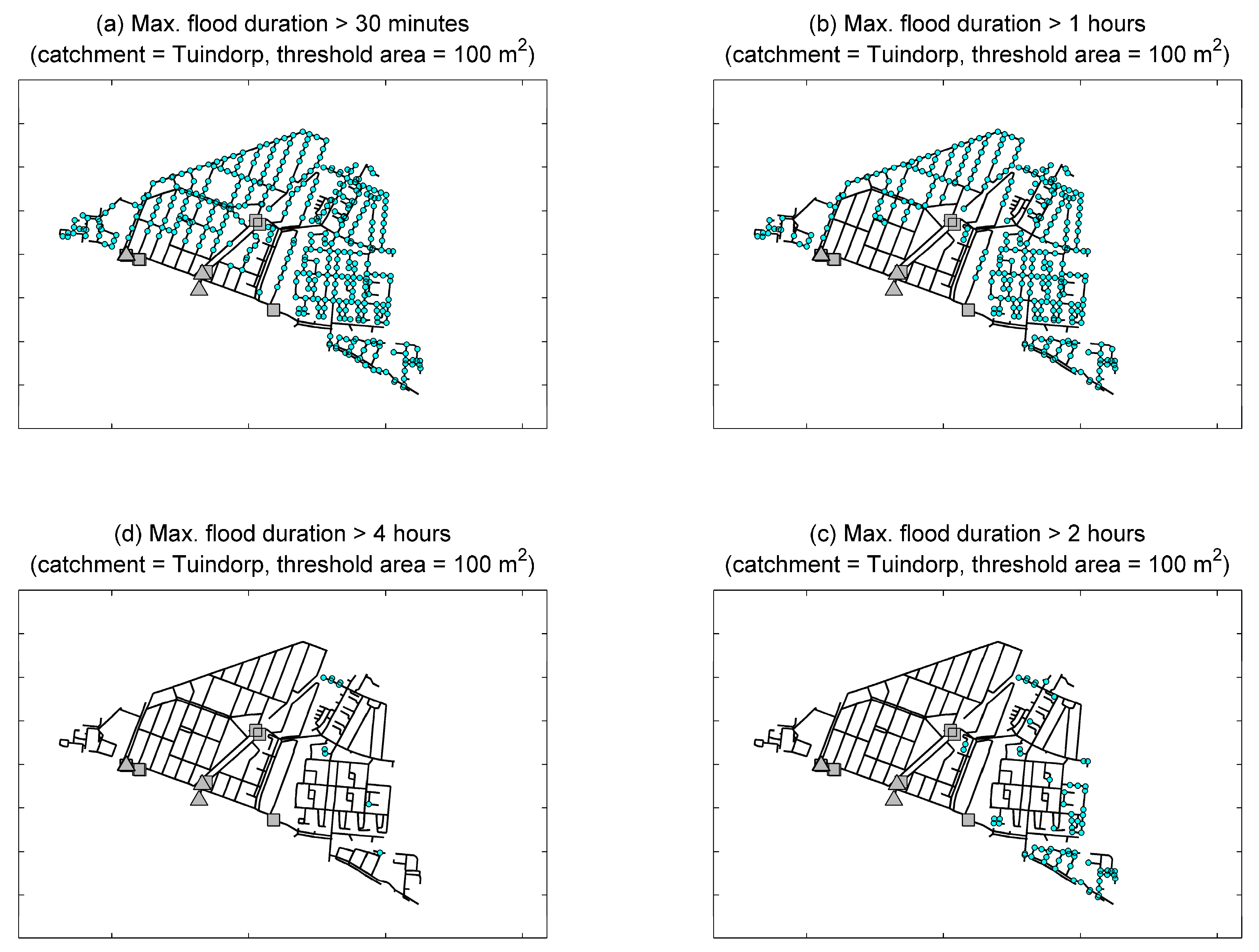
Figure 8). This Figure shows the maximum flood duration per manhole for different thresholds. Starting at the top left figure, the threshold of the maximum duration per manhole increases clock-wise (30 min, one hour, two hours, and four hours respectively).
Manholes with larger flood durations (>2 h) are concentrated in the eastern part of the catchment. Durations over four hours occur at a limited number of top ends in the sewer system. Based on a comparison of
Figure 7 and
Figure 8, it is concluded that in the eastern part of the catchment, flooding events occur more often and last longer relative to the rest of the catchment area. The coincidence of higher frequencies and longer durations increases infection probabilities in this sub-catchment.
Table 2 presents the summary statistics for the duration of flooding events in the ‘Tuindorp’ catchment. Both mean values and 95% uncertainty intervals of average, minimum, and maximum event duration (in minutes) are displayed for three different threshold area dimensions. An event is defined as a combination of a rainfall event and a system state (i.e., 322 × 750 events).
The mean value of the average flood duration per event is limited to approximately 20 min. However, the spread is relatively large (1–64 min), with a long tail towards the higher values. The mean of the maximum flood duration per event is approximately 37 min, also exhibiting a large spread (1–127 min).
Table 2 also demonstrates that the selected rainfall events are independent with respect to flood impacts. The upper value of the 95% interval of the maximum flood duration per event (approximately two hours) is much smaller than the total duration of the rainfall events (12 h and more).
3.1.3. Probability of Infection
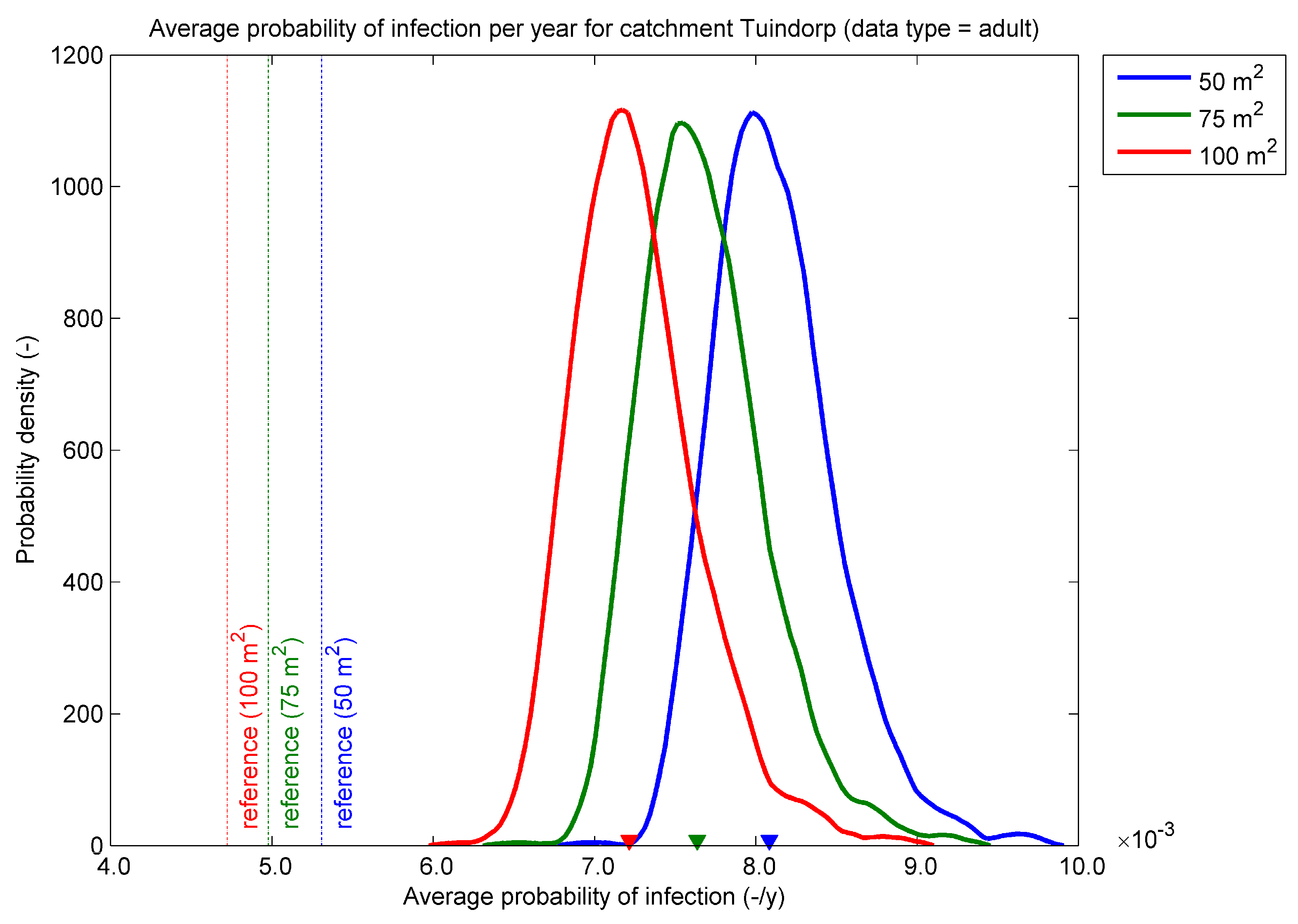
Overall for ‘Tuindorp’, the average infection probability for adults increases (
Figure 9). This figure shows the catchment-wide density function of infection probabilities for three different threshold area dimensions. The density function is calculated using kernel smoothing based on an Epanechnikov kernel [
33]. This kernel has the shape of the positive part of a parabola (i.e., has no long tails). The selected bandwidth performs well for normal distributions.
The median value of the infection probability decreases with increasing threshold area. This simply means that the probability of a smaller flooded area is larger and, as a result, the infection probability is also larger. The spread is due to the different system states in the Monte Carlo sample.
There is a shift in infection probabilities due to sedimentation. This shift equals an approximate factor of 1.5 (
Table 3). This table shows the summary statistics for adults in the ‘Tuindorp’ catchment.
The shift from a reference to sewer system with sediment deposits has the same order of magnitude for all three threshold area dimensions. The reference system represents a single run of the hydrodynamic simulation with the complete collection of selected (and independent) storm events for the sewer system without sediment deposits.
The shift from the reference to the median of the Monte Carlo simulations is statistically significant. The significance is tested for each threshold area dimension (50, 75 and 100 m2) using a t-test. The test statistic for the t-test is calculated as follows. The difference between the reference value and the median of distribution function is divided by the standard error of the distribution function. This standard error equals the standard deviation of the distribution function divided by the square root of the sample size (i.e., the number of Monte Carlo runs). The corresponding p-value of the test statistic is calculated using the cumulative distribution function of the Students’ t-distribution with 1 degree of freedom for a one-tailed p-value. The calculated p-value is compared with a significance level of 0.5%. Since the distribution functions are not Gaussian and, therefore, violate t-test assumptions, the data are transformed prior to significance testing. For ‘Tuindorp’ the transformation equals 1/x3.
For children in the ‘Tuindorp’ catchment the infection probability increases as well due to sediment deposits. Summary statistics are shown in
Table 4. The calculated probability accounts for the non-homogeneous distribution of children in the catchment area as shown in
Figure 10.
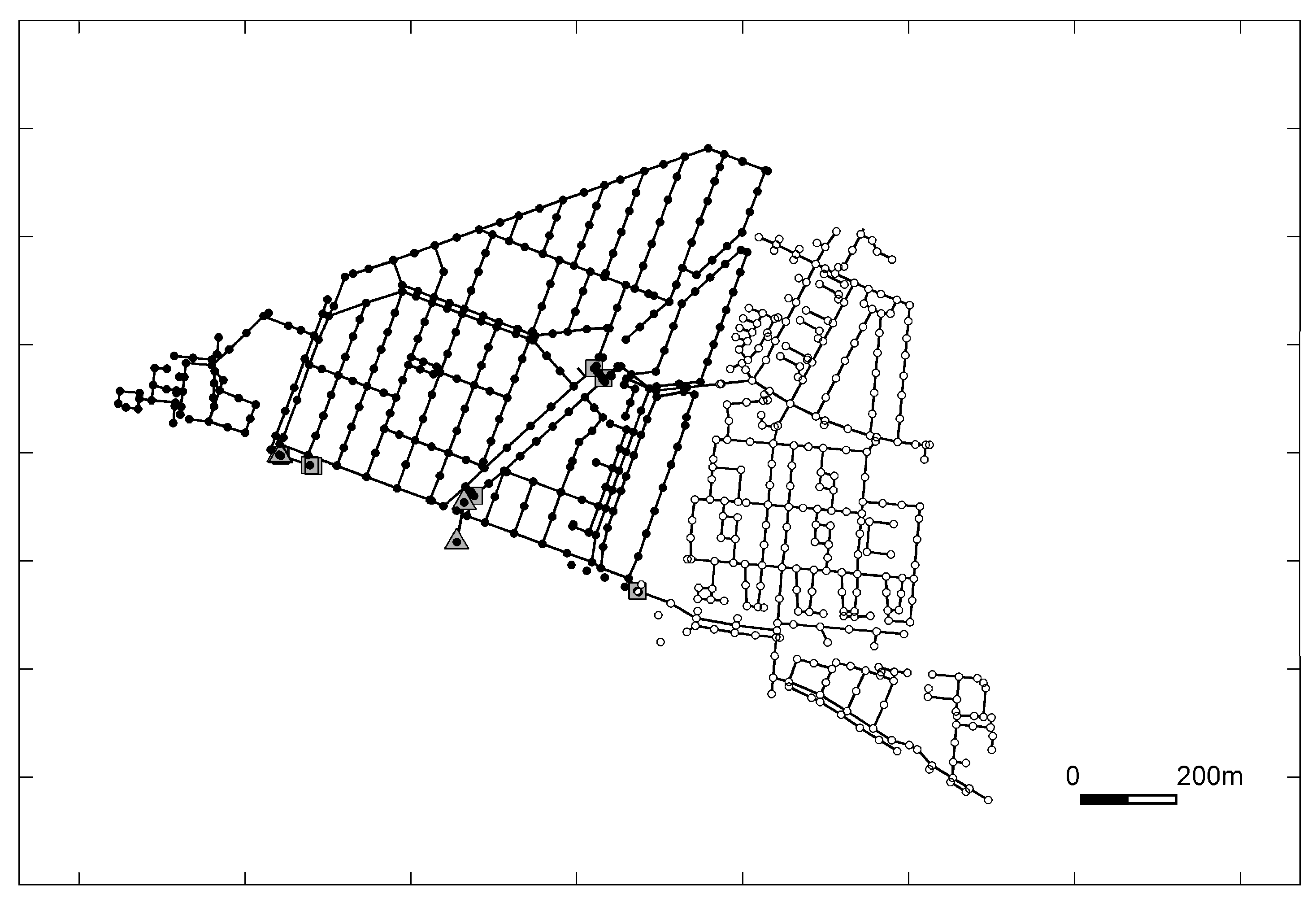
Although the infection probability per event is 10 times higher for children compared to adults, the average infection probability per year only increases by a factor of 9.6. This is due to the afore-mentioned distribution of percentages of children [
34]. Comparison of
Figure 7 and
Figure 10 shows that the frequency of flooding events is higher in the area with a lower proportion of children (12% of population) and lower in the area with a higher proportion (21% of population).
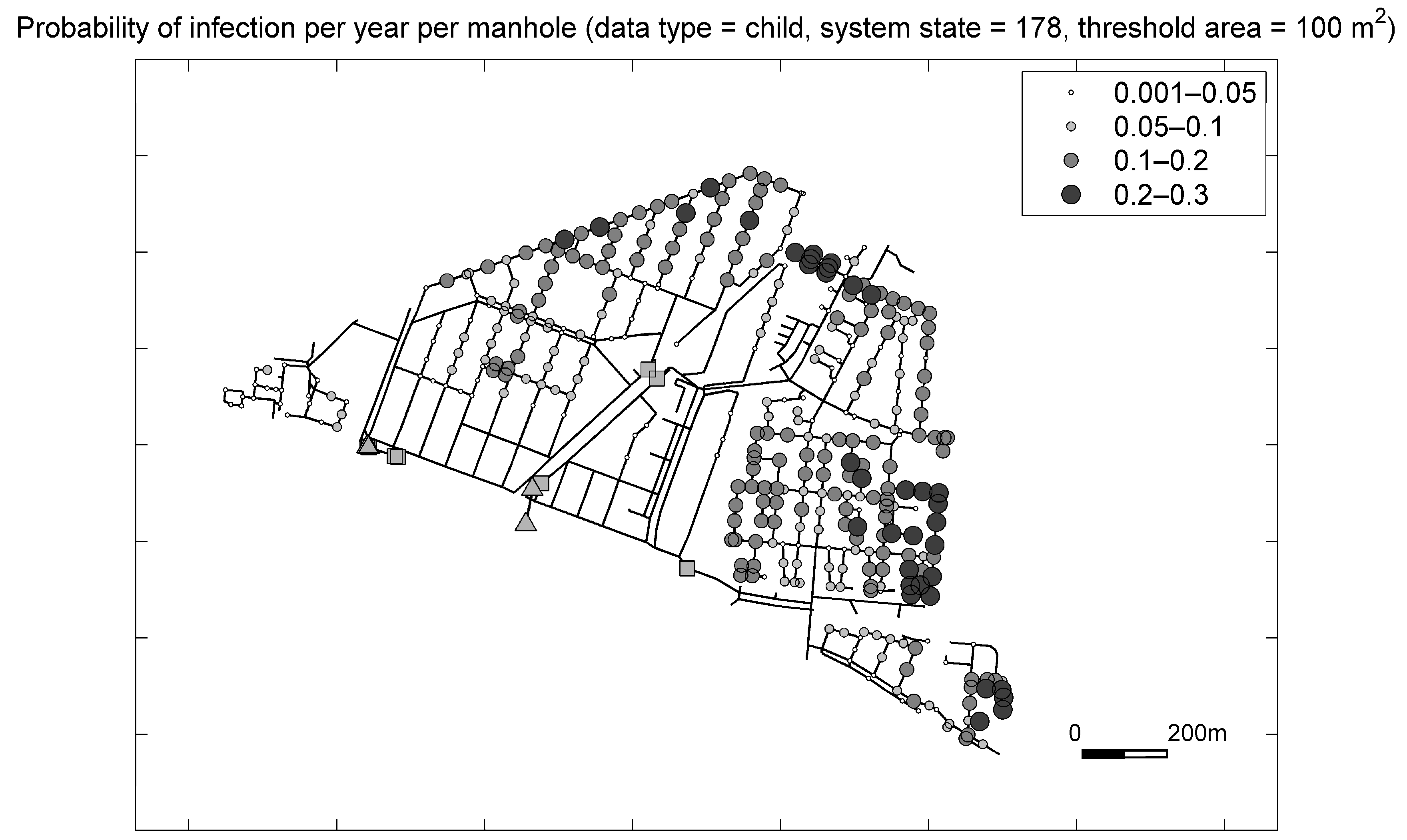
The spatial distribution of infection probabilities per manhole per year for children in the ‘Tuindorp’ catchment for one system state (i.e., one Monte Carlo run) and a threshold area of 100 m
2 is illustrated in
Figure 11. This figure shows that the impact of sedimentation on infection probability varies within the catchment.
3.2. Results ‘Loenen’ Catchment
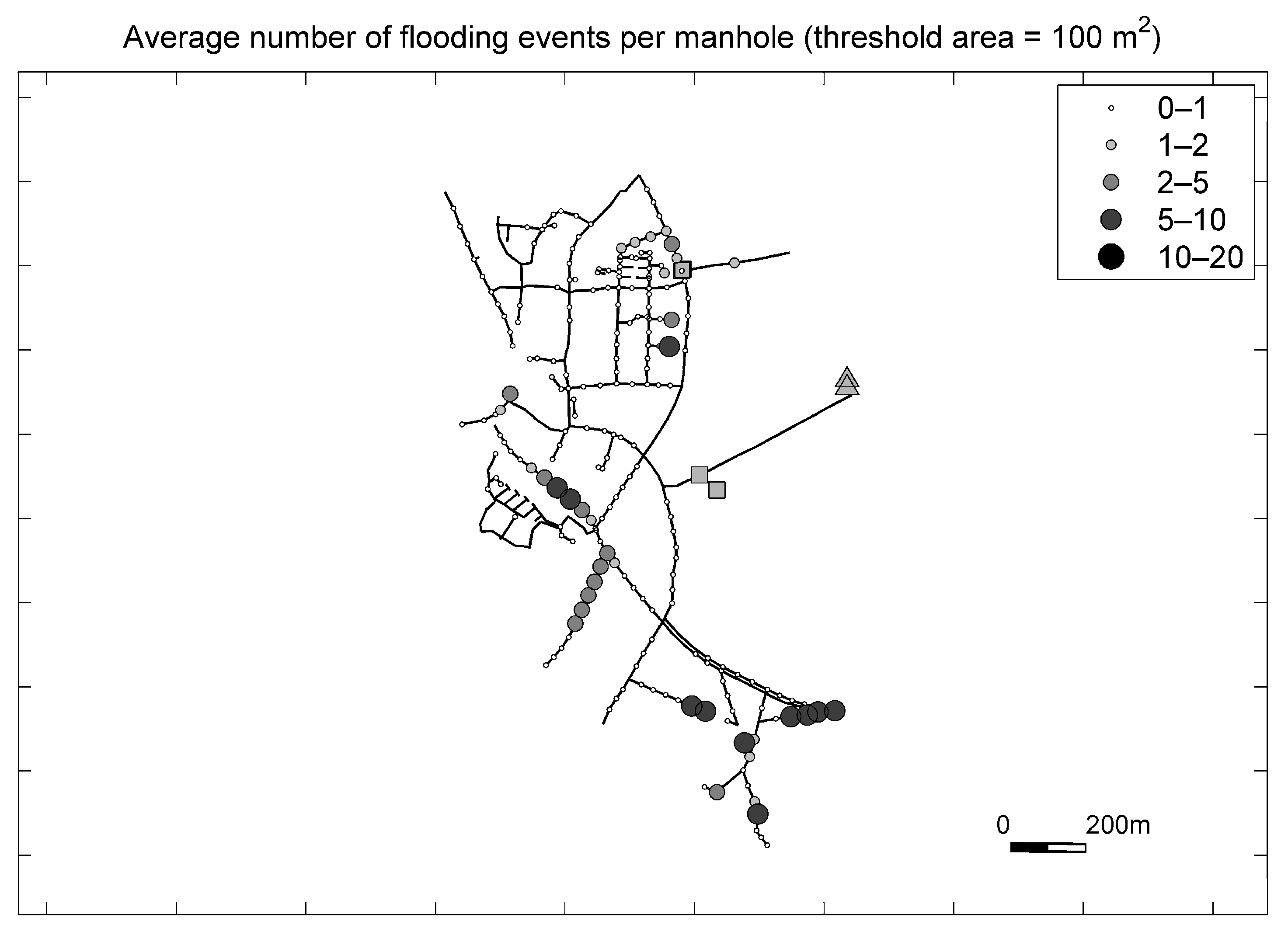
3.2.1. Frequency of Flooding
In the partly branched ‘Loenen’ catchment, the average number of flooding events per manhole is more or less evenly distributed over the catchment area. The number of more sensitive sewers is limited (
Figure 12).
3.2.2. Probability of Infection
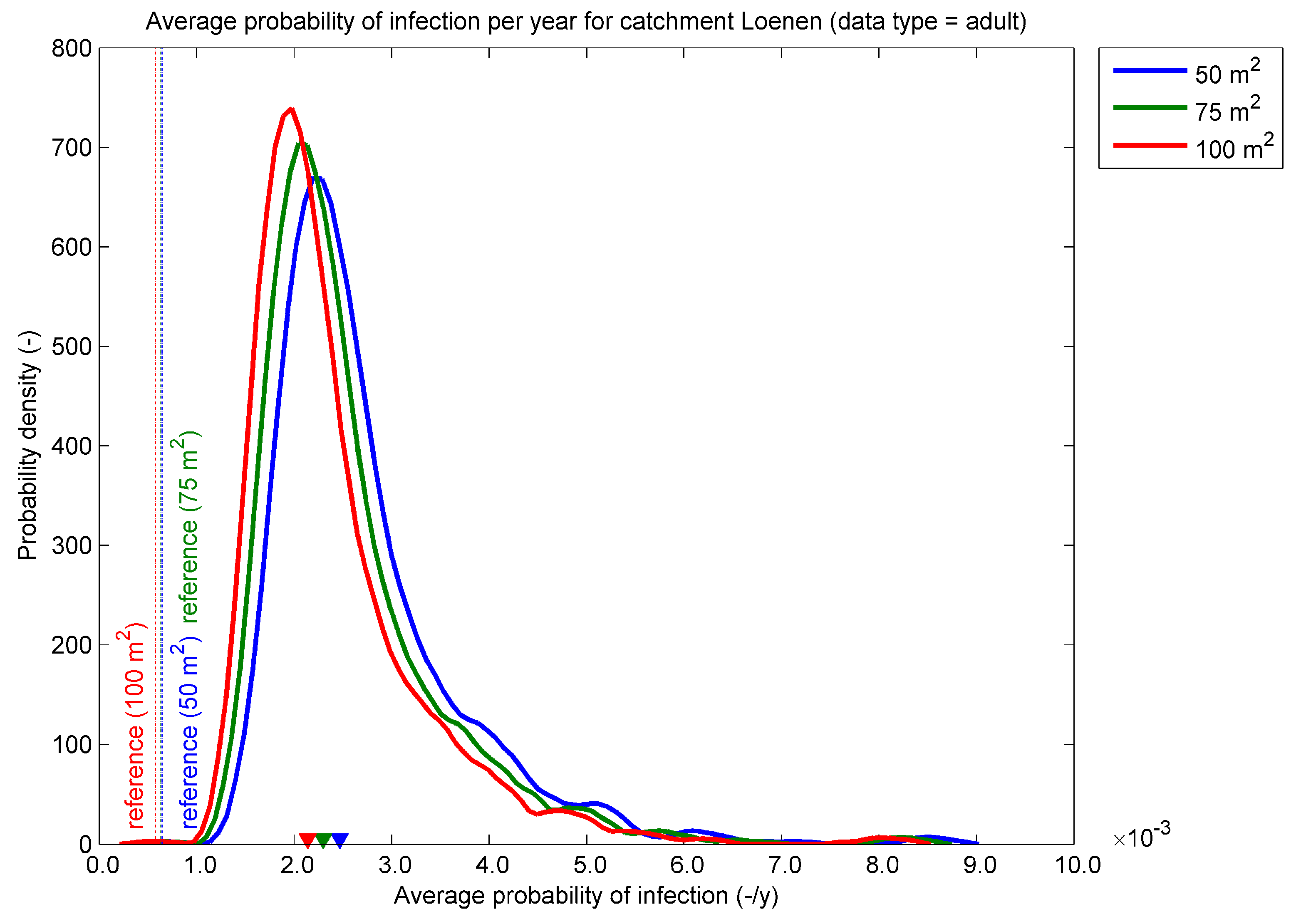
The impact of in-sewer defects on infection probabilities for adults in the ‘Loenen’ catchment is shown in
Figure 13. As for ‘Tuindorp’, the density functions are calculated using kernel smoothing. The figure shows that the infection probability increases for adults due to sedimentation. Again, the calculated median probability for the different threshold area dimensions decreases with increasing flooded areas.
For adults, the median of the probability distribution of the system with sediment deposits is almost four times larger than the reference (
Table 5). This shift from the reference to the median of the Monte Carlo simulations is statistically significant. This was tested using a
t-test. In order to avoid violations of
t-test assumptions, the data are transformed to normal with a factor of 1/
x.
4. Discussion
A comparison of the results for both catchments in this paper shows that the impact of sediment deposits on infection probabilities is system-dependent. One difference is that the tail of the distribution functions for the infection probability for ‘Loenen’ is much longer than for ‘Tuindorp’. This can most probably be explained by the partly branched character of the sewer system and the steeper catchment area in ‘Loenen’. As a result, the impact of sediment deposits in a relatively limited set of sewer pipes most important for draining the area spreads out over a relatively large part of the catchment. Another difference is that the distance between the median values of the probability distributions for the three threshold area dimensions is larger for ‘Tuindorp’ than for ‘Loenen’. This relates to the looped character of the sewer system and the flatter catchment area in ‘Tuindorp’.
The average infection probability per year in this paper is determined from the overall probability of infection per exposure event and the frequency of flooding events. Flood duration is not incorporated in this approach. However, the results in this paper demonstrate that flood duration may vary considerably over the catchment, possibly affecting infection probabilities. Despite recent developments in methods to quantify infection risks [
3,
5,
7], knowledge on the impact of flood duration on infection probability is still very limited. Moreover, none of the methods take the timing of the flooding event (time of the day, time of the year) into account, although it can be expected that the infection probability is also strongly related to this. Consequently, further research is needed on the impact of duration and timing on infection probabilities.
In this paper, flood cones are applied for estimating flooding levels above a street instead of a 2D overland flow model (as in e.g., [
8]). The use of flood cones significantly accelerates calculations, which is useful for the Monte Carlo simulations. Compared to the situation in Dhaka as described in Mark et al. [
8], the flood levels in ‘Tuindorp’ and ‘Loenen’ are much lower and the differences in ground levels are much smaller. Consequently, a 2D overland flow model is not crucial for accurate results in ‘Tuindorp’ and ‘Loenen’ in contrast to areas comparable to Dhaka.
Call data of the municipality have been used to validate model results. This shows that not all locations with calculated flooding coincide with registered calls. Based on interviews with inhabitants in the ‘Tuindorp’ catchment, it can be concluded that media attention emphasising the possible increase of flooding events and impacts due to climate change reduces the tendency to call the municipality to register a flooding event when the flood duration is relatively short. In addition, the registration of calls is not always sufficient for correctly analysing reported flood events. For example, information on the location of the flooding, duration, and the total affected area is not present or understandable. For a better understanding of call data, further research is needed on the psychological background of calls.
Van Bijnen et al. [
19] demonstrated that the return period of flooding, number of flooded locations, and flooded volumes are substantially affected by in-sewer defects. This increases the possibility of exposure to pluvial flooding and its high amounts of pathogens. In order to reduce risks of exposure, it is recommended that proactive maintenance strategies are developed to optimize hydraulic performance. If the importance of an element for the total network is known, maintenance can be adjusted accordingly instead of maintaining all elements to the same quality level. Methods to determine the importance of individual elements in relation to the total network are described in Arthur et al. [
35], Arthur and Crow [
36], Mair et al. [
37], Möderl et al. [
38], Möderl and Rauch [
39], and Meijer et al. [
40]. When the critical elements are known, hydraulic properties of the sewer system at these locations can be monitored to safeguard performance [
20]. If no monitoring equipment is available, rapid and cost-effective inspection methods, such as a manhole-zoom camera and the Sewerbatt instrument, can be used to examine the sewer condition more often and to determine whether maintenance is necessary [
41].
The methods presented here may serve to further rationalise decision making in sewer asset management. As shown by van Riel et al. [
42], decision making in sewer asset management is largely based on intuition and economic considerations, while the original motivation for constructing sewer systems was protection from infectious diseases. Using the methods presented here, designers and sewer managers have a tool to quantify health effects of design and/or maintenance activities on the actual protection level offered by a sewer system and take these into account in their decision making.
5. Conclusions
Exposure to urban pluvial flooding can cause health risks for humans because floodwater may contain a variety of contaminants. The contaminations depend on the origin of the floodwater. These include human enteric pathogens from urban wastewater and Campylobacter, Giardia, and Cryptosporidium from both animal faeces and human wastewater.
In-sewer defects affect the hydraulic performance of a sewer system and may cause increased pluvial flooding. This paper shows that the occurrence of flooding, and therefore the infection probability, are significantly enlarged due to sediment deposits, thus providing input for risk-informed sewer asset management actions such as proactive maintenance strategies to preserve hydraulic performance. The average catchment-wide infection probability is calculated using Quantitative Microbial Risk Assessment (QMRA) and flooding frequencies from Monte Carlo simulations with a hydrodynamic model.
The impact of sediment deposits on the infection probabilities is significant and depends on sewer systems characteristics. The overall picture for the flat and looped ‘Tuindorp’ catchment is that the catchment-wide average infection probability increases due to sedimentation, both for adults and children. In comparison with a sewer system without sediment deposits, the median of the probability distribution of the system with sediment deposits is approximately 1.5 times larger. This shift is statistically significant. The average infection probability for children is almost 10 times larger than for adults. For the partly branched and mildly sloping ‘Loenen’ catchment, it can be concluded that the median of the average infection probability distribution is approximately four times larger due to sedimentation compared to the reference. The shift in Loenen is also significant.
The results in this paper demonstrate that flood duration may vary considerably over the catchment, possibly affecting infection probabilities. However, flood duration is not incorporated in QMRA approaches for urban flooding presented in literature. In order to account for flood duration in catchment-wide infection probabilities, further research is needed.
Municipalities should inform inhabitants that floodwater is contaminated with pathogens and that exposure to this floodwater has to be avoided. Furthermore, special attention is needed for avoiding contamination of precipitation with pathogens in rehabilitation projects, reconstruction works, and the design and construction of new drainage systems [
43].
Acknowledgments
This paper describes the results of a research project, which was financially supported by and carried out in close co-operation with the municipality of Utrecht. The authors would like to thank the municipality of Utrecht for its support. The research is performed within the Dutch ‘Kennisprogramma Urban Drainage’ (Knowledge Programme Urban Drainage). The involved parties are: ARCADIS, Deltares, Evides, Gemeente Almere, Gemeente Arnhem, Gemeente Breda, Gemeente ’s-Gravenhage, Gemeentewerken Rotterdam, Gemeente Utrecht, GMB Rioleringstechniek, Grontmij, KWR Watercycle Research Institute, Royal HaskoningDHV, Stichting RIONED, STOWA, Tauw, vandervalk + degroot, Waterboard De Dommel, Waternet, and Witteveen+Bos.
Author Contributions
Marco van Bijnen and Hans Korving wrote the initial version. Jeroen Langeveld and François Clemens contributed by editing and suggesting revisions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fewtrell, L.; Kay, D.; Ashley, R. Flooding and health—An evaluation of the health impacts of urban pluvial flooding in the UK. In Health Impact Assessment for Sustainable Water Management; IWA Publishing: London, UK, 2008; pp. 121–154. ISBN 9781843391333. [Google Scholar]
- Lau, C.L.; Smythe, L.D.; Craig, S.B.; Weinstein, P. Climate change, flooding, urbanization and leptospirosis: Fueling the fire? Trans. R. Soc. Trop. Med. Hyg. 2010, 104, 613–638. [Google Scholar] [CrossRef] [PubMed]
- Fewtrell, L.; Kay, D.; Watkins, J.; Davies, C.; Francis, C. The microbiology of urban UK floodwaters and a quantitative microbial risk assessment of flooding and gastrointestinal illness. J. Flood Risk Manag. 2011, 4, 77–87. [Google Scholar] [CrossRef]
- Cann, K.F.; Thomas, D.R.; Salmon, R.L.; Wyn-Jones, A.P.; Kay, D. Extreme water-related weather events and waterborne disease. Epidemiol. Infect. 2013, 141, 671–686. [Google Scholar] [CrossRef] [PubMed]
- De Man, H.; Van den Berg, H.H.J.L.; Leenen, E.J.T.M.; Schijven, J.F.; Schets, F.M.; Van der Vliet, J.C.; Van Knapen, F.; De Roda Husman, A.M. Quantitative assessment of infection risk from exposure to waterborne pathogens in urban floodwater. Water Res. 2014, 48, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, M.; Suetsugi, T.; Ichikawa, Y.; Sunada, K.; Nishida, K.; Kondo, N.; Ishidaira, H. Assessing the relationship between inundation and diarrhoeal cases by flood simulations in low-income communities of Dhaka City, Bangladesh. Hydrol. Res. Lett. 2014, 8, 96–102. [Google Scholar] [CrossRef]
- Andersen, S.T. Urban Flooding and Health Risk Analysis by Use of Quantitative Microbial Risk Assessment—Limitations and Improvements. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2015. [Google Scholar]
- Mark, O.; Jørgensen, C.; Hammond, M.; Khan, D.; Tjener, R.; Erichsen, A.; Helwigh, B. A new methodology for modelling of health risk from urban flooding exemplified by cholera—Case Dhaka, Bangladesh. J. Flood Risk Manag. 2015. [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2015. [CrossRef]
- Harder-Lauridsen, N.M.; Kuhn, K.G.; Erichsen, A.C.; Mølbak, K.; Ethelberg, S. Gastrointestinal Illness among Triathletes Swimming in Non-Polluted versus Polluted Seawater Affected by Heavy Rainfall. PLoS ONE 2013, 8, e78371. [Google Scholar] [CrossRef]
- Stephenson, J.; Vaganay, M.; Cameron, R.; Joseph, P. The long-term health impacts of repeated flood events. WIT Press 2014, 184. [Google Scholar] [CrossRef]
- Lodder, W.J.; De Roda Husman, A.M. Presence of noroviruses and other enteric viruses in sewage and surface waters in The Netherlands. Appl. Environ. Microbiol. 2005, 71, 1453–1461. [Google Scholar] [CrossRef] [PubMed]
- Schets, F.M.; Van Wijnen, J.H.; Schijven, J.F.; Schoon, H.; De Roda Husman, A.M. Monitoring of waterborne pathogens in surface waters in Amsterdam, The Netherlands, and the potential health risk associated with exposure to Cryptosporidium and Giardia in these waters. Appl. Environ. Microbiol. 2008, 74, 2069–2078. [Google Scholar] [CrossRef] [PubMed]
- Koenraad, P.M.F.J.; Hazeleger, W.C.; Vanderlaan, T.; Beumer, R.R.; Rombouts, F.M. Survey of Campylobacter spp. in sewage plants in The Netherlands. Food Microbiol. 1994, 11, 65–75. [Google Scholar] [CrossRef]
- De Wit, M.A.S.; Koopmans, M.P.G.; Kortbeek, L.M.; Van Leeuwen, N.J.; Bartelds, A.I.M.; Van Duynhoven, Y.T.H.P. Gastroenteritis in sentinel general practices, The Netherlands. Emerg. Infect. Dis. 2001, 7, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Mead, P.S.; Slutsker, L.; Dietz, V.; McCaig, L.F.; Bresee, J.S.; Shapiro, C.; Griffin, P.M.; Tauxe, R.V. Food-related illness and death in the United States. Emerg. Infect. Dis. 1999, 5, 607–625. [Google Scholar] [CrossRef] [PubMed]
- Stanić, N.; Langeveld, J.G.; Clemens, F.H.L.R. HAZard and OPerability (HAZOP) analysis for identification of information requirements for sewer asset management. Struct. Infrastruct. Eng. 2014, 10, 1345–1356. [Google Scholar] [CrossRef]
- Bennis, S.; Bengassem, J.; Lamarre, P. Hydraulic performance index of a sewer network. J. Hydraul. Eng. 2003, 129, 504–510. [Google Scholar] [CrossRef]
- Van Bijnen, M.; Korving, H.; Clemens, F. Impact of sewer condition on urban flooding: An uncertainty analysis based on field observations and Monte Carlo simulations on full hydrodynamic models. Water Sci. Technol. 2012, 65, 2219–2227. [Google Scholar] [CrossRef] [PubMed]
- Van Bijnen, M.; Korving, H.; Langeveld, J.; Clemens, F. Calibration of hydrodynamic model-driven sewer maintenance. Struct. Infrastruct. Eng. 2017, 13, 1167–1185. [Google Scholar] [CrossRef]
- Crabtree, R. Sediments in Sewers. Water Environ. J. 1989, 36, 569–578. [Google Scholar] [CrossRef]
- Dirksen, J.; Clemens, F. The role of uncertainties in urban drainage decisions: Uncertainty in inspection data and their impact on rehabilitation decisions. In Proceedings of the 2nd Leading Edge Conference on Strategic Asset Management, Lisbon, Portugal, 17–19 October 2007. [Google Scholar]
- Korving, H. Probabilistic Assessment of the Performance of Combined Sewer Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2004. [Google Scholar]
- Van Mameren, H.J.; Clemens, F.H.L.R. Dutch guidelines for hydrodynamic design, overview and principles. Water Sci. Technol. 1997, 36, 247–252. [Google Scholar]
- Clemens, F.H.L.R. Hydrodynamic Models in Urban Drainage: Application and Calibration. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2001. [Google Scholar]
- Stichting RIONED. Leidraad Riolering. Module C2100—Rioleringsberekeningen, Hydraulisch Functioneren; Kluwer: Alphen aan de Rijn, The Netherlands, 2004. (In Dutch) [Google Scholar]
- Leandro, J.; Djordjević, S.; Chen, A.S.; Savić, D.A.; Stanić, M. Calibration of 1D/1D urban flood models with 1D/2D model results in the 1 absence of real data. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Spekkers, M.H.; Clemens, F.H.L.R.; Ten Veldhuis, J.A.E. On the occurrence of rainstorm damage based on home insurance and weather data. Nat. Hazard Earth Syst. 2015, 15, 261–272. [Google Scholar] [CrossRef]
- Stichting RIONED. Urban Drainage Guideline. Module C2100 ‘Hydraulic performance sewerage calculations’. In Module C2100—Rioleringsberekeningen, Hydraulisch Functioneren; Kluwer: Alphen aan den Rijn, The Netherlands, 2004. (In Dutch) [Google Scholar]
- Alderman, K.; Turner, L.R.; Tong, S. Floods and human health: A systematic review. Environ. Int. 2012, 47, 37–47. [Google Scholar] [CrossRef] [PubMed]
- De Man, H.; Mughini Gras, L.; Schimmer, B.; Friesema, I.H.; De Roda Husman, A.M.; Van Pelt, W. Gastrointestinal, influenza-like illness and dermatological complaints following exposure to floodwater: A cross-sectional survey in The Netherlands. Epidemiol. Infect. 2015, 144, 1445–1454. [Google Scholar] [CrossRef]
- Hashizume, M.; Armstrong, B.; Hajat, S.; Wagatsuma, Y.; Faruque, A.; Hayashi, T.; Sack, D. The Effect of Rainfall on the Incidence of Cholera in Bangladesh. Epidemiology 2008, 19, 103–110. [Google Scholar] [CrossRef] [PubMed]
- Wand, M.P.; Jones, M.C. Kernel Smoothing. Monographs on Statistics and Applied Probability; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- CBS. Available online: http://www.cbsinuwbuurt.nl/#buurten2016_perc_personen_tot_15_jaar (accessed on 26 September 2017).
- Arthur, S.; Crow, H.; Pedezert, L.; Karikas, N. Using serviceability to prioritise proactive sewer maintenance. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, Scotland, UK, 31 August–5 September 2008; pp. 1–11. [Google Scholar]
- Arthur, S.; Crow, H. Prioritising sewerage maintenance using serviceability criteria. Proc. ICE Water Manag. 2007, 160, 189–194. [Google Scholar] [CrossRef]
- Mair, M.; Sitzenfrei, R.; Kleidorfer, M.; Möderl, M.; Rauch, W. GIS-based applications of sensitivity analysis for sewer models. Water Sci. Technol. 2012, 65, 1215–1222. [Google Scholar] [CrossRef] [PubMed]
- Möderl, M.; Kleidorfer, M.; Sitzenfrei, R.; Rauch, W. Identifying weak points of urban drainage systems by means of VulNetUD. Water Sci. Technol. 2009, 60, 2507–2513. [Google Scholar] [CrossRef] [PubMed]
- Möderl, M.; Rauch, W. Spatial risk assessment for critical network infrastructure using sensitivity analysis. Front. Earth Sci. 2011, 5, 414–420. [Google Scholar] [CrossRef]
- Meijer, D.; Van Bijnen, M.; Langeveld, J.; Korving, H.; Post, P.; Clemens, F. Identifying Critical Elements in Sewer Networks Using Graph-Theory. Water 2018, 10, 136. [Google Scholar] [CrossRef]
- Plihal, H.; Kretschmer, F.; Bin Ali, M.T.; See, C.H.; Romanova, A.; Horoshenkov, K.V.; Ertl, T. A novel method for rapid inspection of sewer networks: Combining acoustic and optical means. Urban Water J. 2016, 13, 3–14. [Google Scholar] [CrossRef]
- Van Riel, W. On Decision-Making for Sewer Replacement. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.L.; et al. SUDS, LID, BMPs, WSUD and more—The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
Figure 1.
Procedure for calculating average catchment-wide infection probabilities.
Figure 1.
Procedure for calculating average catchment-wide infection probabilities.
Figure 2.
Layout of the ‘Tuindorp’ and ‘Loenen’ catchments.
Figure 2.
Layout of the ‘Tuindorp’ and ‘Loenen’ catchments.
Figure 3.
Comparison of reported and simulated flood areas in the ‘Tuindorp’ catchment during the rainfall event on 4 November 2013 in order to validate the InfoWorks model.
Figure 3.
Comparison of reported and simulated flood areas in the ‘Tuindorp’ catchment during the rainfall event on 4 November 2013 in order to validate the InfoWorks model.
Figure 4.
Long-term rainfall series of De Bilt (The Netherlands). Observed rainfall volumes (by the Royal Dutch Meteorological Institute) during the period 1955–1964. (a) 15-min time serie of rainfall; (b) 1-day time series of rainfall.
Figure 4.
Long-term rainfall series of De Bilt (The Netherlands). Observed rainfall volumes (by the Royal Dutch Meteorological Institute) during the period 1955–1964. (a) 15-min time serie of rainfall; (b) 1-day time series of rainfall.
Figure 5.
Average (top) and standard deviation (bottom) of relevant model output parameter (i.e., average infection probability per year). (a) Average value of model output parameter; (b) Standard deviation of model output parameter.
Figure 5.
Average (top) and standard deviation (bottom) of relevant model output parameter (i.e., average infection probability per year). (a) Average value of model output parameter; (b) Standard deviation of model output parameter.
Figure 6.
Flood cone on top of a manhole in the hydrodynamic model storing water above street level. (a) The relationship between flood volume and water level above the street; (b) Three threshold areas 50, 75, and 100 m2, including the corresponding threshold water levels h50, h75, and h100 for assessing the sensitivity of the results.
Figure 6.
Flood cone on top of a manhole in the hydrodynamic model storing water above street level. (a) The relationship between flood volume and water level above the street; (b) Three threshold areas 50, 75, and 100 m2, including the corresponding threshold water levels h50, h75, and h100 for assessing the sensitivity of the results.
Figure 7.
Average number of flooding events per manhole based on the Monte Carlo simulations for the ‘Tuindorp’ catchment.
Figure 7.
Average number of flooding events per manhole based on the Monte Carlo simulations for the ‘Tuindorp’ catchment.
Figure 8.
Manholes in the ‘Tuindorp’ catchment with an increasing maximum flood duration: (a) Larger than 30 min; (b) Larger than one hour; (c) Larger than two hours; (d) Larger than four hours.
Figure 8.
Manholes in the ‘Tuindorp’ catchment with an increasing maximum flood duration: (a) Larger than 30 min; (b) Larger than one hour; (c) Larger than two hours; (d) Larger than four hours.
Figure 9.
Infection probability for adults per year in the ‘Tuindorp’ catchment.
Figure 9.
Infection probability for adults per year in the ‘Tuindorp’ catchment.
Figure 10.
Spatial distribution of children in the ‘Tuindorp’ catchment: black dots (21% of population) and white dots (12% of population) [
34].
Figure 10.
Spatial distribution of children in the ‘Tuindorp’ catchment: black dots (21% of population) and white dots (12% of population) [
34].
Figure 11.
Example of spatial distribution of infection probability for children per year per manhole for a specific system state (i.e., Monte Carlo run) of the ‘Tuindorp’ catchment.
Figure 11.
Example of spatial distribution of infection probability for children per year per manhole for a specific system state (i.e., Monte Carlo run) of the ‘Tuindorp’ catchment.
Figure 12.
Average number of flooding events per manhole based on the Monte Carlo simulations for the ‘Loenen’ catchment.
Figure 12.
Average number of flooding events per manhole based on the Monte Carlo simulations for the ‘Loenen’ catchment.
Figure 13.
Infection probability for adults per year in the ‘Loenen’ catchment.
Figure 13.
Infection probability for adults per year in the ‘Loenen’ catchment.
Table 1.
Main characteristics of ‘Tuindorp’ and ‘Loenen’ catchments.
Table 1.
Main characteristics of ‘Tuindorp’ and ‘Loenen’ catchments.
| Characteristics | Tuindorp Catchment | Loenen Catchment |
|---|
| Area use | Residential | Residential |
| Catchment area | Flat | Mildly sloping |
| System type | Combined | Combined |
| System structure | Looped | Partly branched |
| Ground level/surface level (m above average sea level) | 0.75–2.25 | 17.8–28.6 |
| Average surface slope (mm/m) | 3.0 | 8.8 |
| Average pipe slope (mm/m) | 2.8 | 3.8 |
| Contributing area (ha) | 56.9 | 23.4 |
| Number of CSO structures (-) | 5 | 2 |
| Storage volume (m3) | 4669 (=8.2 mm) | 900 (=3.85 mm) |
| Volume storage settling tank (m3) | 822 (=1.4 mm) | 0 |
| Number of pumping stations (-) | 1 | 1 |
| Pumping capacity (m3/h) | 800 a | 209 |
| Number of inhabitants (-) | 10,656 | 2100 |
| Dry weather flow (m3/h) (including leakage water) | 157 | 78 |
Table 2.
Summary statistics of duration (in minutes) of flooding events in the ‘Tuindorp’ catchment.
Table 2.
Summary statistics of duration (in minutes) of flooding events in the ‘Tuindorp’ catchment.
| | Flooded Area |
|---|
| 50 m2 | 75 m2 | 100 m2 |
|---|
| Average event duration (min) | Mean | 19.60 | 19.32 | 19.05 |
| 95%-interval | 2–64.08 | 1.67–63.98 | 1–63.62 |
| Min. event duration (min) | Mean | 4.23 | 4.17 | 4.02 |
| 95%-interval | 1–36 | 1–33 | 1–31 |
| Max. event duration (min) | Mean | 37 | 36.77 | 36.49 |
| 95%-interval | 3–127 | 3–127 | 1–127 |
Table 3.
Summary statistics of probability of infection per year for adults in the ‘Tuindorp’ catchment.
Table 3.
Summary statistics of probability of infection per year for adults in the ‘Tuindorp’ catchment.
| Flooded Area | Reference (×10−3)
(No Sedimentation) | Median (×10−3)
(MC Simulation) | Shifta (×10−3) | 95% (×10−3) |
|---|
| 50 m2 | 5.3 | 8.1 | 2.8 | 1.4 |
| 75 m2 | 5.0 | 7.6 | 2.7 | 1.5 |
| 100m2 | 4.7 | 7.2 | 2.5 | 1.5 |
Table 4.
Summary statistics of probability of infection per year for children in the ‘Tuindorp’ catchment.
Table 4.
Summary statistics of probability of infection per year for children in the ‘Tuindorp’ catchment.
| Flooded Area | Reference (×10−2)
(No Sedimentation) | Median (×10−2)
(MC Simulation) | Shifta (×10−2) | 95% (×10−2) |
|---|
| 50 m2 | 5.1 | 7.5 | 2.5 | 1.2 |
| 75 m2 | 4.8 | 7.1 | 2.4 | 1.3 |
| 100 m2 | 4.5 | 6.8 | 2.2 | 1.3 |
Table 5.
Summary statistics of probability of infection per year for adults in the ‘Loenen’ catchment.
Table 5.
Summary statistics of probability of infection per year for adults in the ‘Loenen’ catchment.
| Flooded Area | Reference (×10−3)
(No Sedimentation) | Median (×10−3)
(MC Simulation) | Shifta (×10−3) | 95% (×10−3) |
|---|
| 50 m2 | 0.64 | 2.5 | 1.8 | 3.6 |
| 75 m2 | 0.62 | 2.3 | 1.7 | 3.5 |
| 100 m2 | 0.58 | 2.1 | 1.6 | 3.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).