4.1. Results Analysis
The AWOA is employed to solve the Handan water resource allocation optimization model. The initialization swarm size is 150 and there are 180 iterations. There are 20 runs, and each run starts with a different random initialization swarm. Through numerous simulation experiments, the maximum and minimum inertia weights of the AWOA are finally determined to be and , respectively.
The aforementioned parameters are entered into the MATLAB (MATLAB 9.0, R2016a, MathWorks, Natick, MA, USA) for solving in order to obtain the Pareto front. Nine solutions are included on the Pareto front, as shown in
Table 4. The Pareto optimal solution set cannot explain further how to choose a scenario as the final decision on the Pareto front. For any non-inferior solution of multi-objective models, there is no other possibility that the two objective function values corresponding to the non-inferior solutions can be improved from the two objective functions corresponding to other non-inferior solutions. Policymakers can sacrifice only one goal in a certain range in return for another goal improvement. They show their preferences in the alternative tradeoff between such goals. After one operation, a number of Pareto optimal solutions are obtained under the AWOA, which results in higher solution efficiency, and provides greater choices for policymakers.
Table 4 shows that if there is a special preference for the minimum amount of water, we can choose scenario 1; if there is a special preference for the best economic benefits, we can choose scenario 9; and if we consider the minimum amount of water shortage and the best economic benefits, we can choose one of the scenarios from 2 to 8. As there is a serious shortage of water resources in Handan, meeting the water demand of different water sectors is an urgent challenge, which must be solved to improve current water resources management. Thus, scenario 1 better reflects the fairness of water consumption among different households. Therefore, it is chosen as an effective scenario, and this study analyzes it in detail.
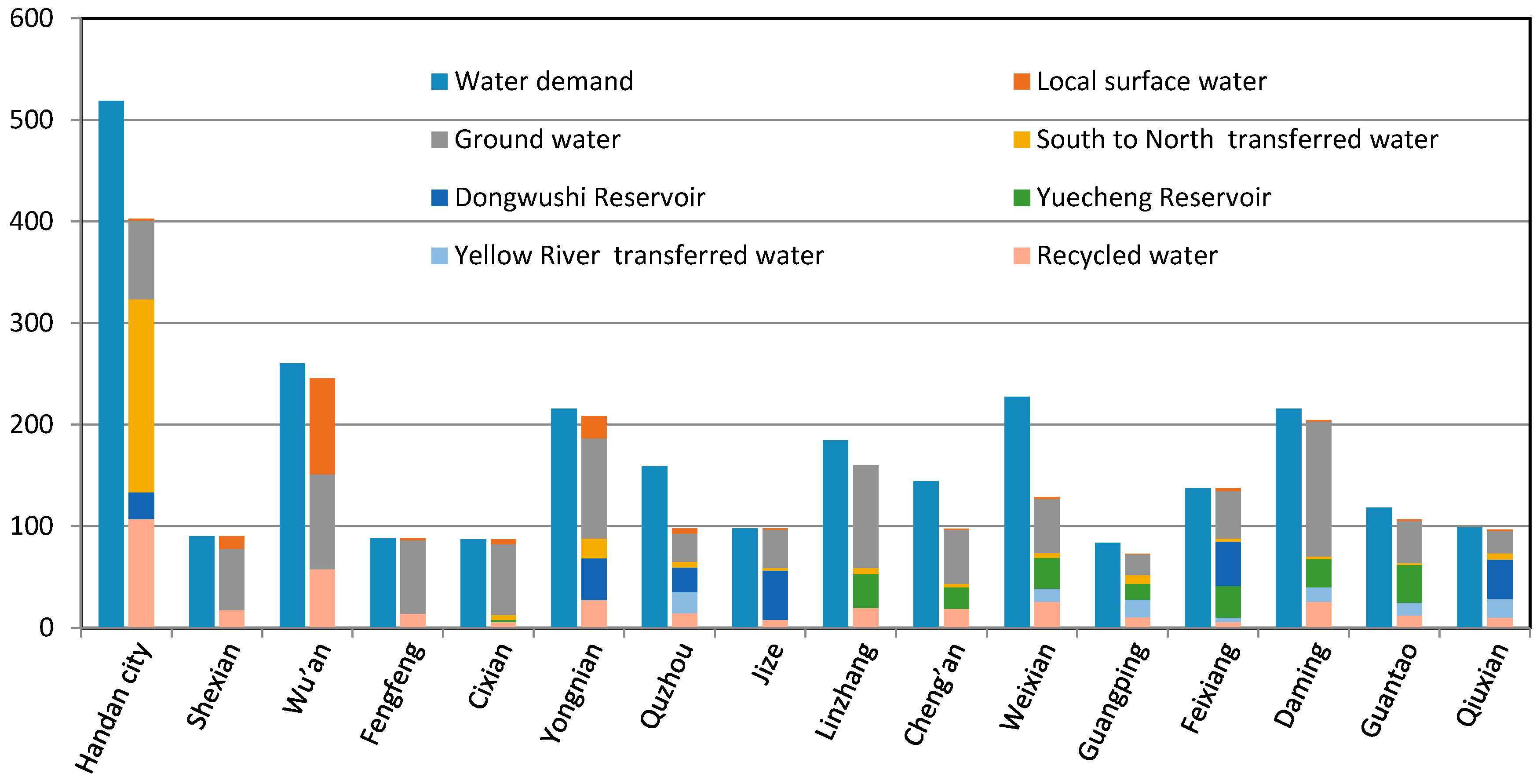
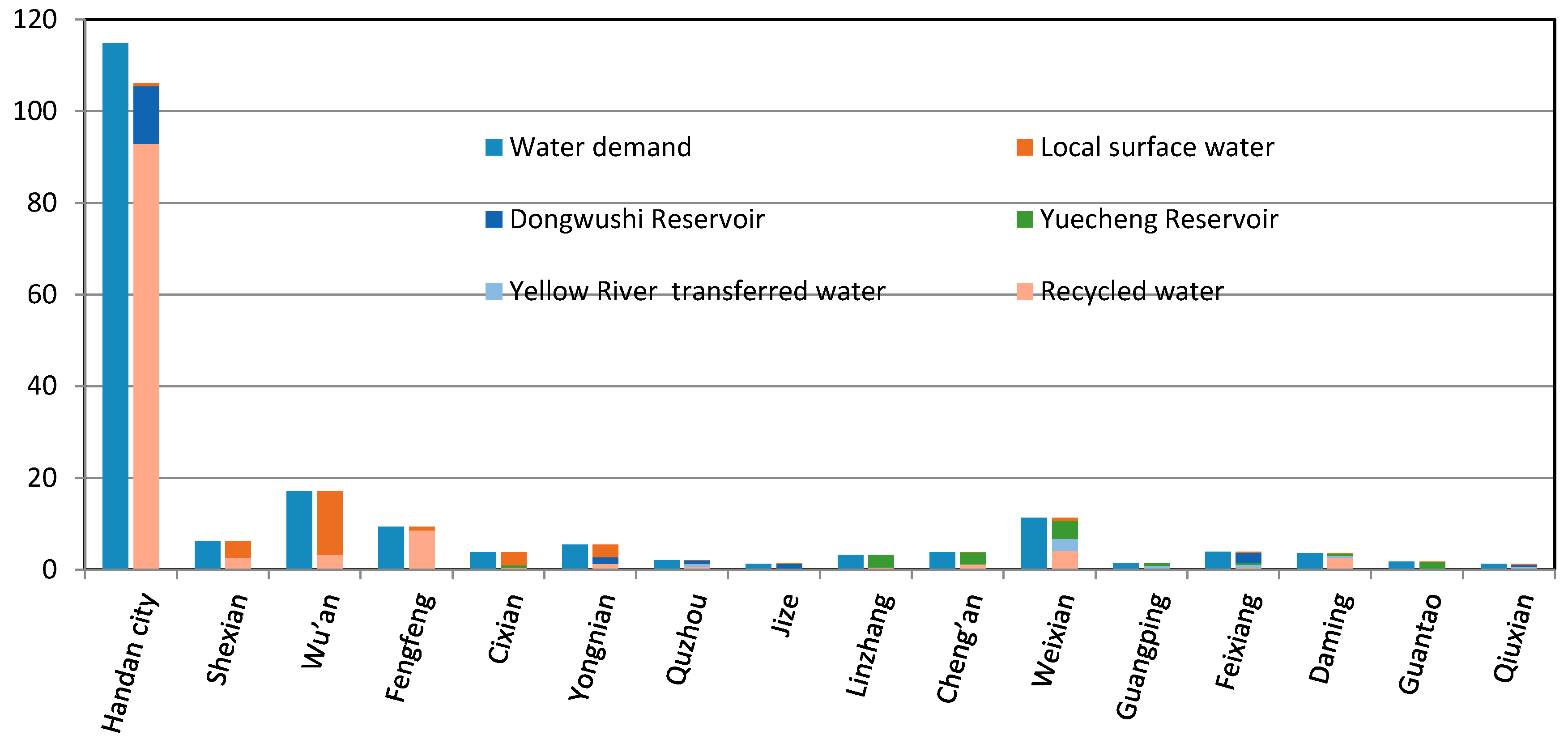
The optimal water resource allocation results in each sub-region in Handan are shown in
Figure 3. The total water demand for all users in the region is 2726.08 × 10
6 m
3, and the total allocated volume is 2321.74 × 10
6 m
3, resulting in a total water shortage of 404.34 × 10
6 m
3 and a shortage rate of 14.8%. The four sub-regions with relatively high shortage rates are Weixian, Quzhou, Cheng’an, and Handan city, with rates of 43.3%, 38.5%, 32.4%, and 22.3%, respectively. In Shexian, Fengfeng, Cixian, Jize, and Feixiang, the allocated volume can meet the water demand, and there is no water shortage. The allocated volumes by local surface water, groundwater, water transferred through the South–North Water Transfer Project, the Dongwushi reservoir, the Yuecheng reservoir, imported water from the Yellow River, and recycled water in Handan are 153.06 × 10
6 m
3, 1007.32 × 10
6 m
3, 259.11 × 10
6 m
3, 221.79 × 10
6 m
3, 197.56 × 10
6 m
3, 100.00 × 10
6 m
3, and 382.90 × 10
6 m
3, respectively. They account for 6.6%, 43.4%, 11.2%, 9.6%, 8.5%, 4.3%, and 16.5%, respectively, of the total water allocation in the region. It is noteworthy that groundwater resources are the main water source of Handan.
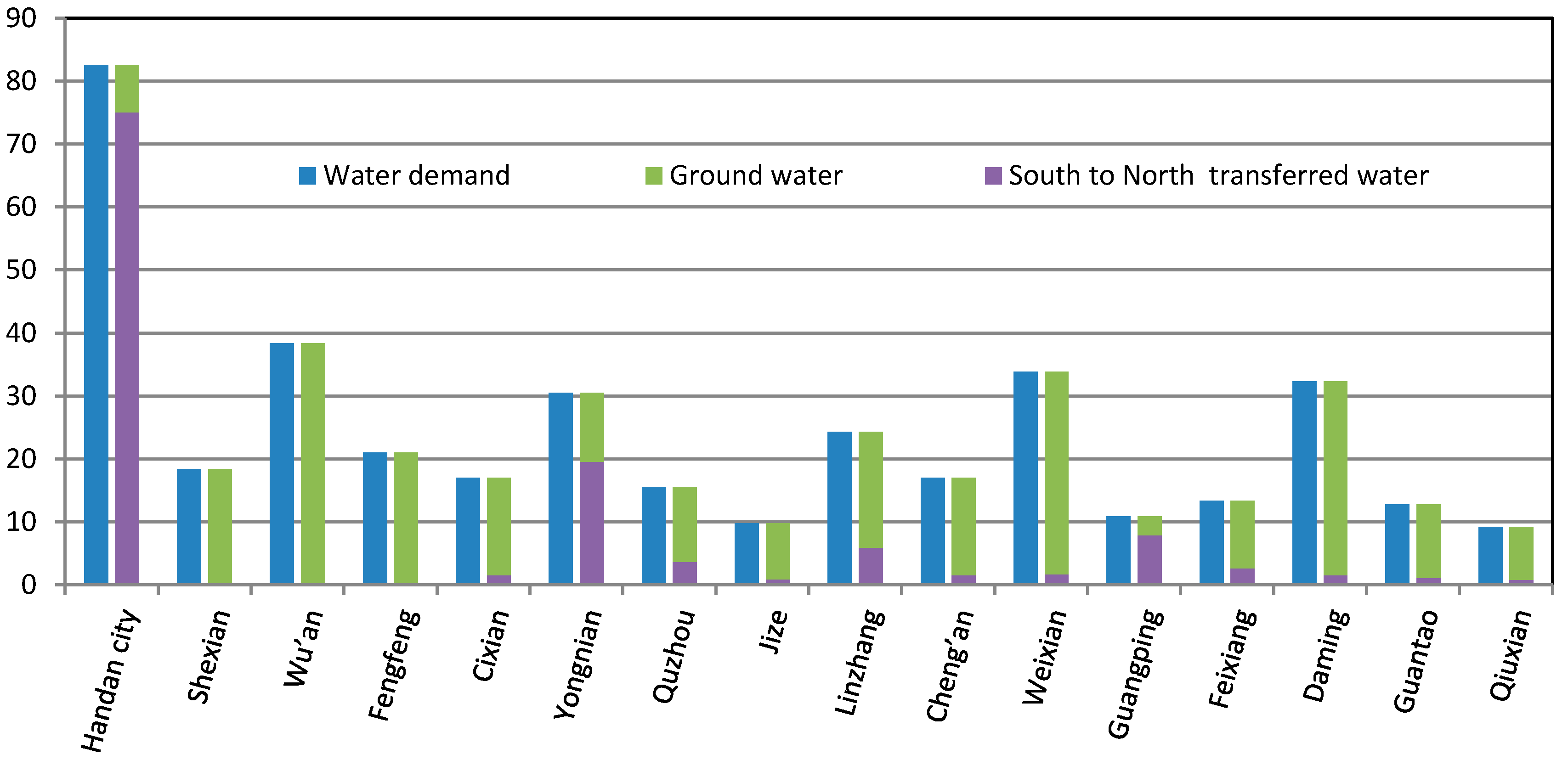
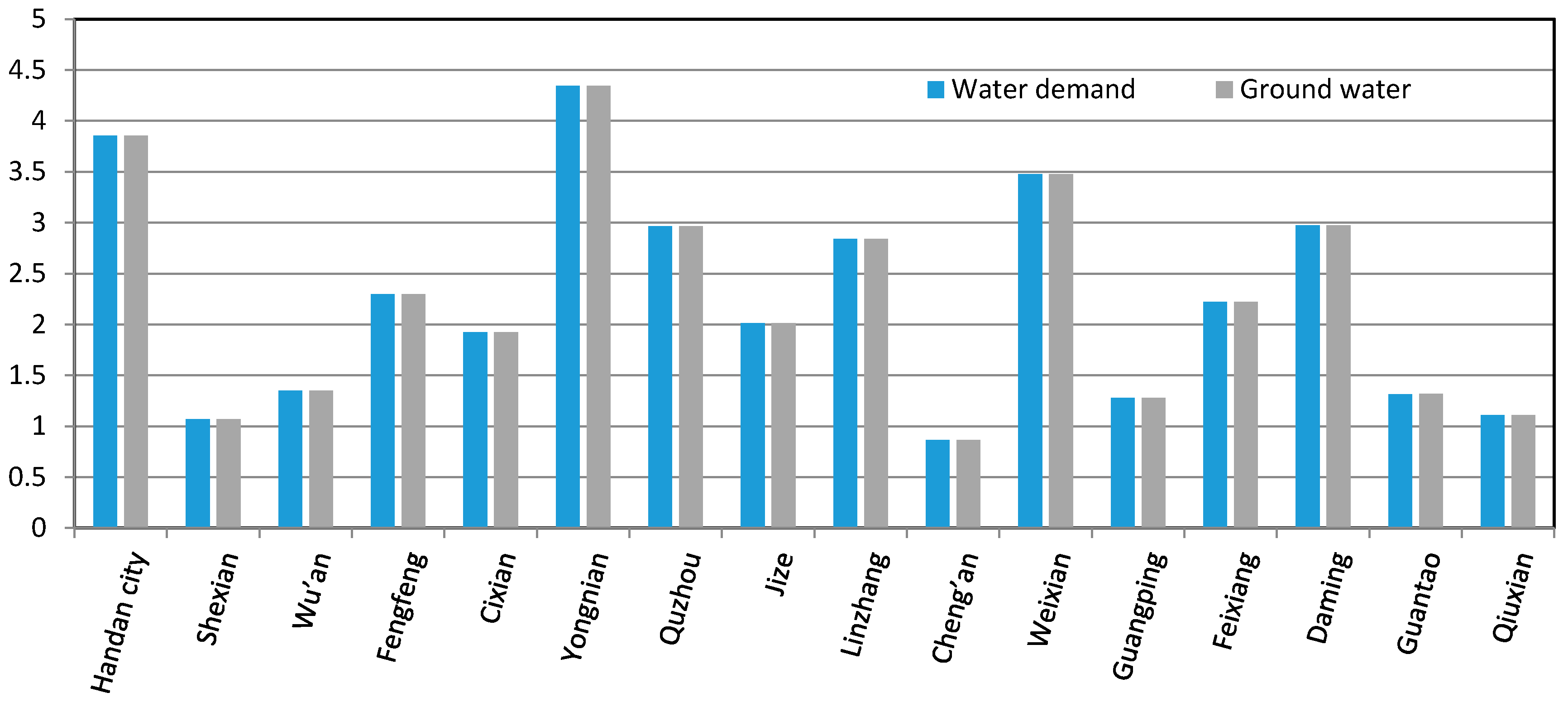
Figure 4 illustrates the urban domestic water allocation in each sub-region in Handan. The total urban domestic water demand is 387.16 × 10
6 m
3 while the total allocated volume is 387.16 × 10
6 m
3. The water supply can fully satisfy the urban domestic water demand in all sub-regions. The water demand is mainly supported by groundwater and water transferred through the South–North Water Transfer Project, the allocated volumes of which are 263.07 × 10
6 m
3 and 124.09 × 10
6 m
3, respectively, accounting for 67.9% and 32.1%, respectively, of the total supply. It is noteworthy that groundwater is the dominant water source for urban domestic water demand.
Figure 5 gives the rural domestic water allocation in each sub-region in Handan. The rural domestic water supply is able to meet the demand in all sub-regions. The total rural domestic water demand is 35.91 × 10
6 m
3 while the total allocated volume is 35.91 × 10
6 m
3, supported wholly by groundwater.
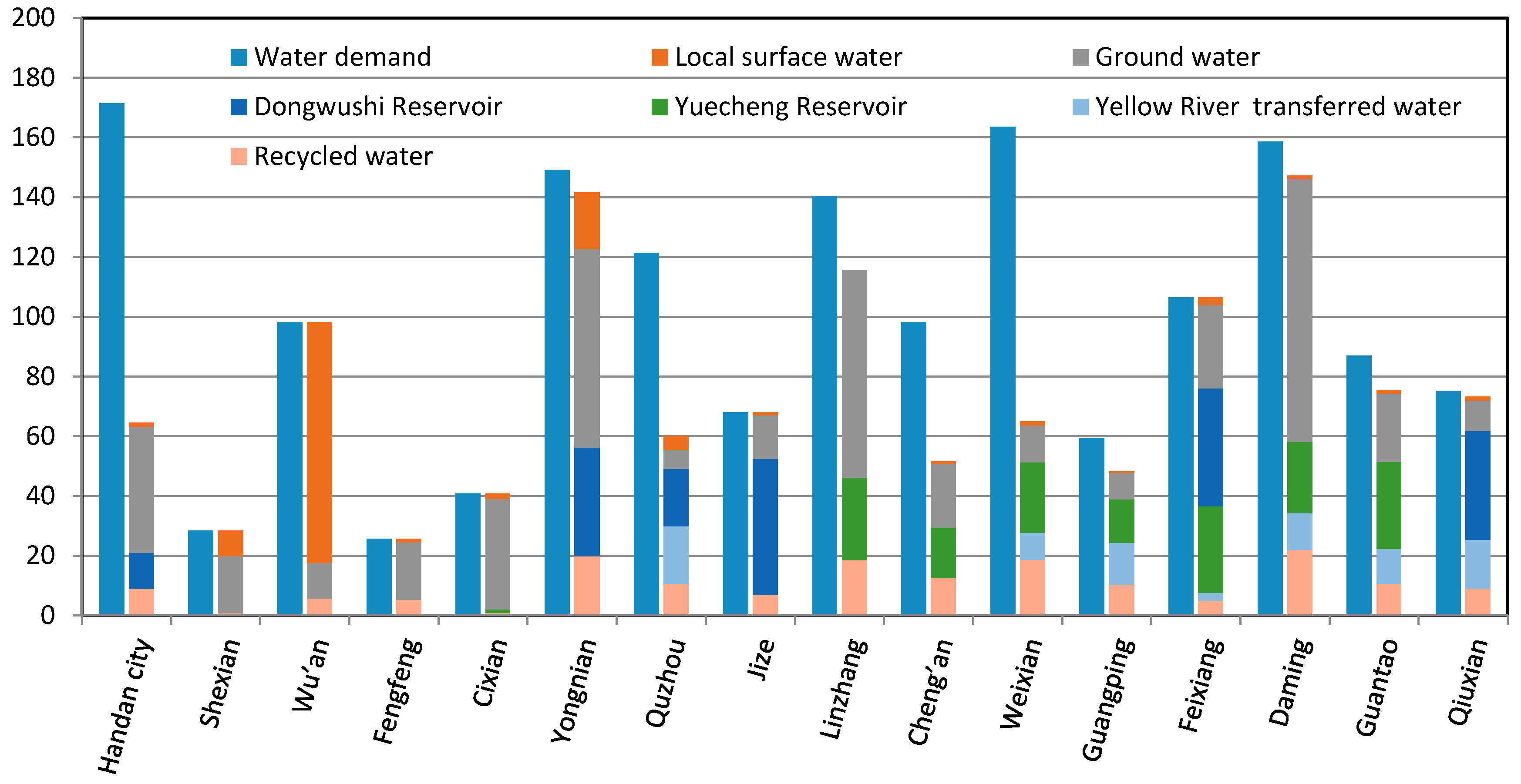
Figure 6 shows the primary sector water allocation in each sub-region in Handan. The total water demand of the primary sector in the region is 1591.82 × 10
6 m
3, whereas the total allocated volume is 1210.66 × 10
6 m
3, with a shortage of 381.15 × 10
6 m
3, and an average shortage rate of 23.9%. The four sub-regions with relatively great shortages are Handan city, Weixian, Quzhou, and Cheng’an and their shortage rates are 62.4%, 60.3%, 50.4%, and 47.5%, respectively. In Shexian, Wu’an, Fengfeng, Cixian, Jize, and Feixiang, water supply can meet the primary sector water demand. The allocated volume supported by local surface water, groundwater, the Dongwushi reservoir, the Yuecheng reservoir, imported water from the Yellow River, and recycled water are 127.18 × 10
6 m
3, 477.69 × 10
6 m
3, 189.08 × 10
6 m
3, 165.70 × 10
6 m
3, 85.83 × 10
6 m
3, and 165.19 × 10
6 m
3, respectively, accounting for 10.5%, 39.5%, 15.6%, 13.7%, 7.1%, and 3.6% of the total supply, respectively. Again, groundwater is the main water source for the primary sector.
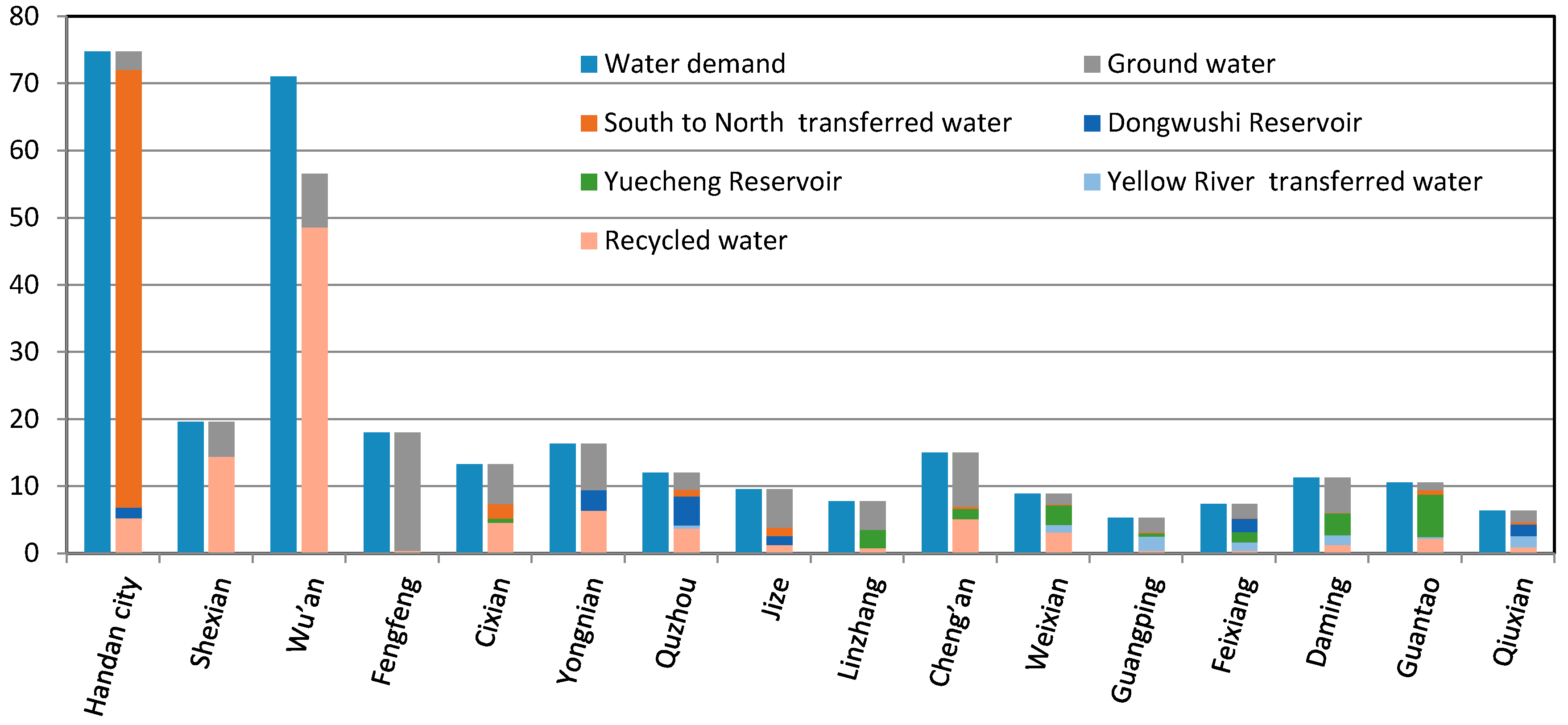
The secondary sector water allocation in each sub-region in Handan is shown in
Figure 7. The total water demand of the secondary sector is 307.06 × 10
6 m
3, and the total allocated volume is 292.60 × 10
6 m
3, leading to a shortage of 14.46 × 10
6 m
3, and an average shortage rate of 4.7%. In all sub-regions except Wu’an, the supply meets the demand. In Wu’an, the demand is 71.00 × 10
6 m
3, and the allocated volume is 56.54 × 10
6 m
3. There is a shortage of 14.46 × 10
6 m
3. Water sources for the secondary sector water supply include groundwater, water transferred through the South–North Water Transfer Project, the Dongwushi reservoir, the Yuecheng reservoir, imported water from the Yellow River, and recycled water. Their allocated volumes are 81.02 × 10
6 m
3, 71.26 × 10
6 m
3, 14.03 × 10
6 m
3, 19.35 × 10
6 m
3, 8.40 × 10
6 m
3, and 98.55 × 10
6 m
3, and contribute to total supply by 26.4%, 23.2%, 4.6%, 6.3%, 2.7%, and 32.1%, respectively. The main water source for the secondary sector is recycled water.
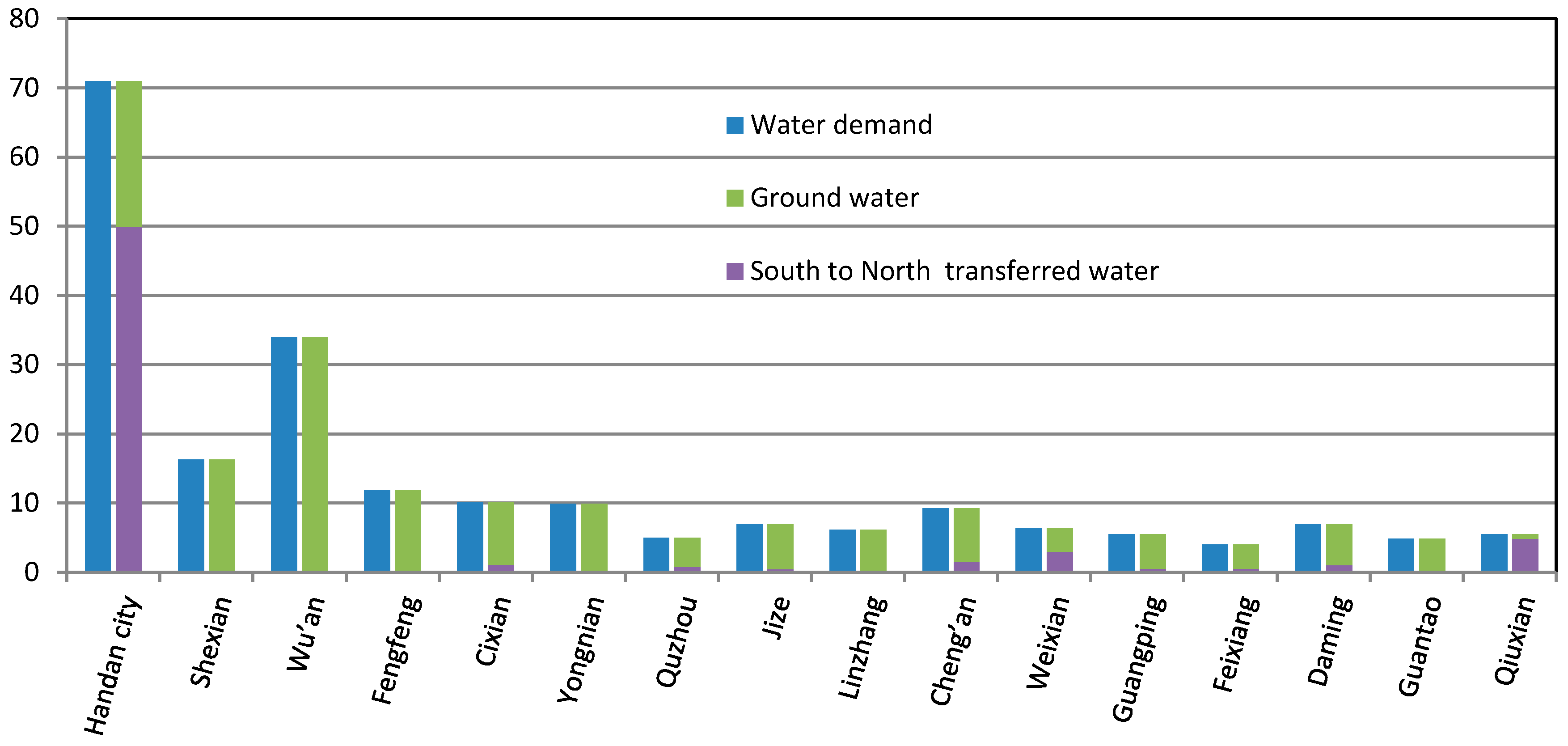
Figure 8 shows the tertiary sector water allocation in each sub-region in Handan. As shown in
Figure 8, the total water demand and allocated volume are 213.41 × 10
6 m
3 and 213.41 × 10
6 m
3, respectively. In all sub-regions, the supply can satisfy the demand. The tertiary sector water demand is wholly supported by groundwater and water transferred through the South–North Water Transfer Project, the supplies of which are 8.40 × 10
6 m
3 and 98.55 × 10
6 m
3, respectively, and account for 70.1% and 29.9% of the total, respectively. Groundwater is the dominant water source for the tertiary sector.
Figure 9 shows the ecological water allocation in each sub-region in Handan. The total water demand and total allocated volume are 190.72 × 10
6 m
3 and 182.00 × 10
6 m
3, respectively. The shortage is 8.72 × 10
6 m
3, and the shortage rate is 4.6%. In all sub-regions, except Handan city, the supply can satisfy the demand. In Handan city, the demand is 114.84 × 10
6 m
3, while the allocated volume is 106.12 × 10
6 m
3, resulting in a deficiency of 8.72 × 10
6 m
3. The supplies by local surface water, the Dongwushi reservoir, the Yuecheng reservoir, imported water from the Yellow River, and recycled water are 25.88 × 10
6 m
3, 18.68 × 10
6 m
3, 12.50 × 10
6 m
3, 5.77 × 10
6 m
3, and 119.17 × 10
6 m
3, respectively, accounting for 14.2%, 10.3%, 6.9%, 3.2%, and 65.5%, respectively, of the total. Recycled water is the main source for the ecological water demand.
Table 5 lists the volumes of local surface water allocated to each user in each sub-region in Handan. Due to the water quality, local surface water is allocated only to the primary sector and ecology. The corresponding allocated volumes are 127.18 × 10
6 m
3 and 25.88 × 10
6 m
3, respectively, and the total is 153.06 × 10
6 m
3. Since the total available water supply by local surface water in the region is 236.58 × 10
6 m
3, 83.52 × 10
6 m
3 of water not utilized. From
Figure 6 and
Figure 9, local surface water accounts for 10.5% and 14.2% of the total volumes allocated to the primary sector and ecology, respectively. In Wu’an, the highest volumes of local surface water are allocated to the primary sector and ecology. The corresponding volumes are 80.68 × 10
6 m
3 and 13.93 × 10
6 m
3, which account for 63.4% and 53.8%, respectively, of the total volumes of local surface water allocated. This is because Wu’an has abundant local surface water, or 48.6% of the total in Handan.
Table 6 shows the volumes of groundwater allocated to each user in each sub-region in Handan. Groundwater is allocated to urban domestic, rural domestic, primary sector, secondary sector, and tertiary sector uses in volumes of 263.07 × 10
6 m
3, 35.91 × 10
6 m
3, 477.69 × 10
6 m
3, 81.02 × 10
6 m
3, and 149.63 × 10
6 m
3, respectively. These account for 26.1%, 3.6%, 47.4%, 8.0%, and 14.9% of the total volume of groundwater allocated, respectively. Groundwater is mostly supplied to the primary sector. This is in line with actual local groundwater usage. The total available water supply by groundwater and total allocated volume are 1130.42 × 10
6 m
3 and 1007.32 × 10
6 m
3, respectively. There is 123.10 × 10
6 m
3 of unallocated water remaining.
The allocation results of water transferred through the South–North Water Transfer Project to each user in each sub-region in Handan are listed in
Table 7. The transferred water is mostly supplied for urban domestic, secondary, and tertiary sector uses. The total available water supply and total allocated volumes are 388.62 × 10
6 m
3 and 259.11 × 10
6 m
3, respectively, resulting in a surplus of 129.51 × 10
6 m
3 not allocated for any use. The allocated volumes for urban domestic, secondary, and tertiary sector uses are 124.09 × 10
6 m
3, 71.26 × 10
6 m
3, and 63.77 × 10
6 m
3, respectively. These account for 47.9%, 27.5%, and 24.6%, respectively, of the total allocated volume of water transferred through the South–North Water Transfer Project. The transferred water is mainly supplied for urban domestic use, since its quality is relatively high and consequently, it is able to fulfill the quality requirements for urban domestic water.
The total available water supply by the Dongwushi reservoir and the total allocated volume are both 221.79 × 10
6 m
3, signifying that the total available supply is completely allocated for different uses. The results are listed in
Table 8. The Dongwushi reservoir is a public water source and mainly supplies water to Handan city, Yongnian, Quzhou, Jize, Feixiang, and Qiuxian. The Dongwushi reservoir mostly supports the primary and secondary sector and ecological water uses. From
Table 8, the allocated volumes to the primary sector, secondary sector, and ecology are 189.08 × 10
6 m
3, 14.03 × 10
6 m
3, and 18.68 × 10
6 m
3, respectively, accounting for 85.3%, 6.3%, and 8.4%, respectively, of the total allocated volume from the Dongwushi reservoir. Most of the water from the reservoir is supplied to the primary sector because the water quality is not high enough to satisfy domestic requirements, but is suitable for irrigation in the primary sector. The allocation results are consistent with the current allocation situation of the reservoir.
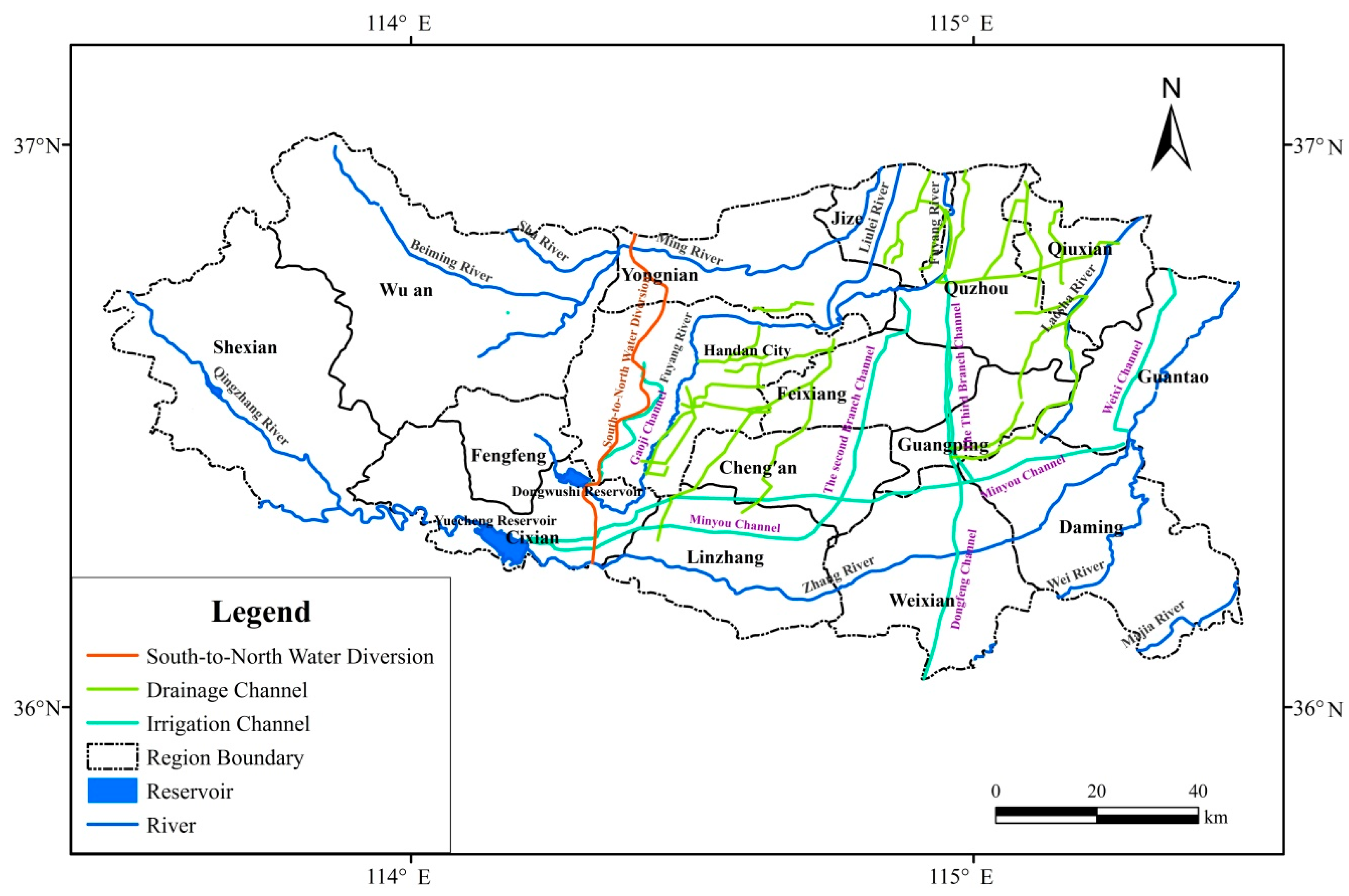
The Yuecheng reservoir is a public water source mainly supplied to Cixian, Linzhang, Cheng’an, Weixian, Guangping, Feixiang, Daming, and Guantao. The main users are primary sector, secondary sector, and ecology. The allocation results are shown in
Table 9. The total available water supply equals the total allocated volume, which is 197.56 × 10
6 m
3. Thus, the total available supply is completely allocated. The volumes allocated to the primary sector, secondary sector, and ecology are 165.70 × 10
6 m
3, 19.35 × 10
6 m
3, and 12.50 × 10
6 m
3, respectively. These account for 83.9%, 9.8%, and 6.3% of the total allocated volume, respectively, indicating that the main user of the Yuecheng reservoir is the primary sector.
Imported water from the Yellow River is a public water source. The imported water is mainly supplied to Quzhou, Weixian, Guangping, Feixiang, Daming, Guantao, and Qiuxian. It is mostly allocated for the primary sector, secondary sector, and ecological uses. From
Table 10, the allocated volumes to the primary sector, secondary sector, and ecology are 85.83 × 10
6 m
3, 8.40 × 10
6 m
3, and 5.77 × 10
6 m
3, respectively, accounting for 85.8%, 8.4%, and 5.8%, respectively, of the total allocated volume of 100.00 × 10
6 m
3. All imported water is allocated completely, and mostly to the primary sector.
The allocation results for recycled water in Handan are listed in
Table 11. Recycled water is mostly allocated to the primary sector, secondary sector, and ecology in volumes of 165.19 × 10
6 m
3, 98.55 × 10
6 m
3, and 119.17 × 10
6 m
3, respectively. These account for 43.1%, 25.7%, and 31.1% of the total allocated volume, respectively. The total available supply by recycled water is 421.75 × 10
6 m
3 and the total allocated volume is 382.90 × 10
6 m
3, resulting in a surplus of 38.85 × 10
6 m
3 not utilized.
In Handan, the total water demand of all users, the total available water supply, and the total allocated volume are 2726.07 × 10
6 m
3, 2696.71 × 10
6 m
3, and 2321.74 × 10
6 m
3, respectively. There is a surplus of 374.97 × 10
6 m
3 not allocated, and the volumes are listed in
Table 12. Water from the Dongwushi reservoir, Yuecheng reservoir, and water imported from the Yellow River are fully allocated for different uses. Moreover, 83.52 × 10
6 m
3 of local surface water, 123.10 × 10
6 m
3 of groundwater, 129.51 × 10
6 m
3 of water transferred through the South–North Water Transfer Project, and 38.84 × 10
6 m
3 of recycled water are not used. In five sub-regions, namely, Shexian, Fengfeng, Cixian, Jize, and Feixiang, the allocated volume can completely satisfy the water demand, and there is a surplus of 223.23 × 10
6 m
3 of water. In Handan city, the water demand of the primary sector and ecology are not satisfied, while that of other users is entirely met. In Handan city, 106.30 × 10
6 m
3 of water transferred through the South–North Water Transfer Project is not utilized. Since the water transferred can only be allocated to urban domestic, secondary sector, or tertiary sector uses, the surplus cannot be used to make up the shortage in the primary sector and ecology. In Wu’an, the water demand of the secondary sector is not satisfied while that of other users is fully met. Although 20.29 × 10
6 m
3 of local surface water remains unutilized, it cannot supplement the insufficient supply to the secondary sector, as the local surface water is supplied only to the primary sector and ecology. In Yongnian, Quzhou, Linzhang, Cheng’an, Weixian, Guangping, Daming, Guantao, and Qiuxian, the water demand of the primary sector is not satisfied. The surplus in these nine sub-regions consists solely of water transferred through the South–North Water Transfer Project. Due to the relatively high cost of the transferred water, it cannot be used to make up the shortage in the primary sector. Lastly, 9.91 × 10
6 m
3 of groundwater is not utilized in Weixian and Guangping.