A Smoothed Version of the Lassosum Penalty for Fitting Integrated Risk Models Using Summary Statistics or Individual-Level Data
Abstract
:1. Introduction
1.1. Literature Review
2. Methodology
2.1. Brief Overview of Nesterov Smoothing
2.2. A Smoothed Version of the Lassosum Objective Function
2.3. Theoretical Guarantees
3. Application to Experimental Data
- “NeuralNetwork”: a neural network implemented with the Keras interface [43] to the Tensorflow machine learning platform [44]. We train a network with four layers, having 20, 8, 4 and 2 nodes. We employ the LeakyReLU activation function; a dropout rate of ; a validation splitting rate of ; the he_normal truncated normal distribution for kernel initialization; and kernel, bias, and activity regularization with penalty. The last layer employs the sigmoid (for Section 3.1) or ReLU (for Section 3.2) activation functions. The model is compiled for binary crossentropy loss (for Section 3.1) or mean absolute error loss (for Section 3.2) using the Adam optimizer, evaluated with the AUC (for Section 3.1) or the mean squared error (for Section 3.2) using 1000 epochs.
- “MegaPRS”: we employ the robust version Bolt Predict of the MegaPRS algorithm [28] as suggested by the authors. We use default parameters given in the example section of the MegaPRS website (a cross validation proportion of , the—ignore-weights option and a power parameter of ). MegaPRS is implemented in the LDAK package [46].
- “EpiOnly”: we perform a simple linear regression using epidemiological covariates only.
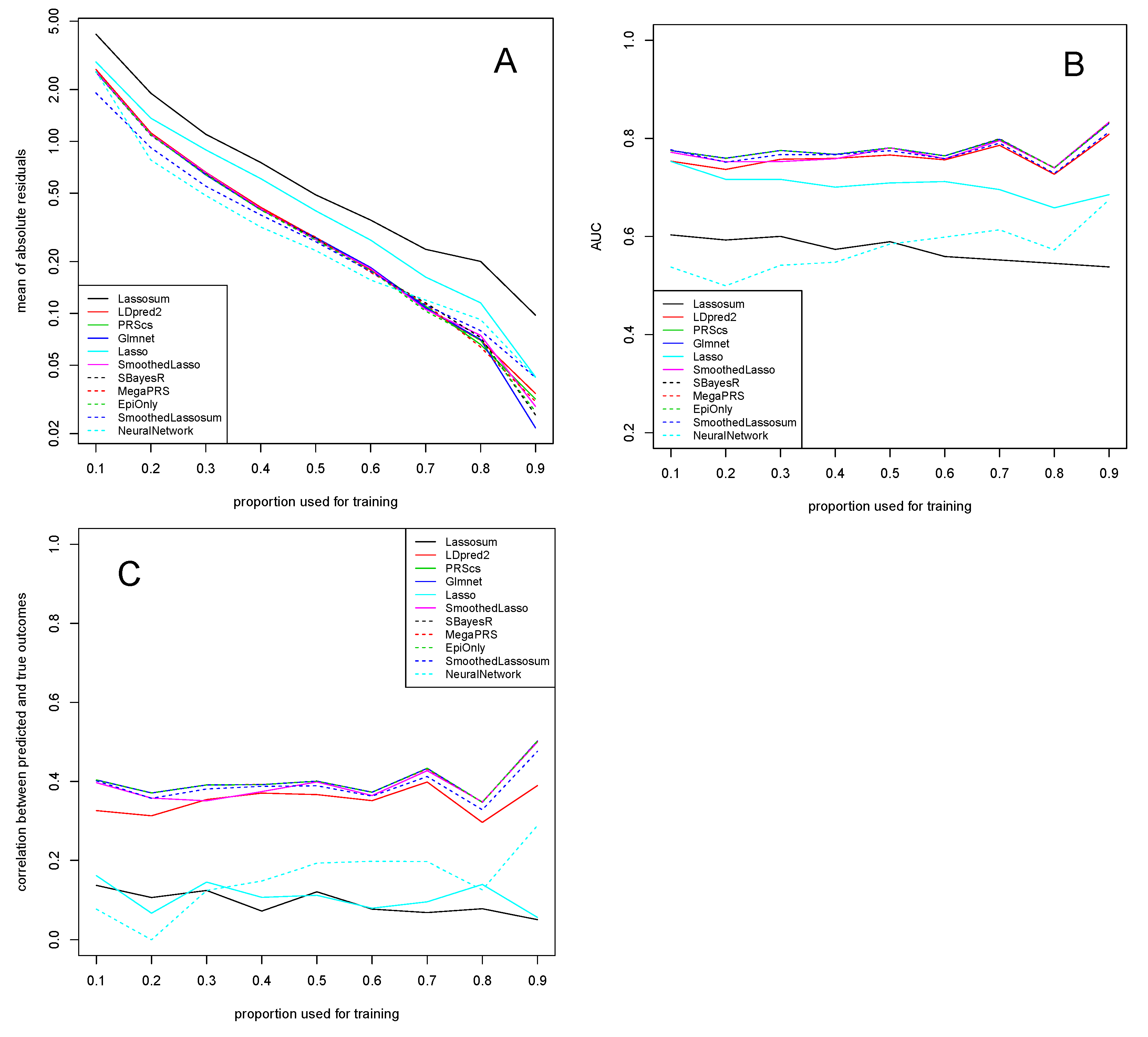
3.1. Alzheimer’s Disease Study
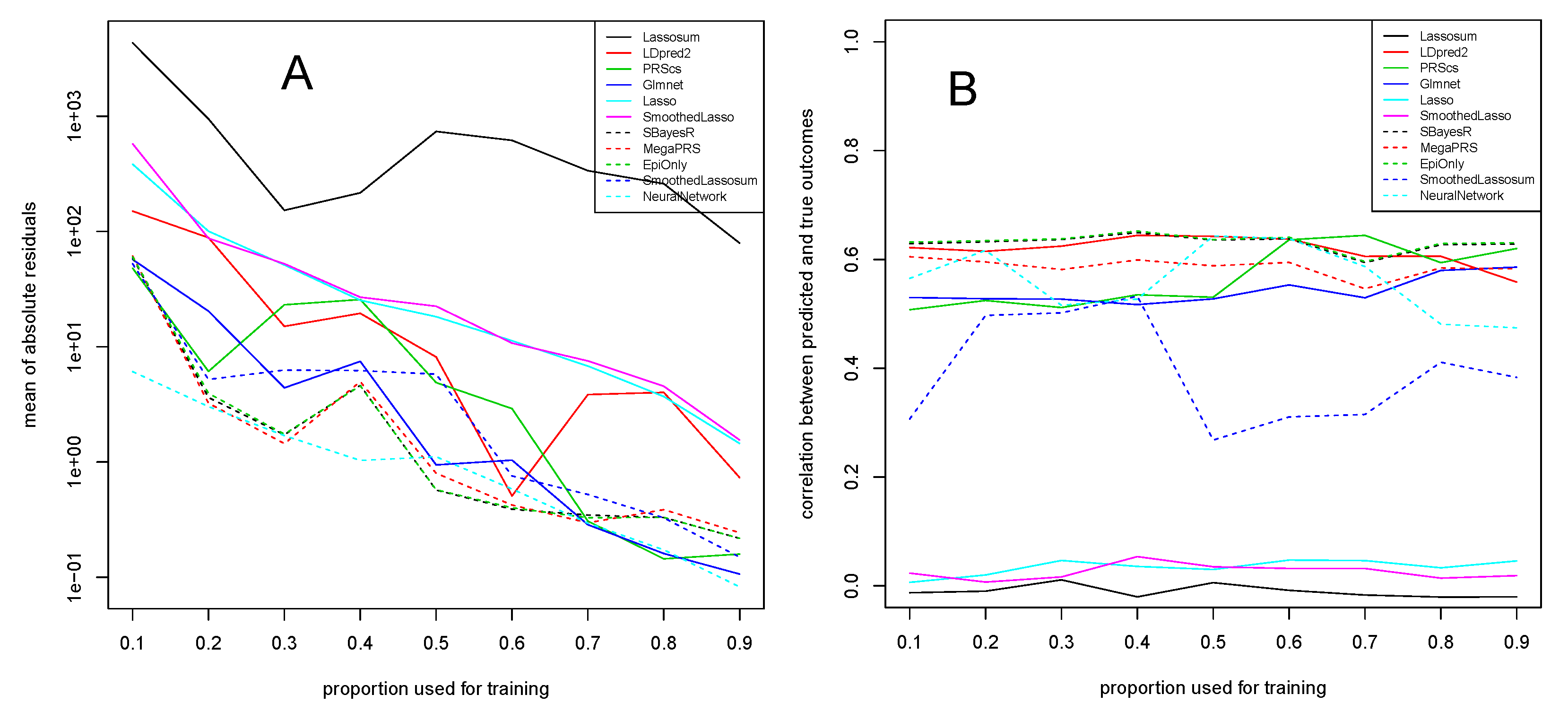
3.2. COPD Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Principal Component Plots

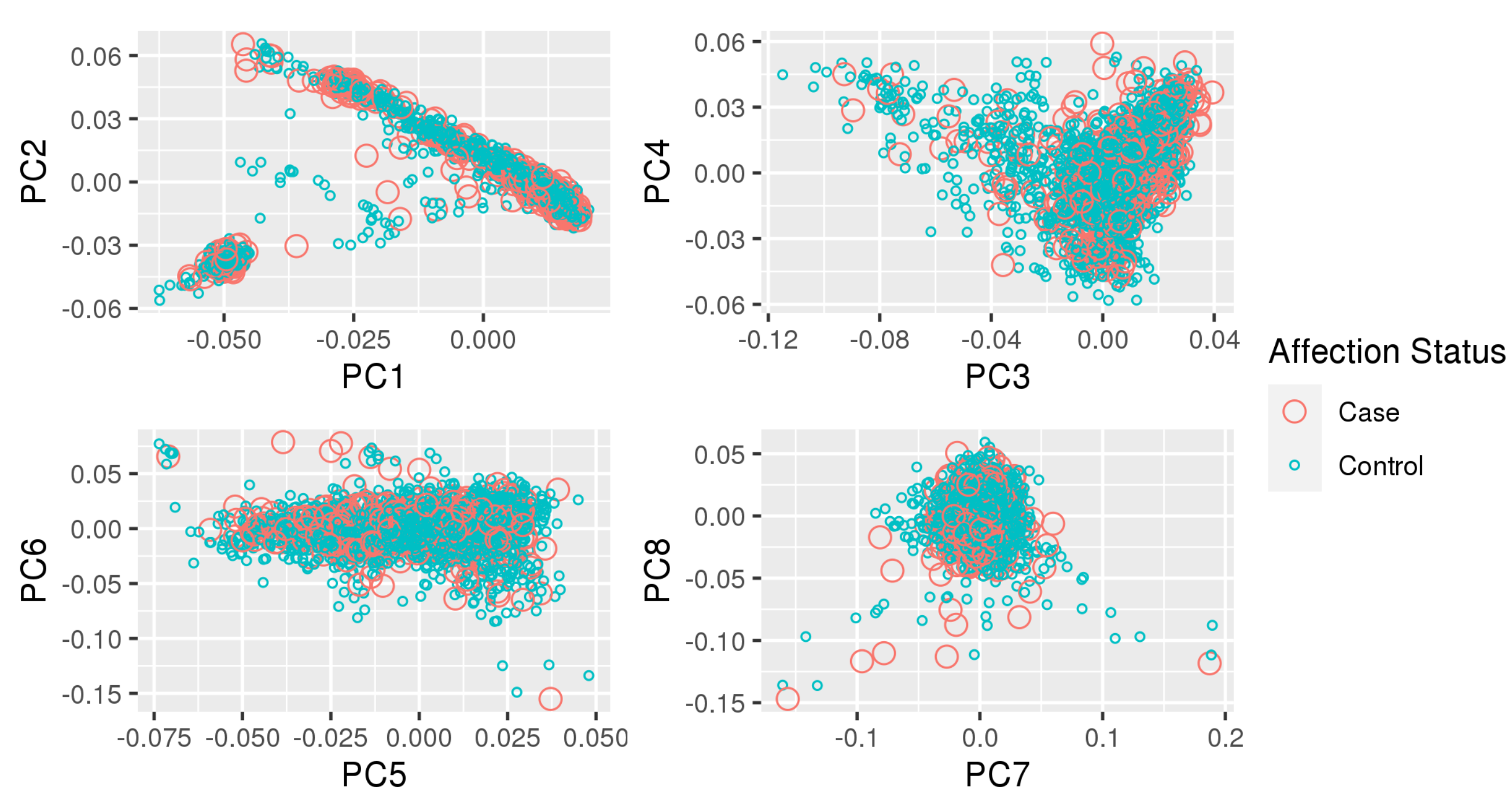
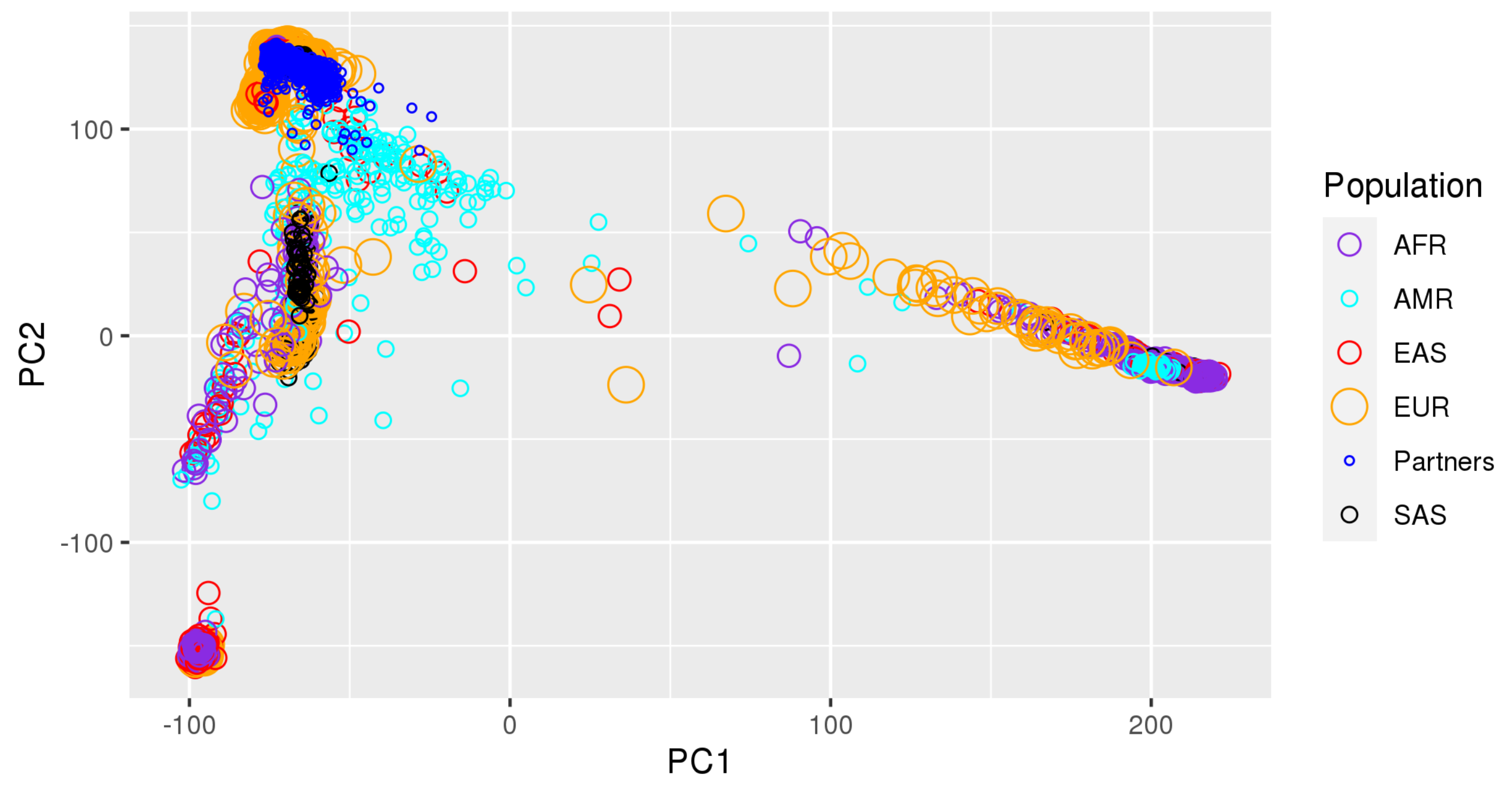
| TOPMed | TOPMed Study | TOPMed | TOPMed | Omics Center | Omics Support | Omics Type |
|---|---|---|---|---|---|---|
| Accession # | Short Name | Phase | Project | Short Name | ||
| phs000951 | COPDGene | 5 | COPD | NWGC | HHSN268201600032I | Methylomics |
| phs000951 | COPDGene | 2.5 | COPD | Broad Genomics | HHSN268201500014C | WGS |
| phs000951 | COPDGene | 1 | COPD | NWGC | 3R01HL089856-08S1 | WGS |
| phs000951 | COPDGene | 2 | COPD | Broad Genomics | HHSN268201500014C | WGS |
| phs000951 | COPDGene | 4 | COPD | NWGC | HHSN268201600032I | RNASeq |
References
- Wand, H.; Lambert, S.A.; Tamburro, C.; Iacocca, M.A.; O’Sullivan, J.W.; Sillari, C.; Kullo, I.J.; Rowley, R.; Dron, J.S.; Brockman, D.; et al. Improving reporting standards for polygenic scores in risk prediction studies. Nature 2021, 591, 211–219. [Google Scholar] [CrossRef]
- Khera, A.V.; Chaffin, M.; Aragam, K.G.; Haas, M.E.; Roselli, C.; Choi, S.H.; Natarajan, P.; Lander, E.S.; Lubitz, S.A.; Ellinor, P.T.; et al. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018, 50, 1219–1224. [Google Scholar] [CrossRef]
- Duncan, L.; Shen, H.; Gelaye, B.; Meijsen, J.; Ressler, K.; Feldman, M.; Peterson, R.; Domingue, B. Analysis of polygenic risk score usage and performance in diverse human populations. Nat. Commun. 2019, 10, 3328. [Google Scholar] [CrossRef]
- Knowles, J.; Ashley, E. Cardiovascular disease: The rise of the genetic risk score. PLoS Med. 2018, 15, e1002546. [Google Scholar] [CrossRef] [PubMed]
- Schizophrenia Working Group of the Psychiatric Genomics Consortium. Biological insights from 108 schizophrenia-associated genetic loci. Nature 2014, 511, 421–427. [Google Scholar] [CrossRef] [Green Version]
- Mandrekar, J.N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mak, T.; Porsch, R.; Choi, S.; Zhou, X.; Sham, P. Polygenic scores via penalized regression on summary statistics. Genet. Epidemiol. 2017, 41, 469–480. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Darbar, D. Genetic Risk Scores for Atrial Fibrillation: Do they Improve Risk Estimation? Can. J. Cardiol. 2017, 33, 422–424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosmer, D.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2000; pp. 160–164, Chapter 5. [Google Scholar]
- Nesterov, Y. Smooth minimization of non-smooth functions. Math. Program. Ser. A 2005, 103, 127–152. [Google Scholar] [CrossRef]
- Hahn, G.; Lutz, S.M.; Laha, N.; Lange, C. A framework to efficiently smooth L1 penalties for linear regression. bioRxiv 2020, 1–35. [Google Scholar] [CrossRef]
- Hahn, G.; Lutz, S.; Laha, N.; Cho, M.; Silverman, E.; Lange, C. A fast and efficient smoothing approach to LASSO regression and an application in statistical genetics: Polygenic risk scores for Chronic obstructive pulmonary disease (COPD). Stat. Comput. 2021, 31, 35. [Google Scholar] [CrossRef]
- Kunkle, B.; Grenier-Boley, B.; Sims, R.; Bis, J.; Damotte, V.; Naj, A.; Boland, A.; Vronskaya, M.; van der Lee, S.; Amlie-Wolf, A.; et al. Genetic meta-analysis of diagnosed Alzheimer’s disease identifies new risk loci and implicates Aβ, tau, immunity and lipid processing. Nat. Genet. 2019, 51, 414–430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jansen, I.; Savage, J.; Watanabe, K.; Bryois, J.; Williams, D.; Steinberg, S.; Sealock, J.; Karlsson, I.; Hägg, S.; Athanasiu, L.; et al. Genome-wide meta-analysis identifies new loci and functional pathways influencing Alzheimer’s disease risk. Nat. Genet. 2019, 51, 404–413. [Google Scholar] [CrossRef]
- Regan, E.; Hokanson, J.; Murphy, J.; Make, B.; Lynch, D.; Beaty, T.; Curran-Everett, D.; Silverman, E.; Crapo, J. Genetic epidemiology of COPD (COPDGene) study design. COPD 2010, 7, 32–43. [Google Scholar] [CrossRef]
- Privé, F.; Arbel, J.; Vilhjálmsson, B.J. LDpred2: Better, faster, stronger. Bioinformatics 2019. [Google Scholar] [CrossRef]
- Ge, T.; Chen, C.Y.; Ni, Y.; Feng, Y.C.A.; Smoller, J.W. PRS-CS: A Polygenic Prediction Method That Infers Posterior SNP Effect Sizes under Continuous Shrinkage (CS) Priors Using GWAS Summary Statistics and an External LD Reference Panel. 2020. Available online: https://github.com/getian107/PRScs (accessed on 8 May 2021).
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. B Meter. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hahn, G.; Lutz, S.M.; Laha, N.; Lange, C. smoothedLasso: Smoothed LASSO Regression via Nesterov Smoothing. 2020. R-Package Version 1.4. Available online: https://cran.r-project.org/src/contrib/Archive/smoothedLasso/smoothedLasso_1.4.tar.gz (accessed on 8 May 2021).
- Choi, S.W.; Mak, T.S.H.; O’Reilly, P.F. Tutorial: A guide to performing polygenic risk score analyses. Nat. Protoc. 2020, 15, 2759–2772. [Google Scholar] [CrossRef]
- Purcell, S.; Wray, N.; Stone, J.; Visscher, P.; O’Donovan, M.C.; Sullivan, P.; Sklar, P. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 2009, 460, 748–752. [Google Scholar] [PubMed]
- Wray, N.; Lee, S.; Mehta, D.; Vinkhuyzen, A.; Dudbridge, F.; Middeldorp, C. Research Review: Polygenic methods and their application to psychiatric traits. J. Child Psychol. Psychiatry 2014, 55, 1068–1087. [Google Scholar] [CrossRef] [Green Version]
- Vilhjálmsson, B.; Yang, J.; Finucane, H.; Gusev, A.; Lindström, S.; Ripke, S.; Genovese, G.; Loh, P.; Bhatia, G.; Do, R.; et al. Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores. Am. J. Hum. Genet. 2015, 97, 576–592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mak, T.; Kwan, J.; Campbell, D.; Sham, P. Local true discovery rate weighted polygenic scores using GWAS summary data. Behav. Genet. 2016, 46, 573–582. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, G.; Park, J.H.; Chatterjee, N. Estimation of complex effect-size distributions using summary-level statistics from genome-wide association studies across 32 complex traits. Nat. Genet. 2018, 50, 1318–1326. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Jones, L.R.; Zeng, J.; Sidorenko, J.; Yengo, L.; Moser, G.; Kemper, K.E.; Wang, H.; Zheng, Z.; Magi, R.; Esko, T.; et al. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun. 2019, 10, 5086. [Google Scholar] [CrossRef] [Green Version]
- Ge, T.; Chen, C.Y.; Ni, Y.; Feng, Y.C.A.; Smoller, J.W. Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun. 2019, 10, 1776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Q.; Privé, F.; Vilhjálmsson, B.; Speed, D. Improved genetic prediction of complex traits from individual-level data or summary statistics. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.; Hastie, T.; Tibshirani, R.; Narasimhan, B.; Tay, K.; Simon, N.; Qian, J. glmnet: Lasso and Elastic-Net Regularized Generalized Linear Models. 2020. R-Package Version 4.0. Available online: https://cran.r-project.org/package=glmnet (accessed on 8 May 2021).
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.W.; O’Reilly, P.F. PRSice-2: Polygenic Risk Score software for biobank-scale data. Gigascience 2019, 8, giz082. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, J.; Wang, N. Using the Machine Learning Approach to Predict Patient Survival from High-Dimensional Survival Data. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016; pp. 1–5. [Google Scholar]
- Mamaniab, N.M. Machine Learning techniques and Polygenic Risk Score application to prediction genetic diseases. Adv. Distrib. Comput. Artif. Intell. 2020, 9, 5–14. [Google Scholar]
- Badré, A.; Zhang, L.; Muchero, W.; Reynolds, J.C.; Pan, C. Deep neural network improves the estimation of polygenic risk scores for breast cancer. J. Hum. Genet. 2021, 66, 359–369. [Google Scholar] [CrossRef]
- Huang, S.; Ji, X.; Cho, M.; Joo, J.; Moore, J. DL-PRS: A novel deep learning approach to polygenic risk scores. BMC Bioinform. 2021. [Google Scholar] [CrossRef]
- Peng, J.; Li, J.; Han, R.; Wang, Y.; Han, L.; Peng, J.; Wang, T.; Hao, J.; Shang, X.; Wei, Z. A Deep Learning-based Genome-wide Polygenic Risk Score for Common Diseases Identifies Individuals with Risk. medRxiv 2021. [Google Scholar] [CrossRef]
- Gola, D.; Erdmann, J.; Müller-Myhsok, B.; Schunkert, H.; König, I.R. Polygenic risk scores outperform machine learning methods in predicting coronary artery disease status. Genet. Epidemiol. 2020, 44, 125–138. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Stat Comp.: Vienna, Austria, 2014. [Google Scholar]
- Mak, T.; Porsch, R.; Choi, S.; Zhou, X.; Sham, P. Lassosum: A Method for Computing LASSO/Elastic Net Estimates of a Linear Regression Problem Given Summary Statistics from GWAS and Genome-Wide Meta-Analyses. 2020. Available online: https://github.com/tshmak/lassosum (accessed on 8 May 2021).
- Privé, F.; Blum, M.; Aschard, H. bigsnpr: Analysis of Massive SNP Arrays. 2020. R-Package Version 1.5.2. Available online: https://cran.r-project.org/package=bigsnpr (accessed on 8 May 2021).
- Hahn, G.; Lutz, S.M.; Laha, N.; Lange, C. smoothedLasso: Smoothed LASSO Regression via Nesterov Smoothing. 2020. R-Package Version 1.5. Available online: https://cran.r-project.org/package=smoothedLasso (accessed on 8 May 2021).
- Falbel, D.; Allaire, J.; Chollet, F.; Studio, R.; Tang, Y.; Bijl, W.V.D.; Studer, M.; Keydana, S. keras: R Interface to ‘Keras’. 2020. R-Package Version 2.3.0.0. Available online: https://cran.r-project.org/package=keras (accessed on 8 May 2021).
- Falbel, D.; Allaire, J.; Studio, R.; Tang, Y.; Eddelbuettel, D.; Golding, N.; Kalinowski, T. Tensorflow: R Interface to ‘TensorFlow’. 2020. R-Package Version 2.2.0. Available online: https://cran.r-project.org/package=tensorflow (accessed on 8 May 2021).
- Zeng, J.; Yang, J.; Zhang, F.; Zheng, Z.; Lloyd-Jones, L.; Goddard, M. GCTB: A Tool for Genome-Wide Complex Trait Bayesian Analysis. 2020. Available online: https://cnsgenomics.com/software/gctb/#Overview (accessed on 8 May 2021).
- Speed, D. MegaPRS. 2021. Available online: http://dougspeed.com/prediction/ (accessed on 8 May 2021).
- McCarthy, S.; Das, S.; Kretzschmar, W.; Delaneau, O.; Wood, A.R.; Teumer, A.; Kang, H.M.; Fuchsberger, C.; Danecek, P.; Sharp, K.; et al. A reference panel of 64,976 haplotypes for genotype imputation. Nat. Genet. 2016, 48, 1279–1283. [Google Scholar]
- Partners. Partners Healthcare Biobank. 2020. Available online: https://biobank.partners.org (accessed on 8 May 2021).
- World Health Organization. International Statistical Classification of Diseases and Related Health Problems (ICD); World Health Organization: Geneva, Switzerland, 2021; Available online: https://www.who.int/standards/classifications/classification-of-diseases (accessed on 8 May 2021).
- Charlson, M.; Szatrowski, T.; Peterson, J.; Gold, J. Validation of a combined comorbidity index. J. Clin. Epidemiol. 1994, 47, 1245–1251. [Google Scholar] [CrossRef]
- Karlson, E.W.; Boutin, N.T.; Hoffnagle, A.G.; Allen, N.L. Building the Partners HealthCare Biobank at Partners Personalized Medicine: Informed Consent, Return of Research Results, Recruitment Lessons and Operational Considerations. J. Pers. Med. 2016, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Manichaikul, A.; Mychaleckyj, J.C.; Rich, S.S.; Daly, K.; Sale, M.; Chen, W.M. Robust relationship inference in genome-wide association studies. Bioinformatics 2010, 26, 2867–2873. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.M. KING: Kinship-Based INference for Gwas. 2021. Available online: https://kingrelatedness.com/ (accessed on 8 May 2021).
- Purcell, S.; Chang, C. PLINK2 (v2.00, 31 Aug 2020). 2020. Available online: www.cog-genomics.org/plink/2.0/ (accessed on 8 May 2021).
- Zhang, Q.; Sidorenko, J.; Couvy-Duchesne, B.; Marioni, R.E.; Wright, M.J.; Goate, A.M.; Marcora, E.; lin Huang, K.; Porter, T.; Laws, S.M.; et al. Risk prediction of late-onset Alzheimer’s disease implies an oligogenic architecture. Nat. Commun. 2020, 11, 4799. [Google Scholar] [CrossRef] [PubMed]
- Ware, E.B.; Faul, J.D.; Mitchell, C.M.; Bakulski, K.M. Considering the APOE locus in Alzheimer’s disease polygenic scores in the Health and Retirement Study: A longitudinal panel study. BMC Med. Genom. 2020, 13, 164. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef] [Green Version]
- NHLBI TOPMed. Genetic Epidemiology of COPD (COPDGene) Funded by the National Heart, Lung, and Blood Institute (NHLBI) in the NHLBI Trans-Omics for Precision Medicine (TOPMed) Program. 2018. Available online: https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000951.v5.p5 (accessed on 13 October 2021).
- Lutz, S.M.; Cho, M.H.; Young, K.; Hersh, C.P.; Castaldi, P.J.; McDonald, M.L.; Regan, E.; Mattheisen, M.; DeMeo, D.L.; Parker, M.; et al. A genome-wide association study identifies risk loci for spirometric measures among smokers of European and African ancestry. BMC Genet. 2015, 16, 138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bolli, A.; Domenico, P.D.; Bottà, G. Software as a Service for the Genomic Prediction of Complex Diseases. 2019. Available online: http://xxx.lanl.gov/abs/10.1101/763722 (accessed on 8 May 2021).
- Wald, N.J.; Old, R. The illusion of polygenic disease risk prediction. Genet. Med. 2019, 21, 1705–1707. [Google Scholar] [CrossRef] [PubMed]
- NIAGADS. NG00075—IGAP Rare Variant Summary Statistics—Kunkle et al. (2019). 2016. Available online: https://www.niagads.org/datasets/ng00075 (accessed on 8 May 2021).
- CTG Lab. Summary Statistics for Alzheimer’s Dementia from Iris Jansen et al., 2019. 2021. Available online: https://ctg.cncr.nl/software/summary_statistics (accessed on 8 May 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hahn, G.; Prokopenko, D.; Lutz, S.M.; Mullin, K.; Tanzi, R.E.; Cho, M.H.; Silverman, E.K.; Lange, C.; on the behalf of the NHLBI Trans-Omics for Precision Medicine (TOPMed) Consortium. A Smoothed Version of the Lassosum Penalty for Fitting Integrated Risk Models Using Summary Statistics or Individual-Level Data. Genes 2022, 13, 112. https://doi.org/10.3390/genes13010112
Hahn G, Prokopenko D, Lutz SM, Mullin K, Tanzi RE, Cho MH, Silverman EK, Lange C, on the behalf of the NHLBI Trans-Omics for Precision Medicine (TOPMed) Consortium. A Smoothed Version of the Lassosum Penalty for Fitting Integrated Risk Models Using Summary Statistics or Individual-Level Data. Genes. 2022; 13(1):112. https://doi.org/10.3390/genes13010112
Chicago/Turabian StyleHahn, Georg, Dmitry Prokopenko, Sharon M. Lutz, Kristina Mullin, Rudolph E. Tanzi, Michael H. Cho, Edwin K. Silverman, Christoph Lange, and on the behalf of the NHLBI Trans-Omics for Precision Medicine (TOPMed) Consortium. 2022. "A Smoothed Version of the Lassosum Penalty for Fitting Integrated Risk Models Using Summary Statistics or Individual-Level Data" Genes 13, no. 1: 112. https://doi.org/10.3390/genes13010112
APA StyleHahn, G., Prokopenko, D., Lutz, S. M., Mullin, K., Tanzi, R. E., Cho, M. H., Silverman, E. K., Lange, C., & on the behalf of the NHLBI Trans-Omics for Precision Medicine (TOPMed) Consortium. (2022). A Smoothed Version of the Lassosum Penalty for Fitting Integrated Risk Models Using Summary Statistics or Individual-Level Data. Genes, 13(1), 112. https://doi.org/10.3390/genes13010112







