Statistical Learning Methods Applicable to Genome-Wide Association Studies on Unbalanced Case-Control Disease Data
Abstract
1. Introduction
2. Why Does the Imbalance Cause an Issue from a Statistic Aspect?
3. Generalized Linear Mixed Model Association Test
4. Scalable and Accurate Implementation of GEneralized Mixed Model
5. Bayesian Multiple Logistic Regression Method
6. Support Vector Machine
7. AdaBoost
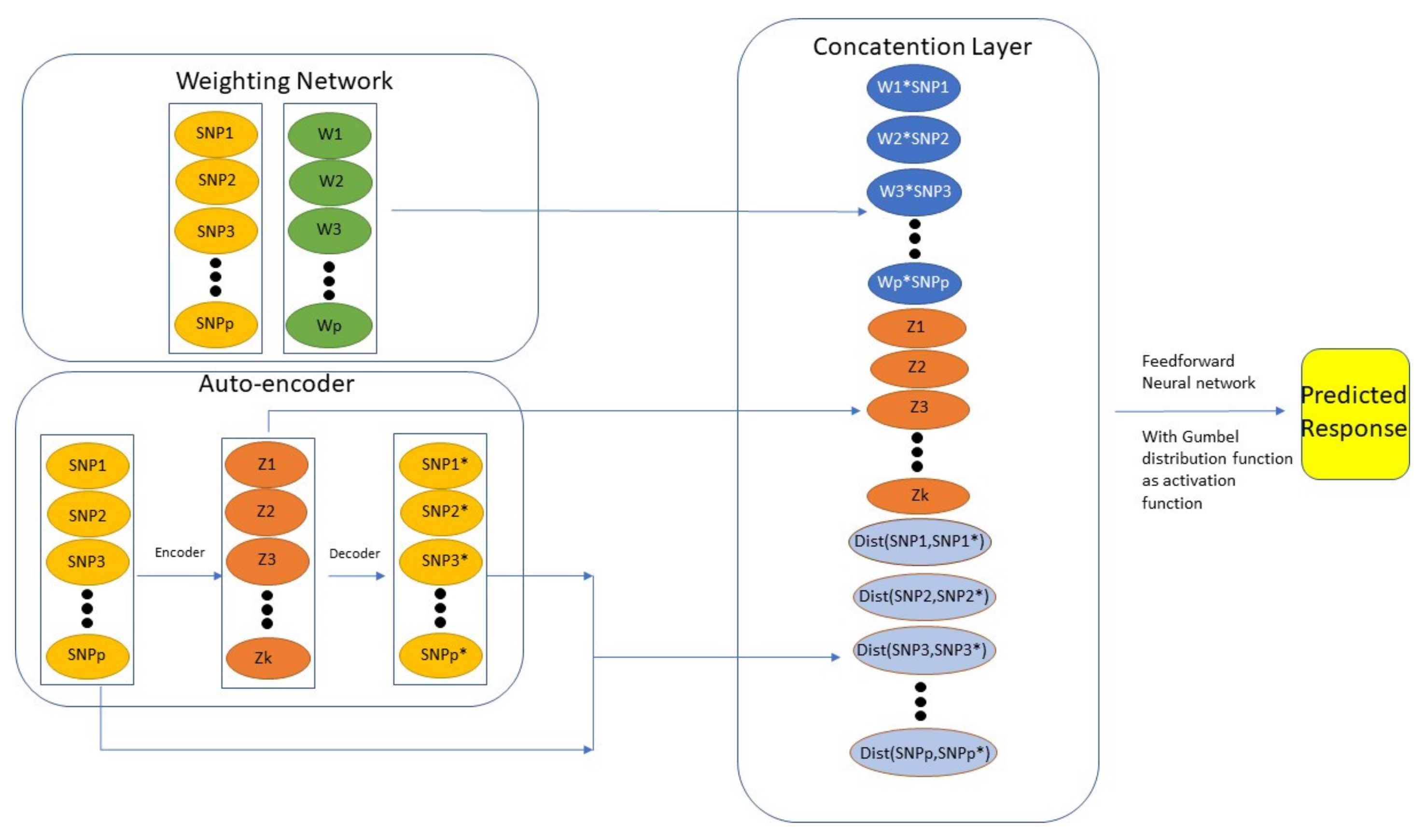
8. Neural Network
9. Significance Test
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sudlow, C.; Gallacher, J.; Allen, N.; Beral, V.; Burton, P.; Danesh, J.; Downey, P.; Elliott, P.; Green, J.; Landray, M.; et al. UK Biobank: An Open Access Resource for Identifying the Causes of a Wide Range of Complex Diseases of Middle and Old Age. PLoS Med. 2015, 12, e1001779. [Google Scholar] [CrossRef]
- Chen, H.; Wang, C.; Conomos, M.P.; Stilp, A.M.; Li, Z.; Sofer, T.; Szpiro, A.A.; Chen, W.; Brehm, J.M.; Celedón, J.C.; et al. Control for Population Structure and Relatedness for Binary Traits in Genetic Association Studies via Logistic Mixed Models. Am. J. Hum. Genet. 2016, 98, 653–666. [Google Scholar] [CrossRef]
- Dey, R.; Schmidt, E.M.; Abecasis, G.R.; Lee, S. A Fast and Accurate Algorithm to Test for Binary Phenotypes and Its Application to PheWAS. Am. J. Hum. Genet. 2017, 101, 37–49. [Google Scholar] [CrossRef]
- Fritsche, L.G.; Gruber, S.B.; Wu, Z.; Schmidt, E.M.; Zawistowski, M.; Moser, S.E.; Blanc, V.M.; Brummett, C.M.; Kheterpal, S.; Abecasis, G.R.; et al. Association of Polygenic Risk Scores for Multiple Cancers in a Phenome-wide Study: Results from The Michigan Genomics Initiative. Am. J. Hum. Genet. 2018, 102, 1048–1061. [Google Scholar] [CrossRef] [PubMed]
- MacArthur, J.; Bowler, E.; Cerezo, M.; Gil, L.; Hall, P.; Hastings, E.; Junkins, H.; McMahon, A.; Milano, A.; Morales, J.; et al. The new NHGRI-EBI Catalog of published genome-wide association studies (GWAS Catalog). Nucleic Acids Res. 2017, 45, D896–D901. [Google Scholar] [CrossRef]
- Visscher, P.M.; Wray, N.R.; Zhang, Q.; Sklar, P.; McCarthy, M.I.; Brown, M.A.; Yang, J. 10 Years of GWAS Discovery: Biology, Function, and Translation. Am. J. Hum. Genet. 2017, 101, 5–22. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Nielsen, J.B.; Fritsche, L.G.; Dey, R.; Gabrielsen, M.E.; Wolford, B.N.; LeFaive, J.; VandeHaar, P.; Gagliano, S.A.; Gifford, A.; et al. Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic associa-tion studies. Nat. Genet. 2018, 50, 1335–1341. [Google Scholar] [CrossRef]
- Wellcome Trust Case Control Consortium. Genome-wide association study of 14,000 cases of seven common diseases and 3000 shared con-trols. Nature 2007, 447, 661. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.D.; The Type I Diabetes Genetics Consortium; Walker, N.M.; Smyth, D.J.; Downes, K.; Healy, B.C.; Todd, J.A. Follow-up of 1715 SNPs from the Wellcome Trust Case Control Consortium genome-wide association study in type I diabetes families. Genes Immun. 2009, 10, S85–S94. [Google Scholar] [CrossRef]
- Maller, J.B.; The Wellcome Trust Case Control Consortium; McVean, G.; Byrnes, J.; Vukcevic, D.; Palin, K.; Su, Z.; Howson, J.M.M.; Auton, A.; Myers, S.; et al. Bayesian refinement of association signals for 14 loci in 3 common diseases. Nat. Genet. 2012, 44, 1294–1301. [Google Scholar] [CrossRef] [PubMed]
- Reilly, M.P.; Li, M.; He, J.; Ferguson, J.F.; Stylianou, I.M.; Mehta, N.N.; Burnett, M.S.; Devaney, J.M.; Knouff, C.W.; Thompson, J.R.; et al. Identification of ADAMTS7 as a novel locus for coronary atherosclerosis and association of ABO with my-ocardial infarction in the presence of coronary atherosclerosis: Two genome-wide association studies. Lancet 2011, 377, 383–392. [Google Scholar] [CrossRef]
- Holmans, P.; Green, E.K.; Pahwa, J.S.; Ferreira, M.A.; Purcell, S.M.; Sklar, P.; Owen, M.J.; O’Donovan, M.C.; Craddock, N. Gene Ontology Analysis of GWA Study Data Sets Provides Insights into the Biology of Bipolar Disorder. Am. J. Hum. Genet. 2009, 85, 13–24. [Google Scholar] [CrossRef]
- Thomson, W.; Barton, A.; Ke, X.; Eyre, S.; Hinks, A.; Bowes, J.; Donn, R.; Symmons, D.; Hider, S.; Bruce, I.N.; et al. Rheu-matoid arthritis association at 6q23. Nat. Genet. 2007, 39, 1431. [Google Scholar] [CrossRef]
- Eyre, S.; Bowes, J.; Diogo, D.; Lee, A.; Barton, A.; Martin, P.; Zhernakova, A.; Stahl, E.; Viatte, S.; McAllister, K.; et al. High-density genetic mapping identifies new susceptibility loci for rheumatoid arthritis. Nat. Genet. 2012, 44, 1336–1340. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Fu, G.; Reese, R. Detecting PCOS susceptibility loci from genome-wide association studies via iterative trend corre-lation based feature screening. BMC Bioinform. 2020, 21, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Bycroft, C.; Freeman, C.; Petkova, D.; Band, G.; Elliott, L.T.; Sharp, K.; Motyer, A.; Vukcevic, D.; Delaneau, O.; O’Connell, J.; et al. Genome-wide genetic data on ~500,000 UK Biobank participants. BioRxiv 2017, 166298. [Google Scholar] [CrossRef]
- Wang, H.; Smith, K.P.; Combs, E.; Blake, T.; Horsley, R.D.; Muehlbauer, G.J. Effect of population size and unbalanced data sets on QTL detection using genome-wide association mapping in barley breeding germplasm. Theor. Appl. Genet. 2011, 124, 111–124. [Google Scholar] [CrossRef]
- Cortes, A.; Hadler, J.; Pointon, J.P.; Robinson, P.C.; Karaderi, T.; Leo, P.; Cremin, K.; Pryce, K.; Harris, J.; Lee, S.; et al. Identification of multiple risk variants for ankylosing spondylitis through high-density genotyping of immune-related lo-ci. Nat. Genet. 2013, 45, 730. [Google Scholar]
- Dawson, J.C.; Endelman, J.B.; Heslot, N.; Crossa, J.; Poland, J.; Dreisigacker, S.; Manès, Y.; Sorrells, M.E.; Jannink, J.-L. The use of unbalanced historical data for genomic selection in an international wheat breeding program. Field Crop. Res. 2013, 154, 12–22. [Google Scholar] [CrossRef]
- Fakiola, M.; Strange, A.; Cordell, H.J.; Miller, E.N.; Pirinen, M.; Su, Z.; Mishra, A.; Mehrotra, S.; Monteiro, G.R.; Band, G.; et al. Common variants in the HLA-DRB1–HLA-DQA1 HLA class II region are associated with susceptibility to visceral leishmaniasis. Nat. Genet. 2013, 45, 208–213. [Google Scholar] [CrossRef] [PubMed]
- Fingerlin, T.E.; Murphy, E.; Zhang, W.; Peljto, A.L.; Brown, K.K.; Steele, M.P.; Loyd, J.E.; Cosgrove, G.P.; Lynch, D.; Groshong, S.; et al. Genome-wide association study identifies multiple susceptibility loci for pulmonary fibrosis. Nat. Genet. 2013, 45, 613–620. [Google Scholar] [CrossRef]
- Liu, J.Z.; The UK-PSCSC Consortium; Hov, J.R.; Folseraas, T.; Ellinghaus, E.; Rushbrook, S.M.; Doncheva, N.T.; Andreassen, O.A.; Weersma, R.K.; Weismüller, T.J.; et al. Dense genotyping of immune-related disease regions identifies nine new risk loci for primary sclerosing cholangitis. Nat. Genet. 2013, 45, 670–675. [Google Scholar] [CrossRef]
- Ma, C.; Blackwell, T.; Boehnke, M.; Scott, L.J. the GoT2D Investigators Recommended Joint and Meta-Analysis Strategies for Case-Control Association Testing of Single Low-Count Variants. Genet. Epidemiol. 2013, 37, 539–550. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Zeng, L.; Schunkert, H.; Söding, J. Bayesian multiple logistic regression for case-control GWAS. PLoS Genet. 2018, 14, e1007856. [Google Scholar] [CrossRef]
- Li, Y.; Levran, O.; Kim, J.; Zhang, T.; Chen, X.; Suo, C. Extreme sampling design in genetic association mapping of quantita-tive trait loci using balanced and unbalanced case-control samples. Sci. Rep. 2019, 9, 1–9. [Google Scholar]
- Zhang, X.; Basile, A.O.; Pendergrass, S.A.; Ritchie, M.D. Real world scenarios in rare variant association analysis: The impact of imbalance and sample size on the power in silico. BMC Bioinform. 2019, 20, 46. [Google Scholar] [CrossRef] [PubMed]
- Barr, R.G.; Avilés-Santa, L.; Davis, S.M.; Aldrich, T.K.; Ii, F.G.; Henderson, A.G.; Kaplan, R.C.; LaVange, L.; Liu, K.; Loredo, J.S.; et al. Pulmonary Disease and Age at Immigration among Hispanics. Results from the Hispanic Community Health Study/Study of Latinos. Am. J. Respir. Crit. Care Med. 2016, 193, 386–395. [Google Scholar] [CrossRef]
- Schubach, M.; Re, M.; Robinson, P.N.; Valentini, G. Imbalance-Aware Machine Learning for Predicting Rare and Common Disease-Associated Non-Coding Variants. Sci. Rep. 2017, 7, 2959. [Google Scholar] [CrossRef]
- Sun, Y.; Wong, A.K.C.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, Number 401–403; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Sammut, C.; Webb, G.I. Encyclopedia of Machine Learning; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Xue, J.-H.; Titterington, D.M. Do unbalanced data have a negative effect on LDA? Pattern Recognit. 2008, 41, 1558–1571. [Google Scholar] [CrossRef]
- Drummond, C.; Holte, R.C. Severe Class Imbalance: Why Better Algorithms Aren’t the Answer. In Proceedings of the Computer Vision; Springer Science and Business Media LLC: Berlin, Germany, 2005; Volume 3720, pp. 539–546. [Google Scholar]
- Chawla, N.V.; Japkowicz, N.; Kotcz, A. Special issue on learning from imbalanced data sets. ACM SIGKDD Explor. Newsl. 2004, 6, 1–6. [Google Scholar] [CrossRef]
- Ling, C.X.; Huang, J.; Zhang, H. AUC: A statistically consistent and more discriminating measure than accuracy. Ijcai 2003, 3, 519–524. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef]
- Zhou, L. Performance of corporate bankruptcy prediction models on imbalanced dataset: The effect of sampling methods. Knowl.-Based Syst. 2013, 41, 16–25. [Google Scholar] [CrossRef]
- Kang, H.M.; Zaitlen, N.A.; Wade, C.M.; Kirby, A.; Heckerman, D.; Daly, M.J.; Eskin, E. Efficient control of population struc-ture in model organism association mapping. Genetics 2008, 178, 1709–1723. [Google Scholar] [CrossRef]
- Kang, H.M.; Sul, J.H.; Service, S.K.; Zaitlen, N.A.; Kong, S.-Y.; Freimer, N.B.; Sabatti, C.; Eskin, E. Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 2010, 42, 348–354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ersoz, E.; Lai, C.-Q.; Todhunter, R.J.; Tiwari, H.K.; Gore, M.; Bradbury, P.J.; Yu, J.; Arnett, D.K.; Ordovas, J.M.; et al. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 2010, 42, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Lippert, C.; Listgarten, J.; Liu, Y.; Kadie, C.M.; Davidson, R.I.; Heckerman, D. FaST linear mixed models for genome-wide association studies. Nat. Methods 2011, 8, 833–835. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lee, S.H.; Goddard, M.E.; Visscher, P.M. GCTA: A Tool for Genome-wide Complex Trait Analysis. Am. J. Hum. Genet. 2011, 88, 76–82. [Google Scholar] [CrossRef]
- Svishcheva, G.R.; Axenovich, T.I.; Belonogova, N.M.; Van Duijn, C.M.; Aulchenko, Y.S. Rapid variance components–based method for whole-genome association analysis. Nat. Genet. 2012, 44, 1166–1170. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef]
- Loh, P.-R.; Tucker, G.J.; Bulik-Sullivan, B.K.; Vilhjálmsson, B.J.; Finucane, H.K.; Salem, R.M.; Chasman, D.I.; Ridker, P.M.; Neale, B.M.; Berger, B.; et al. Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 2015, 47, 284–290. [Google Scholar] [CrossRef]
- Breslow, N.E.; Clayton, D.G. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 1993, 88, 9–25. [Google Scholar]
- Gilmour, A.R.; Thompson, R.; Cullis, B.R. Average information REML: An efficient algorithm for variance parameter esti-mation in linear mixed models. Biometrics 1995, 1440–1450. [Google Scholar] [CrossRef]
- Imhof, J.P. Computing the distribution of quadratic forms in normal variables. Biometrika 1961, 48, 419–426. [Google Scholar] [CrossRef]
- Kuonen, D. Miscellanea. Saddlepoint approximations for distributions of quadratic forms in normal variables. Biometrika 1999, 86, 929–935. [Google Scholar] [CrossRef]
- Hestenes, M.; Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Inst. Stand. Technol. 1952, 49, 409. [Google Scholar] [CrossRef]
- Kaasschieter, E. Preconditioned conjugate gradients for solving singular systems. J. Comput. Appl. Math. 1988, 24, 265–275. [Google Scholar] [CrossRef]
- Carlsen, M.; Fu, G.; Bushman, S.; Corcoran, C. Exploiting Linkage Disequilibrium for Ultrahigh-Dimensional Genome-Wide Data with an Integrated Statistical Approach. Genetics 2016, 202, 411–426. [Google Scholar] [CrossRef] [PubMed]
- Hoggart, C.J.; Whittaker, J.C.; De Iorio, M.; Balding, D.J. Simultaneous Analysis of All SNPs in Genome-Wide and Re-Sequencing Association Studies. PLoS Genet. 2008, 4, e1000130. [Google Scholar] [CrossRef]
- Weeks, D.E.; Lathrop, G. Polygenic disease: Methods for mapping complex disease traits. Trends Genet. 1995, 11, 513–519. [Google Scholar] [CrossRef]
- Van Rheenen, W.; Peyrot, W.J.; Schork, A.J.; Lee, S.H.; Wray, N.R. Genetic correlations of polygenic disease traits: From the-ory to practice. Nat. Rev. Genet. 2019, 20, 567–581. [Google Scholar] [CrossRef]
- Wald, N.J.; Old, R. The illusion of polygenic disease risk prediction. Genet. Med. 2019, 21, 1705–1707. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Carbonetto, P.; Stephens, M. Polygenic Modeling with Bayesian Sparse Linear Mixed Models. PLoS Genet. 2013, 9, e1003264. [Google Scholar] [CrossRef] [PubMed]
- Servin, B.; Stephens, M. Imputation-based analysis of association studies: Candidate regions and quantitative traits. PLoS Genet. 2007, 3, e114. [Google Scholar] [CrossRef]
- Guan, Y.; Stephens, M. Bayesian variable selection regression for genome-wide association studies and other large-scale problems. Ann. Appl. Stat. 2011, 5, 1780–1815. [Google Scholar] [CrossRef]
- Li, J.; Das, K.; Fu, G.; Li, R.; Wu, R. The Bayesian lasso for genome-wide association studies. Bioinformatics 2010, 27, 516–523. [Google Scholar] [CrossRef] [PubMed]
- Carbonetto, P.; Stephens, M. Scalable Variational Inference for Bayesian Variable Selection in Regression, and Its Accuracy in Genetic Association Studies. Bayesian Anal. 2012, 7, 73–108. [Google Scholar] [CrossRef]
- Bottolo, L.; Chadeau-Hyam, M.; Hastie, D.I.; Zeller, T.; Liquet, B.; Newcombe, P.; Yengo, L.; Wild, P.S.; Schillert, A.; Ziegler, A.; et al. GUESS-ing Polygenic Associations with Multiple Phenotypes Using a GPU-Based Evolutionary Stochastic Search Algorithm. PLoS Genet. 2013, 9, e1003657. [Google Scholar] [CrossRef]
- Liquet, B.; Bottolo, L.; Campanella, G.; Richardson, S.; Chadeau-Hyam, M. R2GUESS: A Graphics Processing Unit-Based R Package for Bayesian Variable Selection Regression of Multivariate Responses. J. Stat. Softw. 2016, 69, 1–32. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- Ishwaran, H.; Rao, J.S. Spike and slab variable selection: Frequentist and Bayesian strategies. Ann. Stat. 2005, 33, 730–773. [Google Scholar] [CrossRef]
- Shang, Z.; Clayton, M.K. Consistency of Bayesian linear model selection with a growing number of parameters. J. Stat. Plan. Inference 2011, 141, 3463–3474. [Google Scholar] [CrossRef]
- Narisetty, N.N.; He, X. Bayesian variable selection with shrinking and diffusing priors. Ann. Stat. 2014, 42, 789–817. [Google Scholar] [CrossRef]
- Marron, J.S.; Todd, M.J.; Ahn, J. Distance-Weighted Discrimination. J. Am. Stat. Assoc. 2007, 102, 1267–1271. [Google Scholar] [CrossRef]
- Qiao, X.; Zhang, H.H.; Liu, Y.; Todd, M.J.; Marron, J.S. Weighted distance weighted discrimination and its asymptotic prop-erties. J. Am. Stat. Assoc. 2010, 105, 401–414. [Google Scholar] [CrossRef] [PubMed]
- Qiao, X.; Liu, Y. Adaptive Weighted Learning for Unbalanced Multicategory Classification. Biometrics 2008, 65, 159–168. [Google Scholar] [CrossRef]
- Kittler, J.; Hatef, M.; Duin, R.P.W.; Matas, J. On combining classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef]
- Fu, G.; Dai, X.; Symanzik, J.; Bushman, S. Quantitative gene-gene and gene-environment mapping for leaf shape variation using tree-based models. New Phytol. 2017, 213, 455–469. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class AdaBoost. Stat. Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- Sun, Y.; Kamel, M.S.; Wong, A.K.; Wang, Y. Cost-sensitive boosting for classification of imbalanced data. Pattern Recognit. 2007, 40, 3358–3378. [Google Scholar] [CrossRef]
- Frasca, M.; Bertoni, A.; Re, M.; Valentini, G. A neural network algorithm for semi-supervised node label learning from un-balanced data. Neural Netw. 2013, 43, 84–98. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Gao, W.; Song, J.; Jiang, J. An imbalanced data classification algorithm of improved autoencoder neural network. In Proceedings of the 2016 Eighth International Conference on Advanced Computational Intelligence (ICACI), Chiang Mai, Thailand, 14–16 February 2016; pp. 95–99. [Google Scholar]
- Elkan, C. The Foundations of Cost-Sensitive Learning. International Joint Conference on Artificial Intelligence; Lawrence Erlbaum Associates Ltd.: Mahwah, NJ, USA, 2001; Volume 17, pp. 973–978. [Google Scholar]
- Munkhdalai, L.; Munkhdalai, T.; Ryu, K.H. GEV-NN: A deep neural network architecture for class imbalance problem in binary classification. Knowl.-Based Syst. 2020, 194, 105534. [Google Scholar] [CrossRef]
- Kweon, S.; Kim, Y.; Jang, M.J.; Kim, Y.; Kim, K.; Choi, S.; Chun, C.; Khang, Y.H.; Oh, K. Data resource profile: The Korea na-tional health and nutrition examination survey (KNHANES). Int. J. Epidemiol. 2014, 43, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural net-works from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ojala, M.; Garriga, G.C. Permutation Tests for Studying Classifier Performance. In Proceedings of the 2009 Ninth IEEE International Conference on Data Mining, Miami, FL, USA, 6 December 2009; pp. 908–913. [Google Scholar] [CrossRef]
- Modarres, R.; Good, P. Permutation Tests: A Practical Guide to Resampling Methods for Testing Hypotheses. J. Am. Stat. Assoc. 1995, 90, 384. [Google Scholar] [CrossRef]
- Chen, X.; Liu, C.-T.; Zhang, M.; Zhang, H. A forest-based approach to identifying gene and gene gene interactions. Proc. Natl. Acad. Sci. USA 2007, 104, 19199–19203. [Google Scholar] [CrossRef]
- Qian, J.; Tanigawa, Y.; Du, W.; Aguirre, M.; Chang, C.; Tibshirani, R.; Rivas, M.A.; Hastie, T. A fast and scalable framework for large-scale and ultrahigh-dimensional sparse regression with application to the UK Biobank. PLoS Genet. 2020, 16, e1009141. [Google Scholar] [CrossRef]
- Yang, Q.; Khoury, M.J.; Sun, F.; Flanders, W.D. Case-Only Design to Measure Gene-Gene Interaction. Epidemiology 1999, 10, 167–170. [Google Scholar] [CrossRef]
- Howard, T.D.; Koppelman, G.H.; Xu, J.; Zheng, S.L.; Postma, D.S.; Meyers, D.A.; Bleecker, E.R. Gene-Gene Interaction in Asthma: IL4RA and IL13 in a Dutch Population with Asthma. Am. J. Hum. Genet. 2002, 70, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.Q.; Zhao, S.P.; Nie, S.; Li, J. Gene-gene interaction of PPARγ and ApoE affects coronary heart disease risk. Int. J. Cardiol. 2003, 92, 257–263. [Google Scholar] [CrossRef]
- Dong, C.; Chu, X.; Wang, Y.; Wang, Y.; Jin, L.; Shi, T.; Huang, W.; Li, Y. Exploration of gene–gene interaction effects using entropy-based methods. Eur. J. Hum. Genet. 2007, 16, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Cordell, H.J. Detecting gene–gene interactions that underlie human diseases. Nat. Rev. Genet. 2009, 10, 392–404. [Google Scholar] [CrossRef] [PubMed]
- Yung, L.S.; Yang, C.; Wan, X.; Yu, W. GBOOST: A GPU-based tool for detecting gene–gene interactions in genome–wide case control studies. Bioinformatics 2011, 27, 1309–1310. [Google Scholar] [CrossRef]
- Howson, J.M.; Cooper, J.D.; Smyth, D.J.; Walker, N.M.; Stevens, H.; She, J.-X.; Eisenbarth, G.S.; Rewers, M.; Todd, J.A.; Akolkar, B.; et al. Evidence of Gene-Gene Interaction and Age-at-Diagnosis Effects in Type 1 Diabetes. Diabetes 2012, 61, 3012–3017. [Google Scholar] [CrossRef] [PubMed]
- Van Steen, K. Travelling the world of gene-gene interactions. Brief. Bioinform. 2011, 13, 1–19. [Google Scholar] [CrossRef]
- Fathima, N.; Narne, P.; Ishaq, M. Association and gene–gene interaction analyses for polymorphic variants in CTLA-4 and FOXP3 genes: Role in susceptibility to autoimmune thyroid disease. Endocrine 2019, 64, 591–604. [Google Scholar] [CrossRef] [PubMed]
- Damen, J.A.A.G.; Hooft, L.; Schuit, E.; Debray, T.P.; Collins, G.S.; Tzoulaki, I.; Lassale, C.M.; Siontis, G.C.M.; Chiocchia, V.; Roberts, C.; et al. Prediction models for cardiovascular disease risk in the general population: Systematic review. BMJ 2016, 353, i2416. [Google Scholar] [CrossRef] [PubMed]
- Farzadfar, F. Cardiovascular disease risk prediction models: Challenges and perspectives. Lancet Glob. Health 2019, 7, e1288–e1289. [Google Scholar] [CrossRef]
| Simulation Settings | Standard Error | p-Value |
|---|---|---|
| Balanced data | 0.5956 (0.0275) | 0.0275 (0.0689) |
| Unbalanced data | 0.9731 (0.1410) | 0.1916 (0.2664) |
| Can the Method Be Applied to Genomic Selections? | Can the Method Be Applied to Genomic Predictions? | Can the Method Handle Unbalanced Binary Response? | |
|---|---|---|---|
| GMMAT | √ GMMAT is designed for performing the significance test of each variant. | ✘ GMMAT is a single-SNP method and is not good for prediction. | ✘ Its significance test assumes a Gaussian distribution, which is not the case for unbalanced data. |
| SAIGE | √ SAIGE is designed for performing the significance test of each variant. | ✘ SAIGE is a single-SNP method and is not good for prediction. | √ SAIGE use the entire cumulant generating function to approximate p- values. |
| B-LORE | √ B-LORE is a joint Bayesian variable selection regression method designed for high-dimensional variants. | √ B-LORE is a joint Bayesian regression and can be used for prediction. | ✘ B-LORE cannot handle extremely unbalanced binary data. |
| SVM | √ SVM has not been widely used in GWAS field yet, but it has the potential to select important variants or use permutation-based testing to obtain significance. | √ SVM is a machine method with the strength of producing accurate prediction. | √ SVM with weighted DWD can handle extremely unbalanced binary data. |
| AdaBoost | √ AdaBoost has not been widely used in GWAS field yet, but it has the potential to select important variants or use permutation-based testing to obtain significance. | √ AdaBoost is a machine method with the strength of producing accurate prediction. | √ AdaBoost can handle extremely unbalanced binary data by assigning higher misclassification costs to the minority class. |
| Neural Network | √ Neural Network has not been widely used in GWAS field yet, but it has the potential to select important variants or use permutation-based testing to obtain significance. | √ Neural Network is a machine method with the strength of producing accurate prediction. | √ The RCOSNet and GEV-NN can handle extremely unbalanced binary data. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Fu, G.; Zhao, S.; Zeng, Y. Statistical Learning Methods Applicable to Genome-Wide Association Studies on Unbalanced Case-Control Disease Data. Genes 2021, 12, 736. https://doi.org/10.3390/genes12050736
Dai X, Fu G, Zhao S, Zeng Y. Statistical Learning Methods Applicable to Genome-Wide Association Studies on Unbalanced Case-Control Disease Data. Genes. 2021; 12(5):736. https://doi.org/10.3390/genes12050736
Chicago/Turabian StyleDai, Xiaotian, Guifang Fu, Shaofei Zhao, and Yifei Zeng. 2021. "Statistical Learning Methods Applicable to Genome-Wide Association Studies on Unbalanced Case-Control Disease Data" Genes 12, no. 5: 736. https://doi.org/10.3390/genes12050736
APA StyleDai, X., Fu, G., Zhao, S., & Zeng, Y. (2021). Statistical Learning Methods Applicable to Genome-Wide Association Studies on Unbalanced Case-Control Disease Data. Genes, 12(5), 736. https://doi.org/10.3390/genes12050736





