Population Divergence along a Genetic Line of Least Resistance in the Tree Species Eucalyptus globulus
Abstract
1. Introduction
2. Materials and Methods
2.1. Study System and Measured Traits
2.2. Data Analysis
2.2.1. Estimation and Comparison of G Matrices for the Mainland and Island Population Groups
2.2.2. Evolutionary Divergence among Populations
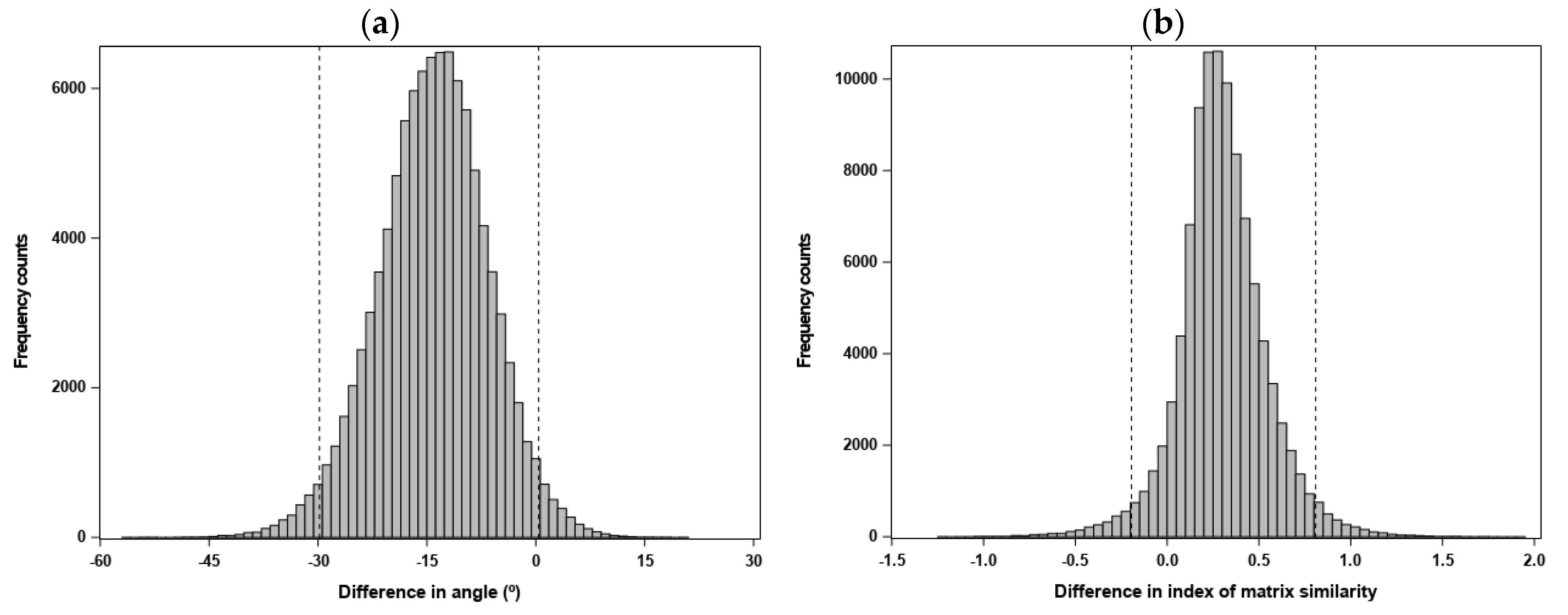
2.2.3. Estimation of Sampling Error for the Measures Used to Compare Matrices
2.2.4. Evaluating the Statistical Support for Similarity of Two Estimated (Co)Variance Matrices
- .
- measures were computed separately for each matrix and then compared between matrices (i.e., measures that capture the potential for evolution; measures of matrix size and shape), where we generated the sampling distribution for the difference between matrices in a measure, based on 100,000 REML-MVN matrix samples drawn from either estimated matrix; or
- .
- measures were directly calculated from a between-matrix comparison (i.e., , and the angle between gmax and dmax), where we computed the statistic —for a measure m, evaluates whether differences within matrices due to sampling error are similar to differences between matrices (Equation (9) in [86])—and drew 100,000 pairs of REML-MVN matrix samples from either estimated matrix to generate the sampling distribution of .
3. Results
3.1. Comparison of G Matrices for the Mainland and Island Population Groups
3.2. Evolutionary Divergence among Populations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoffmann, A.A.; Sgro, C.M. Climate change and evolutionary adaptation. Nature 2011, 470, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Lande, R. Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 1979, 33, 402–416. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.F.; Stinchcombe, J.R. How much do genetic covariances alter the rate of adaptation? Proc. R. Soc. B Biol. Sci. 2009, 276, 1183–1191. [Google Scholar] [CrossRef] [PubMed]
- Walsh, B.; Blows, M.W. Abundant genetic variation + strong selection = multivariate genetic constraints: A geometric view of adaptation. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 41–59. [Google Scholar] [CrossRef]
- Blows, M.W.; Hoffmann, A.A. A reassessment of genetic limits to evolutionary change. Ecology 2005, 86, 1371–1384. [Google Scholar] [CrossRef]
- Hansen, T.F.; Houle, D. Measuring and comparing evolvability and constraint in multivariate characters. J. Evol. Biol. 2008, 21, 1201–1219. [Google Scholar] [CrossRef]
- Schluter, D. Adaptive radiation along genetic lines of least resistance. Evolution 1996, 50, 1766–1774. [Google Scholar] [CrossRef]
- Blows, M.W.; Higgie, M. Genetic constraints on the evolution of mate recognition under natural selection. Am. Nat. 2003, 161, 240–253. [Google Scholar] [CrossRef][Green Version]
- Hansen, T.F.; Voje, K.L. Deviation from the line of least resistance does not exclude genetic constraints: A comment on Berner et al. (2010). Evolution 2011, 65, 1821–1822. [Google Scholar] [CrossRef][Green Version]
- Jones, A.G.; Arnold, S.J.; Bürger, R. Stability of the G-matrix in a population experiencing pleiotropic mutation, stabilizing selection, and genetic drift. Evolution 2003, 57, 1747–1760. [Google Scholar] [CrossRef]
- Haber, A. Phenotypic covariation and morphological diversification in the ruminant skull. Am. Nat. 2016, 187, 576–591. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, M.J.; Haber, A.; Thurman, C.L. Constraints on geographic variation in fiddler crabs (Ocypodidae: Uca) from the western Atlantic. J. Evol. Biol. 2016, 29, 1553–1568. [Google Scholar] [CrossRef] [PubMed]
- Chenoweth, S.F.; Rundle, H.D.; Blows, M.W. The contribution of selection and genetic constraints to phenotypic divergence. Am. Nat. 2010, 175, 186–196. [Google Scholar] [CrossRef] [PubMed]
- Bégin, M.; Roff, D.A. From micro- to macroevolution through quantitative genetic variation: Positive evidence from field crickets. Evolution 2004, 58, 2287–2304. [Google Scholar] [CrossRef] [PubMed]
- Colautti, R.I.; Barrett, S.C.H. Population divergence along lines of genetic variance and covariance in the invasive plant Lythrum salicaria in eastern North America. Evolution 2011, 65, 2514–2529. [Google Scholar] [CrossRef]
- Innocenti, P.; Chenoweth, S.F. Interspecific divergence of transcription networks along lines of genetic variance in Drosophila: Dimensionality, evolvability, and constraint. Mol. Biol. Evol. 2013, 30, 1358–1367. [Google Scholar] [CrossRef]
- Bolstad, G.H.; Hansen, T.F.; Pélabon, C.; Falahati-Anbaran, M.; Pérez-Barrales, R.; Armbruster, W.S. Genetic constraints predict evolutionary divergence in Dalechampia blossoms. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130255. [Google Scholar] [CrossRef]
- McGlothlin, J.W.; Kobiela, M.E.; Wright, H.V.; Mahler, D.L.; Kolbe, J.J.; Losos, J.B.; Brodie III, E.D. Adaptive radiation along a deeply conserved genetic line of least resistance in Anolis lizards. Evol. Lett. 2018, 2, 310–322. [Google Scholar] [CrossRef]
- Teplitsky, C.; Robinson, M.R.; Merilä, J. Evolutionary potential and constraints in wild populations. In Quantitative Genetics in the Wild; Charmantier, A., Garant, D., Kruuk, L., Eds.; Oxford University Press: Oxford, UK, 2014; pp. 190–208. [Google Scholar]
- Lande, R. The genetic covariance between characters maintained by pleiotropic mutations. Genetics 1980, 94, 203–215. [Google Scholar]
- Turelli, M. Phenotypic evolution, constant covariances, and the maintenance of additive variance. Evolution 1988, 42, 1342–1347. [Google Scholar] [CrossRef]
- Barton, N.H.; Turelli, M. Evolutionary quantitative genetics—How little do we know. Annu. Rev. Genet. 1989, 23, 337–370. [Google Scholar] [CrossRef] [PubMed]
- Arnold, S.J.; Pfrender, M.E.; Jones, A.G. The adaptive landscape as a conceptual bridge between micro- and macroevolution. Genetica 2001, 112, 9–32. [Google Scholar] [CrossRef] [PubMed]
- Steppan, S.J.; Phillips, P.C.; Houle, D. Comparative quantitative genetics: Evolution of the G matrix. Trends Ecol. Evol. 2002, 17, 320–327. [Google Scholar] [CrossRef]
- Arnold, S.J.; Bürger, R.; Hohenlohe, P.A.; Ajie, B.C.; Jones, A.G. Understanding the evolution and stability of the G-matrix. Evolution 2008, 62, 2451–2461. [Google Scholar] [CrossRef]
- Jones, A.G.; Arnold, S.J.; Burger, R. Evolution and stability of the G-matrix on a landscape with a moving optimum. Evolution 2004, 58, 1639–1654. [Google Scholar] [CrossRef]
- Jones, A.G.; Arnold, S.J.; Bürger, R. The mutation matrix and the evolution of evolvability. Evolution 2007, 61, 727–745. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.G.; Bürger, R.; Arnold, S.J. Epistasis and natural selection shape the mutational architecture of complex traits. Nat. Commun. 2014, 5, 3709. [Google Scholar] [CrossRef]
- Revell, L.J. The G matrix under fluctuating correlational mutation and selection. Evolution 2007, 61, 1857–1872. [Google Scholar] [CrossRef]
- Guillaume, F.; Whitlock, M.C. Effects of migration on the genetic covariance matrix. Evolution 2007, 61, 2398–2409. [Google Scholar] [CrossRef]
- Arnold, S.J.; Phillips, P.C. Hierarchical comparison of genetic variance-covariance matrices. II Coastal-inland divergence in the garter snake, Thamnophis elegans. Evolution 1999, 53, 1516–1527. [Google Scholar]
- Delahaie, B.; Charmantier, A.; Chantepie, S.; Garant, D.; Porlier, M.; Teplitsky, C. Conserved G-matrices of morphological and life-history traits among continental and island blue tit populations. Heredity 2017, 119, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Hangartner, S.; Lasne, C.; Sgrò, C.M.; Connallon, T.; Monro, K. Genetic covariances promote climatic adaptation in Australian Drosophila. Evolution 2020, 74, 326–337. [Google Scholar] [CrossRef] [PubMed]
- Roff, D.A.; Mousseau, T.; Møller, A.P.; de Lope, F.; Saino, N. Geographic variation in the G matrices of wild populations of the barn swallow. Heredity 2004, 93, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Eroukhmanoff, F.; Svensson, E.I. Evolution and stability of the G-matrix during the colonization of a novel environment. J. Evol. Biol. 2011, 24, 1363–1373. [Google Scholar] [CrossRef]
- Wood, C.W.; Brodie III, E.D. Environmental effects on the structure of the G-matrix. Evolution 2015, 69, 2927–2940. [Google Scholar] [CrossRef]
- Walter, G.M.; Aguirre, J.D.; Blows, M.W.; Ortiz-Barrientos, D. Evolution of genetic variance during adaptive radiation. Am. Nat. 2018, 191, E108–E128. [Google Scholar] [CrossRef]
- Teplitsky, C.; Mouawad, N.G.; Balbontin, J.; De Lope, F.; Møller, A.P. Quantitative genetics of migration syndromes: A study of two barn swallow populations. J. Evol. Biol. 2011, 24, 2025–2039. [Google Scholar] [CrossRef]
- Hohenlohe, P.A.; Arnold, S.J. MIPoD: A hypothesis-testing framework for microevolutionary inference from patterns of divergence. Am. Nat. 2008, 171, 366–385. [Google Scholar] [CrossRef]
- Hendry, A.P. Eco-Evolutionary Dynamics; Princeton University Press: Oxford, UK, 2017. [Google Scholar]
- Firmat, C.; Delzon, S.; Louvet, J.M.; Parmentier, J.; Kremer, A. Evolutionary dynamics of the leaf phenological cycle in an oak metapopulation along an elevation gradient. J. Evol. Biol. 2017, 30, 2116–2131. [Google Scholar] [CrossRef]
- Petit, R.J.; Hampe, A. Some evolutionary consequences of being a tree. Annu. Rev. Ecol. Evol. Syst. 2006, 37, 187–214. [Google Scholar] [CrossRef]
- Armbruster, W.S.; Pélabon, C.; Bolstad, G.H.; Hansen, T.F. Integrated phenotypes: Understanding trait covariation in plants and animals. Philos. Trans. R. Soc. B Biol. Sci. 2014, 369, 20130245. [Google Scholar] [CrossRef] [PubMed]
- Preston, K.A.; Cornwell, W.K.; DeNoyer, J.L. Wood density and vessel traits as distinct correlates of ecological strategy in 51 California coast range angiosperms. New Phytol. 2006, 170, 807–818. [Google Scholar] [CrossRef] [PubMed]
- Dutkowski, G.; Potts, B. Drought tolerant Eucalyptus globulus provenances have thick bark, high basic density and grow poorly on wet sites. In Joining Silvicultural and Genetic Strategies to Minimize Eucalyptus Environmental Stresses: From Research to Practice, Proceedings of IUFRO Group 2.08.03 Conference, Porto Seguro, Brazil, 16–18 November 2011; The Luiz de Queiroz College of Agriculture (ESALQ): Piracicaba, São Paulo, Brazil, 2011; pp. 143–148. [Google Scholar]
- O’Brien, M.J.; Engelbrecht, B.M.J.; Joswig, J.; Pereyra, G.; Schuldt, B.; Jansen, S.; Kattge, J.; Landhäusser, S.M.; Levick, S.R.; Preisler, Y.; et al. A synthesis of tree functional traits related to drought-induced mortality in forests across climatic zones. J. Appl. Ecol. 2017, 54, 1669–1686. [Google Scholar] [CrossRef]
- Nabais, C.; Hansen, J.K.; David-Schwartz, R.; Klisz, M.; López, R.; Rozenberg, P. The effect of climate on wood density: What provenance trials tell us? For. Ecol. Manag. 2018, 408, 148–156. [Google Scholar] [CrossRef]
- Hacke, U.G.; Sperry, J.S.; Pockman, W.T.; Davis, S.D.; McCulloh, K.A. Trends in wood density and structure are linked to prevention of xylem implosion by negative pressure. Oecologia 2001, 126, 457–461. [Google Scholar] [CrossRef] [PubMed]
- Chave, J.; Coomes, D.; Jansen, S.; Lewis, S.L.; Swenson, N.G.; Zanne, A.E. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009, 12, 351–366. [Google Scholar] [CrossRef]
- Choat, B.; Brodribb, T.J.; Brodersen, C.R.; Duursma, R.A.; López, R.; Medlyn, B.E. Triggers of tree mortality under drought. Nature 2018, 558, 531–539. [Google Scholar] [CrossRef]
- Poke, F.S.; Wright, J.K.; Raymond, C.A. Predicting extractives and lignin contents in Eucalyptus globulus using near infrared reflectance analysis. J. Wood Chem. Technol. 2004, 24, 55–67. [Google Scholar] [CrossRef]
- Wong, A.H.H.; Wilkes, J.; Heather, W.A. Influence of wood density and extractives content on the decay resistance of the heartwood of Eucalyptus delegatensis R. T. Baker. J. Inst. Wood Sci. 1983, 9, 261–263. [Google Scholar]
- Bush, D.; McCarthy, K.; Meder, R. Genetic variation of natural durability traits in Eucalyptus cladocalyx (sugar gum). Ann. For. Sci. 2011, 68, 1057. [Google Scholar] [CrossRef]
- Poke, F.S.; Potts, B.M.; Vaillancourt, R.E.; Raymond, C.A. Genetic parameters for lignin, extractives and decay in Eucalyptus globulus. Ann. For. Sci. 2006, 63, 812–821. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Handa, N.; Sharma, R.; Kaur, H.; Kohli, S.; Kumar, V.; Kaur, P. Lignins and abiotic stress: An overview. In Physiological Mechanisms and Adaptation Strategies in Plants Under Changing Environment; Ahmad, P., Wani, M., Eds.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Pereira, L.; Domingues-Junior, A.P.; Jansen, S.; Choat, B.; Mazzafera, P. Is embolism resistance in plant xylem associated with quantity and characteristics of lignin? Trees 2018, 32, 349–358. [Google Scholar] [CrossRef]
- Anterola, A.M.; Lewis, N.G. Trends in lignin modification: A comprehensive analysis of the effects of genetic manipulations/mutations on lignification and vascular integrity. Phytochemistry 2002, 61, 221–294. [Google Scholar] [CrossRef]
- Faix, O.; Mozuch, M.D.; Kirk, T.K. Degradation of gymnosperm (guaiacyl) vs. angiosperm (syringyl/guaiacyl) lignins by Phanerochaete chrysosporium. Holzforschung 1985, 39, 203–208. [Google Scholar] [CrossRef]
- Wardlaw, T.; Grove, S.; Hopkins, A.; Yee, M.; Harrison, K.; Mohammed, C. The uniqueness of habitats in old eucalypts: Contrasting wood-decay fungi and saproxylic beetles of young and old eucalypts. Tasforests 2009, 18, 17–32. [Google Scholar]
- Stackpole, D.J.; Vaillancourt, R.E.; Alves, A.; Rodrigues, J.; Potts, B.M. Genetic variation in the chemical components of Eucalyptus globulus wood. G3 GenesGenomesGenet 2011, 1, 151–159. [Google Scholar] [CrossRef]
- Dutkowski, G.W.; Potts, B.M. Geographic patterns of genetic variation in Eucalyptus globulus ssp. globulus and a revised racial classification. Aust. J. Bot. 1999, 47, 237–263. [Google Scholar] [CrossRef]
- Jones, R.C.; Steane, D.A.; Lavery, M.; Vaillancourt, R.E.; Potts, B.M. Multiple evolutionary processes drive the patterns of genetic differentiation in a forest tree species complex. Ecol. Evol. 2013, 3, 1–17. [Google Scholar] [CrossRef]
- Potts, B.M.; Vaillancourt, R.E.; Jordan, G.J.; Dutkowski, G.W.; Costa e Silva, J.; McKinnon, G.E.; Steane, D.A.; Volker, P.W.; Lopez, G.A.; Apiolaza, L.A.; et al. Exploration of the Eucalyptus globulus gene pool. In Eucalyptus in a Changing World, Proceedings of the IUFRO Conference; Aveiro, Portugal, 11–15 October 2004, RAIZ, Instituto de Investigação da Floresta e Papel: Aveiro, Portugal, 2004; pp. 46–61. [Google Scholar]
- Costa e Silva, J.; Potts, B.M.; Dutkowski, G. Genotype by environment interaction for growth of Eucalyptus globulus in Australia. Tree Genet. Genomes 2006, 2, 61–75. [Google Scholar] [CrossRef]
- McKinnon, G.E.; Jordan, G.J.; Vaillancourt, R.E.; Steane, D.A.; Potts, B.M. Glacial refugia and reticulate evolution: The case of the Tasmanian eucalypts. Philos. Trans. R. Soc. Lond.-Ser. B Biol. Sci. 2004, 359, 275–284. [Google Scholar] [CrossRef]
- Steane, D.A.; Conod, N.; Jones, R.C.; Vaillancourt, R.E.; Potts, B.M. A comparative analysis of population structure of a forest tree, Eucalyptus globulus (Myrtaceae), using microsatellite markers and quantitative traits. Tree Genet. Genomes 2006, 2, 30–38. [Google Scholar] [CrossRef]
- Yeoh, S.H.; Bell, J.C.; Foley, W.J.; Wallis, I.R.; Moran, G.F. Estimating population boundaries using regional and local-scale spatial genetic structure: An example in Eucalyptus globulus. Tree Genet. Genomes 2012, 8, 695–708. [Google Scholar] [CrossRef]
- Stackpole, D.J.; Vaillancourt, R.E.; Aguigar, M.; Potts, B.M. Age trends in genetic parameters for growth and wood density in Eucalyptus globulus. Tree Genet. Genomes 2010, 6, 179–193. [Google Scholar] [CrossRef]
- Gilmour, A.R.; Gogel, B.J.; Cullis, B.R.; Welham, S.J.; Thompson, R. ASReml User Guide Release 4.1; VSN International Ltd.: Hemel Hempstead, UK, 2015. [Google Scholar]
- SAS. SAS/STAT® 14.1. User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2015. [Google Scholar]
- R-Core-Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Podolsky, R.H.; Shaw, R.G.; Shaw, F.H. Population structure of morphological traits in Clarkia dudleyana. II. constancy of within-population genetic variance. Evolution 1997, 51, 1785–1796. [Google Scholar]
- Houle, D.; Pélabon, C.; Wagner, G.P.; Hansen, T.F. Measurement and meaning in biology. Q. Rev. Biol. 2011, 86, 3–34. [Google Scholar] [CrossRef]
- Mimura, M.; Barbour, R.C.; Potts, B.M.; Vaillancourt, R.E.; Watanabe, K.N. Comparison of contemporary mating patterns in continuous and fragmented Eucalyptus globulus native forests. Mol. Ecol. 2009, 18, 4180–4192. [Google Scholar] [CrossRef]
- Lynch, M.; Walsh, B. Genetics and Analysis of Quantitative Traits; Sinauer Associates Inc.: Sunderland, MA, USA, 1998. [Google Scholar]
- Stram, D.O.; Lee, J.W. Variance components testing in the longitudinal mixed effects model. Biometrics 1994, 50, 1171–1177. [Google Scholar] [CrossRef]
- Shaw, R.G. The comparison of quantitative genetic parameters between populations. Evolution 1991, 45, 143–151. [Google Scholar] [CrossRef]
- Marroig, G.; Shirai, L.T.; Porto, A.; de Oliveira, F.B.; De Conto, V. The evolution of modularity in the mammalian skull II: Evolutionary consequences. Evol. Biol. 2009, 36, 136–148. [Google Scholar] [CrossRef]
- Cheverud, J.M. Quantitative genetic analysis of cranial morphology in the cotton-top (Saguinus oedipus) and saddle-back (S. fuscicollis) tamarins. J. Evol. Biol. 1996, 9, 5–42. [Google Scholar] [CrossRef]
- Krzanowski, W. Principles of Multivariate Analysis: A User’s Perspective; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Blows, M.W.; Chenoweth, S.F.; Hine, E. Orientation of the genetic variance-covariance matrix and the fitness surface for multiple male sexually selected traits. Am. Nat. 2004, 163, 329–340. [Google Scholar] [CrossRef] [PubMed]
- Kenward, M.G.; Roger, J.H. Small sample inference for fixed effects from restricted maximum likelihood. Biometrics 1997, 53, 983–997. [Google Scholar] [CrossRef] [PubMed]
- Revell, L.J. phytools: An R package for phylogenetic comparative biology (and other things). Methods Ecol. Evol. 2012, 3, 217–223. [Google Scholar] [CrossRef]
- Revell, L.J. Size-correction and principal components for interspecific comparative studies. Evolution 2009, 63, 3258–3268. [Google Scholar] [CrossRef]
- Houle, D.; Meyer, K. Estimating sampling error of evolutionary statistics based on genetic covariance matrices using maximum likelihood. J. Evol. Biol. 2015, 28, 1542–1549. [Google Scholar] [CrossRef]
- Robinson, M.R.; Beckerman, A.P. Quantifying multivariate plasticity: Genetic variation in resource acquisition drives plasticity in resource allocation to components of life history. Ecol. Lett. 2013, 16, 281–290. [Google Scholar] [CrossRef]
- Thornhill, A.H.; Crisp, M.D.; Külheim, C.; Lam, K.E.; Nelson, L.A.; Yeates, D.K.; Miller, J.T. A dated molecular perspective of eucalypt taxonomy, evolution and diversification. Aust. Syst. Bot. 2019, 32, 29–48. [Google Scholar] [CrossRef]
- Jones, R.C.; Nicolle, D.; Steane, D.A.; Vaillancourt, R.E.; Potts, B.M. High density, genome-wide markers and intra-specific replication yield an unprecedented phylogenetic reconstruction of a globally significant, speciose lineage of Eucalyptus. Mol. Phylogenet. Evol. 2016, 105, 63–85. [Google Scholar] [CrossRef]
- De Deckker, P.; van der Kaars, S.; Macphail, M.K.; Hope, G.S. Land-sea correlations in the Australian region: 460 ka of changes recorded in a deep-sea core offshore Tasmania. Part 1: The pollen record. Aust. J. Earth Sci. 2019, 66, 1–15. [Google Scholar] [CrossRef]
- Lambeck, K.; Chappell, J. Sea Level Change through the Last Glacial Cycle. Science 2001, 292, 679–686. [Google Scholar] [CrossRef]
- Freeman, J.S.; Jackson, H.D.; Steane, D.A.; McKinnon, G.E.; Dutkowski, G.W.; Potts, B.M.; Vaillancourt, R.E. Chloroplast DNA phylogeography of Eucalyptus globulus. Aust. J. Bot. 2001, 49, 585–596. [Google Scholar] [CrossRef]
- Petherick, L.; Bostock, H.; Cohen, T.J.; Fitzsimmons, K.; Tibby, J.; Fletcher, M.S.; Moss, P.; Reeves, J.; Mooney, S.; Barrows, T.; et al. Climatic records over the past 30 ka from temperate Australia—A synthesis from the Oz-INTIMATE workgroup. Quat. Sci. Rev. 2013, 74, 58–77. [Google Scholar] [CrossRef]
- Wood, S.W.; Hua, Q.; Allen, K.J.; Bowman, D.M.J.S. Age and growth of a fire prone Tasmanian temperate old-growth forest stand dominated by Eucalyptus regnans, the world’s tallest angiosperm. For. Ecol. Manag. 2010, 260, 438–447. [Google Scholar] [CrossRef]
- Revell, L.J.; Harmon, L.J.; Langerhans, R.B.; Kolbe, J.J. A phylogenetic approach to determining the importance of constraint on phenotypic evolution in the neotropical lizard Anolis cristatellus. Evol. Ecol. Res. 2007, 9, 261–282. [Google Scholar]
- Freeman, J.S.; Potts, B.M.; Downes, G.M.; Pilbeam, D.; Thavamanikumar, S.; Vaillancourt, R.E. Stability of QTL for growth and wood properties across multiple pedigrees and environments in Eucalyptus globulus. New Phytol. 2013, 198, 1121–1134. [Google Scholar] [CrossRef]
- Houle, D.; Bolstad, G.H.; van der Linde, K.; Hansen, T.F. Mutation predicts 40 million years of fly wing evolution. Nature 2017, 548, 447–450. [Google Scholar] [CrossRef]
- Wilkinson, G.R. Population differentiation within Eucalyptus obliqua: Implications for regeneration success and genetic conservation in production forests. Aust. For. 2008, 71, 4–15. [Google Scholar] [CrossRef]
- Hamilton, M.G.; Williams, D.R.; Tilyard, P.A.; Pinkard, E.A.; Wardlaw, T.J.; Glen, M.; Vaillancourt, R.E.; Potts, B.M. A latitudinal cline in disease resistance of a host tree. Heredity 2013, 110, 372–379. [Google Scholar] [CrossRef]
- Hingston, A.B.; Gartrell, B.D.; Pinchbeck, G. How specialized is the plant-pollinator association between Eucalyptus globulus ssp. globulus and the swift parrot Lathamus discolor? Austral Ecol. 2004, 29, 624–630. [Google Scholar]
- Costa e Silva, J.; Potts, B.M.; Lopez, G.A. Heterosis may result in selection favouring the products of long-distance pollen dispersal in Eucalyptus. PLoS ONE 2014, 9, e93811. [Google Scholar] [CrossRef]
- Phillips, P.C.; Whitlock, M.C.; Fowler, K. Inbreeding changes the shape of the genetic covariance matrix in Drosophila melanogaster. Genetics 2001, 158, 1137–1145. [Google Scholar] [PubMed]
- McGuigan, K.; Chenoweth, S.F.; Blows, M.W. Phenotypic divergence along lines of genetic variance. Am. Nat. 2005, 165, 32–43. [Google Scholar] [CrossRef] [PubMed]
- Whitlock, M.C.; Phillips, P.C.; Fowler, K. Persistence of changes in the genetic covariance matrix after a bottleneck. Evolution 2002, 56, 1968–1975. [Google Scholar] [CrossRef] [PubMed]
- Bégin, M.; Roff, D.A.; Debat, V. The effect of temperature and wing morphology on quantitative genetic variation in the cricket Gryllus firmus, with an appendix examining the statistical properties of the Jackknife–manova method of matrix comparison. J. Evol. Biol. 2004, 17, 1255–1267. [Google Scholar] [CrossRef]
- Costa e Silva, J.; Borralho, N.M.G.; Araujo, J.A.; Vaillancourt, R.E.; Potts, B.M. Genetic parameters for growth, wood density and pulp yield in Eucalyptus globulus. Tree Genet. Genomes 2009, 5, 291–305. [Google Scholar] [CrossRef]
- Nickolas, H.; Williams, D.; Downes, G.; Tilyard, P.; Harrison, P.A.; Vaillancourt, R.E.; Potts, B. Genetic correlations among pulpwood and solid-wood selection traits in Eucalyptus globulus. New For. 2020, 51, 137–158. [Google Scholar] [CrossRef]
| Symbol | Measure | Interpretation | Results |
|---|---|---|---|
| A q × 1 (q = number of traits) vector, where its elements were randomly drawn from a normal distribution with a mean of 0 and a variance of 1; each vector was then normalized to unit length. | Selection gradient, representing directional selection acting on each trait. | n/a | |
is the mean-standardized additive genetic variance-covariance matrix for either the Mainland or Island groups; ’ denotes the transpose operator. | , without regard for the presence of constraints reflected in G-matrix structure. | n/a | |
is defined as above; ’ and −1 denote the transpose and the inverse operators, respectively. | . | n/a | |
. | , assumed to be under stabilizing selection. | n/a | |
| f) | of predicted responses to selection for the traits. | Extent to which a G-matrix deflects the response vector from the direction of the selection gradient vector, and thus reflecting the ability of a population to track with the direction of selection (i.e. a more “flexible” population tracks closer to the direction of selection). | n/a |
| Mean unconditional evolvability, . | is proportional to G-matrix size. | Table 5 Figure S2a | |
| Mean conditional evolvability, . | is proportional to G-matrix size and, by accounting for trait genetic covariances, it will also reflect G-matrix shape. | Table 5 Figure S2b | |
| Mean autonomy, . | will decrease with increasing variation among the eigenvalues of G (indicating that the quantitative effects of genetic constraints may be stronger), and it will have a value of one only if all traits are genetically uncorrelated and have the same genetic variance. | Table 5 Figure S2c | |
| Mean flexibility, . | and matrix eccentricity has been reported [11,12,78]. | Table 5 Figure S2d |
| Symbol | Measure | Interpretation | Results |
|---|---|---|---|
| z | A q × 1 (q = number of traits) divergence vector, obtained for each population by (e.g., [11]): (i) calculating the difference between a vector of phenotypic (least-squares) trait means for the population and a vector of phylogenetically- weighted means estimated for each trait over populations; (ii) mean-standardizing the difference vector via the phylogenetically-weighted trait means; and (iii) normalizing the mean-standardized difference vector to a unit length. Based on the reconstructed phylogeny of the studied E. globulus populations (Methods S1; Figure S1), the vector of phylogenetically-weighted means was estimated by using the fastAnc function in the R-package Phytools developed by Revell [83], assuming a Brownian motion model of trait evolution. This vector corresponds to the inferred ancestral states for each trait at the root node of the phylogenetic tree, under the assumed model of trait evolution [84]. | Direction of divergence of a population from the inferred ancestral states. | n/a |
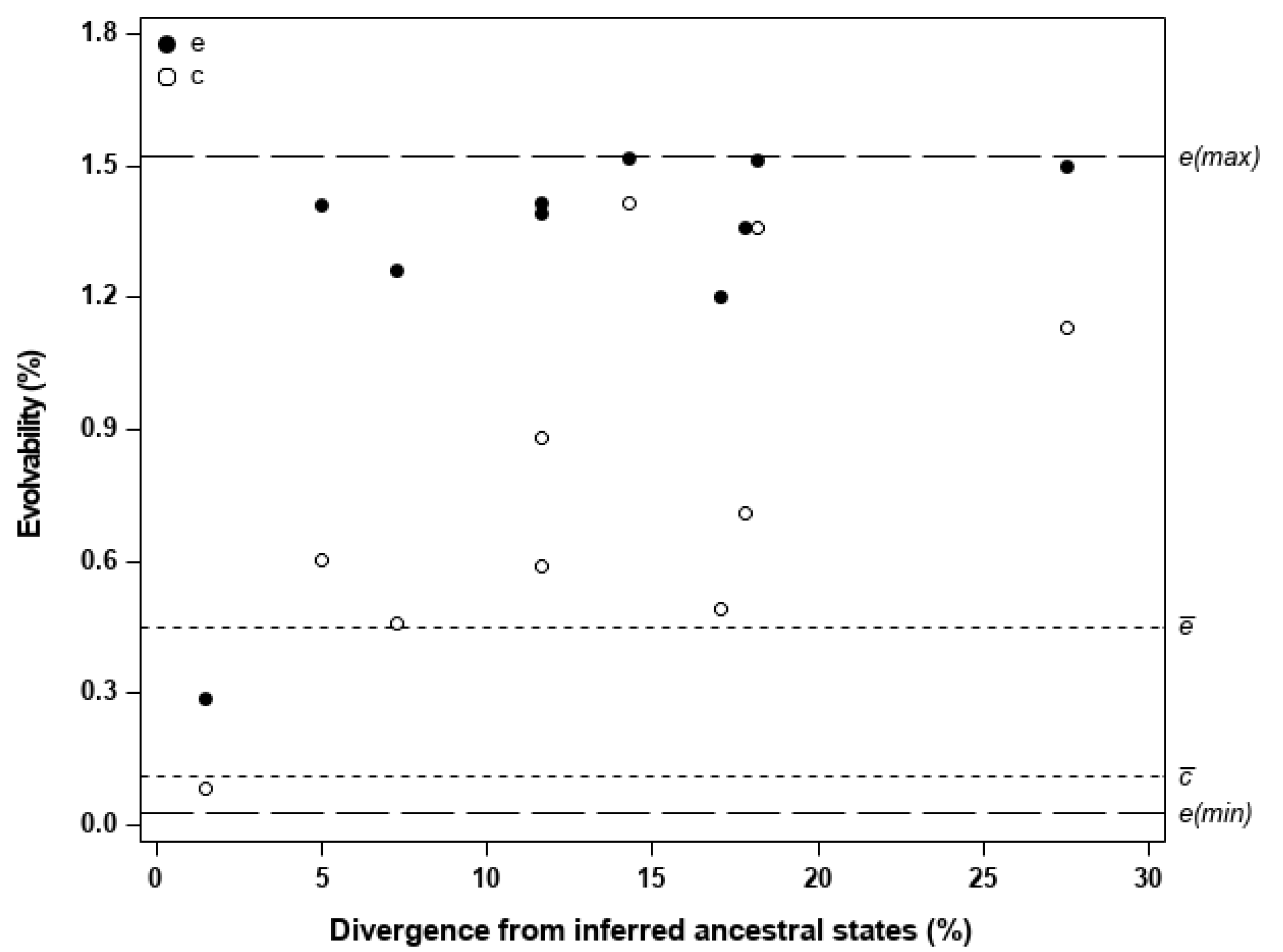
| Unconditional evolvability along z, is the mean-standardized additive genetic variance-covariance matrix common to all populations; ’ denotes the transpose operator. | measures the mean-scaled genetic variance available for a population to diverge along z, without accounting for genetic covariances with trait combinations in directions other than z. | Figure 2 Table S7 | |
| Conditional evolvability along z, is defined as above; ’ and −1 denote the transpose and the inverse operators, respectively. | measures the mean-scaled genetic variance available for a population to diverge along z, assuming that traits are constrained to evolve only in this direction. | Figure 2 Table S7 | |
| Mean unconditional evolvability, . | Expected unconditional evolvability in a random direction. | Figure 2 Table S6 | |
| Mean conditional evolvability, . | Expected conditional evolvability in a random direction. | Figure 2 Table S6 | |
| e(max) | Maximum possible evolvability, given by the eigenvalue of the first eigenvector of G. | Mean-scaled genetic variance available along the direction of the first eigenvector of G. | Figure 2 Table S8 |
| e(min) | Minimum possible evolvability, given by the eigenvalue of the last eigenvector of G. | Mean-scaled genetic variance available along the direction of the last eigenvector of G. | Figure 2 Table S8 |
| Amount of divergence | Amount of divergence in the z-direction, measured by the Euclidean norm of the mean-standardized difference vector [defined as in (ii) above]. | Extent to which a population has diverged from the inferred ancestral states in the z-direction. | Figure 2 Table S7 |
| S/G | KL | BD | EX | |
|---|---|---|---|---|
| Mainland G-matrix | ||||
| S/G | 0.160 ± 0.037 (p < 0.001) | −0.66 ± 0.14 (p < 0.001) | −0.23 ± 0.15 (p > 0.05) (a) | −0.80 ± 0.13 (p < 0.001) |
| KL | −0.062 ± 0.020 (p < 0.001) | 0.056 ± 0.017 (p < 0.001) | 0.04 ± 0.18 (p > 0.05) | 0.78 ± 0.11 (p = 0.002) |
| BD | −0.036 ± 0.026 (p > 0.05) | 0.004 ± 0.017 (p > 0.05) | 0.157 ± 0.034 (p < 0.001) | 0.17 ± 0.19 (p > 0.05) |
| EX | −0.361 ± 0.106 (p < 0.001) | 0.208 ± 0.078 (p = 0.002) | 0.074 ± 0.090 (p > 0.05) | 1.261 ± 0.460 (p < 0.001) |
| Island G-matrix | ||||
| S/G | 0.131 ± 0.029 (p < 0.001) | 0.05 ± 0.18 (p > 0.05) | −0.38 ± 0.14 (p = 0.009) | −0.40 ± 0.14 (p = 0.012) |
| KL | 0.005 ± 0.016 (p > 0.05) | 0.059 ± 0.018 (p < 0.001) | −0.38 ± 0.15 (p = 0.026) | 0.60 ± 0.12 (p = 0.001) |
| BD | −0.058 ± 0.023 (p = 0.009) | −0.039 ± 0.019 (p = 0.026) | 0.176 ± 0.035 (p < 0.001) | −0.13 ± 0.15 (p > 0.05) |
| EX | −0.201 ± 0.085 (p = 0.012) | 0.206 ± 0.073 (p = 0.001) | −0.074 ± 0.089 (p > 0.05) | 1.972 ± 0.448 (p < 0.001) |
| Null Hypothesis | LR Test Statistic | Degrees of Freedom (a) | p-Value |
|---|---|---|---|
| 1: Variances for a trait and covariances between a pair of traits do not differ amongst the two groups | 17.16 | 10 | 0.071 |
| 2: Variances for a trait do not differ amongst the two groups | 2.26 | 4 | 0.688 |
| 3: Covariances between a pair of traits do not differ amongst the two groups (b) | 12.02 | 6 | 0.062 |
| Mainland G-matrix | 0.409 (0.263, 0.667) | 0.085 (0.039, 0.119) | 0.290 (0.138, 0.375) | 0.606 (0.547, 0.676) | 17.0 (10.0, 27.6) |
| Island G-matrix | 0.581 (0.420, 0.860) | 0.118 (0.076, 0.156) | 0.286 (0.174, 0.364) | 0.602 (0.549, 0.656) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa e Silva, J.; Potts, B.M.; Harrison, P.A. Population Divergence along a Genetic Line of Least Resistance in the Tree Species Eucalyptus globulus. Genes 2020, 11, 1095. https://doi.org/10.3390/genes11091095
Costa e Silva J, Potts BM, Harrison PA. Population Divergence along a Genetic Line of Least Resistance in the Tree Species Eucalyptus globulus. Genes. 2020; 11(9):1095. https://doi.org/10.3390/genes11091095
Chicago/Turabian StyleCosta e Silva, João, Brad M. Potts, and Peter A. Harrison. 2020. "Population Divergence along a Genetic Line of Least Resistance in the Tree Species Eucalyptus globulus" Genes 11, no. 9: 1095. https://doi.org/10.3390/genes11091095
APA StyleCosta e Silva, J., Potts, B. M., & Harrison, P. A. (2020). Population Divergence along a Genetic Line of Least Resistance in the Tree Species Eucalyptus globulus. Genes, 11(9), 1095. https://doi.org/10.3390/genes11091095






