Exploring the Full Potential of Reversible Deactivation Radical Polymerization Using Pareto-Optimal Fronts
Abstract
:1. Introduction
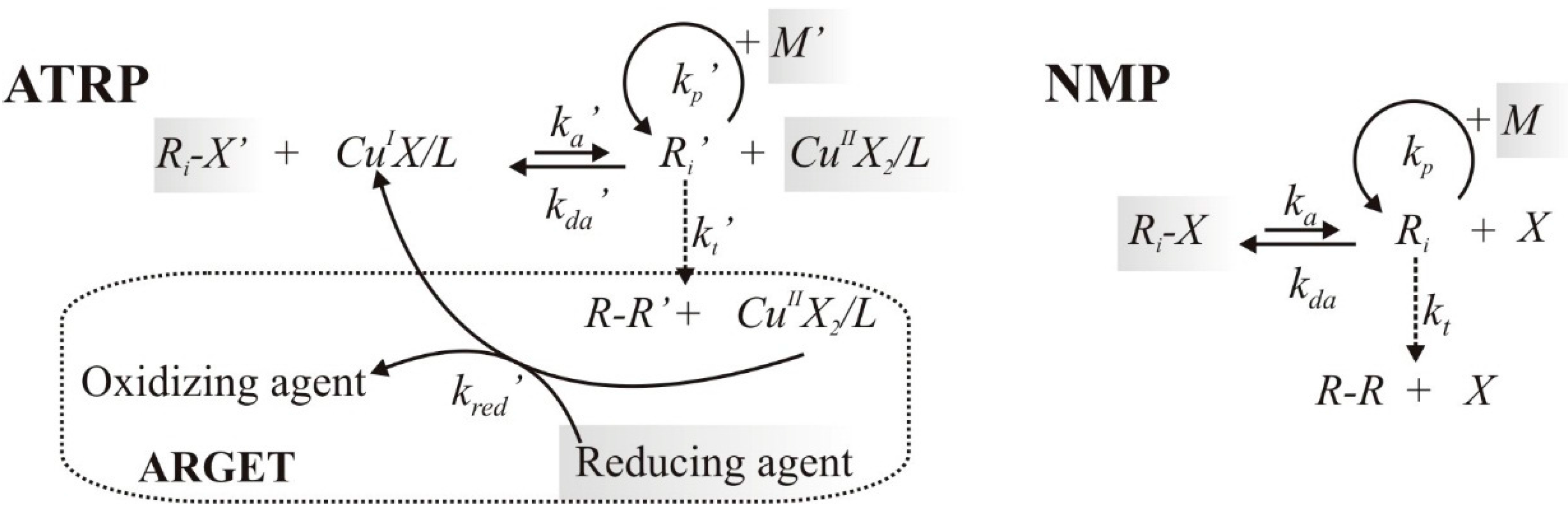
2. Modeling Procedure
2.1. Reaction Schemes and Rate Coefficients
| Reactions | Arrhenius Parameters | |
|---|---|---|
| ARGET ATRP [64] | NMP [61] | |
| ATRP (De)Activation | NMP (De)Activation | ARGET ATRP |
| Aa0' = 5.38 × 104; Ea,a0' = 27.7 | ||
| Ada0' = 3.94 × 108; Ea,da0' = 7.98 | ||
| Aa' = 3.99 × 106; Ea,a' = 27.7 | ||
| Ada' = 1.97 × 108; Ea,da' = 27.7 | ||
| Reduction | Thermal Initiation | Ar1' = 5.55 × 101; Ea,r1' = 14.9 |
| Ar2' = 1.87 × 102; Ea,r2' = 14.9 | ||
| Ap0' = 3.80 × 106; Ea,p0' = 22.9 | ||
| Ap' = 3.80 × 106; Ea,p' = 22.9 | ||
| NMP | ||
| Chain Initiation | Chain Initiation | Aa0 = 1.16 × 1013; Ea,a0 = 105 |
| Ada0 = 2.80 × 106; Ea,da0 = 0.00 | ||
| Aa = 4.04 × 1017; Ea,a = 149 | ||
| Propagation | Propagation | Ada = 1.09 × 106; Ea,da = 0.00 |
| Ad = 4.74 × 105; Ea,d = 93.5 | ||
| Ard = 1.05 × 102; Ea,rd = 44.3 | ||
| Chain Transfer | Athi = 1.51 × 106; Ea,thi = 99.6 | |
| Ap01 = 1.55× 106; Ea,p01 = 16.5 | ||
| Ap0j' = 4.24 × 107; Ea,p0j' = 32.5 | ||
| Ap = 4.24 × 107; Ea,p = 32.5 | ||
| AtrM = 2.30 × 106; Ea,trM = 53.0 | ||
| AtrD = 6.76 × 105; Ea,trD = 27.5 | ||
2.2. Genetic Optimization Algorithm: NSGA-II
3. Results and Discussion
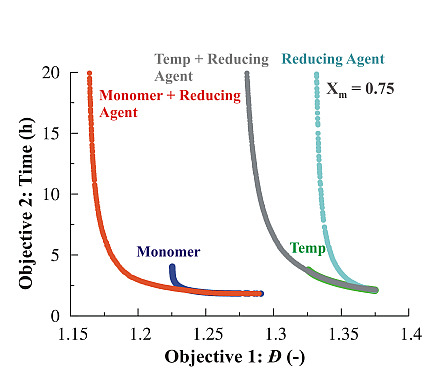
3.1. Multi-Objective Optimization of ARGET ATRP
3.1.1. Variation of Temperature
3.1.2. Variation of Monomer
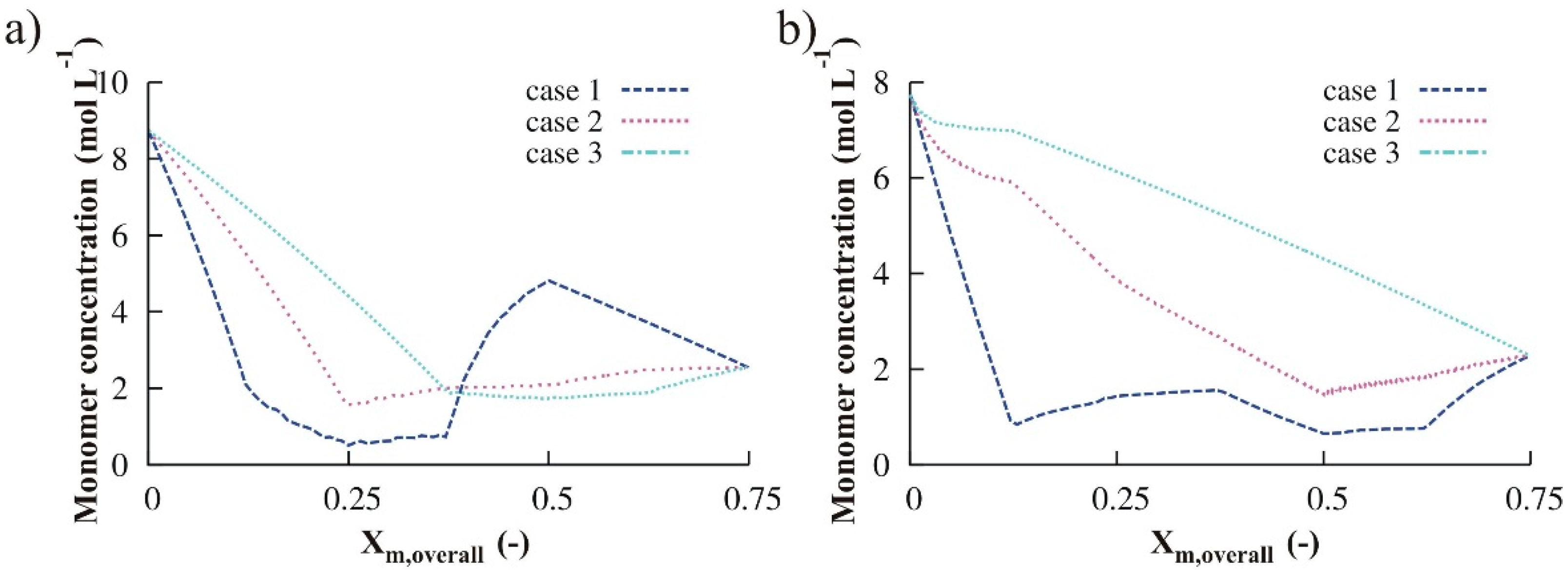
3.1.3. Variation of Reducing Agent
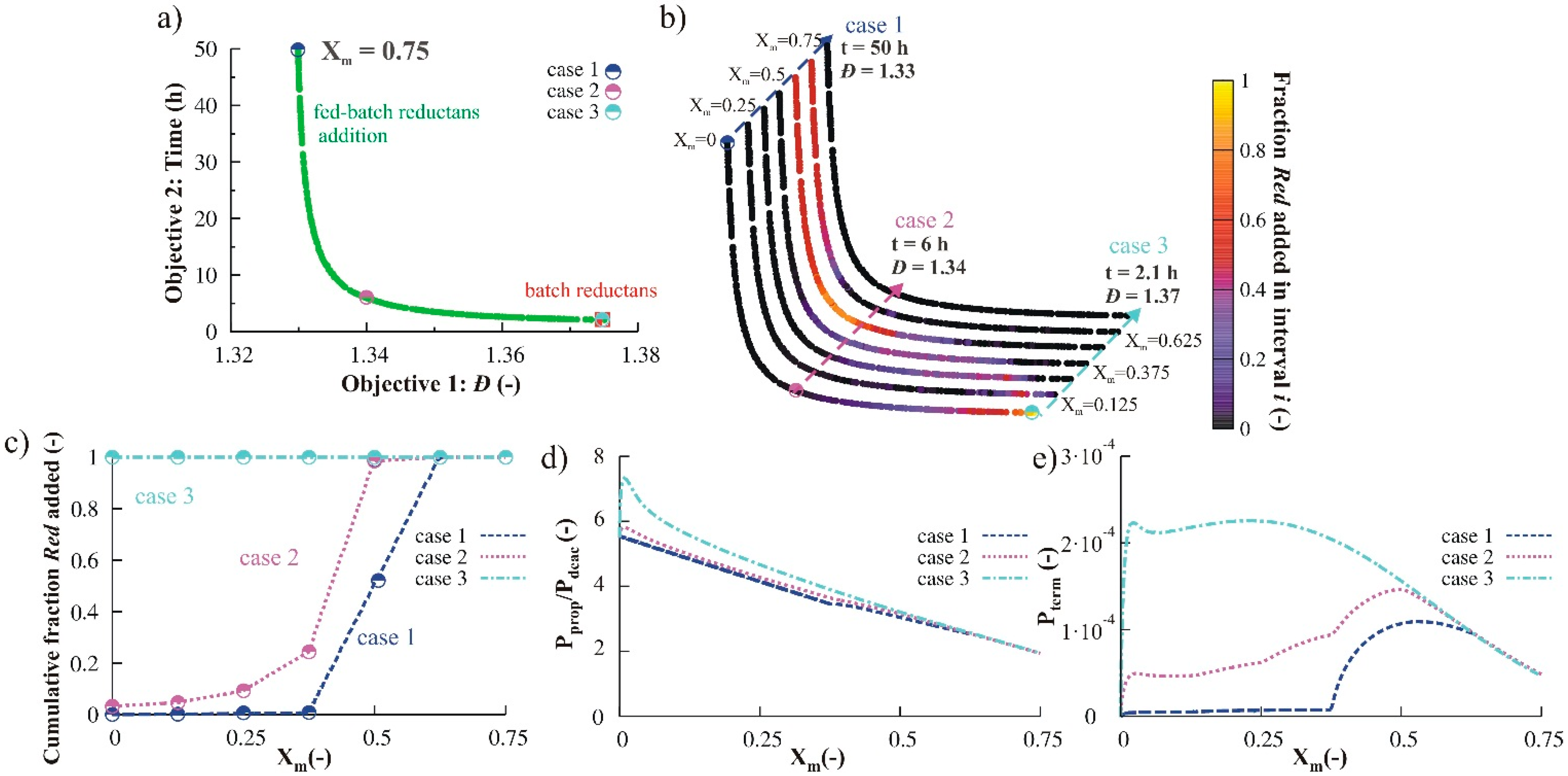
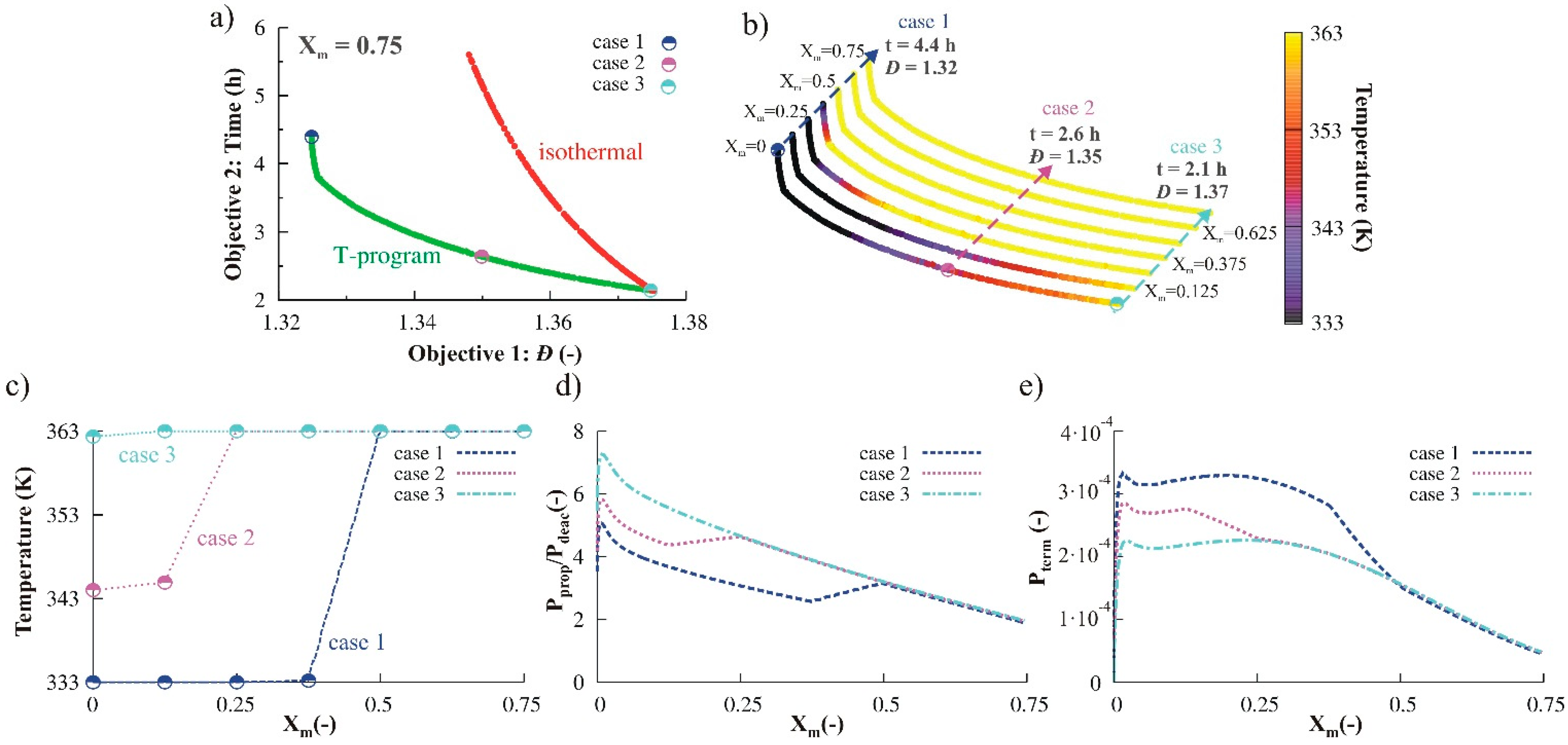
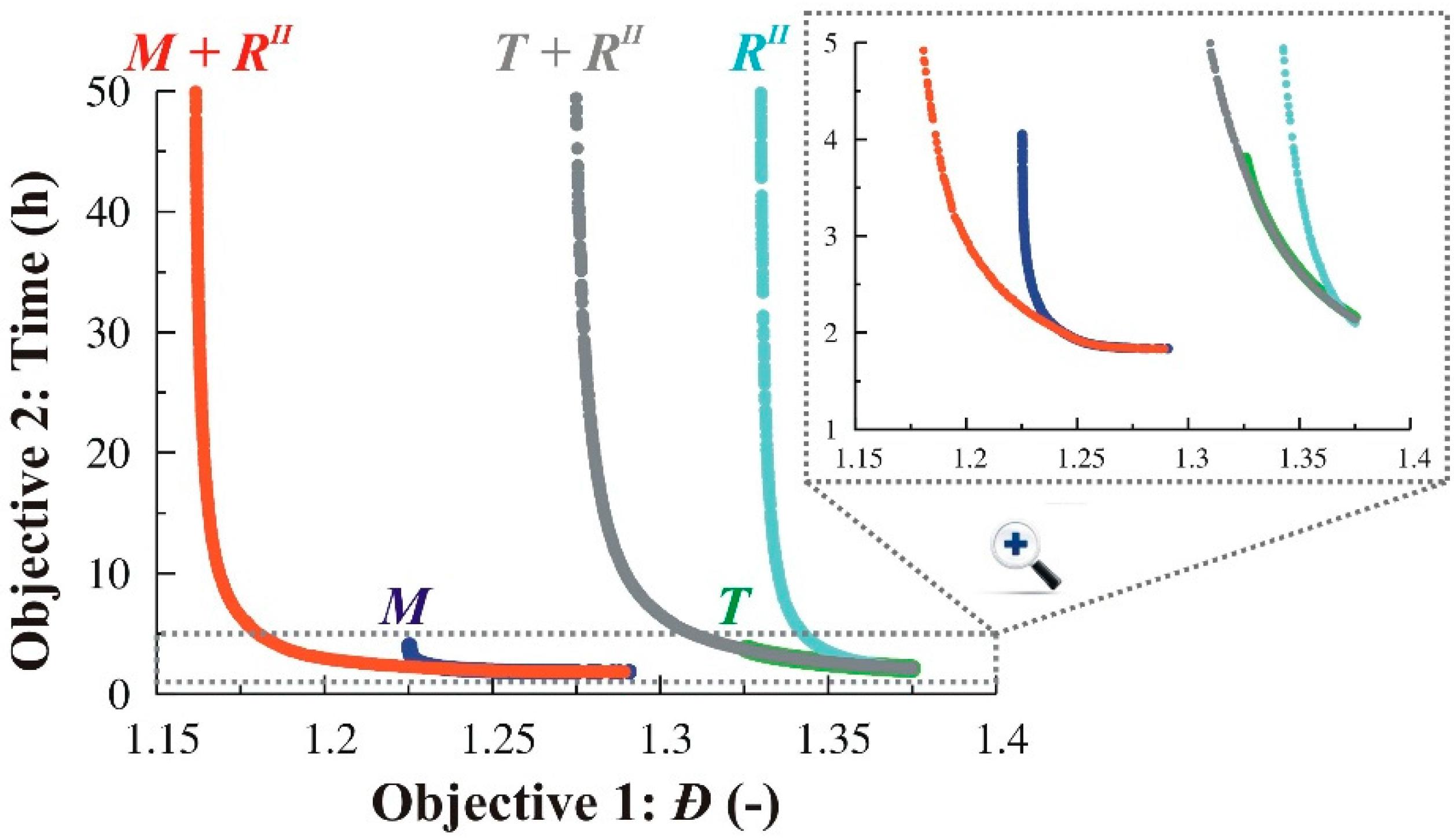
3.1.4. Simultaneous Variation of Different Process Conditions
3.2. Multi-Objective Optimization of NMP
3.2.1. Variation of Temperature
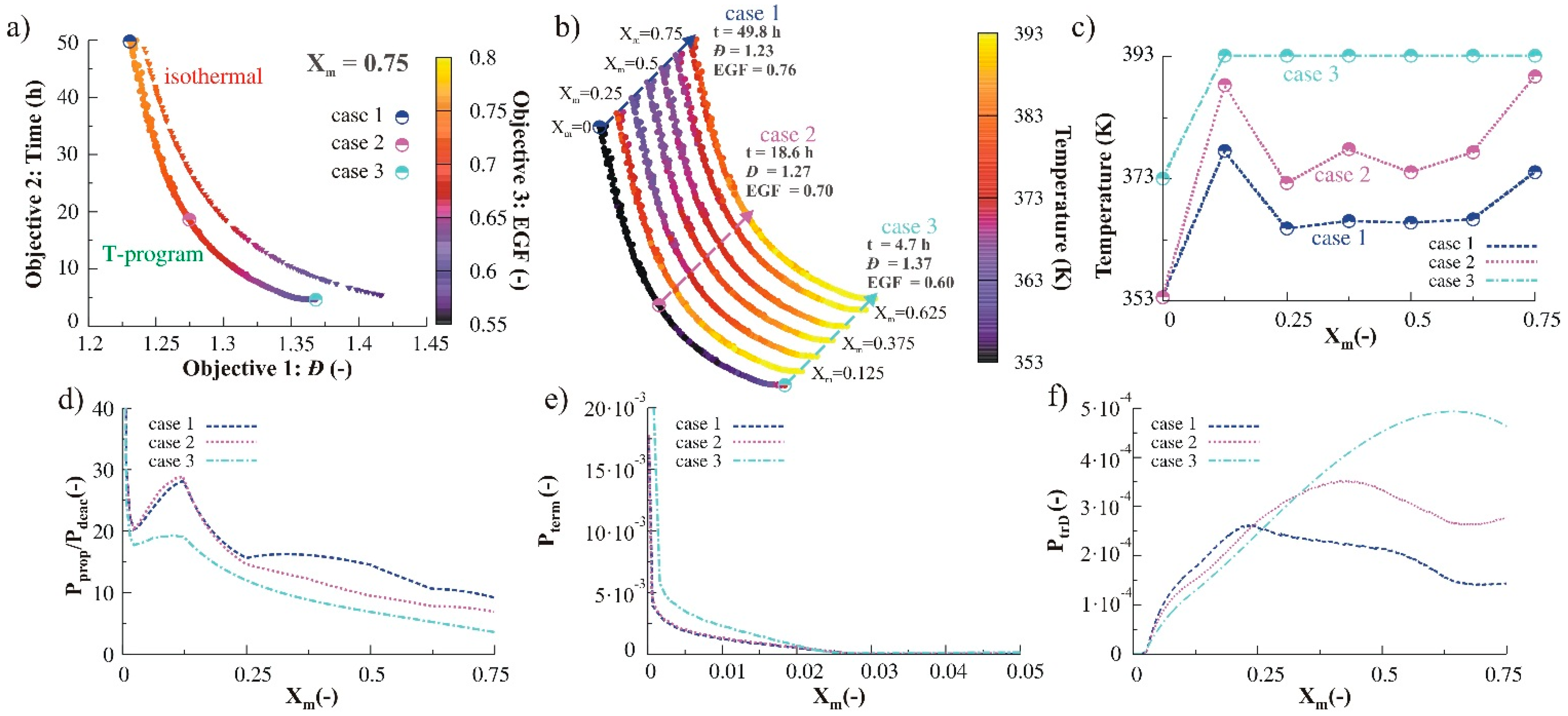
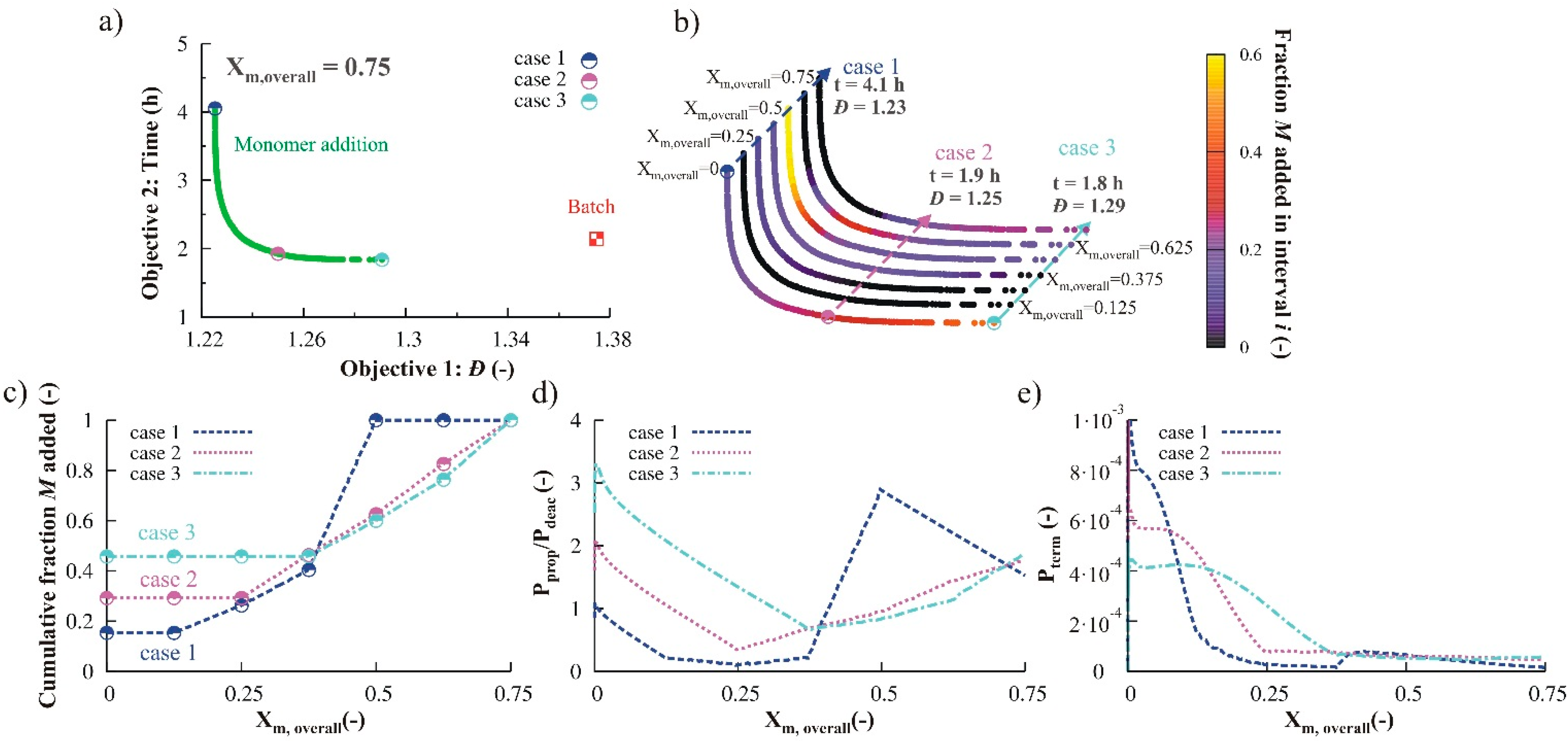
3.2.2. Monomer Addition
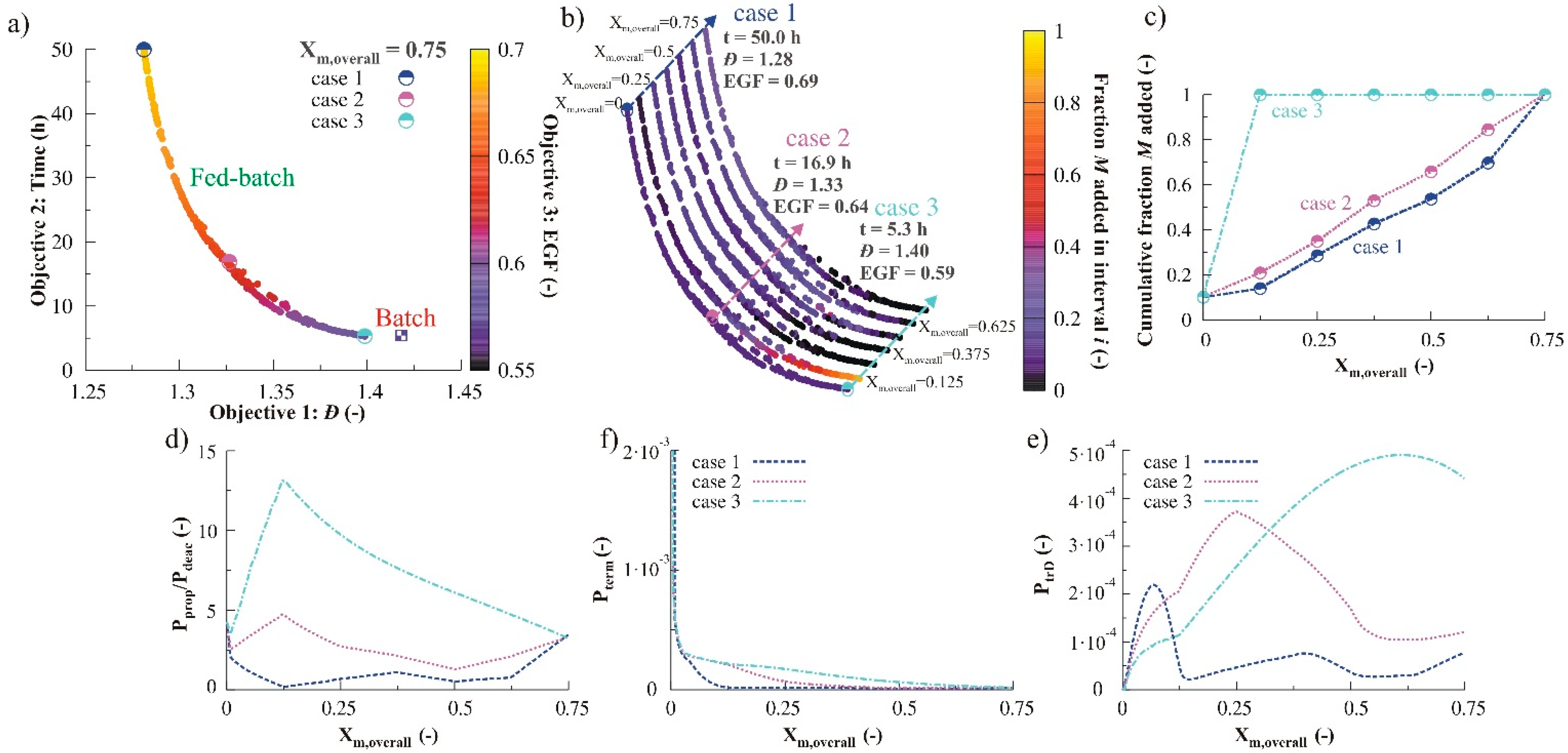
3.2.3. Variation of Initial Nitroxide Loading
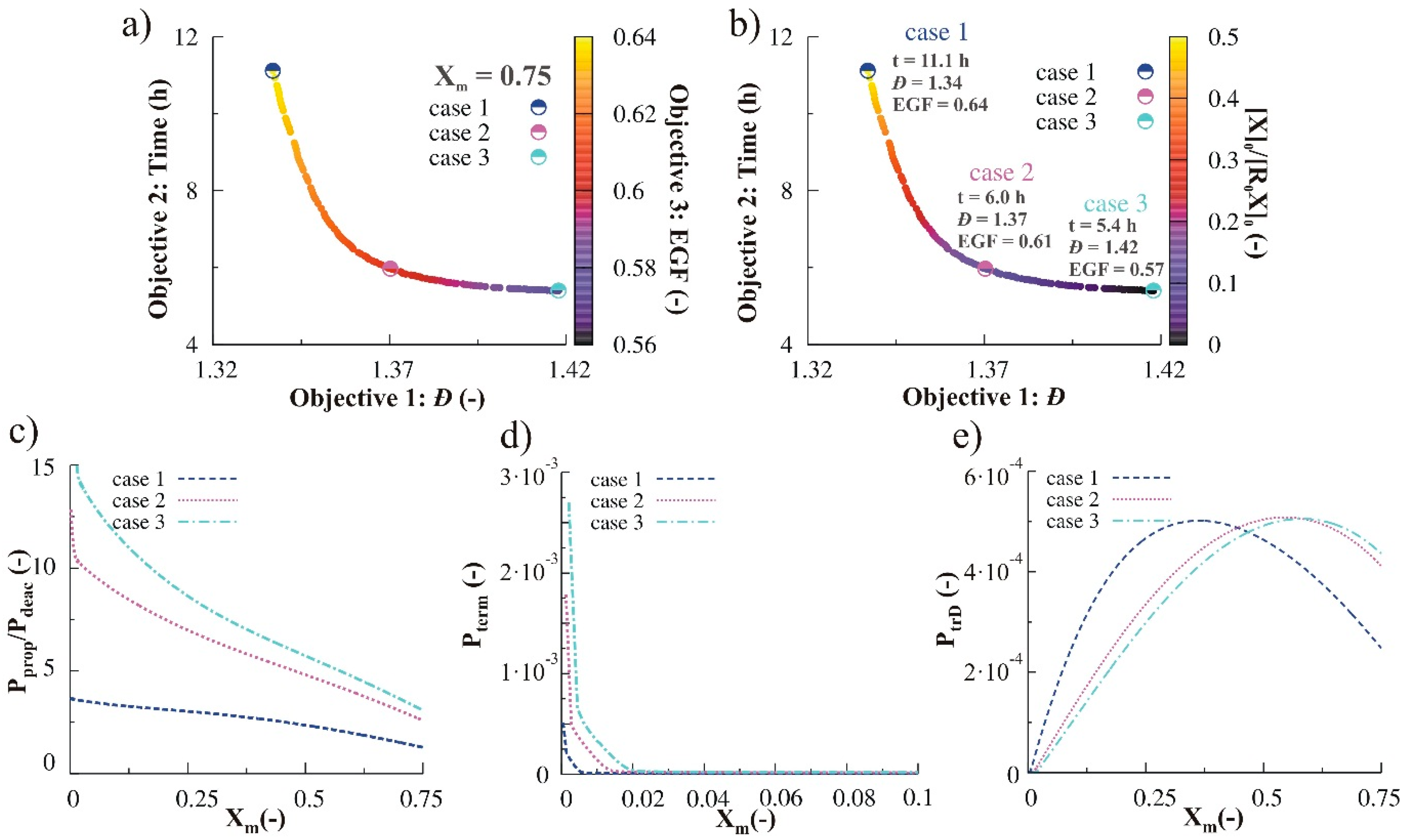
3.2.4. Simultaneous Variation of Different Process Conditions
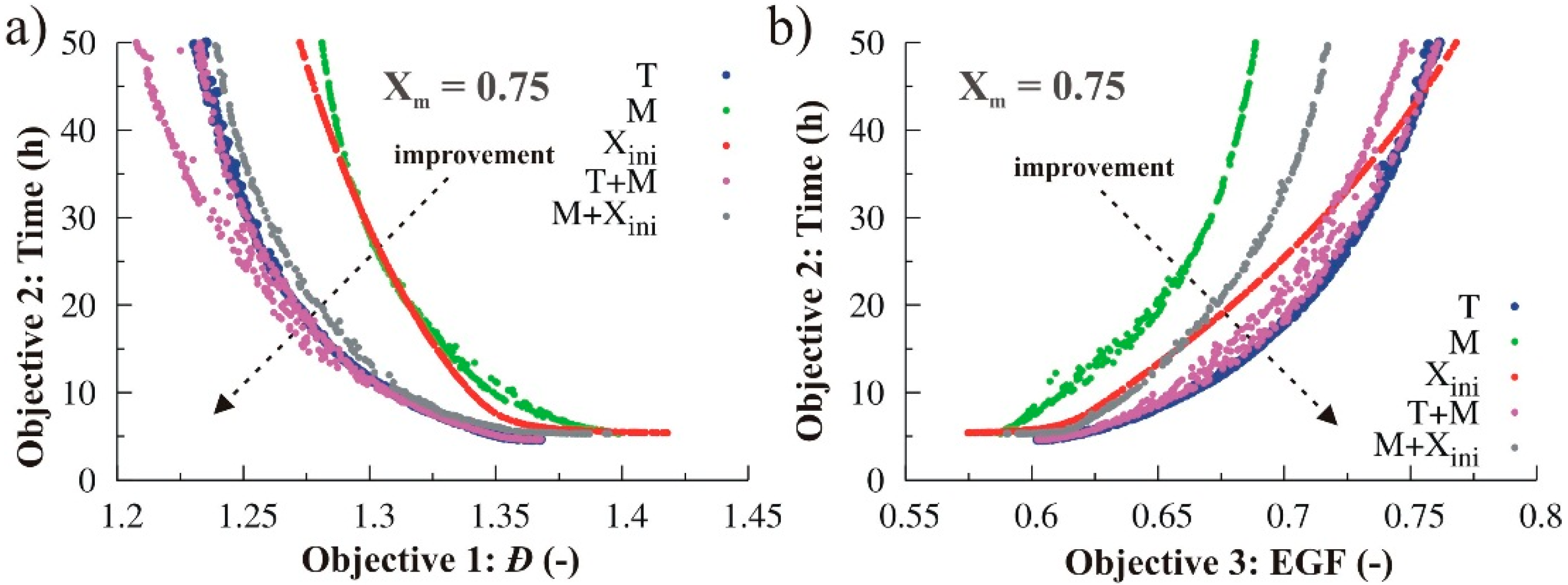
4. Conclusions
Acknowledgments
Supplementary Information
Author Contributions
Conflicts of Interest
References
- Braunecker, W.A.; Matyjaszewski, K. Controlled/living radical polymerization: Features, developments, and perspectives. Progr. Polym. Sci. 2007, 32, 93–146. [Google Scholar] [CrossRef]
- Matyjaszewski, K. Handbook of Radical Polymerization; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Chiefari, J.; Chong, Y.K.; Ercole, F.; Krstina, J.; Jeffery, J.; le, T.P.T.; Mayadunne, R.T.A.; Meijs, G.F.; Moad, C.L.; Moad, G.; et al. Living free-radical polymerization by reversible addition-fragmentation chain transfer: The raft process. Macromolecules 1998, 31, 5559–5562. [Google Scholar] [CrossRef]
- Chong, Y.K.; Le, T.P.T.; Moad, G.; Rizzardo, E.; Thang, S.H. A more versatile route to block copolymers and other polymers of complex architecture by living radical polymerization: The raft process. Macromolecules 1999, 32, 2071–2074. [Google Scholar] [CrossRef]
- Moad, G.; Chiefari, J.; Chong, Y.K.; Krstina, J.; Mayadunne, R.T.A.; Postma, A.; Rizzardo, E.; Thang, S.H. Living free radical polymerization with reversible addition-fragmentation chain transfer (the life of raft). Polym. Int. 2000, 49, 993–1001. [Google Scholar] [CrossRef]
- D’hooge, D.R.; Vachaudez, M.; Stadler, F.J.; Reyniers, M.-F.; Coulembier, O.; Bailly, C.; Dubois, P.; Marin, G.B. Assessment of end-group functionality in atom transfer radical polymerization of N-isopropylacrylamide. Eur. Polym. J. 2013, 49, 2344–2355. [Google Scholar] [CrossRef]
- Metz, N.; Theato, P. Controlled synthesis of poly(acetone oxime acrylate) as a new reactive polymer: Stimuli-responsive reactive copolymers. Eur. Polym. J. 2007, 43, 1202–1209. [Google Scholar] [CrossRef]
- Ferrari, R.; Yu, Y.; Morbidelli, M.; Hutchinson, R.A.; Moscatelli, D. ε-Caprolactone-based macromonomers suitable for biodegradable nanoparticles synthesis through free radical polymerization. Macromolecules 2011, 44, 9205–9212. [Google Scholar] [CrossRef]
- Wang, W.; Hutchinson, R.A. PLP/SEC/NMR study of free radical copolymerization of styrene and glycidyl methacrylate. Macromolecules 2008, 41, 9011–9018. [Google Scholar] [CrossRef]
- Wang, J.-S.; Matyjaszewski, K. Controlled/“living” radical polymerization. Atom transfer radical polymerization in the presence of transition-metal complexes. J. Am. Chem. Soc. 1995, 117, 5614–5615. [Google Scholar] [CrossRef]
- Patten, T.E.; Matyjaszewski, K. Atom transfer radical polymerization and the synthesis of polymeric materials. Adv. Mater. 1998, 10, 901–915. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Xia, J. Atom transfer radical polymerization. Chem. Rev. 2001, 101, 2921–2990. [Google Scholar] [CrossRef] [PubMed]
- Vachaudez, M.; D’hooge, D.R.; Socka, M.; Libiszowski, J.; Coulembier, O.; Reyniers, M.F.; Duda, A.; Marin, G.B.; Dubois, P. Inverse dependencies on the polymerization rate in atom transfer radical polymerization of N-isopropylacrylamide in aqueous medium. React. Funct. Polym. 2013, 73, 484–491. [Google Scholar] [CrossRef]
- Teodorescu, M.; Matyjaszewski, K. Controlled polymerization of (meth)acrylamides by atom transfer radical polymerization. Macromol. Rapid Commun. 2000, 21, 190–194. [Google Scholar] [CrossRef]
- Lutz, J.F.; Matyjaszewski, K. Kinetic modeling of the chain-end functionality in atom transfer radical polymerization. Macromol. Chem. Phys. 2002, 203, 1385–1395. [Google Scholar] [CrossRef]
- Ballard, N.; Salsamendi, M.; Santos, J.I.; Ruipérez, F.; Leiza, J.R.; Asua, J.M. Experimental evidence shedding light on the origin of the reduction of branching of acrylates in ATRP. Macromolecules 2014, 47, 964–972. [Google Scholar] [CrossRef]
- Nicolas, J.; Guillaneuf, Y.; Lefay, C.; Bertin, D.; Gigmes, D.; Charleux, B. Nitroxide-mediated polymerization. Progr. Polym. Sci. 2013, 38, 63–235. [Google Scholar] [CrossRef]
- Moad, G.; Rizzardo, E.; Solomon, D.H. A product study of the nitroxide inhibited thermal polymerization of styrene. Polym. Bull. 1982, 6, 589–593. [Google Scholar] [CrossRef]
- Georges, M.K.; Veregin, R.P.N.; Kazmaier, P.M.; Hamer, G.K. Narrow molecular-weight resins by a free-radical polymerization process. Macromolecules 1993, 26, 2987–2988. [Google Scholar] [CrossRef]
- Hawker, C.J. Molecular weight control by a “living” free-radical polymerization process. J. Am. Chem. Soc. 1994, 116, 11185–11186. [Google Scholar] [CrossRef]
- Hawker, C.J.; Barclay, G.G.; Orellana, A.; Dao, J.; Devonport, W. Initiating systems for nitroxide-mediated “living” free radical polymerizations: Synthesis and evaluation. Macromolecules 1996, 29, 5245–5254. [Google Scholar] [CrossRef]
- Fischer, H. The persistent radical effect in “living” radical polymerization. Macromolecules 1997, 30, 5666–5672. [Google Scholar] [CrossRef]
- Fischer, H. The persistent radical effect in controlled radical polymerizations. J. Polym. Sci. Polym. Chem. 1999, 37, 1885–1901. [Google Scholar] [CrossRef]
- Tang, W.; Tsarevsky, N.V.; Matyjaszewski, K. Determination of equilibrium constants for atom transfer radical polymerization. J. Am. Chem. Soc. 2006, 128, 1598–1604. [Google Scholar] [CrossRef] [PubMed]
- Toloza Porras, C.; Dʼhooge, D.R.; van Steenberge, P.H.M.; Reyniers, M.-F.; Marin, G.B. A theoretical exploration of the potential of icar atrp for one- and two-pot synthesis of well-defined diblock copolymers. Macromol. React. Eng. 2013, 7, 311–326. [Google Scholar] [CrossRef]
- Jakubowski, W.; Matyjaszewski, K. Activator generated by electron transfer for atom transfer radical polymerization. Macromolecules 2005, 38, 4139–4146. [Google Scholar] [CrossRef]
- Jakubowski, W.; Min, K.; Matyjaszewski, K. Activators regenerated by electron transfer for atom transfer radical polymerization of styrene. Macromolecules 2005, 39, 39–45. [Google Scholar] [CrossRef]
- D'hooge, D.R.; Konkolewicz, D.; Reyniers, M.-F.; Marin, G.B.; Matyjaszewski, K. Kinetic modeling of ICAR ATRP. Macromol. Theory Simul. 2012, 21, 52–69. [Google Scholar] [CrossRef]
- Mohammad Rabea, A.; Zhu, S. Achieving high-conversion bulk ATRP with good livingness and well controlled by design and optimization of polymerization temperature profile. Macromol. React. Eng. 2014, 8, 771–776. [Google Scholar] [CrossRef]
- Van Steenberge, P.H.M.; Dʼhooge, D.R.; Wang, Y.; Zhong, M.J.; Reyniers, M.F.; Konkolewicz, D.; Matyjaszewski, K.; Marin, G.B. Linear gradient quality of ATRP copolymers. Macromolecules 2012, 45, 8519–8531. [Google Scholar] [CrossRef]
- Toloza Porras, C.; Dʼhooge, D.R.; Reyniers, M.F.; Marin, G.B. Computer-aided optimization of conditions for fast and controlled ICAR ATRP of N-butyl acrylate. Macromol. Theory Simul. 2013, 22, 136–149. [Google Scholar] [CrossRef]
- Dʼhooge, D.; Van Steenberge, P.; Reyniers, M.-F.; Marin, G. Fed-batch control and visualization of monomer sequences of individual ICAR ATRP gradient copolymer chains. Polymers 2014, 6, 1074–1095. [Google Scholar] [CrossRef]
- Chan, N.; Cunningham, M.F.; Hutchinson, R.A. Copper mediated controlled radical polymerization of methyl acrylate in the presence of ascorbic acid in a continuous tubular reactor. Polym. Chem. 2012, 3, 1322–1333. [Google Scholar] [CrossRef]
- Chan, N.; Meuldijk, J.; Cunningham, M.F.; Hutchinson, R.A. Continuous ARGET ATRP of methyl methacrylate and butyl acrylate in a stirred tank reactor. Ind. Eng. Chem. Res. 2013, 52, 11931–11942. [Google Scholar] [CrossRef]
- Greszta, D.; Matyjaszewski, K. Mechanism of controlled/“living” radical polymerization of styrene in the presence of nitroxyl radicals. Kinetics and simulations. Macromolecules 1996, 29, 7661–7670. [Google Scholar] [CrossRef]
- Solomon, D.H.; Rizzardo, E.; Cacioli, P. Polymerization Process and Polymers Produced Thereby. U.S. Patent 4,581,429, 8 April 1986. [Google Scholar]
- Bertin, D.; Gigmes, D.; Marque, S.R.A.; Tordo, P. Kinetic subtleties of nitroxide mediated polymerization. Chem. Soc. Rev. 2011, 40, 2189–2198. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, T.; Goto, A.; Ohno, K. Mechanisms and kinetics of living radical polymerizations. Macromol. Rapid Commun. 2000, 21, 151–165. [Google Scholar] [CrossRef]
- Gigmes, D.; Bertin, D.; Lefay, C.; Guillaneuf, Y. Kinetic modeling of nitroxide-mediated polymerization: Conditions for living and controlled polymerization. Macromol. Theory Simul. 2009, 18, 402–419. [Google Scholar] [CrossRef]
- Lutz, J.F.; Lacroix-Desmazes, P.; Boutevin, B. The persistent radical effect in nitroxide mediated polymerization: Experimental validity. Macromol. Rapid Commun. 2001, 22, 189–193. [Google Scholar] [CrossRef]
- Hernandez-Ortiz, J.C.; Vivaldo-Lima, E.; Lona, L.M.F.; McManus, N.T.; Penlidis, A. Modeling of the nitroxide-mediated radical copolymerization of styrene and divinylbenzene. Macromol. React. Eng. 2009, 3, 288–311. [Google Scholar] [CrossRef]
- Saldívar-Guerra, E.; Bonilla, J.; Becerril, F.; Zacahua, G.; Albores-Velasco, M.; Alexander-Katz, R.; Flores-Santos, L.; Alexandrova, L. On the nitroxide quasi-equilibrium in the alkoxyamine-mediated radical polymerization of styrene. Macromol. Theory Simul. 2006, 15, 163–175. [Google Scholar] [CrossRef]
- Tang, W.; Fukuda, T.; Matyjaszewski, K. Reevaluation of persistent radical effect in NMP. Macromolecules 2006, 39, 4332–4337. [Google Scholar] [CrossRef]
- Benoit, D.; Chaplinski, V.; Braslau, R.; Hawker, C.J. Development of a universal alkoxyamine for “living” free radical polymerizations. J. Am. Chem. Soc. 1999, 121, 3904–3920. [Google Scholar] [CrossRef]
- Grimaldi, S.; Finet, J.-P.; le Moigne, F.; Zeghdaoui, A.; Tordo, P.; Benoit, D.; Fontanille, M.; Gnanou, Y. Acyclic β-phosphonylated nitroxides: A new series of counter-radicals for “living”/controlled free radical polymerization. Macromolecules 2000, 33, 1141–1147. [Google Scholar] [CrossRef]
- Greszta, D.; Matyjaszewski, K. Tempo-mediated polymerization of styrene: Rate enhancement with dicumyl peroxide. J. Polym. Sci. A Polym. Chem. 1997, 35, 1857–1861. [Google Scholar] [CrossRef]
- He, J.P.; Chen, J.M.; Li, L.; Pan, J.Y.; Li, C.M.; Cao, J.Z.; Tao, Y.F.; Hua, F.J.; Yang, Y.L.; McKee, G.E.; et al. Rate enhancement of nitroxide-mediated living free-radical polymerization by continuous addition of initiator. Polymer 2000, 41, 4573–4577. [Google Scholar] [CrossRef]
- Malmström, E.; Miller, R.D.; Hawker, C.J. Development of a new class of rate-accelerating additives for nitroxide-mediated “living” free radical polymerization. Tetrahedron 1997, 53, 15225–15236. [Google Scholar] [CrossRef]
- Grubbs, R.B. Nitroxide-mediated radical polymerization: Limitations and versatility. Polym. Rev. 2011, 51, 104–137. [Google Scholar] [CrossRef]
- Nayak, A.; Gupta, S.K. Multi-objective optimization of semi-batch copolymerization reactors using adaptations of genetic algorithm. Macromol. Theory Simul. 2004, 13, 73–85. [Google Scholar] [CrossRef]
- Deb, K.; Kalyanmoy, D. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2001; p. 518. [Google Scholar]
- Coello Coello, C.A. Evolutionary multi-objective optimization: A historical view of the field. Comput. Intell. Mag. IEEE 2006, 1, 28–36. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evolut. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mitra, K.; Deb, K.; Gupta, S.K. Multiobjective dynamic optimization of an industrial nylon 6 semibatch reactor using genetic algorithm. J. Appl. Polym. Sci. 1998, 69, 69–87. [Google Scholar] [CrossRef]
- Bhaskar, V.; Gupta, S.K.; Ray, A.K. Multiobjective optimization of an industrial wiped film poly(ethylene terephthalate) reactor: Some further insights. Comput. Chem. Eng. 2001, 25, 391–407. [Google Scholar] [CrossRef]
- Mitra, K.; Majumdar, S.; Raha, S. Multiobjective dynamic optimization of a semi-batch epoxy polymerization process. Comput. Chem. Eng. 2004, 28, 2583–2594. [Google Scholar] [CrossRef]
- Garg, S.; Gupta, S.K. Multiobjective optimization of a free radical bulk polymerization reactor using genetic algorithm. Macromol. Theory Simul. 1999, 8, 46–53. [Google Scholar] [CrossRef]
- Benyahia, B.; Latifi, M.A.; Fonteix, C.; Pla, F. Multicriteria dynamic optimization of an emulsion copolymerization reactor. Comput. Chem. Eng. 2011, 35, 2886–2895. [Google Scholar] [CrossRef]
- Massebeuf, S.; Fonteix, C.; Hoppe, S.; Pla, F. Development of new concepts for the control of polymerization processes: Multiobjective optimization and decision engineering. I. Application to emulsion homopolymerization of styrene. J. Appl. Polym. Sci. 2003, 87, 2383–2396. [Google Scholar] [CrossRef]
- Fierens, S.K.; D’hooge, D.R.; van Steenberge, P.H.M.; Reyniers, M.-F.; Marin, G.B. MAMA-SG1 initiated nitroxide mediated polymerization of styrene: From arrhenius parameters to model-based design. Chem. Eng. J. 2014. [Google Scholar] [CrossRef]
- Bentein, L.; Dʼhooge, D.R.; Reyniers, M.F.; Marin, G.B. Kinetic modeling as a tool to understand and improve the nitroxide mediated polymerization of styrene. Macromol. Theory Simul. 2011, 20, 238–265. [Google Scholar] [CrossRef]
- Petzold, L. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential-equations. SIAM J. Sci. Statist. Comput. 1983, 4, 136–148. [Google Scholar] [CrossRef]
- Payne, K.A.; Dʼhooge, D.R.; van Steenberge, P.H.M.; Reyniers, M.F.; Cunningham, M.F.; Hutchinson, R.A.; Marin, G.B. Arget atrp of butyl methacrylate: Utilizing kinetic modeling to understand experimental trends. Macromolecules 2013, 46, 3828–3840. [Google Scholar] [CrossRef]
- Derboven, P.; D’hooge, D.R.; Reyniers, M.-F.; Marin, G.B.; Barner-Kowollik, C. The long and the short of radical polymerization. Macromolecules 2015, 48, 492–501. [Google Scholar] [CrossRef]
- Tang, W.; Matyjaszewski, K. Kinetic modeling of normal ATRP, normal ATRP with [CuII] 0, reverse ATRP and SR&NI ATRP. Macromol. Theory Simul. 2008, 17, 359–375. [Google Scholar] [CrossRef]
- Mayo, F.R. Chain transfer in the polymerization of styrene. VIII. Chain transfer with bromobenzene and mechanism of thermal initiation1. J. Am. Chem. Soc. 1953, 75, 6133–6141. [Google Scholar] [CrossRef]
- Zetterlund, P.B.; Saka, Y.; McHale, R.; Nakamura, T.; Aldabbagh, F.; Okubo, M. Nitroxide-mediated radical polymerization of styrene: Experimental evidence of chain transfer to monomer. Polymer 2006, 47, 7900–7908. [Google Scholar] [CrossRef]
- Johnston-Hall, G.; Monteiro, M.J. Bimolecular radical termination: New perspectives and insights. J. Polym. Sci. Polym. Chem. 2008, 46, 3155–3173. [Google Scholar] [CrossRef]
- Johnston-Hall, G.; Monteiro, M.J. Kinetic simulations of atom transfer radical polymerization (ATRP) in light of chain length dependent termination. Macromol. Theory Simul. 2010, 19, 387–393. [Google Scholar] [CrossRef]
- Matyjaszewski, K. Mechanistic and synthetic aspects of atom transfer radical polymerization. J. Macromol. Sci. A 1997, 34, 1785–1801. [Google Scholar] [CrossRef]
- Goto, A.; Fukuda, T. Kinetics of living radical polymerization. Progr. Polym. Sci. 2004, 29, 329–385. [Google Scholar] [CrossRef]
- Zhong, M.J.; Matyjaszewski, K. How fast can a CRP be conducted with preserved chain end functionality? Macromolecules 2011, 44, 2668–2677. [Google Scholar] [CrossRef]
- Woloszyn, J.D.; McAuley, K.B. Application of parameter selection and estimation techniques in a thermal styrene polymerization model. Macromol. React. Eng. 2011, 5, 453–466. [Google Scholar] [CrossRef]
- Belincanta-Ximenes, J.; Mesa, P.V.R.; Lona, L.M.F.; Vivaldo-Lima, E.; McManus, N.T.; Penlidis, A. Simulation of styrene polymerization by monomolecular and bimolecular nitroxide-mediated radical processes over a range of reaction conditions. Macromol. Theory Simul. 2007, 16, 194–208. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fierens, S.K.; D'hooge, D.R.; Van Steenberge, P.H.M.; Reyniers, M.-F.; Marin, G.B. Exploring the Full Potential of Reversible Deactivation Radical Polymerization Using Pareto-Optimal Fronts. Polymers 2015, 7, 655-679. https://doi.org/10.3390/polym7040655
Fierens SK, D'hooge DR, Van Steenberge PHM, Reyniers M-F, Marin GB. Exploring the Full Potential of Reversible Deactivation Radical Polymerization Using Pareto-Optimal Fronts. Polymers. 2015; 7(4):655-679. https://doi.org/10.3390/polym7040655
Chicago/Turabian StyleFierens, Stijn K., Dagmar R. D'hooge, Paul H. M. Van Steenberge, Marie-Françoise Reyniers, and Guy B. Marin. 2015. "Exploring the Full Potential of Reversible Deactivation Radical Polymerization Using Pareto-Optimal Fronts" Polymers 7, no. 4: 655-679. https://doi.org/10.3390/polym7040655
APA StyleFierens, S. K., D'hooge, D. R., Van Steenberge, P. H. M., Reyniers, M.-F., & Marin, G. B. (2015). Exploring the Full Potential of Reversible Deactivation Radical Polymerization Using Pareto-Optimal Fronts. Polymers, 7(4), 655-679. https://doi.org/10.3390/polym7040655