Mechanical Behavior of BFRP-Steel Composite Plate under Axial Tension
Abstract
:1. Introduction

2. Experimental Program
2.1. Material Properties and Manufacture of BFRP-Steel Composite Plate (BSP) Specimens
| Type of material | Elastic modulus (GPa) | Yield strength (MPa) | Tensile strength (MPa) | Elongation (%) |
|---|---|---|---|---|
| Basalt fiber fabric | 91 | – | 2350 | 2.6 |
| Steel plate | 190 | 435 | – | 20 |
| Adhesive | 2.7 | – | 48 | 2.7 |


2.2. Specimen Design
| Type | Thickness of steel plate (mm) | Number of BFRP Layers | Total thickness of the specimen (mm) |
|---|---|---|---|
| SP | 3.05 | 0 | 3.05 |
| BSP2 | 3.05 | 2 | 3.85 |
| BSP4 | 3.05 | 4 | 4.46 |
| BSP6 | 3.05 | 6 | 4.85 |
| BSP8 | 3.05 | 8 | 5.32 |
2.3. Testing Setup and Loading Program
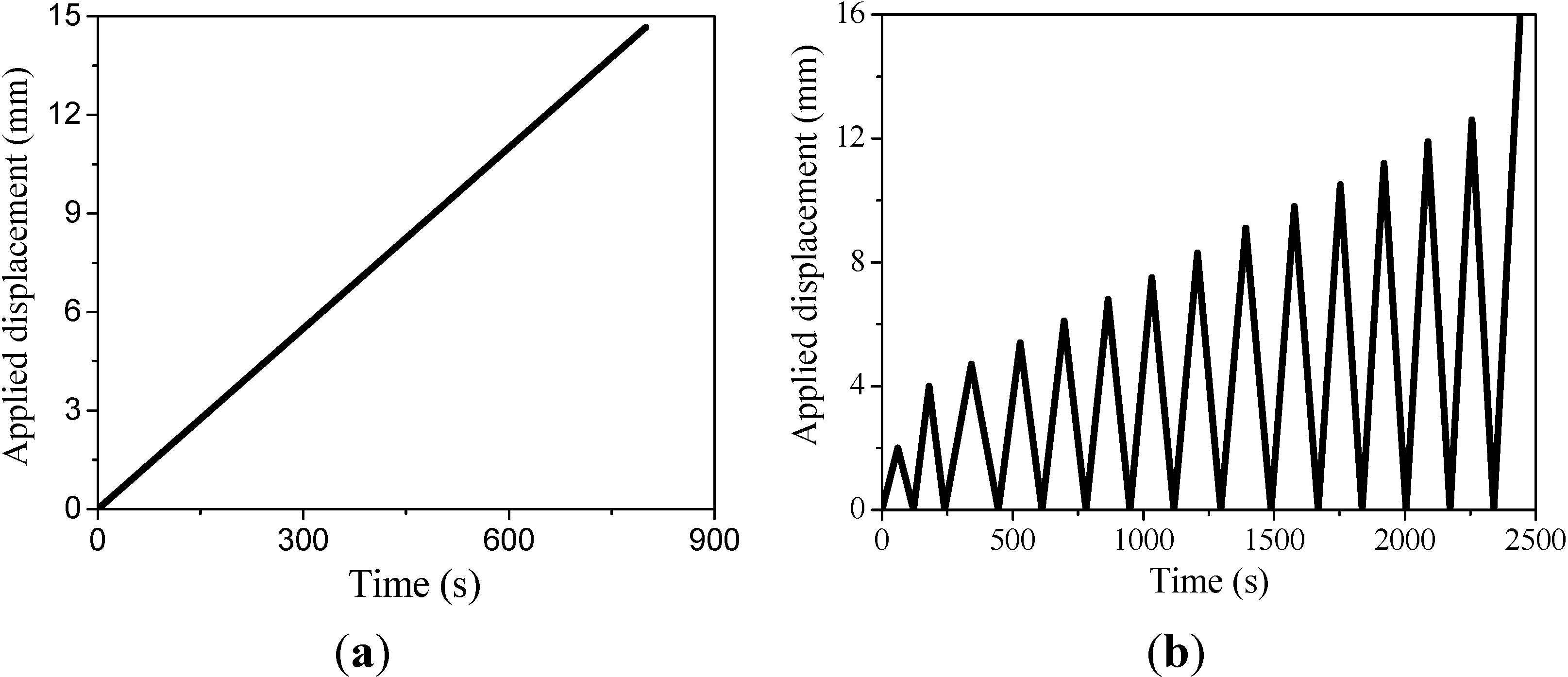
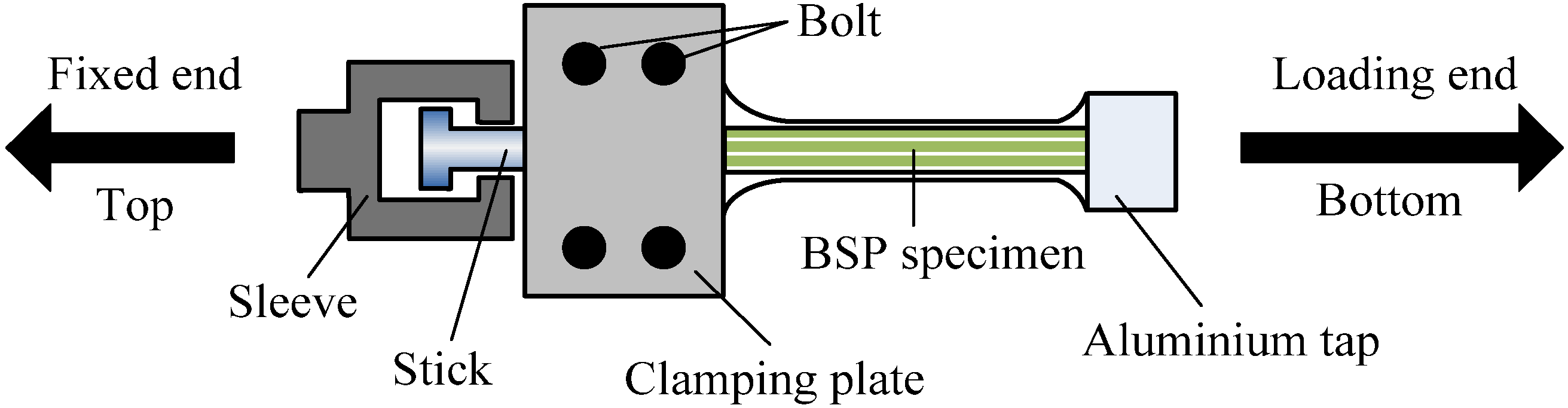
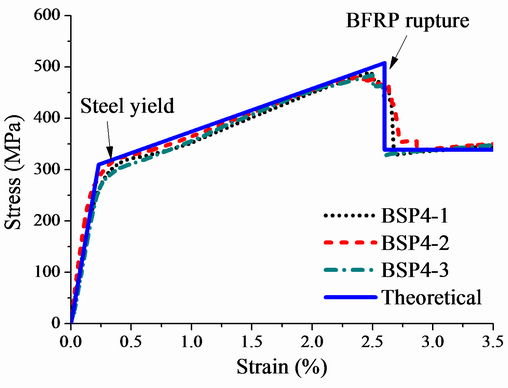
3. Uniaxial Tensile Behaviors of BSP
3.1. Test Results
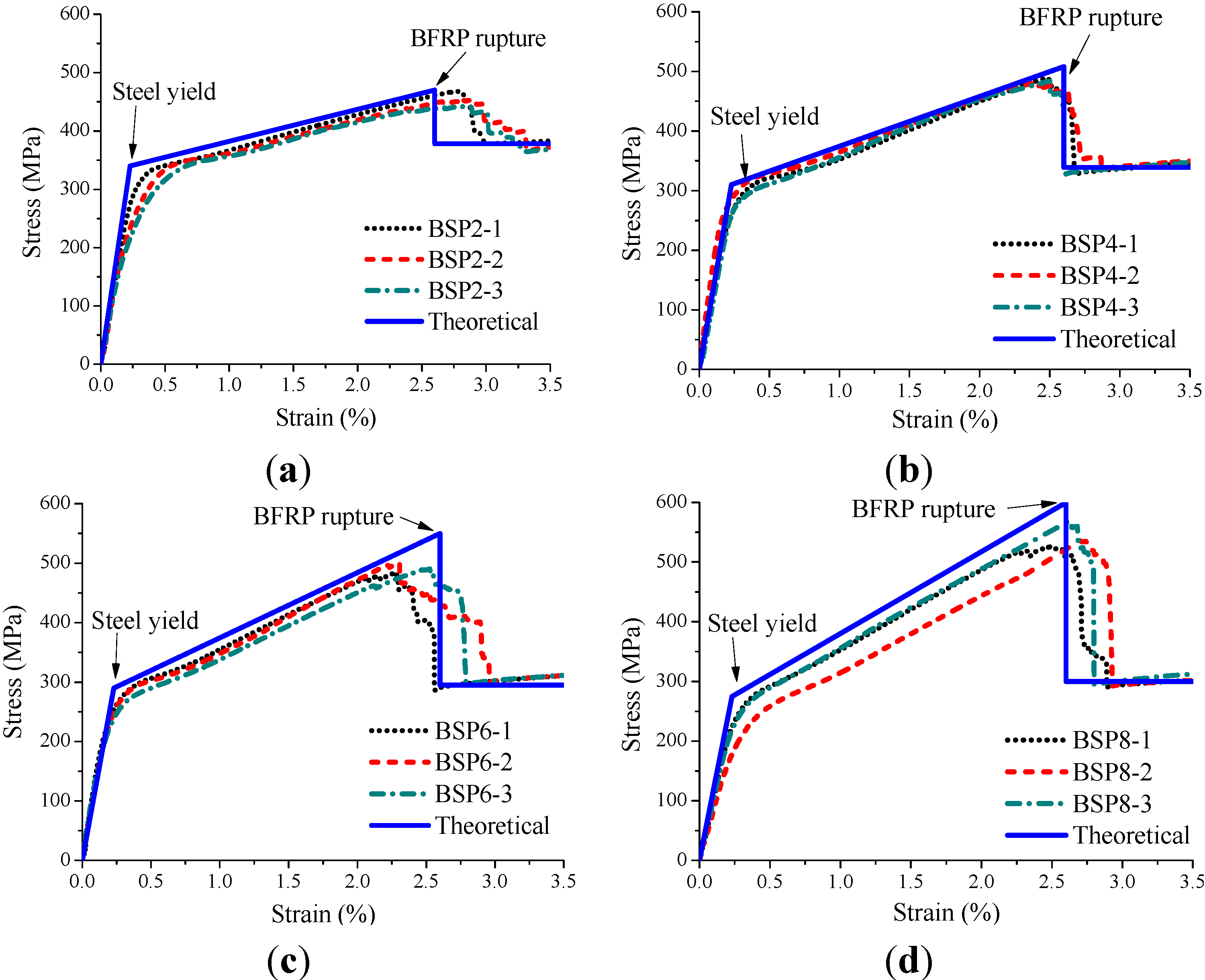
| Type | EI (GPa) | EII (GPa) | ||||
|---|---|---|---|---|---|---|
| Exp. a | Theo. b | R.E. c | Exp. a | Theo. b | R.E. c | |
| BSP2 | 134.2 | 155.3 | 15.7% | 4.5 | 4.7 | 4.4% |
| BSP4 | 130.7 | 138.2 | 5.7% | 8.1 | 8.2 | 1.2% |
| BSP6 | 126.2 | 130.2 | 3.2% | 11.1 | 11.4 | 2.7% |
| BSP8 | 117.4 | 122.8 | 4.6% | 13.5 | 13.9 | 3.0% |
| Type | fbsy (MPa) | fbsu (MPa) | Nu (kN) | ||||
|---|---|---|---|---|---|---|---|
| Exp. a | Theo. b | R.E. c | Exp. a | Theo. b | R.E. c | ||
| BSP2 | 309.4 | 355.6 | 14.9% | 455.2 | 468.9 | 3.0% | 43.8 |
| BSP4 | 293.0 | 316.4 | 8.0% | 483.8 | 512.2 | 5.9% | 53.9 |
| BSP6 | 275.6 | 300.3 | 9.0% | 492.0 | 570.9 | 16.0% | 59.6 |
| BSP8 | 258.6 | 281.1 | 8.7% | 551.2 | 609.4 | 10.6% | 73.3 |

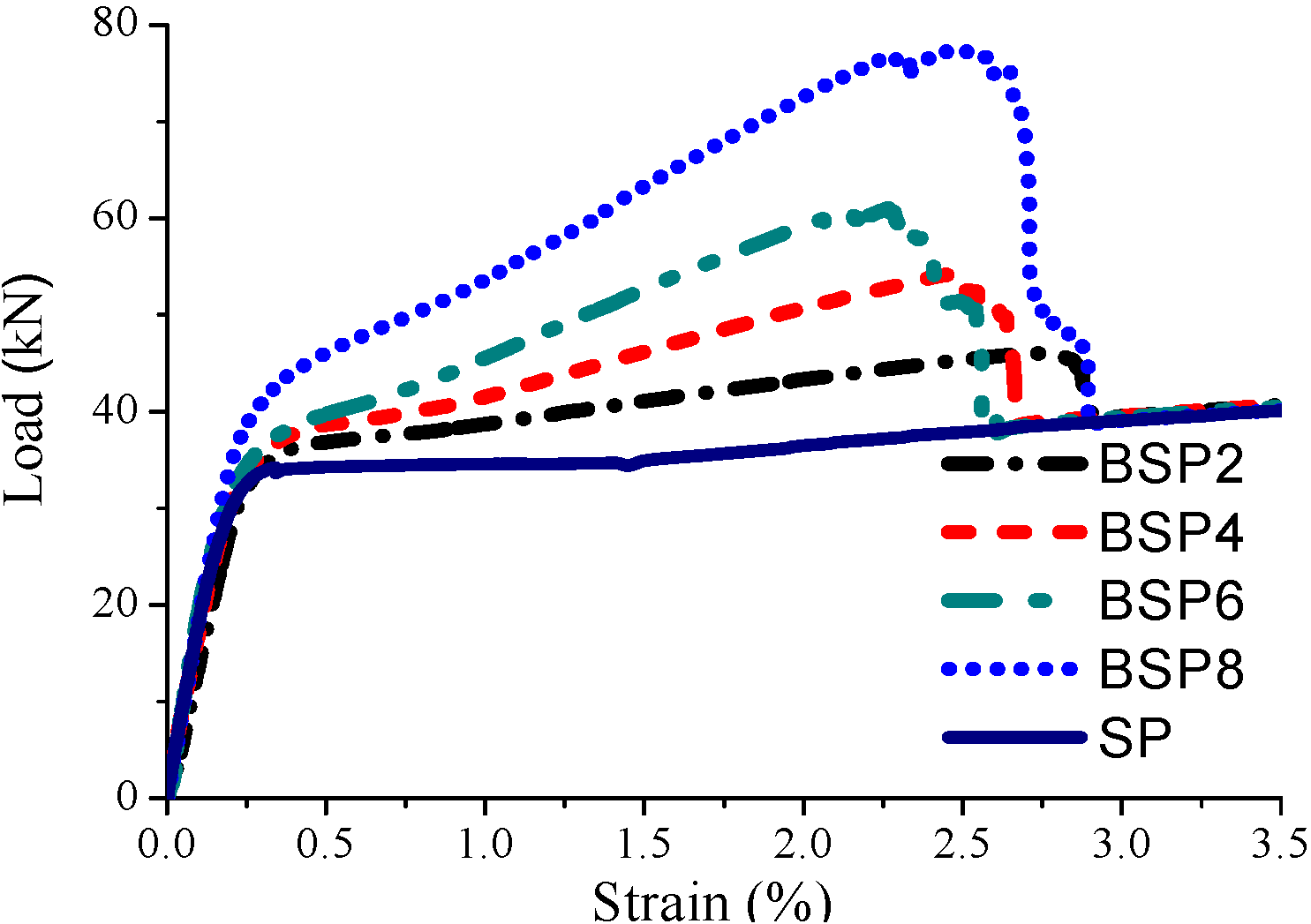

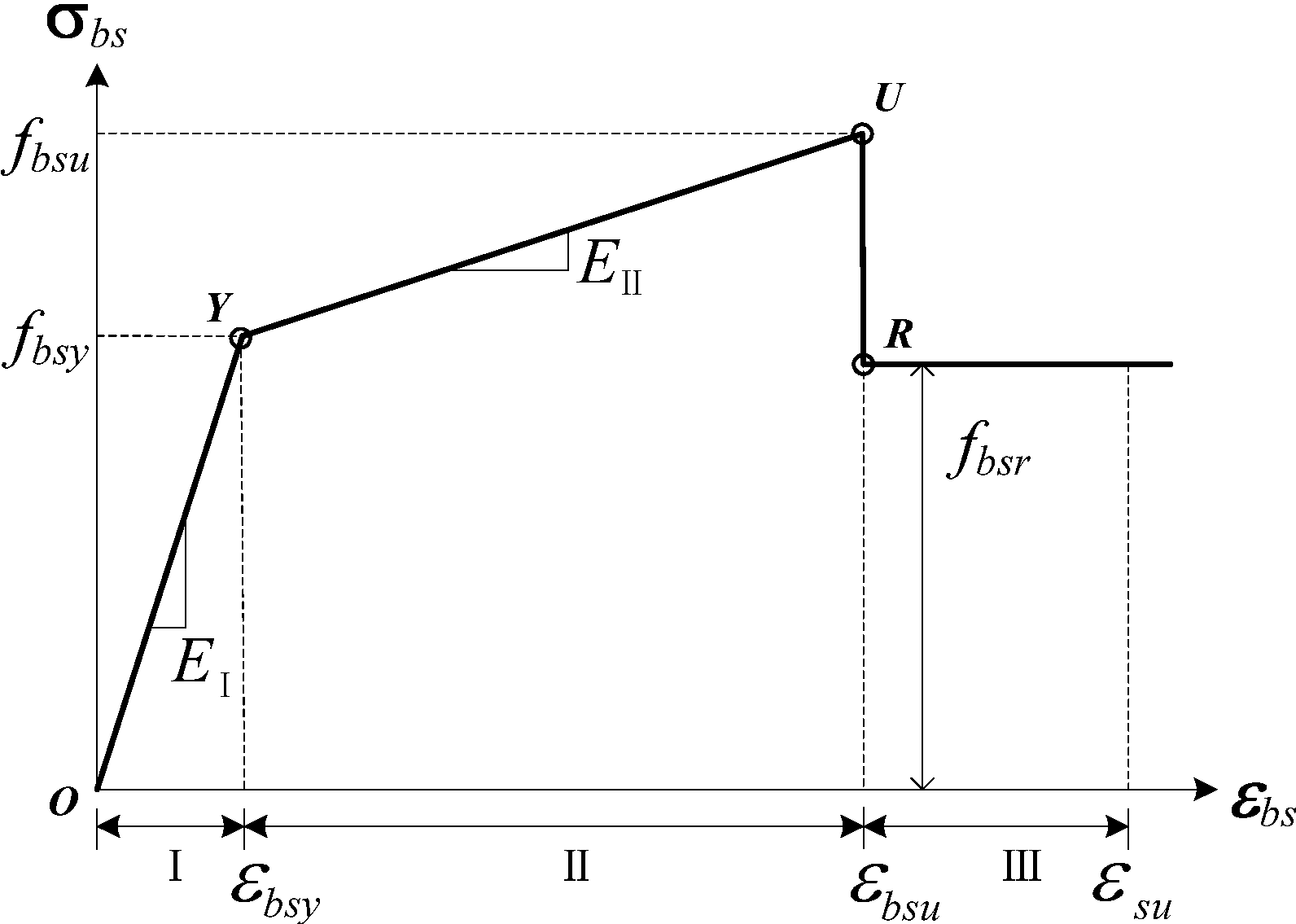
3.2. Theoretical Model of the Stress-Strain Relationship for BSP

4. Cyclic Tensile Behaviors of BSP
4.1. Test Results
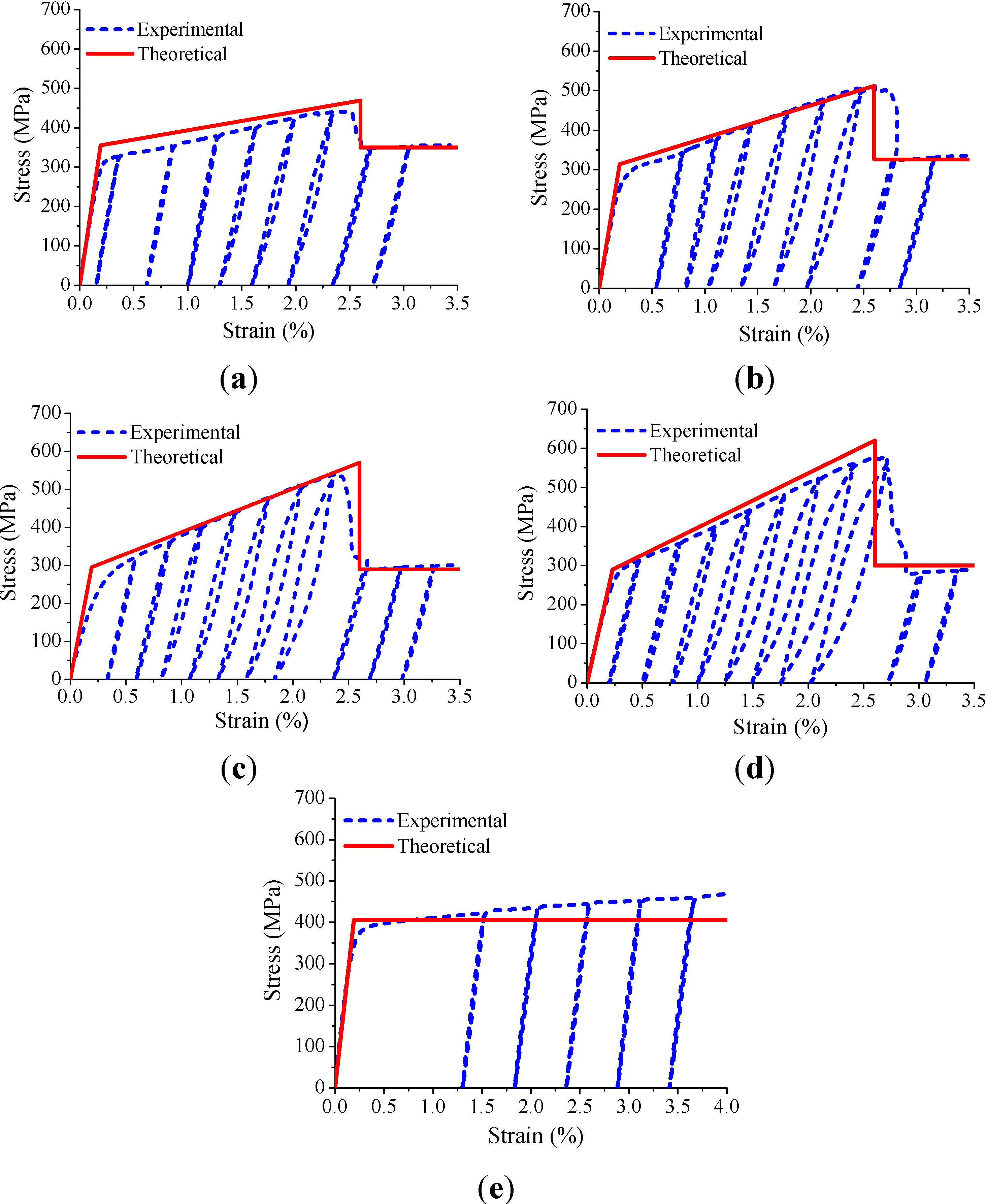

4.2. Stress–Strain Relationship of BSP under Cyclic Tensile Loading

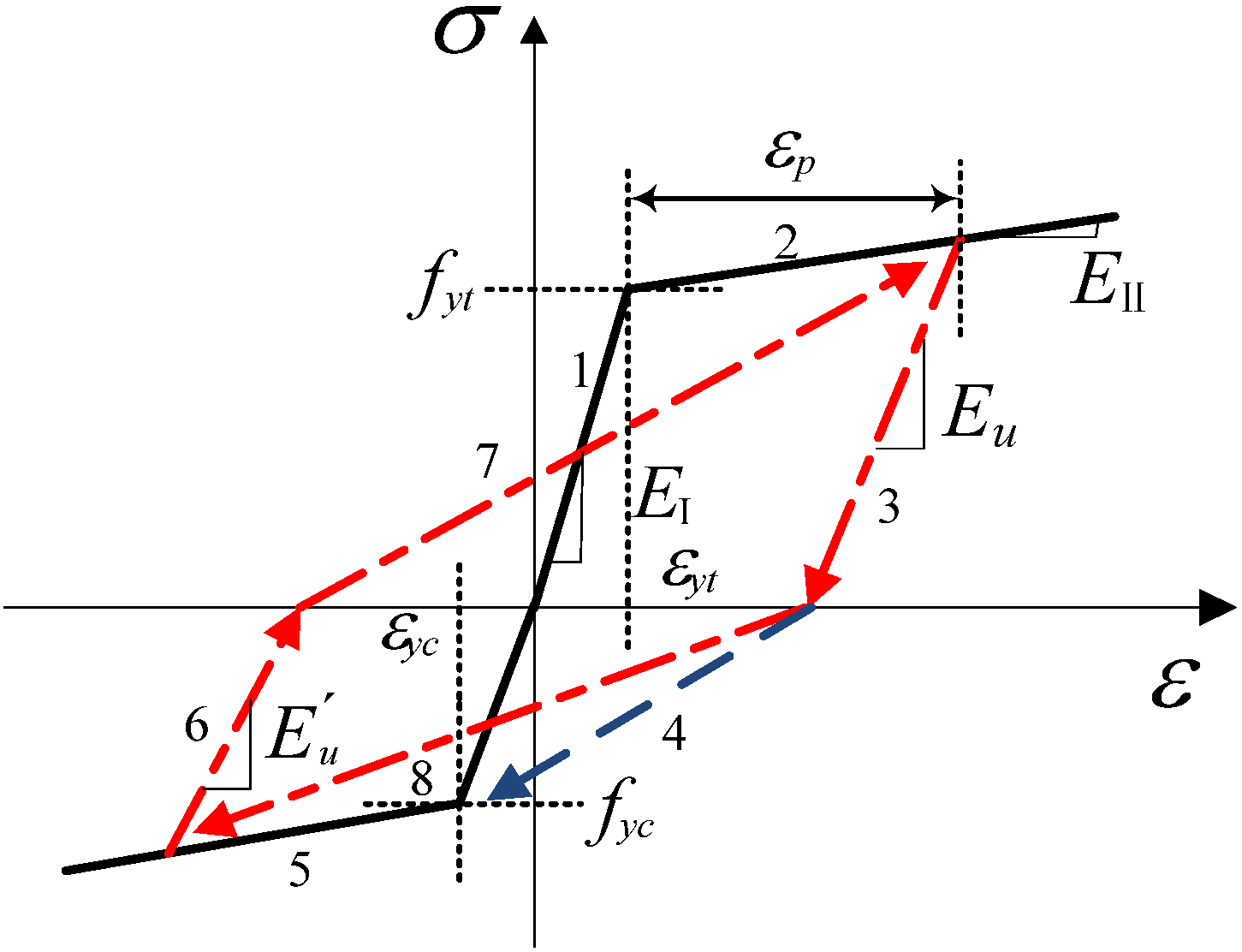
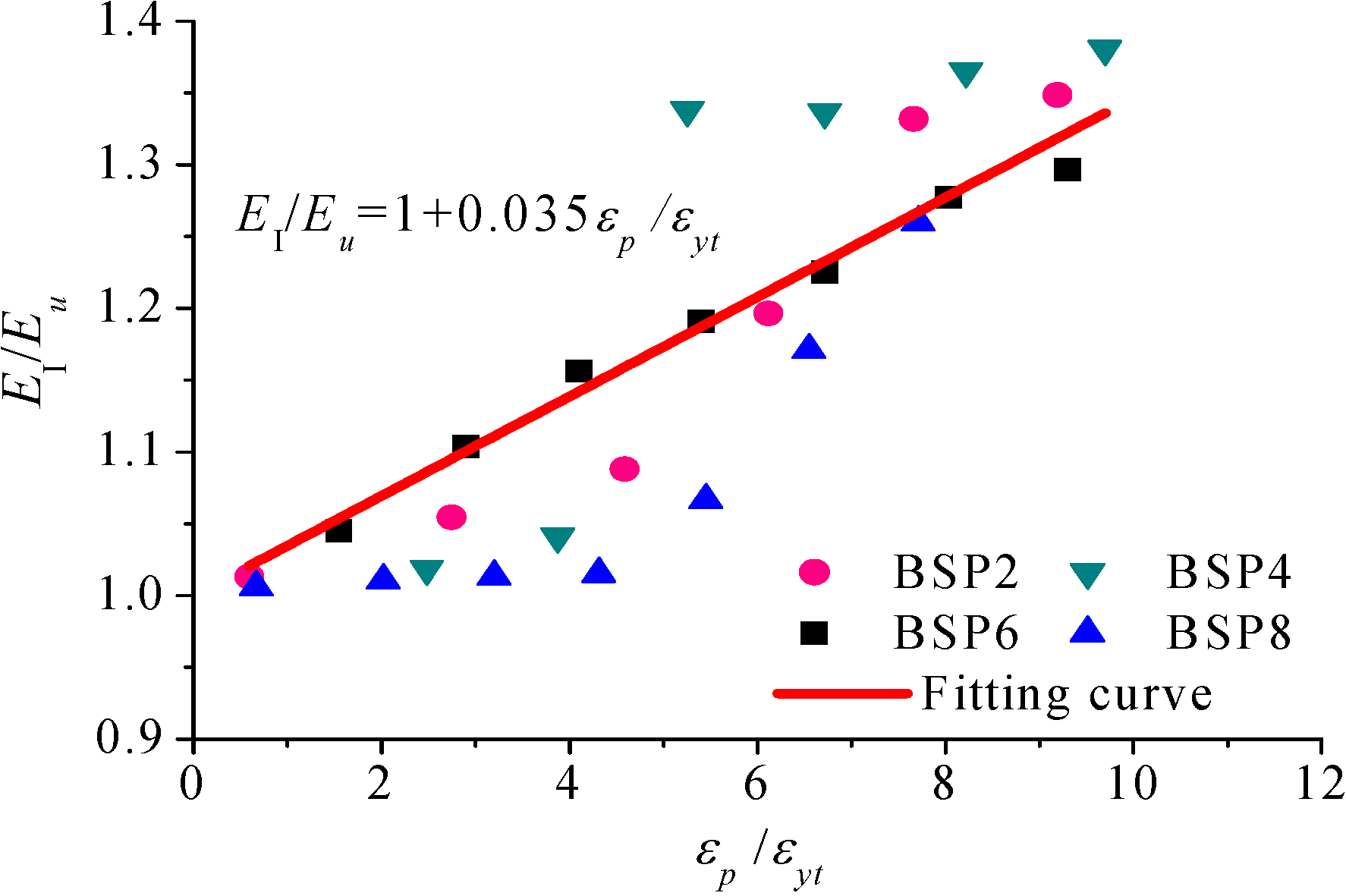

5. Conclusions
- The stress-strain curve of the BSP specimen was bilinear prior to the fracture of the outer BFRP, and the BSP specimen had a stable postyield stiffness after the yielding of the inner steel plate.
- The postyield modulus and the ultimate bearing capacity of the BSP specimens increased almost linearly with the increasing number of outer BFRP layers, respectively.
- The strength and stiffness of the BSP specimens remained unaffected by the cyclic tensile loading, and the BSP specimens had small residual deformation and good recovery of the bearing ability after the yielding of the BSP specimens, as compared with the steel plate, under cyclic tensile loading.
- The selected theoretical stress–strain relationship models for the BSP specimens were in good agreement with the experimental results, which indicated that the theoretical models could be used to predict and design the mechanical behavior of BSP.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hollaway, L.C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Zhao, X.L.; Zhang, L. State-of-the-art review on FRP strengthened steel structures. Eng. Struct. 2007, 29, 1808–1823. [Google Scholar] [CrossRef]
- Bakis, C.E.; Bank, L.C.; Brown, V.L. Fiber-reinforced polymer composites for construction—State-of-the-art review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef]
- Mirmiran, A.; Bank, L.C.; Neale, K.W. World survey of civil engineering programs on fiber reinforced polymer composites for construction. J. Prof. Issues Eng. Educ. Pract. 2003, 129, 155–160. [Google Scholar] [CrossRef]
- Design and Construction of Building Component with Fiber-Reinforced Polymers; CSA S806–02; Canadian Standard Association (CSA): Toronto, Ontario, Canada, 2002.
- Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; ACI 440.2R-08; American Concrete Institute (ACI): Detroit, MI, USA, 2008.
- Recommendation for Design and Construction of Concrete Structures Using Continuous Fiber Reinforcing Materials; Concrete Engineering Series No. 23; Japan Society of Civil Engineers (JSCE): Tokyo, Japan, 1997.
- AASHTO LRFD Bridge Design Guide Specifications for GFRP—Reinforced Concrete Bridge Decks and Traffic Railings; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2009.
- Wu, G.; Sun, Z.Y.; Wu, Z.S.; Luo, Y.B. Mechanical properties of steel-FRP composite bars (SFCBs) and performance of SFCB reinforced concrete structures. Adv. Struct. Eng. 2012, 15, 625–635. [Google Scholar] [CrossRef]
- Rizkalla, S.; Hassan, T. Effectiveness of FRP for strengthening concrete bridges. Struct. Eng. Int. 2002, 12, 89–95. [Google Scholar] [CrossRef]
- Wu, G.; Wu, Z.S.; Luo, Y.B.; Wei, H.C. A new reinforcement material of steel fiber composite bar (SFCB) and its mechanics properties. In Proceedings of the 9th International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures (FRPRCS-9), Sydney, Australia, 13–15 July 2009.
- Wu, G.; Wu, Z.S.; Luo, Y.B.; Sun, Z.Y.; Hu, X.Q. Mechanical properties of steel-FRP composite bar under uniaxial and cyclic tensile loads. J. Mater. Civ. Eng. 2010, 22, 1056–1066. [Google Scholar] [CrossRef]
- Christopoulos, C.; Pampanin, S.; Priestley, M.J. Performance-based seismic response of frame structures including residual deformations, Part I: Single-degree of freedom systems. J. Earthq. Eng. 2003, 7, 97–118. [Google Scholar]
- Christopoulos, C.; Pampanin, S. Towards performance based seismic design of MDOF structures with explicit consideration of residual deformations. J. Earthq. Technol. 2004, 41, 53–73. [Google Scholar]
- Tensile Test of Metallic Material—Part 1: Test Method Atambient Temperature; GB/T 228.1-2010; China Standard Press: Beijing, China, 2010.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, Y.; Wang, Y.; Ou, J. Mechanical Behavior of BFRP-Steel Composite Plate under Axial Tension. Polymers 2014, 6, 1862-1876. https://doi.org/10.3390/polym6061862
Li Y, Wang Y, Ou J. Mechanical Behavior of BFRP-Steel Composite Plate under Axial Tension. Polymers. 2014; 6(6):1862-1876. https://doi.org/10.3390/polym6061862
Chicago/Turabian StyleLi, Yunyu, Yanlei Wang, and Jinping Ou. 2014. "Mechanical Behavior of BFRP-Steel Composite Plate under Axial Tension" Polymers 6, no. 6: 1862-1876. https://doi.org/10.3390/polym6061862
APA StyleLi, Y., Wang, Y., & Ou, J. (2014). Mechanical Behavior of BFRP-Steel Composite Plate under Axial Tension. Polymers, 6(6), 1862-1876. https://doi.org/10.3390/polym6061862