Next Article in Journal
Azetidinium Functionalized Polytetrahydrofurans: Antimicrobial Properties in Solution and Application to Prepare Non Leaching Antimicrobial Surfaces
Next Article in Special Issue
Development of a Biocompatible Layer-by-Layer Film System Using Aptamer Technology for Smart Material Applications
Previous Article in Journal / Special Issue
Structures and Synthesis of Zwitterionic Polymers
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Polymers
Volume 6
Issue 5
10.3390/polym6051602
polymers-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

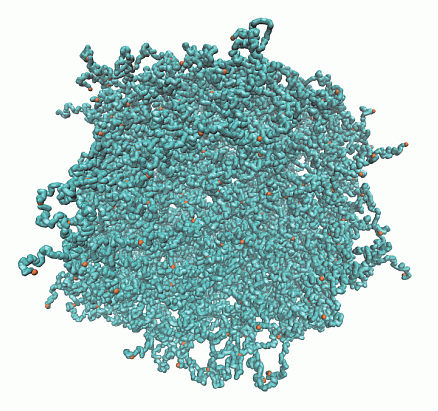
Structure of Microgels with Debye–Hückel Interactions

by
Hideki Kobayashi
and
Roland G. Winkler
*
Theoretical Soft Matter and Biophysics, Institute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany
*
Author to whom correspondence should be addressed.
Polymers 2014, 6(5), 1602-1617; https://doi.org/10.3390/polym6051602
Submission received: 31 March 2014 / Revised: 13 May 2014 / Accepted: 19 May 2014 / Published: 23 May 2014
(This article belongs to the Special Issue Polyelectrolytes 2014)
Browse Figures
Versions Notes

Abstract

:
The structural properties of model microgel particles are investigated by molecular dynamics simulations applying a coarse-grained model. A microgel is comprised of a regular network of polymers internally connected by tetra-functional cross-links and with dangling ends at its surface. The self-avoiding polymers are modeled as bead-spring linear chains. Electrostatic interactions are taken into account by the Debye–Hückel potential. The microgels exhibit a quite uniform density under bad solvent conditions with a rather sharp surface. With increasing Debye length, structural inhomogeneities appear, their surface becomes fuzzy and, at very large Debye lengths, well defined again. Similarly, the polymer conformations change from a self-avoiding walk to a rod-like behavior. Thereby, the average polymer radius of gyration follows a scaling curve in terms of polymer length and persistence length, with an asymptotic rod-like behavior for swollen microgels and self-avoiding walk behavior for weakly swollen gel particles

Graphical Abstract

1. Introduction

Microgels are cross-linked polymers, typically polyelectrolytes, with a network structure. They are able to undergo reversible volume phase-transitions in response to environmental stimuli, such as pH, temperature, the ionic strength of the surrounding medium, the quality of solvent and the action of the external electromagnetic field [1,2,3,4]. This renders them potential candidates for a broad-range of applications in drug delivery, sensing, the fabrication of photonic crystals, template-based synthesis of inorganic nanoparticles and separation and purification technologies [5,6,7,8,9,10,11,12,13].
Theoretical studies of the macroscopic properties of polyelectrolyte gels have a long history; a summary can be found in the review article by Khokhlov et al. [14]. Computer simulations have mainly been performed during the last decade. Such simulations typically consider defect-free microgels applying periodic boundary conditions, i.e., only the bulk properties of the gel are considered [15,16,17,18,19,20,21,22,23,24,25,26,27]. Monte Carlo [15,16,18,20,22,25,26,27] or molecular dynamics [17,19,21,23,24] simulations have been performed using coarse-grained polymer models with an implicit solvent, but explicit counterions. A major aspect of these studies is the swelling behavior of the polyelectrolyte networks. These simulations provide valuable insight into the origin of the driving force responsible for gel swelling. It is generally accepted that the entropy of the free counterions is responsible for swelling, whereas Coulomb repulsion between the charged polymer chains shows no explicit effect [16,21]. A detailed study of the latter aspect shows that this is due to the cancellation of various pressure contributions [21,23].
Comparably little attention has been paid to finite-size cross-linked polyelectrolytes [28,29,30]. A markedly different behavior of the counterion distribution has been observed. Now, no longer are all counterions confined inside the microgel, but rather, a large fraction is distributed outside, around the colloidal gel particle [28,31]. This is caused by the permeability of microgels. Another important aspect is the presence of the surface. We expect that, when the surface effect is non-negligible compared to the bulk effect, this effect will cause inhomogeneities in the structure of microgels.
To characterize the structural properties of microgels, we perform large-scale computer simulations, combining molecular dynamics simulations for the polymers with the Brownian multiparticle collision dynamics (B-MPC) approach [32]. Electrostatic interactions are taken into account by the Debye–Hückel potential. Hence, we consider counterions only implicitly. The study is intended as a reference to discriminate between effects caused by explicit charges and counterions—such as counterion condensation [33,34]—and effects due to repulsive interactions in finite-sized microgel particles. The simulations reveal a significant dependence of the microgel structure on the monomer interactions. Under bad solvent conditions, we find highly compact particles with a rather constant radial monomer distribution. Switching to good solvent conditions implies a swelling of a microgel particle. An additional increase of the Debye length, i.e., an increasing electrostatic repulsion, leads to further swelling, and the monomer distribution becomes inhomogeneous. Thereby, the polymer conformational properties change from self-avoiding walk to rod-like behavior. At the same time, the surface properties of the microgels change from a rather sharp interface to a more fuzzy one for neutral, non-compact gels, back to a rather well-defined one at large Debye lengths.
The rest of the paper is organized as follows. In Section 2, the microgel model and the simulation approach are outlined. The results are presented in Section 3, and Section 4 summarizes our findings.

2. Models

2.1. Microgel

A microgel particle is comprised of a regular network of polymers, which are internally connected by Nc tetra-functional cross-links and with Nd dangling ends at the surface, due to its finite size, as illustrated in Figure 1. The ratio Nd/(Nc − Nd) indicates the relative importance of surface effects [29]. The limit Nd/(Nc − Nd) → 0 corresponds to the case of a macrogel, where surface effects are negligible.
Figure 1. Topological structure of a microgel particle with Nc = 729 cross-links and Nm = 40 monomers per polymer. (Top) Initial state with fully stretched polymers; (bottom) equilibrated structure for lD = 0 under good solvent conditions. Cross-link monomers are indicated in orange.
Figure 1. Topological structure of a microgel particle with Nc = 729 cross-links and Nm = 40 monomers per polymer. (Top) Initial state with fully stretched polymers; (bottom) equilibrated structure for lD = 0 under good solvent conditions. Cross-link monomers are indicated in orange.
An individual polymer is modeled as a linear chain of Nm monomers. A nearly constant bond length, l, is maintained by the harmonic potential:
between successive monomers, i and i + 1. Here, ri denotes the position of monomer i and ks the spring constant. Excluded-volume interactions between non-bonded monomers are taken into account by the truncated Lennard–Jones (LJ) potential:
where rij = |ri − rj|, C = 4ε((σ/rc)12 − (σ/rc)6) and rc is the cut-off radius. The parameter ε characterizes the strength of the interaction, and σ represents the diameter of the monomers. A good solvent is modeled by rc = 21/6σ, using only the repulsive part of the LJ potential. For a poor solvent, the cut-off radius is set to rc = 2.5σ.
Charge-charge interactions between monomers are captured in an effective manner by the Debye–Hückel potential:
where lB is the Bjerrum length, lD = (4πlBn)−1/2 is the Debye length with the ion concentration n, rDH = 5.3lD is the cut-off radius, T is the temperature and kB is the Boltzmann constant. The dynamics of the monomers is governed by Newton’s equations of motion, which are solved by the velocity-Verlet algorithm [35].

2.2. Brownian Multiparticle Collision Dynamics

In order to perform isothermal simulations, we couple the microgel monomers with the Brownian multiparticle collision dynamics method (B-MPC) [32,36,37]. This is a non-hydrodynamic version of the multiparticle collision dynamics approach for fluid systems [36,38]. In B-MPC, a monomer performs a random collision with the fluid after a time increment, Δt, which is denoted as collision time. Thereby, we assign an effective fluid particle to every monomer. The velocity of the fluid particle of mass M (equal to the mass of a monomer) is taken from a Maxwell–Boltzmann distribution of variance MkBT. In the collision, the relative velocity of every monomer, with respect to the center-of-mass velocity:
where P is the fluid particle momentum and vi the monomer velocity, is rotated around a randomly oriented axis by a fixed angle, α. Thus, after a collision step, the velocity of the i-th monomer is:
with the rotation matrix R(α) and the unit matrix I [36].

2.3. Parameters

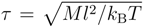We consider microgels comprised of polymers with Nm = 20 and 40 monomers of Nc = 147 and 729 cross-links, respectively. With the number of dangling ends Nd = 64 and 204, the ratios Nd/(Nc − Nd) are 0.39 and 0.77. In the largest system, the total number of monomers is N = 50,169. The topological structure of a microgel for Nc = 729 cross-links is illustrated in Figure 1.
We employ l as the unit of length, kBT as the unit of energy and M as the unit of mass. Thus, the unit of time is . The Lennard–Jones parameters are σ = 0.8l, ε/kBT = 0.5, 1.0 and 1.5 for a poor solvent and 1.0 for a good solvent. For the bonds, we set ks = 103kBT/l2. The collision time is Δt = 0.1τ, and we perform 20 molecular dynamics simulation steps between collisions. To achieve a reasonable statistical accuracy, we performed, at least, 5.0 × 104 collision steps, which corresponds to 106 molecular dynamics simulation steps, after reaching a stationary state in every simulation.

3. Results

3.1. Microgel in Good Solvent (lD = 0)

As a reference, we consider the polymer conformational properties of a microgel under good solvent conditions and lD = 0. Figure 2 displays the chain-length dependence of the polymer radius of gyration for Nc = 0, 147 and 729 . Here, is the square root of the average over all polymers of the mean square radius of gyration, where the radius of gyration of a polymer ( ) itself is defined by:
with the polymer center of mass:
The system with Nc = 0 corresponds to a non-cross-linked network. As expected, the radius of gyration exhibits the power-law dependence ~ (Nm − 1)v with the number of bonds. Thereby, the critical exponent, v, for the non-cross-linked polymers closely follows the theoretical prediction v ≈ 0.59 [39]. Similarly, the values for the systems with Nc = 147 and 729 follow a power law; however, with the somewhat larger exponent v ≈ 0.62. Hence, cross-linking leads to swelling of the polymer chains.
Further insight into the microgel structure is gained by the spherically averaged static structure factor [39]:
where q is the wave number with the magnitude q = |q|. As shown in Figure 3, in the vicinity of ql ≈ 0.05, we find a steep drop of the structure factor due to the spherical shape of a gel particle. For 0.6 < ql < 3, S(q) decays according to the power-law q−1/0.62 with increasing q, indicating the self-similarity of the polymer conformations. This is consistent with the scaling ~ (Nm − 1)0.62. Hence, the polymer conformations are determined by thermal fluctuations, intramolecular and intermolecular interactions and the cross-links.
Figure 2. Dependence of the average root mean square radius of gyration of polymers on the bond number Nm − 1 for Nc = 0 (squares), 147 (open squares) and 729 (bullets) under good solvent conditions (lD = 0). The solid line is proportional to N0.59 and the dashed lineto N0.62.
Figure 2. Dependence of the average root mean square radius of gyration of polymers on the bond number Nm − 1 for Nc = 0 (squares), 147 (open squares) and 729 (bullets) under good solvent conditions (lD = 0). The solid line is proportional to N0.59 and the dashed lineto N0.62.
Figure 3. Spherically averaged static structure factor S(q) of a microgel with Nc = 729 cross-links and a polymer length Nm = 40. The dashed line is proportional to q−1/0.62.
Figure 3. Spherically averaged static structure factor S(q) of a microgel with Nc = 729 cross-links and a polymer length Nm = 40. The dashed line is proportional to q−1/0.62.

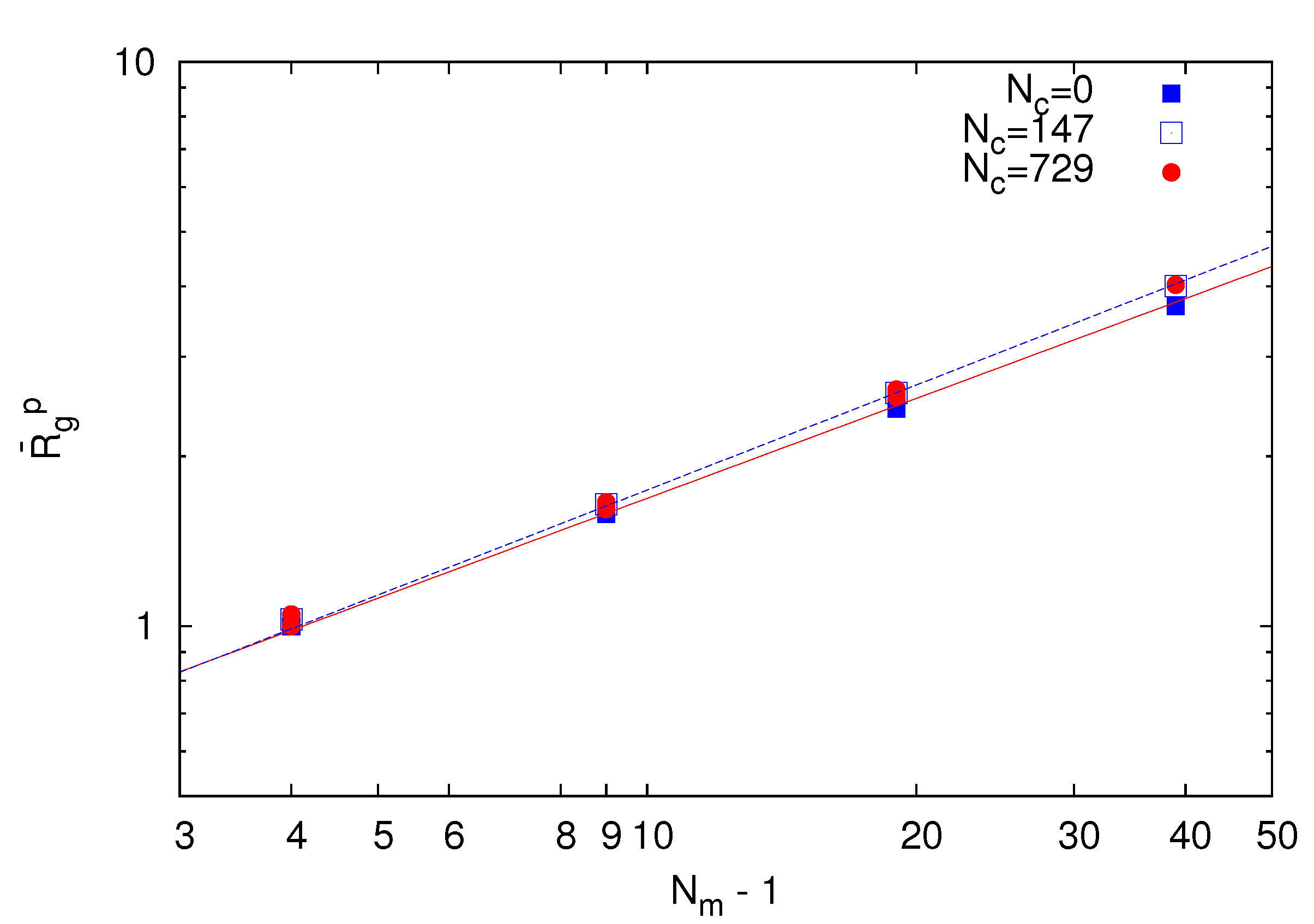
3.2. Microgel in Poor Solvent (lD = 0)

Figure 4 shows radial monomer distribution functions P(r) with respect to the microgel vcenter-of-mass for Nm = 40, Nc = 729 and various attraction strengths ε under poor solvent conditions.In addition, P(r) with lD = 0 under good solvent conditions is shown. The distribution function is normalized, such that:
With increasing ε, the size of a microgel particle shrinks and its density increases. As expected, microgels in a good solvent with lD = 0 are more swollen. This behavior is in qualitative agreement with experimental results [40,41,42]. The inset of Figure 4 indicates that P(r) decreases fast for r > Rg and vanishes at r ≳ 1.5Rg, where Rg is the average microgel radius of gyration. Thereby, the fuzziness of the surface decreases with increasing ε and the interface becomes rather sharper for large ε. The fuzziness for ε/kBT = 0.5 is comparable to that of a microgel in a good solvent with lD = 0.
Figure 4. Radial monomer distribution functions P(r) for a microgel with Nm = 40 and Nc = 729 under poor solvent conditions with ε/(kBT) = 1.5 (red), 1.0 (green) and 0.5 (blue). In addition, P(r) for lD = 0 under good solvent conditions is shown (black). Inset: the same distribution functions normalized by the respective radii of gyration, Rg, of the microgels.
Figure 4. Radial monomer distribution functions P(r) for a microgel with Nm = 40 and Nc = 729 under poor solvent conditions with ε/(kBT) = 1.5 (red), 1.0 (green) and 0.5 (blue). In addition, P(r) for lD = 0 under good solvent conditions is shown (black). Inset: the same distribution functions normalized by the respective radii of gyration, Rg, of the microgels.
The gel compaction is also reflected in the static structure factor displayed in Figure 5. The shift of the strongly dipping part of S(q) at ql ≈ 0.1 with increasing ε is reminiscent of the shrinkage of the microgel. In the range of 0.3 < ql < 2.0, S(q) is proportional to q−4.1 for ε/kBT = 1.0 and 1.5. This behavior is in close agreement with Porod’s law S(q) ∝ q−4 for a system with a sharp interface. In contrast, for ε/kBT = 0.5, S(q) is proportional to q−1/0.6 in the range of 0.6 < ql < 2.0,. 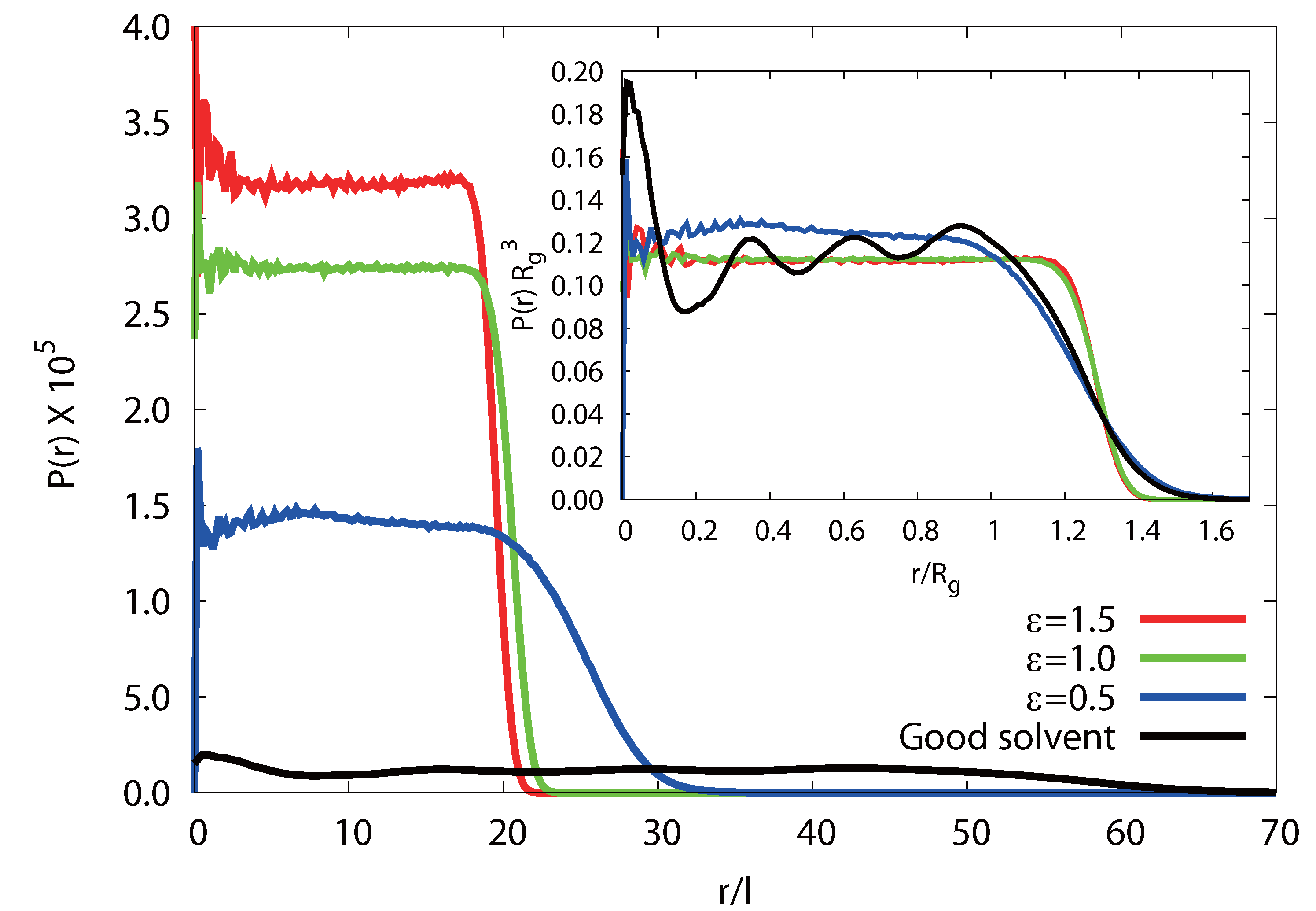Thus, scales as ∝ (Nm − 1)0.6 with polymer length, and the interface is less sharp. The scaling exponent, 0.6, is smaller than 0.62 obtained for microgels in a good solvent. Hence, the polymers are somewhat more compact for ε/kBT = 0.5 as compared to the bare good solvent system. The attractive interaction brings the polymers closer to the scaling behavior of free polymers.
Figure 5. Spherically averaged static structure factors S(q) for Np = 40, Nc = 729 and ε/kBT = 1.5 (red), 1.0 (green) and 0.5 (blue). The straight solid line is proportional to q−4.1 and the straight dashed line to q−1/0.6.
Figure 5. Spherically averaged static structure factors S(q) for Np = 40, Nc = 729 and ε/kBT = 1.5 (red), 1.0 (green) and 0.5 (blue). The straight solid line is proportional to q−4.1 and the straight dashed line to q−1/0.6.

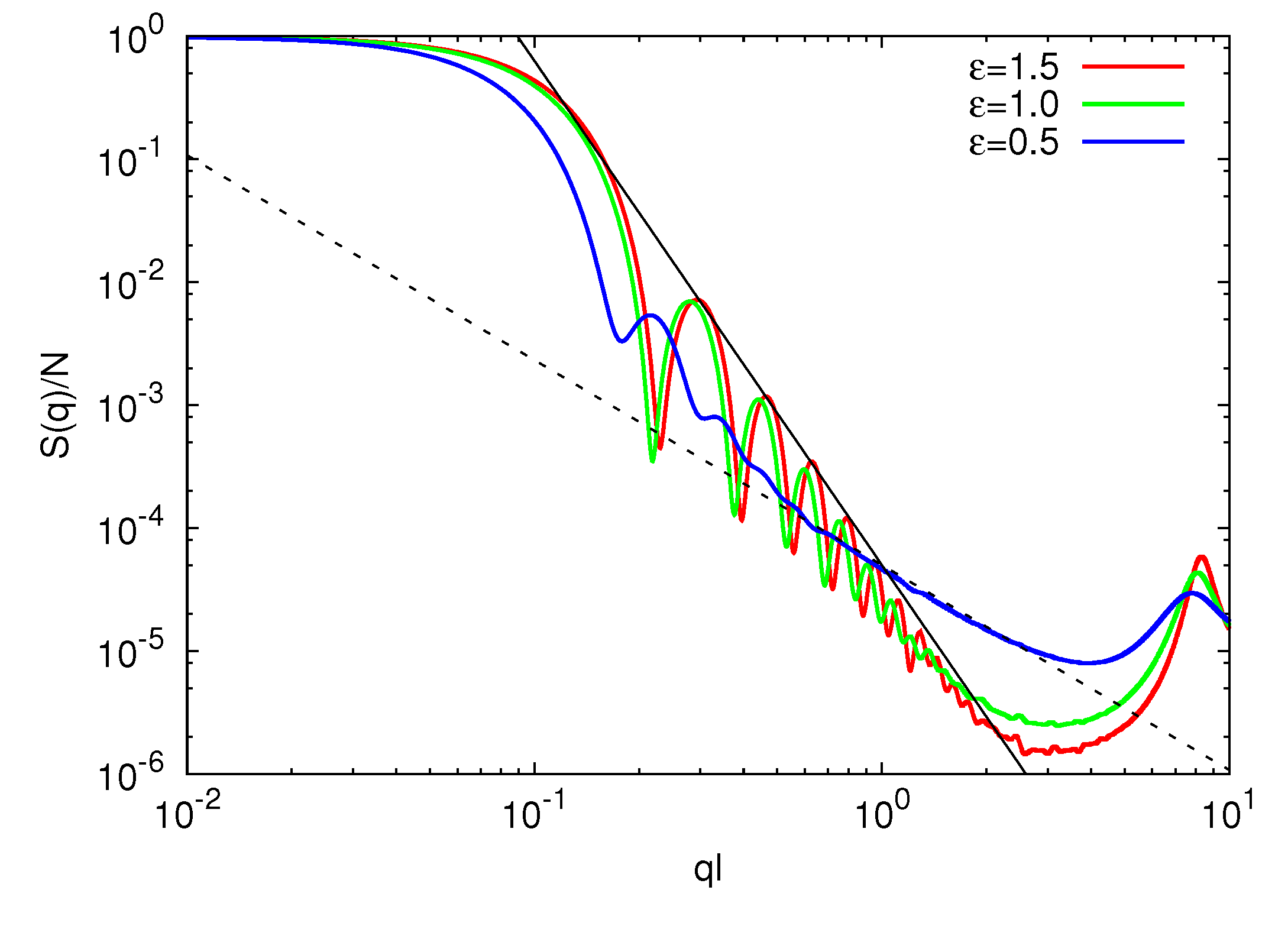
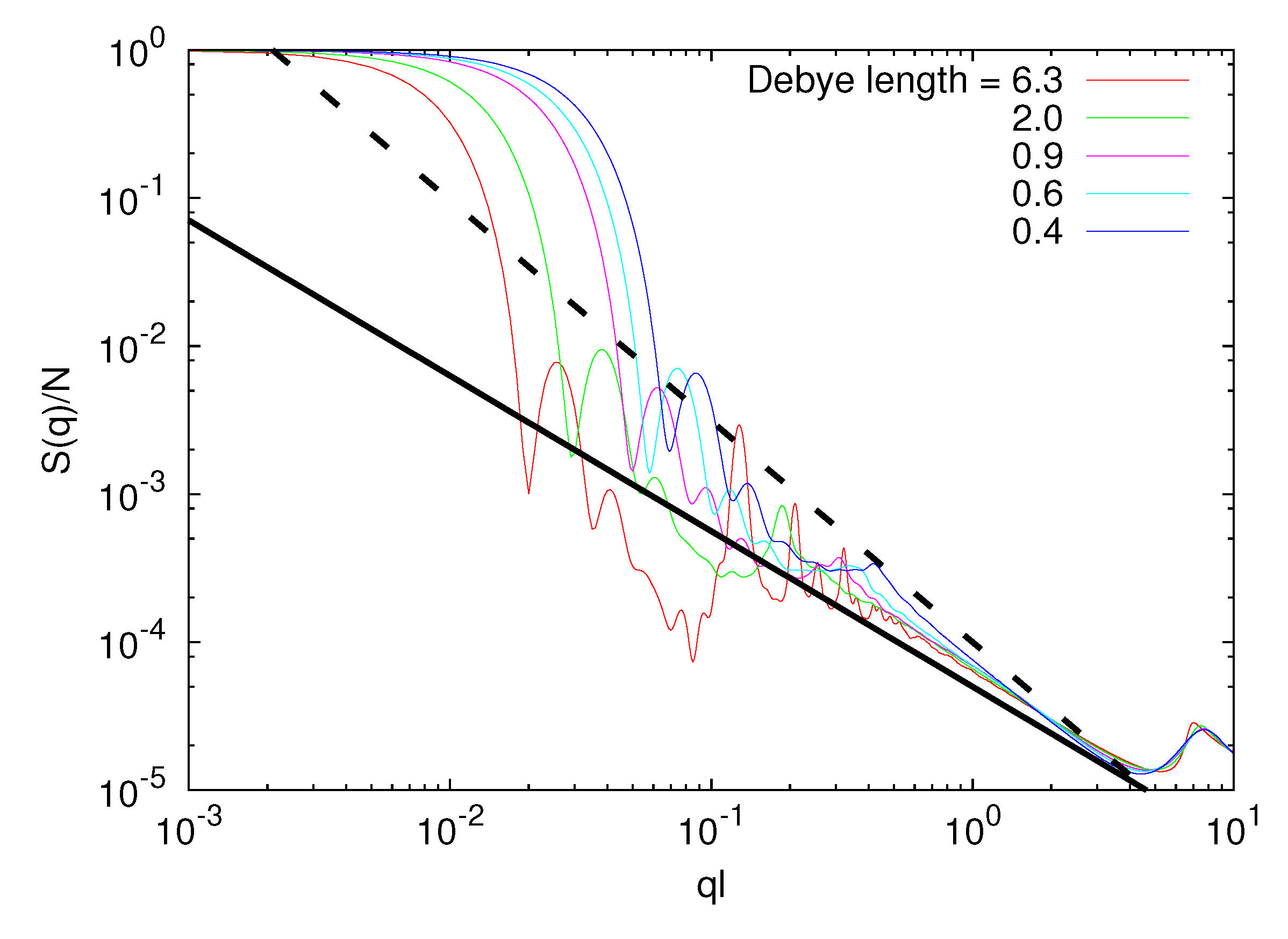
3.3. Microgel with Debye–Hückel Interaction

We now elucidate the conformational properties of microgels, where the monomers interact via the Debye–Hückel potential Equation (3). We focus on good solvent conditions, i.e., only the repulsive part of the Lennard–Jones potential is taken into account.

3.3.1. Microgel Radius of Gyration

The Debye–Hückel potential Equation (3) is a short-range potential, since it decays very fast with the distance between two particles. The actual range depends on the Debye length, lD. For lD ≪ σ < l, UDH decays so fast that it is essentially negligible. This corresponds to the limit where the charge-charge interactions in a system are screened and only excluded volume interactions remain. In the opposite limit, when the Debye length is larger than the microgel particle, there is a strong repulsion between monomers, and we expect the microgel to be swollen. This corresponds to unscreened charge-charge interactions within the microgel. Hence, by increasing lD, we expect a conformational change of the gel particle from a good solvent state to a fully swollen state and essentially stretched polymers. This expectation is reflected in Figure 6, where the microgel radius of gyration is shown for various Bjerrum and Debye lengths. The onset of the increase in particle size depends on the Bjerrum length; the larger the Bjerrum length, the earlier the increase. Moreover, the slope of the increasing curve increases somewhat with increasing lB. Interestingly, the swelling behavior only weakly depends on the number of cross-links. Here, we conclude that the microgel behavior should be very similar to the behavior of a macroscopic gel, i.e., there is little effect due to the finite size of the microgel. However, we observe a polymer-length dependence of the swelling behavior. The microgels with Nm = 40 swell significantly faster with increasing Debye length compared to the shorter polymers. Hence, we speculate that very long polymers will show a very steep increase in the form of a first order phase transition.
Figure 6. The dependence of the radius of gyration, Rg, of a microgel on the Debye length, lD, for various Bjerrum lengths, lB, Nm = 20 and 40, and Nc = 147 and 729. denotes the radius of gyration of a microgel under good solvent conditions.
Figure 6. The dependence of the radius of gyration, Rg, of a microgel on the Debye length, lD, for various Bjerrum lengths, lB, Nm = 20 and 40, and Nc = 147 and 729. denotes the radius of gyration of a microgel under good solvent conditions.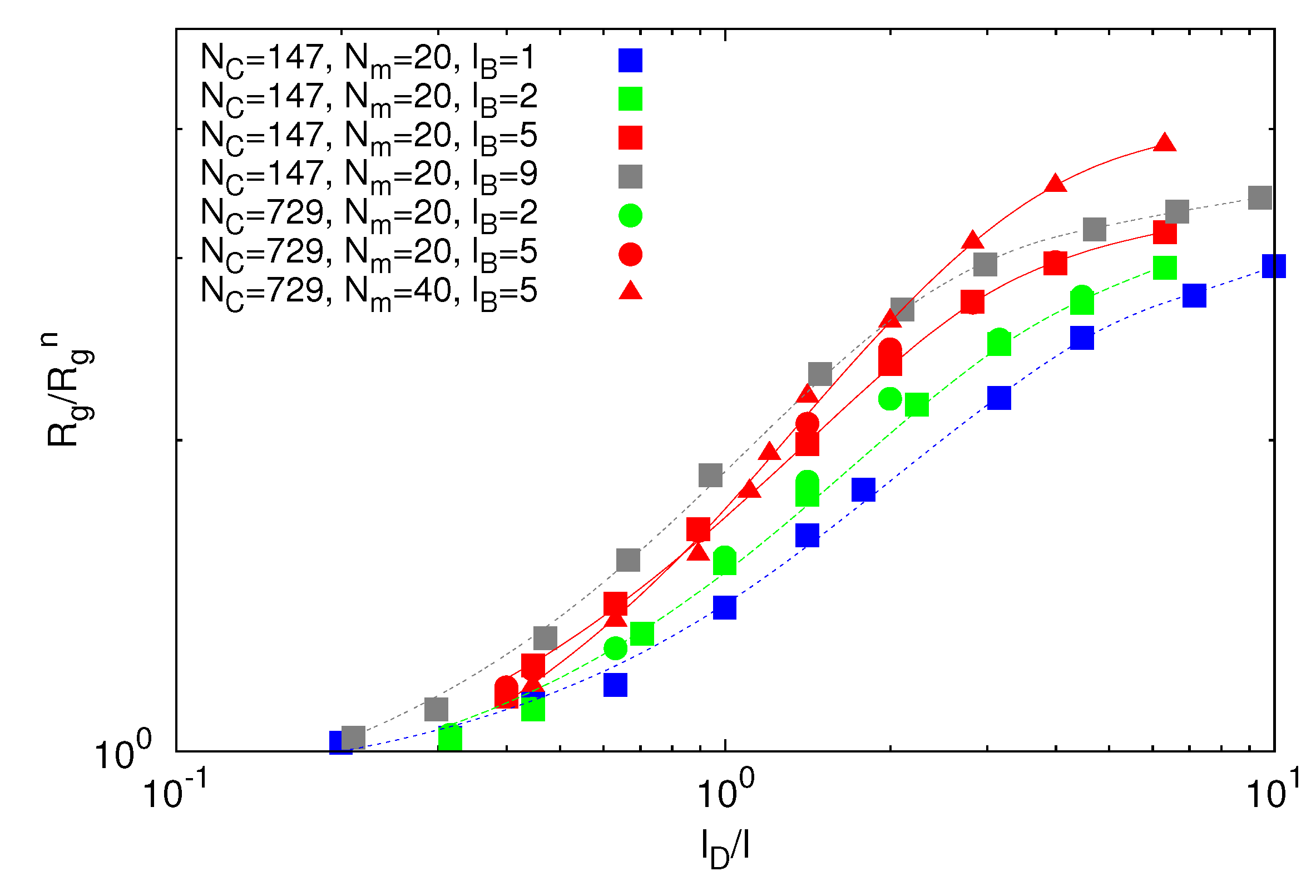

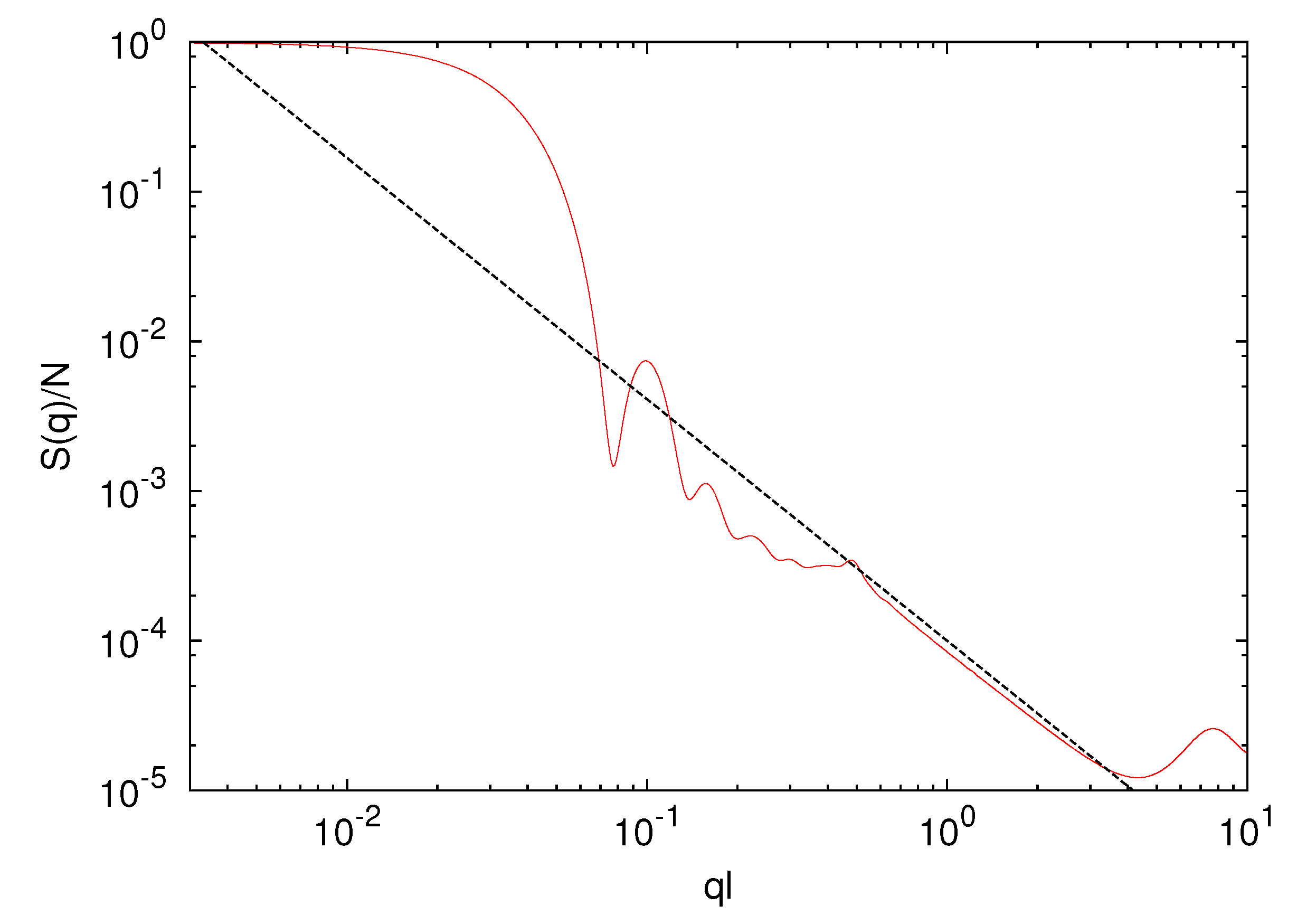
3.3.2. Microgel Structure Factor

Figure 7 displays structure factors of microgels for various Debye lengths. The shift of the initial decay (small q values) with increasing lD toward smaller q values reflects the swelling of the microgel. The surface is rather sharp for all lD, as indicated by the steep decay and the appearing successive oscillations. More importantly, on the length scale of the polymers, we see a crossover in the chain conformations from a self-avoiding to a rod-like polymer. For lD/l = 0.4 and lD/l = 6.3, S(q) is proportional to q−1/0.67 and q−1.05, respectively, in the range of 0.05 ≲ ql ≲ 0.3. We obtain a somewhat larger scaling exponent v = 0.67 compared to the good solvent value due to monomer repulsion.
Figure 7. Spherically averaged static structure factors S(q) for Nc = 729, Nm/ = 40, lB/l = 5 and lD/l = 0.4 − 6.3. The solid line is proportional to q−1.05 and the dashed line to q−1/0.67.
Figure 7. Spherically averaged static structure factors S(q) for Nc = 729, Nm/ = 40, lB/l = 5 and lD/l = 0.4 − 6.3. The solid line is proportional to q−1.05 and the dashed line to q−1/0.67.

3.3.3. Polymer Size Scaling

From simulations, we can extract the average polymer radii of gyration for the various Debye lengths. Since the Debye–Hückel potential is of short-range order, we assume that the polymer radius of gyration obeys the scaling relation:
where L = (Nm − 1)l is the contour length and Lp is the persistence length. L = Lp is the number of persistence lengths per polymer length. This approach is similar to the blob picture with the characteristic length scale Lp [43]. Here, we defined Lp as Lp = l + le, with the persistence length:
due to electrostatic interactions. Equation (11) is the well-known OSF relation, derived by Odijk [44] and Skolnick and Fixman [45] in the limit of a weakly bending charged rod. The relation between le and lD strongly depends on the underlying polymer model [46]. Previous works reported that le ∝ for freely jointed chains with fixed bond lengths [47,48,49]. Figure 8 shows the radii of gyration for the various considered systems. We obtain a rather good scaling behavior for all obtained values. For small L/Lp (≤ 2), /Lp increases linearly with L/Lp, i.e., the polymers exhibit rod-like behavior, whereas for L/Lp ≳ 4, Rg/Lp ~ L0.6, i.e., it crosses over to self-avoiding walk behavior. Similar results have been reported in previous studies on a single polyelectrolyte chain [47,50]. The scaling results are in agreement with the observed dependencies of the structure factors of Figure 7.
Figure 8. Dependence of the ratio /Lp on the ratio L/Lp for Nc = 0, 147 and 729, Np = 20 and 40 and lB/l = 1,2,5 and 9. The black line is proportional to (L/Lp)0.6 and the red line to L/Lp.
Figure 8. Dependence of the ratio /Lp on the ratio L/Lp for Nc = 0, 147 and 729, Np = 20 and 40 and lB/l = 1,2,5 and 9. The black line is proportional to (L/Lp)0.6 and the red line to L/Lp.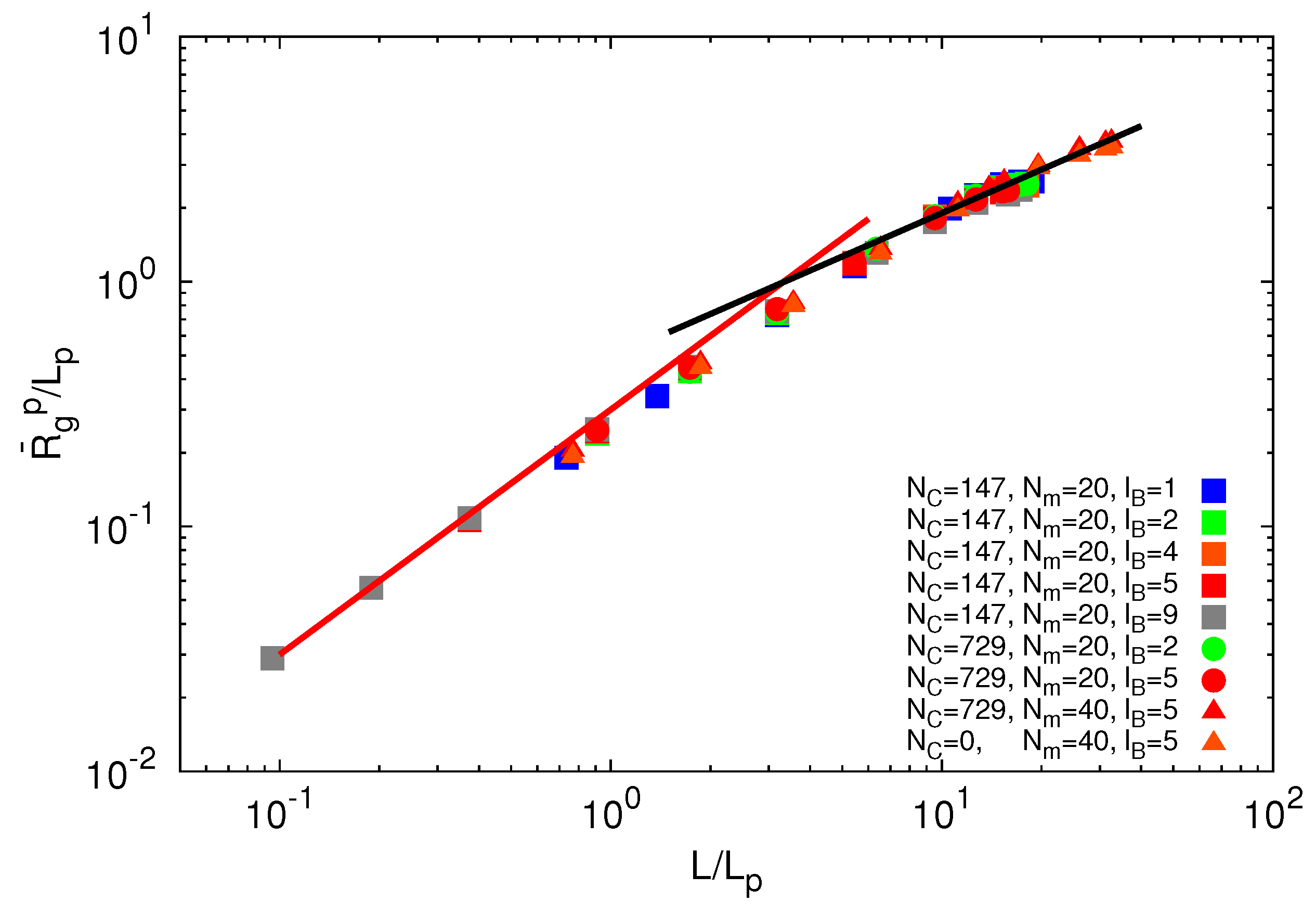

3.3.4. Radial Monomer Distribution

Figure 9 shows radial monomer distribution functions for various Debye lengths and a microgel in a poor solvent. Already for small Debye lengths, characteristic peaks appear due to the underlying diamond lattice structure of the cross-linked microgel. The undulations are weak for lD/l ≲ 1, but they become rather sharp for large lD. Note that the density distribution for a microgel under good solvent conditions with lD = 0 is close to the distribution for lD/l = 0.4. We do not necessarily expect such a detailed structure for a real microgel, since the polymer lengths are rather polydisperse and the cross-link density is inhomogeneous. In the range of r/Rg > 1, the density profiles decrease for lD/l > 3 as fast as P(r) of a microgel in a poor solvent with ε/kBT = 1.5. This indicates that the microgel has a sharp boundary, and peripheral polymers are smaller than internal polymers. For small lD, P(r) gradually decreases in the vicinity of the surface. The fuzzy boundary implies that the radius of gyration of a polymer at the surface is larger than that in the interior.
Figure 9. Radial monomer distribution functions for various Debye lengths, lD/l, Nc = 729, Nm = 40 and lB/l = 5. In addition, P(r) for ε/kBT = 1.5 under poor solvent conditions is shown.
Figure 9. Radial monomer distribution functions for various Debye lengths, lD/l, Nc = 729, Nm = 40 and lB/l = 5. In addition, P(r) for ε/kBT = 1.5 under poor solvent conditions is shown.
We find a rather high monomer concentration in the vicinity of the center-of-mass of the microgel at larger lD. This is a consequence of the on average isotropic distribution of monomers and a cross-link at the location of the center of mass.

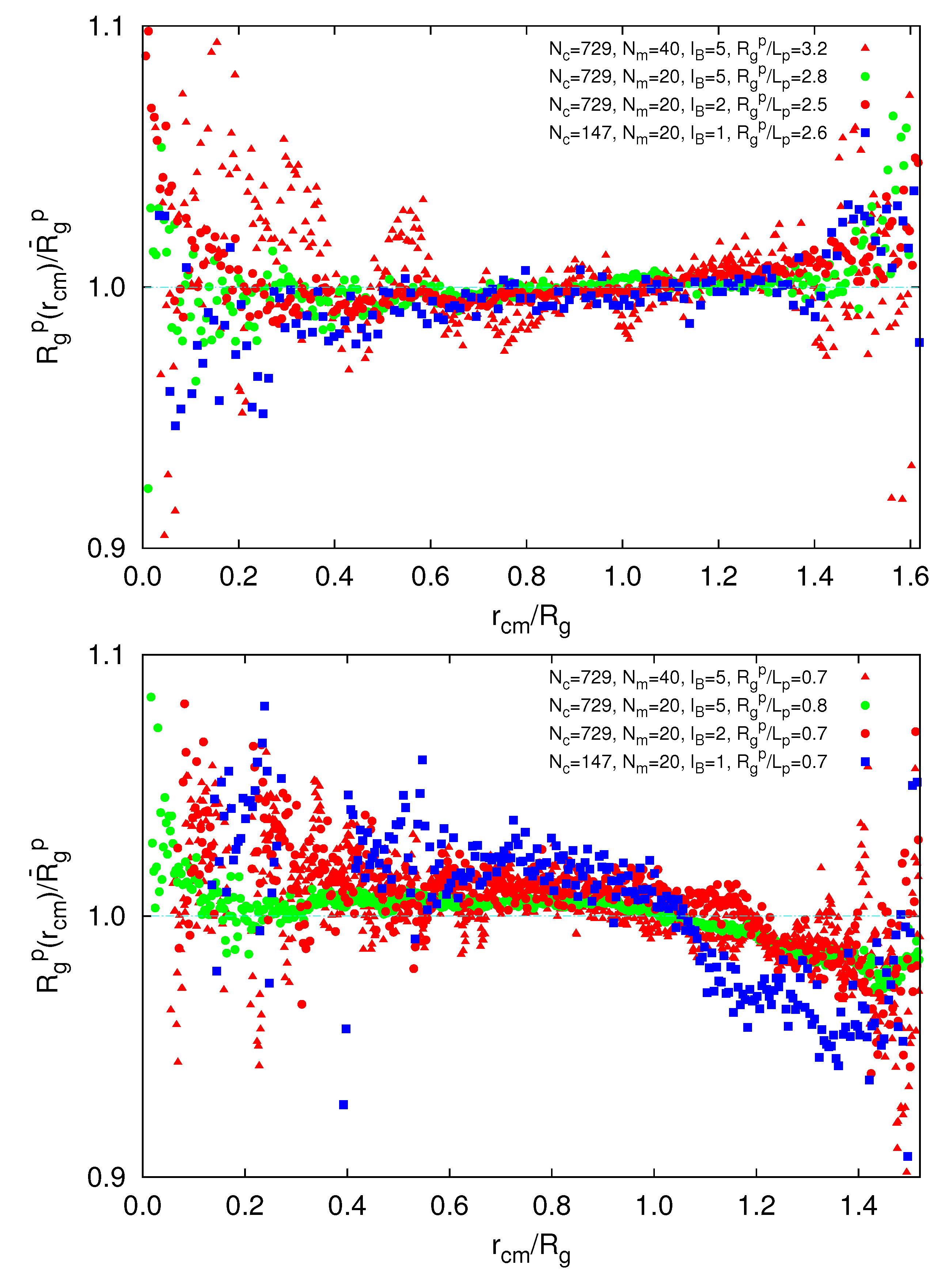
3.3.5. Radial Polymer Conformation

To gain insight into possible inhomogeneous polymer conformations, we consider the radial dependence of the polymer radius of gyration, (rcm), in a microgel. As shown in Figure 10, we find a qualitative difference for /Lp > 2.5 and /Lp < 1. For /Lp > 2.5, i.e., lD/l ≲ 0.45, exceeds the mean value at large rcm/Rg. Hence, polymers near the surface are swollen as compared to internal polymers. We attribute the inhomogeneities to anisotropic intramolecular interactions by short-range repulsion. Internal polymers experience an almost isotropic interaction, whereas at the surface, the symmetry is broken and repulsion is stronger from inside to outside, which leads to a swelling. For /Lp < 1, i.e., lD/l ≳ 2, is smaller than the average value at large rcm/Rg. Thus, the outside polymers are somewhat more compact than the internal polymers. This is attributed to the inhomogeneous radial monomer distribution, as displayed in Figure 9. The larger interaction range of the Debye-Hückel potential for these parameters combined with a larger number of neighbors leads to the stronger swelling of internal polymers than those at the surface. Overall, the effect is small, but is a consequence of the finite size of a microgel and is thus not present in bulk systems.
Figure 10. Dependence of the polymer radius of gyration on its radial center-of-mass position, rcm, for /Lp > 2.5 (top) and /Lp < 1 (bottom), Nc = 147 and 729 and Nm = 20 and 40. The upper bounds of rcm are defined by the condition .
Figure 10. Dependence of the polymer radius of gyration on its radial center-of-mass position, rcm, for /Lp > 2.5 (top) and /Lp < 1 (bottom), Nc = 147 and 729 and Nm = 20 and 40. The upper bounds of rcm are defined by the condition .

4. Summary and Conclusions

We have performed large-scale molecular dynamics simulations to unravel the structural properties of finite-size polyelectrolyte microgel particles and the conformations of their comprising linear polymers. Counterions are treated implicitly via the Debye-Hückel potential. We find radially inhomogeneous polymer conformations due to the finite size of the microgel. Thereby, polymers at the surface are swollen compared to internal polymers for microgels where polymers exhibit self-avoiding walk scaling behavior. Oppositely, peripheral polymers are more compact for microgels where polymers behave rod-like. The difference in polymer conformations is also reflected in the radial monomer distribution function. Due to the swelling of surface polymers, the surface of a microgel becomes fuzzy, and the density decays gradually to zero. Oppositely, microgels display a rather sharp surface with a fast decaying monomer density in the case of more compact polymers. Although differences in the radial dependence of the polymer radii of gyration shown in Figure 10 are small, it is a consequence of the finite size of a microgel.
In general, the radial variations of the polymer properties are surprisingly small. We expected more severe inhomogeneities. The smooth variations suggest that the microgel properties are rather similar to those of the bulk properties of macrogels, at least as along as the Debye-Hückel description applies.
We considered a model microgel with an underlying diamond-lattice structure of the cross-links. This certainly is not the case of typical synthetic microgels. Although we do not expect severe differences between microgels with a more random distribution of polymer lengths and cross-link density for the adopted Debye-Hückle description, a more generalized description is desirable for a quantitative comparison with experimental results. The structure will definitely matter for the transport of particles in the microgel.
The presented results are intended as a reference for simulation studies of microgels where monomers interact by the bare Coulomb potential and where counterions are taken into account explicitly. The comparison will shed light on the influence of explicit ions on the structure of a microgel. Specifically, the inhomogeneous charge distribution of the spherical particle implies an inhomogeneous distribution of counterions (in the simplest case, it can be considered as a radially dependent Debye length), and correspondingly, interesting effects appear, which reach beyond those presented in the current article. Such studies are currently under way.

Acknowledgments

The authors gratefully acknowledge the computing time granted on the supercomputer JUROPA at Jülich Supercomputing Centre (JSC). We also acknowledge financial support from the Deutsche Forschungsgemeinschaft within the Sonderforschungsbereich SFB 985 “Functional Microgels and Microgel Systems”.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tanaka, T. Collapse of gels and the critical endpoint. Phys. Rev. Lett. 1978, 40, 820–823. [Google Scholar] [CrossRef]
  2. Ilmain, F.; Tanaka, T.; Kokufuta, E. Volume transition in a gel driven by hydrogen bonding. Nature 1991, 349, 400–401. [Google Scholar] [CrossRef]
  3. Tanaka, T.; Nishio, I.; Sun, S.T.; Ueno-Nishio, S. Collapse of gels in an electric field. Science 1982, 218, 467–469. [Google Scholar] [CrossRef]
  4. Polotsky, A.A.; Plamper, F.A.; Borisov, O.V. Collapse-to-swelling transitions in pH- and thermoresponsive microgels in aqueous dispersions: The thermodynamic theory. Macromolecules 2013, 46, 8702–8709. [Google Scholar]
  5. Das, M.; Zhang, H.; Kumacheva, E. MICROGELS: Old materials with new applications. Annu. Rev. Mater. Res. 2006, 36, 117–142. [Google Scholar]
  6. Richter, A.; Paschew, G.; Klatt, S.; Lienig, J.; Arndt, K.F.; Adler, H.J.P. Review on hydrogel-based pH sensors and microsensors. Sensors 2008, 8, 561–581. [Google Scholar] [CrossRef]
  7. Oh, J.K.; Drumright, R.; Siegwart, D.J.; Matyjaszewski, K. The development of microgels/nanogels for drug delivery applications. Prog. Polym. Sci. 2008, 33, 448–477. [Google Scholar] [CrossRef]
  8. Saunders, B.R.; Laajam, N.; Daly, E.; Teow, S.; Hu, X.; Stepto, R. Microgels: From responsive polymer colloids to biomaterials. Adv. Colloid Interface Sci. 2009, 147-148, 251–262. [Google Scholar] [CrossRef]
  9. Delcea, M.; Möhwald, H.; Skirtach, A.G. Stimuli-responsive LbL capsules and nanoshells for drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 730–747. [Google Scholar] [CrossRef]
  10. Tan, B.H.; Tam, K.C. Review on the dynamics and micro-structure of pH-responsive nano-colloidal systems. Adv. Colloid Interface Sci. 2008, 136, 25–44. [Google Scholar] [CrossRef]
  11. Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; et al. Emerging applications of stimuli-responsive polymer materials. Nat. Mater 2010, 9, 101–113. [Google Scholar] [CrossRef]
  12. Gokmen, M.T.; Prez, F.E.D. Porous polymer particles: A comprehensive guide to synthesis, characterization, functionalization and applications. Prog. Polym. Sci. 2012, 37. [Google Scholar] [CrossRef]
  13. Thorne, J.B.; Vine, G.J.; Snowden, M.J. Microgel applications and commercial considerations. Colloid Polym. Sci. 2011, 289, 625–646. [Google Scholar]
  14. Khokhlov, A.R.; Starodubtzev, S.G.; Vasilevskay, V.V. Conformational transitions in polymer gels: Theory and experiment. Adv. Polym. Sci. 1993, 109, 123–171. [Google Scholar] [CrossRef]
  15. Schneider, S.; Linse, P. Swelling of cross-linked polyelectrolyte gels. Eur. Phys. J. E Soft Matter 2002, 8, 457–460. [Google Scholar]
  16. Schneider, S.; Linse, P. Monte Carlo simulation of defect-free cross-linked polyelectrolyte gels. J. Phys. Chem. B 2003, 32, 8030–8040. [Google Scholar] [CrossRef]
  17. Lu, Z.Y.; Hentschke, R. Computer simulation study on the swelling of a polyelectrolyte gel by a Stockmayer solvent. Phys. Rev. E 2003, 67. [Google Scholar] [CrossRef]
  18. Yan, Q.; de Pablo, J.J. Monte Carlo simulation of a coarse-grained model of polyelectrolyte networks. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
  19. Mann, B.A.; Everaers, R.; Holm, C.; Kremer, K. Scaling in polyelectrolyte networks. Europhys. Lett. 2004, 67, 786–792. [Google Scholar] [CrossRef]
  20. Schneider, S.; Linse, P. Discontinuous volume transitions in cross-linked polyelectrolyte gelsinduced by short-range attractions and strong electrostatic coupling. Macromolecules 2004, 37, 3850–3856. [Google Scholar] [CrossRef]
  21. Mann, B.A.; Holm, C.; Kremer, K. Swelling of polyelectrolyte networks. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef]
  22. Edgecombe, S.; Linse, P. Monte Carlo simulations of cross-linked polyelectrolyte gels with oppositely charged macroions. Langmuir 2006, 22, 3836–3843. [Google Scholar]
  23. Mann, B.A.; Kremer, K.; Holm, C. The swelling behavior of charged hydrogels. Macromol. Symp. 2006, 237, 90–107. [Google Scholar] [CrossRef]
  24. Yin, D.W.; Horkay, F.; Douglas, J.F.; de Pablo, J.J. Molecular simulation of the swelling of polyelectrolyte gels by monovalent and divalent counterions. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef]
  25. Yin, D.W.; de la Cruz, M.O.; de Pablo, J.J. Swelling and collapse of polyelectrolyte gels in equilibrium with monovalent and divalent electrolyte solutions. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef]
  26. Quesada-Peres, M.; Ramos, J.; Forcada, J.; Martin-Molina, A. Computer simulations of thermo-sensitive microgels: Quantitative comparison with experimental swelling data. J. Chem. Phys. 2012, 136. [Google Scholar] [CrossRef]
  27. Quesada-Peres, M.; Maroto-Centeno, J.A.; Martin-Molina, A. Effect of the counterion valence on the behavior of thermo-sensitive gels and microgels: A monte carlo simulation study. Macromolecules 2012, 45, 8872–8879. [Google Scholar] [CrossRef]
  28. Claudio, G.C.; Kremer, K.; Holm, C.J. Comparison of a hydrogel model to the Poisson-Boltzmann cell model. J. Chem. Phys. 2009, 131. [Google Scholar] [CrossRef]
  29. Jha, P.K.; Zwanikken, J.W.; Detcheverry, F.A.; de Pablo, J.J.; de la Cruz, M.O. Study of volume phase transitions in polymeric nanogels by theoretically informed coarse-grained simulations. Soft Matter 2011, 7, 5965–5975. [Google Scholar] [CrossRef]
  30. Jha, P.K.; Zwanikken, J.W.; de Pablo, J.J.; de la Cruz, M.O. Electrostatic control of nanoscale phase behavior of polyelectrolyte networks. Curr. Opin. Solid State Mater. Sci. 2011, 15, 271–276. [Google Scholar] [CrossRef]
  31. Denton, A.R. Counterion penetration and effective electrostatic interactions in solutions of polyelectrolyte stars and microgels. Phys. Rev. E 2003, 67. [Google Scholar] [CrossRef]
  32. Ripoll, M.; Winkler, R.G.; Gompper, G. Hydrodynamic screening of star polymers in shear flow. Eur. Phys. J. E Soft Matter 2007, 23, 349–354. [Google Scholar] [CrossRef]
  33. Winkler, R.G.; Gold, M.; Reineker, P. Collapse of polyelectrolyte macromolecules by counterion condensation and ion pair formation: A molecular dynamics simulation study. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
  34. Frank, S.; Winkler, R.G. Polyelectrolyte electrophoresis: Field effects and hydrodynamic interactions. EPL 2008, 83, 38004:1–38004:6. [Google Scholar]
  35. Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
  36. Gompper, G.; Ihle, T.; Kroll, D.M.; Winkler, R.G. Multi-Particle Collision Dynamics: A particle-based mesoscale simulation approach to the hydrodynamics of complex Fluids. Adv. Polym. Sci. 2009, 221, 1–87. [Google Scholar]
  37. Winkler, R.G. Flow simulations with multiparticle collision dynamics. In Hierarchical Methods for Dynamics in Complex Molecular Systems: IAS Series; Grotendorst, J., Sutmann, G., Gompper, G., Marx, D., Eds.; Forschungszentrum Jülich GmbH: Jülich, Germany, 2012. [Google Scholar]
  38. Kapral, R. Multiparticle collision dynamics: Simulations of complex systems on mesoscale. Adv. Chem. Phys. 2008, 140. [Google Scholar] [CrossRef]
  39. Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
  40. Senff, H.; Richtering, W. Temperature sensitive microgel suspensions: Colloidal phase behavior and rheology of soft spheres. J. Chem. Phys. 1999, 111. [Google Scholar] [CrossRef]
  41. Stieger, M.; Richtering, W.; Pedersen, J.S.; Lindner, P. Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids. J. Chem. Phys. 2004, 120, 6197–6206. [Google Scholar]
  42. Scherzinger, C.; Holderer, O.; Richter, D.; Richtering, W. Polymer dynamics in responsive microgels: Influence of cononsolvency and microgel architecture. Phys. Chem. Chem. Phys. 2012, 14, 2762–2768. [Google Scholar] [CrossRef]
  43. De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University: Ithaca, Greece, 1979. [Google Scholar]
  44. Odijk, T. Polyelectrolytes near the rod limit. J. Polym. Sci., Polym. Phys. Ed. 1977, 15, 477–483. [Google Scholar] [CrossRef]
  45. Skolnick, J.; Fixman, M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules 1977, 10, 944–948. [Google Scholar] [CrossRef]
  46. Fixman, M. Electrostatic persistence length. J. Chem. Phys. 2010, 114, 3185–3196. [Google Scholar]
  47. Ullner, M. Comments on the scaling behavior of flexible polyelectrolytes within the Debye-Hückel approximation. J. Phys. Chem. B 2003, 107, 8097–8110. [Google Scholar] [CrossRef]
  48. Nguyen, T.T.; Shklovskii, B.I. Persistence length of a polyelectrolyte in salty water: Monte Carlo study. Phys. Rev. E 2002, 66. [Google Scholar] [CrossRef]
  49. Everaers, R.; Milchev, A.; Yamakov, V. The electrostatic persistence length of polymers beyond the OSF limit. Eur. Phys. J. E 2002, 8, 3–14. [Google Scholar] [CrossRef]
  50. Micka, U.; Kremer, K. Persistence length of the Debye-Hückel model of weakly charged flexible polyelectrolyte chains. Phys. Rev. E 1996, 54, 2653–2662. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Kobayashi, H.; Winkler, R.G. Structure of Microgels with Debye–Hückel Interactions. Polymers 2014, 6, 1602-1617. https://doi.org/10.3390/polym6051602

AMA Style

Kobayashi H, Winkler RG. Structure of Microgels with Debye–Hückel Interactions. Polymers. 2014; 6(5):1602-1617. https://doi.org/10.3390/polym6051602

Chicago/Turabian Style

Kobayashi, Hideki, and Roland G. Winkler. 2014. "Structure of Microgels with Debye–Hückel Interactions" Polymers 6, no. 5: 1602-1617. https://doi.org/10.3390/polym6051602

APA Style

Kobayashi, H., & Winkler, R. G. (2014). Structure of Microgels with Debye–Hückel Interactions. Polymers, 6(5), 1602-1617. https://doi.org/10.3390/polym6051602

Article Metrics

Back to TopTop