Abstract
Advances in functionality and reliability of carbon nanotube (CNT) composite materials require careful formulation of processing methods to ultimately realize the desired properties. To date, controlled dispersion of CNTs in a solution or a composite matrix remains a challenge, due to the strong van der Waals binding energies associated with the CNT aggregates. There is also insufficiently defined correlation between the microstructure and the physical properties of the composite. Here, we offer a review of the dispersion processes of pristine (non-covalently functionalized) CNTs in a solvent or a polymer solution. We summarize and adapt relevant theoretical analysis to guide the dispersion design and selection, from the processes of mixing/sonication, to the application of surfactants for stabilization, to the final testing of composite properties. The same approaches are expected to be also applicable to the fabrication of other composite materials involving homogeneously dispersed nanoparticles.
1. Introduction
Remarkable improvements in the electrical and mechanical properties of composite materials, when carbon nanotubes (CNTs) are used as fillers instead of other conventional materials, have been demonstrated by early works from [1,2,3]. New opportunities arise due to the incorporation of CNTs into polymer and elastomer matrices, producing tunable dielectrics and compliant conductors [4,5,6,7] for uses within consumer electronic devices. Further development of such a composite system could also greatly enhance the performance of electrically activated artificial muscles, and the bio-interfacing of electronic devices with soft tissues, e.g., for medical implants [8,9,10]. Advances in functionality and reliability of CNT-composite materials require careful formulation of processing methods to ultimately realize the desired properties. However, in spite of many reports claiming successful preparation, controlling the microstructure of such a composite system remains a challenge. This is primarily due to the strong interaction forces that cause the formations of bundles and clusters in as-produced CNTs. Conventional methods of producing a composite involves directly mixing as-produced CNT fillers into a polymer matrix. The dispersion and arrangement of CNTs in the matrix (including their potential uniaxial alignment) hold a central role in controlling the properties of the resulting composites. Here, we review the dispersion processes of pristine (non-functionalized) carbon nanotubes in a solvent or a polymer solution. Unlike many other studies in the field, which focus on experimentation and testing of a suitable dispersion process, we summarize and adapt relevant theoretical analysis to guide of dispersion design and selection. The Review starts from the processes of mixing/sonication, to the application of surfactants for stabilization, and finally to the testing of composite electrical properties. The same approaches are expected to be also applicable to the fabrication of other composite materials involving homogeneously dispersed nanoparticles.
2. Criteria for Dispersion
When being mixed in a solution, filler aggregates are subjected to shear stresses imparted from the medium (e.g., solvent or polymer melt). Therefore, the flow of the medium in response to an external force (e.g., through the rotation of a mixer blade, or cavitation in ultrasonication) generates the local shear stresses that are ultimately responsible for dispersion. A mixing process can be interpreted as the delivery of a mechanical energy into the solution to separate the aggregates. The opposing factor against separation is the binding energy which holds the aggregates together. Considering the above two factors, one can establish the mixing criteria for effective aggregate separation as: the supplied energy (or, to be more precise, the local energy density) from the chosen mixing technique to be greater than the binding energy of the CNT aggregates (to be more precise, the energy per local volume of the contact). On the other hand, to retain the morphology of individual CNTs, the supplied energy should also be lower than the amount required to fracture a nanotube. Hence, an ideal aggregate separation technique should supply an energy density between the binding energy of the aggregates (lower limit), and the fracture resistance of individual nanotubes (upper limit). In the following sections, the relative energy scale associated with each of the three factors will be evaluated. We will also elucidate how one can predict the likely morphology and microstructure of the CNTs-polymer composite resulted from a particular mixing technique.
2.1. Binding Energies Holding the Nanotube Aggregates
We will first evaluate the binding forces associated with carbon nanotube network and clusters. Real forms of CNTs vary significantly depending on their synthesis methods. They have as-produced lengths ranging from hundreds of nanometers to tens of microns, and often contain defects in their walls, hence are not completely straight over their contours. Furthermore, they are rarely present in isolated entities but instead are found in bundles or clusters. Figure 1 shows two typical examples of CNTs of different morphologies: (a) illustrates the arc-discharged single-wall nanotubes (SWNTs), where each of the fine strands consists of tens or even hundreds of micron-long SWNTs; and (b) shows the common commercially available multi-wall nanotube (MWNT) clusters. Although CNTs see a large variation in their physical attributes across different types, the interaction forces between pairs of nanotubes can be estimated through theoretical models to be illustrated below.
Using a continuum model by integration over the tubular surfaces of two parallel (10,10) SWNT, Girifalco et al. [11] calculated the cohesion energy per unit length between the SWNT pair to be ca. −0.095 eV/Å; the associated energy is −0.36 eV/Å for a bundle formed by the same SWNTs. The equilibrium distance between the tube axes was calculated to be ca. 18 Å, or 2.5 times the radius of the (10,10) SWNT. Since the pair cohesion energy per unit length is much greater in magnitude than the room temperature thermal energy (ca. 0.025 eV), ‘unzipping’ of a SWNT from an existing bundle is unlikely, despite of the fact that tubes in a separated state have higher configurational entropy. The computer simulation [11] also provides a solution to the equilibrium spacing (Hc) of nanotube sections in close proximity. This spacing (outer-wall to outer-wall) is weakly dependent on the diameter of nanotubes; and has a value of 3.14 Å, similar to the inter-plane spacing of graphite.
One can generalize the analysis of van der Waals (VdW) attraction by introducing the relevant Hamaker constant, AH [12]. By modeling each CNT as a meso-scale rod continuum, one can determine the interaction energy associated with different pair configurations through classical solutions (these can be found in text books, like [13]). Hamaker constant is experimentally shown to be ca. 60 × 10−20 J (3.8 eV) for the van der Waals attraction between an outer-wall of the MWNT and the metallic surface at a vacuum of 10−3 Pa. One would expect the AH between the side walls of CNTs to be slightly lower, but not much different from the value reported above. With the knowledge of AH, one can determine the van der Waals energy between a pair of parallel CNTs. This is analogous to the solution which describes the van der Waals interaction energy between two parallel mesoscopic cylinders of length L, diameter d = 2r, separated by a gap H is:
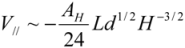 for
for 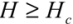 (1)
(1)Taking AH = 3.8 eV and Hc = 3.4 Å to estimate the V// per unit length, for the (10,10) SWNT (diameter of 1.36 nm), Equation (1) yields an attractive potential V// /L ~ −0.09 eV/Å. This matches the pair interaction value V// /L ~ −0.095 eV/Å calculated in [11].
It is noted that, the van der Waals effect alone is not sufficient to account for the different bundling and clustering morphologies present. Analyzing Equation (1), one can note that V// increases with diameter, which predicts that thick nanotubes should pack more favorably in a parallel configuration to maximize the van der Waals interaction. In practice, the opposite is found to be the case, where SWNTs and double-walled nanotubes exist in tightly packed parallel bundles, whereas thick multi-walled nanotubes (MWNTs) usually exist in clusters with a crossed mesh configuration. To form tight bundles, the neighboring nanotubes have to be in close proximity (<1 nm spacing) to each other, and align parallel with respect to the bundle axis. This means that nanotubes in a bundle will need to ‘adjust’ their conformations to confront the packing requirements co-operatively. Inevitably, there is an associated strain energy of deforming (bending) a nanotube to follow the contour of its neighbors; the magnitude of this strain energy scales with the tube diameter to a fourth power, within a classical model of beam bending. Hence for MWNTs, the energy cost resulted from bending much exceeds the energy savings in forming parallel bundles. Although most MWNTs are not closely packed in order to retain their original contour shapes to minimize the strain energy, they are formed into networks and are subjected to van der Waals binding at the contact junctions. The energy associated with each contact can be modeled by two perpendicularly crossed rods of radius r and gap size H:
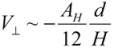 for
for 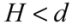 (2)
(2)For a tube diameter of 100 Å (10nm), spaced by 3.4 Å (0.34 nm), 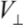 ~ −10 eV per contact is obtained. This value is lower than, but comparable to what was calculated in [14],
~ −10 eV per contact is obtained. This value is lower than, but comparable to what was calculated in [14], 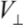 ~ −15 eV per contact, which was calculated based on the surface integral of graphene layers for a similar rolled configuration. The esults from [14] also showed a linear dependence of
~ −15 eV per contact, which was calculated based on the surface integral of graphene layers for a similar rolled configuration. The esults from [14] also showed a linear dependence of 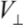 on the diameter d for all MWNTs. From the
on the diameter d for all MWNTs. From the 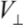 estimate, we can see that the energy associated with each contact is orders of magnitude greater than the room-temperature thermal energy. The number of contacts which can form between neighboring CNT pairs increase dramatically with the length of nanotubes. Therefore, the binding of a clustered network of long MWNTs is extremely strong, where each contact acts effectively as a physical cross-link fixing the network.
estimate, we can see that the energy associated with each contact is orders of magnitude greater than the room-temperature thermal energy. The number of contacts which can form between neighboring CNT pairs increase dramatically with the length of nanotubes. Therefore, the binding of a clustered network of long MWNTs is extremely strong, where each contact acts effectively as a physical cross-link fixing the network.
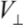 ~ −10 eV per contact is obtained. This value is lower than, but comparable to what was calculated in [14],
~ −10 eV per contact is obtained. This value is lower than, but comparable to what was calculated in [14], 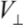 ~ −15 eV per contact, which was calculated based on the surface integral of graphene layers for a similar rolled configuration. The esults from [14] also showed a linear dependence of
~ −15 eV per contact, which was calculated based on the surface integral of graphene layers for a similar rolled configuration. The esults from [14] also showed a linear dependence of 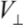 on the diameter d for all MWNTs. From the
on the diameter d for all MWNTs. From the 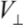 estimate, we can see that the energy associated with each contact is orders of magnitude greater than the room-temperature thermal energy. The number of contacts which can form between neighboring CNT pairs increase dramatically with the length of nanotubes. Therefore, the binding of a clustered network of long MWNTs is extremely strong, where each contact acts effectively as a physical cross-link fixing the network.
estimate, we can see that the energy associated with each contact is orders of magnitude greater than the room-temperature thermal energy. The number of contacts which can form between neighboring CNT pairs increase dramatically with the length of nanotubes. Therefore, the binding of a clustered network of long MWNTs is extremely strong, where each contact acts effectively as a physical cross-link fixing the network.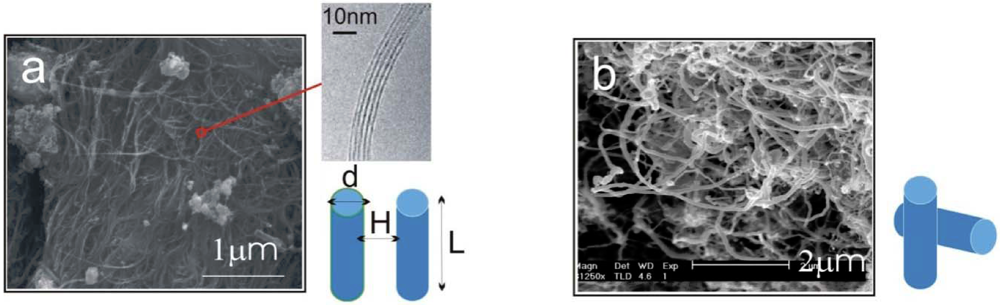
Figure 1.
Scanning electron micrographs showing: (a) Single-wall nanotubes (SWNTs), grown by arc-discharge, with inset showing a bundle of closely-packed SWNTs; (b) multi-walled nanotubes (MWNTs), grown by chemical vapor deposition. The van der Waals (VdW) interaction between a pair of SWNTs or a pair of MWNTs is modeled by a pair of rods with parallel and perpendicular configuration respectively.
To convert the values of these ‘contact’ energy into the more macroscopically meaningful quantity of energy density (ε), the following analysis is applied. For SWNTs, the energy density ε required to separate a pair of parallel tubes of length L and diameter d, bound by an attractive potential energy Vtot, is ε ~ |Vtot|/(Ld)2. Using L = 1 μm, d = 1 nm and Vtot ~V// ~ −103 eV (here, the van der Waals binding energy per unit length is taken as −0.095 eV/Å), ε ~ 100 MPa is obtained. For MWNTs networks, one needs to have additional information about the number density of nanotube contacts in the network, ct (in units of number per cubic meter). Then, the energy density required to separate the raw MWNT network is ε ~ ct|Vtot|. One can estimate ct by looking at the spacing ζ between the direct crossing junctions of the neighboring nanotubes visible on the surface of a cluster (e.g., in a scanning electron micrograph). Then, ct ~ 1/ ζ3. Taking the spacing between MWNT junctions to be ζ ~ 100 nm (estimated from the SEM image of MWNTs with diameters of 60–100 nm in Figure 1 of reference [15]) and  ~ −100 eV [14] for a 80 nm diameter MWNT, we obtain ε ~ 16 kPa. The above two examples demonstrate the vastly different energy levels, with many orders of magnitude difference, required to separate the CNTs of various as-grown morphologies.
~ −100 eV [14] for a 80 nm diameter MWNT, we obtain ε ~ 16 kPa. The above two examples demonstrate the vastly different energy levels, with many orders of magnitude difference, required to separate the CNTs of various as-grown morphologies.
 ~ −100 eV [14] for a 80 nm diameter MWNT, we obtain ε ~ 16 kPa. The above two examples demonstrate the vastly different energy levels, with many orders of magnitude difference, required to separate the CNTs of various as-grown morphologies.
~ −100 eV [14] for a 80 nm diameter MWNT, we obtain ε ~ 16 kPa. The above two examples demonstrate the vastly different energy levels, with many orders of magnitude difference, required to separate the CNTs of various as-grown morphologies.2.2. Energy Density Delivered from Mixing
Separation of nanotubes is usually performed in a solution phase using shear-mixing, [16,17,18] or ultrasonication, [19,20,21,22]. These processes are both governed by the transfer of local shear stress which breaks down the aggregates. It is therefore intuitive to suggest that complete separation of nanotubes would require the shear energy densities delivered to the bundle/cluster to exceed the binding energy (which can be treated as an ‘activation energy barrier’) of the system. Although the exfoliation state achieved may only be a temporary one, it greatly assists the surface adsorption of interfacial molecules (such as surfactants and compatible solvent molecules) which may subsequently stabilize the dispersion of CNTs [23]. During mixing, the level of energy density delivered into a solution is equivalent to the shear stress attainable. Shear stress (σs) is defined as the product of fluid viscosity (η) and fluid strain rate ( 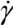 ), i.e.,
), i.e., 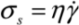 . We next consider the magnitude of the energy density that can be delivered by a mechanical mixing or a sonication technique.
. We next consider the magnitude of the energy density that can be delivered by a mechanical mixing or a sonication technique.
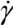 ), i.e.,
), i.e., 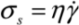 . We next consider the magnitude of the energy density that can be delivered by a mechanical mixing or a sonication technique.
. We next consider the magnitude of the energy density that can be delivered by a mechanical mixing or a sonication technique.Mechanical shear-mixing through stirring or extrusion can be performed in both low viscosity solvents (e.g., water or organic solvents with or without dissolved polymers), or highly viscous polymer melts. Hence the η values employed in shear mixing can span from 0.01 Pa∙s to 10 Pa∙s. The fluid strain rate ( 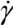 ) for the common melt shear mixing is dependent on the rotational speed of the mixer blade (ω in units of rad/s), and the geometry of the mixer and the container. For a typical Couette (concentric cylinder) shear-mixing geometry,
) for the common melt shear mixing is dependent on the rotational speed of the mixer blade (ω in units of rad/s), and the geometry of the mixer and the container. For a typical Couette (concentric cylinder) shear-mixing geometry, 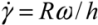 , with R being the radius of the container, and h the spacing between the leading edge of the mixer blade and the inner wall of the container. The standard Couette mixing conditions in reference [15] have yielded a strain rate of 500 s−1; experimental setups of different geometries could obtain a fluid strain rate as high as 4,000 s−1[24]. Therefore, using a viscous polymer melt such as PDMS uncross-linked polymer (η = 5.6 Pa∙s), the shear stress imparted by the mixing medium is below 20 kPa. Note that if one wishes to shear-mix in a low-viscosity solvent (such as water, toluene or chlorophorm), the shear stress delivered to the CNT clusters will drop to below 50 Pa, offering very little hope of achieving dispersion. The simple message of this estimate is: shear mixing is only suitable for dispersion of MWNT clusters in high-viscosity polymer melts.
, with R being the radius of the container, and h the spacing between the leading edge of the mixer blade and the inner wall of the container. The standard Couette mixing conditions in reference [15] have yielded a strain rate of 500 s−1; experimental setups of different geometries could obtain a fluid strain rate as high as 4,000 s−1[24]. Therefore, using a viscous polymer melt such as PDMS uncross-linked polymer (η = 5.6 Pa∙s), the shear stress imparted by the mixing medium is below 20 kPa. Note that if one wishes to shear-mix in a low-viscosity solvent (such as water, toluene or chlorophorm), the shear stress delivered to the CNT clusters will drop to below 50 Pa, offering very little hope of achieving dispersion. The simple message of this estimate is: shear mixing is only suitable for dispersion of MWNT clusters in high-viscosity polymer melts.
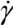 ) for the common melt shear mixing is dependent on the rotational speed of the mixer blade (ω in units of rad/s), and the geometry of the mixer and the container. For a typical Couette (concentric cylinder) shear-mixing geometry,
) for the common melt shear mixing is dependent on the rotational speed of the mixer blade (ω in units of rad/s), and the geometry of the mixer and the container. For a typical Couette (concentric cylinder) shear-mixing geometry, 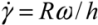 , with R being the radius of the container, and h the spacing between the leading edge of the mixer blade and the inner wall of the container. The standard Couette mixing conditions in reference [15] have yielded a strain rate of 500 s−1; experimental setups of different geometries could obtain a fluid strain rate as high as 4,000 s−1[24]. Therefore, using a viscous polymer melt such as PDMS uncross-linked polymer (η = 5.6 Pa∙s), the shear stress imparted by the mixing medium is below 20 kPa. Note that if one wishes to shear-mix in a low-viscosity solvent (such as water, toluene or chlorophorm), the shear stress delivered to the CNT clusters will drop to below 50 Pa, offering very little hope of achieving dispersion. The simple message of this estimate is: shear mixing is only suitable for dispersion of MWNT clusters in high-viscosity polymer melts.
, with R being the radius of the container, and h the spacing between the leading edge of the mixer blade and the inner wall of the container. The standard Couette mixing conditions in reference [15] have yielded a strain rate of 500 s−1; experimental setups of different geometries could obtain a fluid strain rate as high as 4,000 s−1[24]. Therefore, using a viscous polymer melt such as PDMS uncross-linked polymer (η = 5.6 Pa∙s), the shear stress imparted by the mixing medium is below 20 kPa. Note that if one wishes to shear-mix in a low-viscosity solvent (such as water, toluene or chlorophorm), the shear stress delivered to the CNT clusters will drop to below 50 Pa, offering very little hope of achieving dispersion. The simple message of this estimate is: shear mixing is only suitable for dispersion of MWNT clusters in high-viscosity polymer melts.Compared to mechanical shear mixing, ultrasonication uses a very different mechanism in delivering the shear stress for dispersing aggregates. Cavitation occurs in a low-viscosity fluid above a certain ultrasonic intensity in the low-pressure regions of the travelling wave. Once created, the cavitation bubbles collapse causing an extremely high strain rate in the fluid in the proximate regions of bubble implosion. A strain rate of up to 109 s−1 [25,26] is produced. The distribution of cavities is controlled by the geometry of the sonicator and the sonication settings, and is inhomogeneous throughout the solution [27]. Taking a typical low viscosity solvent of 0.1 Pa∙s, the localized shear stress imparted in the vicinity of an imploding bubble can approach 108 Pa (100 MPa).
2.3. Fracture of CNTs during Mixing
The shear stress imparting on the surface of a CNT can induce a pulling effect (a tensile force) on the nanotube. As a result, dispersion methods supplying high energy input can also induce fracture of CNTs. Mixing-induced fracture is of particular relevance in ultrasonication, where literature studies have confirmed the breakage of CNTs during sonication, with an example illustrated in Figure 2 [28]. Here, we will review a theoretical model for sonication scission [20].
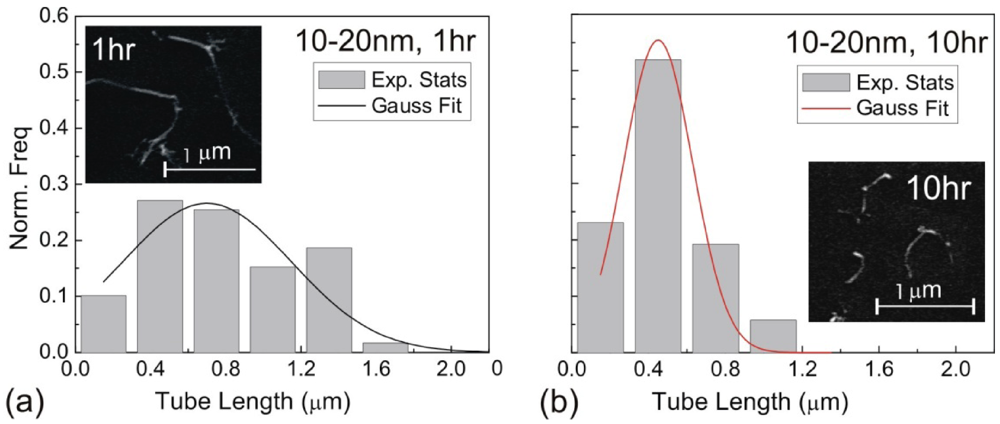
Figure 2.
Histogram of length distribution for d = 10–20 nm MWNTs after the (a) 1 h, and (b) 10 h horn sonication treatment. Gaussian profiles are fitted to both histograms for better statistical analysis. The corresponding SEM images of the MWNTs after sonication treatment are shown as insets.
Let us consider a simple potential-flow description of bubble implosion dynamics which is based on the radial solvent flow around a bubble (i.e., an inverse-square dependence between the fluid velocity V(S) and the distance S from the bubble center). The radial fluid velocity at a distance S from the bubble is estimated by 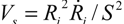 , where Ri is the characteristic bubble radius. It is expected that most nano-filaments, when located close to the imploding bubble (typical sizes of tens of micron), will re-orient themselves to align with the radial flow field. The final configuration of the filament with respect to the imploding bubble and its associated flow field is schematically illustrated in Figure 3(a). Within this framework, an affine estimate is used to calculate the stress that is exerted on a suspended filament by the viscous forces transmitted from the solvent.
, where Ri is the characteristic bubble radius. It is expected that most nano-filaments, when located close to the imploding bubble (typical sizes of tens of micron), will re-orient themselves to align with the radial flow field. The final configuration of the filament with respect to the imploding bubble and its associated flow field is schematically illustrated in Figure 3(a). Within this framework, an affine estimate is used to calculate the stress that is exerted on a suspended filament by the viscous forces transmitted from the solvent.
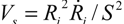 , where Ri is the characteristic bubble radius. It is expected that most nano-filaments, when located close to the imploding bubble (typical sizes of tens of micron), will re-orient themselves to align with the radial flow field. The final configuration of the filament with respect to the imploding bubble and its associated flow field is schematically illustrated in Figure 3(a). Within this framework, an affine estimate is used to calculate the stress that is exerted on a suspended filament by the viscous forces transmitted from the solvent.
, where Ri is the characteristic bubble radius. It is expected that most nano-filaments, when located close to the imploding bubble (typical sizes of tens of micron), will re-orient themselves to align with the radial flow field. The final configuration of the filament with respect to the imploding bubble and its associated flow field is schematically illustrated in Figure 3(a). Within this framework, an affine estimate is used to calculate the stress that is exerted on a suspended filament by the viscous forces transmitted from the solvent.Consider the bubble with an instantaneous radius of 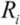 and wall velocity
and wall velocity 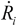 . Near the bubble there is a segment of the filament with a length L (with S1 and S2 being the starting and the ending positions of the filament) and a diameter d, which is accelerated by the surrounding viscous (surface shear) forces. Let us take a frame moving with the instantaneous velocity of the filament and assume the tube is in a quasi-equilibrium and its center of mass moving with a speed of Vtube. Surface shear stresses are created when the local velocity of the fluid flow Vs is different from the velocity of the filament Vtube. Assuming that the tube surface is non-slip and the characteristic length scale of the velocity decay across the cylindrical filament is of the order of its diameter d, the local shear strain on the surface can be approximated as (Vs − Vtube)/d. This gives the local shear stress as
. Near the bubble there is a segment of the filament with a length L (with S1 and S2 being the starting and the ending positions of the filament) and a diameter d, which is accelerated by the surrounding viscous (surface shear) forces. Let us take a frame moving with the instantaneous velocity of the filament and assume the tube is in a quasi-equilibrium and its center of mass moving with a speed of Vtube. Surface shear stresses are created when the local velocity of the fluid flow Vs is different from the velocity of the filament Vtube. Assuming that the tube surface is non-slip and the characteristic length scale of the velocity decay across the cylindrical filament is of the order of its diameter d, the local shear strain on the surface can be approximated as (Vs − Vtube)/d. This gives the local shear stress as 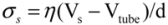 , with η the solvent viscosity.
, with η the solvent viscosity.
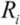 and wall velocity
and wall velocity 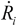 . Near the bubble there is a segment of the filament with a length L (with S1 and S2 being the starting and the ending positions of the filament) and a diameter d, which is accelerated by the surrounding viscous (surface shear) forces. Let us take a frame moving with the instantaneous velocity of the filament and assume the tube is in a quasi-equilibrium and its center of mass moving with a speed of Vtube. Surface shear stresses are created when the local velocity of the fluid flow Vs is different from the velocity of the filament Vtube. Assuming that the tube surface is non-slip and the characteristic length scale of the velocity decay across the cylindrical filament is of the order of its diameter d, the local shear strain on the surface can be approximated as (Vs − Vtube)/d. This gives the local shear stress as
. Near the bubble there is a segment of the filament with a length L (with S1 and S2 being the starting and the ending positions of the filament) and a diameter d, which is accelerated by the surrounding viscous (surface shear) forces. Let us take a frame moving with the instantaneous velocity of the filament and assume the tube is in a quasi-equilibrium and its center of mass moving with a speed of Vtube. Surface shear stresses are created when the local velocity of the fluid flow Vs is different from the velocity of the filament Vtube. Assuming that the tube surface is non-slip and the characteristic length scale of the velocity decay across the cylindrical filament is of the order of its diameter d, the local shear strain on the surface can be approximated as (Vs − Vtube)/d. This gives the local shear stress as 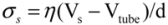 , with η the solvent viscosity.
, with η the solvent viscosity.The quasi-equilibrium condition requires the total shear forces applied on the filament surface add to zero. Hence, between S1 and S2, there must be a position S* at which the surface fluid would have the same velocity as the filament: the fluid stagnation point on the filament surface with Vtube = V (S*). For S1 < S < S*, the surface fluid is traveling at a greater speed than Vtube, thus imposing surface shear forces acting towards the bubble center on the front section of the filament, Figure 3(b); on the other hand, for S* < S < S2, the surface fluid is traveling at a lower speed than Vtube, and the filament is experiencing drag forces on the surface of its rear section. The total surface shear forces acting on the front part of the filament, for S1 < S < S* in Figure 3(c) is:
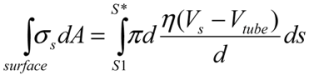 (3)
(3)Similarly, the surface shear forces on the rear part of the filament, for S* < S < S2, is 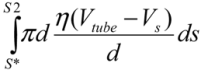 . Since the total shear forces applied on the tube surface add to zero, these two forces are balanced. After cancelation of factors on both sides, one obtains:
. Since the total shear forces applied on the tube surface add to zero, these two forces are balanced. After cancelation of factors on both sides, one obtains:
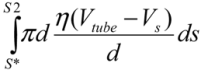 . Since the total shear forces applied on the tube surface add to zero, these two forces are balanced. After cancelation of factors on both sides, one obtains:
. Since the total shear forces applied on the tube surface add to zero, these two forces are balanced. After cancelation of factors on both sides, one obtains: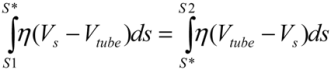 (4)
(4)Substituting 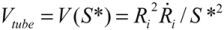 , one can solve Equation (4), giving
, one can solve Equation (4), giving 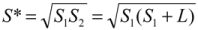 .
.
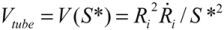 , one can solve Equation (4), giving
, one can solve Equation (4), giving 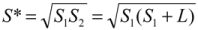 .
.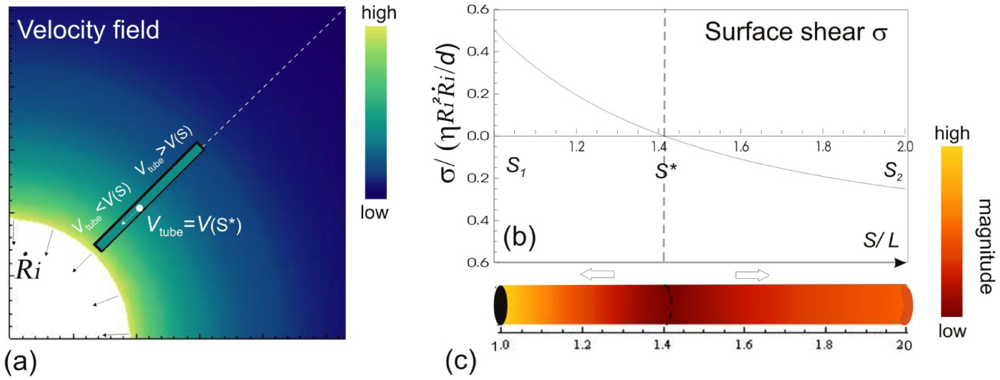
Figure 3.
(a) A snapshot during the cavitation process, showing a bubble of radius Ri collapsing with its wall velocity 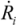 . The instantaneous velocity field of the fluid medium surrounding the bubble Vs is illustrated, of which magnitude is indicated by the color-coded scale bar. The filament immersed in the flow can only have a single velocity Vtube along its entire length, hence local surface shear stresses σs are created. The variation of σs w.r.t the position on the filament are shown in (b) and (c). The values of the surface stresses are normalized against the position-independent parameters, and the distance is normalized against the length of the filament.
. The instantaneous velocity field of the fluid medium surrounding the bubble Vs is illustrated, of which magnitude is indicated by the color-coded scale bar. The filament immersed in the flow can only have a single velocity Vtube along its entire length, hence local surface shear stresses σs are created. The variation of σs w.r.t the position on the filament are shown in (b) and (c). The values of the surface stresses are normalized against the position-independent parameters, and the distance is normalized against the length of the filament.
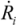 . The instantaneous velocity field of the fluid medium surrounding the bubble Vs is illustrated, of which magnitude is indicated by the color-coded scale bar. The filament immersed in the flow can only have a single velocity Vtube along its entire length, hence local surface shear stresses σs are created. The variation of σs w.r.t the position on the filament are shown in (b) and (c). The values of the surface stresses are normalized against the position-independent parameters, and the distance is normalized against the length of the filament.
. The instantaneous velocity field of the fluid medium surrounding the bubble Vs is illustrated, of which magnitude is indicated by the color-coded scale bar. The filament immersed in the flow can only have a single velocity Vtube along its entire length, hence local surface shear stresses σs are created. The variation of σs w.r.t the position on the filament are shown in (b) and (c). The values of the surface stresses are normalized against the position-independent parameters, and the distance is normalized against the length of the filament.
As a result of the surface shear forces acting on opposite directions of the filament, an axial tensile force is generated. This ‘pulling’ force has a maximum at S*, and is of a magnitude equal to the net surface shear force (e.g., surface force integral between S1 and S*). Therefore, by knowing S*, one can re-calculate the integral in Equation (4) to determine the total force pulling in each direction; dividing this by the tube cross-section area gives the maximum tensile stress exerted on the tube:
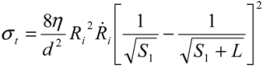 (5)
(5)Taking the typical literature values for the bubble size and rate of implosion ( 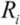 = 10 μm, and mean
= 10 μm, and mean 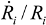 ~ 108 s−1), the CNT diameter d ~ 10 nm, the viscosity of a typical low-molecular weight solvent η ~ 0.1 Pa·s, and S1 ~L ~10 μm (the maximal stress occurs for a filament positioned closest to the bubble such that S1 = Ri), one obtains the estimate for the maximum tensile stress generated by viscous forces near the imploding bubble: σt > 100 GPa. This is enough to break most nanotubes! However, it is also clear from the Equation (5) that the tensile stress on the tube decreases dramatically as the tube length L diminishes, and a characteristic threshold length Llim exists for tube scission, for a set of pre-defined parameters η, d and
~ 108 s−1), the CNT diameter d ~ 10 nm, the viscosity of a typical low-molecular weight solvent η ~ 0.1 Pa·s, and S1 ~L ~10 μm (the maximal stress occurs for a filament positioned closest to the bubble such that S1 = Ri), one obtains the estimate for the maximum tensile stress generated by viscous forces near the imploding bubble: σt > 100 GPa. This is enough to break most nanotubes! However, it is also clear from the Equation (5) that the tensile stress on the tube decreases dramatically as the tube length L diminishes, and a characteristic threshold length Llim exists for tube scission, for a set of pre-defined parameters η, d and 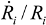 . If the value of breaking stress (ultimate tensile strength) of the nanotube is σ*, then this threshold length, after small-parameter expansion of Equation (5), is:
. If the value of breaking stress (ultimate tensile strength) of the nanotube is σ*, then this threshold length, after small-parameter expansion of Equation (5), is:
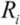 = 10 μm, and mean
= 10 μm, and mean 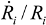 ~ 108 s−1), the CNT diameter d ~ 10 nm, the viscosity of a typical low-molecular weight solvent η ~ 0.1 Pa·s, and S1 ~L ~10 μm (the maximal stress occurs for a filament positioned closest to the bubble such that S1 = Ri), one obtains the estimate for the maximum tensile stress generated by viscous forces near the imploding bubble: σt > 100 GPa. This is enough to break most nanotubes! However, it is also clear from the Equation (5) that the tensile stress on the tube decreases dramatically as the tube length L diminishes, and a characteristic threshold length Llim exists for tube scission, for a set of pre-defined parameters η, d and
~ 108 s−1), the CNT diameter d ~ 10 nm, the viscosity of a typical low-molecular weight solvent η ~ 0.1 Pa·s, and S1 ~L ~10 μm (the maximal stress occurs for a filament positioned closest to the bubble such that S1 = Ri), one obtains the estimate for the maximum tensile stress generated by viscous forces near the imploding bubble: σt > 100 GPa. This is enough to break most nanotubes! However, it is also clear from the Equation (5) that the tensile stress on the tube decreases dramatically as the tube length L diminishes, and a characteristic threshold length Llim exists for tube scission, for a set of pre-defined parameters η, d and 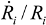 . If the value of breaking stress (ultimate tensile strength) of the nanotube is σ*, then this threshold length, after small-parameter expansion of Equation (5), is:
. If the value of breaking stress (ultimate tensile strength) of the nanotube is σ*, then this threshold length, after small-parameter expansion of Equation (5), is: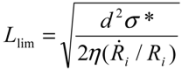 (6)
(6)Tubes shorter than Llim will not experience scission anymore.
One limitation of the above model is that the instant shear force is linearly dependent on viscosity. However, as viscosity increases, ultrasound absorption in the medium also increases and there is a much lower probability of cavitation at higher viscosities. Equations (5) and (6) are therefore only applicable to sonication with low viscosity solvents where cavitation is permitted. Nevertheless, this analysis gives a qualitative picture of the role played by the imploding bubble parameters 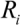 and
and 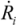 in tube breakage. We can further re-arrange Equation (6) to the form of
in tube breakage. We can further re-arrange Equation (6) to the form of 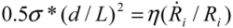 , by replacing Llim with L, the starting length of a filament. We see that the left hand side contains purely the filament parameters, the aspect ratio (L/d), and the strength of the fiber σ*; while the right hand side is equal to the stress induced during cavitation, σson. Therefore, we have obtained an important filament fracture resistance parameter
, by replacing Llim with L, the starting length of a filament. We see that the left hand side contains purely the filament parameters, the aspect ratio (L/d), and the strength of the fiber σ*; while the right hand side is equal to the stress induced during cavitation, σson. Therefore, we have obtained an important filament fracture resistance parameter 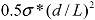 . If a filament has
. If a filament has 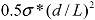 > σson, it will not fracture during sonication; on the other hand, when
> σson, it will not fracture during sonication; on the other hand, when 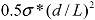 < σson, fracture occurs, and L will decrease until L = Llim as discussed above. Filaments with higher strength and lower aspect ratio are more resistant to fracture during sonication, as one would expect.
< σson, fracture occurs, and L will decrease until L = Llim as discussed above. Filaments with higher strength and lower aspect ratio are more resistant to fracture during sonication, as one would expect.
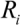 and
and 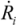 in tube breakage. We can further re-arrange Equation (6) to the form of
in tube breakage. We can further re-arrange Equation (6) to the form of 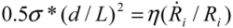 , by replacing Llim with L, the starting length of a filament. We see that the left hand side contains purely the filament parameters, the aspect ratio (L/d), and the strength of the fiber σ*; while the right hand side is equal to the stress induced during cavitation, σson. Therefore, we have obtained an important filament fracture resistance parameter
, by replacing Llim with L, the starting length of a filament. We see that the left hand side contains purely the filament parameters, the aspect ratio (L/d), and the strength of the fiber σ*; while the right hand side is equal to the stress induced during cavitation, σson. Therefore, we have obtained an important filament fracture resistance parameter 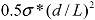 . If a filament has
. If a filament has 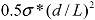 > σson, it will not fracture during sonication; on the other hand, when
> σson, it will not fracture during sonication; on the other hand, when 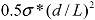 < σson, fracture occurs, and L will decrease until L = Llim as discussed above. Filaments with higher strength and lower aspect ratio are more resistant to fracture during sonication, as one would expect.
< σson, fracture occurs, and L will decrease until L = Llim as discussed above. Filaments with higher strength and lower aspect ratio are more resistant to fracture during sonication, as one would expect.2.4. Effects of Shear-Mixing and Sonication
Combining the above analysis, an energy density diagram is presented in Figure 4, which compares the theoretical values of energy density input, filament fracture resistance, and binding energy of the CNT aggregates. The lower and upper binding energy limits for MWNTs are calculated based on a tube diameter d = 80 nm, for nanotube junctions spaced by distances of four-diameter, and one-diameter apart, respectively. For SWNTs, the ranges of binding energies shown are determined from the energy balances between the bending strain and the van der Waals attraction. The filament fracture resistance parameter is defined as 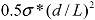 introduced previously (which has a dimension of energy density). The span of values in
introduced previously (which has a dimension of energy density). The span of values in 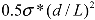 is resulted from the different ranges of strengths reported for CNTs, such that σ∗MWNT ~ 3–100 GPa, and σ∗MWNT ~ 10–100 GPa [29,30,31,32,33]. To understand the diagram, we first focus on the mixing conditions. High speed shear mixing in a high viscosity polymer melt can deliver an energy density reaching 104 Pa (as derived in the previous section). However, this energy level is still orders of magnitude lower than an ultrasonic cavitation event. For an aspect ratio of 10, the fracture resistance of SWNTs is of a slightly higher value than the binding energy of their aggregates. Ultrasonication just delivers a sufficient stress level to separate the SWNT aggregates without causing much fracture to individual nanotubes. For MWNTs, one finds that high viscosity shear mixing is able to separate the aggregates apart. Shear mixing is a better dispersion method because it can effectively separate the MWNTs without causing damage to the filament. For an aspect ratio of 1,000, which is relevant to the as-produced CNT sources, one notices that the fracture resistance of both SWNTs and MWNTs are lower than the stress input level delivered by sonication. On the other hand, shear mixing is not able to achieve a stress level matching the binding energy density. A dilemma therefore arises here, such that for complete separation of long CNTs, the tubes will also be broken during the process.
is resulted from the different ranges of strengths reported for CNTs, such that σ∗MWNT ~ 3–100 GPa, and σ∗MWNT ~ 10–100 GPa [29,30,31,32,33]. To understand the diagram, we first focus on the mixing conditions. High speed shear mixing in a high viscosity polymer melt can deliver an energy density reaching 104 Pa (as derived in the previous section). However, this energy level is still orders of magnitude lower than an ultrasonic cavitation event. For an aspect ratio of 10, the fracture resistance of SWNTs is of a slightly higher value than the binding energy of their aggregates. Ultrasonication just delivers a sufficient stress level to separate the SWNT aggregates without causing much fracture to individual nanotubes. For MWNTs, one finds that high viscosity shear mixing is able to separate the aggregates apart. Shear mixing is a better dispersion method because it can effectively separate the MWNTs without causing damage to the filament. For an aspect ratio of 1,000, which is relevant to the as-produced CNT sources, one notices that the fracture resistance of both SWNTs and MWNTs are lower than the stress input level delivered by sonication. On the other hand, shear mixing is not able to achieve a stress level matching the binding energy density. A dilemma therefore arises here, such that for complete separation of long CNTs, the tubes will also be broken during the process.
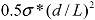 introduced previously (which has a dimension of energy density). The span of values in
introduced previously (which has a dimension of energy density). The span of values in 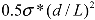 is resulted from the different ranges of strengths reported for CNTs, such that σ∗MWNT ~ 3–100 GPa, and σ∗MWNT ~ 10–100 GPa [29,30,31,32,33]. To understand the diagram, we first focus on the mixing conditions. High speed shear mixing in a high viscosity polymer melt can deliver an energy density reaching 104 Pa (as derived in the previous section). However, this energy level is still orders of magnitude lower than an ultrasonic cavitation event. For an aspect ratio of 10, the fracture resistance of SWNTs is of a slightly higher value than the binding energy of their aggregates. Ultrasonication just delivers a sufficient stress level to separate the SWNT aggregates without causing much fracture to individual nanotubes. For MWNTs, one finds that high viscosity shear mixing is able to separate the aggregates apart. Shear mixing is a better dispersion method because it can effectively separate the MWNTs without causing damage to the filament. For an aspect ratio of 1,000, which is relevant to the as-produced CNT sources, one notices that the fracture resistance of both SWNTs and MWNTs are lower than the stress input level delivered by sonication. On the other hand, shear mixing is not able to achieve a stress level matching the binding energy density. A dilemma therefore arises here, such that for complete separation of long CNTs, the tubes will also be broken during the process.
is resulted from the different ranges of strengths reported for CNTs, such that σ∗MWNT ~ 3–100 GPa, and σ∗MWNT ~ 10–100 GPa [29,30,31,32,33]. To understand the diagram, we first focus on the mixing conditions. High speed shear mixing in a high viscosity polymer melt can deliver an energy density reaching 104 Pa (as derived in the previous section). However, this energy level is still orders of magnitude lower than an ultrasonic cavitation event. For an aspect ratio of 10, the fracture resistance of SWNTs is of a slightly higher value than the binding energy of their aggregates. Ultrasonication just delivers a sufficient stress level to separate the SWNT aggregates without causing much fracture to individual nanotubes. For MWNTs, one finds that high viscosity shear mixing is able to separate the aggregates apart. Shear mixing is a better dispersion method because it can effectively separate the MWNTs without causing damage to the filament. For an aspect ratio of 1,000, which is relevant to the as-produced CNT sources, one notices that the fracture resistance of both SWNTs and MWNTs are lower than the stress input level delivered by sonication. On the other hand, shear mixing is not able to achieve a stress level matching the binding energy density. A dilemma therefore arises here, such that for complete separation of long CNTs, the tubes will also be broken during the process.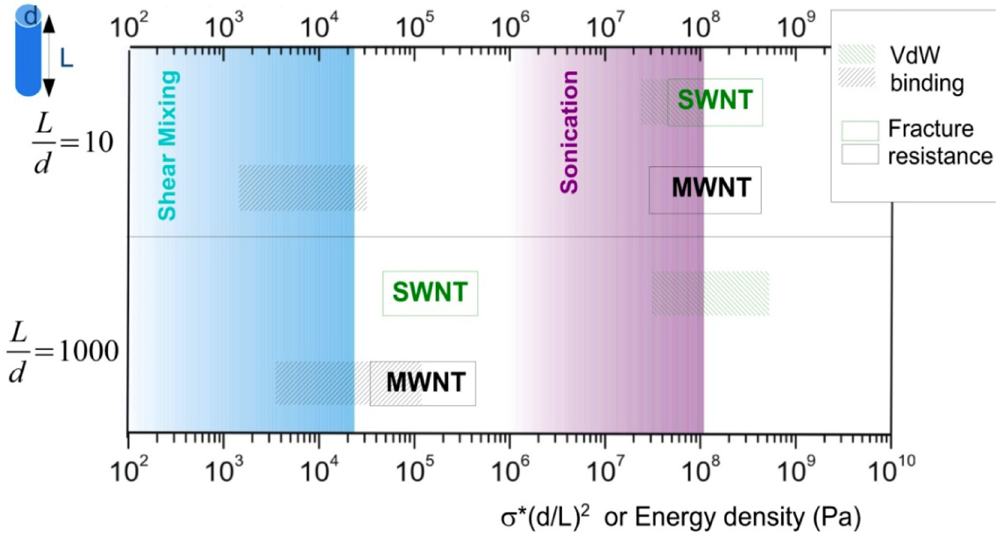
Figure 4.
An energy diagram showing the theoretical capabilities and limitations of shear-mixing and ultrasonication for carbon nanotube (CNT) dispersion, using filament aspect ratios L = d of 10 and 1,000 as examples.
Based on the above, one can predict the morphology of the CNTs immediately after mixing. It is important to emphasize that the findings stated above only hold when there exists a steady state condition during mixing/sonication. For mechanical shear mixing, it is useful to determine the time t*, required to achieve such a steady state condition. A rheological prototype has been developed to determine t* [15], where the evolution of the solution microstructure for t < t* was also studied. The viscous medium also provides a mean to temporarily stabilize the as-produced dispersion state for subsequent composite fabrication. On the other hand, since ultrasonication both disperses and cuts the CNTs [28], finding a good ‘recipe’ for sonication dispersion is system dependent and requires significant trial and error experimentation. Since ultrasonication is performed in a low viscosity solvent/solution, additional means are required to stabilize the as-dispersed state. Various stabilization methods of CNTs in a solution are discussed in Section 3 below.
3. Stability of Carbon Nanotube Dispersion
Upon removal of the external shear stress, the CNTs in solution would reconfigure themselves to a new equilibrium state of low energy, through re-aggregation. This process will take place unless surfactants are added to provide steric hindrance or static charge repulsion to stabilize the particles. The driving force for re-aggregation is provided by the van der Waals attraction; it has also been shown that application of weak shear (with σ << σ*, see Section 2.3 above) subsequent to a well-mixed state can significantly accelerate the re-aggregation process [34]. Moreover, particles in solution tend to sediment if the ratio between gravitational to Brownian forces exceeds unity. For a spherical aggregate, this is 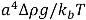 , with a being the particle size,
, with a being the particle size, 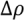 being the density difference between the solute and the surrounding medium. It is thus apparent that re-aggregation can be promoted by sedimentation, due to the power-four dependence on the particle size. Most organic solvents and polymeric melts have densities of the order ~1 g/cm3, which are lower than various types of CNTs (1.4 to 2 g/cm3). This gives an estimate of the critical diameter of CNT cluster for sedimentation ~1 μm (cf. as-produced CNTs commonly have lengths greater than ~1 μm). Although the above formula only provides a very crude estimate without considering the shape effect of the particles, it points out the great difficulty in obtaining a homogenous solution of CNTs with long-time stability. On the other hand, sonication processing can result in apparently enhanced dispersion through ‘sonication cutting’ [20,28], such that the decreased lengths makes the nanotubes less energetically favorable to re-aggregate and sediment after the removal of sonication. Although this process can reduce the bundle sizes of SWNTs, it is unlikely to produce individually separated SWNTs. This is because the critical tens of nanometers length regime (a length required to counteract van der Waals attraction, see Section 2.3 above) is below the limiting tube length (Llim) achievable by ultrasonication [20]. Such a short length also limits the applications of SWNTs.
being the density difference between the solute and the surrounding medium. It is thus apparent that re-aggregation can be promoted by sedimentation, due to the power-four dependence on the particle size. Most organic solvents and polymeric melts have densities of the order ~1 g/cm3, which are lower than various types of CNTs (1.4 to 2 g/cm3). This gives an estimate of the critical diameter of CNT cluster for sedimentation ~1 μm (cf. as-produced CNTs commonly have lengths greater than ~1 μm). Although the above formula only provides a very crude estimate without considering the shape effect of the particles, it points out the great difficulty in obtaining a homogenous solution of CNTs with long-time stability. On the other hand, sonication processing can result in apparently enhanced dispersion through ‘sonication cutting’ [20,28], such that the decreased lengths makes the nanotubes less energetically favorable to re-aggregate and sediment after the removal of sonication. Although this process can reduce the bundle sizes of SWNTs, it is unlikely to produce individually separated SWNTs. This is because the critical tens of nanometers length regime (a length required to counteract van der Waals attraction, see Section 2.3 above) is below the limiting tube length (Llim) achievable by ultrasonication [20]. Such a short length also limits the applications of SWNTs.
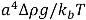 , with a being the particle size,
, with a being the particle size, 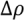 being the density difference between the solute and the surrounding medium. It is thus apparent that re-aggregation can be promoted by sedimentation, due to the power-four dependence on the particle size. Most organic solvents and polymeric melts have densities of the order ~1 g/cm3, which are lower than various types of CNTs (1.4 to 2 g/cm3). This gives an estimate of the critical diameter of CNT cluster for sedimentation ~1 μm (cf. as-produced CNTs commonly have lengths greater than ~1 μm). Although the above formula only provides a very crude estimate without considering the shape effect of the particles, it points out the great difficulty in obtaining a homogenous solution of CNTs with long-time stability. On the other hand, sonication processing can result in apparently enhanced dispersion through ‘sonication cutting’ [20,28], such that the decreased lengths makes the nanotubes less energetically favorable to re-aggregate and sediment after the removal of sonication. Although this process can reduce the bundle sizes of SWNTs, it is unlikely to produce individually separated SWNTs. This is because the critical tens of nanometers length regime (a length required to counteract van der Waals attraction, see Section 2.3 above) is below the limiting tube length (Llim) achievable by ultrasonication [20]. Such a short length also limits the applications of SWNTs.
being the density difference between the solute and the surrounding medium. It is thus apparent that re-aggregation can be promoted by sedimentation, due to the power-four dependence on the particle size. Most organic solvents and polymeric melts have densities of the order ~1 g/cm3, which are lower than various types of CNTs (1.4 to 2 g/cm3). This gives an estimate of the critical diameter of CNT cluster for sedimentation ~1 μm (cf. as-produced CNTs commonly have lengths greater than ~1 μm). Although the above formula only provides a very crude estimate without considering the shape effect of the particles, it points out the great difficulty in obtaining a homogenous solution of CNTs with long-time stability. On the other hand, sonication processing can result in apparently enhanced dispersion through ‘sonication cutting’ [20,28], such that the decreased lengths makes the nanotubes less energetically favorable to re-aggregate and sediment after the removal of sonication. Although this process can reduce the bundle sizes of SWNTs, it is unlikely to produce individually separated SWNTs. This is because the critical tens of nanometers length regime (a length required to counteract van der Waals attraction, see Section 2.3 above) is below the limiting tube length (Llim) achievable by ultrasonication [20]. Such a short length also limits the applications of SWNTs.Significant progress has been made to dissolve CNTs since the first demonstration of CNT dissolution in organic solvents through cutting and subsequently functionalization with octadecylamine (ODA) [35]. CNT dissolution methods can be largely grouped into covalent and non-covalent in nature. Although high solubility is obtainable in covalently functionalized CNTs, the conversion of π (sp2) to σ (sp3) bond can significantly alter the properties of CNTs, depending on the percentage of bond conversion on the surface and this may undermine future applications [36,37]. The current focus, therefore, is placed on the non-covalent dispersion techniques. These are based on two strategies using very different mechanisms. Firstly, a dispersed microstructure can be temporarily sustained (although possibly for a long time) by a liquid medium of high viscosity. On the other hand, unbundling and stabilization of pristine CNTs can be achieved by the choice of a chemically compatible solvent, or the use of appropriate dispersants. Both of these approaches require the molecules (solvent or surfactant) having favorable interaction with the curved graphene wall of the CNT surface.
3.1. Kinetically Sustained Metastable State
Un-modified CNTs can be temporarily kept in their separated state by a highly viscous medium, even if the solvent is chemically incompatible with the CNTs. Commonly, this state is automatically attained after the high viscosity mechanical shear-mixing for a sufficient length of time. Using a rheological technique to monitor the state of dispersion, reference [15] provides a detailed study of the stability and re-aggregation process of MWNTs in PDMS (polydimethylsiloxane) melt subjected to various degrees of shear-mixing. It was found that the stabilization mechanisms are different for filler concentrations below or above the entanglement (overlap) concentration of the order ~2 wt%. For 1 wt% MWNTs in PDMS (an example of a mixture with concentration smaller than the overlap), the viscosity of the aged mixture may be altered depending on the initial dispersion state. The sample mixed for just 2 min showed a large drop in viscosity after aging for 2 weeks, essentially recovering a pure PDMS value. In contrast, very little change in viscosity was registered for the same aging of the originally well-mixed samples. Therefore, it was suggested that sparse non-interacting nanotubes dispersed in a highly viscous matrix do not have enough Brownian mobility to re-aggregate within the time period. Moreover, storage conditions can also be modified to minimize the re-aggregation process, e.g., by cooling the matrix below the polymer glass transition.
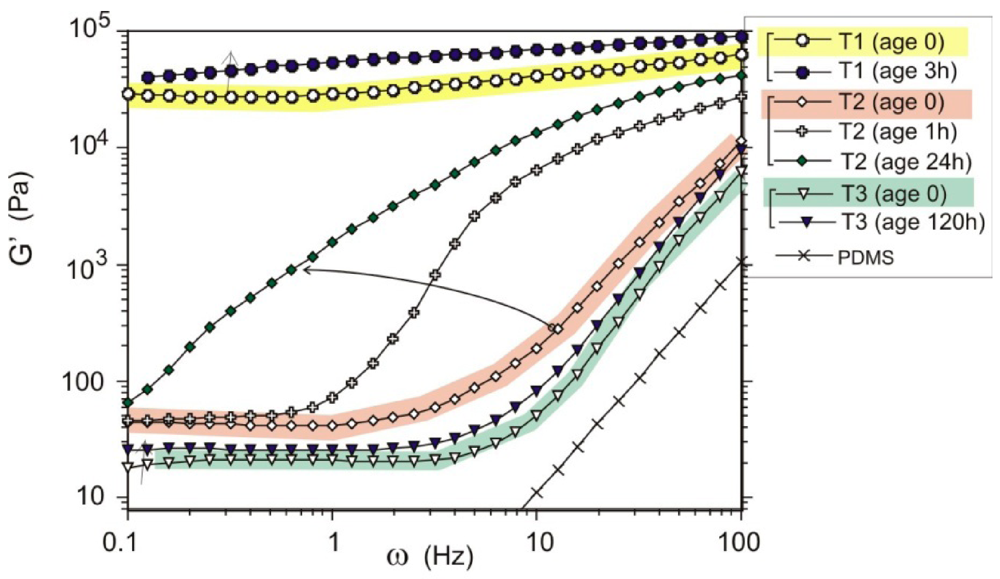
Figure 5.
Plots of shear modulus (G’) against shear frequency (ω) for 7 wt% MWCNT samples. Three groups of data are labeled: T1 for the short mixing time, T2 for the intermediate state of mixing, and T3 for the well-dispersed composite. The age of each sample is labeled in the legend.
Above the overlap concentration (which, incidentally, should not be mixed with the electrical percolation concentration that we discuss separately in Section 4), the kinetic stabilization mechanism changes to the formation of a homogenous inter-connecting entangled network of nanotubes in the matrix. Due to the strong binding of crossed MWNTs, Figure 1(b), providing the physical crosslinks and the very low thermal fluctuations in the stiff MWNT, the resulting network is very stable and has an equilibrium shear modulus, which could be measured as the low-frequency limit of the storage modulus G’. Figure 5 (adapted from [15]) shows three groups of measurements of G’ against shear frequency (ω), for the samples mixed for a short time (tmix =1 h, labeled T1 in the plot), for the intermediate stage of mixing (tmix =16 h, labeled T2) and for the well-dispersed composites (tmix = 61 h, labeled T3). The G’-ω functions before and after aging were compared. It was found that both T1 and T3 samples show small changes in their rheological signatures, indicating weak aging. In contrast, the T2 response function G’ evolves most significantly with the aging time. The rheological transition in this metastable gel moves to the lower frequencies as aging proceeds. In effect, one is observing the movement of the dynamic glass transition across the plot in Figure 5. The T3 (well-mixed) sample demonstrates good metastability (over 6 days of standing) and the stable low-frequency shear modulus due to the entangled network of nanotubes, with no clusters left to act as seeds for re-aggregation.
3.2. Thermodynamically Stable Dispersion States
The π bonding of graphene surface renders pristine, undoped CNTs hydrophobic. Additionally, the high curvature of the small tubular geometry makes the surface increasingly electrophilic. Good solvents such as n-methylpyrrolidone and n,n-dimethylformamide, all have common characteristic such as high values for electron pair donation, negligible values for hydrogen bond donation, and high values for solvochromic parameter, as suggested by [38]. The same reference also demonstrated shifts in the electronic transitions of SWNTs when they are dispersed in different compatible organic solvents, revealing strong interactions between the SWNT graphene wall and the solvent at the molecular level. Therefore, surface chemistry controls the compatibility of CNTs in a solvent. The above also qualitatively agrees with the findings from [39], which indicate that successful solvents for CNTs (such as n-methylpyrrolidone, NMP) are those with surface tensions close to that of graphene surfaces. The affinity between the solvent molecules and the graphene walls renders the free-energy of mixing negative, leading to solubility of CNTs in the solvent. However, since the van der Waals interaction remains present when CNTs are immersed in these liquids, pairs of nanotubes in close proximity are still strongly attracted, leading to re-aggregation. Therefore, a stable solution can only be realized in sparse low-concentration dispersion to minimize the van der Waals interactions. This explains the origin of the 0.02 mg/mL solubility limit achieved by the best organic solvents (e.g., NMP). This concentration is just below the transition from a dilute to a semi-dilute regime of filaments of CNT dimensions [40]. For composite fabrication, the dispersion approach of choosing a CNT-compatible solvent imposes some limitations. Firstly, only very selected number of engineering polymers are applicable. Secondly, evaporation of solvents during composite production brings the CNTs into a close proximity which may promote cluster formation.
Non-covalent functionalization generally involves the use of surfactant, or dispersant which physically binds to the nanotube surface. In general, they can be viewed to have an ‘amphiphilic’ structure, with active groups/sites attracted towards the nanotube graphene wall, and moieties matching the chemistry of the solubilizing medium. Regardless of the solubilizing media, most of the binding mechanisms between the CNT surface and the active surfactant moiety can be divided into two origins: hydrophobic interaction, and the more specific π−π stacking (though strictly, π−π stacking is also hydrophobic in nature). To stabilize carbon nanotubes in solution, the groups which interface the solvent act to provide either charge, and/or steric hindrance to isolate individual carbon nanotubes after mixing or sonication.
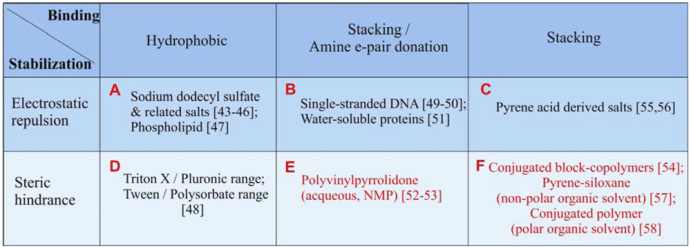
The combined mechanisms of binding and stabilization are summarized in Table 1, covering many commonly used surfactants in aqueous or organic solvents. For the surfactants which stabilize CNTs through electrostatic repulsion (Groups A–C), zeta-potential of the surfactant/CNT complex governs the stability of the solution [41,42]. Since charge dissociation is only significant in an aqueous medium (high dielectric constant), electrostatic repulsion is only effective in aqueous medium. Overall, one notices some characteristic structures typical to each group of the surfactant/CNT complex. Firstly, members of Group A [43,44,45,46,47], and Group D [48], are signified by micelle formation. These molecules can be seen as formed by separate blocks of hydrophobic and hydrophilic (charged or uncharged) regions. The hydrophobic block of the surfactant is relatively small, thus multiple surfactant molecules can pack around the circumference of a CNT. On the other hand, biomolecules (Group B [49,50,51]) and some polymeric surfactants (e.g., polyvinylpyrrolidone, PVP [52,53] tend to wrap or twist around the CNT center through their flexible or semi-flexible backbones. The CNT-affine groups are on the side chain of the molecules. Lastly, the molecular structure associated with the π−π stacking complex can vary considerably depending on the location of the rigid π-bondings. They can be in a block [54,55,56,57], or in the backbone [58]. The resultant supramolecular structure is usually formed to maximize the π-stacking interaction, inducing alignment of the π bonding with respect to the CNT chirality. The surfactants available for organic solvents are less readily available than those for the aqueous solvents. Especially, surfactants designed for non-polar organic solvent are rare, and a pyrene-siloxane based surfactant is only recently developed [57].

Table 1.
Summary of dispersion mechanisms for various surfactants. The surfactants are divided into six generic groups, labeled A–F. The ones which are highlighted in red are for dispersion in organic solvents, whereas the rest are for dispersion in aqueous solution.
 |
For engineering composite fabrication, often the purpose of the surfactants is to assist homogenous dispersion of CNTs in a matrix both during solution processing and after solvent removal. The cases of ‘surfactants’ which are deliberately added to impart functionalities to the composite (such as for the biopolymers and the conjugated polymers) are relatively uncommon. Therefore, careful consideration should be taken to evaluate whether the improvement in dispersion does enhance the desired functionality. Since surfactants inevitably leave a coating layer on the surface of the CNT, increased electron tunneling distance is resulted at the CNT contact junction. The effect of surfactant addition on the electrical performance of CNT-polymer composite is discussed in Section 4.
4. Correlating the Physical Properties and the Microstructure
A basic question one needs to address is that whether complete separation of the aggregates is desirable. For application utilizing the optical properties of SWNTs, isolated SWNTs are essential because aggregation can reduce the absorption, and quench the fluorescence emission of excited nanotubes [59]. For applications involving conductivity of a composite, the effect is different because conduction of electrons requires percolation of conductive paths in the matrix. It had been demonstrated that a partially re-aggregated state (after long time mixing) shows a lower percolation threshold than the original well-mixed state [60,61]. Furthermore, under strong shearing conditions, the composites which have been shear-mixed with shorter times show better conductivity [62]. An example experiment was illustrated in [63], which is to be described here. MWNTs are shear-mixed in an un-crosslinked PDMS (polydimethylsiloxane) polymer, under the condition that the supplied shear stress is greater than the binding energy of the clusters, but lower than the fracture resistance of the MWNTs. The mixtures were taken out after different mixing times for rheology and electrical measurement. Through the rheological measurement, the storage modulus (G’) was extrapolated, which reflects the solid-like property of the mixture. Figure 6 shows that the storage modulus (square symbols) gradually decreases with increasing mixing time. Combining with scanning electron microscopy, it was found that high values of G’ resulted from chains of hard CNT clusters present in the mixture (the jamming effect in colloidal system). The separation of the clusters into a spread network morphology decreases the G’ values. The conductivity values, which are shown by the red symbols, follow the same trend as the storage modulus. The above correlation seems to support the hypothesis that a composite morphology consists of phase separated regions of clusters and dangling bridges result in more effective electron transport than an evenly-spread CNT network [63,64,65]. A recent study by Kyrylyuk et al. [66] provided theoretical reasoning to this counter-intuitive effect, and showed that a multi-component CNT dispersion can achieve better electrical percolation than a single phase one.
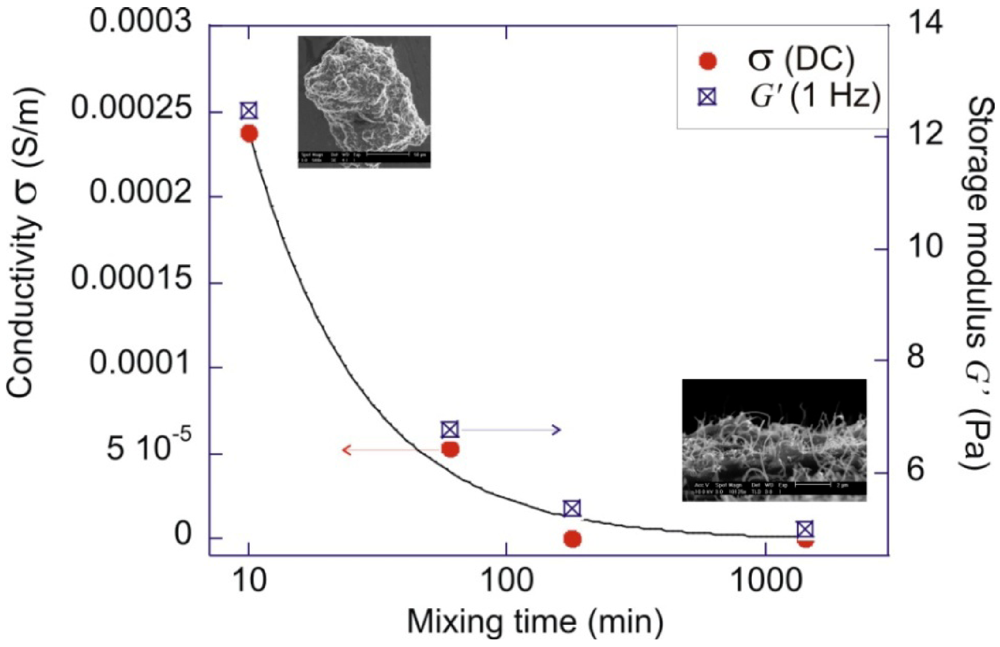
Figure 6.
Plot of DC conductivity σ, and the shear storage modulus G’ at 1 Hz, for pure 2 wt% MWNTs-PDMS composites mechanically mixed for different times. The result indicates a strong correlation between the DC conductivity and the amount of non-dispersed CNT clusters present in the matrix.
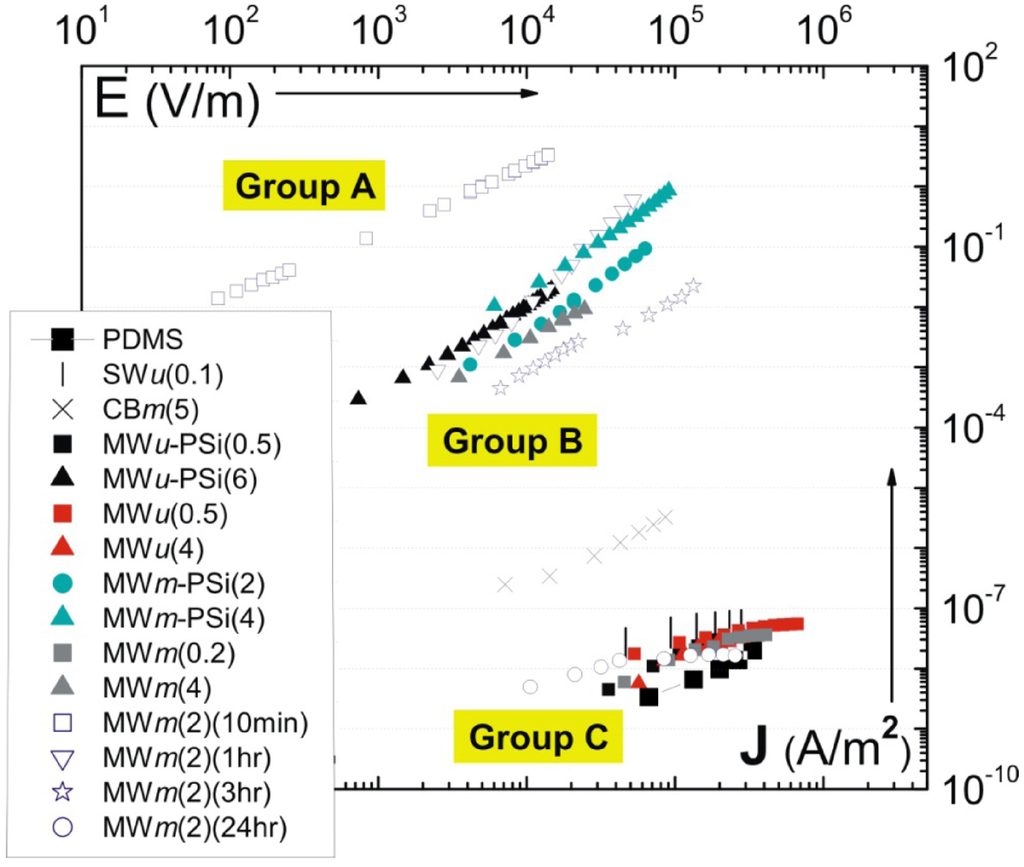
Figure 7.
Master plot of current density vs. applied field J-E for a range of carbon polymer composites (this is analogous to I–V, but presents the relevant intensive parameters). The details of fabrication process corresponding to each sample are illustrated in Table 2.

Table 2.
Listing the fabrication conditions represented by each sample label in Figure 6.
| Notation | Filler addition | Processing method | Mixing time |
|---|---|---|---|
| MWu (wt%) | MWNTs: 0.5 wt%, 4 wt% | ultrasonication | 8 h |
| MWu -PSi(wt%) | MWNTs: 0.5 wt% (filtered) | Psi assisted dispersion | 8 h |
| 6 wt% (filtered) | ultrasonication | ||
| MWm (wt%) | MWNTs: 0.2 wt% to 4 wt% | Shear mixing | 24 h |
| MWm -PSi(wt%) | MWNTs: 2 wt%, 4 wt% | PSi assisted dispersion, | 24 h |
| Shear mixing | |||
| MWm (2)(t) | MWNTs: 2 wt% | Shear mixing | t: 10 min; 1 h; |
| 3 h; 24 h | |||
| SWu (0.1) | SWNTs: 0.1 wt% | ultrasonication | 40 min |
| CBm (5) | Carbon Black: 5 wt% | Shear mixing | 24 h |
In addition to the effect of shear-mixing time on the electrical properties, other processing parameters have also been studied in [63]. This includes the variation in sonication time, and the addition of surfactant. The brief fabrication method for each composite is illustrated in Table 2. Of particular interest is a master plot of current density-electric field (J-E) characteristics for the composites fabricated under different conditions. This master plot is illustrated in Figure 6. One observes a clear separation in the J-E response, making three different groups as labeled on the plot. Crossing the percolation threshold, i.e., moving from Group C to Group B, one finds a jump in the current density of around 6 orders of magnitude for the same applied field. However, the composites in Group A, with a high conductivity, have the current density another 2–3 orders of magnitude higher. Based on this master plot, we will select a few examples to illustrate how the variation in fabrication could ultimately change the electrical properties of the composites.
Firstly, comparing the ultrasonicated samples (MWu-) with their mechanically mixed counterparts (MWm-) reveals a strong dependence of composite conductivity on the aspect ratio of tubes. After long time sonication, the MWNTs were shortened to approximately 1/3 of the original length [20] (which still gives an aspect ratio of ca. 100). Figure 7 shows that MWu(4) has a conductivity value 6 orders of magnitude lower than the MWm(4) sample. Despite the high MWNTs content, MWu(4) exhibits a much lower conductivity than even the carbon black shear-mixed composite CBm(5). This result suggests that long-time sonication has not only resulted in significant tube scission (as indicated by Figure 8), but also caused detrimental amorphization of the graphene walls, making the MWu(4) composite effectively an insulator. For the conductive composites, the MWu-PSi(6) composite also has the conductivity lower than the MWm-PSi(4) sample. The effect of surfactants assisting exfoliation, was also studied on an example of purpose-developed pyrene-siloxane (PSi) [57]. Although one might assume that a surfactant coating would prevent good electric contact between tubes, PSi has induced an electrical percolation in the 2 wt% MWNT-PDMS composite which is otherwise insulating in the pure form (compare MWm-PSi(2) and MWm(2)(24hr)). For concentrations well above percolation, the addition of PSi also leads to approximately an order of magnitude increase in conductivity for the same MWNT doping (compare MWm-PSi(4) and MWm(4)). A possible explanation for the improvement in conductivity was that PSi is in a liquid state at room temperatures; thin layers of PSi surrounding the CNTs provide a capillary force for the connection of the loose dangling ends/loops of CNT in the matrix. Electron transport through the contact junctions of CNTs has been shown to be the dominant mechanism for macroscopic conductivity [67]. This is unlike surfactants such as SDS (sodium dodecyl sulfate) [68] or Tergitol [69], which form a dense shell layer surrounding the CNTs, increasing the tunneling barrier for electron transport across the CNT junctions. Surfactants studied elsewhere (e.g., [69,70]) also appear to have similar effect of improving the electrical percolation behavior of CNTs in polymer matrices.
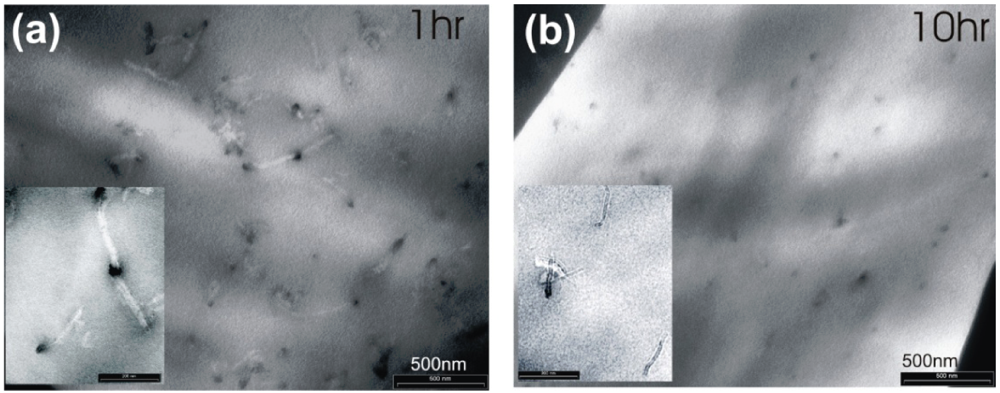
Figure 8.
TEM images of the MWNTs embedded in PDMS, after a sonication treatment of 1 h and 10 h.
4. Conclusions
To conclude, comparing the estimates of inter-tube binding forces and shear forces suggest that only at sufficiently high shear energy density, one can achieve complete separation of CNTs. The considerable energy density input also induces unwanted fiber breakage. A model describing sonication-induced tube scission was illustrated. Various approaches to slow down or to prevent CNT re-aggregation after shear-stress removal are demonstrated. This includes a kinetic approach of using a highly viscous solution/melt (only for shear-mixed samples), or a thermodynamic approach of choosing a compatible solvent or surfactant. An important conclusion reached is that the level of CNT dispersion as well as the choice of stabilizing agent should be adjusted according to the final application of the composites. For the purpose of conductivity enhancement, a full dispersion of CNT network may be considered undesirable. The key factors which influence the apparent electrical properties of CNT/polymer composites are summarized. It was shown that inhomogeneous microstructure consisting of non-dispersed CNT clusters bridged by dangling chains tend to result in higher DC conductivity. Such microstructure is obtained by short-time shear-mixing or weak sonication. The addition of surfactants can have contrasting effects on conductivity, depending on the surfactant layer thickness and the dielectric property. Modification in the dispersion method can sometimes lead to dramatic changes in conductivity from insulting to conducting even for the same composition. Overall, it is hoped that this review would form a general reference to facilitate the fit-for-purpose CNT or nanoparticle dispersion in polymer composites.
Acknowledgements
We thank Y. Ji and J. Marshall for useful discussion. YYH acknowledges the financial support from the Cambridge Gates Trust, the Homerton College and the Oppenheimer Research Fellowships.
References
- Ajayan, P.M.; Stephan, O.; Colliex, C.; Trauth, D. Aligned carbon nanotube arrays formed by cutting a polymer resin nanotube composite. Science 1994, 265, 1212–1214. [Google Scholar]
- Lourie, O.; Cox, D.M.; Wagner, H.D. Buckling and collapse of embedded carbon nanotubes. Phys. Rev. Lett. 1998, 81, 1638–1642. [Google Scholar]
- Schadler, L.S.; Giannarisand, S.C.; Ajayan, P.M. Load transfer in carbon nanotube epoxy composites. Appl. Phys. Lett. 1998, 73, 3842–3845. [Google Scholar] [CrossRef]
- Sekitani, T.; Nakajima, H.; Maeda, H.; Fukushima, T.; Aida, T.; Hata, K.; Someya, T. Stretchable active-matrix organic light-emitting diode display using printable elastic conductors. Nature Mater. 2009, 8, 494–499. [Google Scholar]
- Yu, C.; Masarapu, C.; Rong, J.; Wei, B.; Jiang, H. Stretchable supercapacitors based on buckled single-walled carbon-nanotube macrofilms. Adv. Mater. 2009, 21, 4793–4797. [Google Scholar] [CrossRef]
- Hu, L.; Pasta, M.; Mantia, F.L.; Cui, L.; Jeong, S.; Deshazer, H.D.; Choi, J.W.; Han, S.M.; Cui, Y. Stretchable, porous, and conductive energy textiles. Nano Lett. 2010, 10, 708–714. [Google Scholar]
- Huang, Y.Y.; Terentjev, E.M. Transparent electrodes with a nanostructured coating. ACS Nano 2011, 5, 2082–2089. [Google Scholar]
- Ahir, S.V.; Terentjev, E.M. Actuation in polymer-nanotube composites. Nature Mater. 2005, 4, 491–495. [Google Scholar]
- Pelrine, R.; Kornbluh, R.; Pei, Q.; Joseph, J. High-speed electrically actuated elastomers with strain greater than 100%. Science 2000, 287, 836–839. [Google Scholar] [CrossRef]
- Bar-Cohen, Y. Electroactive Polymer (EAP) Actuators as Artificial Muscles: Reality, Potential, and Challenges, 2nd ed; SPIE Press Book: Bellingham, WA, USA, 2011. [Google Scholar]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 2000, 62, 13104–13110. [Google Scholar]
- Hamaker, H.C. The London van der Waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar] [CrossRef]
- Israelachvili, J. Intermolecular and Surface Forces, 2nd ed; Academic Press: London, UK, 1992. [Google Scholar]
- Zhbanov, A.I.; Pogorelov, E.G.; Chang, Y.C. Van der Waals interaction between two crossed carbon nanotubes. ACS Nano 2010, 4, 5937–5945. [Google Scholar]
- Huang, Y.Y.; Ahir, S.V.; Terentjev, E.M. Rheology of carbon nanotube dispersions. Phys. Rev. B 2006, 73, 125422. [Google Scholar]
- Andrews, R.; Jacques, D.; Minot, M.; Rantell, T. Fabrication of carbon multi-wall nanotube/polymer composites by shear mixing. Macromol. Mater. Eng. 2002, 287, 395–403. [Google Scholar] [CrossRef]
- Park, J.H.; Alegaonkar, P.S.; Jeon, S.Y.; Yoo, J.B. Carbon nanotube composite: Dispersion routes and field emission parameters. Compos. Sci. Technol. 2008, 68, 753–759. [Google Scholar] [CrossRef]
- Wichmann, M.H.G.; Sumeth, J.; Fiedler, B.; Gojny, F.H.; Schulte, K. Multi-wall carbon nanotube/epoxy composites produced with a masterbatch process. Mech. Comp. Mater. 2006, 42, 395–406. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Terentjev, E.M. Dispersion and rheology of carbon nanotubes in polymers. Int. J. Mater. Form. 2008, 1, 63–74. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Knowles, T.P.J.; Terentjev, E.M. Strength of nanotubes, filaments, and nanowires from sonication-induced scission. Adv. Mater. 2009, 21, 3945–3948. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Miyauchi, Y.; Motoyanagi, J.; Fukushima, T.; Aida, T.; Kato, M.; Maruyama, S. Improved bath sonication method for dispersion of individual single-walled carbon nanotubes using new triphenylene-based surfactant. Jpn. J. Appl. Phys. 2008, 47, 2000–2004. [Google Scholar]
- Ramasubramaniama, R.; Chen, J. Homogeneous carbon nanotube/polymer com-posites for electrical applications. Appl. Phys. Lett. 2003, 83, 2928–2930. [Google Scholar] [CrossRef]
- Strano, M.; Moore, V.C.; Miller, M.K.; Allen, M.; Haroz, E.; Kittrell, C.; Hauge, R.H.; Smalley, R.E.J. The role of surfactant adsorption during ultrasonication in the dispersion of single-walled carbon nanotubes. Nanosci. Nanotechnol. 2003, 3, 81–86. [Google Scholar] [CrossRef]
- Chen, G.X.; Li, Y.J.; Shimizu, H. Ultrahigh-shear processing for the preparation of polymer/carbon nanotube composites. Carbon 2007, 45, 2334–2340. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Liang, Q.Z.; Kausch, H.H. Kinetics of ultrasonic and transient elongational flow degradation: A comparative study. Polymer 1997, 38, 3783–3793. [Google Scholar]
- Lohse, D. Sonoluminescence-cavitation hots up. Nature 2005, 434, 33–34. [Google Scholar]
- Gedanken, A. Using sonochemistry for the fabrication of nanomaterials. Ultrason. Sonochem. 2004, 11, 47–55. [Google Scholar] [CrossRef]
- Kerr, C.J.; Huang, Y.Y.; Marshall, J.E.; Terentjev, E.M. Effect of filament aspect ratio on the dielectric response of multiwalled carbon nanotube composites. J. Appl. Phys. 2011, 109, 094109. [Google Scholar]
- Wong, E.W.; Sheehan, P.E.; Lieber, C.M. Nanobeam mechanics: Elasticity, strength, and toughness of nanorods and nanotubes. Science 1997, 277, 1971–1975. [Google Scholar] [CrossRef]
- Xie, S.S.; Li, W.Z.; Pan, Z.W.; Chang, B.H.; Sun, L.F. Mechanical and physical properties on carbon nanotube. J. Phys. Chem. Sol. 2000, 61, 1153–1158. [Google Scholar] [CrossRef]
- Ding, W.; Calabri, L.; Kohlhaas, K.M.; Chen, X.; Dikin, D.A.; Ruo, R.S. Modulus, fracture strength, and brittle vs. plastic response of the outer shell of arc-grown multi-walled carbon nanotubes. Exp. Mech. 2007, 47, 25–36. [Google Scholar] [CrossRef]
- Peng, B.; Locascio, M.; Zapol, P.; Li, S.; Mielke, S.L.; Schatz, G.C.; Es-pinosa, H.D. Measurements of near-ultimate strength for multiwalled carbon nanotubes and irradiation-induced crosslinking improvements. Nat. Nanotechnol. 2008, 3, 626–631. [Google Scholar] [CrossRef]
- Barber, A.H.; Andrews, R.; Schadler, L.S.; Wagner, H.D. On the tensile strength distribution of multiwalled carbon nanotubes. Appl. Phys. Lett. 2005, 87, 203106. [Google Scholar]
- Lin-Gibson, S.; Pathak, J.A.; Grulke, E.A.; Wang, H.; Hobbie, E.K. Elastic flow instability in polymer-dispersed nanotubes. Phys. Rev. Lett. 2004, 92, 48302. [Google Scholar]
- Chen, J.; Hamon, M.A.; Hu, H.; Chen, Y.S.; Rao, A.M.; Eklund, P.C.; Haddon, R.C. Solution properties of single-walled carbon nanotubes. Science 1998, 282, 95–98. [Google Scholar] [CrossRef]
- Hamon, M.A.; Hu, H.; Bhowmik, P.; Niyogi, S.; Zhao, B.; Itkis, M.E.; Haddon, R.C. End-group and defect analysis of soluble single-walled carbon nanotubes. Chem. Phys. Lett. 2001, 347, 8–12. [Google Scholar] [CrossRef]
- Sinnott, S. Chemical functionalization of carbon nanotubes. J. Nanosci. Nanotech. 2002, 2, 112–123. [Google Scholar]
- Ausman, K.; Piner, R.; Lourie, O.; Ruoff, R. Organic solvent dispersions of single-walled carbon nanotubes: Toward solutions of pristine nanotubes. J. Phys. Chem. B 2000, 104, 8911–8915. [Google Scholar] [CrossRef]
- Bergin, S.D.; Nicolosi, V.; Streich, P.V.; Giordani, S.; Sun, Z.; Windle, A.H.; Ryan, P.; Niraj, N.P.P.; Wang, Z.T.T.; Carpenter, L.; et al. Towards solutions of single-walled carbon nanotubes in common solvents. Adv. Mater. 2008, 20, 1876–1881. [Google Scholar]
- Giordani, S.; Bergin, S.D.; Nicolosi, V.; Lebedkin, S.; Kappes, M.M.; Blau, W.J.; Coleman, J.N. Debundling of single-walled nanotubes by dilution: Observation of large populations of individual nanotubes in amide solvent dispersions. J. Phys. Chem. B 2006, 110, 15708–15718. [Google Scholar]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Sun, Z.; Nicolosi, V.; Rickard, D.; Bergin, S.D.; Aherne, D.; Coleman, J.N. Quantitative evaluation of surfactant-stabilized single-walled carbon nanotubes: Dispersion quality and its correlation with zeta potential. J. Phys. Chem. C 2008, 112, 10692–10699. [Google Scholar]
- Bonard, J.M.; Stora, T.; Salvetat, J.P.; Maier, F.; Stockli, T.; Duschl, C.; Forro, L.; de Heer, W.A.; Chatelain, A. Purification and size-selection of carbon nanotubes. Adv. Mater. 1997, 9, 827–831. [Google Scholar] [CrossRef]
- Islam, M.F.; Rojas, E.; Bergey, E.M.; Johnson, A.T.; Yodh, A.G. High weight fraction surfactant solubilization of single-wall carbon nanotubes in water. Nano Lett. 2003, 3, 269–273. [Google Scholar] [CrossRef]
- Li, S.; Daniel Blankschtein, D. Role of the bile salt surfactant sodium cholate in enhancing the aqueous dispersion stability of single-walled carbon nanotubes: A molecular dynamics simulation study. J. Phys. Chem. B 2010, 114, 15616–15625. [Google Scholar]
- Liu, Z.; Tabakman, S.M.; Chen, Z.; Dai, H. Preparation of carbon nanotube bioconjugates for biomedical applications. Nat. Protoc. 2009, 4, 1372–1381. [Google Scholar] [CrossRef]
- Wu, Y.; Hudson, J.A.S.; Lu, Q.; Moore, J.M.; Mount, A.S.; Apparao, M.; Rao, A.M.; Alexov, E.; Ke, P.C. Coating single-walled carbon nanotubes with phospholipids. J. Phys. Chem. B 2006, 110, 2475–2478. [Google Scholar]
- Rastogia, R.; Kaushala, R.; Tripathib, S.K.; Sharmaa, A.L.; Kaura, I.; Bharadwaj, L.M. Comparative study of carbon nanotube dispersion using surfactants. J. Colloid Interface Sci. 2008, 328, 421–428. [Google Scholar] [CrossRef]
- Zheng, M.; Jagota, A.; Semke, E.; Diner, B.; Mclean, R.; Lustig, S.; Richardson, R.; Tassi, N. DNA-assisted dispersion and separation of carbon nanotubes. Nat. Mater. 2003, 2, 338–342. [Google Scholar] [CrossRef]
- Tu, X.; Manohar, S.; Jagota, A.; Zheng, M. DNA sequence motifs for structure-specific recognition and separation of carbon nanotubes. Nature 2009, 460, 250–253. [Google Scholar]
- Karajanagi, S.S.; Yang, H.; Asuri, P.; Sellitto, E.; Dordick, J.S.; Kane, R.S. Protein-assisted solubilization of single-walled carbon nanotubes. Langmuir 2006, 22, 1392–1395. [Google Scholar]
- O’Connell, M.J.; Boul, P.B.; Ericson, L.M.; Huffman, C.; Wang, Y.; Haroz, E.; Kuper, C.; Tour, J.; Ausman, K.D.; Smalley, R.E. Reversible water-solubilization of single-walled carbon nanotubes by polymer wrapping. Chem. Phys. Lett. 2001, 342, 265–271. [Google Scholar] [CrossRef]
- Hasan, T.; Scardaci, V.; Tan, P.H.; Rozhin, A.G.; Milne, W.I.; Ferrari, A.C. Stabilization and “debundling” of single-wall carbon nanotube dispersions in N-methyl-2-pyrrolidone (NMP) by polyvinylpyrrolidone (PVP). J. Phys. Chem. C 2007, 111, 12594–12602. [Google Scholar]
- Zou, J.H.; Liu, L.W.; Chen, H.; Khondaker, S.I.; McCullough, R.D.; Huo, Q.; Zhai, L. Dispersion of pristine carbon nanotubes using conjugated block copolymers. Adv. Mater. 2008, 20, 2055–2060. [Google Scholar] [CrossRef]
- Christian, E.; Rahman, G.M.A.; Jux, N.; Balbinot, D.; Guldi, D.M.; Paolucci, F.; Marcaccio, M.; Paolucci, D.; Melle-Franco, M.; Zerbetto, F.; et al. Interactions in single wall carbon nanotubes/pyrene/porphyrin nanohybrids. J. Am. Chem. Soc. 2006, 128, 11222–11231. [Google Scholar]
- Nakashima, N.; Tomonari, Y.; Murakami, H. Water-soluble single-walled carbon nanotubes via noncovalent sidewall-functionalization with a pyrene-carrying ammonium ion. Chem. Lett. 2002, 31, 638–639. [Google Scholar]
- Ji, Y.; Huang, Y.Y.; Tajbakhsh, A.R.; Terentjev, E.M. Polysiloxane surfactants for the dispersion of carbon nanotubes in non-polar organic solvents. Langmuir 2009, 25, 12325–12331. [Google Scholar]
- Chen, J.; Liu, H.; Weimer, W.A.; Halls, M.D.; Waldeck, D.H.; Walker, G.C. Noncovalent engineering of carbon nanotube surfaces by rigid, functional conjugated polymers. J. Am. Chem. Soc. 2002, 124, 9034–9035. [Google Scholar]
- Hasan, T.; Sun, Z.; Wang, F.; Bonaccorso, F.; Tan, P.H.; Rozhin, A.G.; Ferrari, A.C. Nanotube-polymer composites for ultrafast photonics. Adv. Mater. 2009, 21, 3874–3899. [Google Scholar]
- Lisunova, M.O.; Mamunya, Y.P.; Lebovka, N.I.; Melezhyk, A.V. Percolation be-haviour of ultrahigh molecular weight polyethylene/multi-walled carbon nanotubes composites. Eur. Polym. J. 2007, 43, 949–958. [Google Scholar] [CrossRef]
- Bryning, M.B.; Islam, M.F.; Kikkawa, J.M.; Yodh, A.G. Very low conductivity threshold in bulk isotropic single wall carbon nanotube epoxy composites. Adv. Mater. 2005, 17, 1186–1191. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Marshall, J.E.; Gonzalez Lopez, C.; Terentjev, E.M. Variation in carbon nanotube polymer composite conductivity from the effects of processing, dispersion, aging and sample size. 2012, in press.. [Google Scholar]
- Huang, Y.Y.; Terentjev, E.M. Tailoring the electrical properties of carbon nanotubes-polymer composite. Adv. Funct. Mater. 2010, 20, 4062–4068. [Google Scholar] [CrossRef]
- Bai, J.B.; Allaoui, A. Effect of the length and aggregate size of MWNTs on the mechanical and electrical properties of the nanocomposites. Compos. A 2003, 34, 689–694. [Google Scholar]
- Rahatekar, S.S.; Shaffer, M.S.P.; Elliott, J.A. Modelling percolation in fibre and sphere mixtures: Routes to more efficient network formation. Compos. Sci. Technol. 2010, 70, 356–362. [Google Scholar] [CrossRef]
- Kyrylyuk, A.V.; Hermant, M.C.; Schilling, T.; Klumperman, B.; Koning, C.E.; van der Schoot, P. Controlling electrical percolation in multicomponent carbon. Nat. Nanotech. 2011, 6, 364–369. [Google Scholar] [CrossRef]
- Kyrylyuk, A.V.; van der Schoot, P. Continuum percolation of carbon nanotubes in polymeric and colloidal media. Proc. Natl. Acad. Sci. USA 2008, 105, 8221–8226. [Google Scholar]
- Zhang, Q.; Rastogi, S.; Chen, D.; Lippits, D.; Lemstra, P.J. Low percolation threshold in single-walled carbon nanotube/high density polyethylene composites prepared by melt processing technique. Carbon 2006, 44, 778–785. [Google Scholar] [CrossRef]
- Cui, S.; Caneta, R.; Derrea, A.; Couzib, M.; Delhaes, P. Characterization of multiwall carbon nanotubes and influence of surfactant in the nanocomposite processing. Carbon 2003, 41, 797–809. [Google Scholar] [CrossRef]
- Mitchell, C.A.; Krishnamoorti, R. Dispersion of single-walled carbon nanotubes in poly (e-caprolactone). Macromolecules 2007, 40, 1538–1545. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).