Modeling Textural Processes during Self-Assembly of Plant-Based Chiral-Nematic Liquid Crystals

Abstract

Biological liquid crystalline polymers are found in cellulosic, chitin, and DNA based natural materials. Chiral nematic liquid crystalline orientational order is observed frozen-in in the solid state in plant cell walls and is known as a liquid crystal analogue characterized by a helicoidal plywood architecture. The emergence of the plywood architecture by directed chiral nematic liquid crystalline self assembly has been postulated as the mechanism that leads to optimal cellulose fibril organization. In natural systems, tissue growth and development takes place in the presence of inclusions and secondary phases leaving behind characteristic defects and textures, which provide a unique testing ground for the validity of the liquid crystal self-assembly postulate. In this work, a mathematical model, based on the Landau-de Gennes theory of liquid crystals, is used to simulate defect textures arising in the domain of self assembly, due to presence of secondary phases representing plant cells, lumens and pit canals. It is shown that the obtained defect patterns observed in some plant cell walls are those expected from a truly liquid crystalline phase. The analysis reveals the nature and magnitude of the viscoelastic material parameters that lead to observed patterns in plant-based helicoids through directed self-assembly. In addition, the results provide new guidance to develop biomimetic plywoods for structural and functional applications.

1. Introduction

Biological liquid crystalline polymers (BLCP) are anisotropic viscoelastic materials formed by polypeptides [1,2,3,4,5,6,7,8,9], polysaccharides [1,2,3,4,10,11] and polynucleotides [1,3,12,13,14]. BLCPs exhibit long-range orientational order and, in some cases, partial positional order [15]. These materials possess the anisotropic elastic behavior of oriented media and the anisotropic viscous behavior of concentrated solutions of rod or disk like molecules. BLCPs are structural and functional materials that are responsive to a range of stimuli including electro-magnetic fields, curvatures and interfaces, temperature and concentration gradients, and pH [1]. For example, cellulose in plant cell walls, chitin in exocuticle of insects, and collagen fibrils in human compact bones, adopt a chiral nematic (cholesteric) phase to provide structural strength [2]. Table 1 shows a compilation of biological mesogens that exhibit mesophases in forms of tissues, cells, and supramolecular self-assembled materials. The observed mesophases of BLCPs can be classified into [1]: (i) Liquid crystalline analogues (left column), where the liquid crystalline type of packing is observed frozen-in in the solid state; (ii) liquid crystalline phases observed in biopolymer solutions in a controlled environment (middle column); and (iii) mesophases observed in the native state of the biopolymer (right column).

Table 1. Compilation of self-assembling BLCPs and liquid crystalline analogues observed in nature [Adapted from Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402-3429].

Biological Analogues	In vitro Solutions	In vivo Solutions
Connective tissues in mammals [2] Dermal scutes of fish [3] Exoskeleton of insects and crustaceans [2,3] Membranes of animal eggs [2,4] Plant cell walls [2]	Collagen [4] Cellulose [4,19,11] Chitin [4] DNA [12,13] Viral suspensions [16] Actin [17] Flagella of Salmonella typhimurium [17] Mucin [18]	DNA [3,13] Chromosomes of dinoflagellate and bacteria [14] Collagen in egg shell and glands of dogfish [5] Oothecal gland protein of S. tenuidentata [6] Spider silk [7] Sickle cell hemoglobin [8] Synovial fluid [9]

Table 1. Compilation of self-assembling BLCPs and liquid crystalline analogues observed in nature [Adapted from Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402-3429].

Biological Analogues	In vitro Solutions	In vivo Solutions
Connective tissues in mammals [2] Dermal scutes of fish [3] Exoskeleton of insects and crustaceans [2,3] Membranes of animal eggs [2,4] Plant cell walls [2]	Collagen [4] Cellulose [4,19,11] Chitin [4] DNA [12,13] Viral suspensions [16] Actin [17] Flagella of Salmonella typhimurium [17] Mucin [18]	DNA [3,13] Chromosomes of dinoflagellate and bacteria [14] Collagen in egg shell and glands of dogfish [5] Oothecal gland protein of S. tenuidentata [6] Spider silk [7] Sickle cell hemoglobin [8] Synovial fluid [9]

A host of endophytic fungal metabolites, such as hypericin [19,20], protohypericin [21], blennione [22], necatorone [22] and camptothecin [23], have also drawn interest in recent years owing to their medicinal importance and their tendency to self-assemble into columnar phases in vitro. Another fungal metabolite, Mycenaaurin A [24], is a candidate of interest owing to its nematic self-assembly in vitro. The varied biochemical groups and biological origin of the mesogens presented in Table 1 show that mesophase order is ubiquitous in development of functional and structural biological materials. The present work seeks to describe the structure, dynamics, and process involved in formation of liquid crystalline analogues in representative plant cell walls using well-established liquid crystal models and principles. This knowledge is of significant importance for researchers in the fields of material science and tissue engineering trying to mimic the ultrastructure and mechanical properties of bone tissue using cellulosic material [25,26].

The plant cell wall is a biological composite made of cellulose microfibrils (CMFs), of up to 20 nm diameter [27], and a few micrometers in length, coated with hemicelluloses and embedded in a lignin/pectin matrix [1]. The CMFs ensure support, protection and conduction in plant tissue. The liquid crystal analogues observed in these plant cell walls arise from the CMFs being strategically oriented to produce plywood-like laminated structures called twisted plywood architectures or helicoidal plywoods or Bouligand structures [28]. The twisted plywood architecture and its variations have been reported in algae, lower plants and higher plants, in a variety of tissues such as root hair, petiole, leaf epidermis, hypocotyl, fruit endocarp, seed epidermal walls [2]. They may occur in both primary and secondary plant cell walls, although in the primary cell wall they are transient and fragile [29].

The helicoidal plywoods have the chiral order of a chiral-nematic liquid crystal, which possess orientational order with a superposed rotation and layer periodicity [2]. Figure 1 shows a schematic of helicoidal plywood, where the CMF orientation is represented by lines. Figure 1(a) shows the parallel CMF arrangement on each plane and the rotation of CMF orientation angle by a small degree when traversing normal to each plane, as in chiral nematic LCs. On each plane shown in Figure 1(a) the orientation of CMFs is like in nematic LCs, but on a larger scale it has a layer structure like smectic LCs. The distance through which these planes undergo a 2π rotation is called the pitch p_o, the magnitude of which is usually a few μm. In Figure 1(b), oblique section of the helicoidal plywood shows the characteristic arced pattern, widely observed in many plant cell walls and other extracellular fibrous biological composites, such as insect cuticles and bones [2]. The normal section of the helicoidal plywood in Figure 1(c) shows the cholesteric helix defined by its axis orientation unit vector h, its pitch p_o, and the rotation sense (left or right). The mechanical advantage of helicoidal fiber orientation in the secondary cell wall is that the structure has good properties in all directions which increase the fracture strength since the path of any crack will be diverted by the change in orientation, resulting in an increased capacity to dissipate energy.

Figure 1. (a-b) Schematics of the helicoidal plywood found in some plant cell walls. Oblique sections (b) give rise to characteristic arc patterns. (c) Normal view schematic of the helix axis, defined by the helix orientation h (dashed line in c) and the pitch p_o. See reference [2] for examples of biological plywoods. [Adapted from Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402-3429].

Figure 1. (a-b) Schematics of the helicoidal plywood found in some plant cell walls. Oblique sections (b) give rise to characteristic arc patterns. (c) Normal view schematic of the helix axis, defined by the helix orientation h (dashed line in c) and the pitch p_o. See reference [2] for examples of biological plywoods. [Adapted from Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402-3429].

Owing to the structural similarity between helicoidal plywoods and chiral nematic LCs, it has been hypothesized that these structures arise through liquid crystalline self assembly that occurs at sufficiently high concentration of BLCPs, when the excluded volume of the CMFs is minimized in presence of chiral interactions [2]. A review supporting this hypothesis by analyzing it from the aspects of anatomy and developmental biology has emphasized on the necessity of characterizing the nature of the forces inducing this self-assembly [30]. Although there is no in vivo experimental evidence supporting this hypothesis, it is known that the cellulose microfibrils extracted from plant cell walls by acid-hydrolysis self-assemble to form chiral-nematic phases in vitro [10,11].

In addition to chiral interactions, other factors that influence the formation of liquid crystalline phase include: the shape anisotropy of the fibers, the ionic environment that regulates the charges on the fibers, the concentration of the fibers that drive the minimization of excluded volume and the type of LC organization in either single and/or biphasic states. 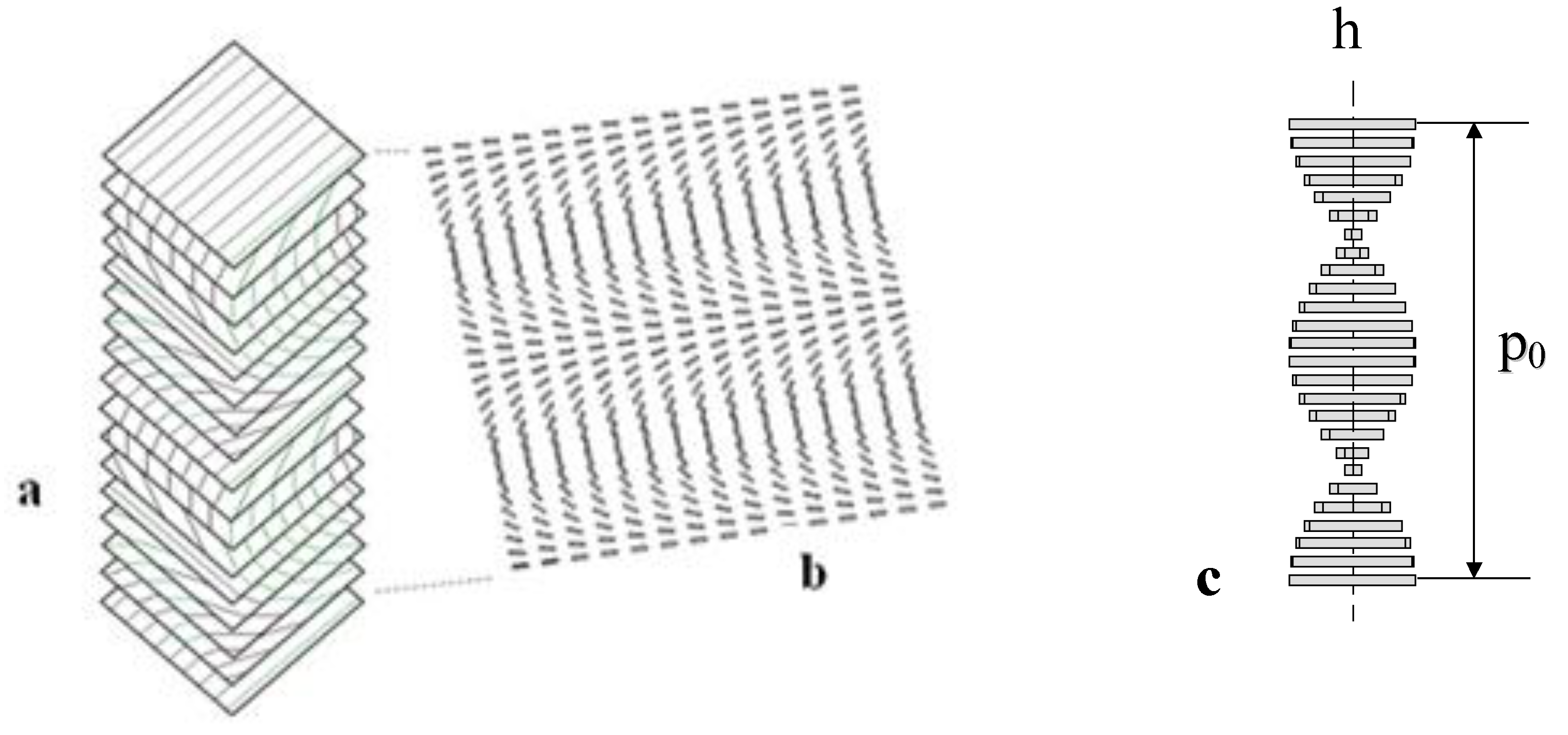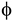According to Onsager theory, this concentration driven lyotropic liquid crystallinity appears in solutions of rods when the shape anisotropy (L_eff/D_eff) times the volume fraction ( ), i.e., 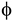L_eff/D_eff, exceed a critical value (usually close to 4) at which excluded volume is minimized [31]. For semi-flexible chain BLCPs, like cellulose fibrils, L_eff is the persistence length of the polymer chain and D_eff is effective diameter that takes into account deviations from uncharged rigid-rods (due to dispersion forces, hydration interactions, and surface charges) [1]. The persistence length of cellulose chains obtained from various cellulose-solvent systems in vitro has been reported in the range of 11–25 nm [32]. It is erroneous to arrive at a conclusion that there is not enough material to form a LC phase during development of helicoidal plywoods in plant cell walls solely based on this calculation for the following reasons: (a) These calculations use absolute diameter instead of D_eff of the CMFs, due to the lack of in vivo experiments in plant cell wall; (b) it has been frequently observed that the isotropic-nematic transition predicted by the Onsager theory may be an order-of-magnitude larger than that observed experimentally, perhaps due to other factors such as molecular interactions. Theory and simulations based on well established liquid crystal theory can be used as a tool to resolve these uncertainties arising due to the lack of in vivo experimental evidence and/or data. This is evident from the recent review [33] that emphasizes the Landau-de Gennes theory that yields testable and verifiable predictions of thermodynamical, textural, and rheological phenomena observed in BLCPs. For an extensive review of mesoscopic models employed to quantitatively describe the biological liquid crystalline phases and processes, refer to [33].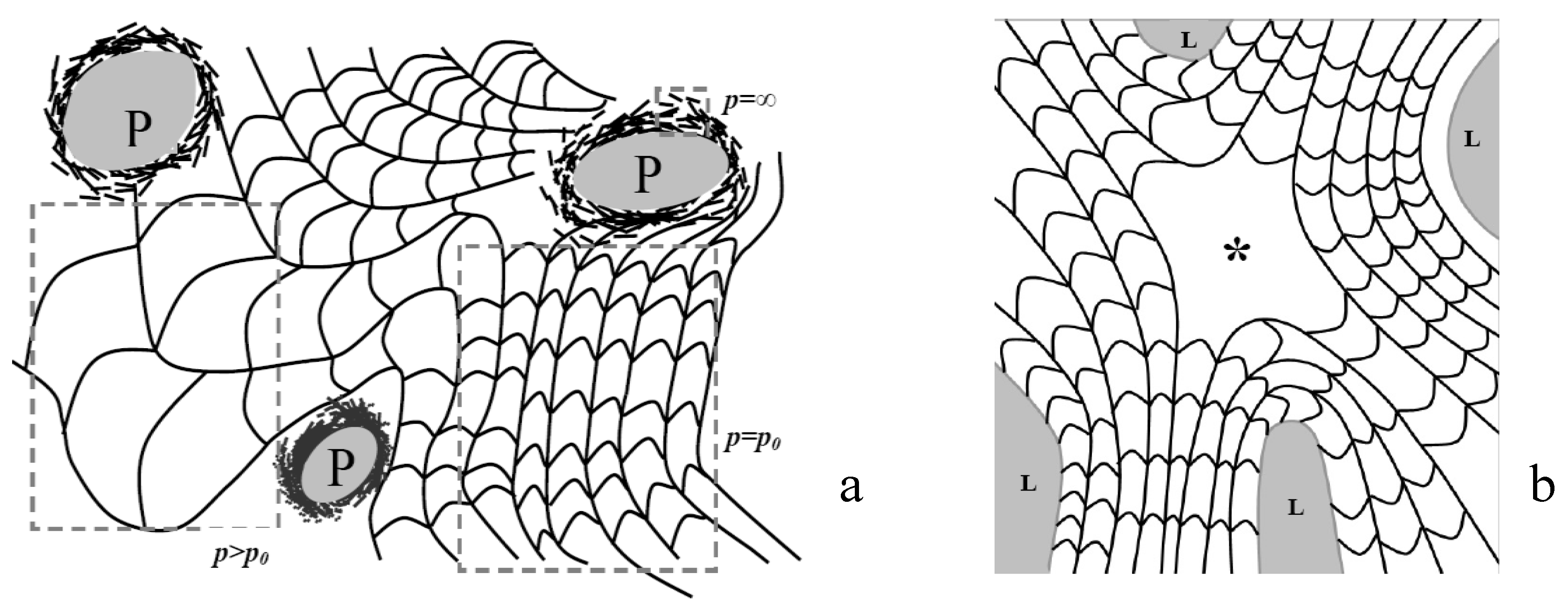

Previously a computationally implemented mathematical model based on the Landau-de Gennes theory has been employed to investigate the effect of constraining surfaces on the development of structure in a lyotropic chiral nematic liquid crystalline mesophase [34,35]. These computations elucidated the need for a constraining surface that can direct the chiral nematic helix in a direction normal to it, to form a defect free monodomain twisted plywood structure [34,35]. Recently, an integrated mechanical model describing nematic liquid crystalline self-assembly of rigid rods on an arbitrarily curved membrane has been presented and relative predictions of cellulose ordering and orientation in the plant cell wall are presented. An integrated shape and nematic order equation developed in this work gives a complete model whose solution describes the coupled membrane shape and fiber order state [36]. When integrated with the Gibbs- Duhem equation, the model can describe the role of temperature and adsorption on membrane shape and fiber order [37]. A viscoelastic model that integrates the statics of anisotropic membranes, the planar nematodynamics of fibers and the dynamics of isotropic membranes, has been reported to predict transitions between axial and azimuthal fiber arrangements of interest to cellulose fiber orientation in plant morphogenesis [38].

The presence of secondary phases, such as plant cells and pit canals in the domain of self‑assembling cell wall material, are evidently the origin of surface constraints that results in distortions, vortices and defect disclinations, such as saddle-like patterns [39,40]. LC analogues in plant cell walls having the structure of chiral-nematic LC phases, can nucleate disclination characteristics of orientationally ordered nematic LCs, as well as dislocations characteristic of layered Smectic-A LCs. As discussed below, the core of disclinations can be singular, when the equilibrium orientational order is distorted or non-singular, such that the rod-like molecules escape into the third dimension avoiding gradients in molecular order. The type and number of defects stabilized in these materials and the nature of the corresponding defect cores (singular or non-singular), affect crack propagation and, hence, determine the strength of the material. Figure 2(a) shows an example of structure adaptation of a helicoidal plywood, involving the pitch expansion and helix rotation to avoid stress concentration around pit canals (denoted by P) in plant cell walls. Figure 2(b) shows a schematic of a disclination line defect of strength -1, in a natural helicoidal plywood found in walnut, due to inclusion of four cell lumens (denoted by L). These disclination line defect patterns observed in electron micrographs of plant cell walls can be used as fingerprints to identify the LC phases involved in their formation and their material properties. Understanding the disclination line, defect nucleation and stabilization mechanism in helicoidal plywoods can be used as a model for gaining insight into similar phenomenon in other lamellar systems, such as diblock co-polymers and SmA LCs [41].

Figure 2. (a) Adaptation of helicoidal plywood to embedded pit canals (P inside the gray circles) by dilation of layers (shown by width changes in arc-patterns) and bending of layers (bending of arced patterns) [39] (b) a–1 saddle defect (denoted by *) defect in a natural helicoidal plywood due to inclusion of four (L) lumens in walnut [40] [Adapted from Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402-3429].

Figure 2. (a) Adaptation of helicoidal plywood to embedded pit canals (P inside the gray circles) by dilation of layers (shown by width changes in arc-patterns) and bending of layers (bending of arced patterns) [39] (b) a–1 saddle defect (denoted by *) defect in a natural helicoidal plywood due to inclusion of four (L) lumens in walnut [40] [Adapted from Rey, A.D. Liquid crystal models of biological materials and processes. Soft Matter 2010, 6, 3402-3429].

A computational modeling study of texture formation in a nematic carbonaceous mesophase matrix with embedded circular carbon fibers, has concluded that the number and type of disclinations that arise invariably obey the experimentally observed Zimmer’s rule; the disclination line strength is equal to –(N–2)/2, where N is the number of inclusions [42,43]. A Landau-de Gennes type model for defect coarsening process of the isotropic/smectic-A phase transition, has been used to simulate elementary dislocations, total dislocation content and defect annihilation laws for smectic disclinations has been established [44]. The model has also been used to characterize edge dislocation arising in SmA LC [45].

The main objectives of this work are: (1) To elucidate the role of liquid crystalline self-assembly in the formation of helicoidal plywoods in plant cell walls, using computational modeling of defect texture formation in chiral-nematic mesophases; and (2) to determine the specific viscoelastic material properties, the specific geometric conditions involving the pitch of the plywood and the characteristic length scale of inclusions, and strength of interfacial interactions between the inclusion and the mesophase, that are required to observe typical hyperbolic textures in plant cell walls. In this paper, the defects textures analysis in a self assembling chiral nematic LC phase, due to four cylindrical inclusions representing cell lumens, are simulated using the Landau de Gennes theory. The number and types of disclinations and dislocations arising in the chiral-nematic phases are characterized. By comparing the texture simulation results and typical natural defect patterns in helicoidal plywoods, confirmation of the directed self-assembly process in the presence of curved inclusion assemblies can be established. Furthermore by exploring the viscoelastic-geometric parametric space, a semi-quantitative characterization of the relevant material properties of CMF and the role of the pitch of the chiral phase-to-domain length are revealed. By comparing the present results with previous simulations and experiments on fiber-filled nematics, it is also possible to demonstrate that cellulosic mesophases respond as expected from layered anisotropic soft matter under complex confinement.

The organization of this paper is as follows. In Section 2, the quadrupolar order parameter that describes the orientation and degree of alignment of CMFs is introduced; the dimensionless form of Landau- de Gennes model for chiral nematics, in terms of length scales of the model and material properties, is presented; and the dimensionless coarse-grained Lubensky- de Gennes model used to analyze some aspects of the results in terms of layer properties of the liquid crystalline phase, is also presented. In Section 3, the computational domain under investigation is introduced and the anisotropic confinement in the domain that results due to the chosen geometry is discussed. The imposed initial and boundary conditions, and the material properties used in the simulations, as well as the classification of defects observed in our simulations, are also presented. In Section 4, the defect textures arising from our simulation while exploring the viscoelastic-geometric parametric space are presented and the defects are characterized. In this section the effect of confinement on the type of dislocations stabilized is discussed, the role of pitch of the chiral phase-to-domain length and elastic anisotropy constant of the material on layer bending and dilation and defect formation mechanism are investigated, and the material properties and length scales that result in the saddle defect observed in plant-based helicoidal plywood are obtained. Section 5 presents the conclusions of this work on structure, dynamics, and processes involved in the formation of liquid crystalline analogues in plant cell walls.

2. Theory and Governing Equations

2.1. Description of Long-Range Orientational Order

As mentioned earlier, liquid crystalline phases possess long range orientational order of their constituent molecules. This long range molecular order is described by an orientation distribution function, whose second moment is known as the quadrupolar symmetric and traceless tensor order parameter Q [15,33]:

(1a)

where the following restrictions apply:

Q = Q^T

(1b)

tr(Q) = 0

(1c)

(1d)

(1e)

n.n = m.m = 1.1

(1f)

The molecular orientation is defined completely by the orthogonal director triad (n, m, l). The measure of molecular alignment is defined by the uniaxial (S) and biaxial (P) scalar order parameters. The quadrupolar symmetry of the Q tensor retains the head-tail invariance i.e., n(z) and −n(z) are equal. The chiral nematic phase being periodic: Q(z) = Q(z + p_o). The chiral nematic phase is inherently biaxial (S ≠ 0, P ≠ 0) and the three eigenvalues μ_n, μ_m, μ₁ are non-zero and distinct.

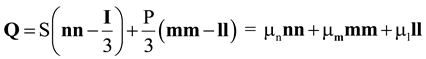
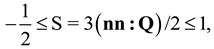
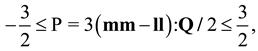
2.2. Landau- de Gennes Theory for Liquid Crystalline Materials

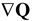The Landau- de Gennes theory expresses the free energy density of the liquid-crystalline material in terms of homogeneous and gradient elastic effects. The homogeneous (gradient) elastic effects are represented by power series of scalar invariants of tensor parameter Q (gradient of tensor order parameter ). In the absence of an external field, the total free energy density of the mesophase (f) can be given in the following dimensionless form [15,33,34,46]:

F=f_iso + f_lr

2(a)

2(b)

2(c)

where f_iso is the free energy density of the isotropic state which depends on conventional thermodynamic parameters, such as temperature, pressure, and concentration. f_sr and f_lr are, respectively, the short- and long-range contributions to the total free energy density f. The dimensionless parameter U is a thermodynamic potential proportional to the dimensionless concentration of anisotropic molecules which drives the isotropic- chiral-nematic phase transition; U is related to the concentration C by the relation U = 3C/C*, where C* is the concentration at the phase transition. The parameter ξ is a coherence/internal length that gives the distance over which variations of long-range orientational order can occur. This length furnishes the order of magnitude for the size of the core of a disclination defect. The parameter h₀ is an external/geometric length that gives the size of the domain. The parameter p₀ is the pitch of the chiral-nematic liquid-crystalline material. It is essential to recognize that this model is therefore of a mesoscopic nature since it includes a molecular length scale (ξ) and a macroscopic (h₀) length scale. The remaining parameter υ represents a measure of the elastic anisotropy of the material. This parameter is constrained to be greater than 1/2 in order to ensure the positivity and thermodynamic stability of the long-range contribution to the free energy.

The time evolution of the tensor order parameter Q is given by a standard dimensionless gradient flow equation:

(3)

where the superscript [s] denotes symmetric and traceless tensors, and where γ is a rotational viscosity [47]. Substituting Equation 2 into Equation 3 yields the equation for spatio-temporal evolution of tensor order parameter Q(x,t).

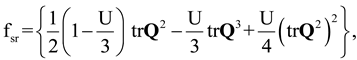
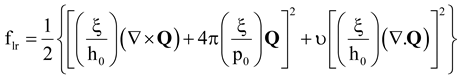
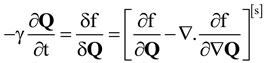
2.3. Characterization Methods: Lubensky- de Gennes Coarse Grained Elastic Theory and Chiral Order Parameter

To guide the exploration of the model to significant biological ranges and to characterize the numerical results, we use the coarse grained model of Lubensky- de Gennes [15] and the chiral order parameter, as follows. At scales larger than the equilibrium pitch p_o, chiral nematic LC phases are layered structures characterized in terms of layer bending and dilation using a coarse grained elastic theory. According to the Lubensky- de Gennes theory, the dimensionless free energy density due to the layer displacement “u” reads [15]:

4(a)

4(b)

4(c)

4(d)

The penetration length λ₁ defines the dilation strain required to produce bending in a set of parallel layers and it is smaller than the pitch p_o. The dimensionless bending (K₁) and dilation (B) parameters of this model are expressed in terms of the scalar order parameter (S), the length-scale ratios ξ/h₀, ξ/p₀, and the elastic anisotropy (υ) of the original LdG model (Equation 2). Hence changes in the coarse grained parameters (K₁, B) that control the layer geometry can be predicted by changes in the primitive LdG parameters.

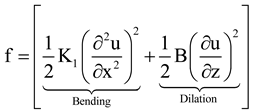
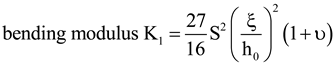
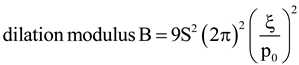
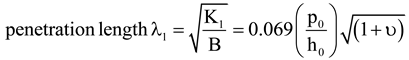
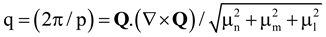To quantify the layer dilation (difference between actual pitch and equilibrium pitch: |p−p_o|) and to identify a non-singular disclination defect core due to escape into the third dimension, which cannot be identified from changes in the uniaxial order parameter S, a chiral order parameter is defined: , where p is the modified pitch due to layer dilation. Hence by tracking q(x), dislocation defects associated with q changes are identified.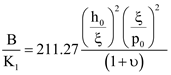

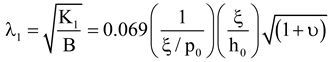
As per Equations 2, 3 the defect textures given by Q(x,t) are modulated by the length scales (ξ/h₀), (ξ/p₀), the elastic anisotropy υ and the thermodynamic potential U. In this study, the parametric space has been limited to (ξ/p₀), (ξ/h₀) and υ. Increasing elastic anisotropy decreases the dilation/bending ratio

(5)

Since a high value of B/K₁ (small λ₁) promotes defect nucleation, large anisotropy, large pitches, and smaller samples will tend to decrease defect proliferation. In terms of penetration length:

(6)

we see that large anisotropy υ, large pitch p_o, and smaller samples h_o increase λ₁ which decreases defect content.

The elastic anisotropy ratio in our model, relates to the well-known Frank’s bending and twist elastic constants as [1,15]: υ = [2(K₃₃/K₂₂) − 1] and the present model assumes equal bend and splay deformations i.e., K₁₁ = K₃₃. For monomeric mesogens far from phase transitions, the elastic anisotropic constant is modest (υ ≈ 1) [1,15], but for polymeric rods it is large (υ >> 1), changing the relative energetic costs of bending/dilation and the defect density in the observed textures.

3. Computational Modeling

In order to understand the directed self-assembly process and material parameters which lead to defect textures observed in the plant cell wall, we simulate the time evolution of the tensor order parameter Q in a lyotropic cholesteric liquid-crystalline material using relevant geometric conditions, including circular inclusions. Since the tensor order parameter has five independent components (symmetric and traceless), five coupled time-dependent nonlinear partial differential equations (Equations 2) need to be solved simultaneously.

3.1. Computational Domain

The dimensionless computational domain is the unit square (0 < x < 1, 0 < y < 1) with four circular inclusions as shown in Figure 3. The internal boundaries 1–4 represent four plant cells embedded in a self assembling extracellular material. Although in reality these cells are often irregular in shape and surface profile, the cells are represented by uniform circles in this model. Allowing this discrepancy is validated by the fact, known both from experiments [40] and simulations [35], that chiral nematic mesophase is robust enough to overcome surface irregularities and can form a monodomain after a finite healing length (usually in the order p₀). This geometry inherently generates anisotropic confinement in the domain of self assembly. The region represented by S (W) imposes stronger (weaker) confinement on the self assembling material. This aspect of the model is essential in understanding the effect of confinement on the type of defects nucleated. It is also important to note that, despite the fact that simulation domain is two dimensional (2D), Q conserves its five degrees of freedom. The Q tensor field is visualized using the MATLAB function plotDTI developed by Barmpoutis et al. [48].

Figure 3. The computational domain, 1–4 internal boundaries, 5–8 external boundries, S—Stronger confinement region, W—Weaker confinement region.

Figure 3. The computational domain, 1–4 internal boundaries, 5–8 external boundries, S—Stronger confinement region, W—Weaker confinement region.

3.2. Boundary and Initial Conditions

In order to restrict the influence of physical boundaries on the material bulk, periodic boundary conditions are employed on external boundaries 5–8. On the internal boundaries 1–4, the molecules exhibit a strong planar anchoring, making them the constraining layers that direct the liquid crystalline phase ordering; for discussion on interfacial modeling of liquid crystal see [49,50,51]. Initially the liquid crystalline material is taken to be in a stable isotropic state. This disordered state is imposed by using Q₀ = Q(t = 0) = 0. The governing equations are then solved using the Finite Element Method software package COMSOL, using adaptive finite elements and biquadratic basis functions with the generalized minimal residual (GMRES) solver method and a time-dependent backward Euler method. Convergence, mesh-independence, and stability are confirmed for each simulation result.

3.3. Elastic Constants for BLCPs

The three basic elastic modes of nematic liquid crystals are splay (K₁₁), twist (K₂₂), and bend (K₃₃). For long chain polymers, it is known that the twist elastic constant K₂₂ is always the smallest of the three elastic constants and the ratio of splay to bend elastic constant has been known to vary from slightly above one, up to three orders of magnitude in different solvents. Whether this difference can solely be attributed to the choice of the solvent has not yet been elucidated [1]. In the present work, based on experimental measurements of PBLG and theoretical predictions [52], the following representative elastic constant ratios were used: K₁₁/K₂₂ = 11 and K₁₁ = K₃₃. The simulations were run for K₁₁/K₂₂ = 1 (single constant approximation) and U = 6. The three dimensional parametric phase space explored for this paper was:

(a)

internal/external length scale ratio (ξ/h₀)

(b)

internal/pitch length scale ratio (ξ/p₀)

(c)

elastic anisotropy (υ).

3.4. Classification of Defects in Chiral Nematic LCs

Chiral nematic LC phases having the orientation characteristics of nematic LCs at small length scales and layer characteristics of smectic LCs at large length scales, are known to nucleate disclinations and dislocations. Disclination is a defect involving discontinuity in the director field, around a line or a point. Dislocations are translational defects which correspond to addition or removal of cholesteric layers. The disclinations and dislocations necessary to discuss the defect textures obtained in our simulations are illustrated in Figure 4; Reference [41] presents a more extensive classification of defects in chiral nematics. Disclinations are characterized by core type and strength, where cores can be singular or non-singular, and where the strength characterizes the amount and sense of rotation when encircling the defect.

Figure 4. The Q tensor field is visualized using the MATLAB function plotDTI developed by Barmpoutis et al. [48]. Disclination lines of τ type and splitting disclination cores into different pairs of disclinations: (a) τ^+1/2, (b) τ^−1/2, (c) λ⁻¹, (d) τ^−1/2λ^+1/2, (e) λ^−1/2λ^+1/2 (f) τ^−1/2τ^+1/2.

Figure 4. The Q tensor field is visualized using the MATLAB function plotDTI developed by Barmpoutis et al. [48]. Disclination lines of τ type and splitting disclination cores into different pairs of disclinations: (a) τ^+1/2, (b) τ^−1/2, (c) λ⁻¹, (d) τ^−1/2λ^+1/2, (e) λ^−1/2λ^+1/2 (f) τ^−1/2τ^+1/2.

Figure 4 shows computed Q-tensor visualization of classical disclinations and disclination pairs arising in chiral nematics. τ disclination lines (a,b) are singular cored, while λ disclination lines (c) are coreless (non-singular). The sign of the disclination lines is positive or negative depending on whether the direction of rotation of director field around a disclination line is anticlockwise or clockwise. These τ and λ disclinations of opposite signs can associate themselves to produce dislocations (d,e,f) [41]. A ± 1 singular disclination may either be energetically unstable and split into two singular defects of half the strength and same sign as the parent or be topologically unstable and then the nonsingular disclination line can escape in the third dimension (as in Figure 4(c)). The escaped unit strength disclination is non-singular and has a larger defect core size [1].

4. Results and Discussion

4.1. Defect Textures and Charge Balance

This section presents simulation results of defect textures while varying the elastic anisotropy υ and keeping the length scales constant, thus changing K₁ and λ₁ (see Equations 4(b,d)). The chiral nematic layering is visualized by plotting the out-of-plane component |n_z| of the director field (see Equation 1(a)). The chiral order parameter q surface plots are used to identify defect cores. All the results presented in this work are at a representative dimensionless time of t = 100 where time dependence vanishes. The number, type and charge of the defects in the region bounded by the four inclusions represented by the dotted line in Figure 3, are identified and tabulated in Table 2.

From Table 2, it is evident that the presence of four circular inclusions result in defect textures of a net charge of −1 as predicted by Zimmer’s rule [42,43]. The number of defects nucleated decreases with increasing elastic anisotropy. This observation will be further reasoned using Lubensky- de Gennes coarse grained elastic theory detailed in Section 4.3

Table 2. The number and types of defects as a function of elastic anisotropy υ (see Figure 5 for parametric values, orientation n_z and chirality q fields).

Type of defect	υ = 1	υ = 5	υ = 21
τ+1/2	5	Absent	Absent
τ−1/2	7	Absent	Absent
λ−1	Absent	1	1
τ−1/2λ+1/2	8	4	Absent
λ−1/2λ+1/2	Absent	8	Absent
τ−1/2τ+1/2	5	Absent	Absent
Total number of defects	25	13	1
Net Charge	−1	−1	−1

Table 2. The number and types of defects as a function of elastic anisotropy υ (see Figure 5 for parametric values, orientation n_z and chirality q fields).

Type of defect	υ = 1	υ = 5	υ = 21
τ+1/2	5	Absent	Absent
τ−1/2	7	Absent	Absent
λ−1	Absent	1	1
τ−1/2λ+1/2	8	4	Absent
λ−1/2λ+1/2	Absent	8	Absent
τ−1/2τ+1/2	5	Absent	Absent
Total number of defects	25	13	1
Net Charge	−1	−1	−1

4.2. Effect of Confinement on the Type of Dislocations Nucleated

As mentioned in Section 3.1, the geometry of the domain under investigation imposes anisotropic confinement on the self assembling material. The material between two consecutive inclusions is strongly confined, yet weakly confined between diagonally opposite inclusions. It is known from Grandjean-Cano cholesteric wedge experiments [41] that dislocations of Burger vector b = p/2 (τ^−1/2λ^+1/2, λ^−1/2τ^+1/2) are stable in regions of strong confinement, when the height of the self assembling region h is less than a critical height h_c. When h exceeds h_c, dislocations of Burger vector b = p (λ^−1/2λ^+1/2, τ^−1/2τ^+1/2) are nucleated [41]. Our simulation results are in accord with this experimental observation. In Figure 5 (a–d), τ^−1/2λ^+1/2, dislocations appear in regions of stronger confinement and λ^−1/2λ^+1/2, τ^−1/2τ^+1/ dislocations appear in regions of weaker confinement. The stability of a certain type of dislocation in a domain is determined by the competition between the core energies of the defects and the compression and dilation terms of the free energy due to the model geometry. In the regions of weaker confinement, the core energy of the b = p defects is minimized by forming a dislocation of lower core energy. On the other hand, dislocation that requires less bending and dilation energies are nucleated and stabilized in regions of stronger confinement [41].

Figure 5. Simulation results for chiral nematic self assembly at dimensionless time t = 100, for length scales ξ/p₀ = 0.05, h/p_o = 20, and U = 6 for varying υ. Surface plots of out‑of‑plane component |n_z| of the director field (left) and chiral order parameter q (right). The elastic anisotropies are 1 (a),(b); 5 (c),(d); 21 (e)(f).

Figure 5. Simulation results for chiral nematic self assembly at dimensionless time t = 100, for length scales ξ/p₀ = 0.05, h/p_o = 20, and U = 6 for varying υ. Surface plots of out‑of‑plane component |n_z| of the director field (left) and chiral order parameter q (right). The elastic anisotropies are 1 (a),(b); 5 (c),(d); 21 (e)(f).

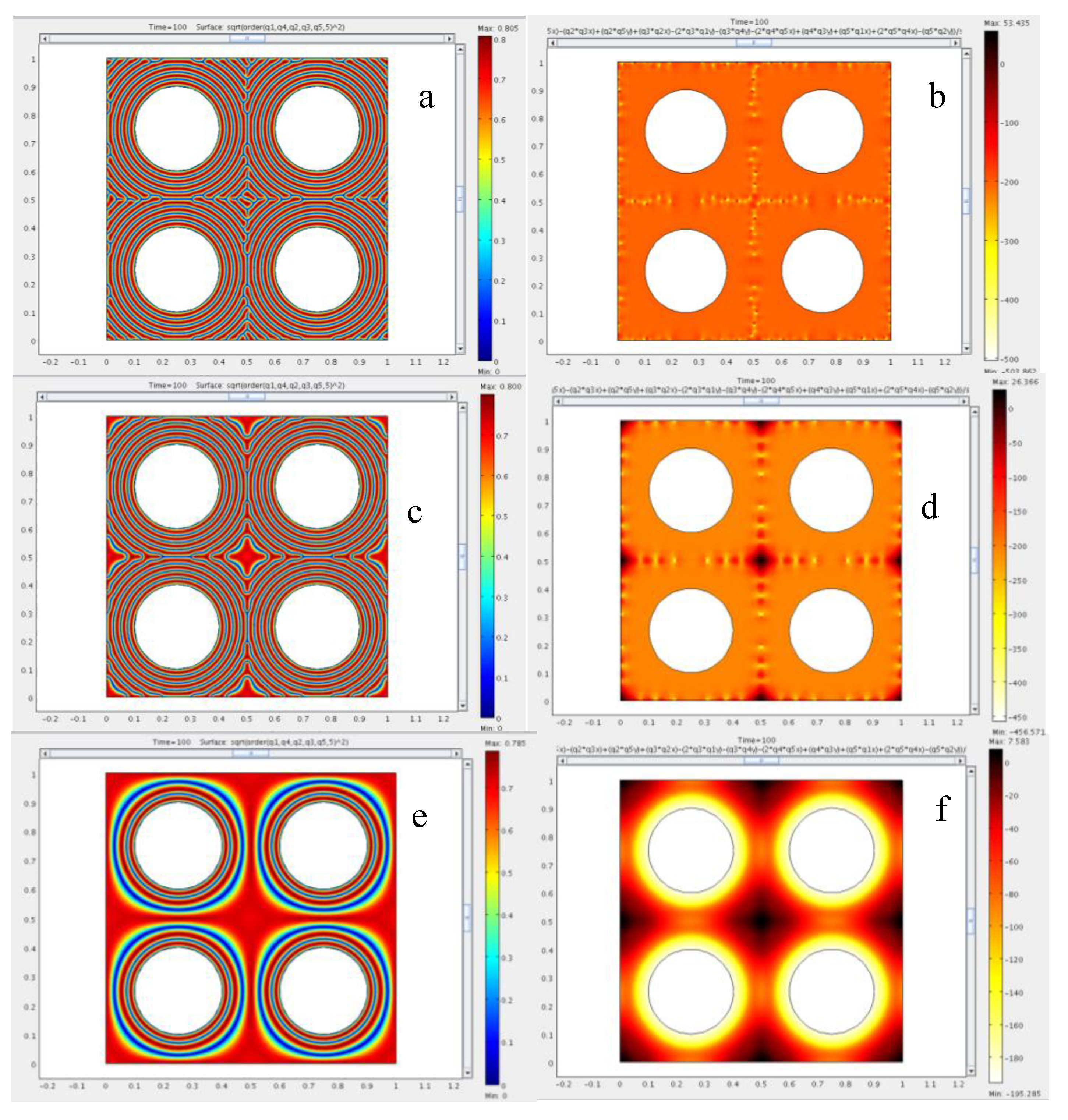
4.3. The Role of Bending and Dilation Energies on Defect Texture

In this section the effect of varying the bending and dilation energies on defect nucleation and layer properties, are investigated. According to Equation 4(b) the bending modulus K₁ of a layered LC phase is a function of elastic anisotropy (υ) and length scale (ξ/h₀). According to Equation 4(c), the dilation modulus B is a function of length scale (ξ/p₀).

(A) Varying υ, while fixing the length scales, changes the bending free energy contribution to the layer deformation. In Figure 5, by varying the values υ from 1 to 21, the penetration length λ₁ varies from 4.873 × 10⁻³ to 1.61 × 10⁻². For the same number of equilibrium pitches in a defect free monodomain per unit thickness of LC material (p₀/h₀), the number of pitches formed in a confined domain decreased with increasing υ. It can also be seen that larger elastic anisotropy decreased the stiffness of the layers, resulting in a reduced number of defects consistent with Equation 6.

(B) The defect textures arising from varying length scale (ξ/p₀), while keeping the material properties U and υ length scale (ξ/h₀) constant, are shown in Figure 6. This variation of (ξ/p₀) from 0.05 to 0.0125 corresponds to the increase in penetration length from 4.873 × 10⁻³ to 1.949 × 10⁻².

Figure 6. Simulation results for chiral nematic self assembly at t = 100, for length scales ξ/h₀ = 0.0025, υ= 1 and U = 6, for varying (ξ/p₀). Surface plots of chiral order parameter q (left) and out-of-plane component |n_z| of the director field (right). (ξ/p₀) are 0.05 (a) and (b); 0.025 (c) and (d); 0.025 (e) and (f).

Figure 6. Simulation results for chiral nematic self assembly at t = 100, for length scales ξ/h₀ = 0.0025, υ= 1 and U = 6, for varying (ξ/p₀). Surface plots of chiral order parameter q (left) and out-of-plane component |n_z| of the director field (right). (ξ/p₀) are 0.05 (a) and (b); 0.025 (c) and (d); 0.025 (e) and (f).

From Figure 6, it can be seen that the layer dilates considerably while decreasing the (ξ/p₀), and the number of defects also reduces from 25 to 6 (four τ^−1/2 and two τ^+1/2 disclinations), consistent with Equation 6.

(C) The defect textures arising from varying length scale (ξ/h₀), while keeping the material properties U and υ length scale (ξ/p₀) constant, are shown in Figure 7. This variation of (ξ/h₀) from 0.0025 to 0.01 corresponds to the increase in penetration length λ₁ from 4.873 × 10⁻³ to 9.746 × 10⁻³.

From Figure 7, it can be seen that the layer dilates considerably while increasing the (ξ/h₀) and the number of defects also reduces from 25 to 6 (four τ^−1/2 and two τ^+1/2 disclinations), consistent with Equation 6.

In plant cell walls, the layer bending and dilation mechanism discussed in this section are essential for the structural adaptation of helicoids without nucleating many defects.

Figure 7. Simulation results for chiral nematic self assembly at t = 100, for length scales (ξ/p₀) = 0.05, υ = 1and U = 6, for varying (ξ/h₀). Surface plots of chiral order parameter q (left) and out-of-plane component |n_z| of the director field (right). (ξ/h₀) are 0.0025 (a) and (b); 0.005 (c) and (d); 0.01 (e) and (f).

Figure 7. Simulation results for chiral nematic self assembly at t = 100, for length scales (ξ/p₀) = 0.05, υ = 1and U = 6, for varying (ξ/h₀). Surface plots of chiral order parameter q (left) and out-of-plane component |n_z| of the director field (right). (ξ/h₀) are 0.0025 (a) and (b); 0.005 (c) and (d); 0.01 (e) and (f).

4.4. Saddle Defect in a Plant-Based Helicoidal Plywood

The saddle defect observed in natural helicoidal plywood due to inclusion of four (L) lumens in walnut (Figure 2(b)) corresponds to Figure 5(e) and (f) in the simulation results. This structure with a non-singular λ⁻¹ disclination in the center results from using the following model parameters: (a) elastic anisotropy υ = 21; (b) (ξ/h₀) = 0.0025; (c) (ξ/p₀) = 0.05; and a thermodynamic potential U = 6. The high elastic anisotropy that leads to saddle texture is consistent with high lyotropic nematic polymer elasticity values. The ratio (h₀/p₀) = 20 indicates that the saddle texture form in the presence of a significant number of layers, consistent with the biological case. The value U = 6 (C = 2C*) correspond to a concentration of CMFs significantly larger than the critical concentration for the onset of mesophase formation, which is consistent with the fact that plant plywoods only arise where cellulose fibrils have higher concentrations.

In addition to providing information on material properties and length scales that cannot be experimentally measured in vivo, the simulated transient defect pattern acts as a fingerprint for the formation of helicoidal plant-based plywoods [2,33].

5. Conclusions

A model based on the Landau-de Gennes theory (Equation 4) was used to simulate dynamic self‑assembly of a lyotropic chiral-nematic liquid crystalline material, in order to understand the structure, dynamics, and processes involved in formation of liquid crystalline analogues in some plant cell walls [2]. The defect textures arising due to inclusions representing the presence of secondary phases in plant cell walls are obtained as a function of elastic anisotropy, internal-to-pitch length scale ratio (ξ/p₀) and internal-to-external length scale ratio (ξ/h₀) that are the parameters that control defect density (Equation 6). The following defects were identified: τ^+1/2, τ^−1/2, λ⁻¹, τ^−1/2λ^+1/2, λ^−1/2λ^+1/2, τ^−1/2τ^+1/2 (Figure 5, Figure 6 and Figure 7). At equilibrium, the number and type of defects arising in all the simulations obeys the rule [42,43] that states that the net charge of defects nucleated in a domain confined by four circular inclusions is always −1. This observation is in accord with defect texture studies on nematic LCs with inclusions [42]. The presented textural results comply with observations on the type of dislocation cores under the effect of confinement from Grandjean-Cano cholesteric wedge experiments [41]. Dislocations of Burger vector b = p/2 (τ^−1/2λ^+1/2, λ^−1/2τ^+1/2) are stable in strongly confined regions and dislocations of Burger vector b = p (λ^−1/2λ^+1/2, τ^−1/2τ^+1/2) are stable in weakly confined regions (Figure 6(a–d)). Increasing the elastic anisotropy and/or length scale (ξ/h₀), and/or decreasing the length scale (ξ/p₀), results in a reduced number of defects by bending and dilating the chiral nematic layers. In the natural helicoidal plywoods observed in plant cell walls [2,39,40], the layer bending and dilation mechanism is employed to structurally adapt to the presence of secondary phases such as cells, lumens and pit canals, thus avoiding energetically costly defects (Figure 2 and Figure 5(f)). The present model is able to reproduce the experimentally observed saddle defect observed in secondary cell wall of walnut [40]. The defect is characterized to be a non-singular λ⁻¹ defect. The theory and simulations presented in this paper indicate that the material property and length scales that result in this biological structure are: large elastic anisotropy, large number of pitches within the confined space, and high concentration of rods (corresponding parameters in Equation 6: υ = 21, U = 6, (ξ/p₀) = 0.05, (ξ/h₀) = 0.0025). In addition to narrowing the parametric space to biological-relevant values that lead to the saddle texture of a biological plywood, the transient directed chiral self-assembly simulations in the presence of curved second phases provides support to Neville’s model that the origin of the frozen‑in architecture in Bouligand’s plywood is the chiral nematic phase [2]. The present model can be extended to explore other biological relevant features of plywoods including pitch gradients and surface melting [2].