Specimen Size and Environmental Exposure Effects on Initial Diffusion in E-Glass/Vinylester Pultruded Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Process Details
2.2. Specimen Details
2.3. Moisture Uptake Test Procedures
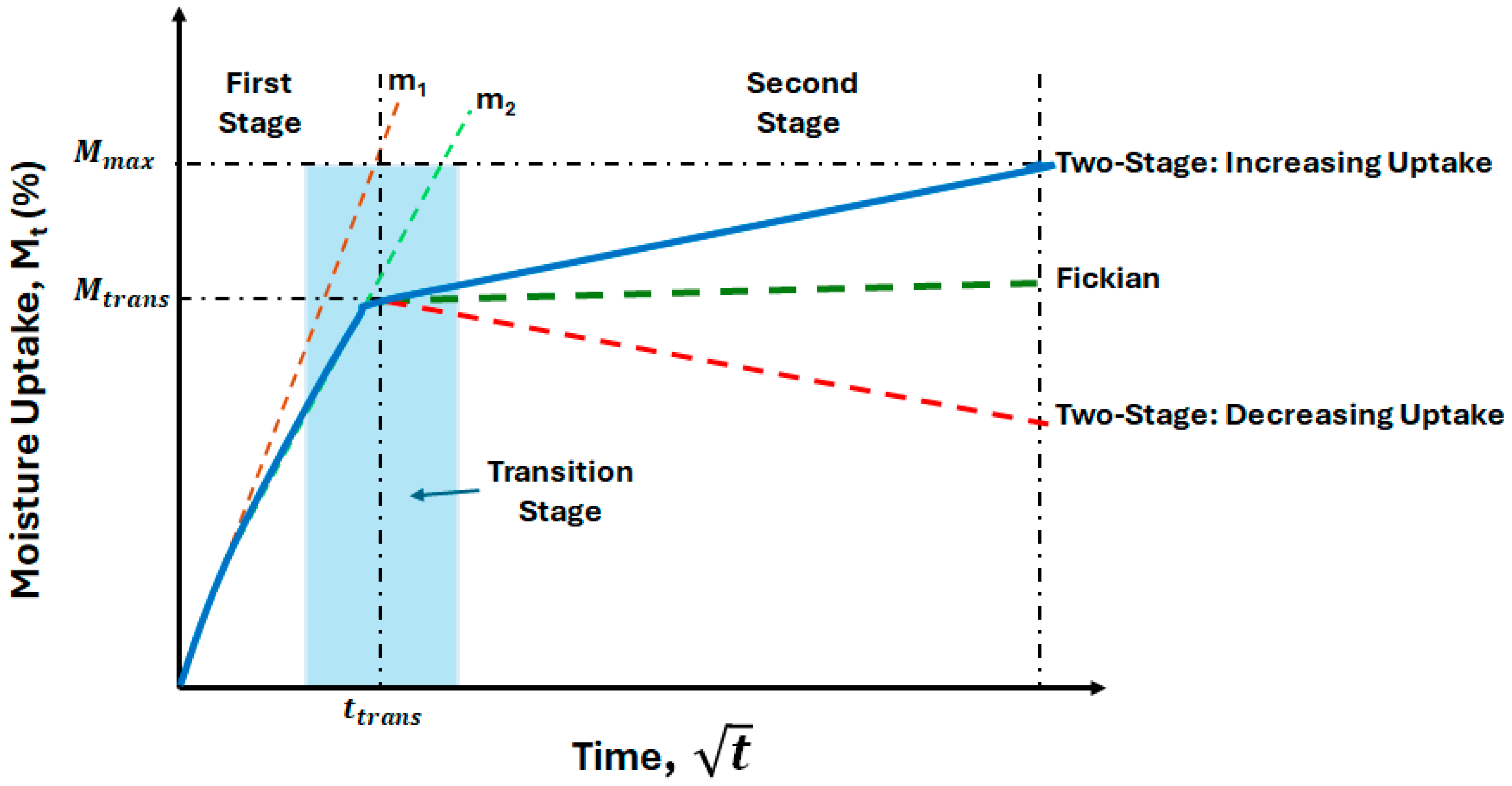
3. Moisture Kinetics
4. Summary and Conclusions
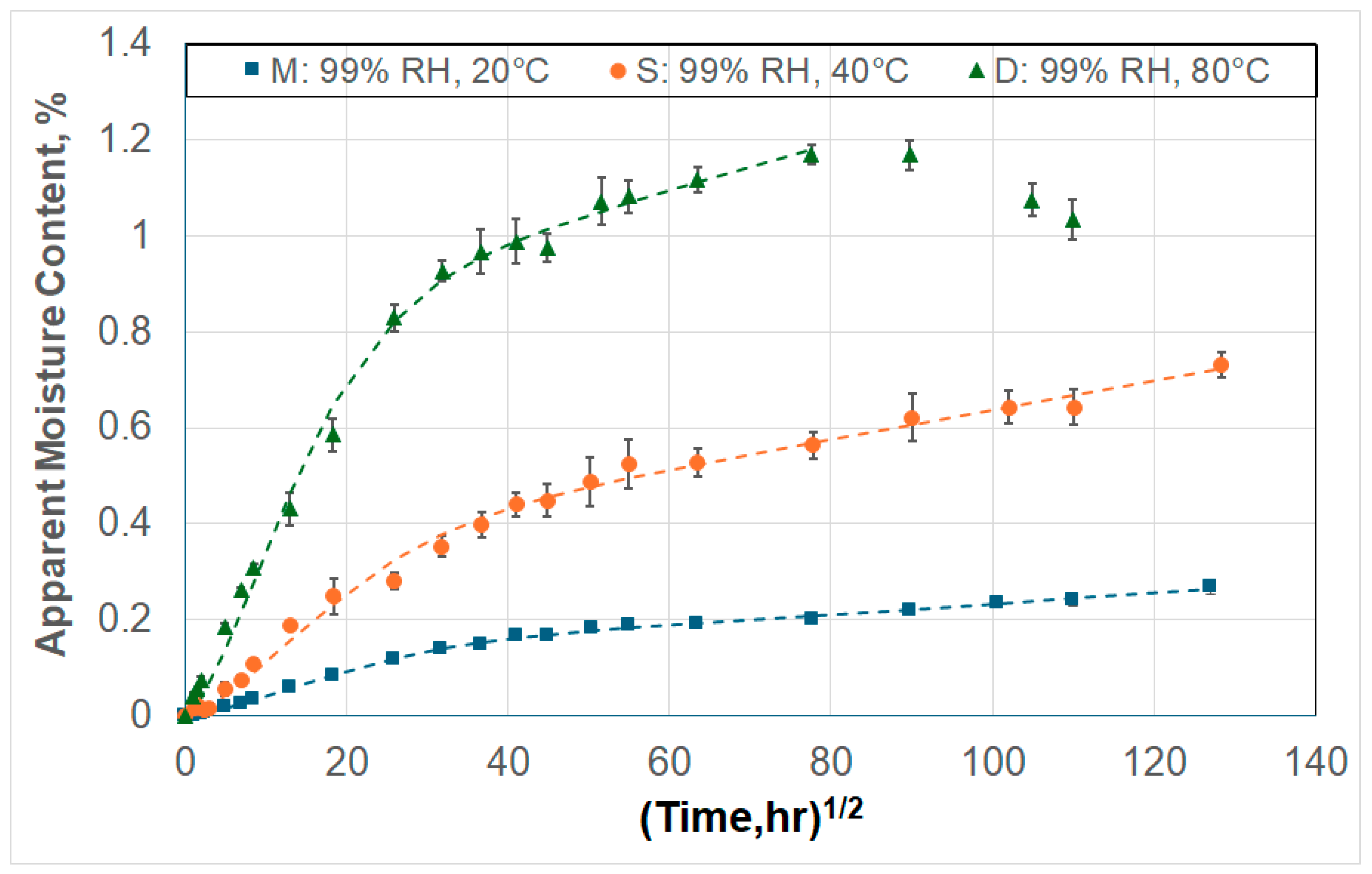
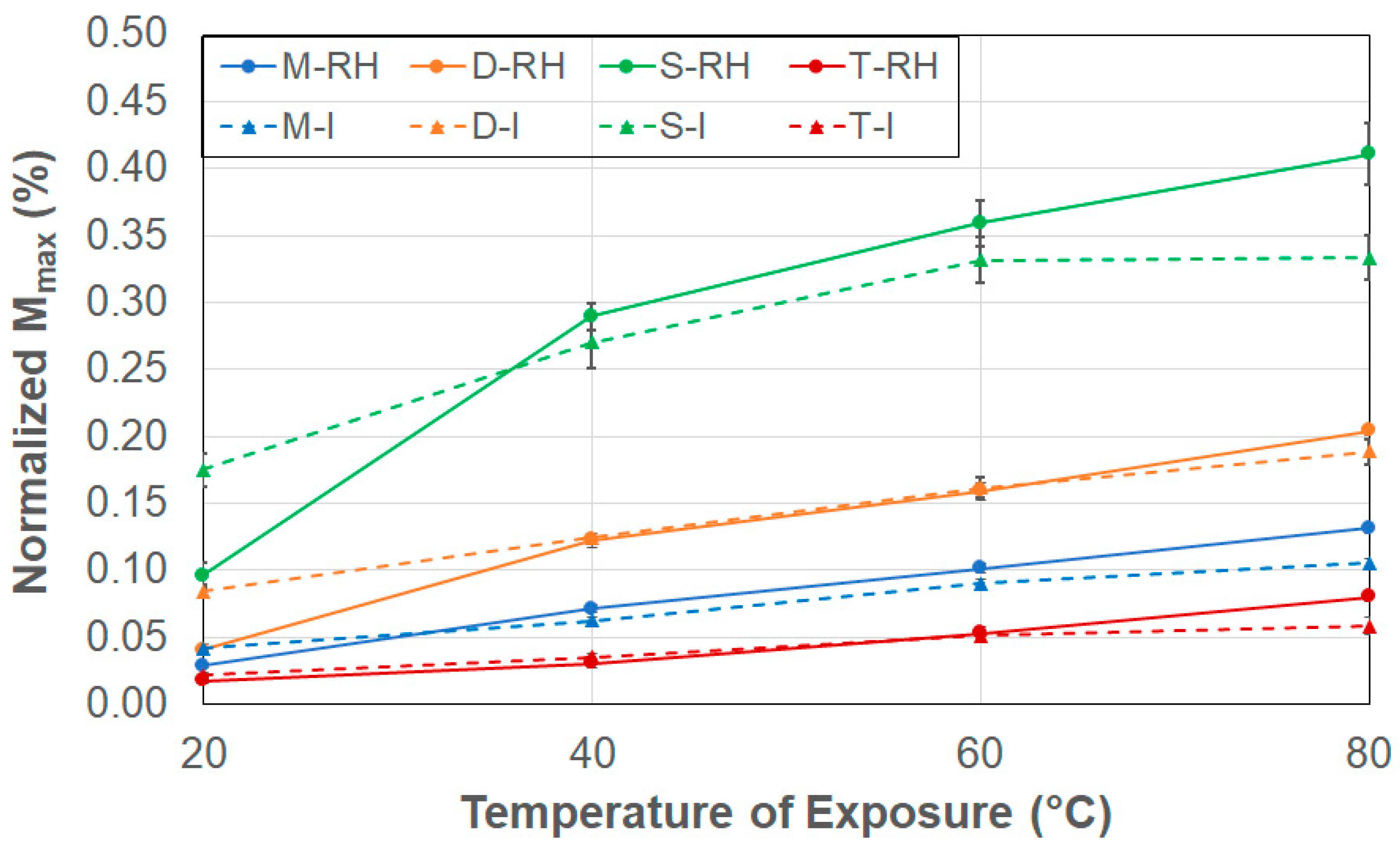
- Peak moisture uptake levels, Mmax, increase with temperature, with levels being higher under the case of immersion at the lowest temperature of immersion, and higher under conditions of 99% RH at the higher temperatures.
- Moisture uptake levels are noted to increase as the surface-to-edge area ratio decreases, indicating that edge diffusion and capillary action at the fiber–matrix interface play a dominant role in smaller specimens in contrast to larger specimens where surface induced through-the-thickness bulk diffusion dominates.
- The transition moisture uptake level, Mtrans, increases with temperature, but immersion conditions exhibit non-monotonic trends, suggesting a shift in the dominant transport mechanism beyond 60 °C, where polymer swelling, microcracking, and matrix relaxation lead to deviations from simple Fickian diffusion.
- Diffusion coefficients determined using a two-stage model show an increase with temperature for the two specimens with the larger surface-to-edge area ratios, M and T, as a result of exposure to both 99% RH and immersion conditions, with the values from immersion being higher. In contrast, the smaller specimens, D and S, show significant variation with temperature, suggesting competing effects and different dominant modes with changes in temperature and edge effects. When diffusion coefficients are normalized by the surface-to-edge area ratios, the lowest normalized coefficient values are indicated by the specimens with the highest surface-to-edge area ratios for all temperatures and for both conditions of exposure.
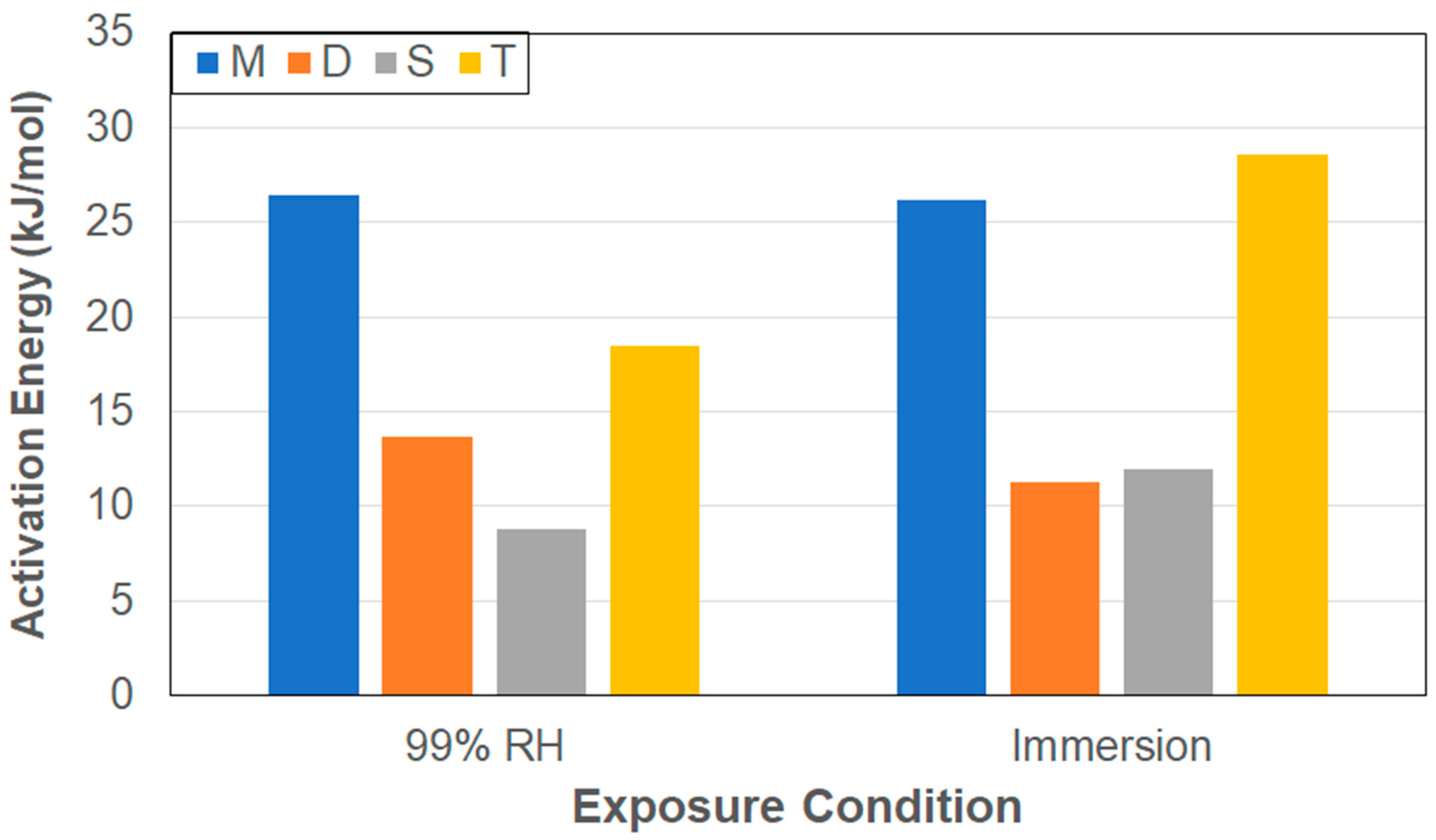
- Diffusion coefficients derived from initial uptake rates, Di, assuming Fickian responses over 60% of the regime prior to attainment of Mtrans show that immersion results in faster initial uptake due to higher driving forces resulting from saturation boundary conditions. The values of the activation energies are lower in the case of immersion due to the greater driving force from the saturation boundary conditions. The highest value for each condition is shown by the T specimens, which have the greatest surface-to-edge area ratios, and the lowest by the S specimens, which have the lowest surface-to-edge area ratios.
- Values of the activation energies are lower in the case of immersion due to the greater driving force from the saturation boundary conditions. Further, smaller specimens are noted to require significantly less energy for moisture ingress than larger specimens.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vedernikov, A.; Safonov, A.; Tucci, F.; Carlone, P.; Akhator, I. Pultruded materials and structures: A review. J. Compos. Mater. 2020, 5426, 4081–4117. [Google Scholar]
- Volk, M.; Yuksel, O.; Baran, I.; Hattel, J.H.; Spagenberg, J.; Sandberg, M. Cost-efficient, automated, and sustainable composite profile manufacture: A review of the state-of-the-art, innovations, and future of pultrusion technologies. Compos. B 2022, 246, 110135. [Google Scholar]
- Arora, R.; Mosch, W. High Voltage and Electrical Insulation Engineering; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Syamsir, A.; Ean, L.-W.; Asyraf, M.R.M.; Supian, A.B.M.; Madenci, E.; Ozkilic, Y.O.; Akseylu, C. Recent advances of GFRP cross arms and energy transmission tower: A short review on design improvements in mechanical properties. Materials 2023, 16, 2778. [Google Scholar] [CrossRef] [PubMed]
- Baran, I.; Tatum, C.C.; Hattel, J.M. The internal stress evaluation of the pultruded blades for a Darrieus wind turbine. Key Eng. Mater. 2013, 554–577, 2127–2137. [Google Scholar]
- Ennis, B.L.; Das, S.; Norris, R.E. Economic competitiveness of protruded fiber composites for wind turbine applications. Compos. B 2023, 265, 110960. [Google Scholar]
- Thomason, J.; Xypolias, G. Hydrothermal ageing of glass fibre reinforced vinyl ester composites: A review. Polymers 2023, 15, 835. [Google Scholar] [CrossRef]
- Sousa, J.M.; Garrido, M.; Correia, J.R.; Cabral-Fonseca, S. Hygrothermal ageing of pultruded GFRP profiles: Comparative study of unsaturated polyester and Vinylester resin matrices. Compos. A 2021, 140, 106193. [Google Scholar]
- Hassanpour, B.; Karbhari, V.M. Characteristics and models of moisture uptake in fiber-reinforced composites: A topical review. Polymers 2024, 16, 2265. [Google Scholar] [CrossRef]
- Adamson, M.J. Thermal expansion and swelling of cured epoxy resin used in graphite/epoxy composite materials. J. Mater. Sci. 1980, 15, 1736–1745. [Google Scholar]
- Apicella, A.; Migliaresi, C.; Nicodemo, L.; Nicolais, L.; Iaccarino, L.; Roccotelli, S. Water sorption and mechanical properties of a glass-reinforced polyester resin. Composites 1982, 13, 406–410. [Google Scholar]
- Nogueira, P.; Ramirez, C.; Torres, A.; Abad, M.J.; Cano, J.; Lopez, J.; Lopez- Bueno, I.; Baral, L. Effect of water sorption on the structure and mechanical properties of an epoxy resin system. J. Appl. Polym. Sci. 2001, 80, 71–80. [Google Scholar]
- Cairns, D.S.; Adams, D.F. Moisture and thermal expansion properties of unidirectional composite materials and the epoxy matrix. J. Reinf. Plast. Compos. 1983, 2, 239–255. [Google Scholar]
- Chateauminois, A.; Vincent, L.; Chabert, B.; Soulier, J.P. Study of the interfacial degradation of a glass-epoxy composite during hygrothermal ageing using water diffusion measurements and dynamic mechanical thermal analysis. Polymer 1994, 35, 4766–4774. [Google Scholar]
- Chu, W.; Wu, L.; Karbhari, V.M. Durability evaluation of moderate temperature cured Eglass/vinylester systems. Compos. Struct. 2004, 66, 367–376. [Google Scholar]
- Boinard, E.; Pethrick, R.A.; Dalzel-Job, J.; Macfarlane, C.J. Influence of resin chemistry on water uptake and environmental ageing in glass fibre reinforced composites-polyester and vinyl ester laminates. J. Mater. Sci. 2000, 35, 1931–1937. [Google Scholar]
- Karbhari, V.M.; Wang, Q. Multi-frequency dynamic mechanical thermal analysis of moisture uptake in E-glass/vinylester composites. Compos. B 2004, 35, 299–304. [Google Scholar]
- Jansen, K.M.B.; Zhang, M.F.; Ernst, L.J.; Vu, D.-K.; Weiss, L. Effect of temperature and humidity on moisture diffusion in an epoxy molding compound. Microelectron. Reilabil. 2020, 107, 113596. [Google Scholar]
- Berens, A.R.; Hopfenberg, H.B. Diffusion and relaxation in glassy polymer powder: 2. Separation of diffusion and relaxation parameters. Polymer 1978, 19, 489–496. [Google Scholar]
- Jacobs, P.M.; Jones, F.R. Diffusion of moisture into two-phase polymers. Part 1. The development of an analytical model and its application to styrene-ethylene butylene styrene block copolymer. J. Mater. Sci. 1989, 24, 2331–2336. [Google Scholar]
- Bao, L.-R.; Yee, A.F.; Lee, C.Y.-C. Moisture absorption and hygrothermal aging in a bismaleimide resin. Polymer 2001, 42, 7327–7333. [Google Scholar]
- Bratasyuk, N.A.; Ostanin, S.A.; Mokeev, M.V.; Zuev, V.V. Water transport in epoxy/polyurethane interpenetrating networks. Polym. Adv. Technol. 2022, 33, 3173–3191. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Zhuo, H. Study on the moisture absorption of pyridine containing polyurethane for moisture responsive shape memory polymers. J. Mater. Sci. 2011, 46, 6581–6588. [Google Scholar] [CrossRef]
- Placette, M.D.; Fan, X.; Zhao, J.H.; Edwards, D. Dual stage modeling of moisture absorption and desorption in epoxy mold compounds. Microelectron. Reliab. 2012, 52, 1401–1408. [Google Scholar] [CrossRef]
- Shen, C.-H.; Springer, G.S. Moisture absorption and desorption of composite materials. J. Compos. Mater. 1976, 10, 2–20. [Google Scholar] [CrossRef]
- Post, N.L.; Riebel, F.; Zhou, A.; Keller, T.; Case, S.W.; Lesko, J.J. Investigation of 3D moisture diffusion coefficients and damage in a pultruded E-glass/polyester structural composite. J. Compos. Mater. 2009, 43, 75–96. [Google Scholar] [CrossRef]
- Broughton, W.R.; Maxwell, A.S. Accelerated Aging of Polymeric Materials; Measurement Good Practice Guide No. 103; National Physical Laboratory: Teddington, UK, 2023. [Google Scholar] [CrossRef]
- Chin, J.W.; Nguyen, T.; Aouadi, K. Sorption and diffusion of water, salt water, and concrete pore solution in composite matrices. J. Appl. Polym. Sci. 1999, 71, 483–492. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Hassanpour, B. Water, saltwater, and concrete leachate solution effects on durability of ambient-temperature cure carbon-epoxy composites. J. Appl. Polym. Sci. 2022, 139, e52496. [Google Scholar] [CrossRef]
- Scott, P.; Lees, J.M. Water, salt water, and alkaline solution uptake in epoxy thin films. J. Appl. Polym. Sci. 2013, 130, 1898–1908. [Google Scholar] [CrossRef]
- Kondo, K.; Taki, T. Moisture diffusivity of unidirectional composites. J. Compos. Mater. 1982, 16, 82–93. [Google Scholar] [CrossRef]
- Choi, H.S.; Ahn, K.J.; Nam, J.D.; Chun, H.J. Hygroscopic aspects of epoxy/carbon fiber composite laminates in aircraft environments. Compos. A 2001, 32, 709–720. [Google Scholar] [CrossRef]
- Arao, Y.; Koyanagi, J.; Hatta, H.; Kawada, H. Analysis of time-dependent deformation of CFRP considering the anisotropy of moisture diffusion. Adv. Compos. Mater. 2008, 17, 359–372. [Google Scholar]
- Bao, L.R.; Yee, A.F. Moisture diffusion and hygrothermal aging in bismaleimide matrix carbon fiber composites—Part II: Woven and hybrid composites. Compos. Sci. Technol. 2002, 62, 2111–2119. [Google Scholar] [CrossRef]
- Korkees, F. Moisture absorption behavior and diffusion characteristics of continuous carbon fiber reinforced epoxy composites: A review. Polym.-Plast. Technol. Mater. 2023, 62, 1789–1822. [Google Scholar]
- Jianmao, T.; Springer, G.S. Effects of cure and moisture on the properties of FIberite 976 resin. J. Compos. Mater. 1988, 22, 2–14. [Google Scholar] [CrossRef]
- ASTM D5229/D5229M-20; Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- ISO 62; Plastics—Determination of Water Absorption. ISO: Geneva, Switzerland, 2008.
- Arnold, J.C.; Alston, S.M.; Korkees, F. An assessment of methods to determine the directional moisture diffusion coefficients of composite materials. Compos. A 2013, 55, 120–128. [Google Scholar]
- Korkees, F.; Alston, S.; Arnold, C. Directional diffusion of moisture into unidirectional carbon fiber/epoxy composites: Experiments and modeling. Polym. Compos. 2018, 39, E2305–E2315. [Google Scholar] [CrossRef]
- Grogan, D.M.; Flanagan, M.; Walls, M.; Leen, S.B.; Doyle, A.; Harrison, N.H.; Mamalis, D.; Goggins, J. Influence of microstructural defects and hydrostatic pressure on water absorption in composite materials for tidal energy. J. Compos. Mater. 2018, 52, 2899–2917. [Google Scholar]
- Gillet, C.; Tamssaouet, F.; Hassoune-Rhabbour, B.; Tchalla, T.; Nassiet, V. Parameter influencing moisture diffusion in epoxy-based materials during hygrothermal ageing—A review by statistical analysis. Polymers 2022, 14, 2832. [Google Scholar] [CrossRef]
- Bao, L.-R.; Yee, A.F. Effect of temperature on moisture absorption in a bismaleimide resin and its carbon fiber composite. Polymer 2002, 43, 3987–3997. [Google Scholar]
- Starink, M.J.; Starink, L.M.P.; Chambers, A.R. Moisture uptake in monolithic and composite materials: Edge correction for rectanguloid samples. J. Mater. Sci. 2002, 37, 287–294. [Google Scholar]
- Abeysinghe, H.E.; Edwards, W.; Pritchard, G.; Qwampillai, G.J. Degradation of crosslinked resins in water and electrolyte solution. Polymer 1982, 23, 1785–1790. [Google Scholar]
- Bond, D.A. Moisture diffusion in a fiber-reinforced composite: Part I—Non-Fickian transport and the effect of fiber spatial distribution. J. Compos. Mater. 2005, 39923, 2113–2141. [Google Scholar]
- Xiao, G.Z.; Delamar, M.; Shanahan, M.E.R. Irreversible interactions between water and DGEBA/DDA epoxy resin during hydrothermal aging. J. Appl. Polym. Sci. 1977, 65, 449–458. [Google Scholar]
- Hassanpour, B.; Karbhari, V.M. Moisture and glass transition temperature kinetics of ambient-cured carbon/epoxy composites. J. Compos. Sci. 2023, 7, 447. [Google Scholar] [CrossRef]
- Marshall, J.M.; Marshall, G.P.; Pinzelli, R.F. The diffusion of liquids into resins and composites. Polym. Compos. 1982, 13, 131–137. [Google Scholar]
- Ghorbel, I.; Valentin, D. Hydrothermal effects on the physico-chemical properties of pure and glass-fiber reinforced polyester and vinylester resins. Polym. Compos. 1993, 14, 324–334. [Google Scholar]
- Apicella, A.; Migliaresi, C.; Nicolais, L.; Iaccarino, L.; Roccotelli, S. The water aging of unsaturated polyester-based composites: Influence of resin composite structure. Composites 1983, 14, 387–392. [Google Scholar]
- Korkees, F.; Arnold, C.; Alston, S. An investigation of the long-term water uptake behavior and mechanisms of carbon fiber/977-2 epoxy composites. Polym. Eng. Sci. 2018, 1–2, 2175–2184. [Google Scholar]
- Karbhari, V.M. Long-term hydrothermal aging of carbon-epoxy materials for rehabilitation of civil infrastructure. Compos. A 2022, 153, 106705. [Google Scholar]
- Grammatikos, S.A.; Zafari, B.; Evernden, M.C.; Mottram, J.T.; Mitchels, J.M. Moisture uptake characteristics of a pultruded fibre reinforced polymer flat sheet subjected to hot/wet aging. Polym. Degrad. Stab. 2015, 121, 407–419. [Google Scholar]
- Gilormini, P.; Verdu, J. On the role of hydrogen bonding on water absorption in polymers. Polymer 2018, 142, 164–169. [Google Scholar]
- Ramesh, N.; Davies, P.K.; Zielinski, J.M.; Danner, R.P.; Duda, J.L. Application of free-volume theory to self diffusion of solvents in polymers below the glass transition temperature: A review. J. Polym. Sci. B Polym. Phys. 2011, 49, 1629–1644. [Google Scholar]
- Crank, J.; Park, G.S. Diffusion in Polymers; Academic Press: London, UK, 1968. [Google Scholar]
- Bazli, M.; Ashrafi, H.; Oskouei, A.V. Effect of harsh environments on mechanical properties of GFRP pultruded profiles. Compos. B 2016, 99, 203–215. [Google Scholar]
- Chu, W.; Karbhari, V.M. Effect of water sorption on performance of pultruded E-glass/vinylester composites. ASCE J. Mater. Civ. Eng. 2005, 17, 63–71. [Google Scholar]
- Harper, J.F.; Naeem, M. The moisture absorption of glass fibre reinforced vinylester and polyester composites. Mater Des 1989, 10, 297–300. [Google Scholar]
- Karbhari, V.M.; Zhang, S. E-glass/vinylester composites in aqueous environments—I: Experimental results. Appl. Compos. Mater. 2003, 10, 19–48. [Google Scholar]
- Cavasin, M.; Snngermano, M.; Thomson, B.; Giannis, S. Exposure of glass fiber reinforced polymer composites in seawater and the effect on their physical performance. Materials 2019, 12, 807. [Google Scholar] [CrossRef]
- Cervenka, A.J.; Young, R.J.; Kueseng, K. Gravimetric determination of the diffusion characteristics of polymers using small specimens. J. Polym. Sci. B Polym. Phys. 2004, 42, 2122–2128. [Google Scholar]


| Specimen Type | Symbol | Dimensions (mm) | Surface-to-Edge Area Ratio | ||
|---|---|---|---|---|---|
| l * | w | h | |||
| Moisture | M | 25.4 | 25.4 | 1.36 | 9.338 |
| DMTA | D | 10 | 35 | 1.36 | 5.79 |
| Short-beam-shear | S | 11 | 5 | 1.36 | 2.528 |
| Tension | T | 254 | 25.4 | 1.36 | 16.979 |
| Characteristic | Specimen Type | 99% Relative Humidity | Immersion in Deionized Water | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 °C | 40 °C | 60 °C | 80 °C | 20 °C | 40 °C | 60 °C | 80 °C | ||
| Mmax (%) | M | 0.2688 | 0.6658 | 0.9481 | 1.2288 | 0.3932 | 0.5856 | 0.8455 | 0.9886 |
| D | 0.2312 | 0.7003 | 0.9103 | 1.1690 | 0.4834 | 0.7121 | 0.9235 | 1.0796 | |
| S | 0.2436 | 0.7320 | 0.9076 | 1.0376 | 0.4426 | 0.6823 | 0.8388 | 0.8432 | |
| T | 0.3026 | 0.5198 | 0.9007 | 1.3616 | 0.3725 | 0.6042 | 0.8675 | 0.9896 | |
| Mtrans (%) | M | 0.1240 | 0.2445 | 0.2477 | 0.3945 | 0.0919 | 0.3458 | 0.1733 | 0.2980 |
| D | 0.0899 | 0.2453 | 0.2592 | 0.8037 | 0.0908 | 0.3283 | 0.2474 | 0.6181 | |
| S | 0.1258 | 0.3300 | 0.2080 | 0.8264 | 0.1084 | 0.3494 | 0.2714 | 0.6572 | |
| T | 0.0746 | 0.2377 | 0.2353 | 0.6844 | 0.0999 | 0.2725 | 0.1596 | 0.2869 | |
| D (×10−6 mm2/s) | M | 0.097 | 0.111 | 0.277 | 0.574 | 0.168 | 0.197 | 0.584 | 0.899 |
| D | 0.523 | 0.245 | 0.413 | 0.151 | 0.270 | 0.111 | 0.441 | 0.424 | |
| S | 0.183 | 0.099 | 0.806 | 0.173 | 0.250 | 0.123 | 0.493 | 0.410 | |
| T | 0.094 | 0.099 | 0.254 | 0.289 | 0.106 | 0.160 | 0.396 | 0.728 | |
| Specimen Type | 99% Relative Humidity | Immersion in Deionized Water | ||||||
|---|---|---|---|---|---|---|---|---|
| 20 °C | 40 °C | 60 °C | 80 °C | 20 °C | 40 °C | 60 °C | 80 °C | |
| M | 46.12% | 36.73% | 26.12% | 32.10% | 23.38% | 59.06% | 20.50% | 30.14% |
| D | 38.87% | 35.03% | 28.48% | 68.75% | 18.79% | 46.10% | 26.79% | 57.25% |
| S | 51.66% | 45.08% | 22.91% | 79.65% | 24.49% | 51.20% | 32.36% | 77.94% |
| T | 24.66% | 45.73% | 26.12% | 50.26% | 26.82% | 45.10% | 18.40% | 29.00% |
| Characteristic | Specimen Type | 99% Relative Humidity | Immersion in Deionized Water | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 °C | 40 °C | 60 °C | 80 °C | 20 °C | 40 °C | 60 °C | 80 °C | ||
| D (×10−6 mm2/s) | M | 3.80 | 19.63 | 45.62 | 188.69 | 5.52 | 37.94 | 47.78 | 225.65 |
| D | 5.11 | 28.27 | 89.08 | 243.28 | 9.08 | 39.59 | 86.59 | 411.87 | |
| S | 8.30 | 33.18 | 103.87 | 283.53 | 13.20 | 44.18 | 105.68 | 420.91 | |
| T | 1.43 | 13.53 | 37.39 | 158.00 | 2.41 | 28.27 | 37.39 | 202.32 | |
| Characteristic | Specimen Type | 99% Relative Humidity | Immersion in Deionized Water | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 °C | 40 °C | 60 °C | 80 °C | 20 °C | 40 °C | 60 °C | 80 °C | ||
| D (×10−6 mm2/s) | M | 3.75 | 19.67 | 45.05 | 187.57 | 5.71 | 37.66 | 47.46 | 224.66 |
| D | 10.28 | 32.16 | 59.68 | 240.82 | 13.96 | 56.36 | 66.81 | 261.18 | |
| S | 10.61 | 39.38 | 79.01 | 322.68 | 14.93 | 71.27 | 86.42 | 363.90 | |
| T | 1.40 | 13.57 | 36.86 | 156.99 | 2.52 | 28.02 | 37.07 | 201.32 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karbhari, V.M. Specimen Size and Environmental Exposure Effects on Initial Diffusion in E-Glass/Vinylester Pultruded Composites. Polymers 2025, 17, 815. https://doi.org/10.3390/polym17060815
Karbhari VM. Specimen Size and Environmental Exposure Effects on Initial Diffusion in E-Glass/Vinylester Pultruded Composites. Polymers. 2025; 17(6):815. https://doi.org/10.3390/polym17060815
Chicago/Turabian StyleKarbhari, Vistasp M. 2025. "Specimen Size and Environmental Exposure Effects on Initial Diffusion in E-Glass/Vinylester Pultruded Composites" Polymers 17, no. 6: 815. https://doi.org/10.3390/polym17060815
APA StyleKarbhari, V. M. (2025). Specimen Size and Environmental Exposure Effects on Initial Diffusion in E-Glass/Vinylester Pultruded Composites. Polymers, 17(6), 815. https://doi.org/10.3390/polym17060815







