1. Introduction
Many traditional models [
1,
2] of polymer solution dynamics predict that mean-square displacements
of polymer molecules in solutions or in melts have the form of a power-law dependence,
where
is a time-dependent displacement,
denotes an average,
t is an elapsed time,
is an exponent, and
A is a prefactor. Power-law dependencies are claimed to be valid over time intervals, with multiple power laws being separated by transition regimes serving to cover the full range of times.
is the collective notation for a group of different displacements, notably
, which describes the mean-square displacement of all the atoms in a polymer molecule, and
, which describes the mean-square displacement of the polymer’s center of mass. The traditional models [
1,
2] predict the order in which different power-law regimes and exponents are encountered with increasing time, but do not, in general, predict the prefactor
A or the time dependence of
in transition regimes between neighboring power-law regions. To display
as a function of time, recourse has uniformly been had to log–log plots, on which power laws such as that seen in Equation (
1) appear as straight lines, each line’s slope being the corresponding exponent
.
Our objective in this proof-of-principle paper is to present a quantitative model-independent method for analyzing the time dependence of
. Our method does not assume that
has a particular functional form, such as the power law of Equation (
1). Contrast will be seen between our method and entirely legitimate studies that assumed that power-law behavior is present, so that segments of
were fit to Equation (
1) in order to obtain values for
.
Here, we invoke a general functional form that uniformly describes the time dependence of
over the entirety of times for which
has been obtained, without any assumption other than that the original data are consistent with a continuous line. Reported measurements appear to lie on smooth, monotonically increasing curves, so a reasonable choice of general form is a finite Taylor series expansion. The statistical spread in the data, in the reports we have examined, appears to be relatively independent of time on a log–log plot, so it is appropriate to take
and write
for the series. Here, the
are the fitting parameters, and
N is the order of the fit. The
are obtained by linear-least-squares. The scatter in measurements of
appears to be nearly independent of
t, so issues concerning the statistical weights to be assigned to different points do not arise. As a cautionary note, Taylor series are used here as approximate interpolants covering the range over which measurements were made. It is not claimed that the series would be valid as an extrapolant beyond the range of
t of the original measurements. What order of fit is appropriate? By increasing
N, one reaches values of
N for which the Taylor expansion agrees with the measurements, with further modest increases in
N having no significant effect on the form of the fitted curve.
To clarify the behavior of
, we also determined its first and second logarithmic derivatives, with the first logarithmic derivative being
Note that , being a logarithmic derivative, is dimensionless.
Our general search for papers on simulations of polymer dynamics revealed a considerable number of reports of
for one or another definition of
. The reports are, uniformly, graphical. Measurements were digitized using Un-Scan-It 7.0, for the most part in manual mode [
3]. Numerical analysis was made using Mathematica 12.1 [
4].
This is a proof-of-principle paper. The objective is to demonstrate that our method works, not to discuss what it reveals about polymer physics. We selected three measurements of
that serve to demonstrate significant aspects of our approach, namely Padding and Briels [
5], with their Figure 1 showing mean-square atomic displacements, Brodeck et al. [
6], with their Figure 1 showing the 400 K mean-square displacements, and Peng et al. [
7], with their Figure 9a showing the mobility of their B beads. Why did we choose these three data sets? Analysis of the Padding and Briels results tests if the approach can usefully represent simple power-law behavior. One might be concerned as to how large an
N is needed to represent a
with multiple features, and what consequences would follow if the order of the fit was increased above the order needed to represent
accurately. The effect of increasing the fit order is revealed by study of results from Brodeck et al. [
6]. Finally, around an inflection point in
, a tangent line might mimic a power law. We inquire if actual power law regimes and inflection points can be distinguished, using results of Peng et al. [
7].
It is legitimate to ask if the approach described here is generally applicable, or if the method leads to new physical results. A full-length paper answering these questions, based on close to a hundred sets of data as obtained by more than a dozen research groups, is now in preparation.
2. Tests of Finite Taylor Series as a General Functional Form
In a series of papers, Padding and Briels [
5,
8,
9,
10] report simulations of a united-atom model for linear polyethylene, reporting, among other dynamic quantities, the diffusion coefficient, the shear relaxation modulus, the end-to-end vector’s time autocorrelation function, the single-chain coherent dynamic structure factor, and, of central interest here, various mean-square displacements. Figure 1 shows Padding and Briels’ determination of
, the mean-square displacement of their individual united atoms. We fit
to an eighth-order polynomial in
. One sees in
Figure 1 that the agreement between our polynomial fit (circles) and the original measurements (heavy line) is excellent.
The original authors report that
can be described by two power laws, one with
for
ps and another with
for
ps. On a log–log plot, a power law would appear as a straight line whose slope equals
. Our results are seen in
Figure 1. As seen in the figure, for times of a few picoseconds up to 200 ps, the calculated slope
is very nearly constant, corresponding to
in agreement with Padding and Briels. For
ps, our polynomial fit reveals that the slope decreases very slightly, to perhaps 0.53 or so, and then increases again back toward 0.65. This gentle modulation of the slope is revealed by our fitting process, but would have been masked a fit to an assumed power-law behavior. A simple power law would be approximately consistent with these measurements, as seen in Padding and Briels’ Figure 1, with the deviations of the data from a simple power law being modest.
Our fitting process is thus seen to reveal power-law behavior when such is present.
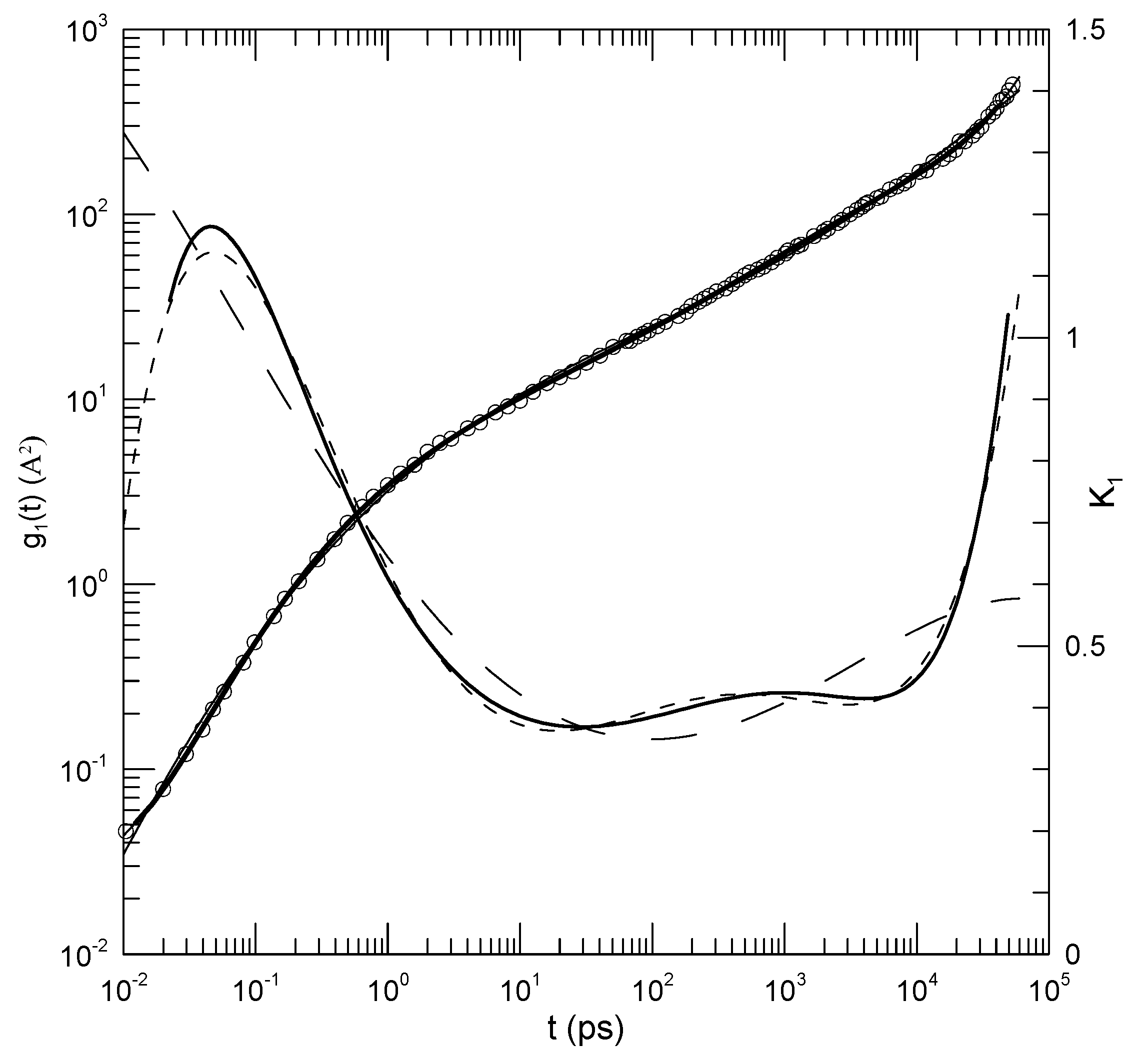
Brodeck et al. [
6] report atomistic molecular dynamics simulations of a polyethylene oxide-polymethylmethacrylate mixture at four temperatures. Their interest was the dynamic asymmetry between the two components, with polymethylmethacrylate density fluctuations relaxing much more slowly than polyethylene oxide density fluctuations. They report an analysis using Rouse mode decomposition, mean-square displacements, non-Gaussian parameters for the distribution of mean-square displacements, and comparison with a simple bead-spring model.
Figure 2 shows their calculated mean-square displacements for their blend at 400 K. Fits to fifth-, sixth-, and eighth-order polynomials lead to the solid lines that pass very nearly uniformly through the data points. The lines are almost completely overlapping, except noting the upper right. The computed first logarithmic derivative
corresponds to the thin solid and dashed lines. Over times
×
×
, the first derivative from the eighth-order fit (solid line) increases from approximately 0.37 to 1.03. At the lower extremum, the slope becomes considerably larger, reaching
1.2 at short times. At times
×
, we find that
follows a smooth curve having a continuously increasing slope, with, as reported by Brodeck et al., a tangent having slope
1 at time
×
.
The fitting process is thus seen to describe time dependencies that are more complex than single power laws.
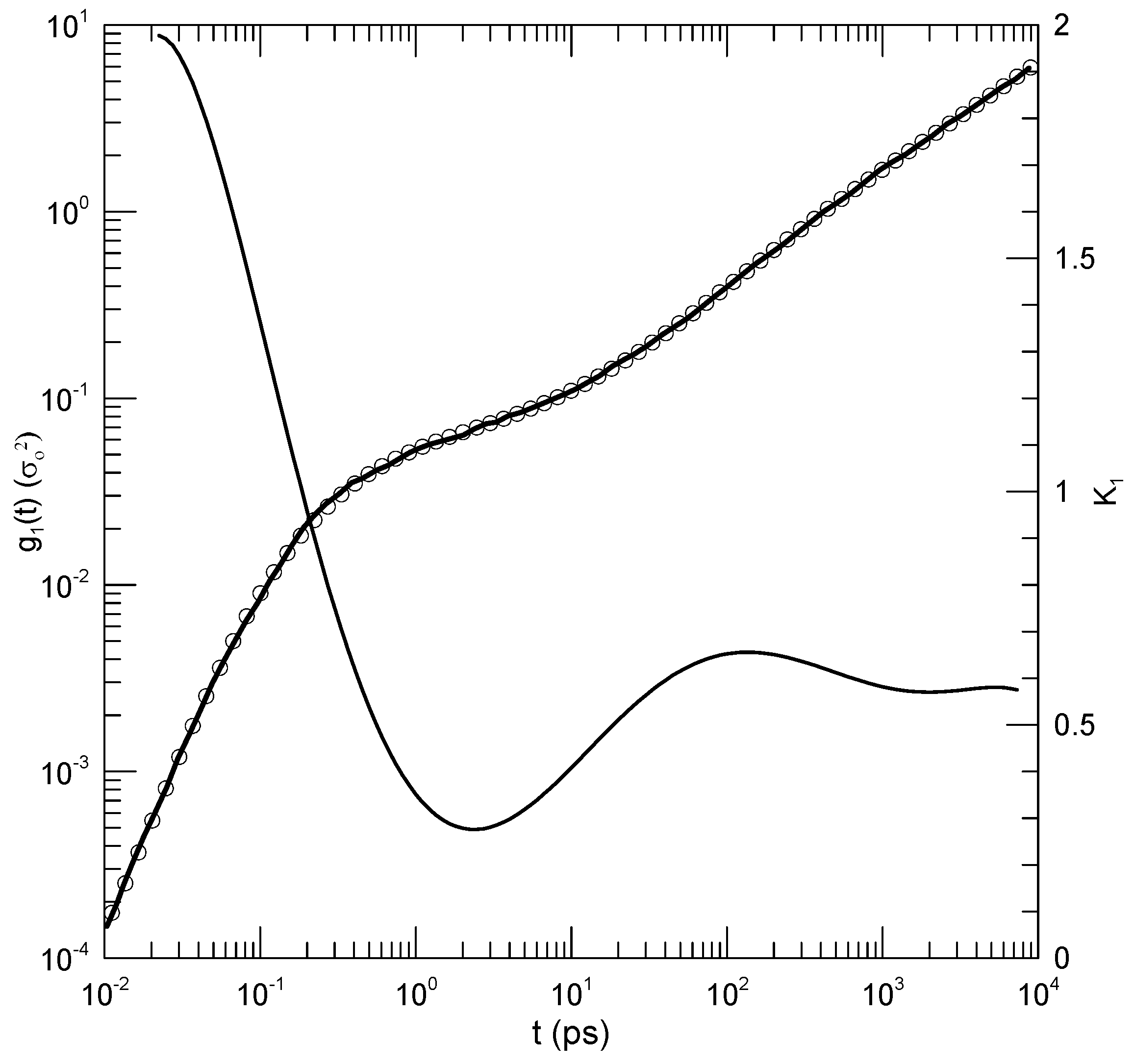
Peng et al. [
7] report simulations of a united-atom model of flexible polymers having bead-bead Lennard-Jones interactions, beads of each chain being linked with a finitely extensible nonlinear-elastic potential. To these were added chains made more rigid by giving them significant bond-bending and torsional potentials. The blends were of interest because they contained two polymer species with very different glass temperatures and mobilities.
Figure 3 shows mean-square displacements of beads of the non-rigid polymers in a mixture to which a small amount of the more rigid polymer has been added (Peng et al.’s Figure 9a,
). The solid line represents an eighth-order polynomial fit, which describes
well at almost all times. We see for long times (
) that
increases nearly linearly in time, with a slope
. At short times (
),
increases rapidly with increasing time, with a slope approaching 2. Of particular interest for this paper is the behavior of
for times near
. In this range,
superficially appears to increase linearly with increasing time, implying power-law behavior
. However,
, the first derivative, simply has a minimum at
, the slope having a parabolic dependence on
around this point. The region near
is thus revealed to be an inflection point of
, not a local power-law regime.