Numerical Simulation of Fatigue Damage in Cross-Ply CFRP Laminates: Exploring Frequency Dependence and Internal Heat Generation Effects
Abstract
1. Introduction
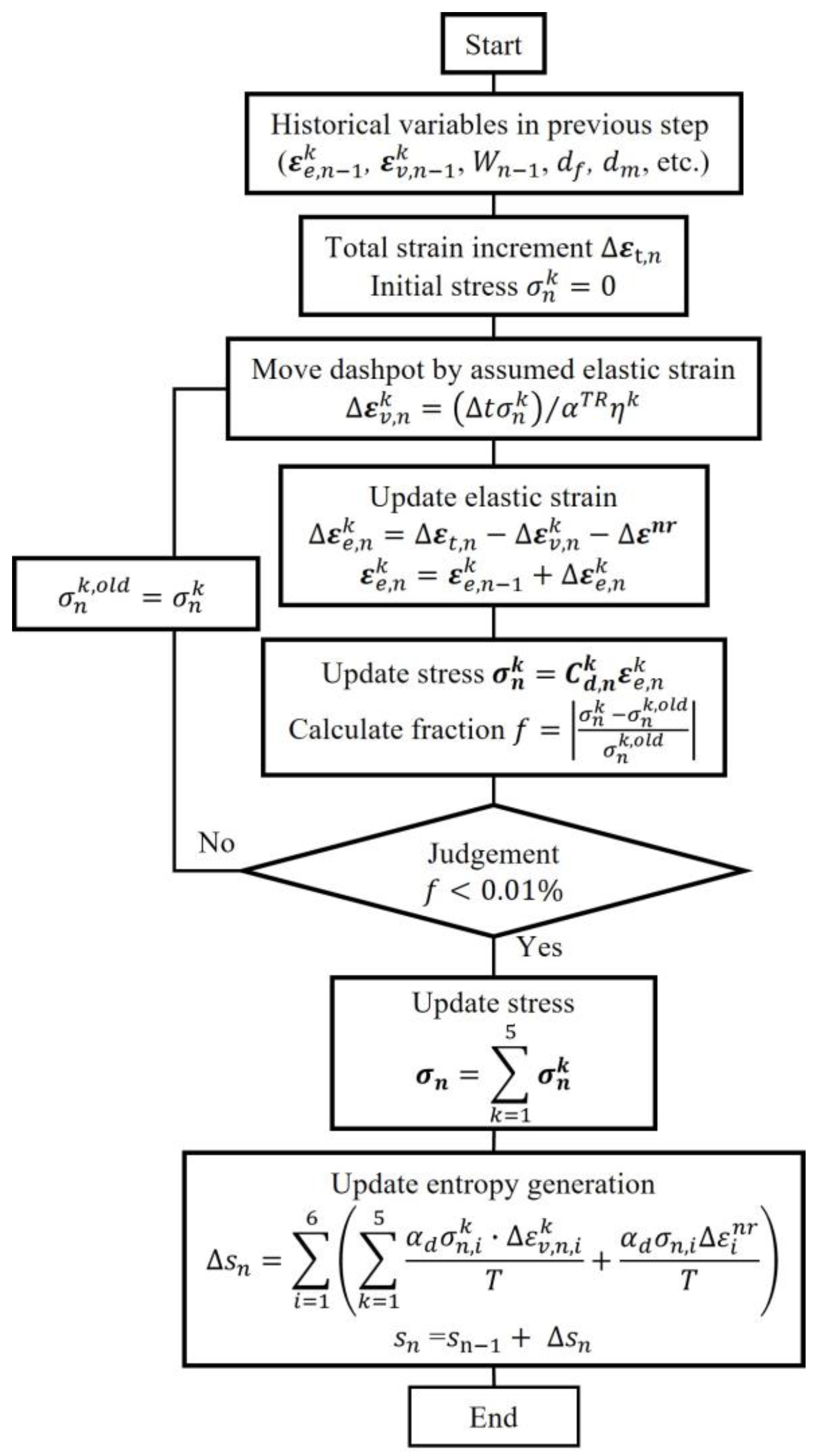
2. Numerical Procedure
2.1. Viscoelastic Constitutive Law
2.2. Heat Conduction and Heat Release
2.3. Reductions in Strength and Failure Criteria
2.4. Material Properties and Damage Variables
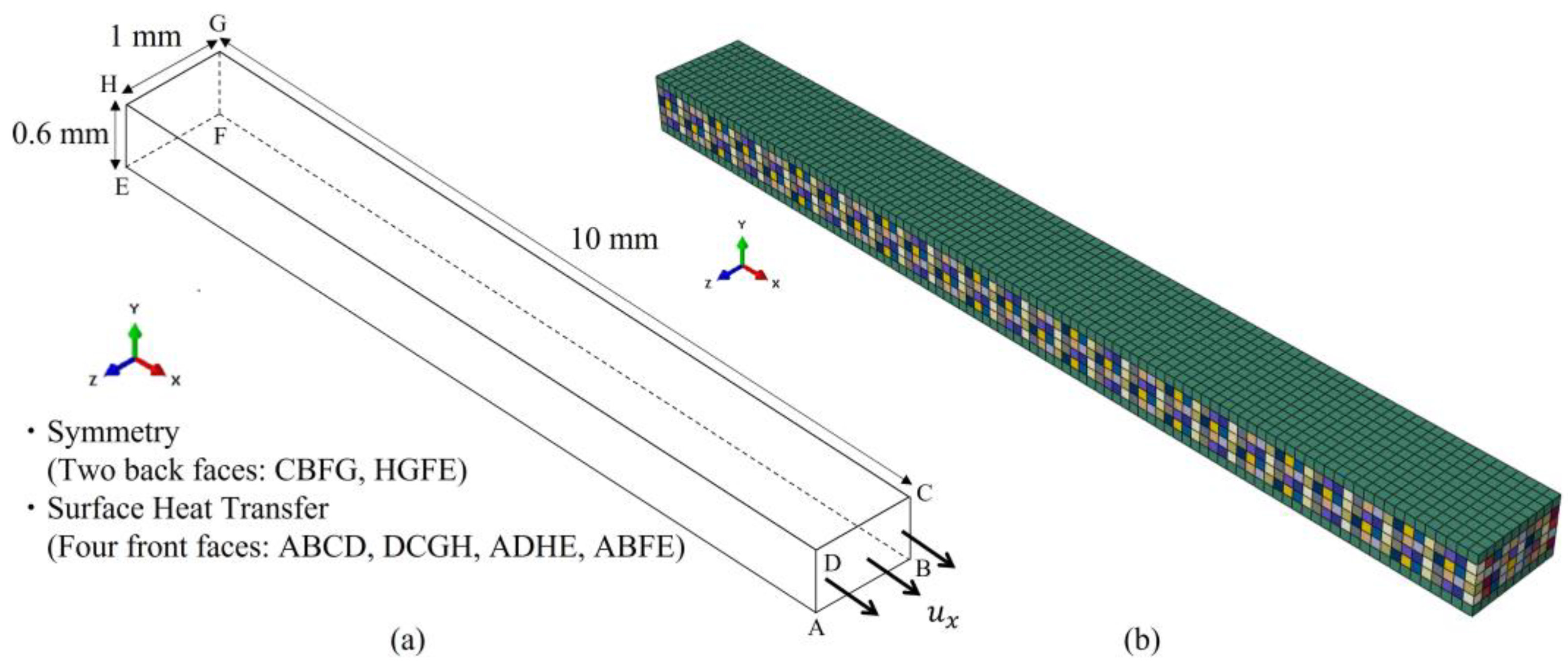
2.5. Numerical Simulation
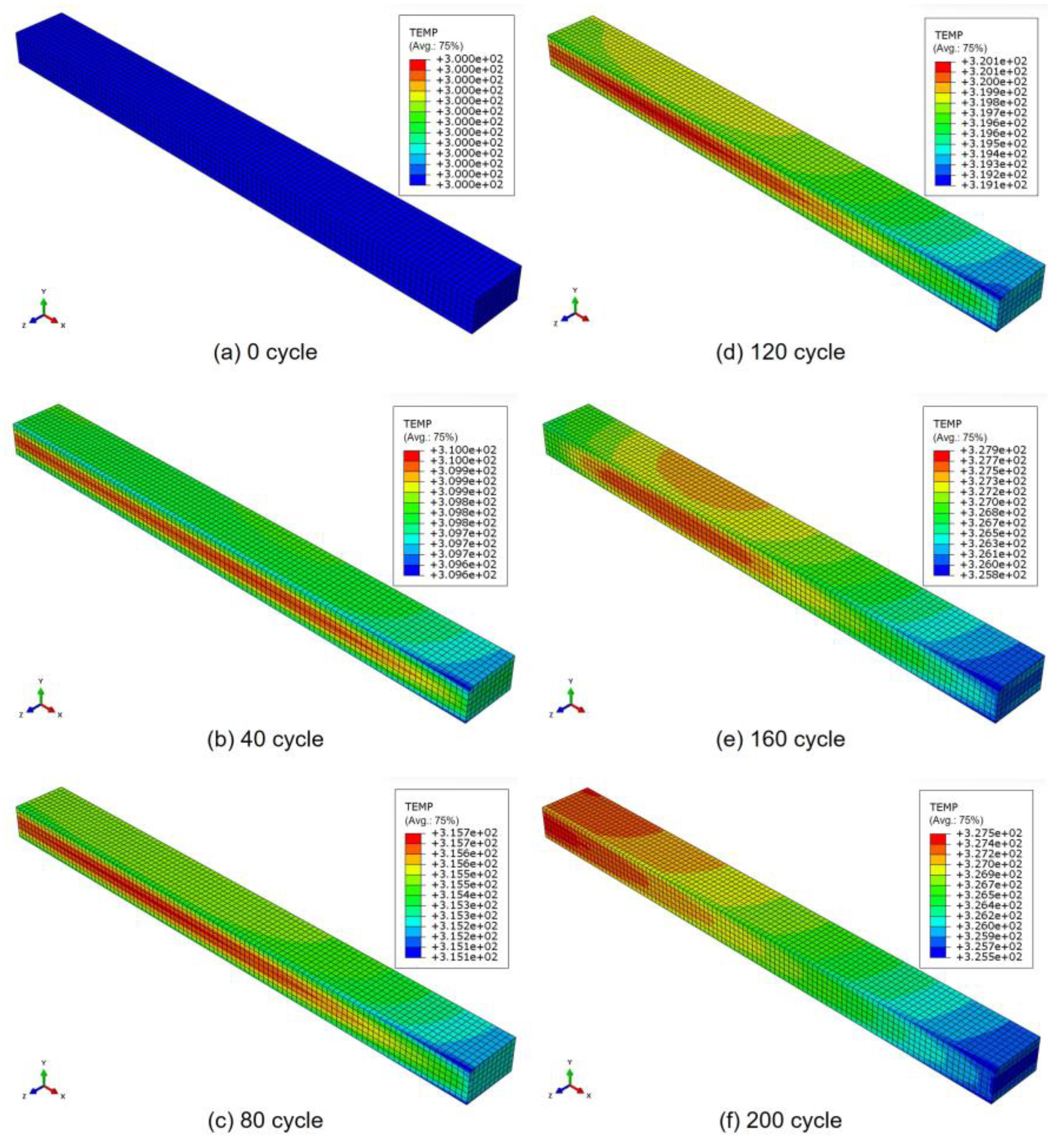
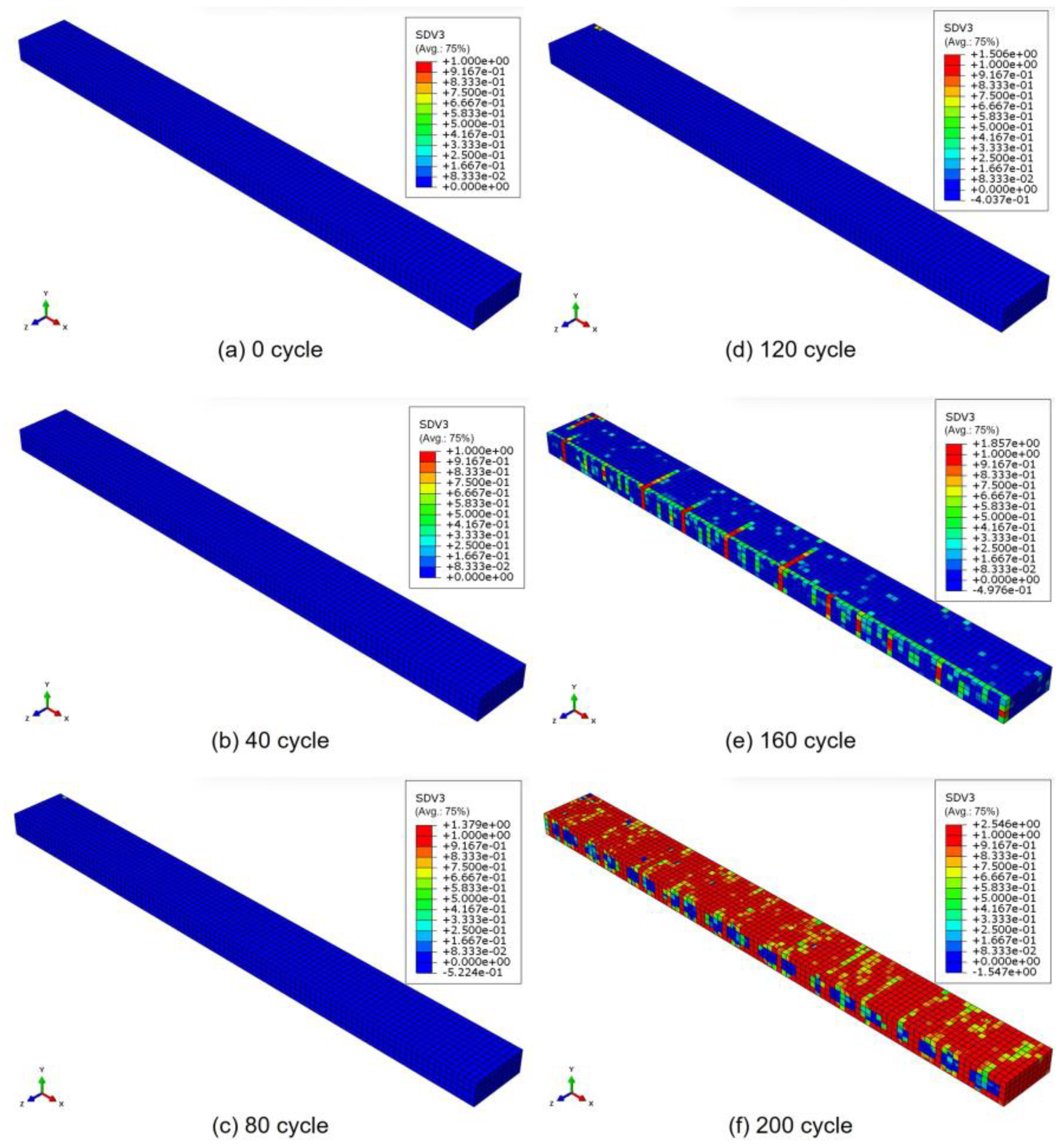
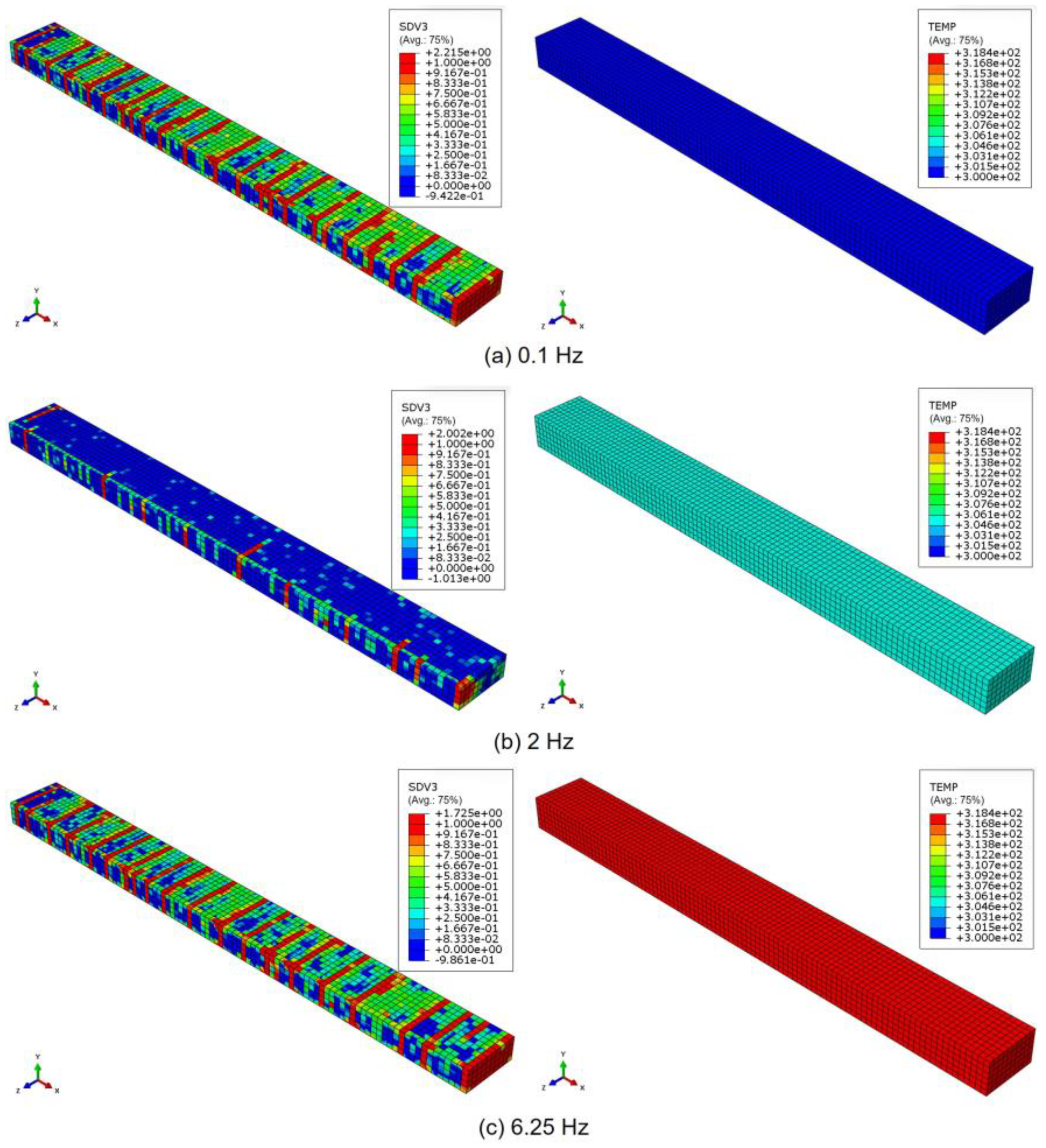
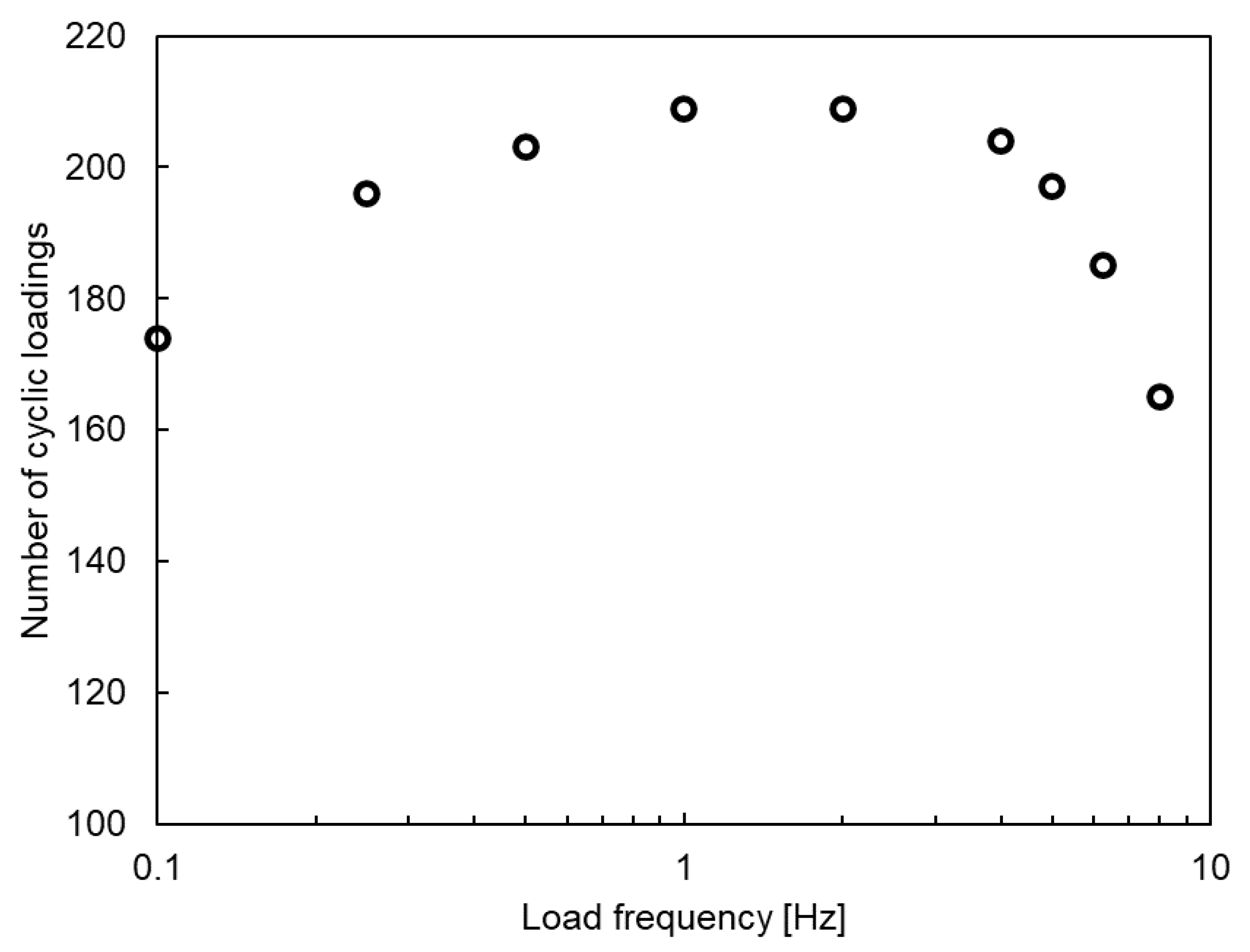
3. Results and Discussion
3.1. Numerical Results
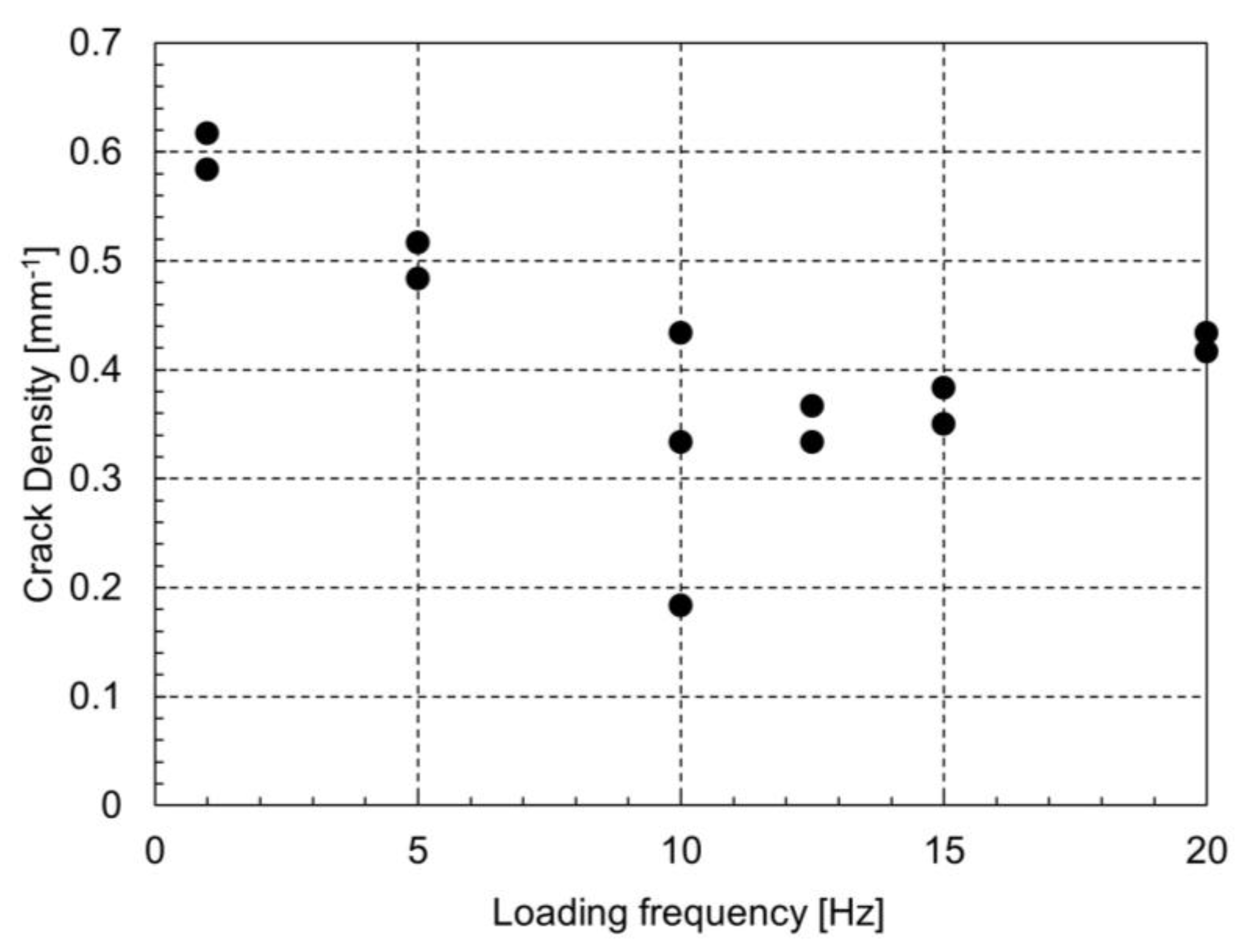
3.2. Comparison with Experimental Findings
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ke, L.; Li, Y.; Li, C.; Cheng, Z.; Ma, K.; Zeng, J. Bond behavior of CFRP-strengthened steel structures and its environmental influence factors: A critical review. Sustain. Struct. 2024, 4, 000038. [Google Scholar] [CrossRef]
- Guo, R.; Li, C.; Niu, Y.; Xian, G. The fatigue performances of carbon fiber reinforced polymer composites—A review. J. Mat. Res. Technol. 2022, 21, 4773–4789. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Fatigue simulation for progressive damage in CFRP laminates using intra-laminar and inter-laminar fatigue damage models. Int. J. Fatigue 2021, 143, 106051. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Progressive damage and residual strength of open-hole thin-ply CFRP laminates under tensile fatigue loading. Compos. Struct. 2023, 314, 116981. [Google Scholar] [CrossRef]
- Brod, M.; Dean, A.; Scheffler, S.; Gerendt, C.; Rolfes, R. Numerical modeling and experimental validation of fatigue damage in cross-ply CFRP composites under inhomogeneous stress states. Compos. Part B Eng. 2020, 200, 108265. [Google Scholar] [CrossRef]
- Brunbauer, J.; Pinter, G. Effects of mean stress and fibre volume content on the fatigue-induced damage mechanisms in CFRP. Int. J. Fatigue 2015, 75, 28–38. [Google Scholar] [CrossRef]
- Hosoi, A.; Takamura, K.; Sato, N.; Kawada, H. Quantitative evaluation of fatigue damage growth in CFRP laminates that changes due to applied stress level. Int. J. Fatigue 2011, 33, 781–787. [Google Scholar] [CrossRef]
- Panella, F.W.; Pirinu, A. Fatigue and damage analysis on aeronautical CFRP elements under tension and bending loads: Two cases of study. Int. J. Fatigue 2021, 152, 106413. [Google Scholar] [CrossRef]
- Guo, Y.E.; Shang, D.G.; Zuo, L.X.; Qu, L.F.; Hou, G.; Cai, D.; Jin, T.; Yin, X. Identification of fatigue damage modes for carbon fiber/epoxy composites using acoustic emission monitoring under fully reversed loading. Polym. Compos. 2022, 43, 3371–3385. [Google Scholar] [CrossRef]
- Just, G.; Koch, I.; Brod, M.; Jansen, E.; Gude, M.; Rolfes, R. Influence of reversed fatigue loading on damage evolution of cross-ply carbon fibre composites. Materials 2019, 12, 1153. [Google Scholar] [CrossRef]
- Longbiao, L. A hysteresis dissipated energy-based parameter for damage monitoring of carbon fiber-reinforced ceramic-matrix composites under fatigue loading. Mater. Sci. Eng. A 2015, 634, 188–201. [Google Scholar] [CrossRef]
- Longbiao, L. A hysteresis dissipated energy-based damage parameter for life prediction of carbon fiber-reinforced ceramic-matrix composites under fatigue loading. Compos. Part B Eng. 2015, 82, 108–128. [Google Scholar] [CrossRef]
- Skinner, T.; Datta, S.; Chattopadhyay, A.; Hall, A. Fatigue damage behavior in carbon fiber polymer composites under biaxial loading. Compos. Part B Eng. 2019, 174, 107013. [Google Scholar] [CrossRef]
- Xu, C.; Fu, J.; Sun, L.; Masuya, H.; Zhang, L. Fatigue damage self-sensing of bridge deck component with built-in giant piezoresistive cementitious carbon fiber composites. Compos. Struct. 2021, 276, 114499. [Google Scholar] [CrossRef]
- Ogi, K.; Takahashi, M.; Yashiro, S. Empirical models for matrix cracking in a CFRP cross-ply laminate under static- and cyclic-fatigue loadings. Polym. Compos. 2011, 32, 1652–1660. [Google Scholar] [CrossRef]
- Ogi, K.; Yashiro, S.; Takahashi, M.; Ogihara, S. A probabilistic static fatigue model for transverse cracking in CFRP cross-ply laminates. Compos. Sci. Technol. 2009, 69, 469–476. [Google Scholar] [CrossRef]
- Yashiro, S.; Okabe, T. Estimation of fatigue damage in holed composite laminates using an embedded FBG sensor. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1962–1969. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Arai, M.; Yoshimura, A.; Goto, K. Prediction of transverse crack multiplication of CFRP cross-ply laminates under tension-tension fatigue load. Adv. Compos. Mater. 2023, 32, 419–436. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Sasaki, K.; Arai, M.; Yoshimura, A.; Goto, K. Experimental evaluation of fatigue properties of carbon fiber/epoxy matrix interface and numerical simulation of transverse cracking under cyclic load. Adv. Compos. Mater. 2024, 33, 212–232. [Google Scholar] [CrossRef]
- Deng, H.; Mochizuki, A.; Fikry, M.; Abe, S.; Ogihara, S.; Koyanagi, J. Numerical and experimental studies for fatigue damage accumulation of CFRP cross-ply laminates based on entropy failure criterion. Materials 2023, 16, 388. [Google Scholar] [CrossRef] [PubMed]
- Koyanagi, J.; Mochizuki, A.; Higuchi, R.; Tan, V.B.C.; Tay, T.E. Finite element model for simulating entropy-based strength-degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings. Int. J. Fatigue 2022, 165, 107132. [Google Scholar] [CrossRef]
- Ma, H.; Bai, X.; Ran, Y.; Wei, X.; An, Z. Modeling the effect of stress ratio, loading frequency and fiber orientation on the fatigue response of composite materials. Polymers 2022, 14, 2772. [Google Scholar] [CrossRef]
- Maillet, I.; Michel, L.; Souric, F.; Gourinat, Y. Mode II fatigue delamination growth characterization of a carbon/epoxy laminate at high frequency under vibration loading. Eng. Fract. Mech. 2015, 149, 298–312. [Google Scholar] [CrossRef]
- Marin, J.C.; Justo, J.; París, F.; Cañas, J. The effect of frequency on tension-tension fatigue behavior of unidirectional and woven fabric graphite-epoxy composites. Mech. Adv. Mater. Struct. 2019, 26, 1430–1436. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A.; Mellott, S.R.; Khosrovaneh, A. Effect of cycling frequency and self-heating on fatigue behavior of reinforced and unreinforced thermoplastic polymers. Polym. Eng. Sci. 2015, 55, 2355–2367. [Google Scholar] [CrossRef]
- Zhou, Y.D.; Fei, Q.G.; Wu, S.Q.; Tan, Z.Y. Numerical investigation of the loading frequency for fatigue test of C/SiC materials. Zhendong Gongcheng Xuebao/J. Vib. Eng. 2016, 29, 985–991. [Google Scholar]
- Kharrazi, M.R.; Sarkani, S. Frequency-dependent fatigue damage accumulation in fiber-reinforced plastics. J. Compos. Mater. 2001, 35, 1924–1953. [Google Scholar] [CrossRef]
- Holmes, J.W.; Wu, X.; Sørensen, B.F. Frequency dependence of fatigue life and internal heating of a fiber-reinforced/ceramic-matrix composite. J. Am. Ceram. Soc. 1994, 77, 3284–3286. [Google Scholar] [CrossRef]
- Nakada, M.; Miyano, Y.; Nonaka, T.; Morisawa, Y.; Isaki, T.; Hirano, T.; Uzawa, K. Statistical tensile and flexural fatigue lives of unidirectional CF/PP laminates. J. Reinf. Plast. Compos. 2024, 43, 195–204. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M.; Morisawa, Y. Statistical fatigue failure life of unidirectional CFRP under bending load. J. Compos. Mater. 2022, 56, 4173–4181. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M.; Muki, R. Prediction of fatigue life of a conical shaped joint system for fiber reinforced plastics under arbitrary frequency, load ratio and temperature. Mech. Time-Depend. Mater. 1997, 1, 143–159. [Google Scholar] [CrossRef]
- Kudo, N.; Sekino, T.; Fikry, M.J.M.; Koyanagi, J. Numerical simulation of the frequency dependence of fatigue failure for a viscoelastic medium considering internal heat generation. Materials 2024, 17, 6202. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. An experimental approach to low-cycle fatigue damage based on thermodynamic entropy. Int. J. Solids Struct. 2010, 47, 875–880. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. Real-time fatigue life monitoring based on thermodynamic entropy. Struct. Health Monit. 2011, 10, 189–197. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Jirandehi, A.P.; Amooie, M.A.; Khonsari, M.M. Entropy-based damage model for assessing the remaining useful fatigue life. Int. J. Damage Mech. 2024, 33, 223–244. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; Khonsari, M.M. On the application of fracture fatigue entropy to variable frequency and loading amplitude. Theor. Appl. Fract. Mech. 2018, 98, 30–37. [Google Scholar] [CrossRef]
- Nourian-Avval, A.; Khonsari, M.M. Rapid prediction of fatigue life based on thermodynamic entropy generation. Int. J. Fatigue 2021, 145, 106073. [Google Scholar] [CrossRef]
- Deng, H.; Toda, K.; Sato, M.; Koyanagi, J. Micro-scale numerical simulation of fatigue failure for CFRP subjected to multiple-amplitude cyclic loadings based on entropy damage criterion. Materials 2023, 16, 6120. [Google Scholar] [CrossRef]
- Kagawa, H.; Umezu, Y.; Sakaue, K.; Koyanagi, J. Numerical simulation for the tensile failure of randomly oriented short fiber reinforced plastics based on a viscoelastic entropy damage criterion. Compos. Part C Open Access 2023, 10, 100319. [Google Scholar] [CrossRef]
- Li, Y.; Deng, H.; Takamura, M.; Koyanagi, J. Durability analysis of CFRP adhesive joints: A study based on entropy damage modeling using FEM. Materials 2023, 16, 6821. [Google Scholar] [CrossRef]
- Sato, M.; Hasegawa, K.; Koyanagi, J.; Higuchi, R.; Ishida, Y. Residual strength prediction for unidirectional CFRP using a nonlinear viscoelastic constitutive equation considering entropy damage. Compos. Part A Appl. Sci. Manuf. 2021, 141, 106225. [Google Scholar] [CrossRef]
- Yoshimori, S.; Koyanagi, J.; Matsuzaki, R. Efficient prediction of fatigue damage analysis of carbon fiber composites using multi-timescale analysis and machine learning. Polymers 2024, 16, 3448. [Google Scholar] [CrossRef]
- Li, Y.; Fikry, M.J.M.; Koyanagi, J. Numerical simulation for durability of a viscoelastic polymer material subjected to variable loadings fatigue based on entropy damage criterion. Polymers 2024, 16, 2857. [Google Scholar] [CrossRef]
- Sekino, T.; Kudo, N.; Koyanagi, J. Micro-Scale Numerical Simulation for Residual Strength of CFRP After Cyclic Tensile or Out-of-Plane Shear Loadings Fatigue. J. Compos. Sci. 2025, 9, 28. [Google Scholar] [CrossRef]
- Zha, X.; Wang, T.; Chen, F.; Wang, J.; Lin, L.; Lin, F.; Xie, H.; Jiang, F. Investigation of the fatigue impact behavior and wear mechanisms of bilayer micro-structured and multilayer nano-structured coatings on cemented carbide tools in milling titanium alloy. Int. J. Refract. Met. Hard Mat. 2022, 103, 105738. [Google Scholar] [CrossRef]
- Alam, P.; Mamalis, D.; Robert, C.; Floreani, C.; Ó Brádaigh, C.M. The fatigue of carbon fibre reinforced plastics: A review. Compos. Part B Eng. 2019, 166, 555–579. [Google Scholar] [CrossRef]
- Thamburaja, P.; Sarah, K.; Srinivasa, A.; Reddy, J.N. Fracture of viscoelastic materials: FEM implementation of a non-local and rate form-based finite-deformation constitutive theory. Comput. Methods Appl. Mech. Eng. 2019, 354, 871–903. [Google Scholar] [CrossRef]
- Sarah, K.; Thamburaja, P.; Srinivasa, A.; Reddy, J.N. Numerical simulations of damage and fracture in viscoelastic solids using a nonlocal fracture criterion. Mech. Adv. Mater. Struct. 2020, 27, 1085–1097. [Google Scholar] [CrossRef]
- Koyanagi, J.; Sugiyama, T.; Fikry, M.J.M.; Yutong, Y.; Tsukada, T. Numerical simulations for damage and failure of polymer composite materials subjected to thermal fatigue loading. Compos. Part A Appl. Sci. Manuf. 2024, under review. [Google Scholar]
- Li, C.; Xian, G. A novel wedge-shaped bond anchorage system for pultruded CFRP plates. Mat. Struct. 2018, 51, 162. [Google Scholar] [CrossRef]



| Strength | Equation |
|---|---|
| Transverse tensile and compressive strengths | |
| Shear strengths | |
| Elastic Modulus (MPa) | |||||
| 128,000 | 80 | 80 | 80 | 80 | |
| 4290 | 267 | 267 | 267 | 267 | |
| 1810 | 133 | 133 | 133 | 133 | |
| 1610 | 101 | 101 | 101 | 101 | |
| Viscosity (MPa·s) | |||||
| 6.00 × 1030 | 3.50 × 106 | 3.00 × 106 | 3.00 × 105 | 6.00 × 103 | |
| 6.00 × 1030 | 1.17 × 107 | 1.00 × 107 | 1.00 × 106 | 2.01 × 104 | |
| 6.00 × 1030 | 5.83 × 106 | 5.00 × 106 | 5.00 × 105 | 9.99 × 103 | |
| 6.00 × 1030 | 4.45 × 106 | 3.81 × 106 | 3.81 × 105 | 7.63 × 103 |
| Material Properties | Value |
|---|---|
| Initial axial tensile strength | 3930 MPa |
| Initial axial compressive strength | 2775 MPa |
| Initial transverse tensile strength | 150 MPa |
| Initial transverse compressive strength | 270 MPa |
| Initial axial shear strength , | 117 MPa |
| Initial axial transverse strength | 117 MPa |
| Initial fiber directional tensile fracture energy * | 12 N/mm |
| Initial fiber directional compressive fracture energy * | 6 N/mm |
| Initial transverse tensile fracture energy * | 0.42 N/mm |
| Initial transverse compressive fracture energy * | 1.36 N/mm |
| Degradation coefficient (, , ) | 3000 K·mm3/J |
| 30 |
| Non-Recoverable Strain [32] | Damage Variables | ||
|---|---|---|---|
| 40 MPa | 200 kJ | ||
| 7.00 × 10−5 | 300 K | ||
| 0.2 | |||
| 2 | |||
| 8 | |||
| Parameter | Value |
|---|---|
| Specific heat | 844 J/(kg∙K) |
| Density | 1550 kg/m3 |
| Surface heat transfer coefficient | 20 W/(m2·K) |
| Axial thermal conductivity | 5.47 W/(m·K) |
| Transverse thermal conductivity | 0.358 W/(m·K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudo, N.; Fikry, M.J.M.; Ogihara, S.; Koyanagi, J. Numerical Simulation of Fatigue Damage in Cross-Ply CFRP Laminates: Exploring Frequency Dependence and Internal Heat Generation Effects. Polymers 2025, 17, 432. https://doi.org/10.3390/polym17030432
Kudo N, Fikry MJM, Ogihara S, Koyanagi J. Numerical Simulation of Fatigue Damage in Cross-Ply CFRP Laminates: Exploring Frequency Dependence and Internal Heat Generation Effects. Polymers. 2025; 17(3):432. https://doi.org/10.3390/polym17030432
Chicago/Turabian StyleKudo, Natsuko, M. J. Mohammad Fikry, Shinji Ogihara, and Jun Koyanagi. 2025. "Numerical Simulation of Fatigue Damage in Cross-Ply CFRP Laminates: Exploring Frequency Dependence and Internal Heat Generation Effects" Polymers 17, no. 3: 432. https://doi.org/10.3390/polym17030432
APA StyleKudo, N., Fikry, M. J. M., Ogihara, S., & Koyanagi, J. (2025). Numerical Simulation of Fatigue Damage in Cross-Ply CFRP Laminates: Exploring Frequency Dependence and Internal Heat Generation Effects. Polymers, 17(3), 432. https://doi.org/10.3390/polym17030432






