Geometric Accuracy and Dimensional Precision in 3D Printing-Based Gear Manufacturing: A Study on Interchangeability and Forming Precision
Abstract
1. Introduction
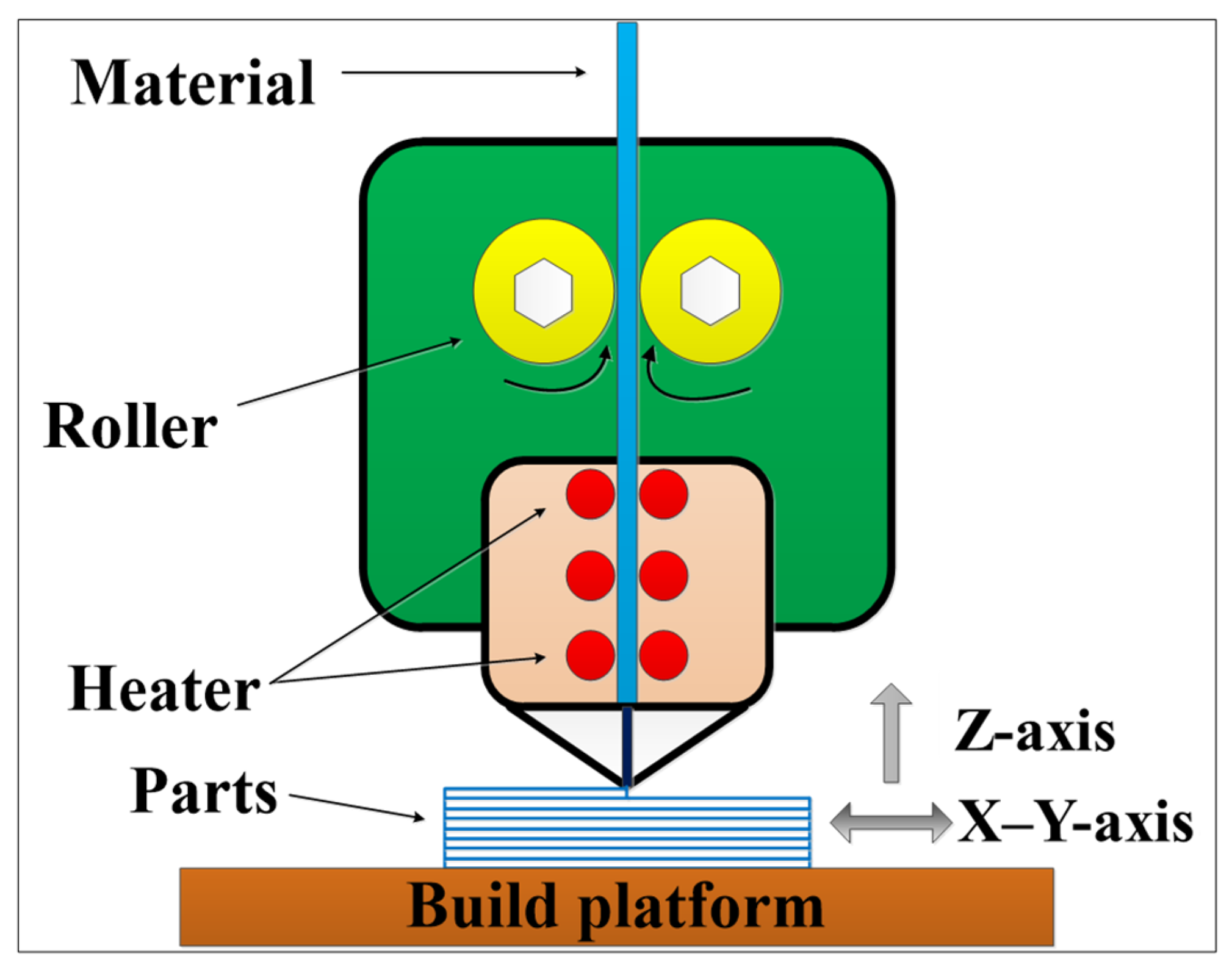
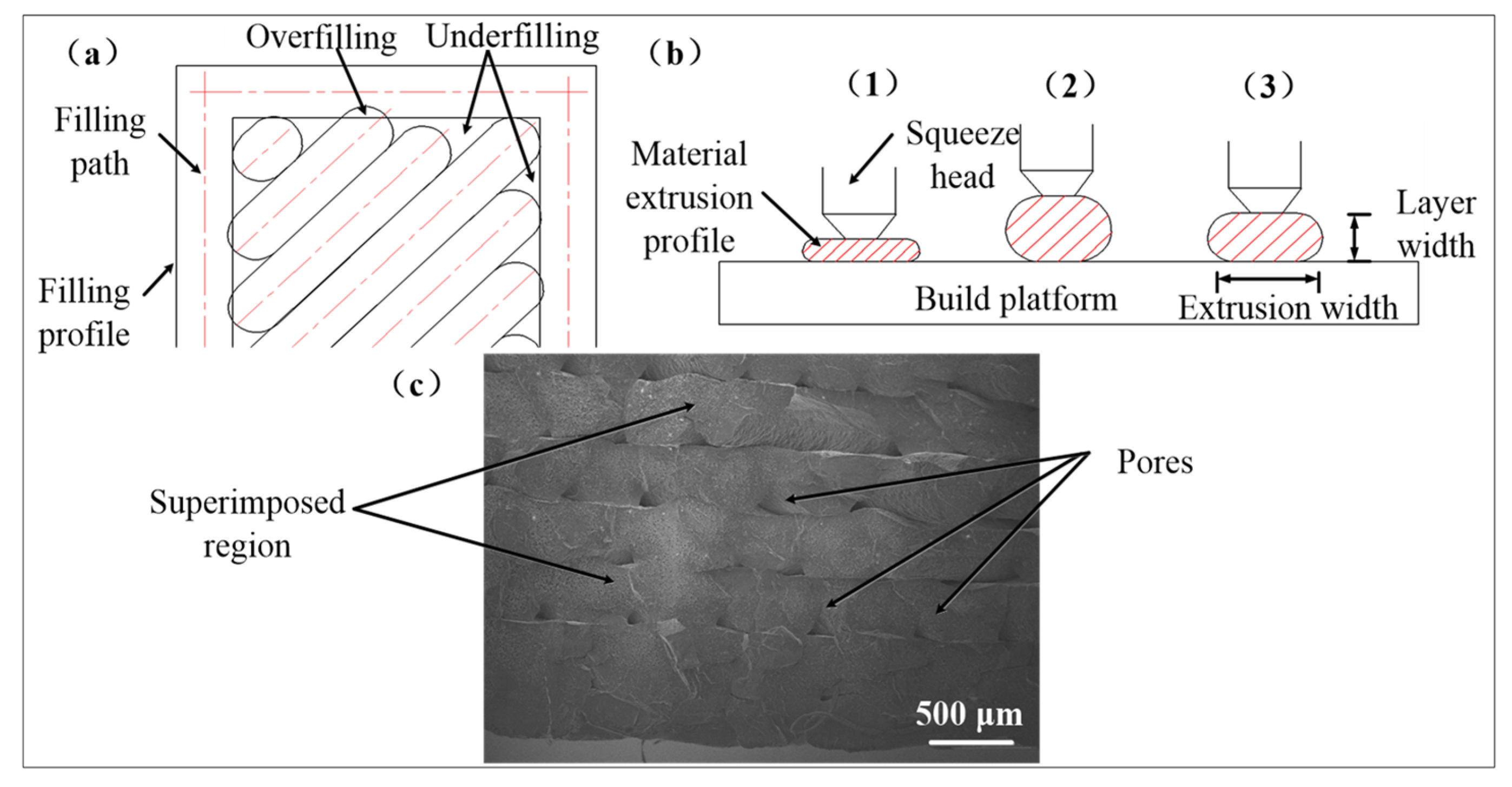
2. Experimental Materials and Methods
3. Experimental Results and Discussion
3.1. Establishment of the Geometric Model
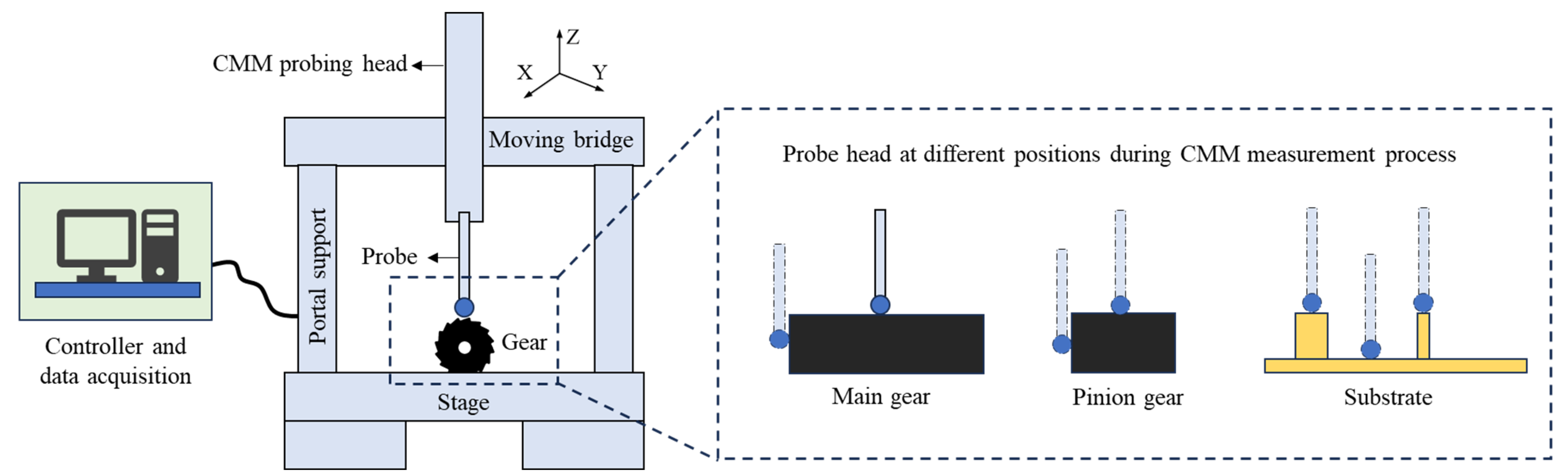
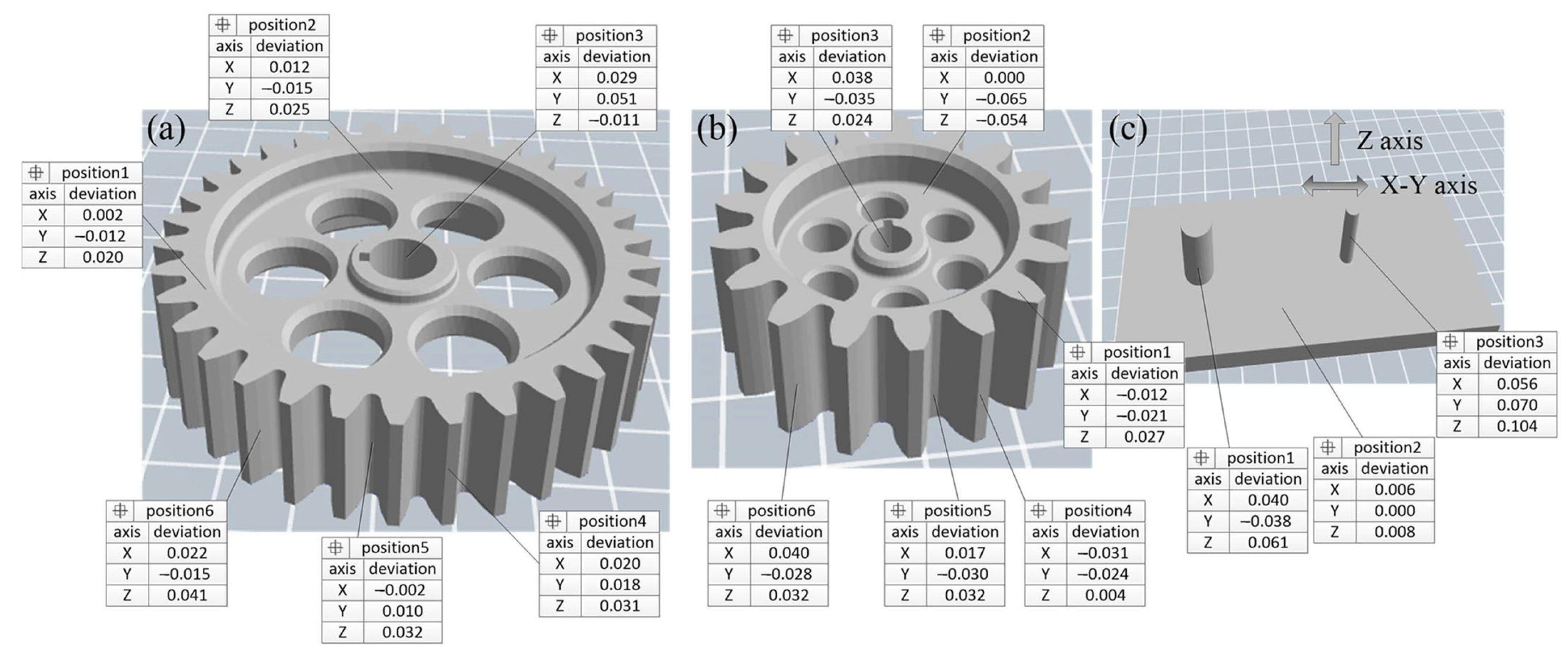
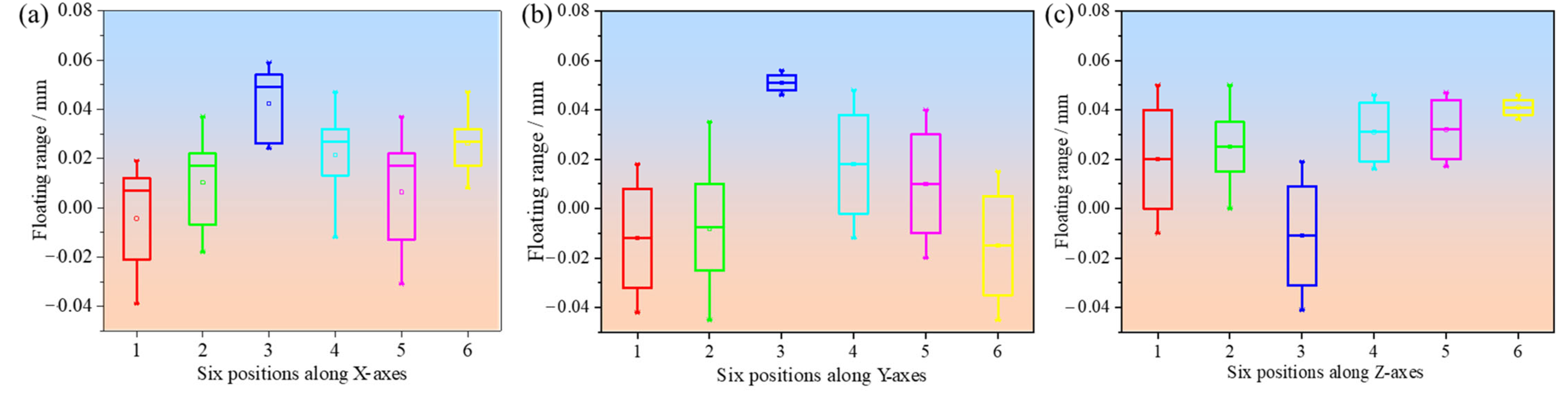
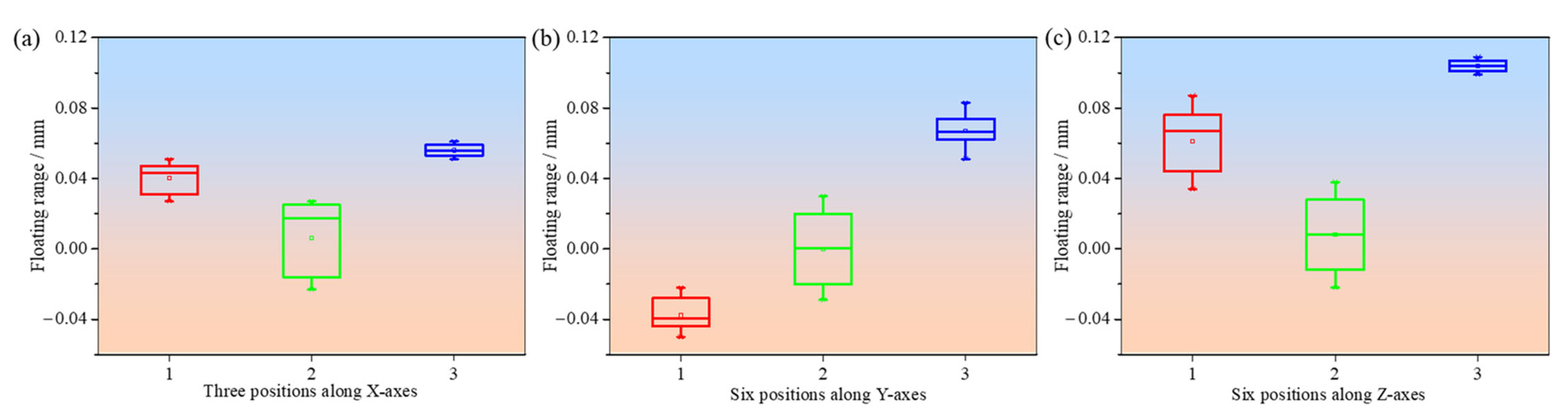
3.2. Dimensional Accuracy Inspection
3.3. Residual Stress Measurement
3.4. Interchangeability Inspection
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liashenko, I.; Rosell-Llompart, J.; Cabot, A. Ultrafast 3D printing with submicrometer features using electrostatic jet deflection. Nat. Commun. 2020, 11, 753. [Google Scholar] [CrossRef] [PubMed]
- Oh, Y.; Ko, H.; Sprock, T.; Bernstein, W.Z.; Kwon, S. Part decomposition and evaluation based on standard design guidelines for additive manufacturability and assemblability. Addit. Manuf. 2021, 37, 101702. [Google Scholar] [CrossRef]
- Khorsandi, D.; Fahimipour, A.; Abasian, P.; Saber, S.S.; Seyedi, M.; Ghanavati, S.; Ahmad, A.; De Stephanis, A.A.; Taghavinezhaddilami, F.; Leonova, A.; et al. 3D and 4D printing in dentistry and maxillofacial surgery: Printing techniques, materials, and applications. Acta Biomater. 2021, 122, 26–49. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Gao, S.; Dong, R.; Ding, X.; Duan, X. Additive Manufacturing of PLA and CF/PLA Binding Layer Specimens via Fused Deposition Modeling. J. Mater. Eng. Perform. 2018, 27, 492–500. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, S.; Almotairy, A.; Bandari, S.; Repka, M.A. Development of multifunctional drug delivery system via hot-melt extrusion paired with fused deposition modeling 3D printing techniques. Eur. J. Pharm. Biopharm. 2023, 183, 102–111. [Google Scholar] [CrossRef]
- Vyavahare, S.; Kumar, S.; Panghal, D. Experimental study of surface roughness, dimensional accuracy and time of fabrication of parts produced by fused deposition modelling. Rapid Prototyp. J. 2020, 26, 1535–1554. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, M. Multi-material fused deposition modelling of structural–functional integrated absorber with multi-scale structure possessing tunable broadband microwave absorption. Mater. Des. 2024, 246, 113315. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Song, Q.; Shi, H.; Hou, Y.; Yue, S.; Wang, R.; Cai, S.; Zhang, Z. Surface micromorphology and nanostructures evolution in hybrid laser processes of slicing and polishing single crystal 4H-SiC. J. Mater. Sci. Technol. 2024, 184, 235–244. [Google Scholar] [CrossRef]
- Rajan, K.; Samykano, M.; Kadirgama, K.; Harun, W.S.W.; Rahman, M.M. Fused deposition modeling: Process, materials, parameters, properties, and applications. Int. J. Adv. Manuf. Technol. 2022, 120, 1531–1570. [Google Scholar] [CrossRef]
- Vyavahare, S.; Teraiya, S.; Panghal, D.; Kumar, S. Fused deposition modelling: A review. Rapid Prototyp. J. 2020, 26, 176–201. [Google Scholar] [CrossRef]
- Adel, M.; Abdelaal, O.; Gad, A.; Nasr, A.B.; Khalil, A. Polishing of fused deposition modeling products by hot air jet: Evaluation of surface roughness. J. Mater. Process. Technol. 2018, 251, 73–82. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Lee, K.M.; Park, H.; Kim, J.; Chun, D.M. Fabrication of a superhydrophobic surface using a fused deposition modeling (FDM) 3D printer with poly lactic acid (PLA) filament and dip coating with silica nanoparticles. Appl. Surf. Sci. 2019, 467–468, 979–991. [Google Scholar] [CrossRef]
- Le Duigou, A.; Chabaud, G.; Matsuzaki, R.; Castro, M. Tailoring the mechanical properties of 3D-printed continuous flax/PLA biocomposites by controlling the slicing parameters. Compos. Part B Eng. 2020, 203, 108474. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters for dimensional accuracy using I-optimality criterion. Measurement 2016, 81, 174–196. [Google Scholar] [CrossRef]
- Chohan, J.S.; Singh, R.; Boparai, K.S.; Penna, R.; Fraternali, F. Dimensional accuracy analysis of coupled fused deposition modeling and vapour smoothing operations for biomedical applications. Compos. Part B Eng. 2017, 117, 138–149. [Google Scholar] [CrossRef]
- Karaki, A.; Masad, E.; Khraisheh, M.; Ouederni, M. Fused deposition modeling of polyethylene (PE): Printability assessment for low-density polyethylene and polystyrene blends. Compos. Part C Open Access 2024, 15, 100499. [Google Scholar] [CrossRef]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, E.; Núñez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Nikzad, M.; Tolouei-Rad, M. Influence of three-dimensional printing parameters on compressive properties and surface smoothness of polylactic acid specimens. Polymers 2023, 15, 3827. [Google Scholar] [CrossRef]
- Kumar, A.; Dixit, A.R.; Sreenivasa, S. Mechanical properties of additively manufactured polymeric composites using sheet lamination technique and fused deposition modeling: A review. Polym. Adv. Technol. 2024, 35, 6396. [Google Scholar] [CrossRef]
- Verma, N.; Awasthi, P.; Gupta, A.; Banerjee, S.S. Fused Deposition Modeling of Polyolefins: Challenges and Opportunities. Macromol. Mater. Eng. 2023, 308, 2200421. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, Q.; Tang, L.; Zhang, L.; Sun, Y.; Xie, Q. Accuracy of a chairside fused deposition modeling 3D-printed single-tooth surgical template for implant placement: An in vitro comparison with a light cured template. J. Cranio-Maxillo-Facial Surg. 2019, 47, 1216–1221. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Anwer, N.; Huang, Q.; Mathieu, L. Machine learning in tolerancing for additive manufacturing. CIRP Ann. 2018, 67, 157–160. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X. Modification the surface quality and mechanical properties by laser polishing of Al/PLA part manufactured by fused deposition modeling. Appl. Surf. Sci. 2019, 492, 765–775. [Google Scholar] [CrossRef]
- Sehhat, M.H.; Mahdianikhotbesara, A.; Yadegari, F. Impact of temperature and material variation on mechanical properties of parts fabricated with fused deposition modeling (FDM) additive manufacturing. Int. J. Adv. Manuf. Technol. 2022, 120, 4791–4801. [Google Scholar] [CrossRef]
- ISO 1101:2017; Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out. ISO: Geneva, Switzerland, 2017.
- Li, Y.; Gao, S. Surface enhanced 316L/SiC nano-composite coatings via laser cladding and following cold-swaging process. Appl. Phys. A 2017, 123, 660. [Google Scholar] [CrossRef]
- Li, N.; Huang, S.; Zhang, G.; Qin, R.; Liu, W.; Xiong, H.; Shi, G.; Blackburn, J. Progress in additive manufacturing on new materials: A review. J. Mater. Sci. Technol. 2019, 35, 242–269. [Google Scholar] [CrossRef]
- Ye, X.; Gao, Q.; Yang, P.; Yang, C.; He, E.; Ye, Y.; Wu, H. Mechanical and microwave absorbing properties of graphene/Mn–Zn ferrite/polylactic acid composites formed by fused deposition modeling. J. Mater. Sci. 2023, 58, 2525–2538. [Google Scholar] [CrossRef]
- Murali, A.; Vakkattil, M.A.; Parameswaran, R. Investigating the Effect of Processing Parameters on Mechanical Behavior of 3D Fused Deposition Modeling Printed Polylactic Acid. J. Mater. Eng. Perform. 2022, 32, 1089–1102. [Google Scholar] [CrossRef]
- Lambiase, F.; Genna, S.; Leone, C. Laser finishing of 3D printed parts produced by material extrusion. Opt. Lasers Eng. 2020, 124, 105801. [Google Scholar] [CrossRef]
- Taufik, M.; Jain, P.K. Laser assisted finishing process for improved surface finish of fused deposition modelled parts. J. Manuf. Process. 2017, 30, 161–177. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.; Gan, S. Effects of laser polishing on surface quality and mechanical properties of PLA parts built by fused deposition modeling. J. Appl. Polym. Sci. 2019, 137, 48288. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Li, Y.; Zhang, Y.; Geng, L.; Shen, F.; Ren, J. Hydrogelation Landscape Engineering and a Novel Strategy to Design Radically Induced Healable and Stimuli-Responsive Hydrogels. ACS Appl. Mater. Interfaces 2019, 11, 19605–19612. [Google Scholar] [CrossRef] [PubMed]
- Mostafaei, A.; Ghiaasiaan, R.; Ho, I.-T.; Strayer, S.; Chang, K.-C.; Shamsaei, N.; Shao, S.; Paul, S.; Yeh, A.-C.; Tin, S.; et al. Additive manufacturing of nickel-based superalloys: A state-of-the-art review on process-structure-defect-property relationship. Prog. Mater. Sci. 2023, 136, 101108. [Google Scholar] [CrossRef]
- Gu, D.; Shi, X.; Poprawe, R.; Bourell, D.L.; Setchi, R.; Zhu, J. Material-structure-performance integrated laser-metal additive manufacturing. Science 2021, 372, eabg1487. [Google Scholar] [CrossRef]
- Zhu, W.L.; Beaucamp, A. Compliant grinding and polishing: A review. Int. J. Mach. Tools Manuf. 2020, 158, 103634. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]






| Properties | PLA |
|---|---|
| Tensile strength (MPa) | 15.5–72.2 |
| Tensile modulus (GPa) | 2.020–3.550 |
| Elongation at break (%) | 0.5–9.2 |
| Flexural strength (MPa) | 52–115.1 |
| Flexural modulus (GPa) | 2.392–4.930 |
| Parameter | Value |
|---|---|
| Filament diameter | 1.75 ± 0.1 mm |
| Nozzle diameter | 0.4 mm |
| Object infill density | 100% |
| Toolpath strategy | ±45° |
| Layer thickness | 0.12 mm |
| Deposition speed | 35 mm/s |
| Feeding speed | 55 mm/s |
| Print temperature | 210 °C |
| Deviation | Fit Hole of Main Gear | Fit Axle of Main Gear | Fit Hole of Pinion | Fit Axle of Pinion |
|---|---|---|---|---|
| Upper deviation | 0.022 | −0.025 | 0.075 | −0.027 |
| Lower deviation | 0 | −0.04 | 0 | −0.345 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Zhang, S.; Sun, L.; Zhao, X.; Sun, M.; Yu, R.; Zhou, X.; Li, Y. Geometric Accuracy and Dimensional Precision in 3D Printing-Based Gear Manufacturing: A Study on Interchangeability and Forming Precision. Polymers 2025, 17, 416. https://doi.org/10.3390/polym17030416
Wei X, Zhang S, Sun L, Zhao X, Sun M, Yu R, Zhou X, Li Y. Geometric Accuracy and Dimensional Precision in 3D Printing-Based Gear Manufacturing: A Study on Interchangeability and Forming Precision. Polymers. 2025; 17(3):416. https://doi.org/10.3390/polym17030416
Chicago/Turabian StyleWei, Xiaofeng, Siwei Zhang, Lingli Sun, Xinyu Zhao, Mengchen Sun, Run Yu, Xingwen Zhou, and Yuhang Li. 2025. "Geometric Accuracy and Dimensional Precision in 3D Printing-Based Gear Manufacturing: A Study on Interchangeability and Forming Precision" Polymers 17, no. 3: 416. https://doi.org/10.3390/polym17030416
APA StyleWei, X., Zhang, S., Sun, L., Zhao, X., Sun, M., Yu, R., Zhou, X., & Li, Y. (2025). Geometric Accuracy and Dimensional Precision in 3D Printing-Based Gear Manufacturing: A Study on Interchangeability and Forming Precision. Polymers, 17(3), 416. https://doi.org/10.3390/polym17030416






