Experimental and Analytical Framework for Predicting Nonlinear Viscoelastic–Viscoplastic Behavior of Polymers
Abstract
1. Introduction
2. Theoretical Part
2.1. Nonlinear Viscoelastic–Viscoplastic Behavior of Polymers
2.2. Reduction to Creep Recovery Data (Two-Step Loading Equation)
2.3. Methodology for Determination of Nonlinear Viscoelastic–Viscoplastic Model Parameters
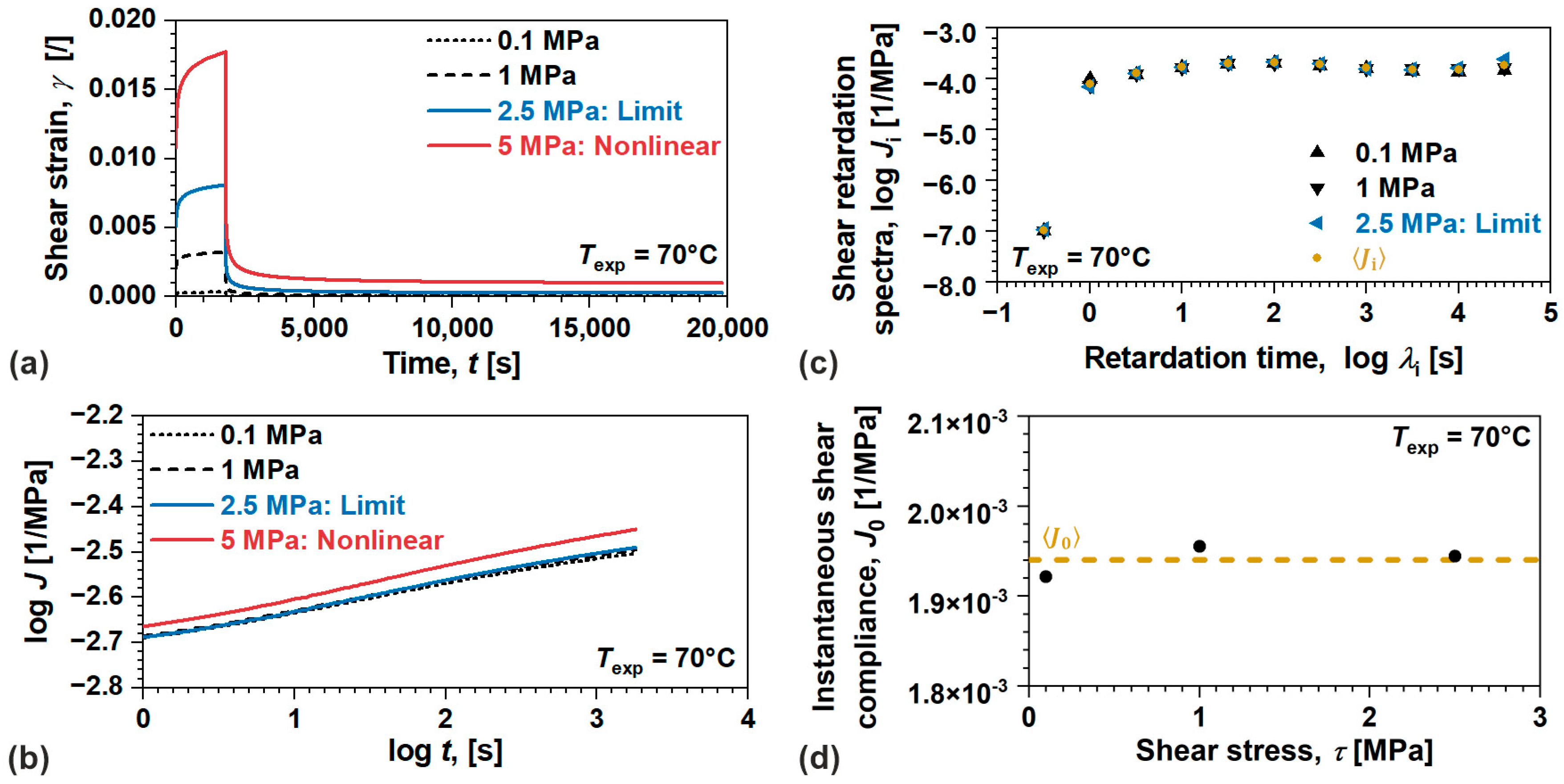
2.3.1. Linear Viscoelastic Behavior
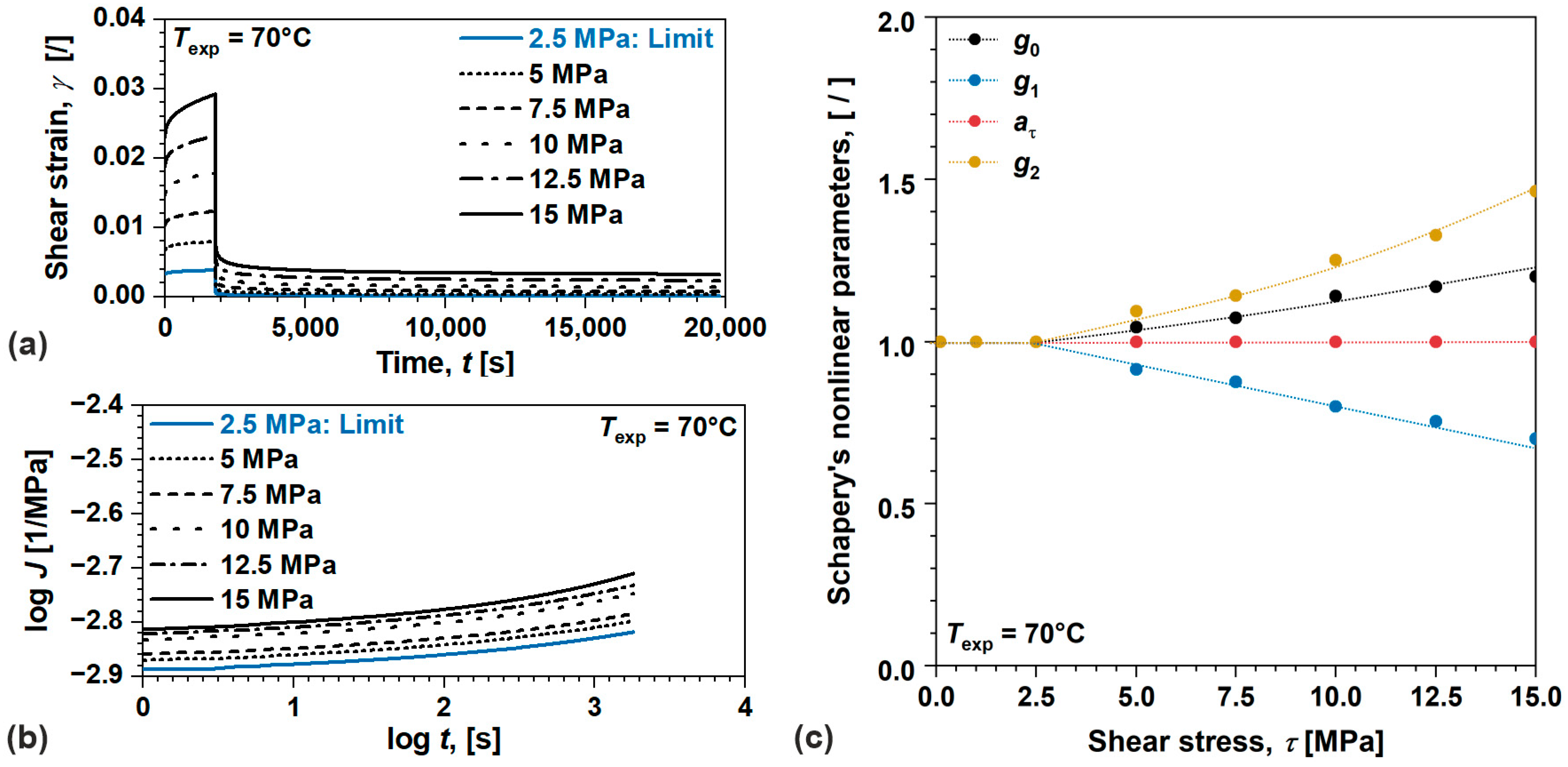
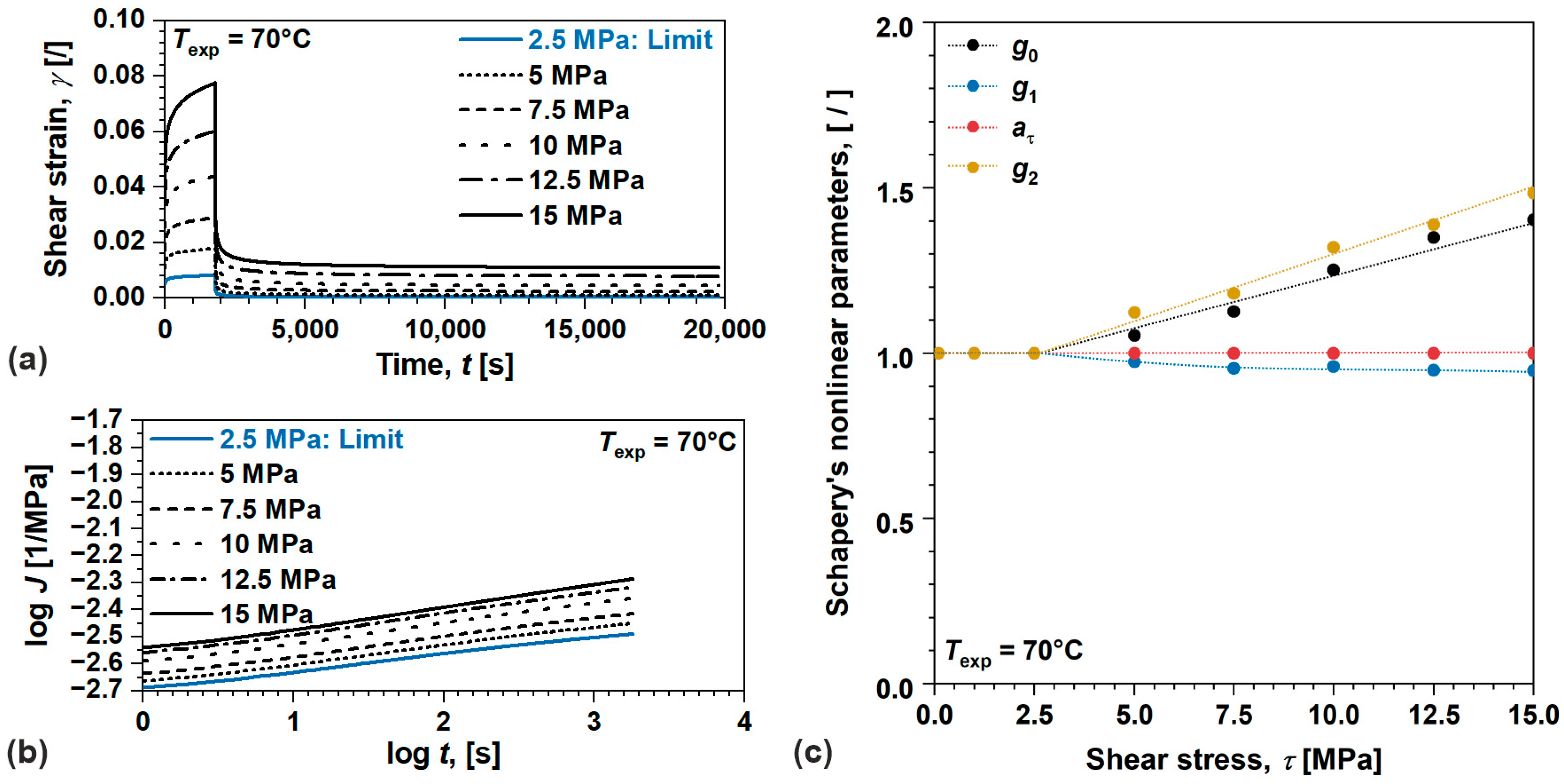
2.3.2. Nonlinear Viscoelastic Behavior
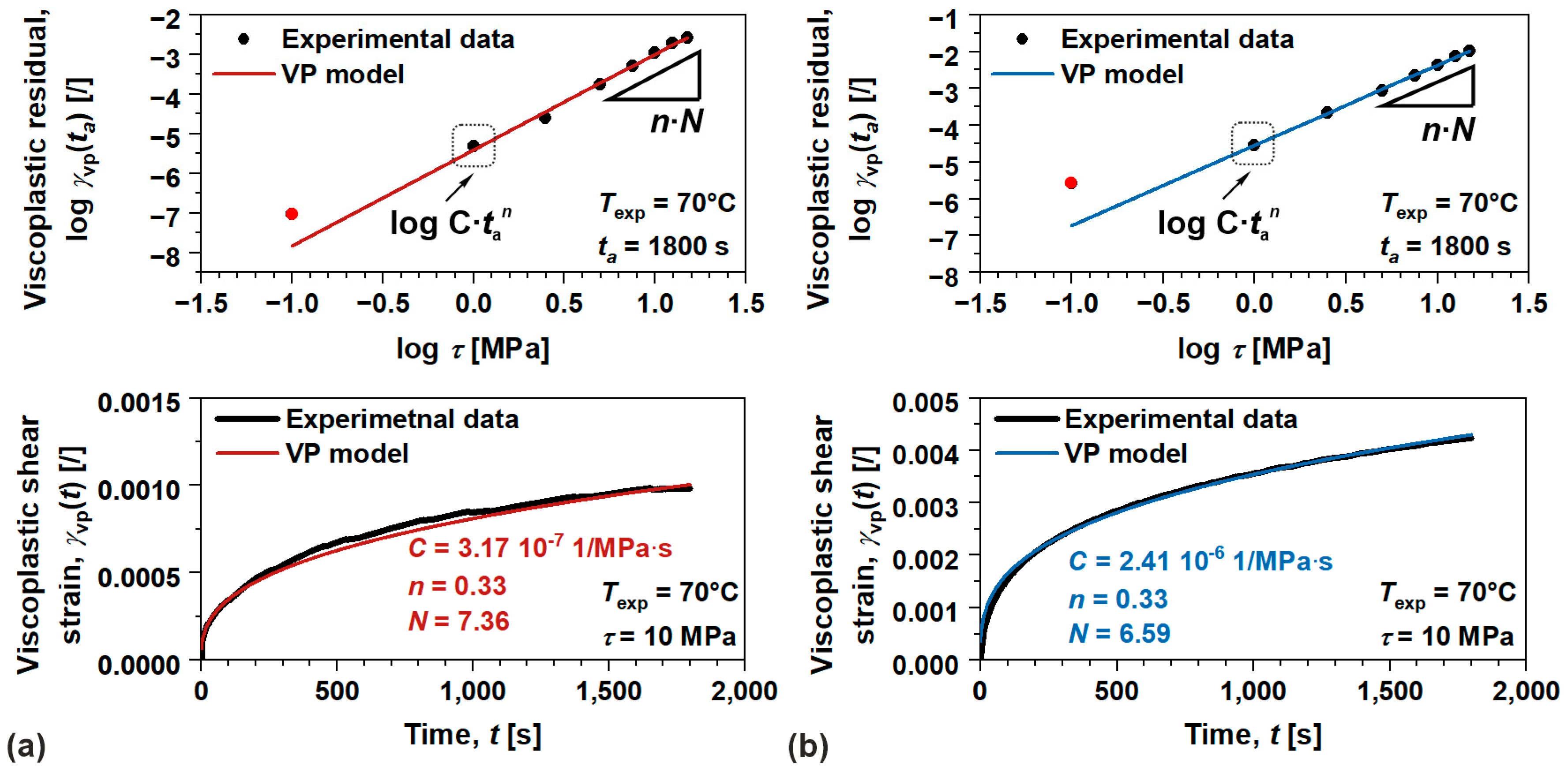
2.3.3. Viscoplastic Behavior
3. Experimental Part
3.1. Materials and Sample Preparation
3.2. Thermal Conditioning and Evaluation of Thermodynamic Equilibrium
3.3. Creep Recovery Tests for Nonlinear Viscoelastic–Viscoplastic Analysis
4. Results and Discussion
4.1. Linear Viscoelastic Behavior of Polymers
4.2. Nonlinear Viscoelastic Behavior of Polymers
4.3. Viscoplastic Behavior of Polymers
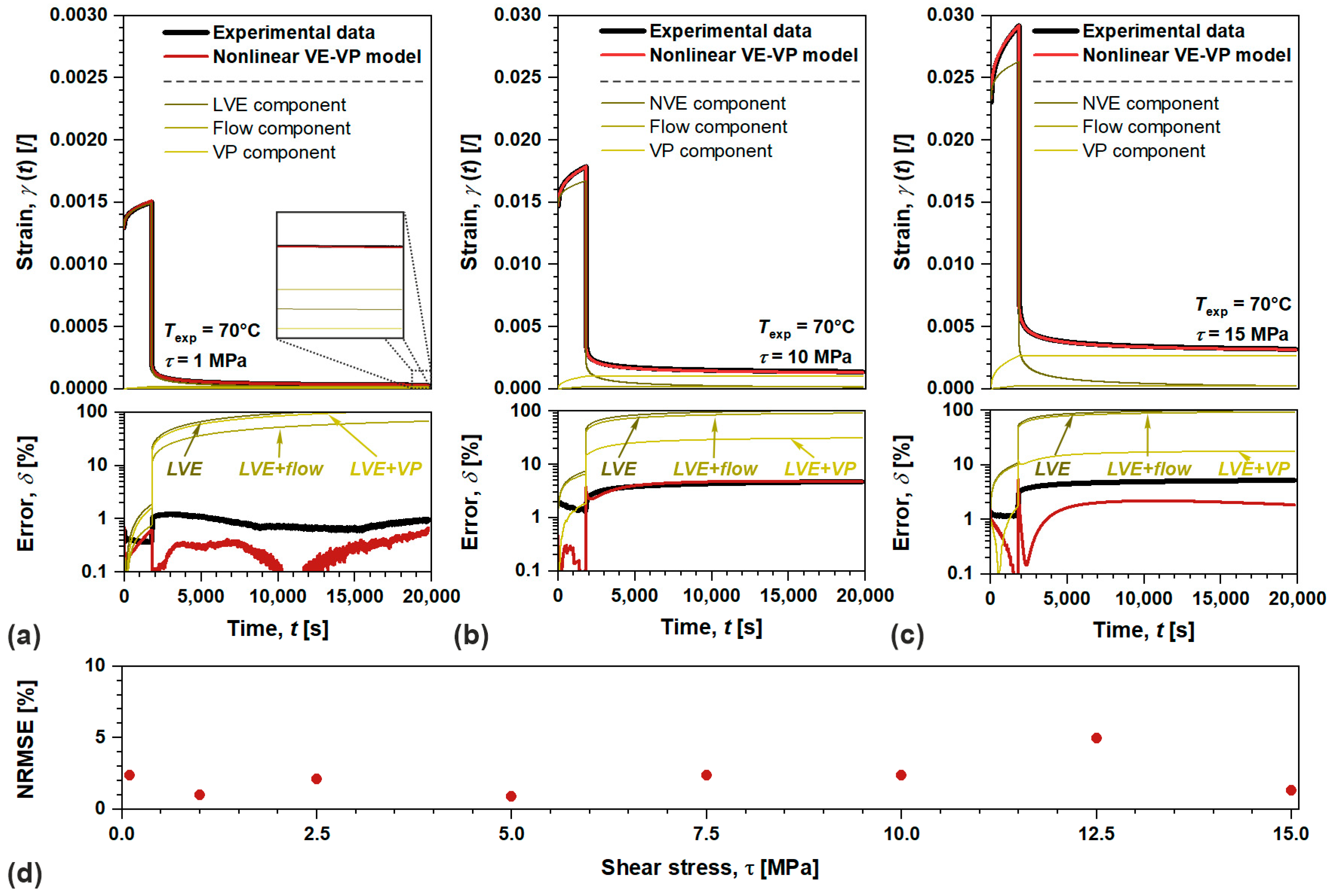
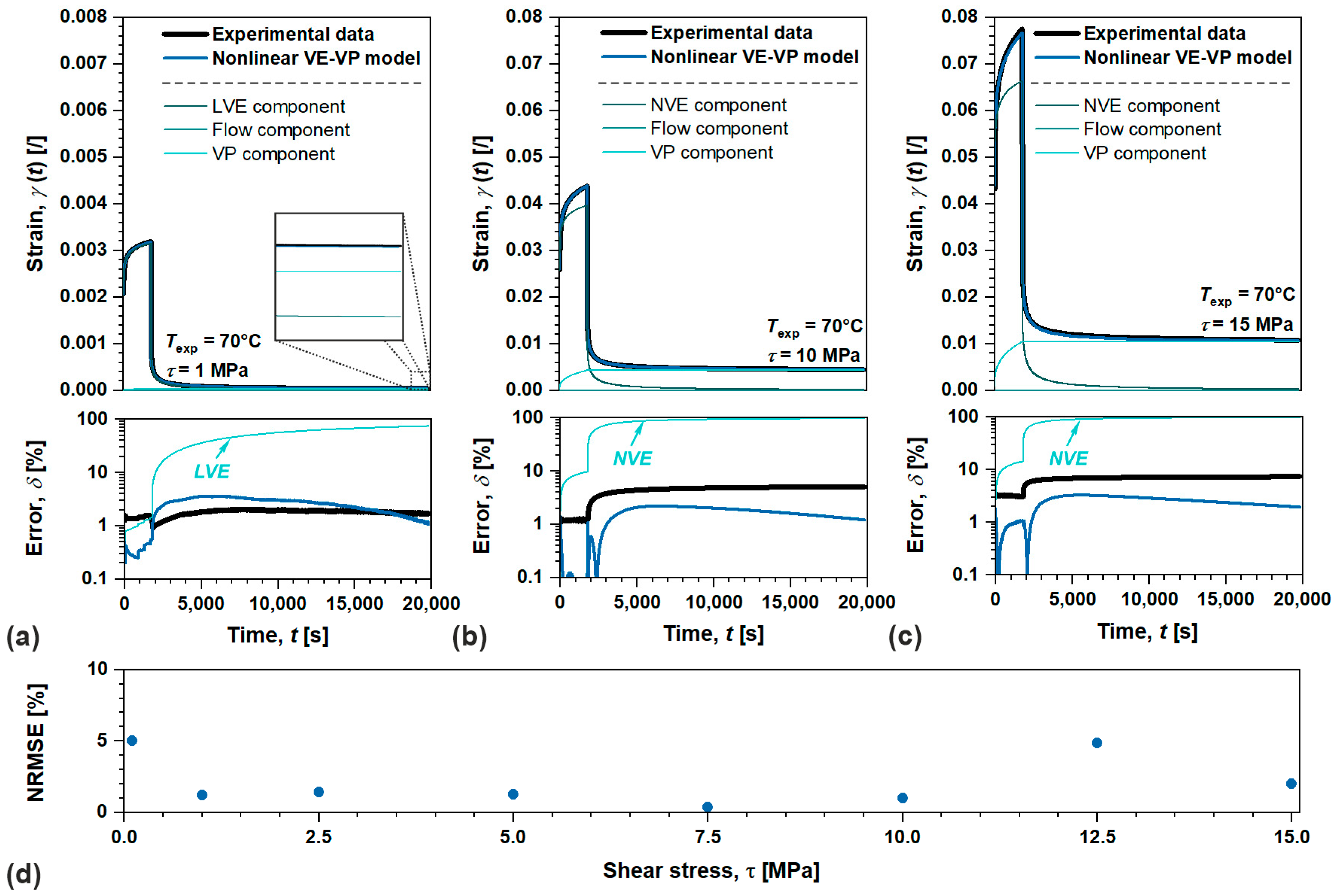
4.4. Evaluation of Nonlinear Viscoelastic–Viscoplastic Model in Linear and Nonlinear Domain
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile Butadiene Styrene |
| POM | Polyoxymethylene |
| TC | Thermal conditioning |
| TD | Thermo-dynamic state |
| DSC | Differential dynamic calorimetry |
| DTMA | Dynamic Thermo-Mechanical Analysis |
| VE | Viscoelastic |
| VP | Viscoplastic |
References
- European Commission. A New Circular Economy Action Plan (2020). EUR-Lex-52020DC0098-EN. Available online: https://eur-lex.europa.eu/legal-content/SL/PIN/?uri=CELEX:52020DC0098 (accessed on 18 November 2025).
- European Commission. Ecodesign for Sustainable Product Regulation (2024). Regulation-EU-2024/1781-EN-EUR-Lex. Available online: https://eur-lex.europa.eu/eli/reg/2024/1781/oj/eng (accessed on 18 November 2025).
- Oseli, A.; Aulova, A.; Gergesova, M.; Emri, I. Effect of temperature on mechanical properties of polymers. In Encyclopedia of Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Aulova, A.; Oseli, A.; Bek, M.; Prodan, T.; Emri, I. Effect of pressure on mechanical properties of polymers. In Encyclopedia of Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Emri, I.; Gergesova, M. Time dependent behavior of solid polymers. In Encyclopedia of Life Support Systems; Eolss Publishers: Oxford, UK, 2010. [Google Scholar]
- Brinson, H.F.; Brinson, L.C. Nonlinear viscoelasticity. In Polymer Engineering Science and Viscoelasticity: An Introduction; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Schapery, R.A. Nonlinear viscoelastic and viscoplastic constitutive equations based on thermodynamics. Mech. Time-Depend. Mater. 1997, 1, 209–240. [Google Scholar] [CrossRef]
- Schapery, R. Nonlinear viscoelastic and viscoplastic constitutive equations with growing damage. Int. J. Fract. 1999, 97, 33–66. [Google Scholar] [CrossRef]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Knauss, W.G.; Emri, I.; Lu, H. Mechanics of polymers: Viscoelasticity. In Springer Handbook of Experimental Solid Mechanics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Yannas, I.V. Nonlinear viscoelasticity of solid polymers (in uniaxial tensile loading). J. Polym. Sci. Macromol. Rev. 1974, 9, 163–190. [Google Scholar] [CrossRef]
- Yannas, I.V.; Lunn, A.C. Transition from linear to nonlinear viscoelastic behavior. Part 1 Creep of polycarbonate. J. Macromol. Sci. Part B 1970, 4, 603–620. [Google Scholar] [CrossRef]
- Yannas, I.V.; Sung, N.H.; Lunn, A.C. Transition from linear to nonlinear viscoelastic behavior. Part 2. stress relaxation of polycarbonate. J. Macromol. Sci. Part B 1971, 5, 487–503. [Google Scholar] [CrossRef]
- Yannas, I.V. Transition from linear to nonlinear viscoelastic behavior. Part 3 Linearity below and above Tg. J. Macromol. Sci. Part B 1972, 6, 91–100. [Google Scholar] [CrossRef]
- Starkova, O.; Aniskevich, A. Limits of linear viscoelastic behavior of polymers. Mech. Time-Depend. Mater. 2007, 11, 111–126. [Google Scholar] [CrossRef]
- Jansson, J.F. Studies of relaxation phenomena in polymers. I. The use of periodic square and triangular stress functions. J. Appl. Polym. Sci. 1973, 17, 2965–2975. [Google Scholar] [CrossRef]
- Maxwell, B.; Guimon, C. Dynamic mechanical spectra and limit of linear viscoelasticity of high polymers. J. Appl. Polym. Sci. 1962, 6, 83–93. [Google Scholar] [CrossRef]
- Starkova, O.; Aniskevich, A. Application of time-temperature superposition to energy limit of linear viscoelastic behavior. J. Appl. Polym. Sci. 2009, 114, 341–347. [Google Scholar] [CrossRef]
- Starkova, O.; Zhang, Z.; Zhang, H.; Park, H.-W. Limits of the linear viscoelastic behavior of polyamide 66 filled with TiO2 nanoparticles: Effect of strain rate, temperature, and moisture. Mater. Sci. Eng. A 2008, 498, 242–247. [Google Scholar] [CrossRef]
- Knauss, W.G.; Emri, I. Volume change and the Nonlinearly Thermo-Viscoelastic Constitution of Polymers. Polym. Eng. Sci. 1987, 13, 123–128. [Google Scholar] [CrossRef]
- Schapery, R.A. On the characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Popelar, C.F.; Liechti, K.M. A distortion-modified free volume theory for nonlinear viscoelastic behavior. Mech. Time-Depend. Mater. 2003, 7, 89–141. [Google Scholar] [CrossRef]
- Chevellard, G.; Ravi-Chandar, K.; Liechti, K.M. Modeling the nonlinear viscoelastic behavior of polyurea using a distortion modified free volume approach. Mech. Time-Depend. Mater. 2012, 16, 181–203. [Google Scholar] [CrossRef]
- Zink, T.; Kehrer, L.; Hirschberg, V.; Wilhelm, M.; Böhlke, T. Nonlinear schapery viscoelastic model for thermoplastic polymers. J. Appl. Polym. Sci. 2021, 139, 52028. [Google Scholar] [CrossRef]
- Tong, X.; Xu, J.; Doghri, I.; El Ghezal, M.I.; Krairi, A.; Chen, X. A nonlinear viscoelastic constitutive model for cyclically loaded solid composite propellant. Int. J. Solids Struct. 2020, 198, 126–135. [Google Scholar] [CrossRef]
- Shim, W.; Jang, J.; Choi, J.-H.; Cho, J.-M.; Yoon, S.-J.; Choi, C.-H.; Yu, W.-R. Simulating rate- and temperature-dependent behaviors of adhesives using a nonlinear viscoelastic model. Mech. Mater. 2020, 147, 103446. [Google Scholar] [CrossRef]
- Nordin, L.-O.; Varna, J. Methodology for parameter identification in nonlinear viscoelastic material model. Mech. Time-Depend. Mater. 2006, 9, 259–280. [Google Scholar] [CrossRef]
- Varna, J.; Pupure, L. Effect of material state and temperature on nonlinear viscoelastic response: 3D constitutive model and incremental formulation for numerical analysis. Mech. Compos. Mater. 2023, 59, 193–218. [Google Scholar] [CrossRef]
- Sun, T.; Yu, C.; Yang, W.; Zhong, J.; Xu, Q. Experimental and numerical research on the nonlinear creep response of polymeric composites under humid environments. Compos. Struct. 2020, 251, 112673. [Google Scholar] [CrossRef]
- Jafaripour, M.; Taheri-Behrooz, F. Creep behavior modeling of polymeric composites using Schapery model based on micromechanical approach. Eur. J. Mech./A Solids 2020, 81, 103963. [Google Scholar] [CrossRef]
- Yang, J.; Ma, X.; Wang, H.; Shang, F.; Hou, D. Characterization of nonlinear viscoelastic behaviors of CF/EP laminates with consideration to physical aging effect under thermos-mechanical loading. Mech. Mater. 2023, 180, 104615. [Google Scholar] [CrossRef]
- Ihuaenyi, R.C.; Deng, J.; Bae, C.; Xiao, X. An orthotropic nonlinear thermoviscoelastic model for polymeric battery separators. J. Electrochem. Soc. 2023, 170, 010520. [Google Scholar] [CrossRef]
- Oseli, A.; Mihelčič, M.; Šobak, M.; Perše, L.S. Nonlinear time-dependent behavior of rheodictic polymers: A theoretical and experimental investigation. Polym. Test. 2024, 137, 108535. [Google Scholar] [CrossRef]
- Perzyna, P. Themodynamic theory of viscoplasticity. Adv. Appl. Mech. 1971, 11, 313–354. [Google Scholar] [CrossRef]
- Takaoka, H.; Sakaue, K. Evaluation of viscoelastic-viscoplastic characteristics and finite element analyses for thermoplastics. Adv. Compos. Mater. 2020, 29, 273–284. [Google Scholar] [CrossRef]
- Chen, Y.; Smith, L.V. A nonlinear viscoelastic–viscoplastic model for adhesives. Mech. Time-Depend. Mater. 2021, 25, 565–579. [Google Scholar] [CrossRef]
- Haddad, M.; Doghri, I.; Pierard, O. Viscoelastic-viscoplastic polymer composites: Development and evaluation of two very dissimilar mean-field homogenization models. Int. J. Solids Struct. 2022, 236-237, 111354. [Google Scholar] [CrossRef]
- Zapas, L.; Crissman, J. Creep and recovery behaviour of ultra-high molecular weight polyethylene in the region of small uniaxial deformations. Polymer 1984, 25, 57–62. [Google Scholar] [CrossRef]
- Nordin, L.-O.; Varna, J. Nonlinear viscoplastic and nonlinear viscoelastic material model for paper fiber composites in compression. Compos. Part A Appl. Sci. Manuf. 2006, 37, 344–355. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley and Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Zupančič, B.; Emri, I. Time-dependent constitutive modeling of drive belts—II. The effect of the shape of material retardation spectrum on the strain accumulation process. Mech. Time-Depend. Mater. 2009, 13, 375–400. [Google Scholar] [CrossRef]
- Park, S.; Schapery, R. Methods of interconversion between linear viscoelastic material functions. Part I-a numerical method based on Prony series. Int. J. Solids Struct. 1999, 36, 1653–1675. [Google Scholar] [CrossRef]
- Emri, I.; Tschoegl, N.W. Determination of mechanical spectra from experimental responses. Int. J. Solids Struct. 1995, 32, 817–826. [Google Scholar] [CrossRef]
- Roths, T.; Maier, D.; Friedrich, C.; Marth, M.; Honerkamp, J. Determination of the relaxation time spectrum from dynamic moduli using an edge preserving regularization method. Rheol. Acta 2000, 39, 163–173. [Google Scholar] [CrossRef]
- Struik, L.C.E. Physical aging in plastics and other glassy materials. Polym. Eng. Sci. 1977, 17, 165–173. [Google Scholar] [CrossRef]
- Oseli, A.; Prodan, T.; Susič, E.; Perše, L.S. The effect of short fiber orientation on long term shear behavior of 40% glass fiber reinforced polyphenylene sulfide. Polym. Test. 2020, 81, 106262. [Google Scholar] [CrossRef]
- ISO 11357:2023; Plastics—Differential Scanning Calorimetry. International Standard Organization: Geneva, Switzerland, 2023.
- ISO 6721:2019; Plastics—Determination of Dynamic Mechanical Properties. International Standard Organization: Geneva, Switzerland, 2019.
- Mark, J.E. Physical Properties of Polymers Handbook; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Menard, K.P.; Menard, N.R. Dynamic Mechanical Analisys: A Practical Introduction; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Zhang, W.; Moumni, Z. A damage-based elastic-viscoplastic constitutive model for amorphous glassy polycarbonate polymers. Mater. Des. 2016, 97, 519–531. [Google Scholar] [CrossRef]
- Aoyagi, Y.; Camboulives, L.N. Modeling of nonlinear viscoelastic-viscoplastic behavior of glassy polymers based on intramolecular rotation of molecular chains. Int. J. Plast. 2025, 189, 104328. [Google Scholar] [CrossRef]
- Huber-Carol, C.; Balakrishnan, N.; Nikulin, M.S.; Mesbah, M. Goodness-of-Fit Tests and Model Validity; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]

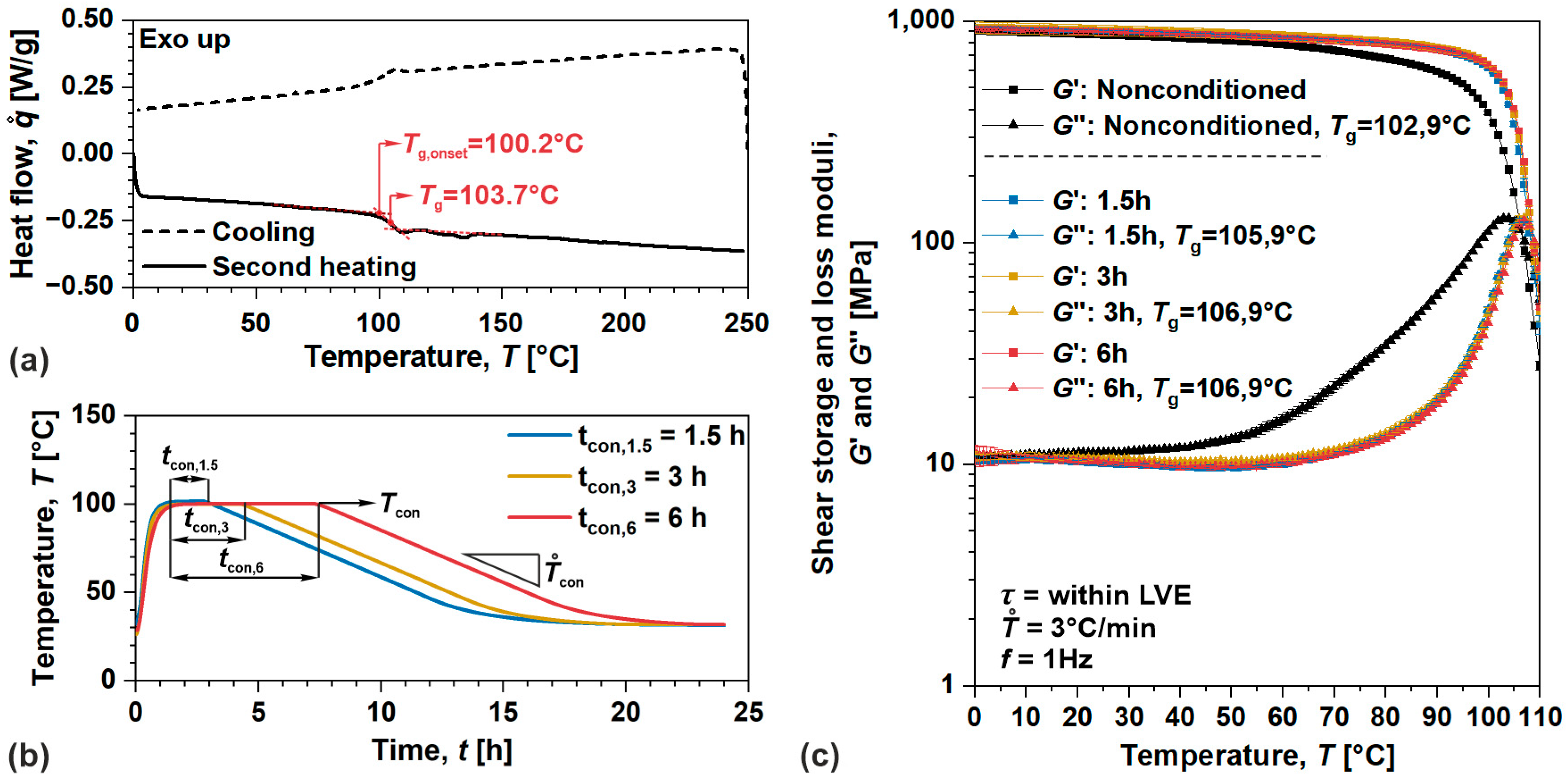
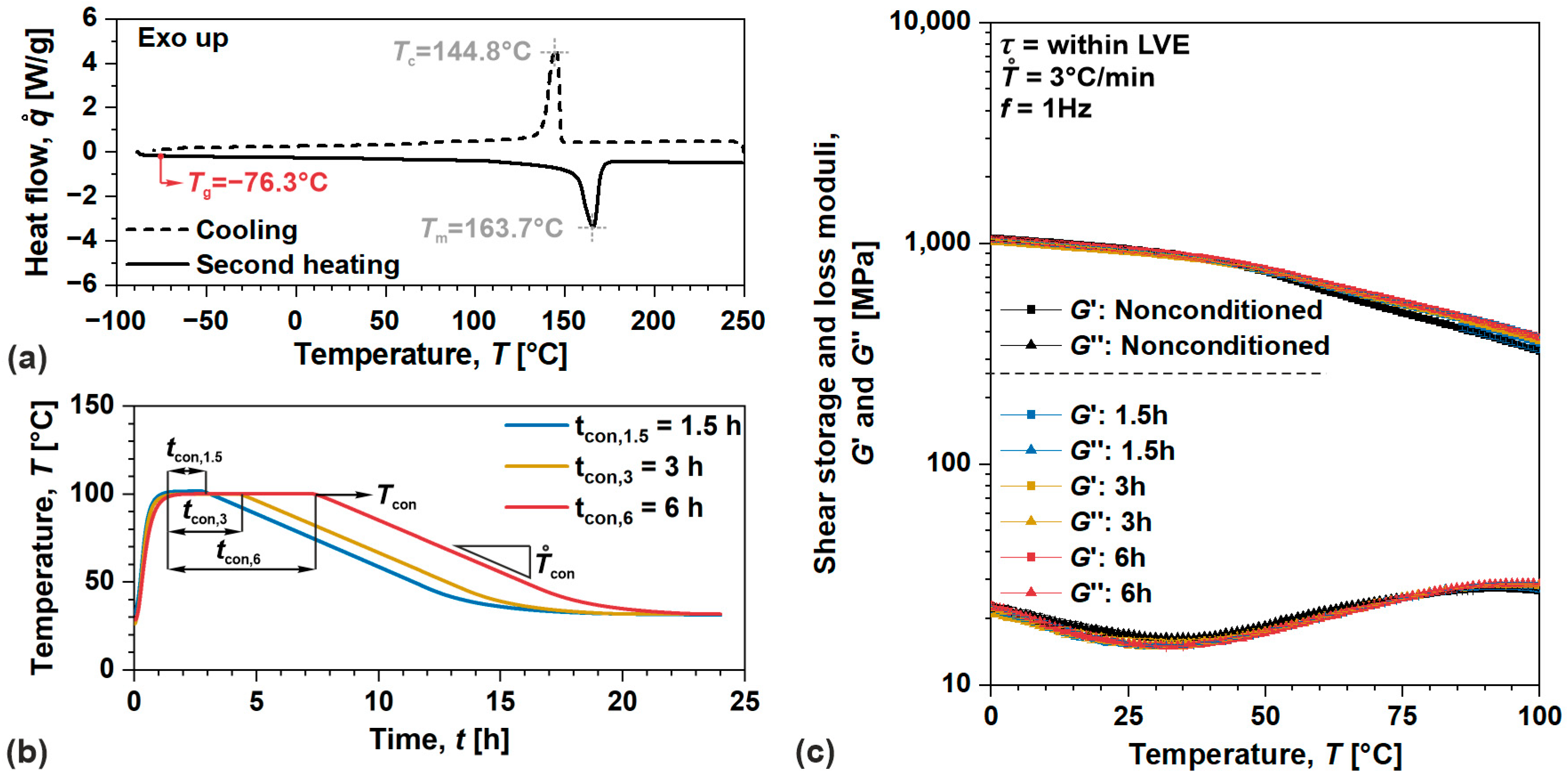
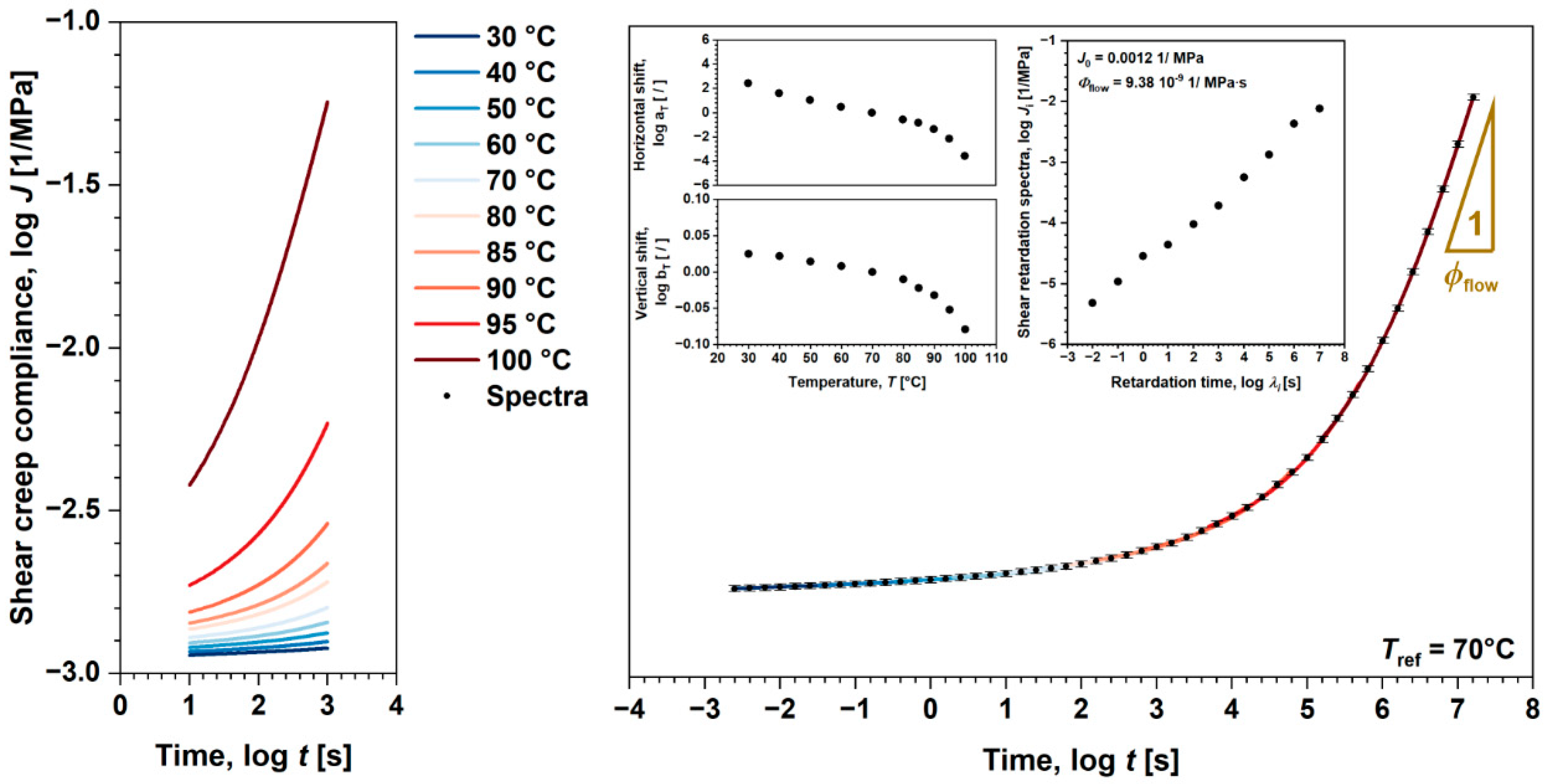
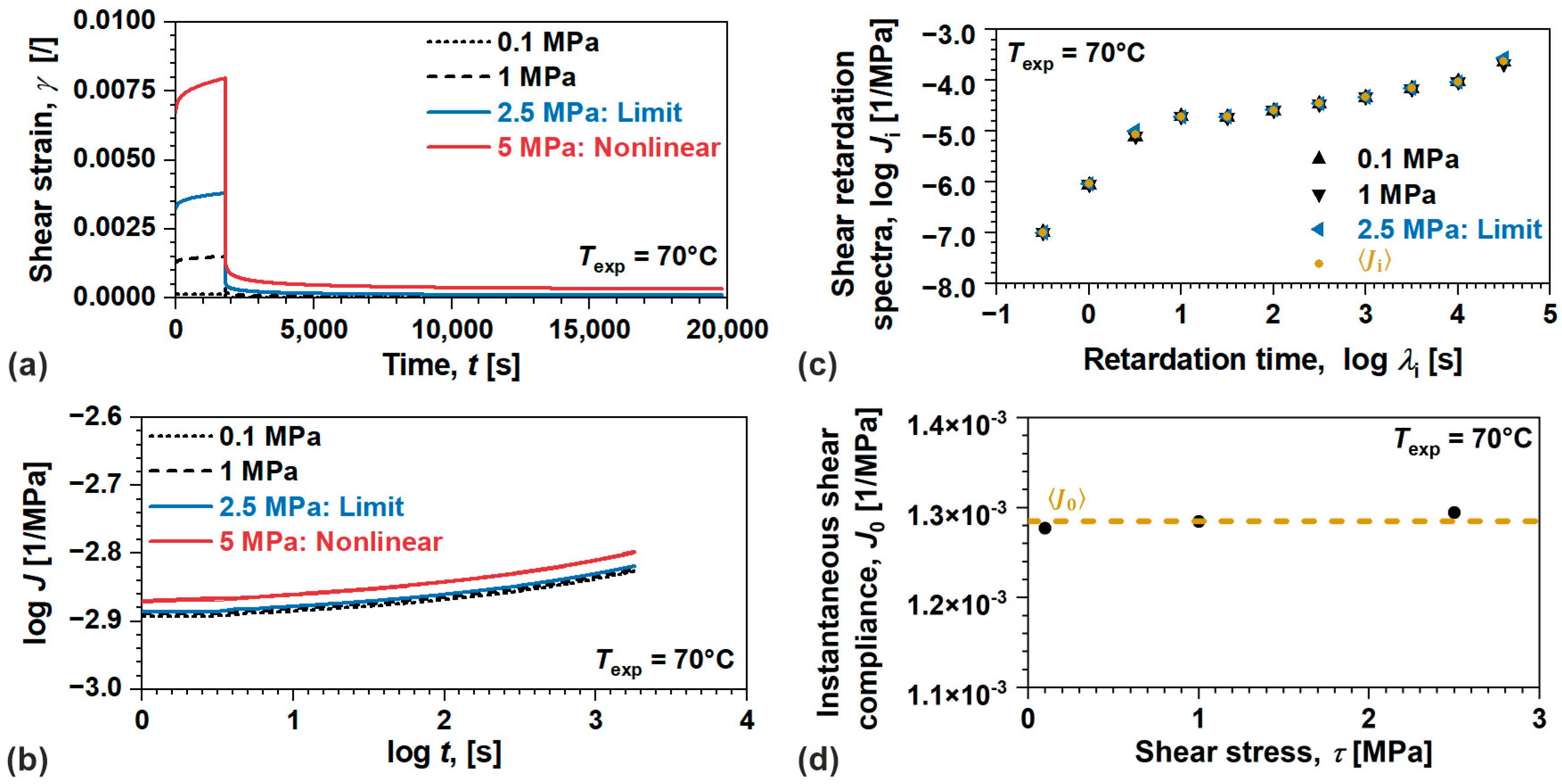
| Process | Process | ABS | POM |
|---|---|---|---|
| Drying | Drying time | ||
| Drying temperature | |||
| Melt mixing | Mixing time | ||
| Mixing temperature | |||
| Screw speed (co-rotating) | |||
| Injection molding | Barrel temperature | ||
| Mold temperature | |||
| Injection pressure | |||
| Injection time | |||
| Holding pressure | |||
| Holding time |
| Amorphous ABS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Linear viscoelastic behavior | ||||||||||
| Nonlinear viscoelastic behavior | ||||||||||
| Viscoplastic behavior | ||||||||||
| Semi-crystalline POM | ||||||||||
| Linear viscoelastic behavior | ||||||||||
| / | ||||||||||
| Nonlinear viscoelastic behavior | ||||||||||
| Viscoplastic behavior | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oseli, A.; Šobak, M.; Slemenik Perše, L. Experimental and Analytical Framework for Predicting Nonlinear Viscoelastic–Viscoplastic Behavior of Polymers. Polymers 2025, 17, 3095. https://doi.org/10.3390/polym17233095
Oseli A, Šobak M, Slemenik Perše L. Experimental and Analytical Framework for Predicting Nonlinear Viscoelastic–Viscoplastic Behavior of Polymers. Polymers. 2025; 17(23):3095. https://doi.org/10.3390/polym17233095
Chicago/Turabian StyleOseli, Alen, Matic Šobak, and Lidija Slemenik Perše. 2025. "Experimental and Analytical Framework for Predicting Nonlinear Viscoelastic–Viscoplastic Behavior of Polymers" Polymers 17, no. 23: 3095. https://doi.org/10.3390/polym17233095
APA StyleOseli, A., Šobak, M., & Slemenik Perše, L. (2025). Experimental and Analytical Framework for Predicting Nonlinear Viscoelastic–Viscoplastic Behavior of Polymers. Polymers, 17(23), 3095. https://doi.org/10.3390/polym17233095







