Development of a Non-Spherical Polymeric Particles Calibration Procedure for Numerical Simulations Based on the Discrete Element Method
Abstract
1. Introduction
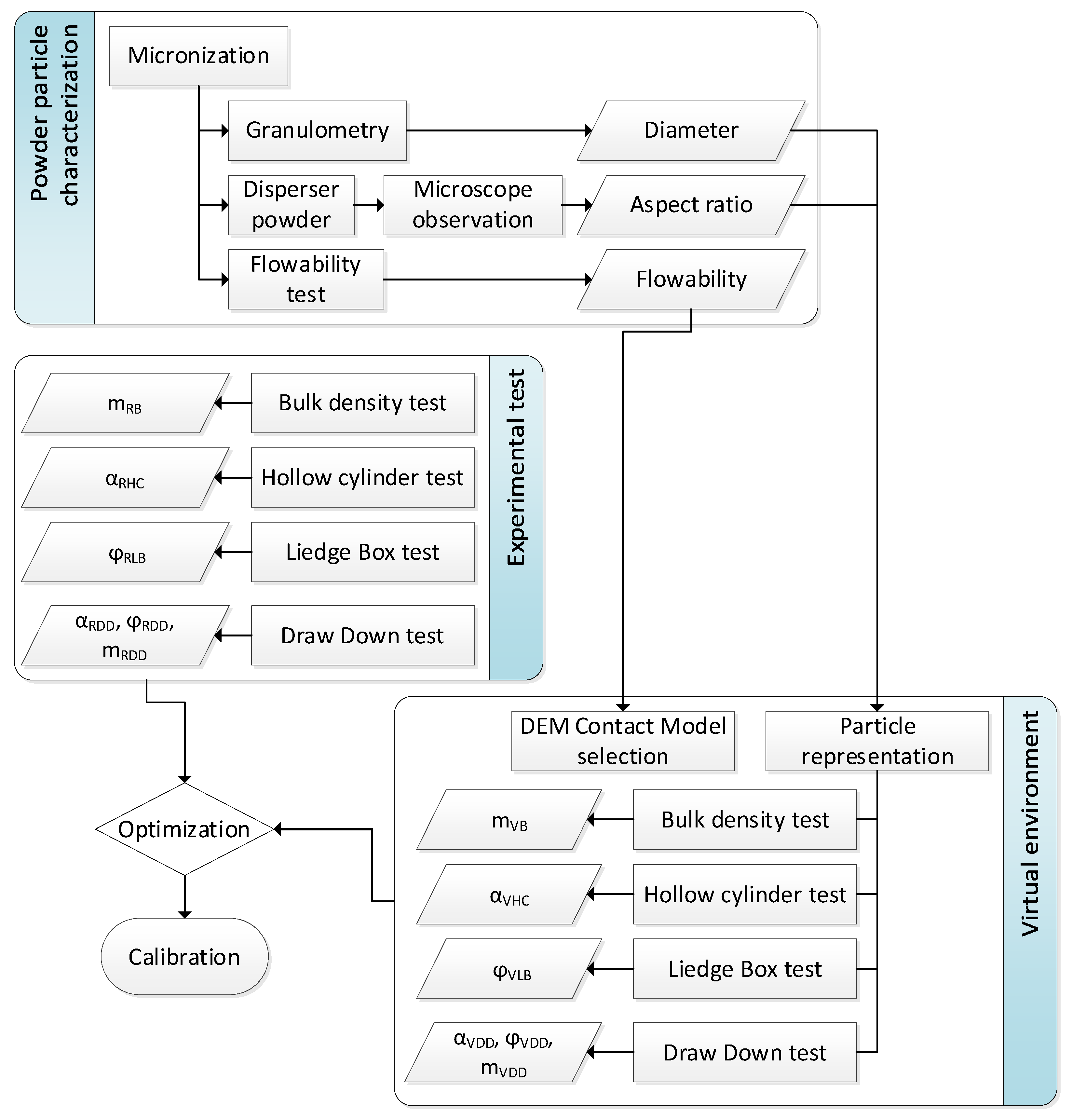
2. Materials and Methods
2.1. Materials
2.2. Experimentation
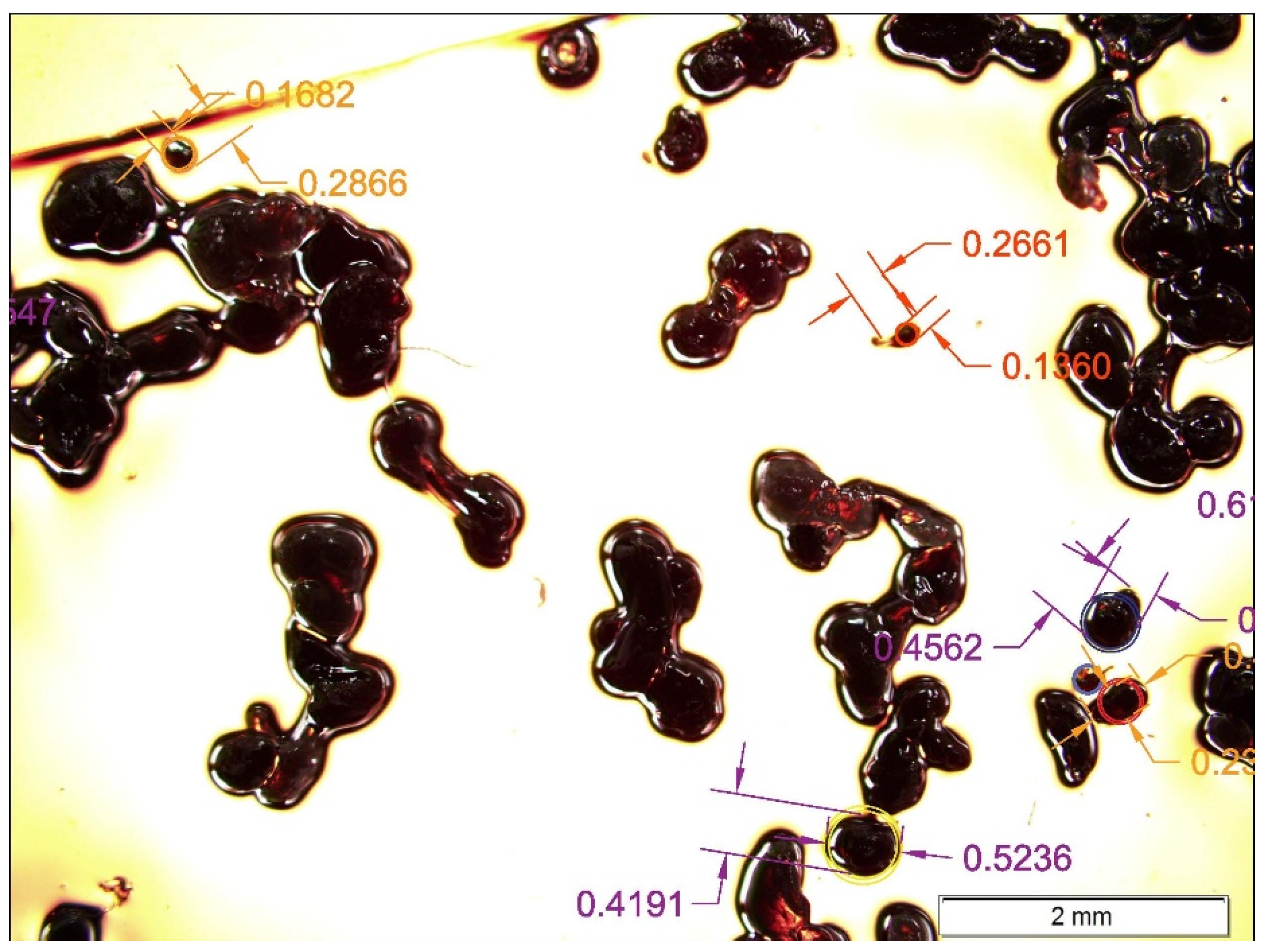
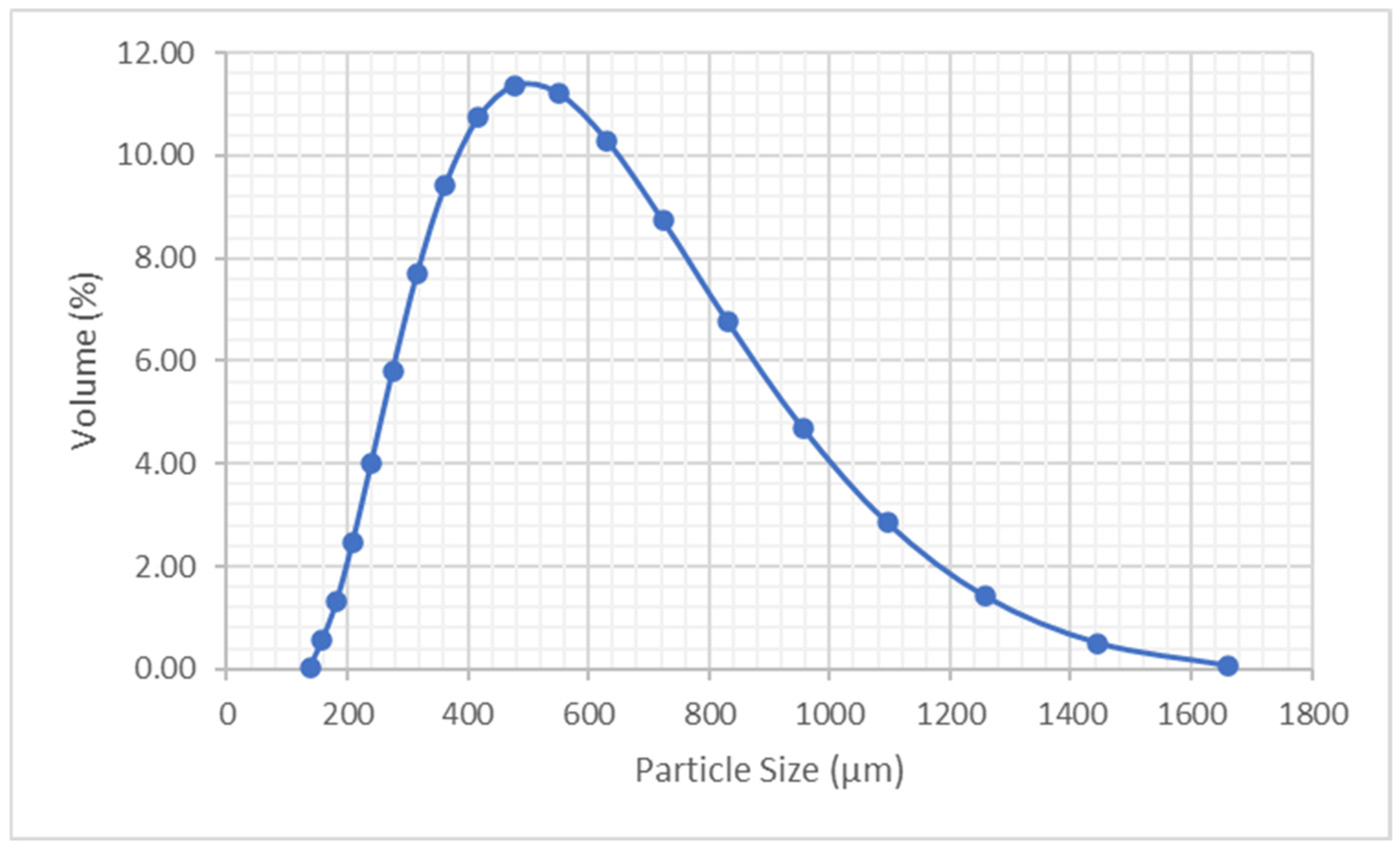
2.2.1. Powder Preparation and Shape Characterization
2.2.2. Determination of the Bulk Density, Tap Density, and Flowability
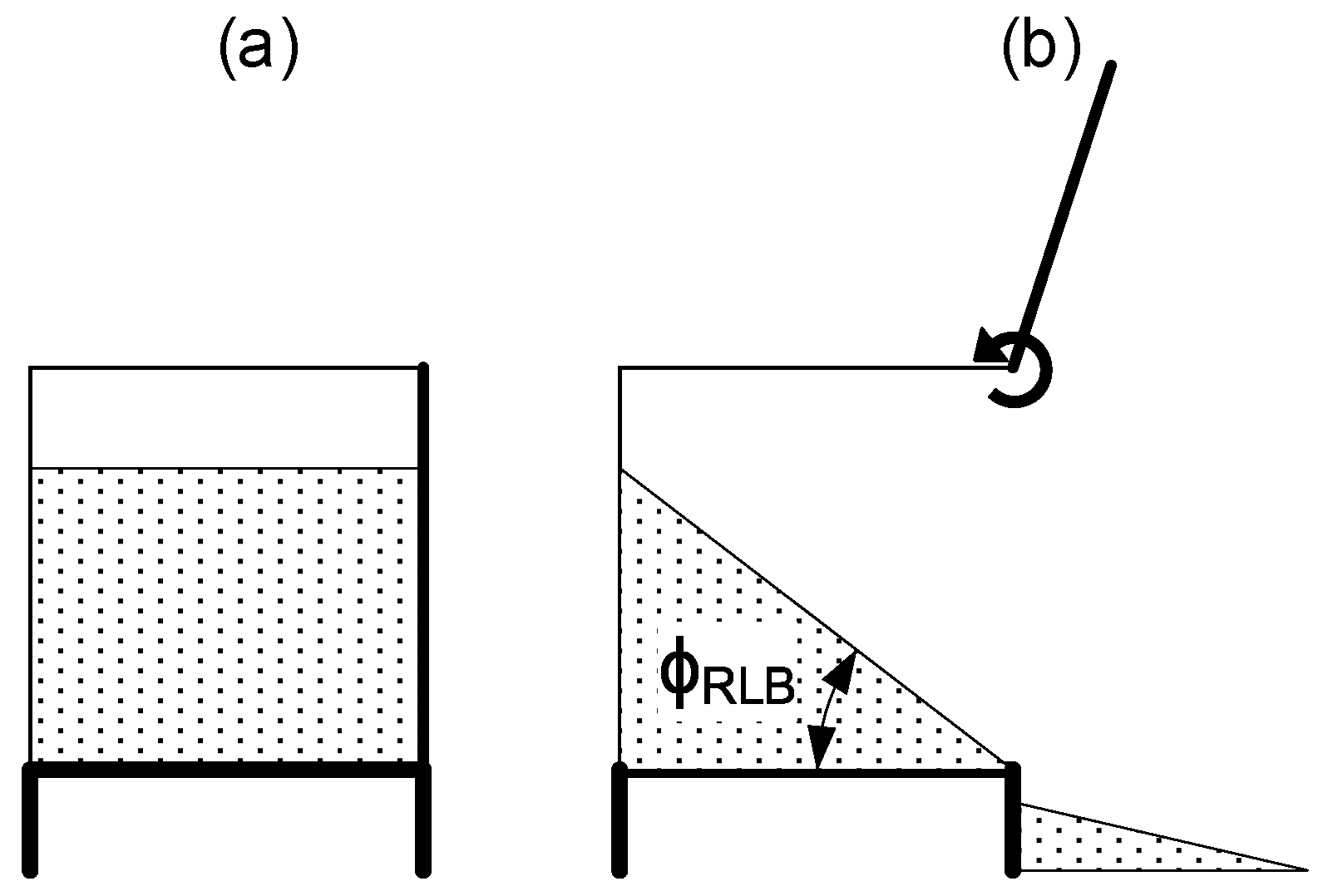
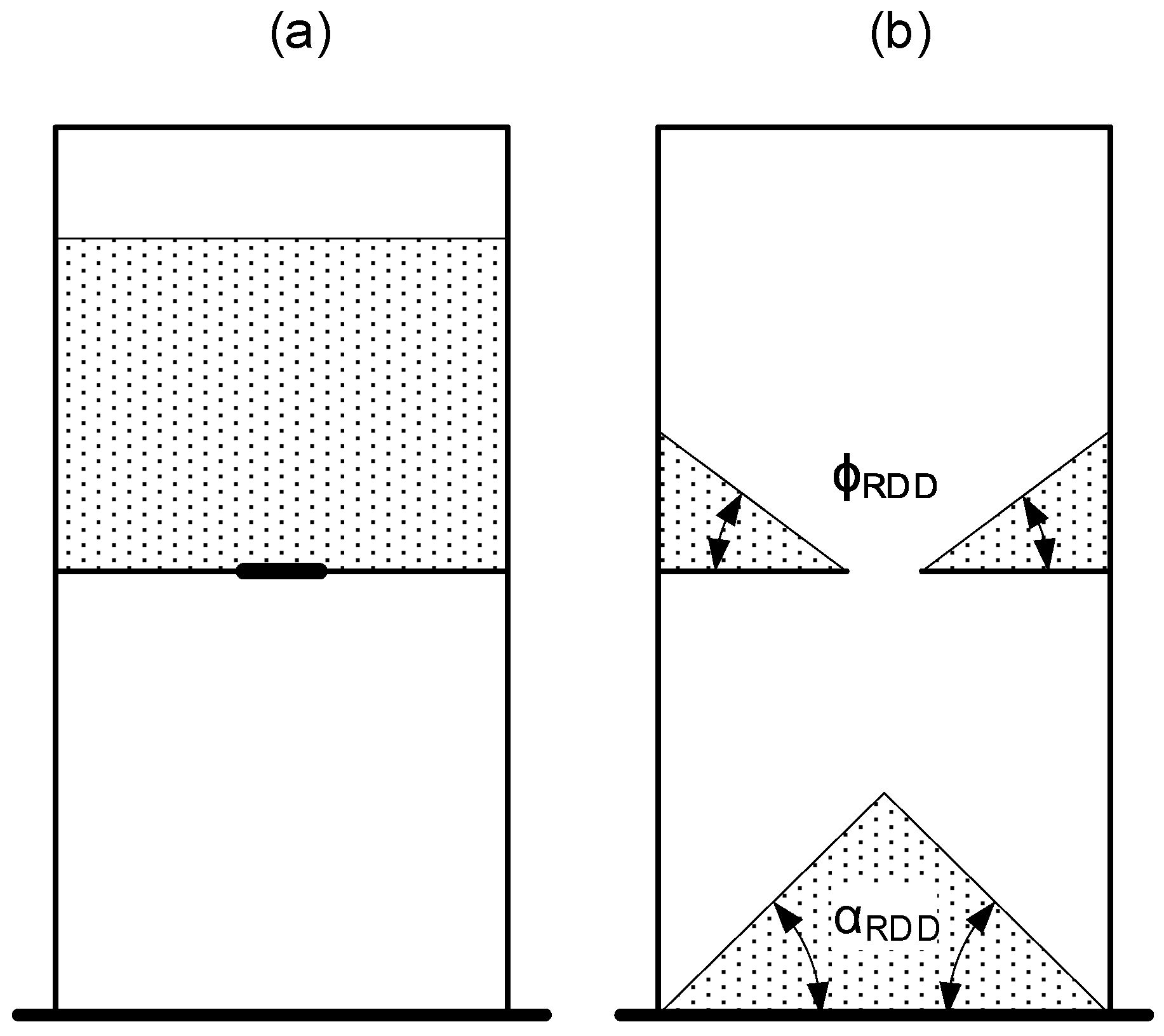
2.2.3. Experimental Reference Tests
Bulk Density Test
Hollow Cylinder Test
Liedge Box Test
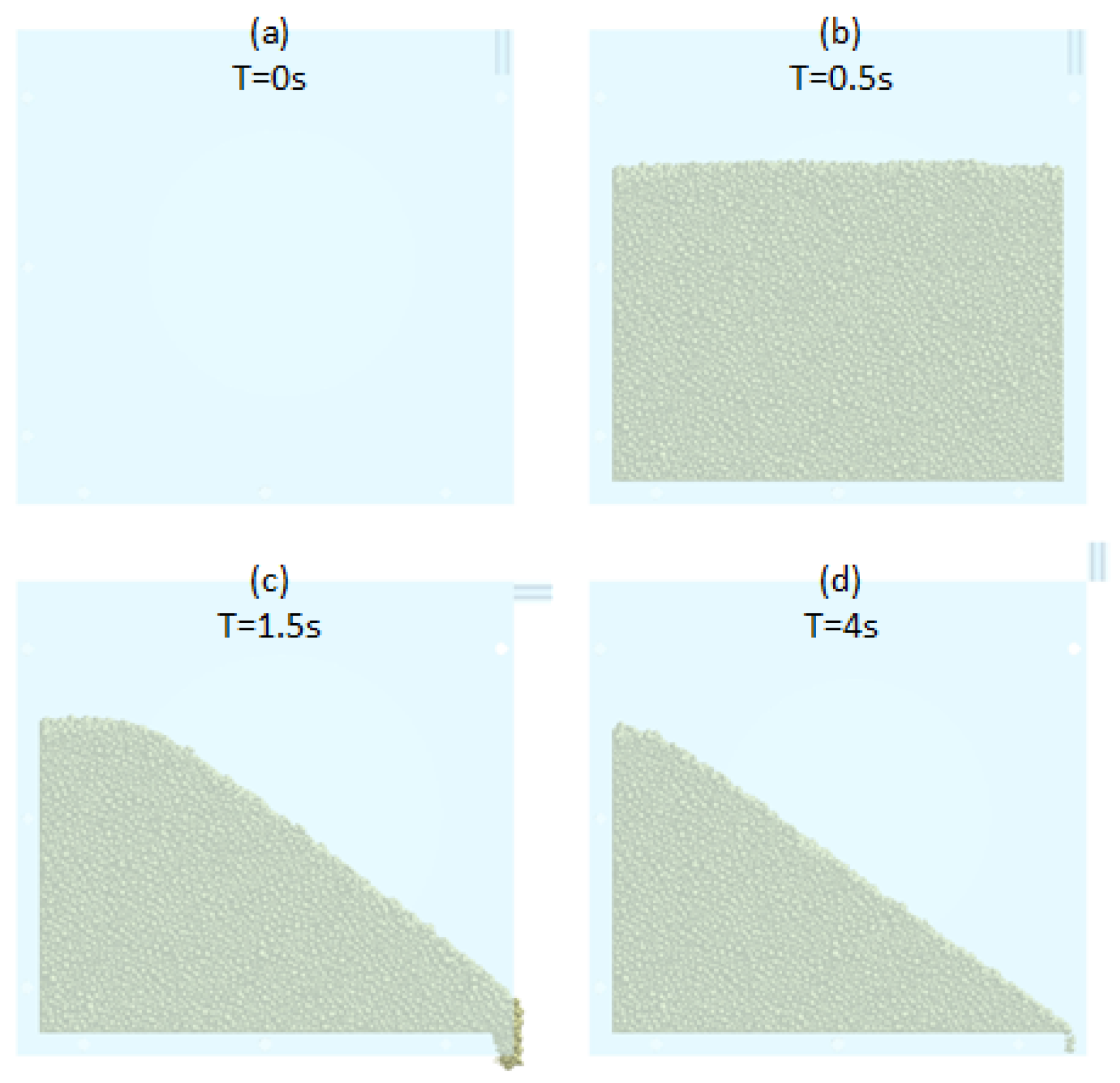
Draw Down Test
2.3. Virtual Environment
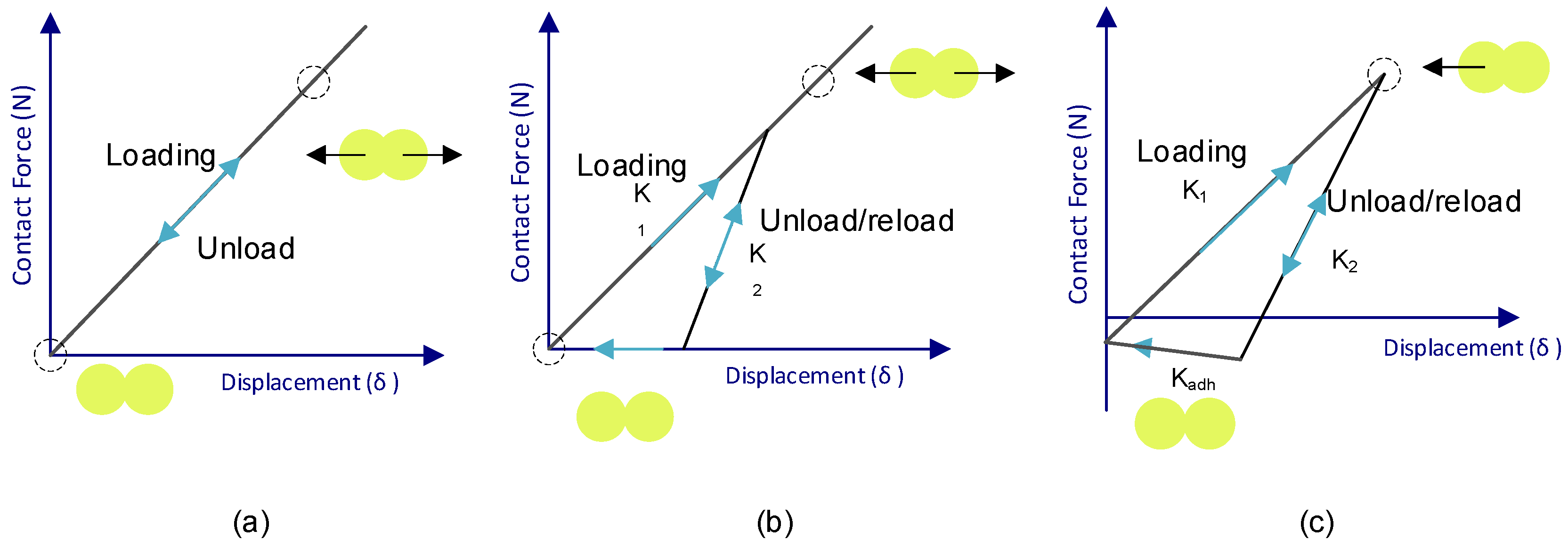
2.3.1. Contact Model DEM Parameters
2.3.2. Particle Shape Design
2.3.3. Test Simulations
Bulk Density Simulation
Hollow Cylinder Simulation
Ledge Box Simulation
Draw Down Simulation
2.4. Angle Measurement Process
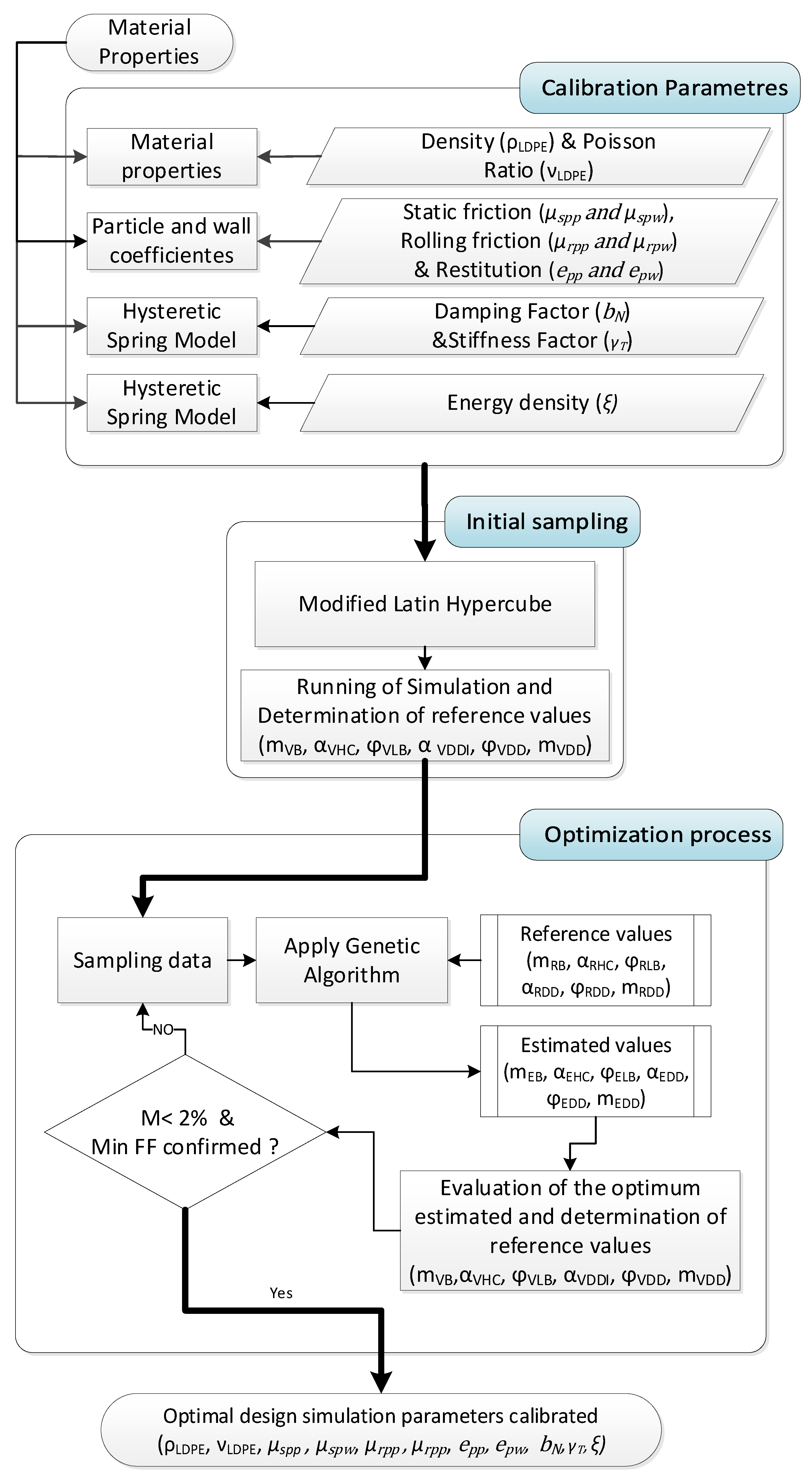
2.5. Optimization with Genetic Algorithms
2.6. Calibration Process
3. Results and Discussion
3.1. Real Environment
3.1.1. Powder Preparation and Shape Characterization
3.1.2. Determination of the Bulk Density, Tap Density, and Flowability
3.1.3. Experimental Reference Tests
3.2. Virtual Environment
3.2.1. Particle Shape Design
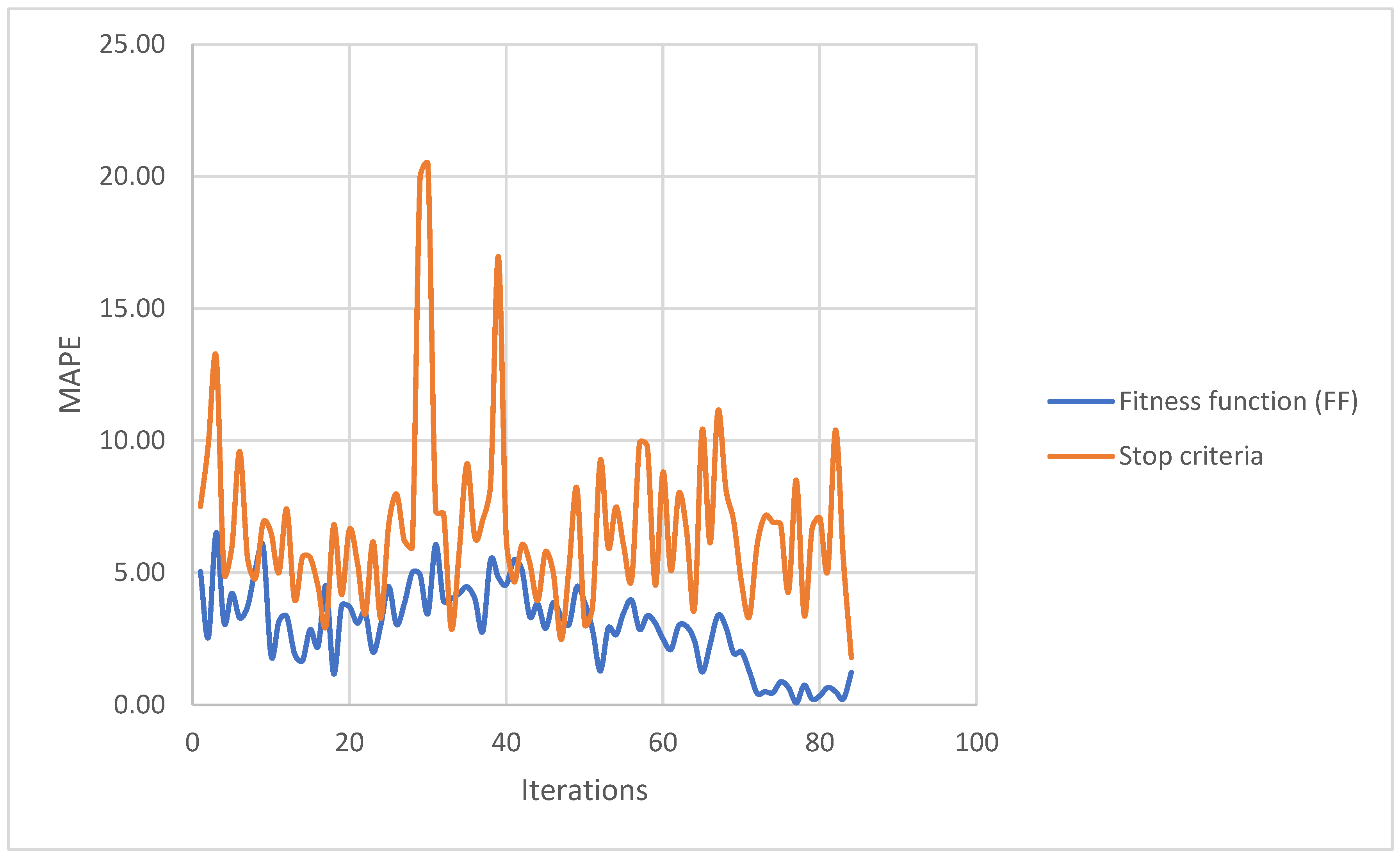
3.2.2. Calibration Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- ISO/ASTM 52900:2021; Additive Manufacturing. General Principles. Fundamentals and Vocabulary. ISO International Organization for Standardization: Geneva, Switzerland, 2021.
- Horabik, J.; Molenda, M. Parameters and Contact Models for DEM Simulations of Agricultural Granular Materials: A Review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Thakur, S.C.; Ooi, J.Y.; Ahmadian, H. Scaling of Discrete Element Model Parameters for Cohesionless and Cohesive Solid. Powder Technol. 2016, 293, 130–137. [Google Scholar] [CrossRef]
- Roessler, T.; Katterfeld, A. Scaling of the Angle of Repose Test and Its Influence on the Calibration of DEM Parameters Using Upscaled Particles. Powder Technol. 2018, 330, 58–66. [Google Scholar] [CrossRef]
- Remy, B.; Glasser, B.J.; Khinast, J.G. The Effect of Mixer Properties and Fill Level on Granular Flow in a Bladed Mixer. AIChE J. 2010, 56, 336–353. [Google Scholar] [CrossRef]
- Janda, A.; Ooi, J.Y. DEM Modeling of Cone Penetration and Unconfined Compression in Cohesive Solids. Powder Technol. 2016, 293, 60–68. [Google Scholar] [CrossRef]
- Coetzee, C.J. Particle Upscaling: Calibration and Validation of the Discrete Element Method. Powder Technol. 2019, 344, 487–503. [Google Scholar] [CrossRef]
- Lommen, S.; Schott, D.; Lodewijks, G. DEM Speedup: Stiffness Effects on Behavior of Bulk Material. Particuology 2014, 12, 107–112. [Google Scholar] [CrossRef]
- Yeom, S.B.; Choi, D.H. Scale-Up Strategy in Quality by Design Approach for Pharmaceutical Blending Process with Discrete Element Method Simulation. Pharmaceutics 2019, 11, 264. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, A.; Larsson, S.; Wersäll, C. Scaling Granular Material with Polygonal Particles in Discrete Element Modeling. Particuology 2023, 75, 151–164. [Google Scholar] [CrossRef]
- Grima, A.P.; Wypych, P.W. Development and Validation of Calibration Methods for Discrete Element Modelling. Granul. Matter 2011, 13, 127–132. [Google Scholar] [CrossRef]
- Hanley, K.J.; O’Sullivan, C.; Oliveira, J.C.; Cronin, K.; Byrne, E.P. Application of Taguchi Methods to DEM Calibration of Bonded Agglomerates. Powder Technol. 2011, 210, 230–240. [Google Scholar] [CrossRef]
- El-Kassem, B.; Salloum, N.; Brinz, T.; Heider, Y.; Markert, B. A Multivariate Regression Parametric Study on DEM Input Parameters of Free-Flowing and Cohesive Powders with Experimental Data-Based Validation. Comp. Part. Mech. 2021, 8, 87–111. [Google Scholar] [CrossRef]
- Kassem, B.E.; Salloum, N.; Brinz, T.; Heider, Y.; Markert, B. A Semi-Automated DEM Parameter Calibration Technique of Powders Based on Different Bulk Responses Extracted from Auger Dosing Experiments. KONA Powder Part. J. 2021, 38, 235–250. [Google Scholar] [CrossRef]
- Bhalode, P.; Ierapetritou, M. Discrete Element Modeling for Continuous Powder Feeding Operation: Calibration and System Analysis. Int. J. Pharm. 2020, 585, 119427. [Google Scholar] [CrossRef]
- Orefice, L.; Khinast, J.G. A Novel Framework for a Rational, Fully-Automatised Calibration Routine for DEM Models of Cohesive Powders. Powder Technol. 2020, 361, 687–703. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, Z.; Chen, J.; Lv, X.; Xie, N. Calibration of DEM Models for Irregular Particles Based on Experimental Design Method and Bulk Experiments. Powder Technol. 2018, 332, 210–223. [Google Scholar] [CrossRef]
- Mohajeri, M.J.; Do, H.Q.; Schott, D.L. DEM Calibration of Cohesive Material in the Ring Shear Test by Applying a Genetic Algorithm Framework. Adv. Powder Technol. 2020, 31, 1838–1850. [Google Scholar] [CrossRef]
- Do, H.Q.; Aragón, A.M.; Schott, D.L. A Calibration Framework for Discrete Element Model Parameters Using Genetic Algorithms. Adv. Powder Technol. 2018, 29, 1393–1403. [Google Scholar] [CrossRef]
- Rackl, M.; Hanley, K.J. A Methodical Calibration Procedure for Discrete Element Models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef]
- Plastics—The Facts 2022 • Plastics Europe; Plastics Europe: Brussels, Belgium, 2022.
- ISO 3953:2011; Metallic Powders. Determination of Tap Density. UNE European Commitee for Standardization: Brussels, Belgium, 2011.
- Gorle, A.P.; Chopade, S.S. Liquisolid Technology: Preparation, Characterization and Applications. J. Drug Deliv. Ther. 2020, 10, 295–307. [Google Scholar] [CrossRef]
- Roessler, T.; Katterfeld, A. DEM Parameter Calibration of Cohesive Bulk Materials Using a Simple Angle of Repose Test. Particuology 2019, 45, 105–115. [Google Scholar] [CrossRef]
- Katterfeld, A.; Donohue, T.; Ilic, D. Application of the Discrete Element Method in Mechanical Conveying of Bulk Materials. In Proceedings of the 7th International Conference for Conveying and Handling of Particulate Solids, Friedrichshafen, Germany, 10–13 September 2012. [Google Scholar]
- Katterfeld, A.; Coetzee, C.; Donohue, T.; Fottner, J.; Grima, A.; Gomez, A.R.; Ilic, D.; Kačianauskas, R.; Necas, J.; Schott, D.; et al. Calibration of DEM Parameters for Cohesionless Bulk Materials Under Rapid Flow Conditions and Low Consolidation; Delft University of Technology: Delft, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Mohajeri, M.J.; Van Den Bos, M.J.; Van Rhee, C.; Schott, D.L. Bulk Properties Variability and Interdependency Determination for Cohesive Iron Ore. Powder Technol. 2020, 367, 539–557. [Google Scholar] [CrossRef]
- Mohajeri, M.J.; Van Rhee, C.; Schott, D.L. Replicating Cohesive and Stress-History-Dependent Behavior of Bulk Solids: Feasibility and Definiteness in DEM Calibration Procedure. Adv. Powder Technol. 2021, 32, 1532–1548. [Google Scholar] [CrossRef]
- Lajeunesse, E.; Mangeney-Castelnau, A.; Vilotte, J.P. Spreading of a Granular Mass on a Horizontal Plane. Phys. Fluids 2004, 16, 2371–2381. [Google Scholar] [CrossRef]
- Qin, R.; Fang, H.; Liu, F.; Xing, D.; Yang, J.; Lv, N.; Chen, J.; Li, J. Study on Physical and Contact Parameters of Limestone by DEM. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 052110. [Google Scholar] [CrossRef]
- Li, T.; Peng, Y.; Zhu, Z.; Yu, Z.; Yin, Z. Effect of the Lifting Velocity and Container Shape on Angle of Repose of Iron Ore Particles. Adv. Mater. Sci. Eng. 2017, 2017, 3405432. [Google Scholar] [CrossRef]
- Cao, X.; Li, Z.; Li, H.; Wang, X.; Ma, X. Measurement and Calibration of the Parameters for Discrete Element Method Modeling of Rapeseed. Processes 2021, 9, 605. [Google Scholar] [CrossRef]
- Derakhshani, S.M.; Schott, D.L.; Lodewijks, G. Micro–Macro Properties of Quartz Sand: Experimental Investigation and DEM Simulation. Powder Technol. 2015, 269, 127–138. [Google Scholar] [CrossRef]
- Coetzee, C. Calibration of the Discrete Element Method: Strategies for Spherical and Non-Spherical Particles. Powder Technol. 2020, 364, 851–878. [Google Scholar] [CrossRef]
- Coetzee, C.J.; Scheffler, O.C. Review: The Calibration of DEM Parameters for the Bulk Modelling of Cohesive Materials. Processes 2022, 11, 5. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Huang, Y.; Ji, J. An Efficient Method for Determining DEM Parameters of a Loose Cohesive Soil Modelled Using Hysteretic Spring and Linear Cohesion Contact Models. Biosyst. Eng. 2022, 215, 283–294. [Google Scholar] [CrossRef]
- Ucgul, M.; Saunders, C.; Fielke, J.M. Particle and Geometry Scaling of the Hysteretic Spring/Linear Cohesion Contact Model for Discrete Element Modelling of Soil-Tool Simulation. In Proceedings of the 2017 ASABE Annual International Meeting, Spokane, WA, USA, 16–19 July 2017; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2017. [Google Scholar]
- Lupo, M.; Barletta, D.; Sofia, D.; Poletto, M. Calibration of DEM for Cohesive Particles in the SLS Powder Spreading Process. Processes 2021, 9, 1715. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.; Zhang, N.; Zhao, H.; Liu, L.; Huang, K.; Chen, X. Local Scour Mechanism of Offshore Wind Power Pile Foundation Based on CFD-DEM. JMSE 2022, 10, 1724. [Google Scholar] [CrossRef]
- Walton, O.R.; Braun, R.L. Viscosity, Granular-temperature, and Stress Calculations for Shearing Assemblies of Inelastic, Frictional Disks. J. Rheol. 1986, 30, 949–980. [Google Scholar] [CrossRef]
- Walton, O.R.; Braun, R.L. Stress Calculations for Assemblies of Inelastic Speres in Uniform Shear. Acta Mech. 1986, 63, 73–86. [Google Scholar] [CrossRef]
- Pasha, M.; Dogbe, S.; Hare, C.; Hassanpour, A.; Ghadiri, M. A Linear Model of Elasto-Plastic and Adhesive Contact Deformation. Granul. Matter 2014, 16, 151–162. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-Dimensional Discrete Element Modelling of Tillage: Determination of a Suitable Contact Model and Parameters for a Cohesionless Soil. Biosyst. Eng. 2014, 121, 105–117. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-Dimensional Discrete Element Modelling (DEM) of Tillage: Accounting for Soil Cohesion and Adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Nalawade, R.D.; Singh, K.P.; Roul, A.K.; Patel, A. Parametric Study and Calibration of Hysteretic Spring and Linear Cohesion Contact Models for Cohesive Soils Using Definitive Screening Design. Comp. Part. Mech. 2023, 10, 707–728. [Google Scholar] [CrossRef]
- Moncada, M.; Betancourt, F.; Rodríguez, C.G.; Toledo, P. Effect of Particle Shape on Parameter Calibration for a Discrete Element Model for Mining Applications. Minerals 2023, 13, 40. [Google Scholar] [CrossRef]
- Marín Pérez, J.; Comlekci, T.; Gorash, Y.; MacKenzie, D. Calibration of the DEM Sliding Friction and Rolling Friction Parameters of a Cohesionless Bulk Material. Particuology 2024, 92, 126–139. [Google Scholar] [CrossRef]
- Bharadwaj, R.; Ketterhagen, W.R.; Hancock, B.C. Discrete Element Simulation Study of a Freeman Powder Rheometer. Chem. Eng. Sci. 2010, 65, 5747–5756. [Google Scholar] [CrossRef]
- He, P.; Fan, Y.; Pan, B.; Zhu, Y.; Liu, J.; Zhu, D. Calibration and Verification of Dynamic Particle Flow Parameters by the Back-Propagation Neural Network Based on the Genetic Algorithm: Recycled Polyurethane Powder. Materials 2019, 12, 3350. [Google Scholar] [CrossRef]
- Coley, D.A. An Introduction to Genetic Algorithms for Scientists and Engineers; World Scientific: Singapore, 1999; ISBN 978-981-02-3602-1. [Google Scholar]
- Paz, R.; Pei, E.; Monzón, M.; Ortega, F.; Suárez, L. Lightweight Parametric Design Optimization for 4D Printed Parts. ICA 2017, 24, 225–240. [Google Scholar] [CrossRef]
- Paz, R.; Monzón, M.D. Optimization Methodology for the Material Assignation in Bioprinted Scaffolds to Achieve the Desired Stiffness over Time. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3248. [Google Scholar] [CrossRef]
- Ulaganathan, S.; Couckuyt, I.; Deschrijver, D.; Laermans, E.; Dhaene, T. A Matlab Toolbox for Kriging Metamodelling. Procedia Comput. Sci. 2015, 51, 2708–2713. [Google Scholar] [CrossRef]
- Wen, J. KrigingToolbox; The MathWorks: Natick, MA, USA, 2025. [Google Scholar]
- Radeke, C.A.; Glasser, B.J.; Khinast, J.G. Large-Scale Powder Mixer Simulations Using Massively Parallel GPUarchitectures. Chem. Eng. Sci. 2010, 65, 6435–6442. [Google Scholar] [CrossRef]
- Barrasso, D.; Ramachandran, R. Multi-Scale Modeling of Granulation Processes: Bi-Directional Coupling of PBM with DEM via Collision Frequencies. Chem. Eng. Res. Des. 2015, 93, 304–317. [Google Scholar] [CrossRef]
- Remy, B.; Khinast, J.G.; Glasser, B.J. Discrete Element Simulation of Free Flowing Grains in a Four-Bladed Mixer. AIChE J. 2009, 55, 2035–2048. [Google Scholar] [CrossRef]
- Sen, M.; Karkala, S.; Panikar, S.; Lyngberg, O.; Johnson, M.; Marchut, A.; Schäfer, E.; Ramachandran, R. Analyzing the Mixing Dynamics of an Industrial Batch Bin Blender via Discrete Element Modeling Method. Processes 2017, 5, 22. [Google Scholar] [CrossRef]
- Roessler, T.; Richter, C.; Katterfeld, A.; Will, F. Development of a Standard Calibration Procedure for the DEM Parameters of Cohesionless Bulk Materials—Part I: Solving the Problem of Ambiguous Parameter Combinations. Powder Technol. 2019, 343, 803–812. [Google Scholar] [CrossRef]
- Richter, C.; Rößler, T.; Kunze, G.; Katterfeld, A.; Will, F. Development of a Standard Calibration Procedure for the DEM Parameters of Cohesionless Bulk Materials—Part II: Efficient Optimization-Based Calibration. Powder Technol. 2020, 360, 967–976. [Google Scholar] [CrossRef]
- Hoshishima, C.; Ohsaki, S.; Nakamura, H.; Watano, S. Parameter Calibration of Discrete Element Method Modelling for Cohesive and Non-Spherical Particles of Powder. Powder Technol. 2021, 386, 199–208. [Google Scholar] [CrossRef]
- Huynh, T.Q.; Nguyen, T.T.; Indraratna, B. Evaluating Cohesive Models in Discrete Element Simulation through Drawdown Test with New Assessment Perspectives. Powder Technol. 2025, 452, 120542. [Google Scholar] [CrossRef]
- Gao, W.; Feng, Y.T. A Coupled Isogeometric/Super-Ellipsoid Discrete Element Method for the Irregular Particle-Structure Contact Interaction Based on Support Point Approach. Comput. Mech. 2025. [Google Scholar] [CrossRef]
- Gao, W.; Feng, Y.T.; Wang, C. A Coupled Isogeometric/Multi-Sphere Discrete Element Approach for the Contact Interaction between Irregular Particles and Structures. Powder Technol. 2023, 430, 118971. [Google Scholar] [CrossRef]











| Flow Character | Hausner Ratio | CI% |
|---|---|---|
| Excellent/very free flow | 1.00–1.11 | ≤10 |
| Good/free flow | 1.12–1.18 | 11-15 |
| Fair | 1.19–1.25 | 16–20 |
| Passable | 1.26–1.34 | 21–25 |
| Poor/cohesive | 1.35–1.45 | 26–31 |
| Very Poor/very cohesive | 1.46–1.59 | 32–37 |
| Very, very poor/Approx. non-flow | >1.6 | >38 |
| Normal Force | |
| Tangential Force | |
| Normal and tangential damping force | |
| Normal and Tangential Stiffness | |
| Equivalent Young modulus | |
| Shear modulus | |
| Equivalent Radio | |
| Equivalent Mass | |
| Rolling friction |
| Normal Force | |
| Tangential Force | |
| Loading Stiffness | |
| Unload Stiffness | |
| Material Yield Strength | |
| Overlap | |
| Normal damping force | |
| Tangential damping force | |
| Moment effect | |
| Rotation moment | |
| Resultant moment |
| Units | Min | Max | Reference | ||
|---|---|---|---|---|---|
| LDPE | νLDPE | Dimensionless | 0.2 | 0.5 | Altair Edem software |
| ρLDPE | kg/m3 | 450 | 1400 | Altair Edem software | |
| G | Pa | 1.00 × 107 | Altair Edem software | ||
| Acrilic | νAcrilic | Dimensionless | 0.4 | [49] | |
| ρAcrilic | kg/m3 | 1385 | [49] | ||
| G | Pa | 1.60 × 1010 | [49] | ||
| Particle-Particle | epp | Dimensionless | 0.1 | 0.78 | [55,56] |
| μspp | Dimensionless | 0.1 | 0.95 | [57,58] | |
| μrpp | Dimensionless | 0 | 0.25 | [20,34] | |
| Particle-Wall | Dimensionless | 0.1 | 0.78 | [55,56] | |
| μspw | Dimensionless | 0.1 | 0.95 | [57,58] | |
| μrpw | Dimensionless | 0 | 0.2 | [13] | |
| Particle-Particle HSCM | bN | Dimensionless | 0 | 0.1 | Altair Edem software |
| γT | Dimensionless | 0.67 | 1 | [40] | |
| Particle-Particle LCCM | ξ | J/m3 | 1 | 8000 | [36] |
| Group of Particles | Average Aspect Ratio | Truncated Group Aspect Ratio |
|---|---|---|
| 1 | 1.75 | 1.64 |
| 2 | 1.70 | |
| 3 | 1.42 | |
| 4 | 1.59 | |
| 5 | 1.54 | |
| 6 | 1.82 | |
| 7 | 1.25 | 1.25 |
| 8 | 1.74 | 1.74 |
| 9 | 1.46 | 1.46 |
| 10 | 1.32 | 1.32 |
| 11 | 1.20 | 1.20 |
| 12 | 1.30 | 1.30 |
| 13 | 1.43 | 1.43 |
| 14 | 1.63 | 1.63 |
| 15 | 1.08 | 1.08 |
| 16 | 1.48 | 1.48 |
| 17 | 1.48 | 1.48 |
| 18 | 1.48 | 1.48 |
| 19 | 1.48 | 1.48 |
| Vb (cm3) | Vt (cm3) | ρb (g/cm3) | ρt (g/cm3) | Ρb (kg/cm3) | ρt (kg/cm3) | H | Ci% | |
|---|---|---|---|---|---|---|---|---|
| 1 | 54.5 | 44.5 | 0.367 | 0.449 | 367 | 449 | 1.22 | 18 |
| 2 | 52.5 | 47 | 0.381 | 0.426 | 381 | 426 | 1.12 | 10 |
| 3 | 56 | 46.75 | 0.357 | 0.428 | 357 | 428 | 1.20 | 17 |
| 4 | 55.5 | 47 | 0.360 | 0.426 | 360 | 426 | 1.18 | 15 |
| 5 | 55 | 47 | 0.364 | 0.426 | 364 | 426 | 1.17 | 15 |
| 6 | 57 | 47.5 | 0.351 | 0.421 | 351 | 421 | 1.20 | 17 |
| 7 | 54 | 47 | 0.370 | 0.426 | 370 | 426 | 1.15 | 13 |
| 8 | 52.5 | 47 | 0.381 | 0.426 | 381 | 426 | 1.12 | 10 |
| Average (standard deviation) | 54.6 (1.60) | 46.71 (0.92) | 0.366 (0.01) | 0.428 (0.01) | 366 (10.76) | 428 (8.77) | 1.17 (0.04) | 14 (2.90) |
| Real Measures | ||||||
|---|---|---|---|---|---|---|
| Test | Variable | Measure | It1 | It2 | It3 | Total Average |
| HC | αRHC (o) | Left | 30.8 | 38.6 | 32.3 | 35.6 |
| Right | 35.8 | 31.8 | 44 | |||
| Average iteration | 33.3 | 35.2 | 38.15 | |||
| LB | ϕRLB (o) | Unique | 50 | 66.3 | 65.7 | 60.7 |
| DD | ϕRDD (o) | Left | 45.2 | 56.1 | 55.3 | 55.4 |
| Right | 52 | 53.3 | 70.3 | |||
| Average iteration | 48.6 | 54.7 | 62.8 | |||
| αRDD (o) | Left | 43.4 | 34.9 | 40.7 | 38.9 | |
| Right | 39.3 | 38.8 | 36.5 | |||
| Average iteration | 41.35 | 36.85 | 38.6 | |||
| mRDD (gr) | Direct | 3.3 | 3 | 3.7 | 3.3 | |
| Bulk density | mRB (gr) | Direct | 60.14 | 59.04 | 58.98 | 59.4 |
| (μm) | |||
|---|---|---|---|
| Particle Group | Radio (R) | Lenth (L) | OD |
| 1–6 | 138 | 501 | 113 |
| 7 | 158 | 394 | 39 |
| 8 | 182 | 632 | 134 |
| 9 | 208 | 610 | 96 |
| 10 | 239 | 630 | 76 |
| 11 | 275 | 660 | 55 |
| 12 | 315 | 822 | 95 |
| 13 | 362 | 1034 | 155 |
| 14 | 416 | 1360 | 264 |
| 15 | 477 | 1033 | 39 |
| 16 | 548 | 1625 | 264 |
| 17 | 629 | 1866 | 304 |
| 18 | 723 | 2143 | 349 |
| 19 | 830 | 2460 | 400 |
| Particle | Particle-Particle | Particle-Walls | P-P HSMC | P-P LCMC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΡLDPE | ΝLDPE | epp | μspp | μrpp | epw | μspw | μrpw | bN | γT | ξ | |
| EP1 | 450 | 0.2 | 0.1 | 0.1 | 0 | 0.1 | 0.1 | 0 | 0 | 0.67 | 1 |
| EP2 | 925 | 0.35 | 0.44 | 0.53 | 0.13 | 0.44 | 0.525 | 0.1 | 0.05 | 0.835 | 4000 |
| EP3 | 1400 | 0.5 | 0.78 | 0.95 | 0.25 | 0.78 | 0.95 | 0.2 | 0.1 | 1 | 8000 |
| EP4 | 623 | 0.26 | 0.207 | 0.479 | 0.044 | 0.503 | 0.739 | 0.085 | 0.054 | 0.776 | 5959 |
| EP5 | 765 | 0.43 | 0.553 | 0.950 | 0.077 | 0.230 | 0.950 | 0.015 | 0.079 | 0.813 | 2543 |
| EP6 | 450 | 0.25 | 0.503 | 0.394 | 0.064 | 0.215 | 0.345 | 0.039 | 0.085 | 0.949 | 1099 |
| EP7 | 1284 | 0.20 | 0.618 | 0.726 | 0.058 | 0.632 | 0.687 | 0.033 | 0.070 | 0.914 | 5181 |
| EP8 | 978 | 0.45 | 0.333 | 0.711 | 0.017 | 0.290 | 0.583 | 0.068 | 0.025 | 0.872 | 8000 |
| EP9 | 1400 | 0.37 | 0.460 | 0.560 | 0.100 | 0.538 | 0.499 | 0.100 | 0.039 | 1.000 | 4037 |
| EP10 | 587 | 0.42 | 0.780 | 0.211 | 0.036 | 0.365 | 0.307 | 0.018 | 0.031 | 0.906 | 2936 |
| EP11 | 1208 | 0.35 | 0.238 | 0.100 | 0.086 | 0.433 | 0.212 | 0.079 | 0.000 | 0.735 | 5061 |
| EP12 | 1130 | 0.32 | 0.100 | 0.617 | 0.023 | 0.100 | 0.411 | 0.000 | 0.012 | 0.846 | 1475 |
| EP13 | 942 | 0.29 | 0.712 | 0.318 | 0.045 | 0.780 | 0.100 | 0.048 | 0.063 | 0.670 | 1 |
| EP14 | 819 | 0.5 | 0.398 | 0.847 | 0.000 | 0.710 | 0.847 | 0.055 | 0.100 | 0.719 | 6788 |
| Simulation Results | Objective (MAPE) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| obj(1) | obj(2) | obj(3) | obj(4) | obj(5) | obj(6) | obj(7) | obj(8) | ||
| αHC | ϕLB | ϕDD | αDD | mDD | mVB | VDD | VLB | ||
| EP1 | 3.3 | 14.6 | 13.3 | 21 | 7 | 50.8 | 1 | 0.5 | 68.86 |
| EP2 | 34.4 | 47.6 | 51.2 | 24 | 2.9 | 92.3 | 0.5 | 0.5 | 23.18 |
| EP3 | 40.6 | 60.2 | 52.2 | 21.6 | 1.8 | 124.5 | 0.5 | 0.5 | 36.81 |
| EP4 | 29.2 | 42.8 | 40.8 | 28.5 | 4.7 | 65.2 | 0.5 | 0.5 | 25.2 |
| EP5 | 33.2 | 43.4 | 50.2 | 24.9 | 3.7 | 70 | 0.5 | 1 | 18.22 |
| EP6 | 35.4 | 43 | 44.3 | 36.1 | 5.4 | 45.4 | 1 | 0.5 | 23.73 |
| EP7 | 28.8 | 46.3 | 48.4 | 38.2 | 2.6 | 121.3 | 1 | 1 | 30.56 |
| EP8 | 25 | 40.8 | 42.6 | 25 | 3.7 | 102.8 | 1 | 0.5 | 34.23 |
| EP9 | 28.5 | 51.2 | 45 | 18.1 | 2.3 | 140.1 | 0.5 | 1 | 45.76 |
| EP10 | 22.2 | 26.5 | 31.6 | 24.1 | 5.7 | 60.8 | 1 | 0.5 | 41.38 |
| EP11 | 17.4 | 22.6 | 23.3 | 28.2 | 4.5 | 134.3 | 1 | 0.5 | 60.07 |
| EP12 | 16.4 | 44.1 | 34.9 | 12.6 | 4 | 123.4 | 0.5 | 0.5 | 52.26 |
| EP13 | 11.1 | 24.3 | 22.1 | 28.5 | 5.6 | 94.9 | 1 | 0.5 | 57.23 |
| EP14 | 24.9 | 31 | 37.7 | 23.9 | 4.5 | 83.6 | 0.5 | 0.5 | 37.53 |
| Particle | Particle-Particle | Particle-Walls | P-P HSMC | P-P LCMC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ | ν | e | μs | μr | e | μs | μr | bN | γT | ξ | |
| Op85 | 664 | 0.20 | 0.662 | 0.526 | 0.149 | 0.463 | 0.950 | 0.107 | 0.081 | 1.000 | 5750 |
| obj(1) | obj(2) | obj(3) | obj(4) | obj(5) | obj(6) | FF | Objetive (MAPE) | |
|---|---|---|---|---|---|---|---|---|
| αHC | ϕLB | ϕDD | αDD | mDD | mVB | |||
| Op85 | 35.0 | 51.0 | 56.9 | 37.0 | 3.3 | 62.7 | 2.98 | 1.8 |
| Experiments | 35.6 | 60.7 | 55.4 | 38.9 | 3.3 | 59.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Montagut, J.; Paz, R.; Monzón, M. Development of a Non-Spherical Polymeric Particles Calibration Procedure for Numerical Simulations Based on the Discrete Element Method. Polymers 2025, 17, 2748. https://doi.org/10.3390/polym17202748
García-Montagut J, Paz R, Monzón M. Development of a Non-Spherical Polymeric Particles Calibration Procedure for Numerical Simulations Based on the Discrete Element Method. Polymers. 2025; 17(20):2748. https://doi.org/10.3390/polym17202748
Chicago/Turabian StyleGarcía-Montagut, Joshua, Rubén Paz, and Mario Monzón. 2025. "Development of a Non-Spherical Polymeric Particles Calibration Procedure for Numerical Simulations Based on the Discrete Element Method" Polymers 17, no. 20: 2748. https://doi.org/10.3390/polym17202748
APA StyleGarcía-Montagut, J., Paz, R., & Monzón, M. (2025). Development of a Non-Spherical Polymeric Particles Calibration Procedure for Numerical Simulations Based on the Discrete Element Method. Polymers, 17(20), 2748. https://doi.org/10.3390/polym17202748








