Directional Entropy Bands for Surface Characterization of Polymer Crystallization
Abstract
1. Introduction
2. Materials and Methods
2.1. Molecular Dynamics Simulation Details
2.2. Order Parameters
2.2.1. Smooth Overlap of Atomic Positions (SOAP) Descriptor
2.2.2. Thermodynamic-like Parameters for Phase Transitions
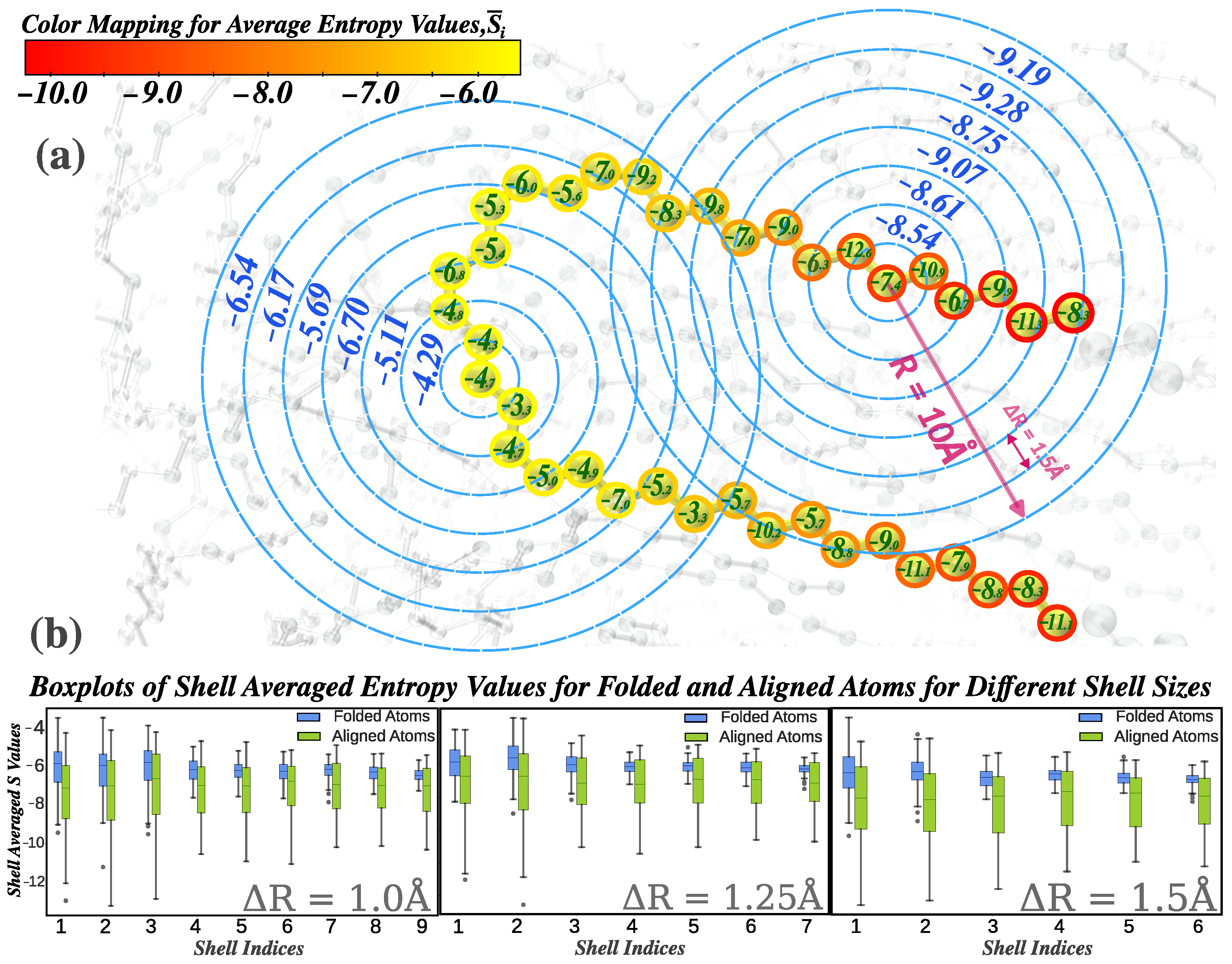
2.2.3. Directional Entropy Bands
- The radial entropy average:where is the value of the scalar entropy of the neighboring atoms within the shell.
- The directional entropy projections along the Cartesian axes:where is the unit displacement vector from the atom (i) to the neighbor (j). These dipole-like projections reflect the first-order directional anisotropy of the local entropy field and are analogous to spherical harmonic components.
- The max-based entropy gradient within the shell:which estimates the steepest local change in entropy and is particularly sensitive to interfacial regions and phase boundaries.
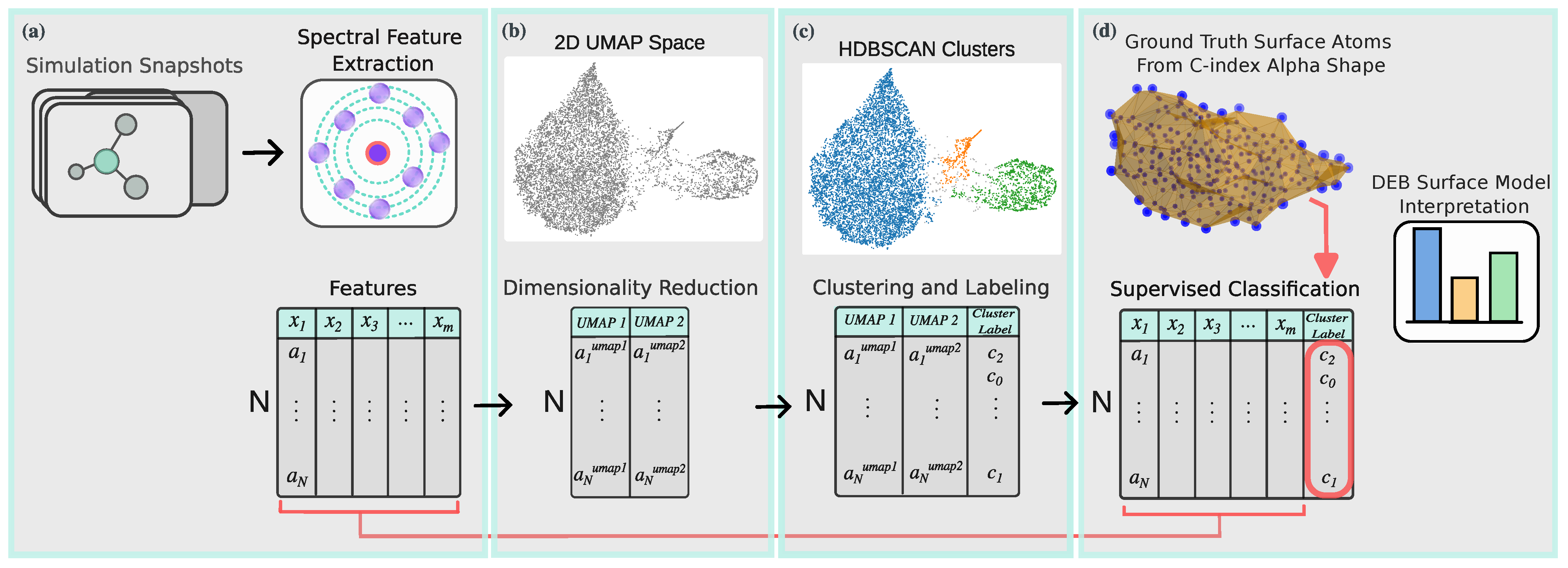
2.2.4. Machine Learning Workflow
3. Results and Discussion
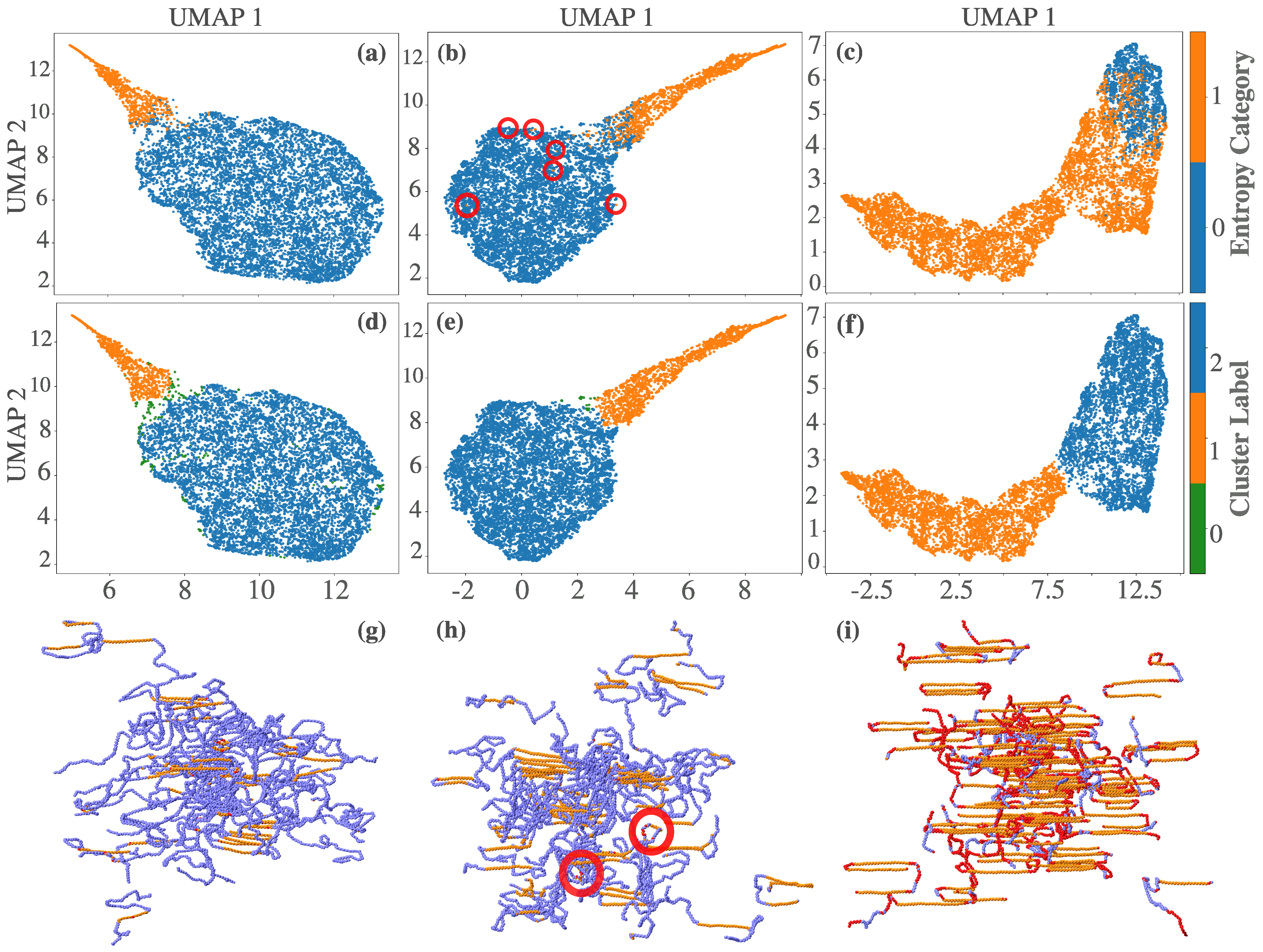
3.1. Smooth Overlap of Atomic Positions (SOAP) Descriptors
3.2. Directional Entropy Bands: Resolving Local Configurational Order
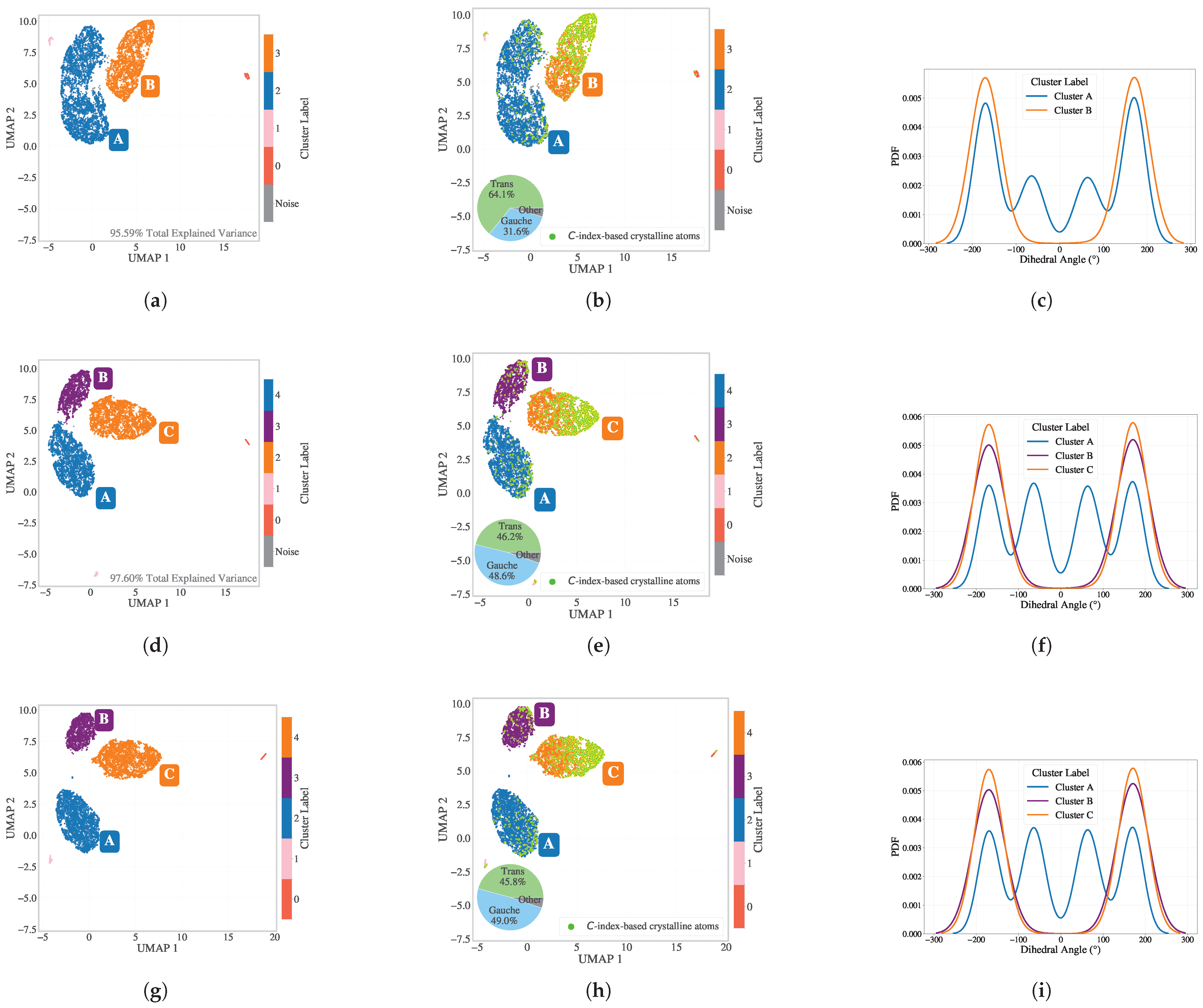
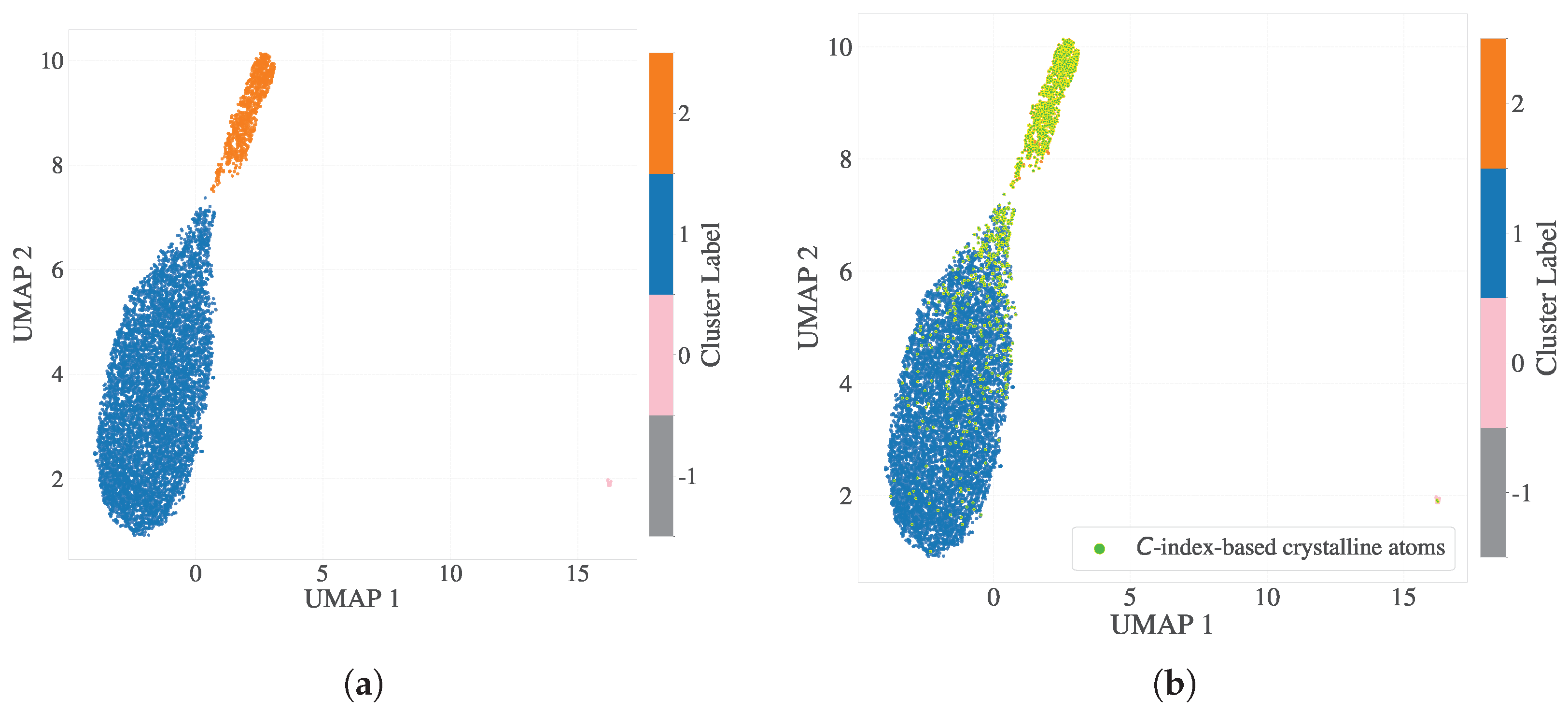
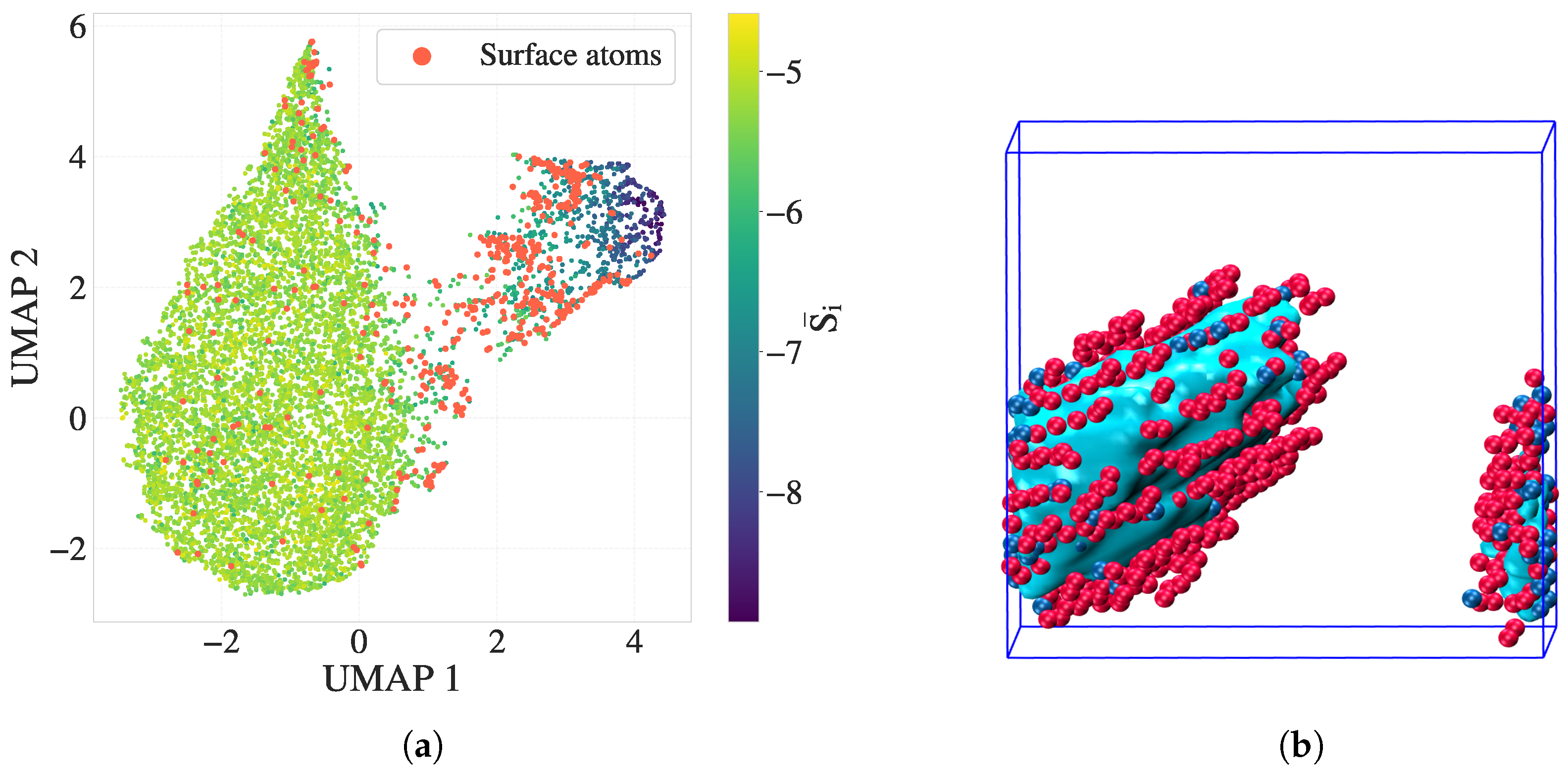
3.2.1. Manifold Learning and Comparison of Band-Averaged and Scalar Entropy
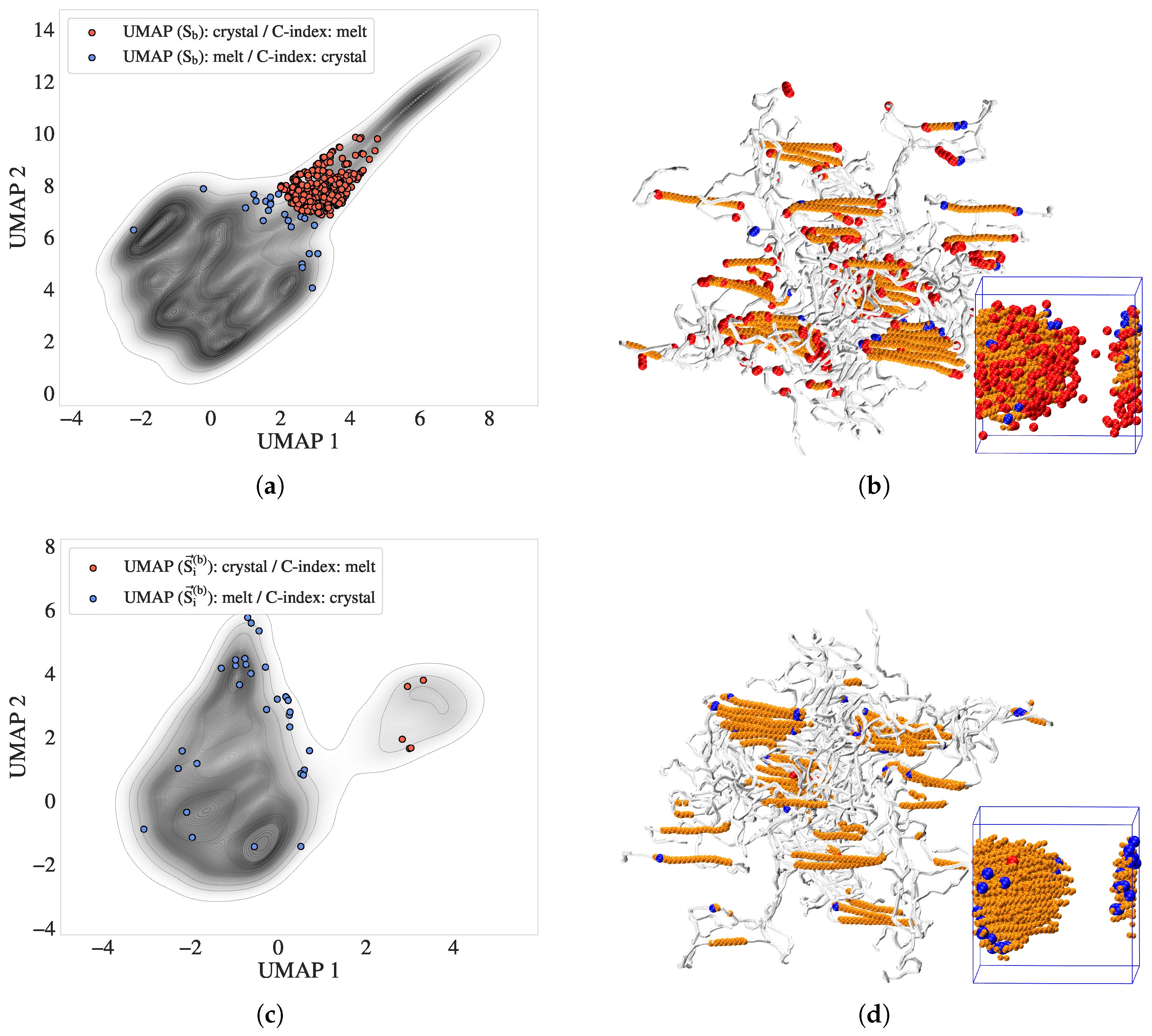
3.2.2. Comparison of Directional Entropy Bands () with the Crystallinity Index (C-index) and Phase Boundaries
3.3. Model Explanation via Supervised Classification
3.3.1. Motivation and Approach
3.3.2. Data Preparation
3.3.3. Model Selection and Training
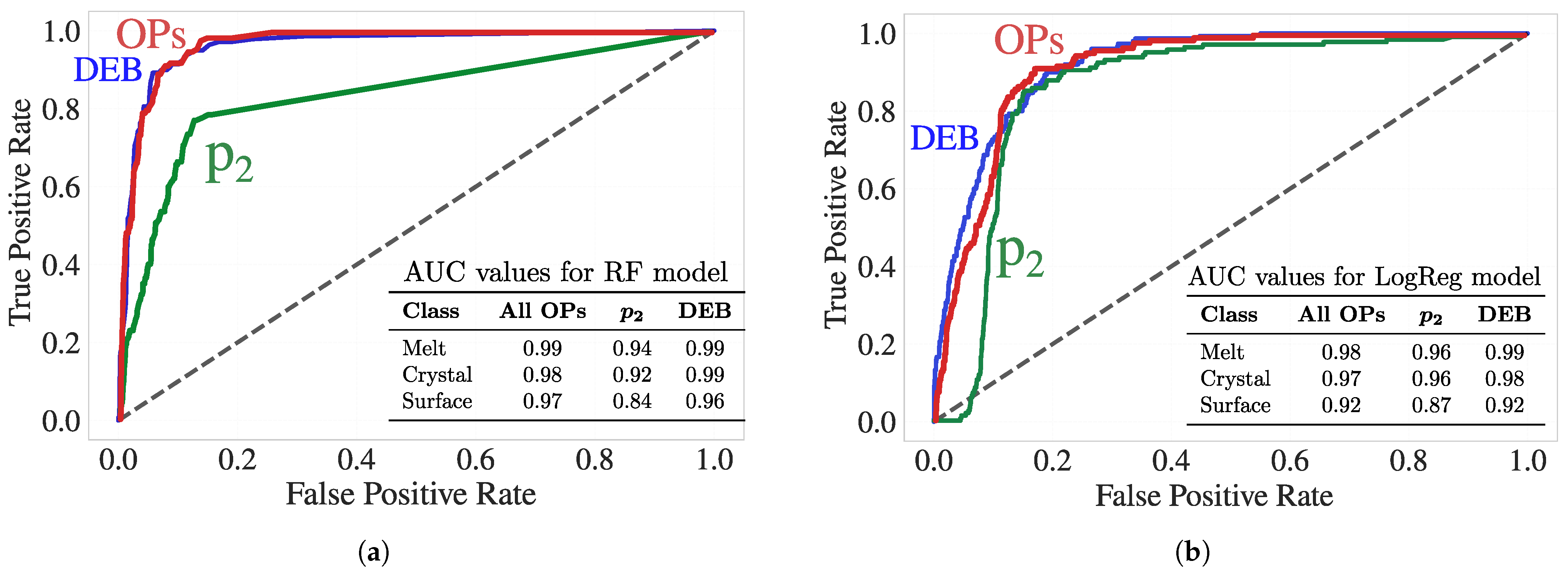
3.3.4. Performance Evaluation: ROC Analysis
3.3.5. Uncertainty of Cluster_Label
3.3.6. Forward Feature Selection and Model Interpretation
3.3.7. Diffuse Nature of Polymer Interfaces and the Role of DEB
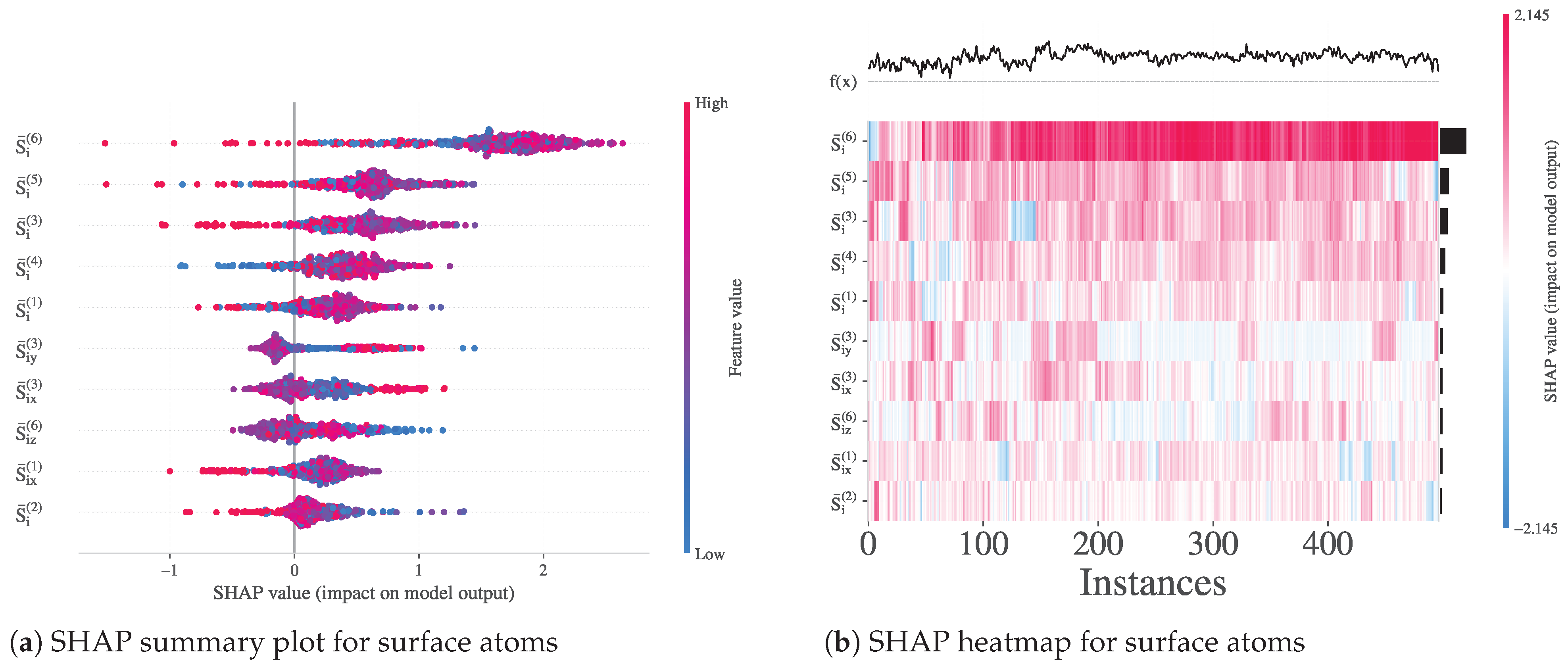
3.3.8. Feature Importance and Local Structure Patterns
3.3.9. Summary of Insights from DEB
4. Conclusions
Future Directions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | Molecular Dynamics |
| PE | Polyethylene |
| UA | United Atom |
| OP | Order Parameter |
| DEB | Directional Entropy Bands |
| UMAP | Uniform Manifold Approximation and Projection |
| SOAP | Smooth Overlap of Atomic Positions |
| HDBSCAN | Hierarchical Density-Based Spatial Clustering of Applications with Noise |
| ROC | Receiver Operating Characteristic |
| AUC | Area Under the Curve (of the ROC) |
| SHAP | SHapley Additive exPlanations |
Appendix A
Appendix A.1. Effect of Skewness Correction on UMAP Embedding
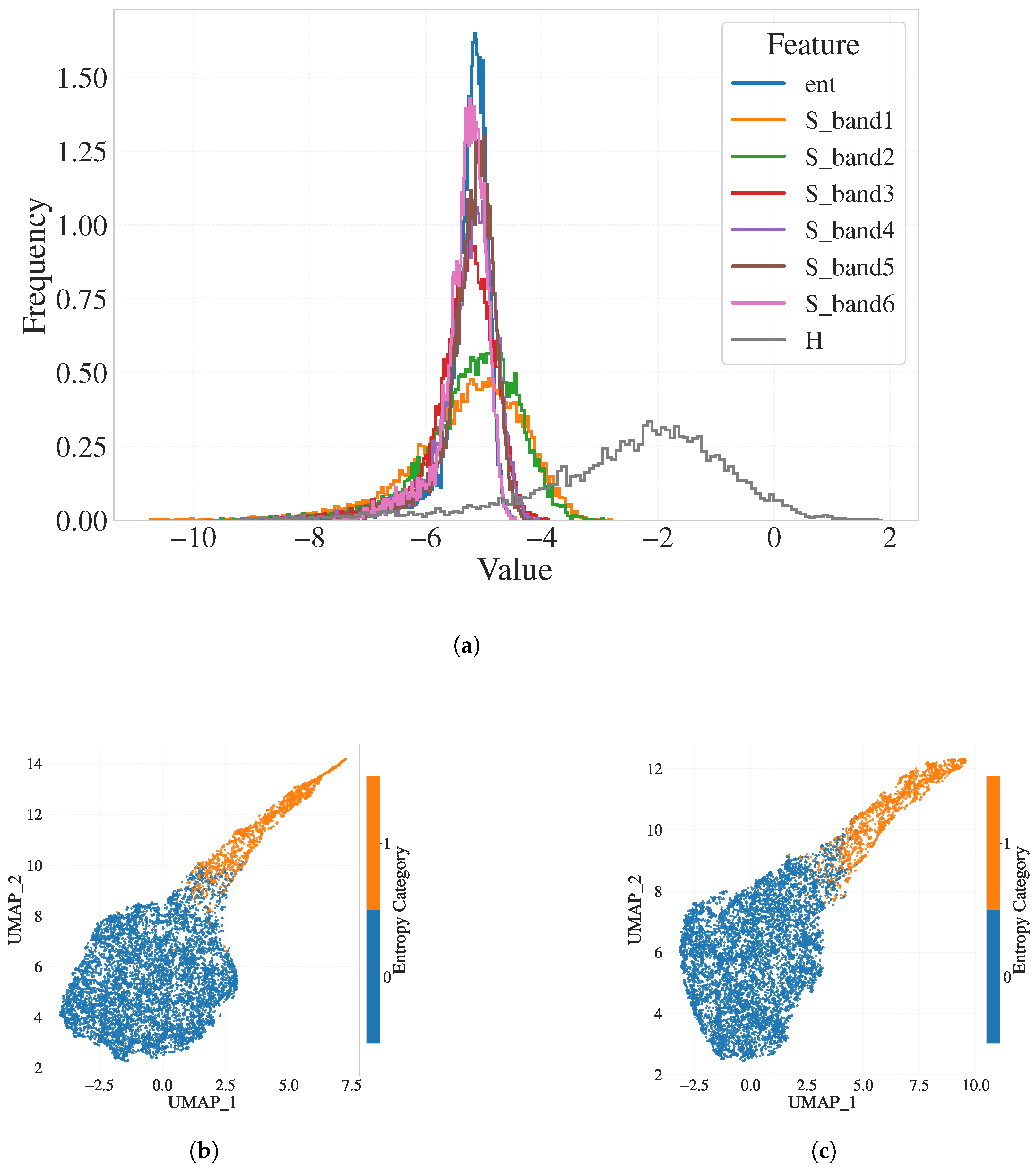
Appendix A.2. PCA for SOAP Descriptors

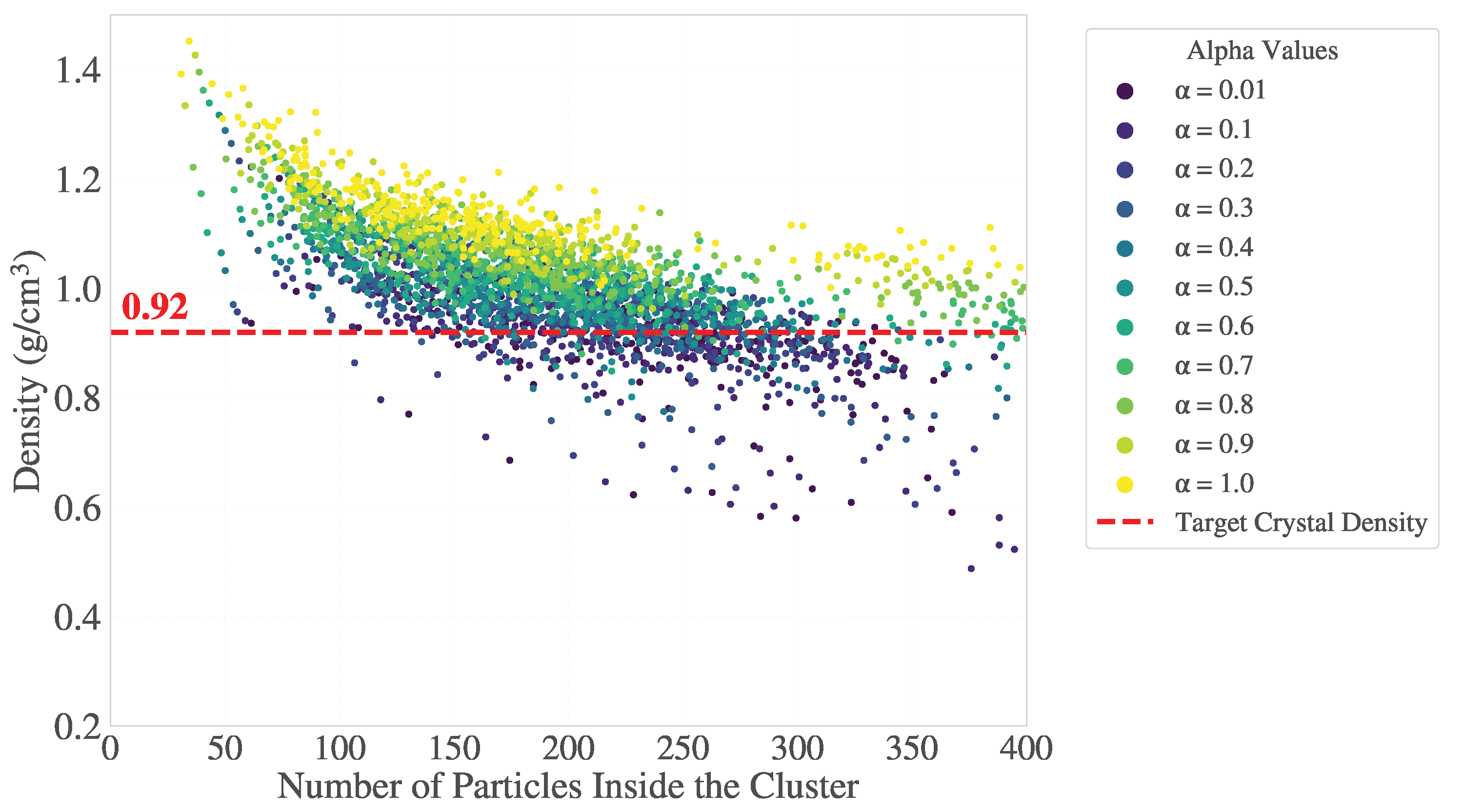
Appendix A.3. Selection of Alpha for Geometric Surface Definition
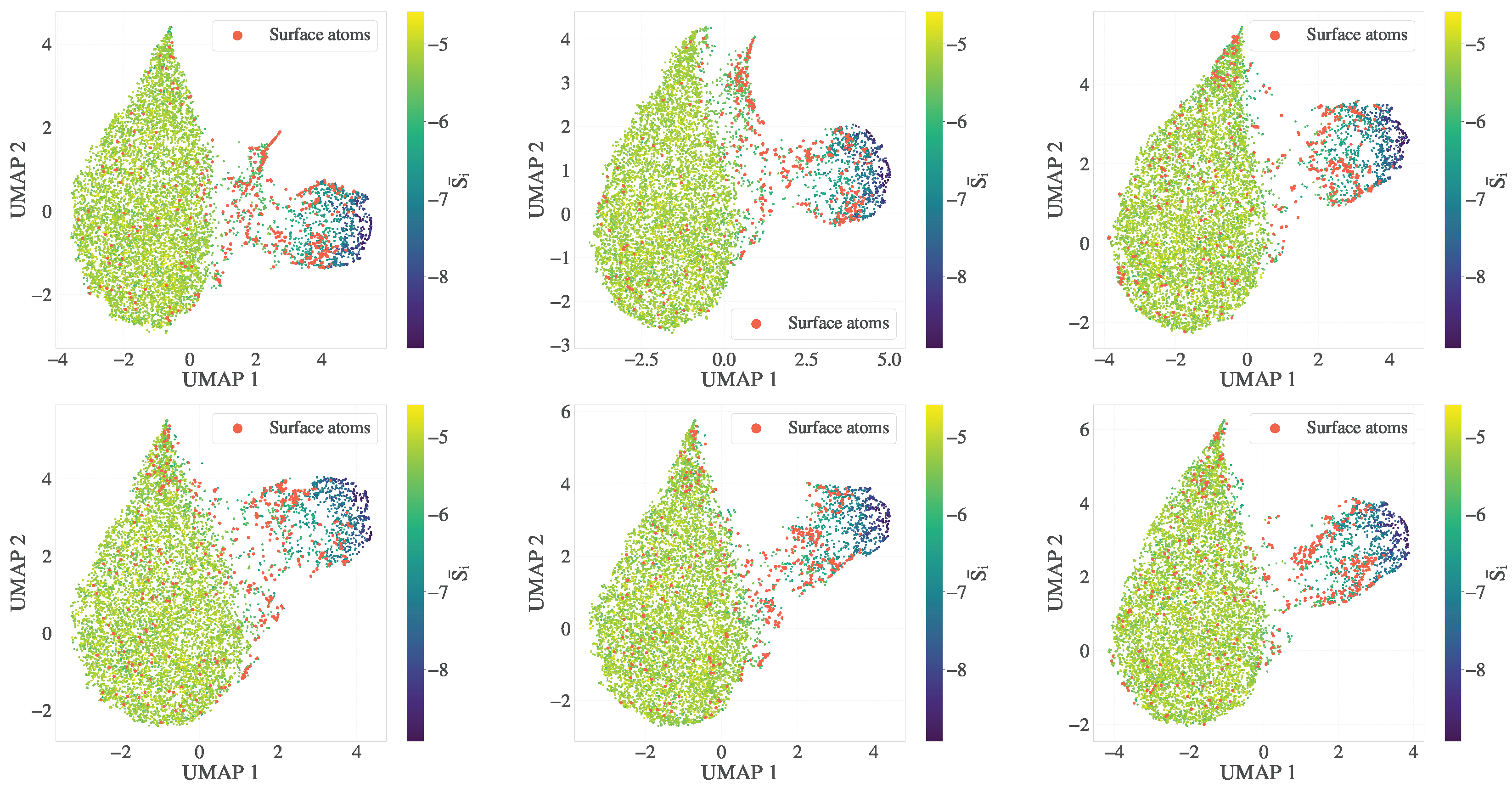
Appendix A.4. UMAP Response to Surface Smoothing Parameter (σs)
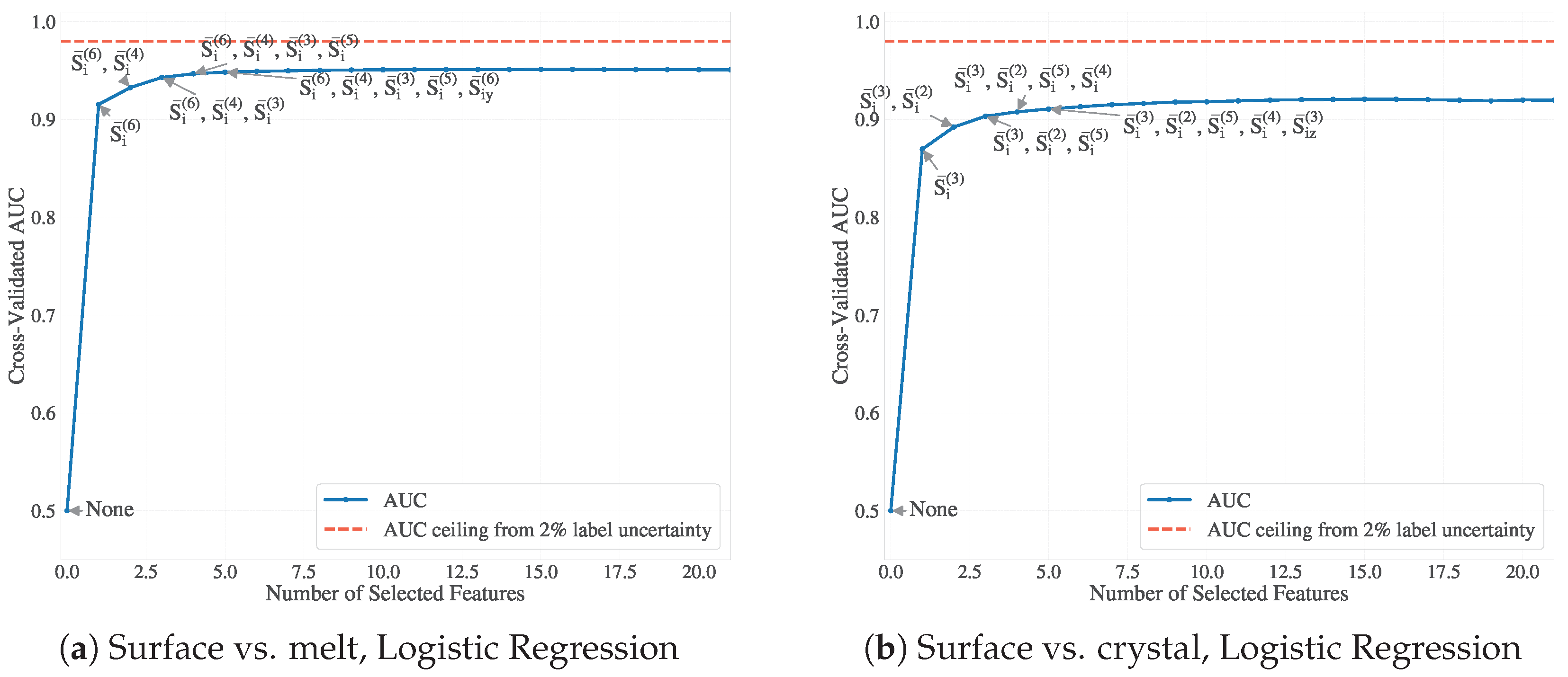
Appendix A.5. Forward Feature Selection Under Alternative Interface Definitions
References
- Keller, A. Morphology of crystallizing polymers. Nature 1952, 169, 913–914. [Google Scholar] [CrossRef]
- Armitstead, K.; Goldbeck-Wood, G.; Keller, A. Polymer crystallization theories. In Macromolecules: Synthesis, Order and Advanced Properties; Springer: Berlin/Heidelberg, Germany, 1992; pp. 219–312. [Google Scholar]
- Gedde, U.L.F. Polymer Physics; Springer Science & Business Media: Berlin, Germany, 1995. [Google Scholar]
- Sawyer, L.; Grubb, D.T.; Meyers, G.F. Polymer Microscopy; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Luo, C.; Kröger, M.; Sommer, J.U. Molecular dynamics simulations of polymer crystallization under confinement: Entanglement effect. Polymer 2017, 109, 71–84. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics simulations of steady-state crystal growth and homogeneous nucleation in polyethylene-like polymer. J. Chem. Phys. 2008, 129, 184903. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Davis, G.T.; Lauritzen, J.I. The Rate of Crystallization of Linear Polymers with Chain Folding. In Treatise on Solid State Chemistry: Vol. 3. Crystalline and Noncrystalline Solids; Hannay, N.B., Ed.; Springer: Boston, MA, USA, 1976; pp. 497–614. [Google Scholar]
- Sadler, D.; Gilmer, G. A model for chain folding in polymer crystals: Rough growth faces are consistent with the observed growth rates. Polymer 1984, 25, 1446–1452. [Google Scholar] [CrossRef]
- Olmsted, P.D.; Poon, W.C.; McLeish, T.; Terrill, N.; Ryan, A. Spinodal-assisted crystallization in polymer melts. Phys. Rev. Lett. 1998, 81, 373. [Google Scholar] [CrossRef]
- Strobl, G. From the melt via mesomorphic and granular crystalline layers to lamellar crystallites: A major route followed in polymer crystallization? Europ. Phys. J. E 2000, 3, 165–183. [Google Scholar] [CrossRef]
- Tang, X.; Yang, J.; Xu, T.; Tian, F.; Xie, C.; Li, L. Local structure order assisted two-step crystal nucleation in polyethylene. Phys. Rev. Mat. 2017, 1, 073401. [Google Scholar] [CrossRef]
- Yi, P.; Rutledge, G.C. Molecular simulation of crystal nucleation in n-octane melts. J. Chem. Phys. 2009, 131, 134902. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics simulation of polymer ordering. II. Crystallization from the melt. J. Chem. Phys. 2001, 115, 8675–8680. [Google Scholar] [CrossRef]
- Anwar, M.; Turci, F.; Schilling, T. Crystallization mechanism in melts of short n-alkane chains. J. Chem. Phys. 2013, 139, 214904. [Google Scholar] [CrossRef]
- Muthukumar, M.; Welch, P. Modeling polymer crystallization from solutions. Polymer 2000, 41, 8833–8837. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics of polymer crystallization revisited: Crystallization from the melt and the glass in longer polyethylene. J. Chem. Phys. 2013, 139, 054903. [Google Scholar] [CrossRef]
- Yi, P.; Locker, C.R.; Rutledge, G.C. Molecular dynamics simulation of homogeneous crystal nucleation in polyethylene. Macromolecules 2013, 46, 4723–4733. [Google Scholar] [CrossRef]
- Anwar, M.; Schilling, T. Crystallization of polyethylene: A molecular dynamics simulation study of the nucleation and growth mechanisms. Polymer 2015, 76, 307–312. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. A thermodynamically inspired method for quantifying phase transitions in polymeric liquids with application to flow-induced crystallization of a polyethylene melt. Macromolecules 2020, 53, 10487–10502. [Google Scholar] [CrossRef]
- Hussain, M.A.; Yamamoto, T.; Adil, S.F.; Yao, S. Coarse-grained simulations on polyethylene crystal network formation and microstructure analysis. Polymers 2024, 16, 1007. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H.; Tong, H.; Shi, R.; Russo, J. Revealing key structural features hidden in liquids and glasses. Nat. Rev. Phys. 2019, 1, 333–348. [Google Scholar] [CrossRef]
- Musil, F.; Grisafi, A.; Bartók, A.P.; Ortner, C.; Csányi, G.; Ceriotti, M. Physics-inspired structural representations for molecules and materials. Chem. Rev. 2021, 121, 9759–9815. [Google Scholar] [CrossRef]
- Esselink, K.; Hilbers, P.; Van Beest, B. Molecular dynamics study of nucleation and melting of n-alkanes. J. Chem. Phys. 1994, 101, 9033–9041. [Google Scholar] [CrossRef]
- Yi, P.; Rutledge, G.C. Molecular simulation of bundle-like crystal nucleation from n-eicosane melts. J. Chem. Phys. 2011, 135, 024903. [Google Scholar] [CrossRef]
- Nicholson, D.A.; Rutledge, G.C. Analysis of nucleation using mean first-passage time data from molecular dynamics simulation. J. Chem. Phys. 2016, 144, 134105. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comp. Mat. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Ackland, G.; Jones, A. Applications of local crystal structure measures in experiment and simulation. Phys. Rev. B 2006, 73, 054104. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085. [Google Scholar] [CrossRef]
- Finney, J. Random packings and the structure of simple liquids. I. The geometry of random close packing. Proc. R. Soc. Lond. Math. Phys. Sci. 1970, 319, 479–493. [Google Scholar]
- Tanemura, M.; Hiwatari, Y.; Matsuda, H.; Ogawa, T.; Ogita, N.; Ueda, A. Geometrical analysis of crystallization of the soft-core model in an FCC crystal formation. Prog. Theor. Phys. 1978, 59, 323–324. [Google Scholar] [CrossRef][Green Version]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Tourani, E.; Edwards, B.J.; Khomami, B. Machine Learning Workflow for Analysis of High-Dimensional Order Parameter Space: A Case Study of Polymer Crystallization from Molecular Dynamics Simulations. arXiv 2025, arXiv:2507.17980. [Google Scholar] [CrossRef]
- Nelson, D.R.; Halperin, B. Dislocation-mediated melting in two dimensions. Phys. Rev. B 1979, 19, 2457–2484. [Google Scholar] [CrossRef]
- Chakravarty, C.; Debenedetti, P.G.; Stillinger, F.H. Lindemann measures for the solid-liquid phase transition. J. Chem. Phys. 2007, 126, 204508. [Google Scholar] [CrossRef]
- Tanaka, H.; Kawasaki, T.; Shintani, H.; Watanabe, K. Critical-like behaviour of glass-forming liquids. Nat. Mater. 2010, 9, 324–331. [Google Scholar] [CrossRef]
- Ikeda, A.; Miyazaki, K. Glass transition of the monodisperse gaussian core model. Phys. Rev. Lett. 2011, 106, 015701. [Google Scholar] [CrossRef] [PubMed]
- Mickel, W.; Kapfer, S.C.; Schröder-Turk, G.E.; Mecke, K. Shortcomings of the bond orientational order parameters for the analysis of disordered particulate matter. J. Chem. Phys. 2013, 138, 044501. [Google Scholar] [CrossRef] [PubMed]
- van Meel, J.A.; Filion, L.; Valeriani, C.; Frenkel, D. A parameter-free, solid-angle based, nearest-neighbor algorithm. J. Chem. Phys. 2012, 136, 234107. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Bartók, A.P.; Kondor, R.; Csányi, G. On representing chemical environments. Phys. Rev. B 2013, 87, 184115. [Google Scholar] [CrossRef]
- Spellings, M.; Glotzer, S.C. Machine learning for crystal identification and discovery. AIChE J. 2018, 64, 2198–2206. [Google Scholar] [CrossRef]
- Adorf, C.S.; Moore, T.C.; Melle, Y.J.; Glotzer, S.C. Analysis of self-assembly pathways with unsupervised machine learning algorithms. J. Phys. Chem. B 2019, 124, 69–78. [Google Scholar] [CrossRef]
- De, S.; Bartók, A.P.; Csányi, G.; Ceriotti, M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 2016, 18, 13754–13769. [Google Scholar] [CrossRef]
- Wang, J.; Ferguson, A. Nonlinear machine learning in simulations of soft and biological materials. Mol. Simul. 2018, 44, 1090–1107. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Barakati, K.; Liu, Y.; Nelson, C.; Ziatdinov, M.; Zhang, X.; Takeuchi, I.; Kalinin, S.V. Reward driven workflows for unsupervised explainable analysis of phases and ferroic variants from atomically resolved imaging data. Adv. Mater. 2024, 2418927. [Google Scholar] [CrossRef]
- Asoudeh, M.; Nguyen, N.; Raith, M.; Denman, D.S.; Anozie, U.C.; Mokhtarnejad, M.; Khomami, B.; Skotty, K.M.; Isaac, S.; Gebhart, T.; et al. PEGylated nanoparticles interact with macrophages independently of immune response factors and trigger a non-phagocytic, low-inflammatory response. J. Control. Release 2024, 366, 282–296. [Google Scholar] [CrossRef]
- Wang, L. Discovering phase transitions with unsupervised learning. Phys. Rev. B 2016, 94, 195105. [Google Scholar] [CrossRef]
- Jadrich, R.B.; Lindquist, B.A.; Truskett, T.M. Unsupervised machine learning for detection of phase transitions in off-lattice systems. I. Foundations. J. Chem. Phys. 2018, 149, 194109. [Google Scholar] [CrossRef] [PubMed]
- Boattini, E.; Dijkstra, M.; Filion, L. Unsupervised learning for local structure detection in colloidal systems. J. Chem. Phys. 2019, 151, 154901. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, A.; Sommer, J.U.; Werner, M. Nucleation patterns of polymer crystals analyzed by machine learning models. Macromolecules 2024, 57, 9711–9724. [Google Scholar] [CrossRef]
- Nettleton, R.; Green, M. Expression in terms of molecular distribution functions for the entropy density in an infinite system. J. Chem. Phys. 1958, 29, 1365–1370. [Google Scholar] [CrossRef]
- Piaggi, P.M.; Valsson, O.; Parrinello, M. Enhancing entropy and enthalpy fluctuations to drive crystallization in atomistic simulations. Phys. Rev. Lett. 2017, 119, 015701. [Google Scholar] [CrossRef]
- Piaggi, P.M.; Parrinello, M. Entropy based fingerprint for local crystalline order. J. Chem. Phys. 2017, 147, 114112. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Flow-induced phase separation and crystallization in entangled polyethylene solutions under elongational flow. Macromolecules 2020, 53, 6432–6451. [Google Scholar] [CrossRef]
- Tapash, A.; DesLauriers, P.J.; White, J.L. Simple NMR experiments reveal the influence of chain length and chain architecture on the crystalline/amorphous interface in polyethylenes. Macromolecules 2015, 48, 3040–3048. [Google Scholar] [CrossRef]
- Lotz, B. Fold surfaces of polymer crystals are nucleation sites: The link between polymer decoration, secondary crystallization, and the rigid amorphous fraction (RAF). Macromolecules 2023, 56, 4135–4152. [Google Scholar] [CrossRef]
- Savage, R.; Mullin, N.; Hobbs, J. Molecular conformation at the crystal-amorphous interface in polyethylene. Macromolecules 2015, 48, 6160–6165. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Huang, Z.; Wu, Y.; Wang, L.; Liu, G.; Chen, Y.; Li, K.; Zhang, W.; Zhou, H. Improved charge-transfer doping in crystalline polymer for efficient and stable Perovskite solar cells. Adv. Energy Mater. 2024, 14, 2403737. [Google Scholar] [CrossRef]
- Heydari Gharahcheshmeh, M.; Dautel, B.; Chowdhury, K. Enhanced carrier mobility and thermoelectric performance by nanostructure engineering of PEDOT thin films fabricated via the OCVD method using SbCl5 oxidant. Adv. Func. Mat. 2025, 35, 2418331. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Siepmann, J.I.; Karaborni, S.; Smit, B. Simulating the critical behaviour of complex fluids. Nature 1993, 365, 330–332. [Google Scholar] [CrossRef]
- Moore, J.; Cui, S.; Cochran, H.; Cummings, P. A molecular dynamics study of a short-chain polyethylene melt.: I. steady-state shear. J. NOn-Newtonian Fluid Mech. 2000, 93, 83–99. [Google Scholar] [CrossRef]
- Baig, C.; Edwards, B.J.; Keffer, D.J.; Cochran, H.D.; Harmandaris, V. Rheological and structural studies of linear polyethylene melts under planar elongational flow using nonequilibrium molecular dynamics simulations. J. Chem. Phys. 2006, 124, 084902. [Google Scholar] [CrossRef]
- Cui, S.; Cummings, P.; Cochran, H. Multiple time step nonequilibrium molecular dynamics simulation of the rheological properties of liquid n-decane. J. Chem. Phys. 1996, 104, 255–262. [Google Scholar] [CrossRef][Green Version]
- Baig, C.; Edwards, B.J.; Keffer, D.J.; Cochran, H.D. Rheological and structural studies of liquid decane, hexadecane, and tetracosane under planar elongational flow using nonequilibrium molecular-dynamics simulations. J. Chem. Phys. 2005, 122, 184906. [Google Scholar] [CrossRef]
- Ionescu, T.C.; Baig, C.; Edwards, B.J.; Keffer, D.J.; Habenschuss, A. Structure formation under steady-state isothermal planar elongational flow of n-eicosane: A comparison between simulation and experiment. Phys. Rev. Lett. 2006, 96, 037802. [Google Scholar] [CrossRef]
- Zhang, M.C.; Guo, B.H.; Xu, J. A review on polymer crystallization theories. Crystals 2016, 7, 4. [Google Scholar] [CrossRef]
- Yamamoto, T. Molecular dynamics simulation of stretch-induced crystallization in polyethylene: Emergence of fiber structure and molecular network. Macromolecules 2019, 52, 1695–1706. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.; Edwards, B.; Khomami, B. Individual chain dynamics of a polyethylene melt undergoing steady shear flow. J. Rheol. 2015, 59, 119–153. [Google Scholar] [CrossRef]
- Gasparotto, P.; Ceriotti, M. Recognizing molecular patterns by machine learning: An agnostic structural definition of the hydrogen bond. J. Chem. Phys. 2014, 141, 174110. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; De, S.; Campbell, J.E.; Li, S.; Ceriotti, M.; Day, G.M. Large-scale computational screening of molecular organic semiconductors using crystal structure prediction. Chem. Mater. 2018, 30, 4361–4371. [Google Scholar] [CrossRef]
- Helfrecht, B.A.; Cersonsky, R.K.; Fraux, G.; Ceriotti, M. Structure-property maps with Kernel principal covariates regression. Mach. Learn. Sci. Technol. 2020, 1, 045021. [Google Scholar] [CrossRef]
- Himanen, L.; Jäger, M.O.; Morooka, E.V.; Canova, F.F.; Ranawat, Y.S.; Gao, D.Z.; Rinke, P.; Foster, A.S. DScribe: Library of descriptors for machine learning in materials science. Comput. Phys. Commun. 2020, 247, 106949. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Direct entropy calculation from computer simulation of liquids. Phys. Rev. A 1989, 40, 3817–3822. [Google Scholar] [CrossRef]
- Laird, B.B.; Haymet, A. Calculation of the entropy from multiparticle correlation functions. Phys. Rev. A 1992, 45, 5680–5689. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. A method for calculating the nonequilibrium entropy of a flowing polymer melt via atomistic simulation. J. Chem. Phys. 2021, 155, 111101. [Google Scholar] [CrossRef]
- Edwards, B.J.; Nafar Sefiddashti, M.H.; Khomami, B. Nonequilibrium thermodynamics of polymeric liquids via atomistic simulation. Entropy 2022, 24, 175. [Google Scholar] [CrossRef]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Atomistic simulation of flow-induced microphase separation and crystallization of an entangled polyethylene melt undergoing uniaxial elongational flow and the role of Kuhn segment extension. Polymers 2023, 15, 1831. [Google Scholar] [CrossRef] [PubMed]
- Nafar Sefiddashti, M.H.; Edwards, B.J.; Khomami, B. Flow-induced phase phenomena in an entangled polyethylene/benzene solution under uniaxial elongational flow. Rheol. Acta 2024, 63, 113–133. [Google Scholar] [CrossRef]
- Baig, C.; Edwards, B.J. Atomistic simulation of flow-induced crystallization at constant temperature. Europhys. Lett. 2010, 89, 36003. [Google Scholar] [CrossRef]
- Baig, C.; Edwards, B.J. Atomistic simulation of crystallization of a polyethylene melt in steady uniaxial extension. J. Non-Newtonian Fluid Mech. 2010, 165, 992–1004. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Astels, S. hdbscan: Hierarchical density based clustering. J. Open Source Softw. 2017, 2, 205. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, J.K.; Farrance, O.E.; Kailas, L. How atomic force microscopy has contributed to our understanding of polymer crystallization. Polymer 2009, 50, 4281–4292. [Google Scholar] [CrossRef]
- Milner, S.T. Polymer crystal–melt interfaces and nucleation in polyethylene. Soft Matter 2011, 7, 2909–2917. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the surprising behavior of distance metrics in high dimensional space. In Database Theory — ICDT 2001; Van den Bussche, J., Vianu, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 420–434. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tourani, E.; Edwards, B.J.; Khomami, B. Directional Entropy Bands for Surface Characterization of Polymer Crystallization. Polymers 2025, 17, 2399. https://doi.org/10.3390/polym17172399
Tourani E, Edwards BJ, Khomami B. Directional Entropy Bands for Surface Characterization of Polymer Crystallization. Polymers. 2025; 17(17):2399. https://doi.org/10.3390/polym17172399
Chicago/Turabian StyleTourani, Elyar, Brian J. Edwards, and Bamin Khomami. 2025. "Directional Entropy Bands for Surface Characterization of Polymer Crystallization" Polymers 17, no. 17: 2399. https://doi.org/10.3390/polym17172399
APA StyleTourani, E., Edwards, B. J., & Khomami, B. (2025). Directional Entropy Bands for Surface Characterization of Polymer Crystallization. Polymers, 17(17), 2399. https://doi.org/10.3390/polym17172399






