Macro-Microscopic Characterization and Long-Term Performance Prediction of Polyvinyl Chloride Under Hydrothermal Aging Based on Creep Behavior Analysis
Abstract
1. Introduction
2. Materials and Experimental Methods
2.1. Material and Sample Preparation
2.2. Aging Experiment in a Hydrothermal Environment
2.3. Tensile Creep Test
2.4. Microstructure Characterization
2.5. Theoretical Analysis Methods
2.5.1. Time–Stress Equivalence Principle
2.5.2. Time–Aging Time Equivalence Principle
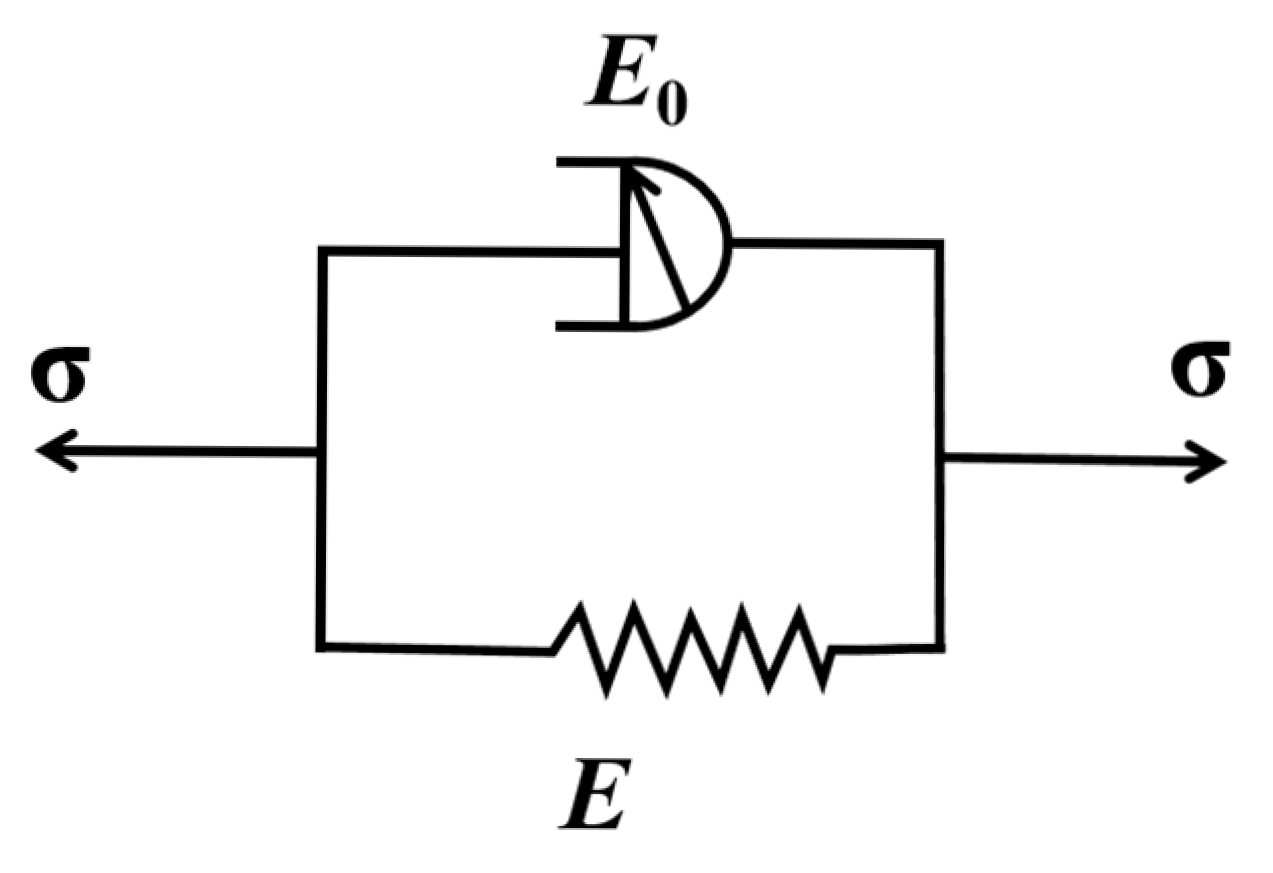
2.5.3. Local Structural Derivative Kelvin Model
3. Creep Test Results and Microscopic Characterization Analysis
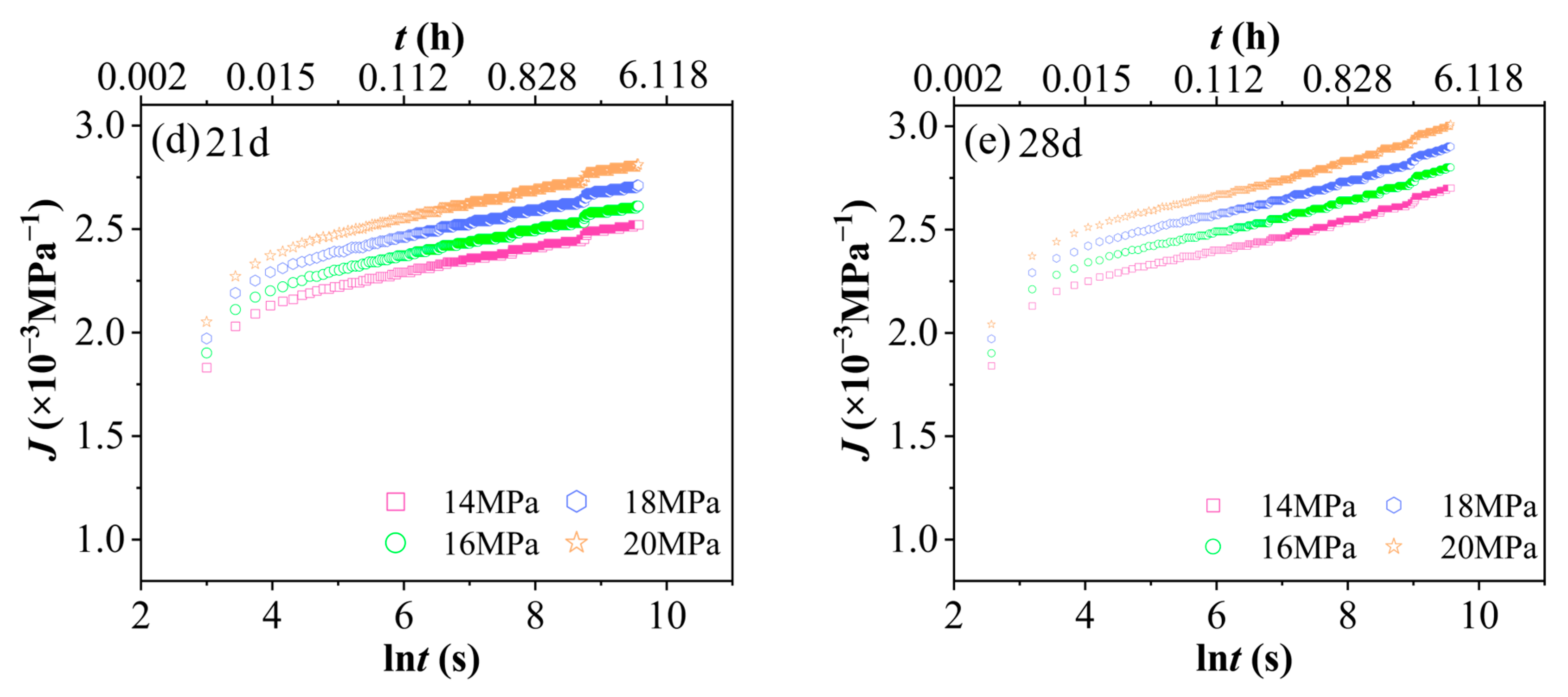
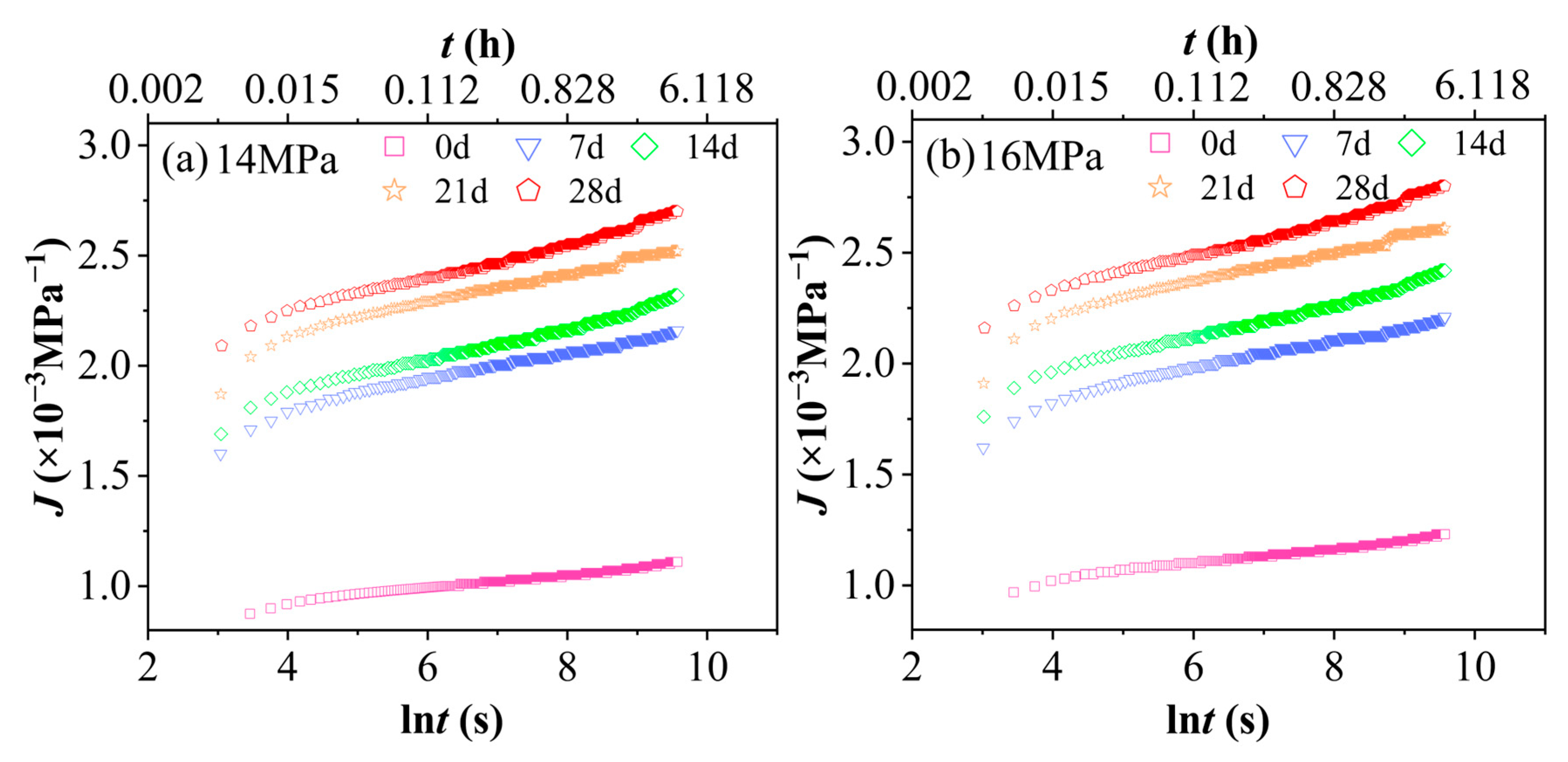
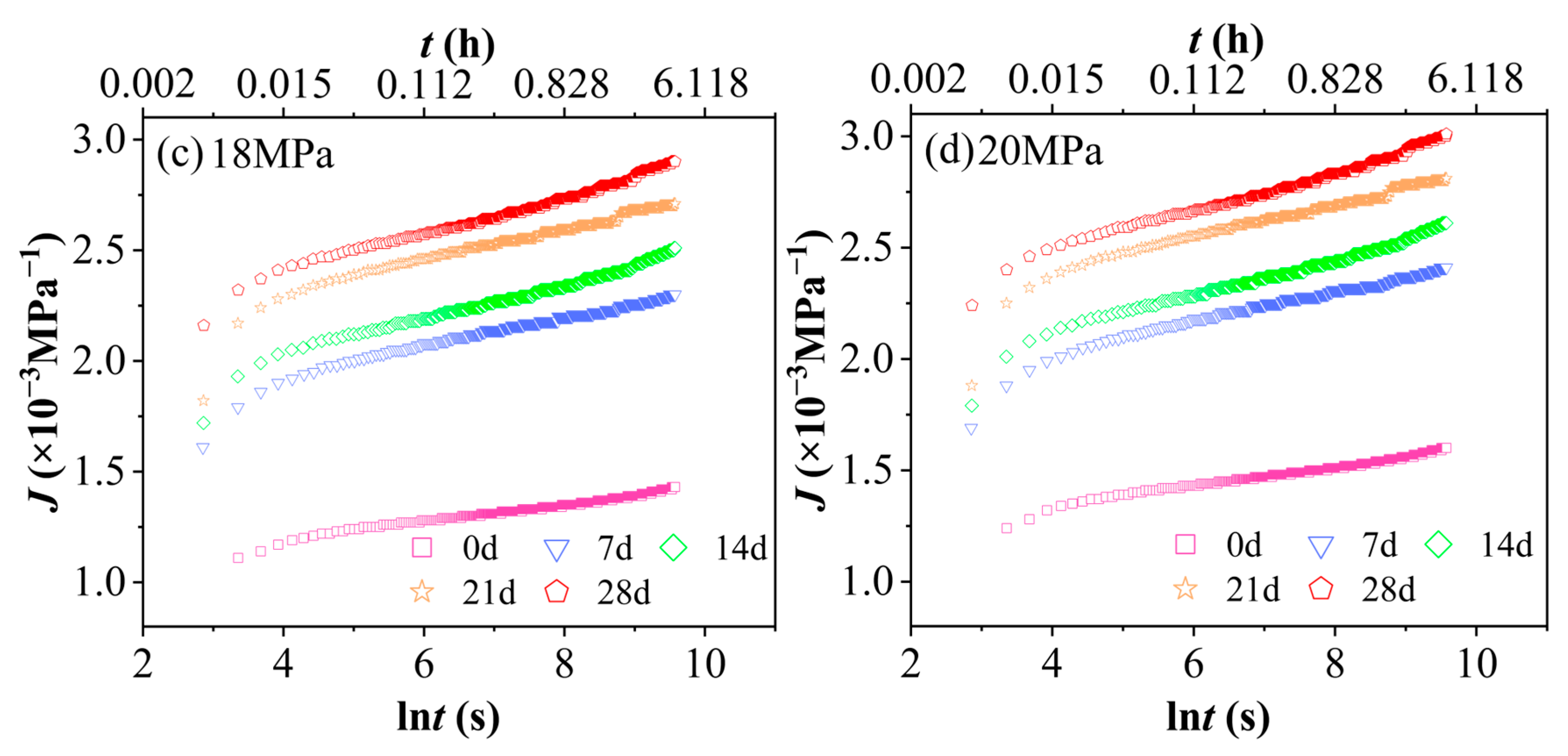
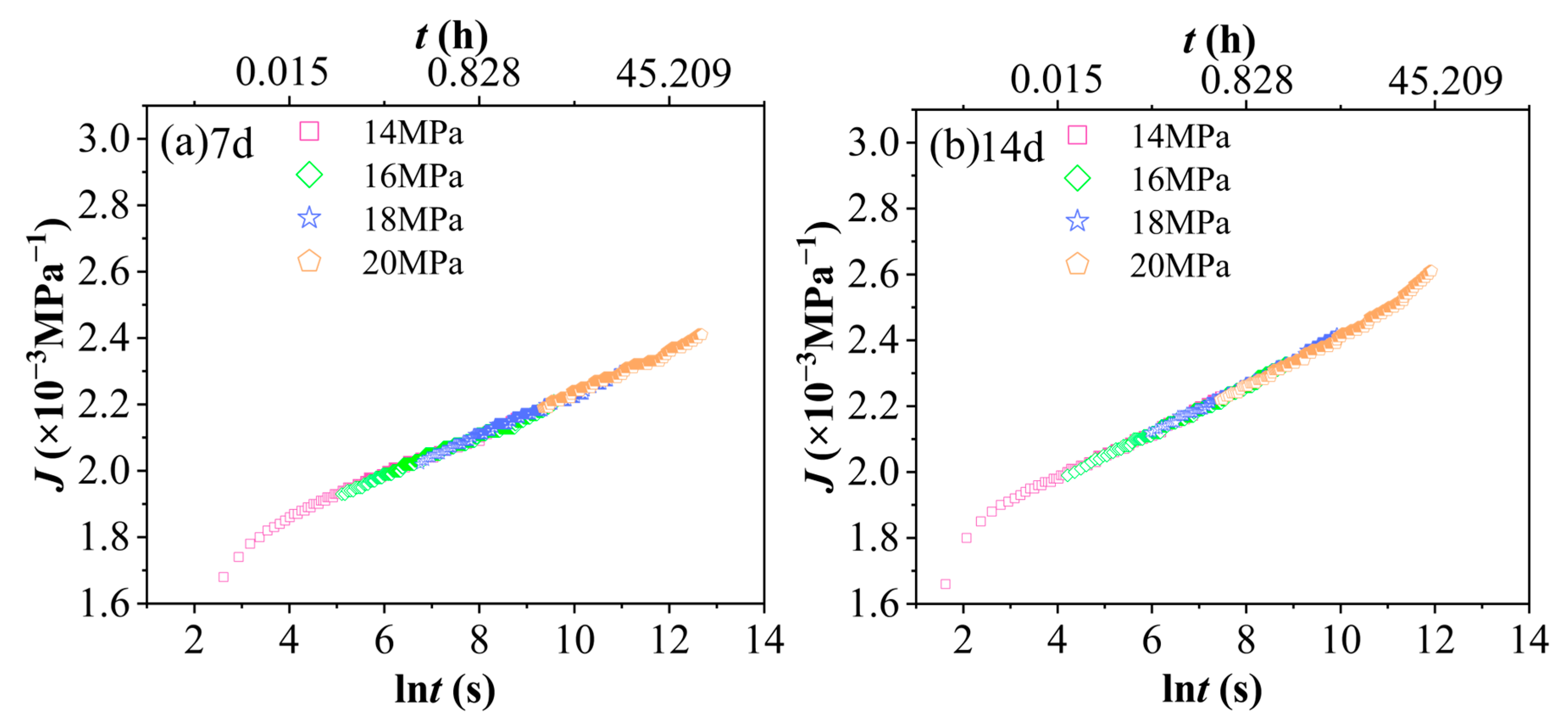
3.1. Characteristic Analysis of Material Creep Curves
3.2. Microscopic Morphology Analysis
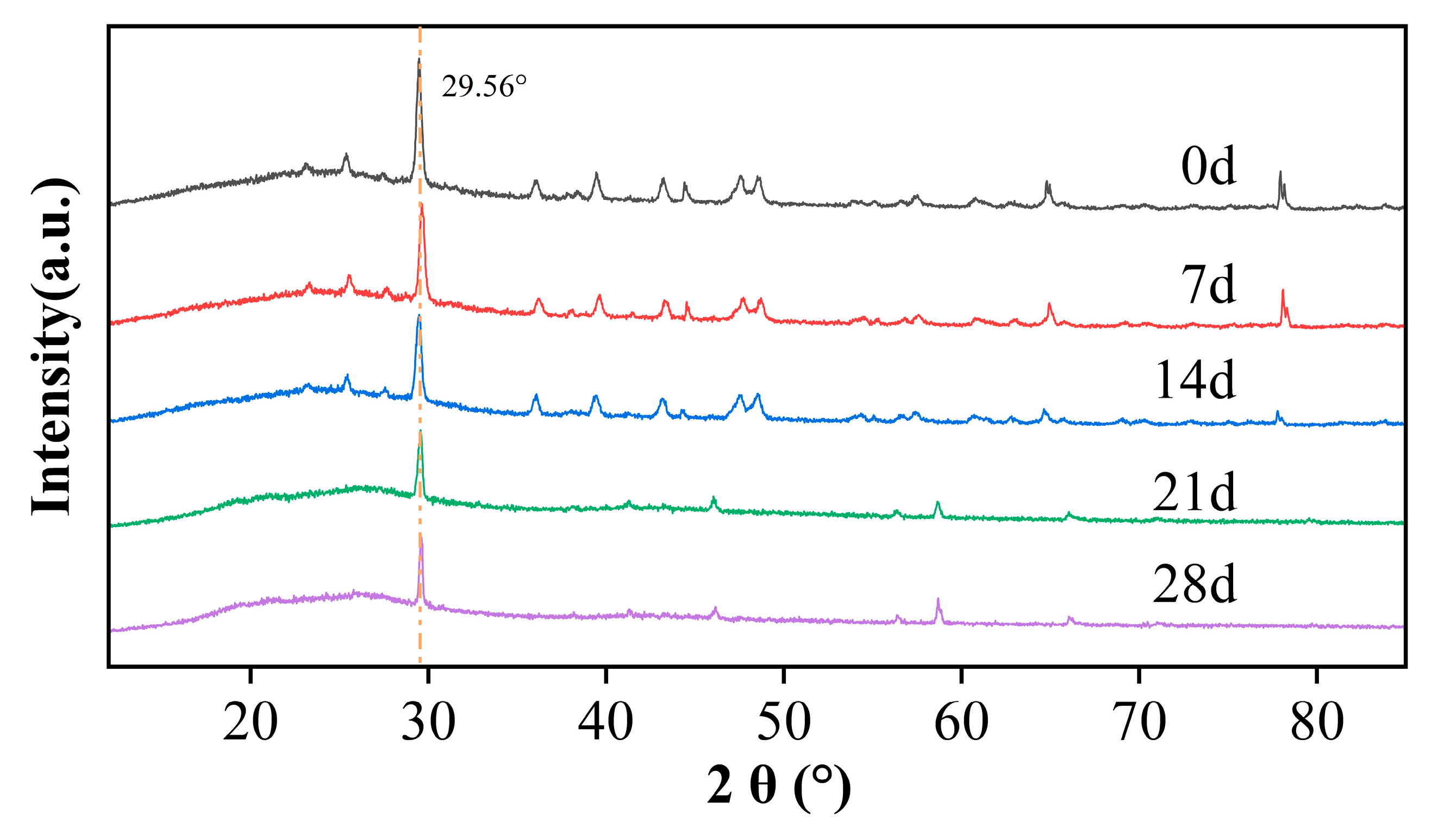
3.2.1. XRD Analysis
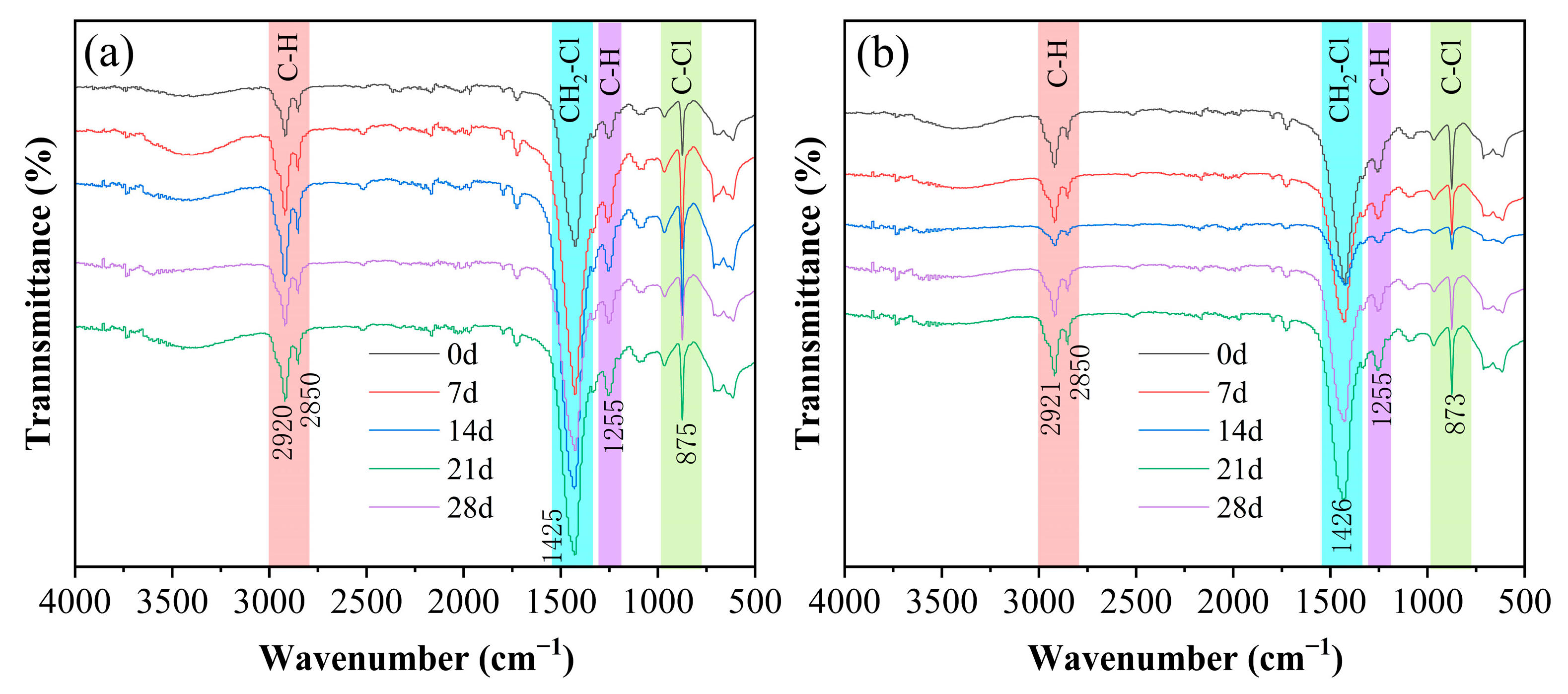
3.2.2. FTIR Analysis
3.2.3. SEM Analysis
4. Theoretical Modeling of Long-Term Creep Behavior and Life Prediction
4.1. The Equivalence Principles of Time–Stress and Time–Aging Time for Accelerated Characterization
4.2. Model Simulation
5. Conclusions
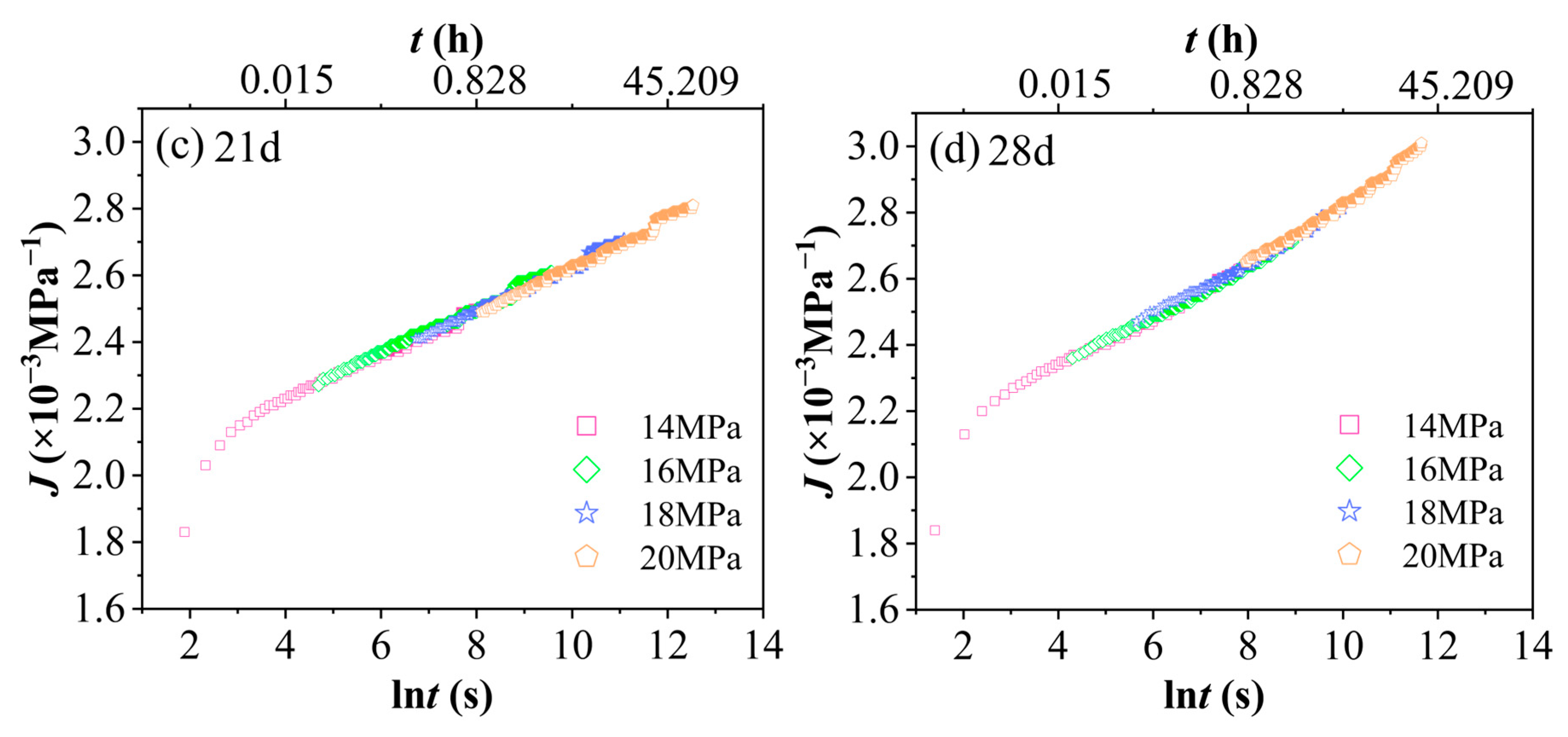
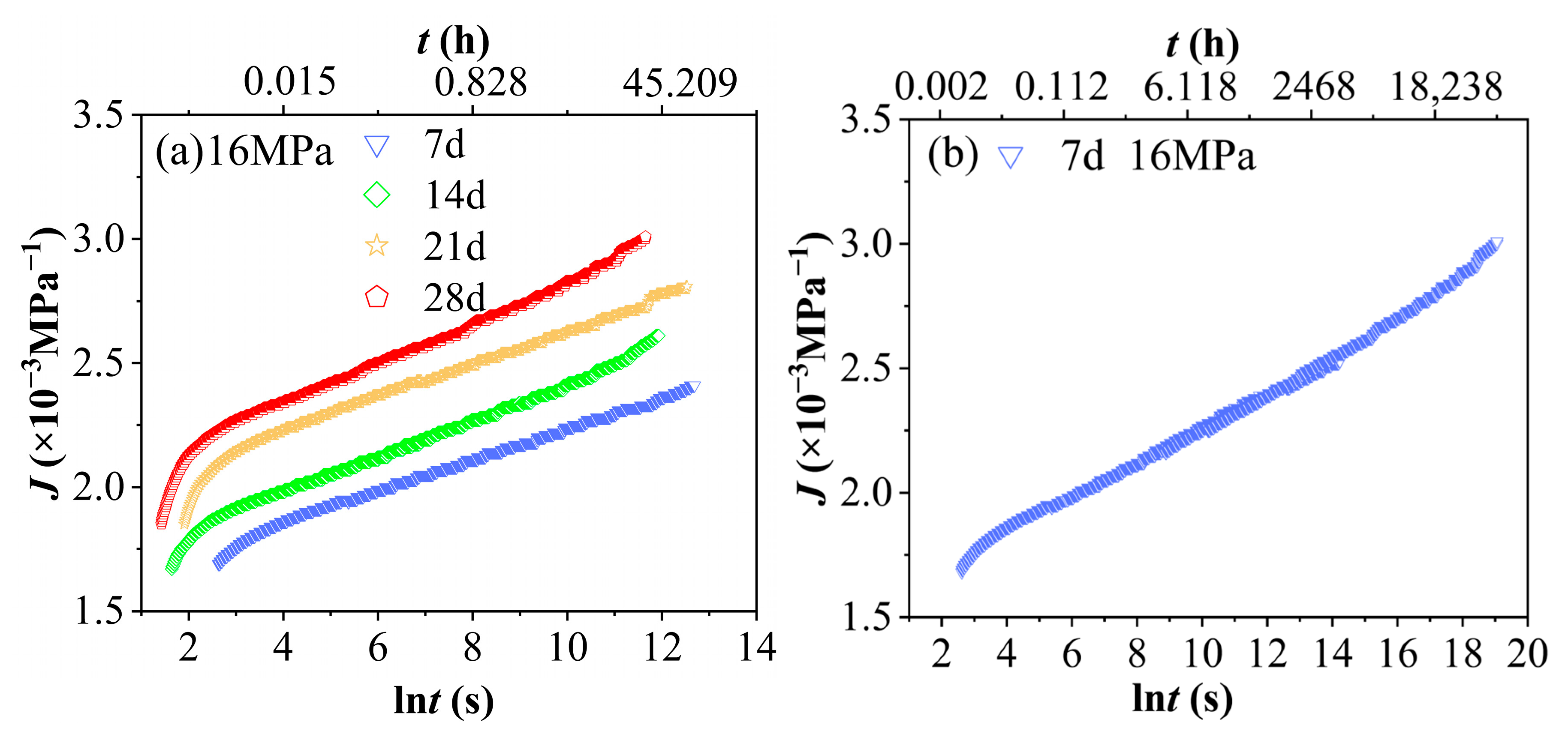
- A hydrothermal aging test was conducted under conditions of 60 °C and 90% relative humidity, followed by short-term tensile creep tests at various stress levels. The results indicate that, for a given aging duration, higher stress levels lead to greater strain accumulation. Similarly, under the same stress level, prolonged aging time also results in increased strain accumulation. The combined effects of temperature and humidity synergistically intensify the viscoelastic response, leading to a reduction in the creep modulus and an increase in the steady-state creep rate. As stress increases, along with extended aging time and the influence of hydrothermal conditions, creep compliance rises significantly, highlighting the material’s high sensitivity to environmental changes.
- Microscopic characterization was conducted using advanced microscopic techniques, including SEM, XRD, and FTIR. The results demonstrated a clear correlation between the evolution of the microstructure—specifically the expansion of amorphous regions, increased surface porosity, and alterations in functional groups—and the observed decline in macroscopic creep modulus as well as an increase in the steady-state creep rate. Such correlations represent a hallmark of polymer aging under hot and humid conditions. This study establishes a microscopic mechanistic foundation for interpreting the changes in macroscopic creep behavior.
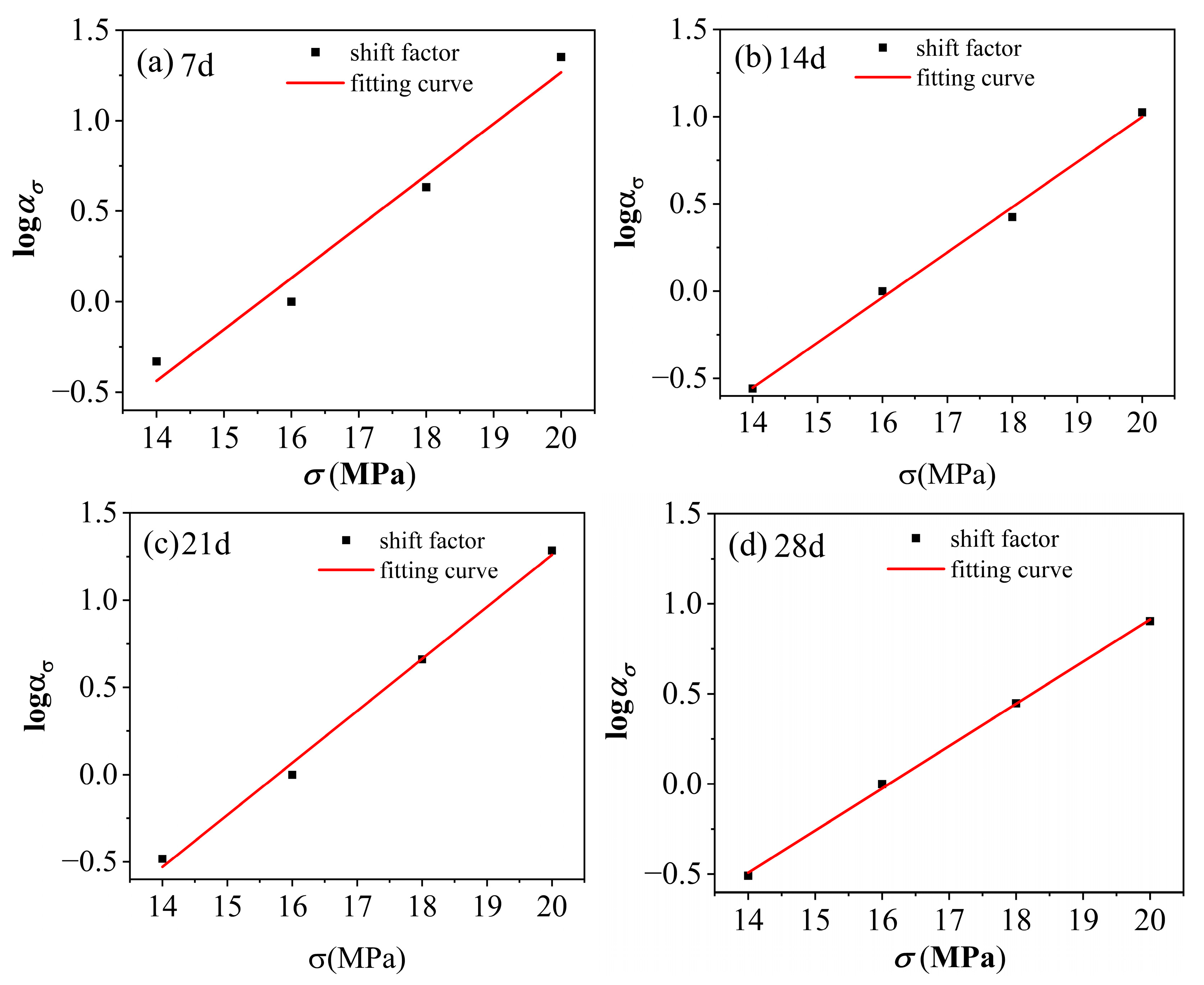
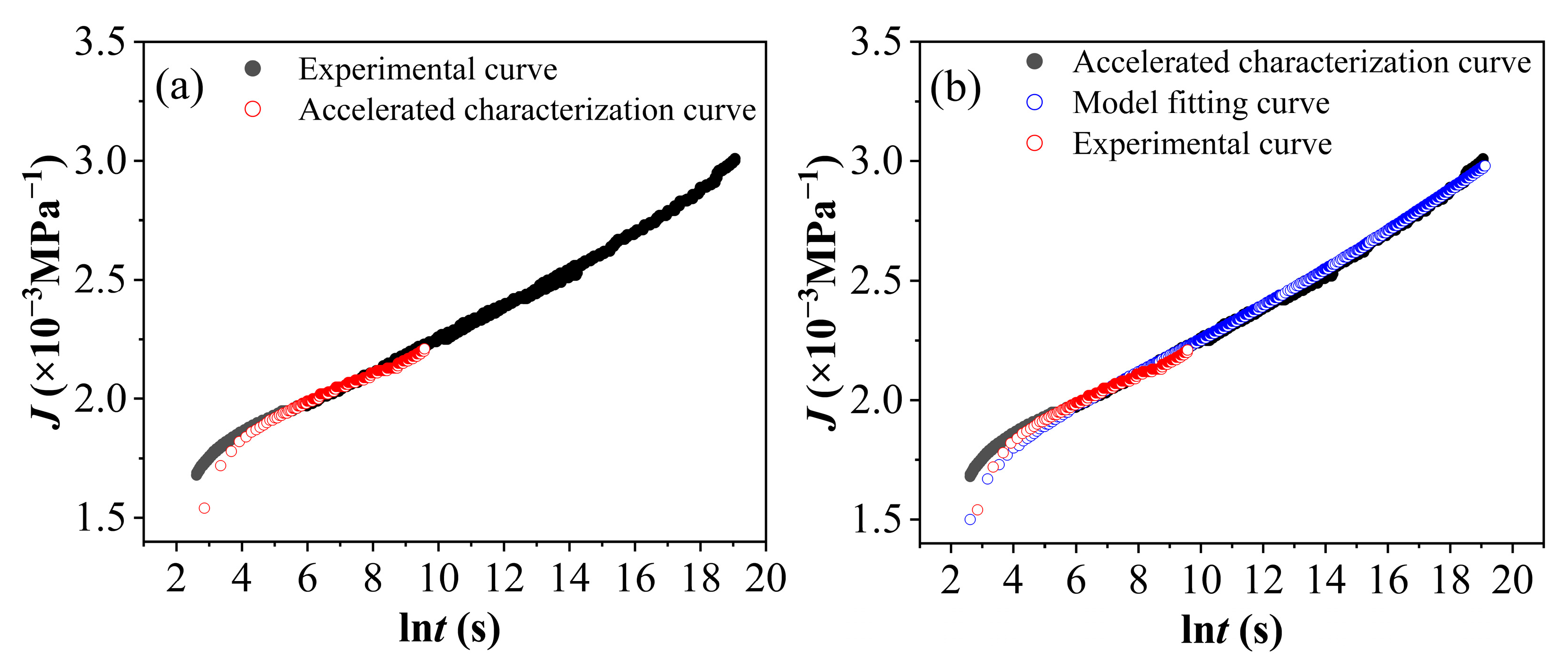
- This study validated the effectiveness of the time–stress equivalence principle and the time–aging equivalence principle under a hygrothermal coupling environment. By selecting appropriate reference stress and reference aging time, the short-term experimental data obtained within 4 h were effectively extrapolated to predict the long-term (approximately 6.5 years) creep behavior. This approach provides a reusable methodological framework for predicting the long-term performance of polyolefin viscoelastic materials. More importantly, when these equivalence principles were applied under accelerated aging conditions, the resulting shift factors exhibited an approximately linear distribution. This suggests that, based on the methodology verified in this study, the shift factors for polyvinyl chloride materials can be determined across different aging times, environmental conditions, or stress levels. Consequently, the creep compliance master curve can be constructed under the selected reference conditions (i.e., reference environment and stress level), significantly reducing both the number of required experimental conditions and the time needed to obtain long-term creep data.
- The local structural derivative Kelvin model was employed to fit the long-term creep behavior of PVC, effectively capturing the time-dependent deformation characteristics under high-temperature and high-humidity conditions. The high goodness-of-fit (R2 ≥ 0.99) of the model for PVC creep data under the coupled effects of heat and humidity confirmed its suitability for this system and indicated its potential for simulating the creep behavior of polymers under multi-factor environmental coupling (e.g., heat, humidity, and stress). However, its applicability across different material systems requires further investigation and validation.
- In future research, we plan to expand the range of experimental temperatures and humidities to obtain more comprehensive data and verify the universality of the conclusions. Furthermore, multiple models will be integrated for comparison with the local structural derivative Kelvin model, enabling a detailed evaluation of the advantages and limitations of each model in characterizing the creep behavior of PVC. This strategy is intended to furnish robust theoretical and methodological support for research in this field and facilitate the broader and safer application of PVC materials in engineering contexts.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, X.R. Current status and prospects of PVC plastic building materials, China. Plastics 2024, 38, 145–153. [Google Scholar] [CrossRef]
- Yarahmadi, N.; Jakubowicz, I.; Hjertberg, T. The effects of heat treatment and ageing on the mechanical properties of rigid PVC. Polym. Degrad. Stab. 2003, 82, 59–72. [Google Scholar] [CrossRef]
- Quennehen, P.; Royaud, I.; Seytre, G.; Gain, O.; Rain, P.; Espilit, T.; François, S. Determination of the aging mechanism of single core cables with PVC insulation. Polym. Degrad. Stab. 2015, 119, 96–104. [Google Scholar] [CrossRef]
- Frigione, M.; Rodríguez-Prieto, A. Can Accelerated Aging Procedures Predict the Long Term Behavior of Polymers Exposed to Different Environments? Polymers 2021, 13, 2688. [Google Scholar] [CrossRef]
- Krauklis, A.E. Modular Paradigm for Composites: Modeling Hydrothermal Degradation of Glass Fibers. Fibers 2021, 9, 83. [Google Scholar] [CrossRef]
- Jemii, H.; Boubakri, A.; Bahri, A.; Hammiche, D.; Elleuch, K.; Guermazi, N. Tribological behavior of virgin and aged polymeric pipes under dry sliding conditions against steel. Tribol. Int. 2020, 154, 106727. [Google Scholar] [CrossRef]
- Sharafi, S.; Santare, M.; Gerdes, J.; Advani, S. A review of factors that influence the fracture toughness of extrusion-based additively manufactured polymer and polymer composites. Addit. Manuf. 2021, 38, 101830. [Google Scholar] [CrossRef]
- Ferreira, M.M.; Lins, V.d.F.C. Failure in automobile headlight lenses. Eng. Fail. Anal. 2019, 104, 844–855. [Google Scholar] [CrossRef]
- Sadasivuni, K.K.; Saha, P.; Adhikari, J.; Deshmukh, K.; Ahamed, M.B.; Cabibihan, J. Recent advances in mechanical properties of biopolymer composites: A review. Polym. Compos. 2019, 41, 32–59. [Google Scholar] [CrossRef]
- Fu, C.; Yang, X. Bending dolution of viscoelastic Timoshenko cracked beam strengthened with fiber-reinforced polymer. J. Xinyang Norm. Univ. 2019, 32, 327–332. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X. A review of polymer electrolyte membrane fuel cell durability for vehicular applications: Degradation modes and experimental techniques. Energy Convers. Manag. 2019, 199, 112022. [Google Scholar] [CrossRef]
- Guedes, R.M. (Ed.) Creep and Fatigue in Polymer Matrix Composites; Woodhead Publishing: Cambridge, UK, 2019. [Google Scholar]
- Jiang, Z.; Fang, Z.; Fang, C.; Li, Q.; Wang, Z. Experimental investigation on high-temperature creep behavior of carbon fiber reinforced polymer cable. Compos. Struct. 2022, 291, 115533. [Google Scholar] [CrossRef]
- Randhawa, K.S.; Patel, A. The effect of environmental humidity/water absorption on tribo-mechanical performance of polymers and polymer composites—A review. Ind. Lubr. Tribol. 2021, 73, 1146–1158. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Liu, Q.; Shi, W.; Li, K. Modeling and Analysis of Performance Degradation Data for Reliability Assessment: A Review. IEEE Access 2020, 8, 74648. [Google Scholar] [CrossRef]
- Hagnell, M.; Kumaraswamy, S.; Nyman, T.; Åkermo, M. From aviation to automotive—A study on material selection and its implication on cost and weight efficient structural composite and sandwich designs. Heliyon 2020, 6, e03716. [Google Scholar] [CrossRef]
- Li, H.; Luo, Y.; Hu, D. Long term creep assessment of room-temperature cured epoxy adhesive by time-stress superposition and fractional rheological model. Appl. Rheol. 2018, 28, 201864796. [Google Scholar] [CrossRef]
- Kumar, V.; Koorata, P.K. Low stress creep response of PTFE sealants applied to PEM fuel cells. J. Appl. Polym. Sci. 2024, 141, 55292. [Google Scholar] [CrossRef]
- Eftekhari, M.; Fatemi, A. Creep behavior and modeling of neat, talc-filled, and short glass fiber reinforced thermoplastics. Compos. Part B Eng. 2016, 97, 68–83. [Google Scholar] [CrossRef]
- Bennis, H.; Elkori, R.; Hachim, A.; El Had, K.; El Maliki, A.; Sandabad, S. Determining the impact of accelerated hydrothermal aging on the mechanical properties of polyvinyl chloride and chlorinated polyvinyl chloride. J. Polym. Res. 2025, 32, 1–8. [Google Scholar] [CrossRef]
- Luo, W.; Wang, C.; Hu, X.; Yang, T. Long-term creep assessment of viscoelastic polymer by time-temperature-stress superposition. Acta Mech. Solida Sin. 2012, 25, 571–578. [Google Scholar] [CrossRef]
- Jiang, C.; Jiang, H.; Zhu, Z.; Zhang, J.; Guo, S.; Xiong, Y. Application of time-temperature-stress superposition principle on the accelerated physical aging test of polycarbonate. Polym. Eng. Sci. 2015, 55, 2215–2221. [Google Scholar] [CrossRef]
- Zhu, Z.; Jiang, C.; Cheng, Q.; Zhang, J.; Guo, S.; Xiong, Y.; Fu, B.; Yang, W.; Jiang, H. Accelerated aging test of hydrogenated nitrile butadiene rubber using the time–temperature–strain superposition principle. RSC Adv. 2015, 5, 90178–90183. [Google Scholar] [CrossRef]
- Sun, T.L.; Luo, F.; Hong, W.; Cui, K.; Huang, Y.; Zhang, H.J.; King, D.R.; Kurokawa, T.; Nakajima, T.; Gong, J.P. Bulk Energy Dissipation Mechanism for the Fracture of Tough and Self-Healing Hydrogels. Macromolecules 2017, 50, 2923–2931. [Google Scholar] [CrossRef]
- Zhu, J.J.; Chen, H.J.; Yu, X.N.; Zhu, J.J. Effect of montmorillonite on microstructure and mechanical properties of epoxy resin. J. Xinyang Norm. Univ. 2014, 27, 247–250. [Google Scholar] [CrossRef]
- Xie, S.L.; Wang, H.T.; Zhang, Y.M. Performance study of Z-pin reinforced composite laminates under hygrothermal conditions. J. Xinyang Norm. Univ. 2022, 35, 304–309. [Google Scholar] [CrossRef]
- Thoral, C.; Soulagnet, G.; Bussiere, P.-O.; Therias, S. Impact of photo- and thermooxidative ageing of NBR/PVC blends on the formation of cracks. Polym. Degrad. Stab. 2023, 220, 110633. [Google Scholar] [CrossRef]
- Rigoli, P.S.; Murakami, L.M.S.; Diniz, M.F.; Azevedo, M.F.P.; Mattos, E.D.C.; Dutra, R.d.C.L.; Cassu, S. Quantification of Aerospace Polymer Blends by Thermogravimetric Analysis and Infrared Spectrometry. J. Aerosp. Technol. Manag. 2019, 11, e0619. [Google Scholar] [CrossRef]
- Gibson, W.; Patterson, J. Observing Nano-Scale Dynamics of Active Soft Materials by In Situ Electrochemistry and Liquid Cell Transmission Electron Microscopy. Microsc. Microanal. 2022, 28, 96–99. [Google Scholar] [CrossRef]
- Ingham, B. X-ray scattering characterisation of nanoparticles. Crystallogr. Rev. 2015, 21, 229–303. [Google Scholar] [CrossRef]
- Saad, M.; Bucki, M.; Bujok, S.; Pawcenis, D.; Rijavec, T.; Górecki, K.; Bratasz, Ł.; Cigić, I.K.; Strlič, M.; Kruczała, K. The impact of heat and humidity on unplasticized poly(vinyl chloride). Polym. Degrad. Stab. 2025, 238, 16121. [Google Scholar] [CrossRef]
- Ouyang, Z.; Zhang, Z.; Jing, Y.; Bai, L.; Zhao, M.; Hao, X.; Li, X.; Guo, X. The photo-aging of polyvinyl chloride microplastics under different UV irradiations. Gondwana Res. 2022, 108, 72–80. [Google Scholar] [CrossRef]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity, An Introduction; Springer Science+Business Media, LLC: New York, NY, USA, 2008. [Google Scholar]
- Yao, C.; Xia, Y.; Zhu, Z.; Yang, Z.; Chen, K.; Jiang, H. Investigation on brittle-ductile transition of PMMA mode-II fracture using time-temperature superposition principle. Eng. Fract. Mech. 2022, 273, 108733. [Google Scholar] [CrossRef]
- Gao, Y.F.; Niu, J.N. Mechanical properties of viscoelastic bodies obeying the fractional-order Zener model. J. Xinyang Norm. Univ. 2019, 32, 191–195. [Google Scholar] [CrossRef]
- Hao, A.; Chen, Y.; Chen, J.Y. Creep and recovery behavior of kenaf/polypropylene nonwoven composites. J. Appl. Polym. Sci. 2014, 131, 8864–8874. [Google Scholar] [CrossRef]
- Martins, C.; Pinto, V.; Guedes, R.M.; Marques, A.T. Creep and Stress Relaxation Behaviour of PLA-PCL Fibres—A Linear Modelling Approach. Procedia Eng. 2015, 114, 768–775. [Google Scholar] [CrossRef][Green Version]
- Tarkashvand, A.; Daneshjou, K.; Golmohammadi, A.; Daneshjoo, Z. Viscoelastic-acoustic response of new polymeric matrix composite shells considering cavity resonances using a new approach: Layered viscoelastic model. Compos. Struct. 2022, 292, 115673. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Alam, M.; Rahman, M.; Islam, A.; Bhowmick, A.K. Model-Based Study of Creep and Recovery of a Glassy Polymer. Adv. Polym. Technol. 2022, 2022, 8032690. [Google Scholar] [CrossRef]
- Jamshidi, M.; Shokrieh, M. On the Schapery nonlinear viscoelastic model: A review. Eur. J. Mech. A/Solids 2024, 108, 105403. [Google Scholar] [CrossRef]
- Hajikarimi, P.; Ehsani, M.; EL Haloui, Y.; Tehrani, F.F.; Absi, J.; Nejad, F.M. Fractional viscoelastic modeling of modified asphalt mastics using response surface method. Constr. Build. Mater. 2022, 317, 125958. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, Y.C.; Gao, Y.F.; Zhang, W.W.; Yan, Q.F.; Liu, L.C. Quasi-Static response analysis of fractional viscoelastic compressible oil and gas well tubing strings. J. Xinyang Norm. Univ. 2021, 34, 331–338+344. [Google Scholar] [CrossRef]
- Xiang, G.; Yin, D.; Meng, R.; Cao, C. Predictive model for stress relaxation behavior of glassy polymers based on variable-order fractional calculus. Polym. Adv. Technol. 2020, 32, 703–713. [Google Scholar] [CrossRef]
- GB/T 1040.1-2018; Plastics—Determination of Tensile Properties—Part 1: General Principles. Standardization Administration of China: Beijing, China, 2018.
- GB/T 1040.2-2022; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. Standardization Administration of China: Beijing, China, 2022.
- IEC 60068-2-67:1995; Environmental Testing—Part 2-67: Tests—Test Cy: Damp Heat, Steady State, Accelerated Test Primarily Intended for Components. IEC: Geneva, Switzerland, 1995.
- GB/T 2918-2018; Plastics—Standard atmospheres for Conditioning and Testing. Standardization Administration of China: Beijing, China, 2018.
- ISO 899-1:2017; Plastics—Determination of Creep Behaviour—Part 1: Tensile Creep. ISO: Geneva, Switzerland, 2017.
- Jazouli, S.; Luo, W.; Bremand, F.; Vu-Khanh, T. Application of time–stress equivalence to nonlinear creep of polycarbonate. Polym. Test. 2005, 24, 463–467. [Google Scholar] [CrossRef]
- Wang, B.; Fancey, K.S. Application of time–stress superposition to viscoelastic behavior of polyamide 6,6 fiber and its “true” elastic modulus. J. Appl. Polym. Sci. 2017, 134, 44971. [Google Scholar] [CrossRef]
- Sharma, J.; Tewari, K.; Arya, R.K. Diffusion in polymeric systems–A review on free volume theory. Prog. Org. Coatings 2017, 111, 83–92. [Google Scholar] [CrossRef]
- Urzhumtsev, Y.S.; Maksimov, R.D. Time-stress superposition in nonlinear viscoelasticity. Mech. Compos. Mater. 1972, 4, 318–320. [Google Scholar] [CrossRef]
- Richert, R. On the origin of time-aging-time superposition. J. Chem. Phys. 2024, 160, 024501. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.P.; Gong, Q.; Li, M.D. Study on time-aging temperature equivalence of polyethylene creep behavior. Int. J. Mech. Res. 2021, 10, 267–274. [Google Scholar] [CrossRef]
- Fonseca, E.; da Silva, V.D.; Amico, S.C.; Pupure, L.; Joffe, R.; Schrekker, H.S. Time-dependent properties of epoxy resin with imidazolium ionic liquid. J. Appl. Polym. Sci. 2021, 138, 51369. [Google Scholar] [CrossRef]
- Al-Maqdasi, Z.; Pupure, L.; Gong, G.; Emami, N.; Joffe, R. Time-dependent properties of graphene nanoplatelets reinforced high-density polyethylene. J. Appl. Polym. Sci. 2021, 138, 507833. [Google Scholar] [CrossRef]
- Basso, M.; Pupure, L.; Simonato, M.; Furlanetto, R.; De Nardo, L.; Joffe, R. Nonlinear creep behaviour of glass fiber reinforced polypropylene: Impact of aging on stiffness degradation. Compos. Part B Eng. 2019, 163, 702–709. [Google Scholar] [CrossRef]
- Yang, X.; Liang, Y.; Chen, W. A local structural derivative PDE model for ultraslow creep. Comput. Math. Appl. 2018, 76, 1713–1718. [Google Scholar] [CrossRef]
- Guan, P.Y.; Liang, Y.J. A local structural derivative constitutive model for ultraslow creep of viscoelastic materials. J. Chongqing Univ. 2022, 45, 49–61. [Google Scholar] [CrossRef]
- Gouinlock, E.V. Degrees of order from X-ray diffraction in highly crystalline poly(vinyl chloride). J. Polym. Sci. Polym. Phys. Ed. 1975, 13, 961–970. [Google Scholar] [CrossRef]
- Dawson, P.C.; Gilbert, M.; Maddams, W.F. Comparison of X-Ray diffraction and thermal analysis methods for assessing order in poly(vinyl chloride). J. Polym. Sci. Part B Polym. Phys. 1991, 29, 1407–1418. [Google Scholar] [CrossRef]
- Guerrero, S.J.; Veloso, H.; Randon, E. On the analysis of wide-angle X-ray diffraction curves of poly(vinyl chloride) samples. Polymer 1990, 31, 1615–1622. [Google Scholar] [CrossRef]

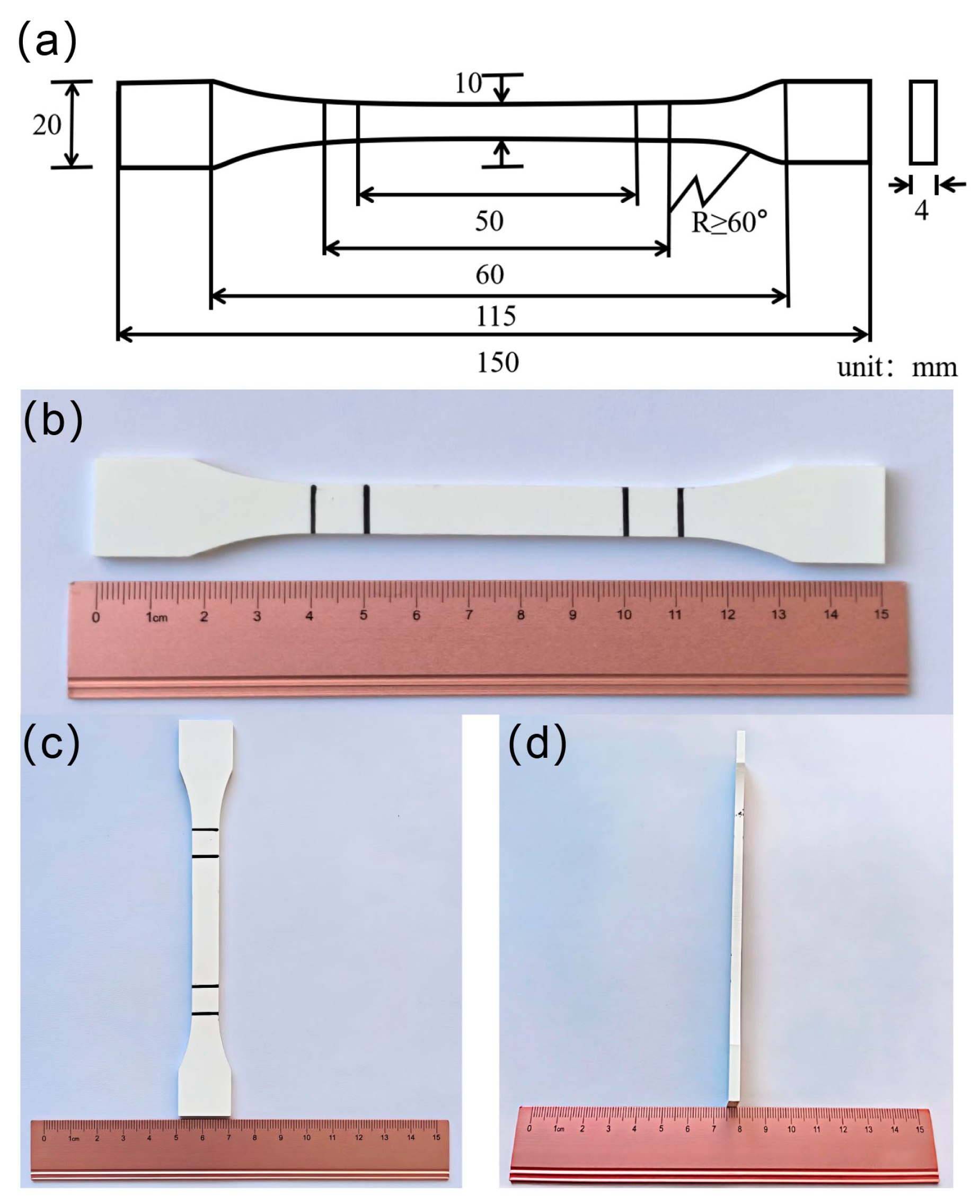








| Aging Time (Days) | Tensile Strength (MPa) | SD | CV (%) | Elongation at Break (%) | SD | CV (%) |
|---|---|---|---|---|---|---|
| 0 | 38.02 | ±0.8 | 2.1 | 16.0 | ±0.5 | 3.1 |
| 7 | 36.22 | ±0.7 | 1.9 | 14.4 | ±0.6 | 4.2 |
| 14 | 35.12 | ±0.9 | 2.6 | 12.8 | ±0.4 | 3.1 |
| 21 | 34.04 | ±1.1 | 3.2 | 11.6 | ±0.6 | 5.2 |
| 28 | 32.35 | ±1.3 | 4.0 | 10.6 | ±0.8 | 7.5 |
| Aging Time (Days) | Stress (MPa) | Mean Creep Rate (h−1) | SD | CV (%) |
|---|---|---|---|---|
| 0 | 14 | 3.96 × 10−4 | 3.37 × 10−5 | 8.5 |
| 16 | 5.02 × 10−4 | 4.67 × 10−5 | 9.3 | |
| 18 | 6.54 × 10−4 | 6.67 × 10−5 | 10.2 | |
| 20 | 8.09 × 10−4 | 9.78 × 10−5 | 12.1 | |
| 7 | 14 | 6.55 × 10−4 | 6.23 × 10−5 | 9.5 |
| 16 | 7.64 × 10−4 | 6.71 × 10−5 | 8.8 | |
| 18 | 8.97 × 10−4 | 9.43 × 10−5 | 10.5 | |
| 20 | 1.04 × 10−3 | 1.25 × 10−4 | 12.0 | |
| 14 | 14 | 9.55 × 10−4 | 7.83 × 10−5 | 8.2 |
| 16 | 1.13 × 10−3 | 1.30 × 10−4 | 11.5 | |
| 18 | 1.31 × 10−3 | 1.18 × 10−4 | 9.0 | |
| 20 | 1.52 × 10−3 | 1.52 × 10−4 | 10.0 | |
| 21 | 14 | 7.75 × 10−4 | 6.74 × 10−5 | 8.7 |
| 16 | 9.13 × 10−4 | 8.95 × 10−5 | 9.8 | |
| 18 | 1.07 × 10−3 | 1.20 × 10−4 | 11.2 | |
| 20 | 1.23 × 10−3 | 1.27 × 10−4 | 10.4 | |
| 28 | 14 | 1.00 × 10−3 | 9.19 × 10−5 | 9.2 |
| 16 | 1.19 × 10−3 | 1.00 × 10−4 | 8.4 | |
| 18 | 1.38 × 10−3 | 1.49 × 10−4 | 10.8 | |
| 20 | 1.59 × 10−3 | 1.83 × 10−4 | 11.5 |
| σ/MPa | 60 °C, 90%RH | |||
|---|---|---|---|---|
| 7 d | 14 d | 21 d | 28 d | |
| 14 MPa | −0.33 | −0.56 | −0.48 | −0.33 |
| 16 MPa | 0 | 0 | 0 | 0 |
| 18 MPa | 0.63 | 0.42 | 0.66 | 0.45 |
| 20 MPa | 1.35 | 1.03 | 1.28 | 0.90 |
| Shift factor equation | y = −4.41 + 0.28x | y = −4.20 + 0.26x | y = −4.68 + 0.30x | y = −3.26 + 0.21x |
| Number of Days | 7 d | 14 d | 21 d | 28 d |
|---|---|---|---|---|
| Shift factor | 0 | 2.12 | 5.68 | 7.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Su, X.; Gong, G.; Shao, A.; Zheng, Y. Macro-Microscopic Characterization and Long-Term Performance Prediction of Polyvinyl Chloride Under Hydrothermal Aging Based on Creep Behavior Analysis. Polymers 2025, 17, 2320. https://doi.org/10.3390/polym17172320
Li H, Su X, Gong G, Shao A, Zheng Y. Macro-Microscopic Characterization and Long-Term Performance Prediction of Polyvinyl Chloride Under Hydrothermal Aging Based on Creep Behavior Analysis. Polymers. 2025; 17(17):2320. https://doi.org/10.3390/polym17172320
Chicago/Turabian StyleLi, Hui, Xiaoxiao Su, Guan Gong, Aoxin Shao, and Yanan Zheng. 2025. "Macro-Microscopic Characterization and Long-Term Performance Prediction of Polyvinyl Chloride Under Hydrothermal Aging Based on Creep Behavior Analysis" Polymers 17, no. 17: 2320. https://doi.org/10.3390/polym17172320
APA StyleLi, H., Su, X., Gong, G., Shao, A., & Zheng, Y. (2025). Macro-Microscopic Characterization and Long-Term Performance Prediction of Polyvinyl Chloride Under Hydrothermal Aging Based on Creep Behavior Analysis. Polymers, 17(17), 2320. https://doi.org/10.3390/polym17172320







