Review of Developed Methods for Measuring Gas Uptake and Diffusivity in Polymers Enriched by Pure Gas under High Pressure
Abstract
1. Introduction
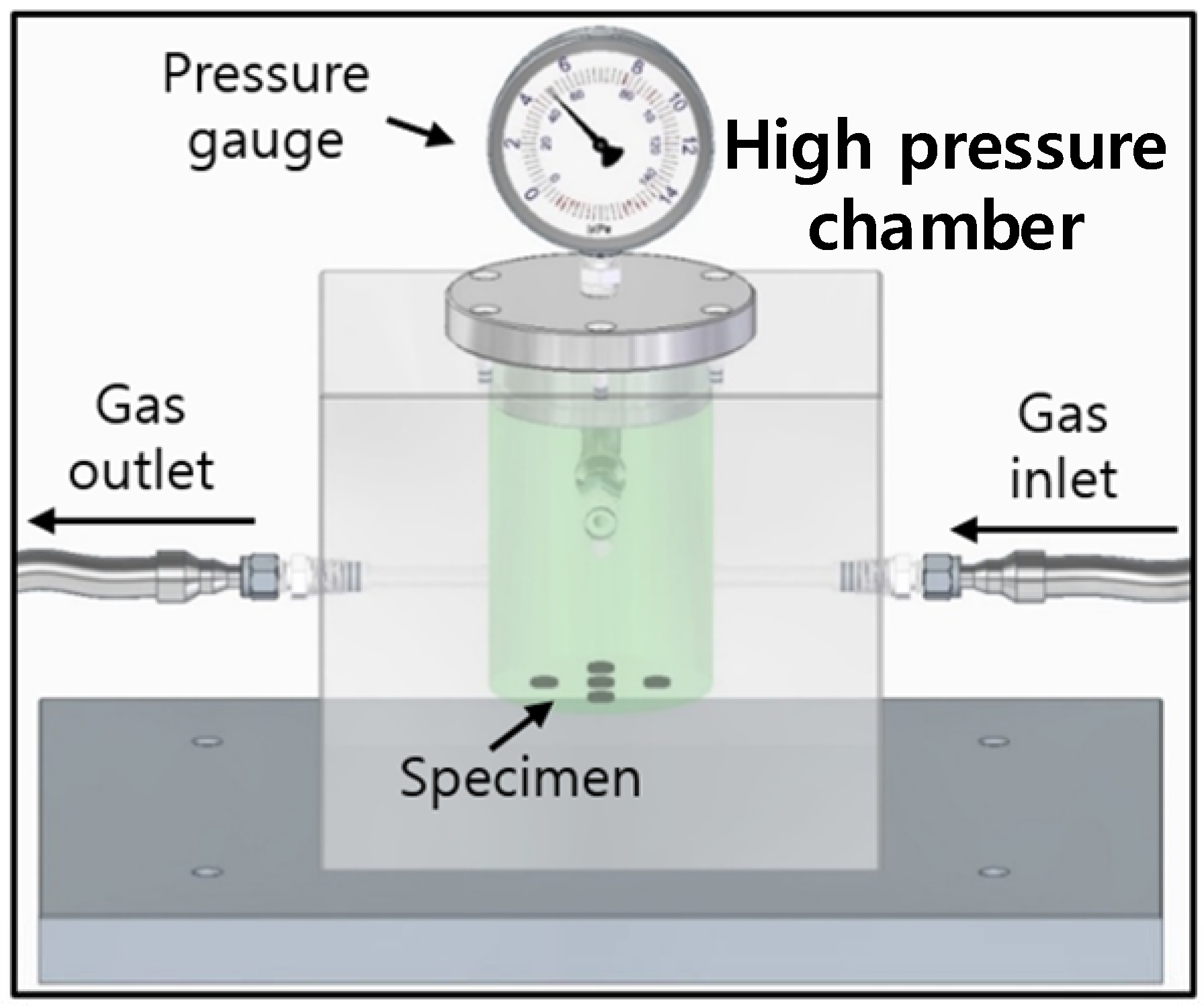
2. Sample Preparation and Gas Exposure under High Pressure Conditions
3. Measuring Principle and Procedure for the Four Methods
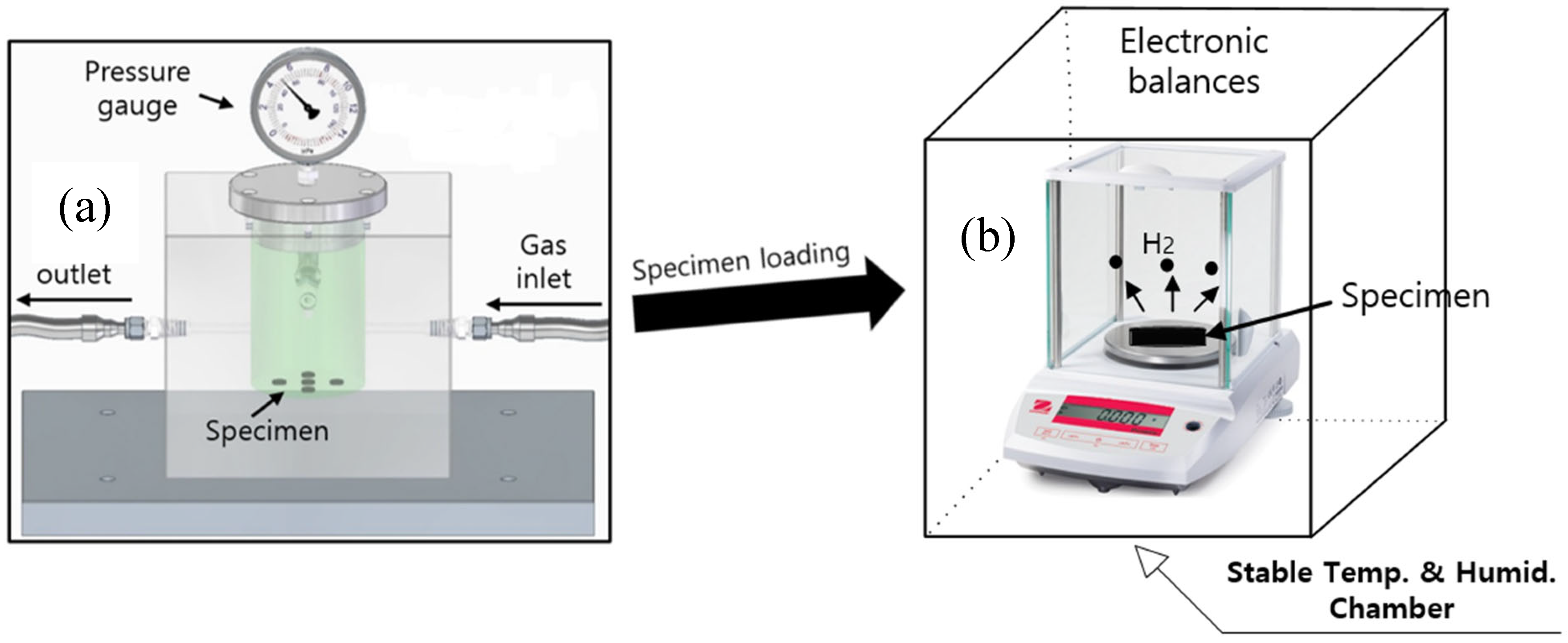
3.1. Gravimetric Measurement of the Gas Emitted by Enriched Specimens
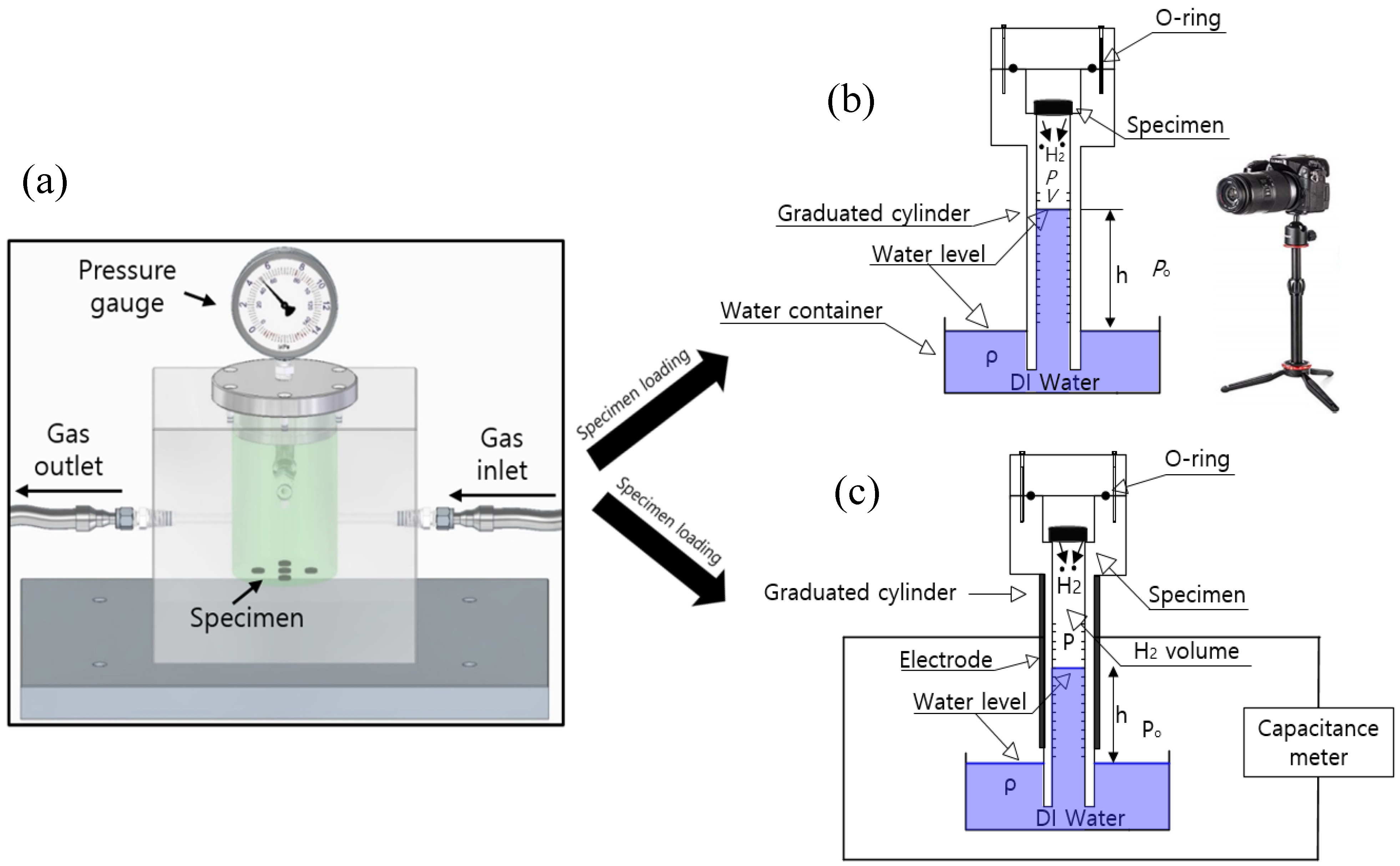
3.2. Volumetric Measurement of the Gas Emitted by Enriched Specimens
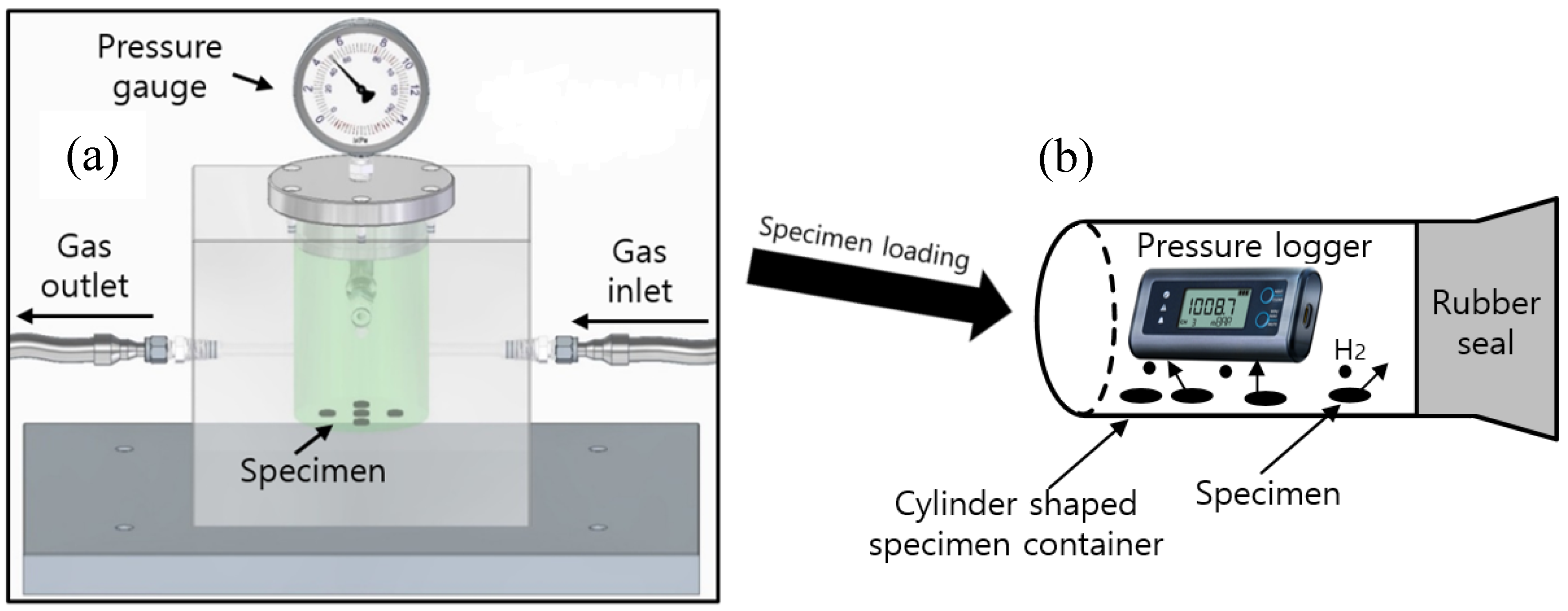
3.3. Manometric Measurement of the Gas Emitted by Enriched Specimens
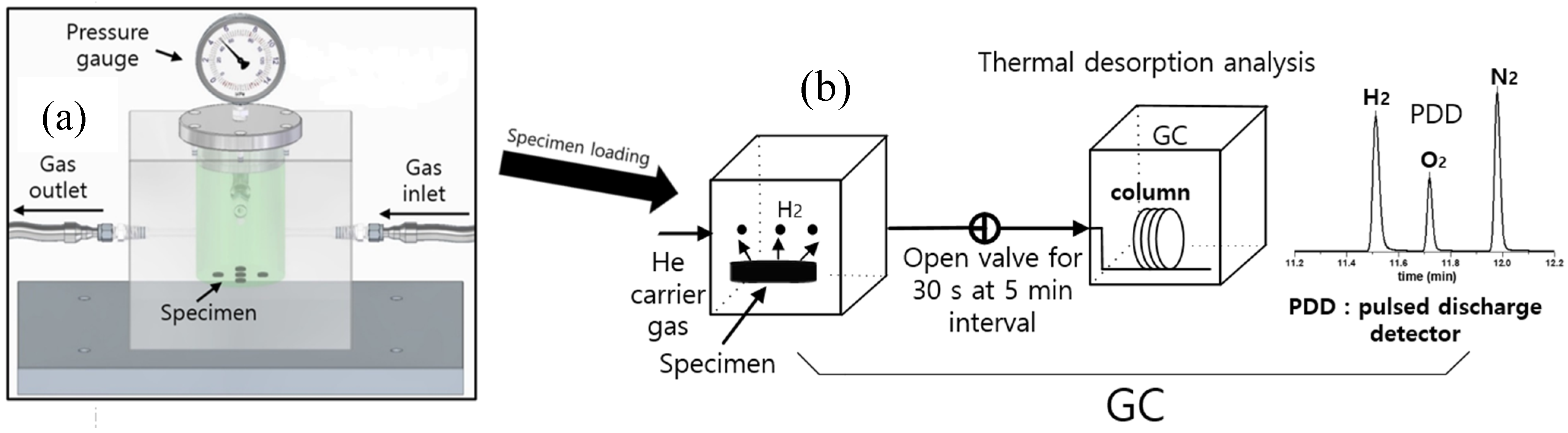
3.4. Gas Chromatography of the Gas Emitted by Enriched Specimens
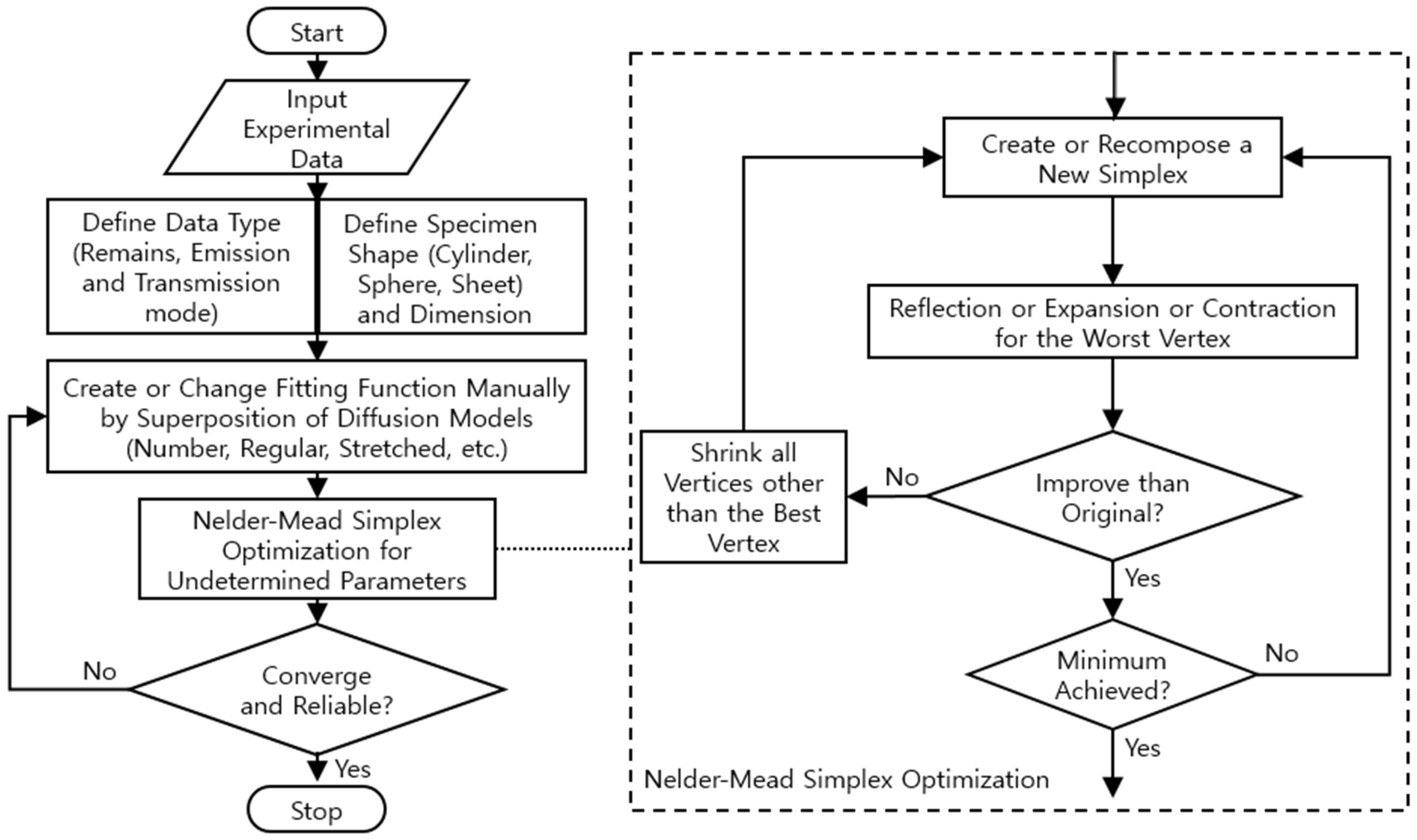
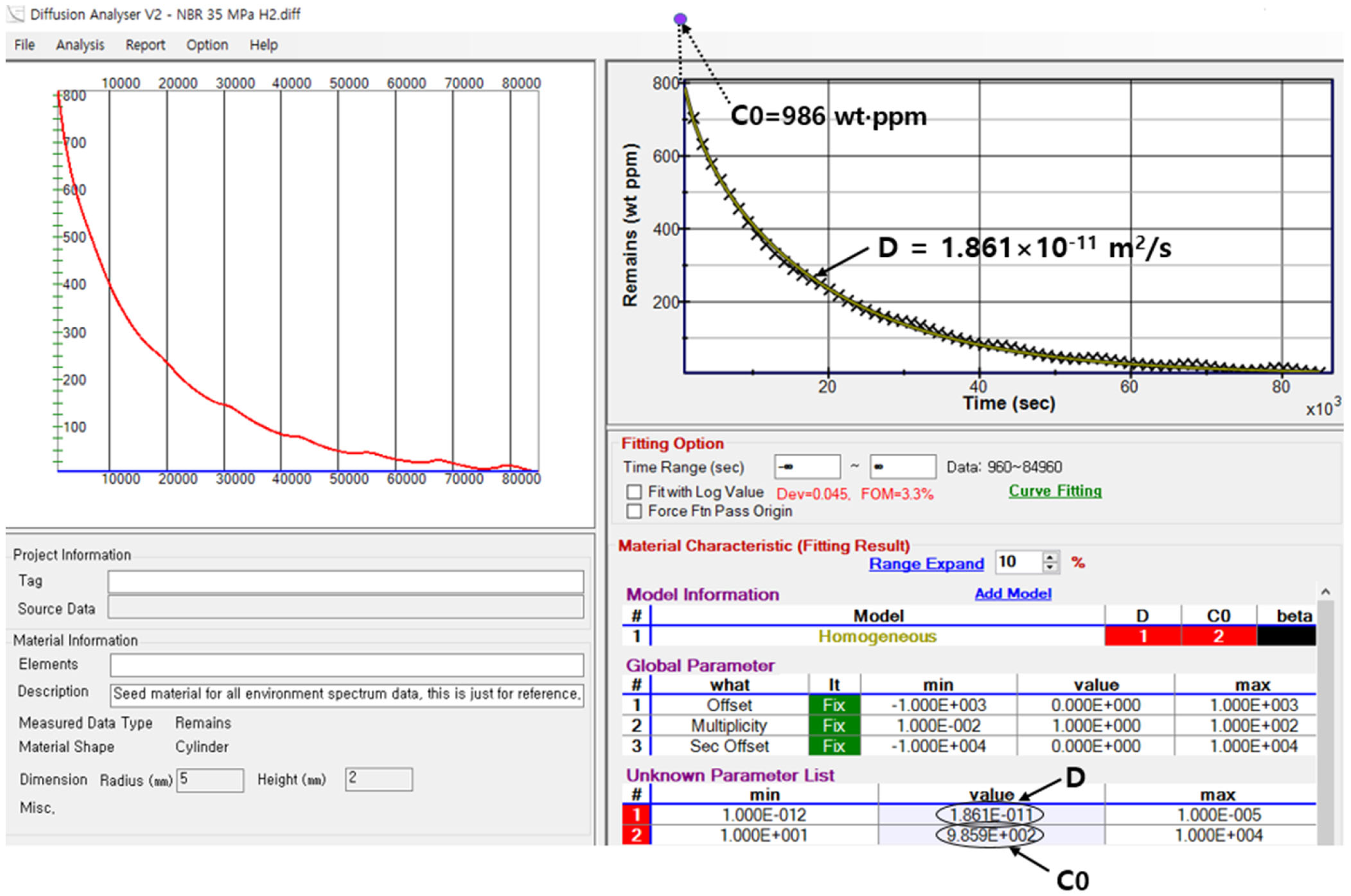
3.5. Diffusion Analysis Program for Obtaining Diffusion Parameters and its Algorithm
4. Results and Discussion
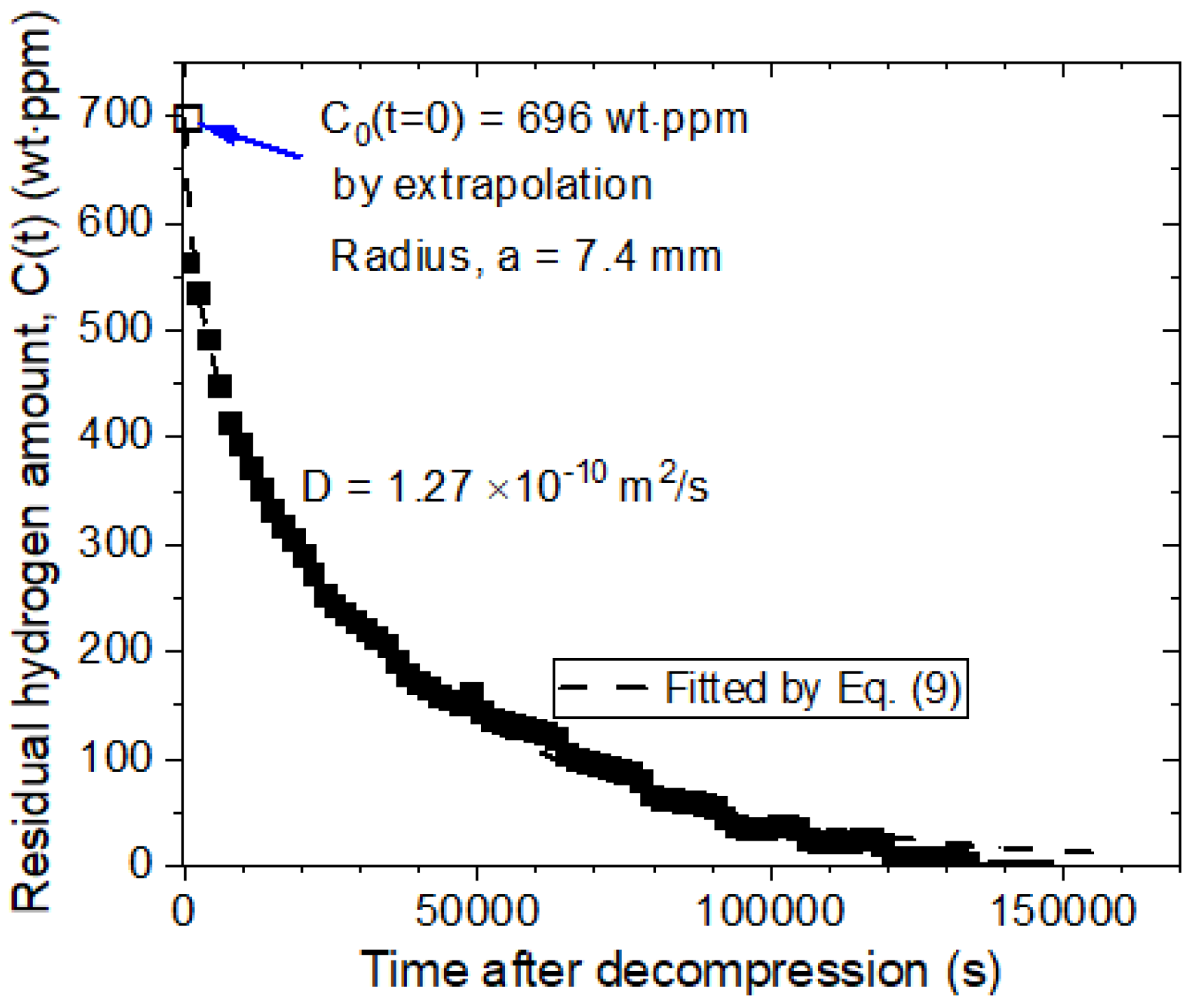
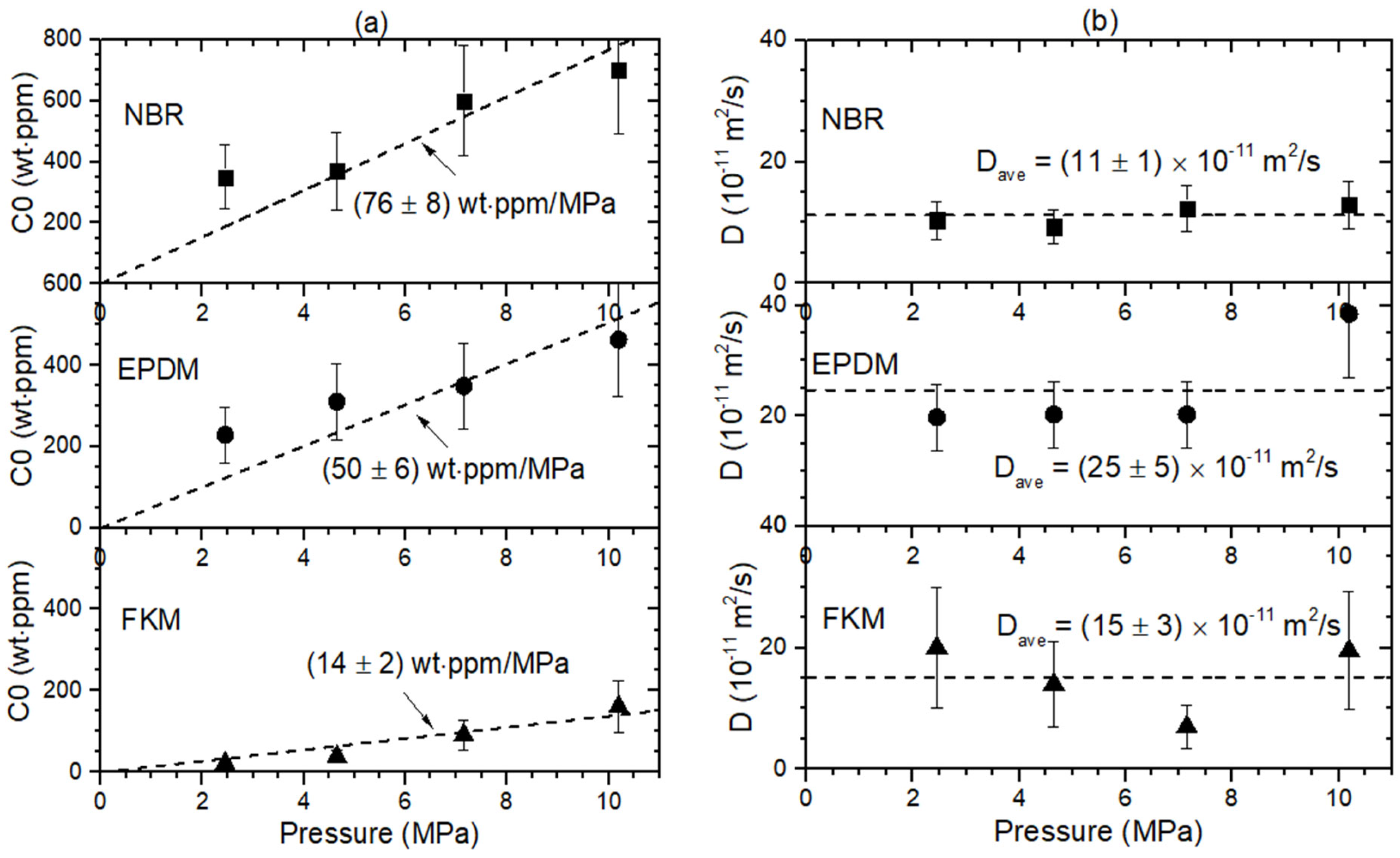
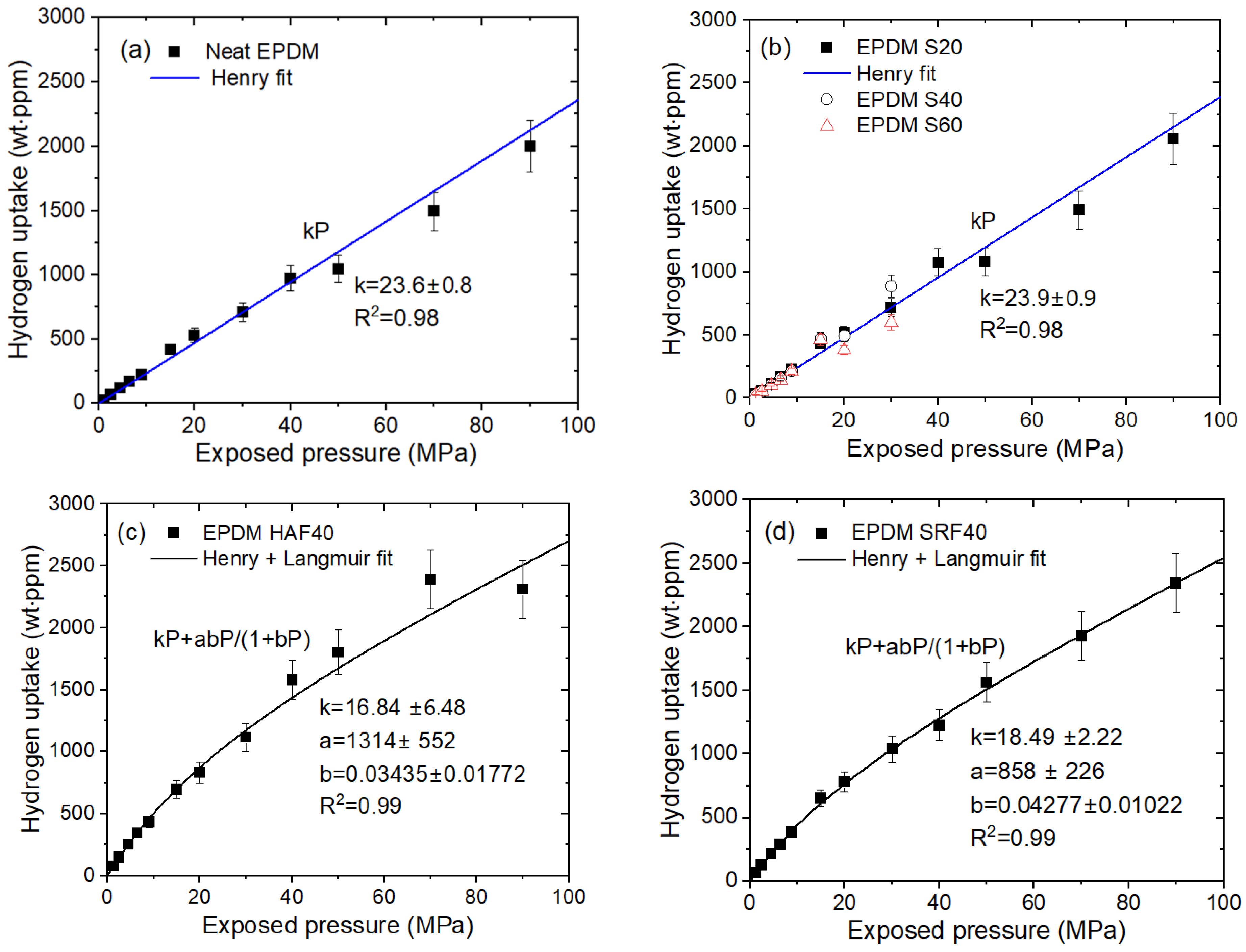
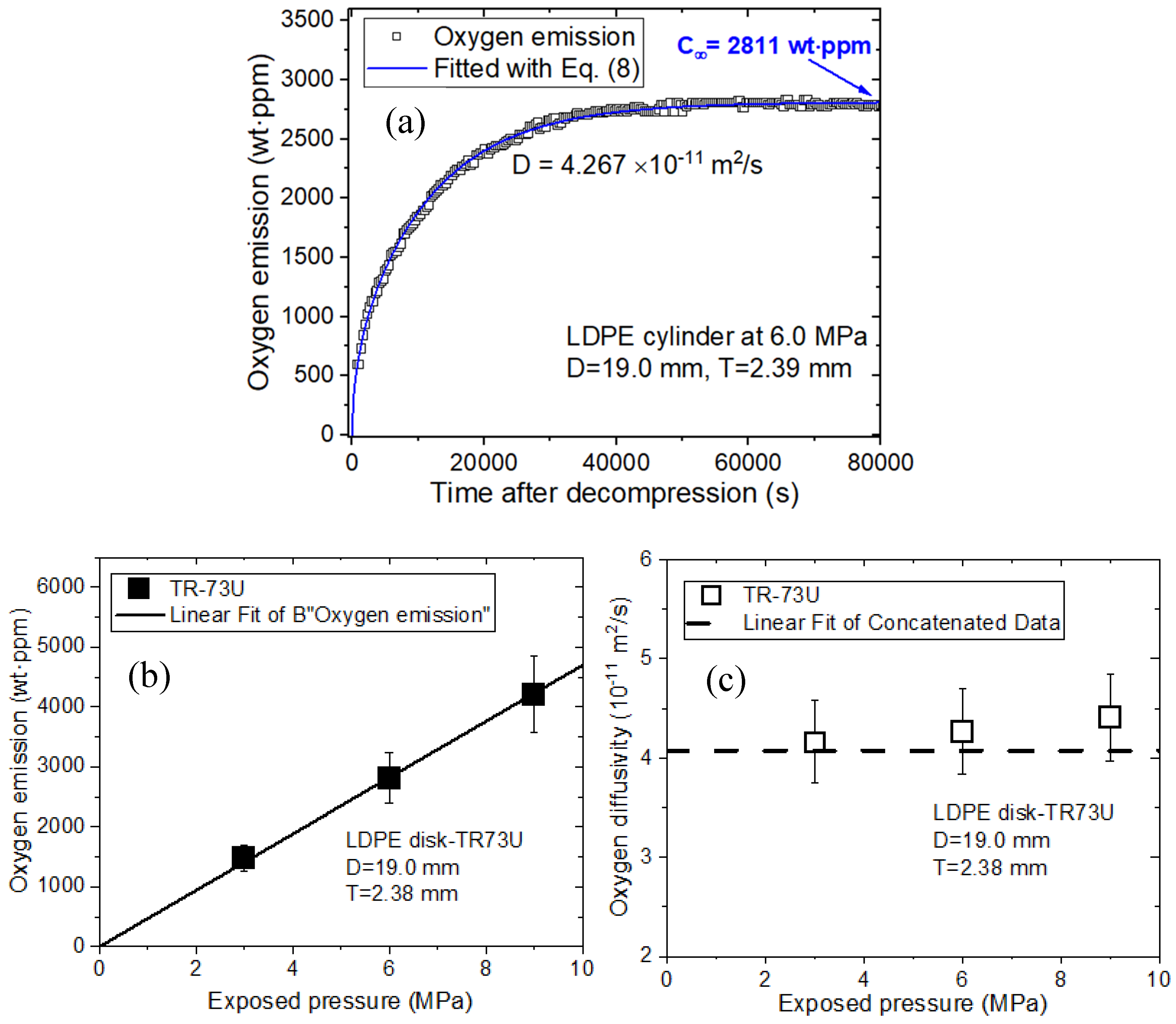
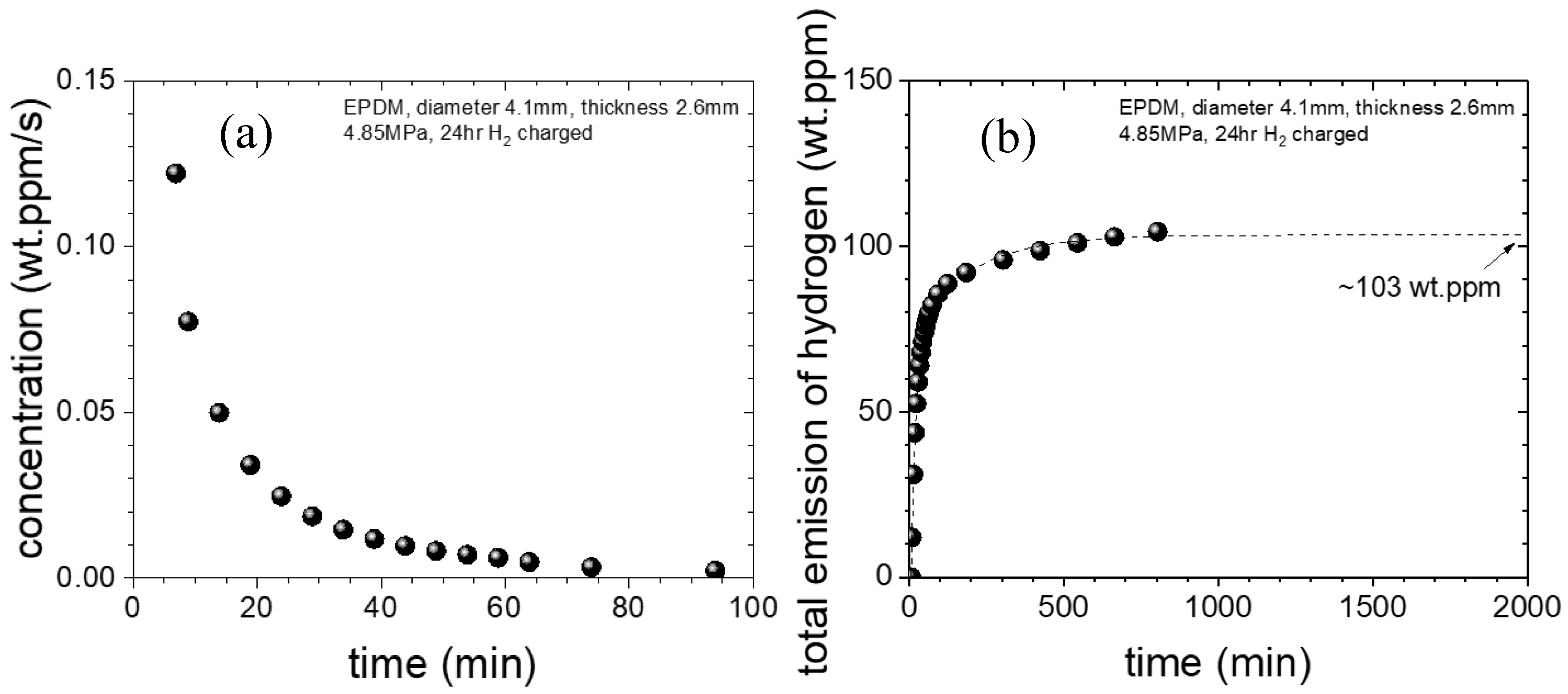
4.1. Gravimetric Method
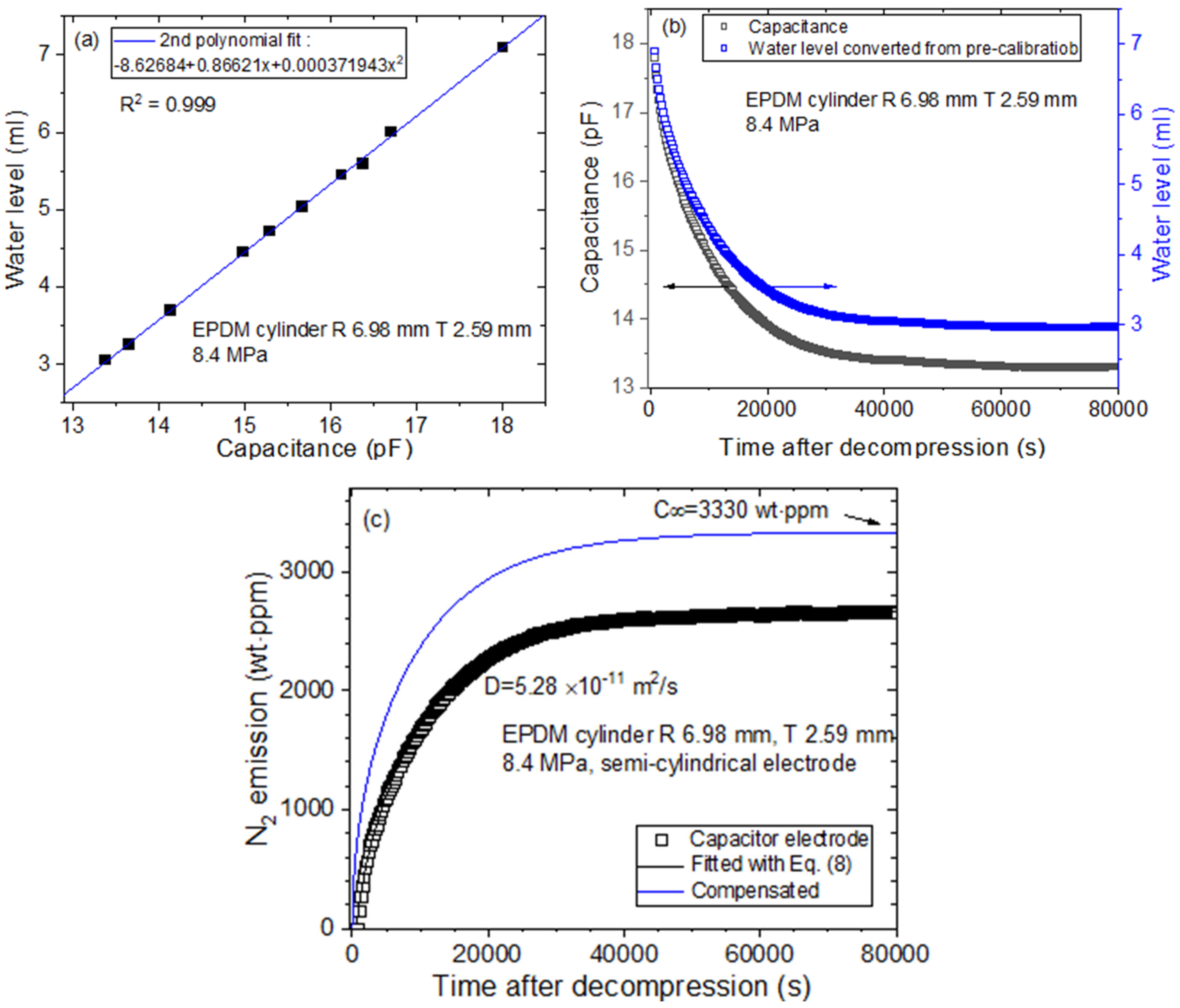
4.2. Volumetric Method
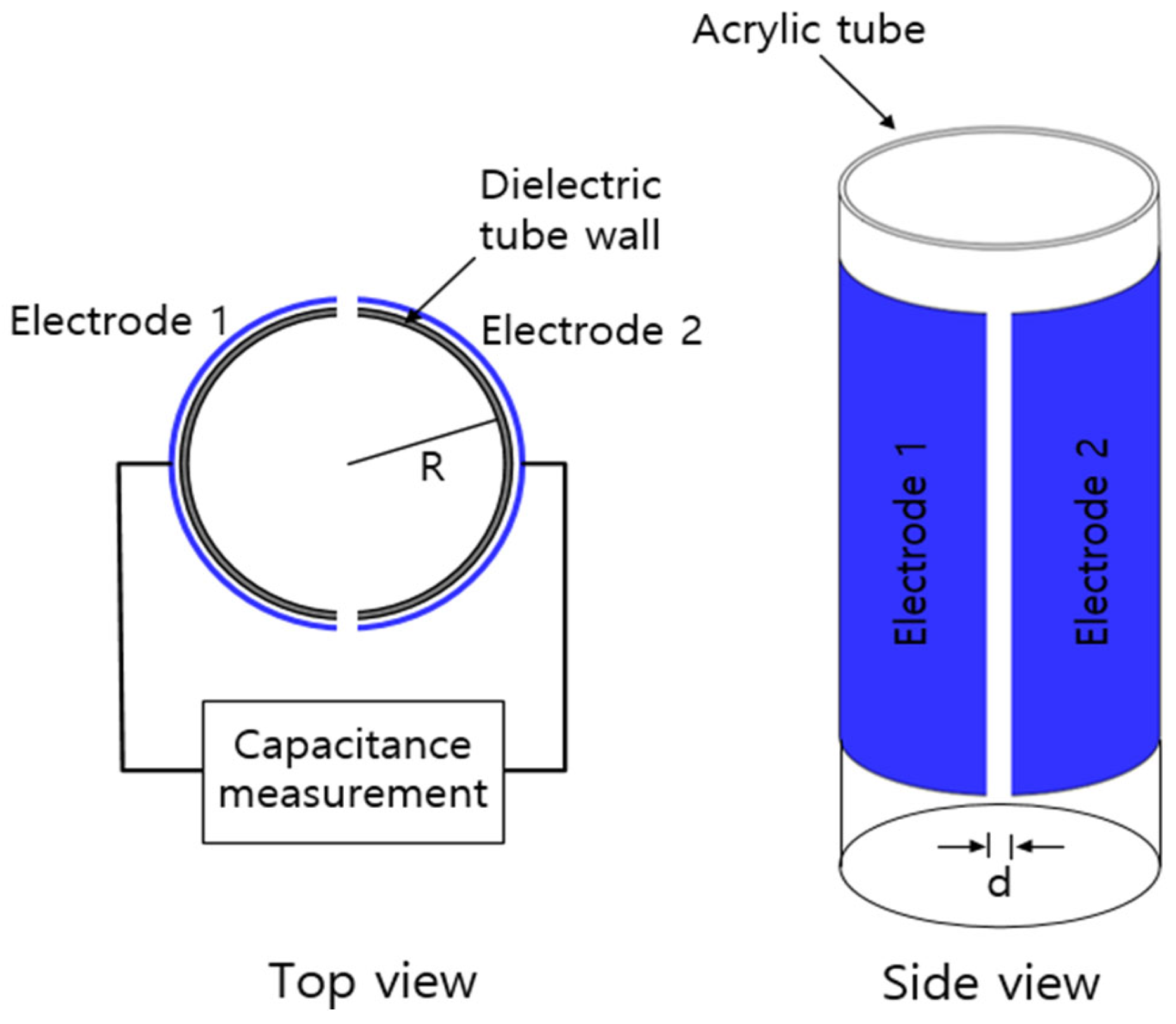
4.3. Manometric Method
4.4. Gas Chromatography
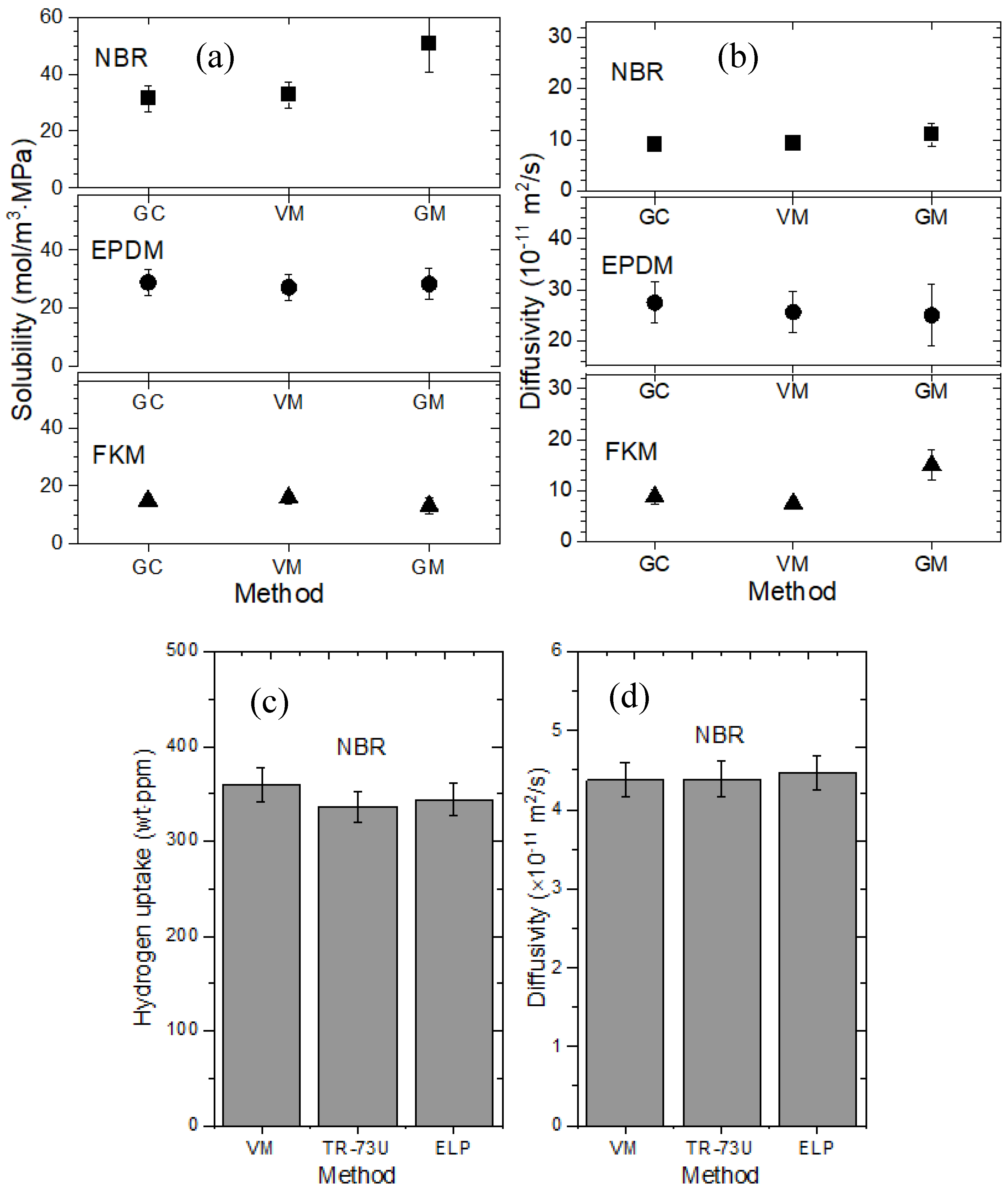
5. Comparisons of the Measured Results and Characteristics of the Four Methods
6. Conclusions
- The three developed methods are inexpensive and simple techniques, except for gas chromatography, for evaluating the gas uptake and diffusion of gas-enriched polymer materials under high-pressure conditions.
- The four developed methods are insensitive to variations in temperature and pressure, regardless of the specimen size, specimen shape, and testing gas species.
- All the methods are exactly calculable by applying the diffusion analysis program, which includes more than 50 terms in the summation of provided equation.
- The volumetric and manometric methods are flexible techniques in which the sensitivity, resolution, and range can be flexibly changed.
- All the methods are independent techniques, without any interaction between the testing gas molecule and gas sensor.
- The volumetric method is visible because the entire process of gas release and leakage can be observed by monitoring the change in water level.
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bessler, W.G. A new computational approach for SOFC impedance from detailed electrochemical reaction–diffusion models. Solid. State Ion. 2005, 176, 997–1011. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, Q.; Eić, M.; Balcom, B.J. CO2 dynamic adsorption/desorption on zeolite 5A studied by 13C magnetic resonance imaging. Langmuir 2005, 21, 4376–4381. [Google Scholar] [CrossRef] [PubMed]
- Primdahl, S.; Mogensen, M. Gas diffusion impedance in characterization of solid oxide fuel cell anodes. J. Electrochem. Soc. 1999, 146, 2827–2833. [Google Scholar] [CrossRef]
- Hagen, G.; Dubbe, A.; Fischerauer, G.; Moos, R. Thick-film impedance based hydrocarbon detection based on chromium(III) oxide/zeolite interfaces. Sens. Actuators B Chem. 2006, 118, 73–77. [Google Scholar] [CrossRef]
- Franke, M.E.; Simon, U. Solvate-supported proton transport in zeolites. ChemPhysChem 2004, 5, 465–472. [Google Scholar] [CrossRef]
- Simon, U.; Flesch, U.; Maunz, W.; Müller, R.; Plog, C. The effect of NH3 on the ionic conductivity of dehydrated zeolites Na beta and H beta. Microporous Mesoporous Mater. 1998, 21, 111–116. [Google Scholar] [CrossRef]
- Nguyen, T.-Q.; Glorius, M.; Breitkopf, C. A new approach to determine gas diffusion coefficients in porous solids by EIS: Application for NH3 and CO2 adsorption on zirconia and zeolite type 5A. Adv. Math. Phys. 2018, 2018, 5462659. [Google Scholar] [CrossRef]
- Luis, P. Gas permeation and supported liquid membranes. In Fundamental Modelling of Membrane Systems Membrane and Process Performance; Elsevier: Amsterdam, The Netherlands, 2018; pp. 103–151. [Google Scholar]
- Robeson, L.M. Polymer membranes. Polym. Sci. Compr. Ref. 2012, 8, 325–347. [Google Scholar] [CrossRef]
- Laciak, D.V.; Langsam, M. Membrane Separations|Gas separations with polymer membranes. In Encyclopedia of Separation Science; Elsevier: Amsterdam, The Netherlands, 2000; pp. 1725–1738. [Google Scholar]
- Sundén, B. Chapter 9-Transport phenomena in fuel cells. In Hydrogen, Batteries and Fuel Cells; Academic Press: Cambridge, MA, USA, 2019; pp. 145–166. [Google Scholar]
- Conlisk, A.T. Essentials of Micro- and Nanofluidics: With Applications to the Biological and Chemical Sciences; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Atkins, P.; Ratcliffe, G.; Wormald, M.; de Paula, J. Physical Chemistry for the Life Sciences, 3rd ed.; Oxford University Press: Oxford, UK, 2023. [Google Scholar]
- Chandra, P.; Koros, W.J. Sorption and transport of methanol in poly(ethylene terephthalate). Polymer 2009, 50, 236–244. [Google Scholar] [CrossRef]
- Mamaliga, I.; Schabel, W.; Kind, M. Measurements of sorption isotherms and diffusion coefficients by means of a magnetic suspension balance. Chem. Eng. Process. Process Intensif. 2004, 43, 753–763. [Google Scholar] [CrossRef]
- Aionicesei, E.; Škerget, M.; Knez, Ž. Measurement of CO2 solubility and diffusivity in poly(l-lactide) and poly(d,l-lactide-co-glycolide) by magnetic suspension balance. J. Supercrit. Fluids 2008, 47, 296–301. [Google Scholar] [CrossRef]
- BS EN ISO 2556:2001; Plastics–Determination of the Gas Transmission Rate of Films and Thin Sheets under Atmospheric–Manometric Method. International Organization for Standardization: Geneva, Switzerland, 2001.
- ASTM D1434–82; Standard Test Methods for Determining Gas Permeability Characteristics of Plastic Film and Sheeting. International Organization for Standardization: Geneva, Switzerland, 1982.
- Minelli, M.; Sarti, G. Gas transport in glassy polymers: Prediction of diffusional time lag. Membranes 2018, 8, 8. [Google Scholar] [CrossRef]
- ISO 15105-1:2007; Plastics, Film and Sheeting, Determination of Gas-Transmission Rate. International Organization for Standardization: Geneva, Switzerland, 1982.
- Stern, S.A.; Gareis, P.J.; Sinclair, T.F.; Mohr, P.H. Performance of a versatile variable-volume permeability cell. Comparison of gas permeability measurements by the variable-volume and variable-pressure methods. J. Appl. Polym. Sci. 1963, 7, 2035–2051. [Google Scholar] [CrossRef]
- Fujiwara, H.; Ono, H.; Onoue, K.; Nishimura, S. High-pressure gaseous hydrogen permeation test method -property of polymeric materials for high-pressure hydrogen devices (1). Int. J. Hydrogen Energy 2020, 45, 29082–29094. [Google Scholar] [CrossRef]
- Guiochon, G.; Guillemin, C.L. Chapter 13 Quantitative analysis by gas chromatography basic problems, fundamental relationships, measurement of the sample size. J. Chromatogr. Libr. 1988, 42, 563–586. [Google Scholar] [CrossRef]
- Jung, J.K.; Kim, I.G.; Chung, K.S.; Baek, U.B. Gas chromatography techniques to evaluate the hydrogen permeation characteristics in rubber: Ethylene propylene diene monomer. Sci. Rep. 2021, 11, 4859. [Google Scholar] [CrossRef] [PubMed]
- Bessarabov, D.; Millet, P. Chapter 5-Gas permeation in PEM water electrolyzers. In PEM Water Electrolysis Hydrogen Energy and Fuel Cells Primers; Academic Press: Cambridge, MA, USA, 2018; pp. 117–158. [Google Scholar]
- Mukaddam, M.; Litwiller, E.; Pinnau, I. Gas sorption, diffusion, and permeation in nafion. Macromolecules 2016, 49, 280–286. [Google Scholar] [CrossRef]
- Jung, J.K.; Kim, I.G.; Kim, K.T.; Ryu, K.S.; Chung, K.S. Evaluation techniques of hydrogen permeation in sealing rubber materials. Polym. Test. 2021, 93, 107016. [Google Scholar] [CrossRef]
- Brijker, F.; Heijdra, Y.F.; Elshout, F.J.; Bosch, F.H.; Folgering, H.T. Volumetric measurements of peripheral oedema in clinical conditions. Clin. Physiol. 2000, 20, 56–61. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.K.; Lee, J.H.; Jang, J.S.; Chung, N.K.; Park, C.Y.; Baek, U.B.; Nahm, S.H. Characterization technique of gases permeation properties in polymers: H2, He, N2 and Ar gas. Sci. Rep. 2022, 12, 3328. [Google Scholar] [CrossRef] [PubMed]
- CSA/ANSI CHMC 2:19; American National Standard Recommended Practice for Electromagnetic Compatibility Limits and Test Levels. National Standard of Canada, American National Standard: Toronto, ON, Canada, 2019.
- Zahariea, D. Dynamic response of the U-tube liquid manometer with equal diameter columns. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012114. [Google Scholar] [CrossRef]
- Jung, J.; Kim, G.; Gim, G.; Park, C.; Lee, J. Determination of gas permeation properties in polymer using capacitive electrode sensors. Sensors 2022, 22, 1141. [Google Scholar] [CrossRef] [PubMed]
- Crank, J. The Mathematics of Diffusion; University Press: Oxford, NY, USA, 1975. [Google Scholar]
- Junichiro, Y.; Shin, N. Influence of fillers on hydrogen penetration properties and blister fracture of rubber composites for O-ring exposed to high-pressure hydrogen gas. Int. J. Hydrogen Energy 2009, 34, 1977–1989. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Sander, R.; Acree, W.E.; De Visscher, A.; Schwartz, S.E.; Wallington, T.J. Henry’s law constants (IUPAC Recommendations 2021). Pure Appl. Chem. 2021, 94, 71–85. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Jung, J.K.; Lee, J.H.; Jeon, S.K.; Baek, U.B.; Lee, S.H.; Lee, C.H.; Moon, W.J. H2 uptake and diffusion characteristics in sulfur-crosslinked ethylene propylene diene monomer polymer composites with carbon black and silica fillers after high-pressure hydrogen exposure reaching 90 MPa. Polymers 2023, 15, 162. [Google Scholar] [CrossRef]
- Kanehashi, S.; Nagai, K. Analysis of dual-mode model parameters for gas sorption in glassy polymers. J. Membr. Sci. 2005, 253, 117–138. [Google Scholar] [CrossRef]
- Wang, J.-S.; Kamiya, Y. Evaluation of gas sorption parameters and prediction of sorption isotherms in glassy polymers. J. Polym. Sci. B Polym. Phys. 2000, 38, 883–888. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, Q.; Liu, Y.; Thaika, M.A. A developed dual-site Langmuir model to represent the high-pressure methane adsorption and thermodynamic parameters in shale. Int. J. Coal Sci. Technol. 2023, 10, 59. [Google Scholar] [CrossRef]
- Tian, H.; Li, T.; Zhang, T.; Xiao, X. Characterization of methane adsorption on overmature lower Silurian-upper Ordovician shales in Sichuan Basin, southwest China: Experimental results and geological implications. Int. J. Coal Geol. 2016, 156, 36–49. [Google Scholar] [CrossRef]
- Xia, J.; Song, Z.; Wang, S.; Zeng, W. Preliminary study of pore structure and methane sorption capacity of the Lower Cambrian shales from the north Gui-zhou province. J. Nat. Gas. Sci. Eng. 2017, 38, 81–93. [Google Scholar] [CrossRef]



| Measuring Methods | GM | VM | MM | GC |
|---|---|---|---|---|
| Measurand | mass | volume | pressure | volume |
| Resolution | 0.3 wt∙ppm | 0.1 wt∙ppm | 0.1 wt∙ppm | 0.01 wt∙ppm |
| Stability | <0.22% | <0.16% | <0.15% | <0.13% |
| Expanded uncertainty | <13% | <10% | <10% | <10% |
| Figure of merit (FOM) | 1.5% | 0.8% | 0.7% | 0.5% |
| Sensitivity to temperature and pressure | sensitive | sensitive | very sensitive | less sensitive |
| Features | very simple and inexpensive | simple, inexpensive and effective | very simple, inexpensive and effective | complicated and delicate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.K. Review of Developed Methods for Measuring Gas Uptake and Diffusivity in Polymers Enriched by Pure Gas under High Pressure. Polymers 2024, 16, 723. https://doi.org/10.3390/polym16050723
Jung JK. Review of Developed Methods for Measuring Gas Uptake and Diffusivity in Polymers Enriched by Pure Gas under High Pressure. Polymers. 2024; 16(5):723. https://doi.org/10.3390/polym16050723
Chicago/Turabian StyleJung, Jae Kap. 2024. "Review of Developed Methods for Measuring Gas Uptake and Diffusivity in Polymers Enriched by Pure Gas under High Pressure" Polymers 16, no. 5: 723. https://doi.org/10.3390/polym16050723
APA StyleJung, J. K. (2024). Review of Developed Methods for Measuring Gas Uptake and Diffusivity in Polymers Enriched by Pure Gas under High Pressure. Polymers, 16(5), 723. https://doi.org/10.3390/polym16050723






