Mechanical Performance of Structural Polymethyl Methacrylate Joints at Different Temperatures
Abstract
1. Introduction
2. Experimental Design
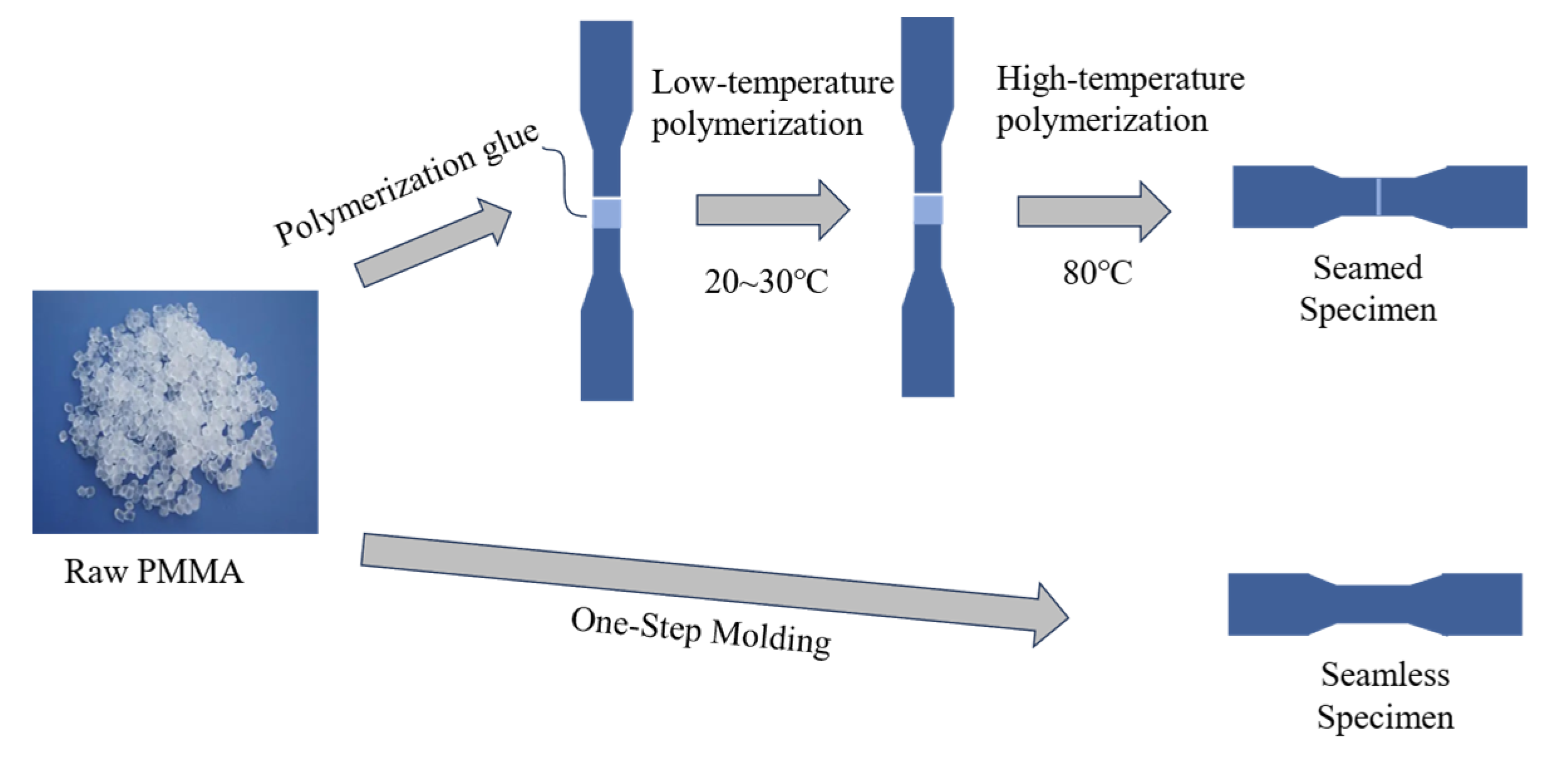
2.1. Specimen Design
2.2. Methodology
2.2.1. PMMA Tensile Tests at Various Temperatures
2.2.2. Post-Thermal Cycling PMMA Tensile Tests
3. Results and Analysis
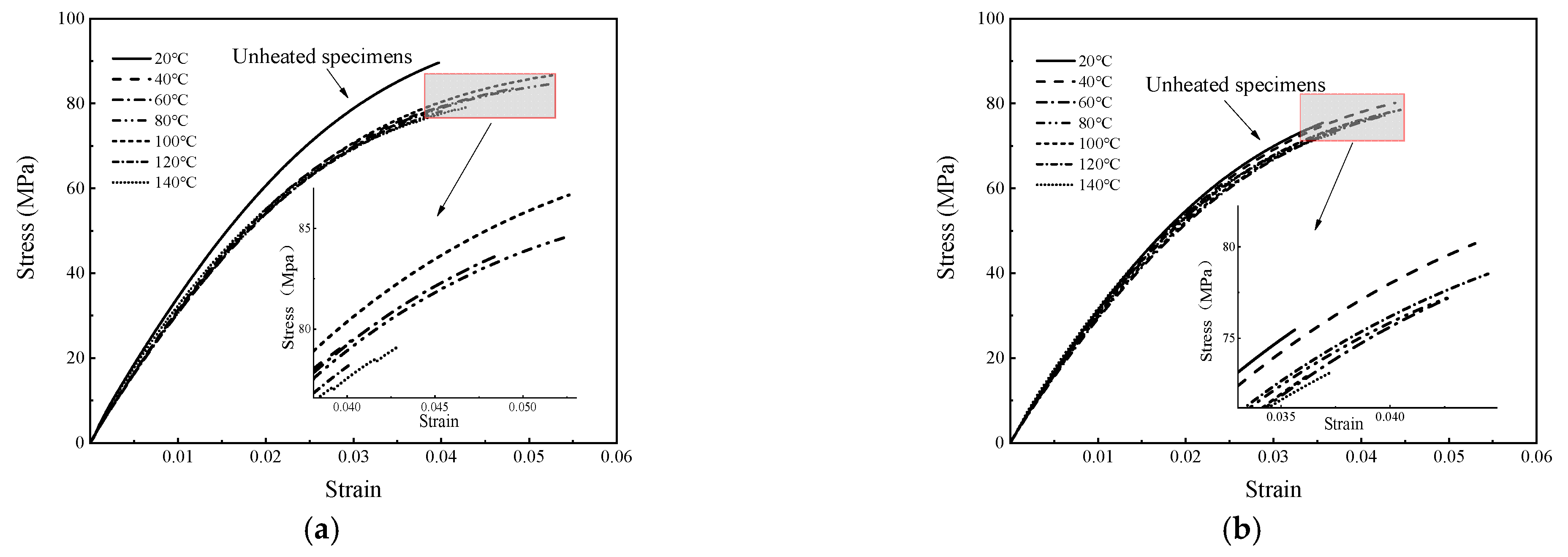
3.1. Tensile Test at Various Temperatures
3.1.1. Forms of Failure
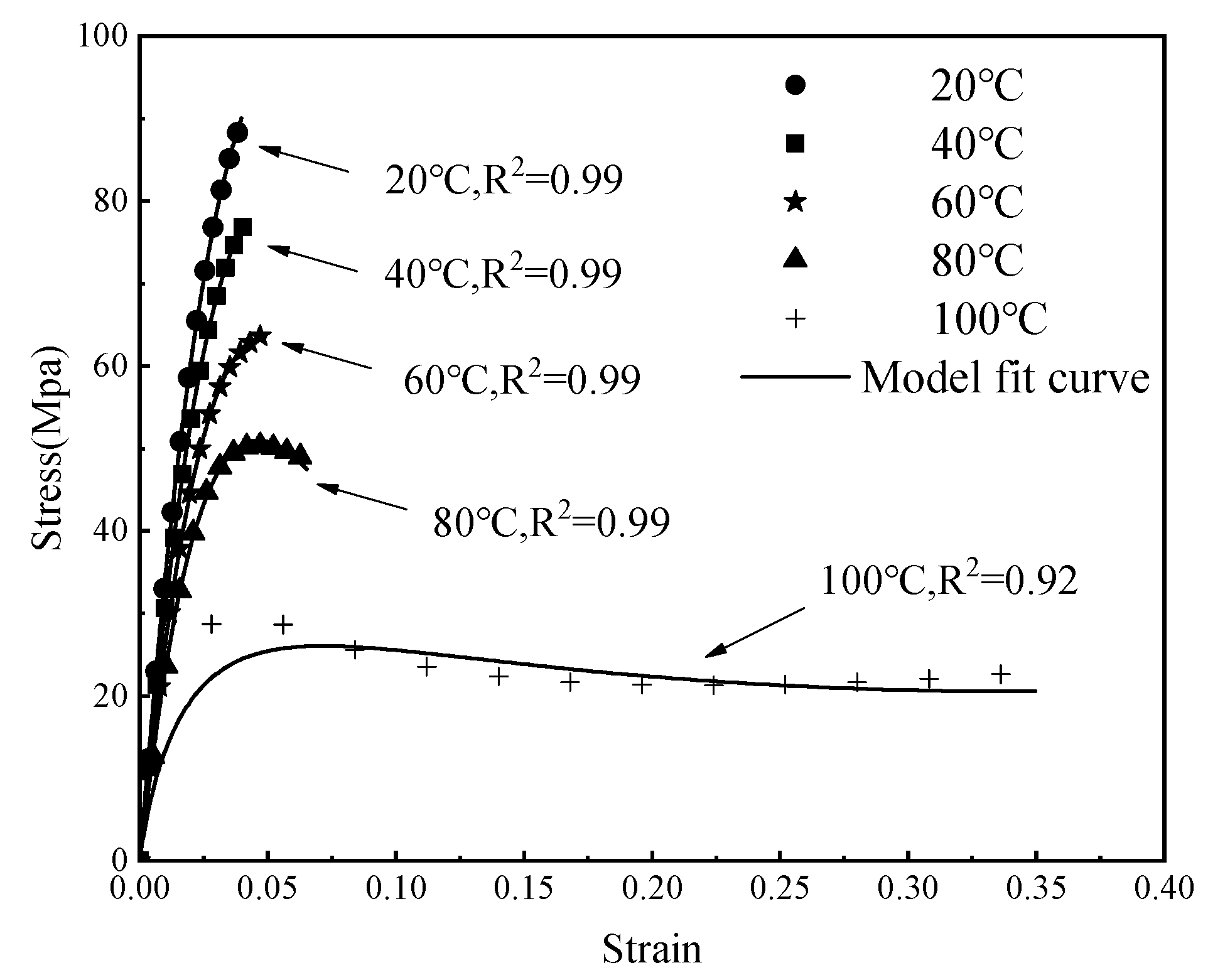
3.1.2. Stress–Strain Curves
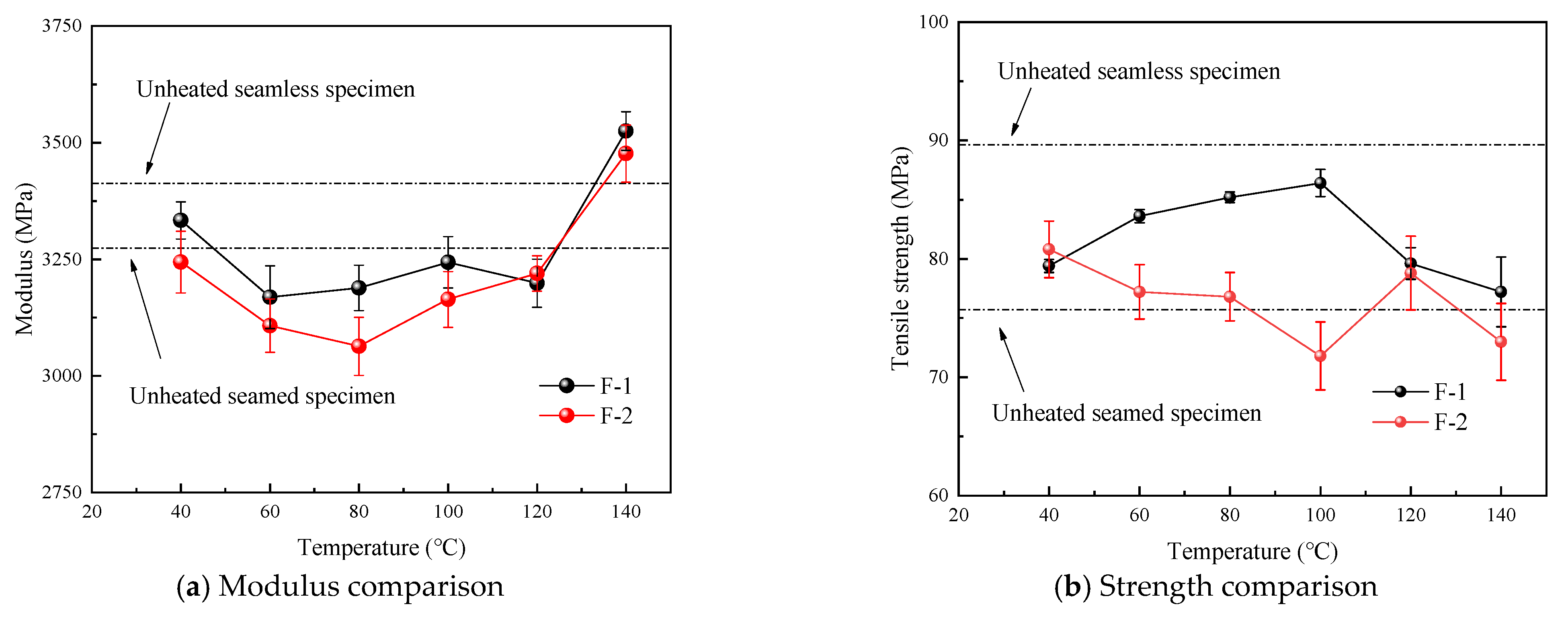
3.2. Thermal Cycling Test
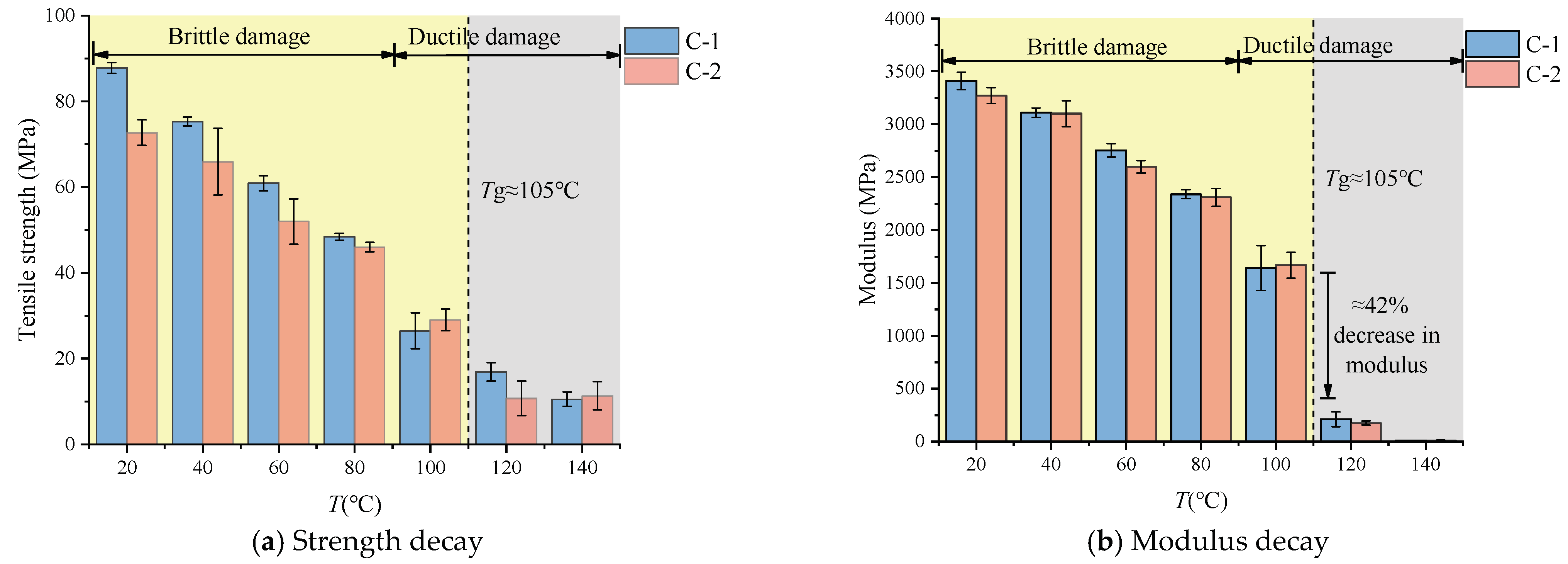
4. Quantitative Analysis of Factorial Impacts on Mechanical Properties
4.1. Effects of Temperature Variations
4.2. Effects of Cooling on Heated Sheets
5. Establishment of Constitutive Modeling
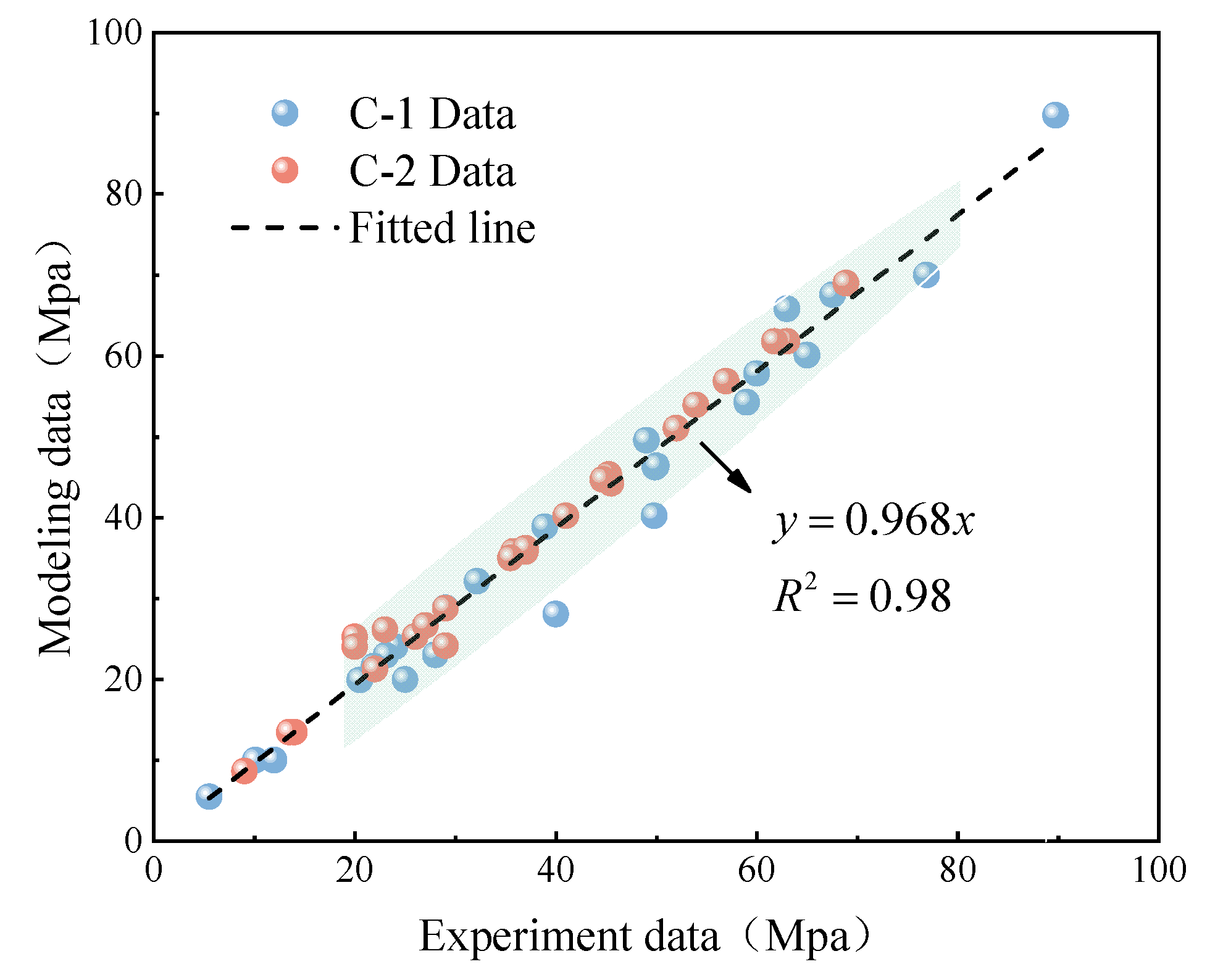
5.1. Matsuoka Model Development and Validation
5.2. Model Improvement and Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gasratova, N.A.; Zuev, V.S. The use of acrylic as a structural material in the design of translucent elements of deep-submergence vehicles. Mater. Sci. Forum 2021, 1031, 196–200. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, B.; Shu, G.; Wang, Z.; Sun, Z.; Tang, Y. Mechanical properties and engineering application of structural acrylic. Build. Struct. 2023, 53, 1–6+35. [Google Scholar]
- Yang, X.-M.; Zhu, Z.-M. Study on material properties of stretched acrylic for civil aircraft transparency. Synth. Mater. Aging Appl. 2023, 53, 8–11. [Google Scholar] [CrossRef]
- Zhang, G. Application of organic glass in new energy vehicles. Plast. Sci. Technol. 2016, 44, 50–53. [Google Scholar]
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Makradi, A. Modeling and validation of the large deformation inelastic response of amorphous polymers over a wide range of temperatures and strain rates. Int. J. Solids Struct. 2007, 44, 7938–7954. [Google Scholar] [CrossRef]
- Ionita, D.; Cristea, M.; Banabic, D. Viscoelastic behavior of PMMA in relation to deformation mode. J. Therm. Anal. Calorim. 2015, 120, 1775–1783. [Google Scholar] [CrossRef]
- Hu, W.; Guo, H.; Chen, Y.; Xie, R.; Jing, H.; He, P. Experimental investigation and modeling of the rate-dependent deformation behavior of PMMA at different temperatures. Eur. Polym. J. 2016, 85, 313–323. [Google Scholar] [CrossRef]
- Liu, W.; Yao, X.; Chen, X. A local stress approach to predict the fatigue life of the U-notched PMMA plate at different temperatures. Int. J. Fatigue 2017, 103, 436–443. [Google Scholar] [CrossRef]
- Gao, Z.Z.; Liu, W.; Liu, Z.Q.; Yue, Z.F. Experiment and Simulation Study on the Creep Behavior of PMMA at Different Temperatures. Polym. -Plast. Technol. Eng. 2010, 49, 1478–1482. [Google Scholar] [CrossRef]
- Huang, F.-Z.; Guo, W.-I.G. Mechanical behavior of MDYB-3PMMA at different temperatures and strain rates. J. Mater. Sci. Eng. 2007, 4, 582–586. [Google Scholar]
- Wu, H.; Ma, G.; Xia, Y. Experimental study of unidirectional tensile mechanical properties of PMMA at low and medium strain rates. J. Exp. Mech. 2005, 85, 193–199. [Google Scholar]
- Jin, T.; Zhou, Z.; Shu, X.; Wang, Z.; Wu, G.; Liu, Z. Effects of strain rate on PMMA failure behavior. Appl. Phys. A 2015, 122, 7. [Google Scholar] [CrossRef]
- Du, Y.; Pei, P.; Suo, T.; Gao, G. Large deformation mechanical behavior and constitutive modeling of oriented PMMA. Int. J. Mech. Sci. 2023, 257, 108520. [Google Scholar] [CrossRef]
- Yadav, D.; Jaya, B.N. Size effects governing damage resistance of architected PMMA. Eng. Fract. Mech. 2023, 290, 109526. [Google Scholar] [CrossRef]
- Zhang, L.; Townsend, D.; Petrinic, N.; Pellegrino, A. Pressure and temperature dependent dynamic flow and failure behavior of PMMA at intermediate strain rates. Int. J. Impact Eng. 2021, 158, 104026. [Google Scholar] [CrossRef]
- Bura, E.; Derpeński, Ł.; Seweryn, A. Fracture in PMMA notched specimens under compression—Experimental study. Polym. Test. 2019, 77, 105923. [Google Scholar] [CrossRef]
- Habeeb, C.N.I.; Osovski, S. Experimental and numerical study of the interaction between dynamically loaded cracks and pre-existing flaws in edge impacted PMMA specimens. Int. J. Impact Eng. 2021, 157, 103973. [Google Scholar] [CrossRef]
- Morales, R.C.; Baek, J.; Sharp, D.; Aderounmu, A.; Wei, H.; Chen, J.S.; Eliasson, V. Mode-II fracture response of PMMA under dynamic loading conditions. J. Dyn. Behav. Mater. 2022, 8, 104–121. [Google Scholar] [CrossRef]
- Zhou, X.-P.; Fu, L.; Ju, W.; Berto, F. An experimental study of the mechanical and fracturing behavior in PMMA specimen containing multiple 3D embedded flaws under uniaxial compression. Theor. Appl. Fract. Mech. 2019, 101, 207–216. [Google Scholar] [CrossRef]
- Du, Q.; Liu, F.; Lei, Q. Numerical simulation of PMMA impact based on the J–C constitutive and damage models under hydrostatic pressure loading. Appl. Sci. 2023, 13, 8640. [Google Scholar] [CrossRef]
- Kochanov, V.; Píštěk, V.; Kondratiev, A.; Yuresko, T.; Kučera, P. Influence of geometric parameters of conical acrylic portholes on their stress–strain behaviour. Polymers 2022, 14, 1041. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhu, H.; Liu, F.; Cao, J.; Ding, Z.; Zhang, Y. Buckling failure analysis of PMMA spherical pressure hull. Ocean Eng. 2022, 245, 110465. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.; Zhang, Y.; Du, Q.; Jiang, Z.; Cui, W. Effect of temperature and nonlinearity of PMMA material in the design of observation windows for a full ocean depth manned submersible. Mar. Technol. Soc. J. 2019, 53, 27–36. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Du, X.; Zhang, T.; Heng, Y. Study on the fracture properties of the PMMA structure for the JUNO central detector. KSCE J. Civ. Eng. 2019, 23, 2584–2597. [Google Scholar] [CrossRef]
- Huang, M.; Wang, Z.; Wang, Y.; Xie, J.; Sun, X. Experimental study on load-bearing capacity of scaled acrylic roof model of future garden. Build. Struct. 2023, 53, 23–28. [Google Scholar]
- ASTM D638; Test Methods for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- GB/T 1040.2-2022; Plastics Determination of Tensile Properties Part 2: Test Conditions for Molded and Extruded Plastics. China General Administration of Market Supervision and Administration China Standardization Administration: Beijing, China, 2022.
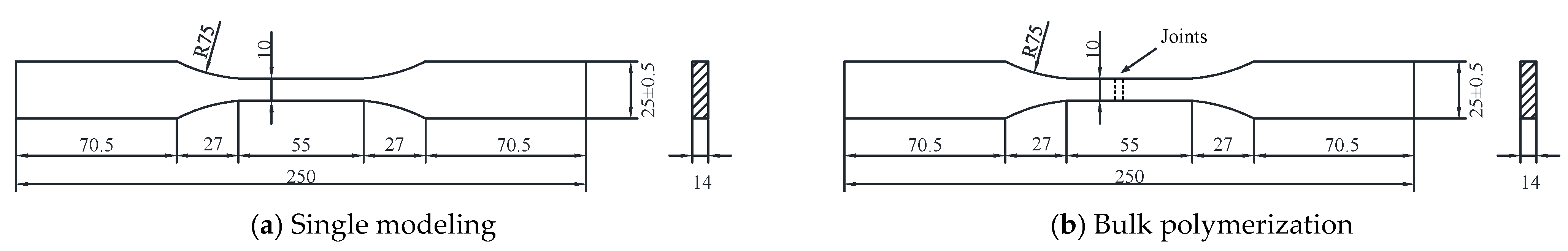




| Group | Specimen Thickness (mm) | Splicing of Specimens | Test Temperature (°C) | Strain Rate (mm/min) |
|---|---|---|---|---|
| C-1 | 14 | Single modeling (seamless) | 20, 40, 60 80, 100 120, 140 | 10 |
| C-2 | 14 | Bulk polymerization (seamed) |
| Group | Specimen Thickness (mm) | Splicing of Specimens | Heating Temperature (°C) | Strain Rate (mm/min) |
|---|---|---|---|---|
| F-1 | 14 | Single modeling (seamless) | 40, 60, 80 100, 120, 140 | 10 |
| F-2 | 14 | Bulk polymerization (seamed) |
| Group | T (°C) | (Gpa) | |||
|---|---|---|---|---|---|
| C-1 | 20 °C | 3.81 | 14.05 | −25.18 | 0.85 |
| 40 °C | 3.39 | 17.34 | −12.06 | 0.83 | |
| 60 °C | 2.95 | 10.02 | −14.87 | 0.82 | |
| 80 °C | 2.79 | 21.07 | −15.69 | 0.77 | |
| 100 °C | 2.31 | 14.45 | −18.12 | 0.72 | |
| C-2 | 20 °C | 3.68 | 8.11 | −21.18 | 0.85 |
| 40 °C | 3.15 | 12.44 | −15.56 | 0.83 | |
| 60 °C | 2.87 | 11.36 | −17.52 | 0.82 | |
| 80 °C | 2.74 | 21.35 | −22.86 | 0.77 | |
| 100 °C | 2.37 | 14.37 | −18.06 | 0.72 | |
| Average | —— | 14.46 | −18.11 | —— | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; Peng, L.; Li, Y.; Zong, J. Mechanical Performance of Structural Polymethyl Methacrylate Joints at Different Temperatures. Polymers 2024, 16, 3243. https://doi.org/10.3390/polym16233243
Kang C, Peng L, Li Y, Zong J. Mechanical Performance of Structural Polymethyl Methacrylate Joints at Different Temperatures. Polymers. 2024; 16(23):3243. https://doi.org/10.3390/polym16233243
Chicago/Turabian StyleKang, Chenxing, Lei Peng, Yantao Li, and Jinhui Zong. 2024. "Mechanical Performance of Structural Polymethyl Methacrylate Joints at Different Temperatures" Polymers 16, no. 23: 3243. https://doi.org/10.3390/polym16233243
APA StyleKang, C., Peng, L., Li, Y., & Zong, J. (2024). Mechanical Performance of Structural Polymethyl Methacrylate Joints at Different Temperatures. Polymers, 16(23), 3243. https://doi.org/10.3390/polym16233243






