Dynamic Light Scattering Microrheology of Phase-Separated Poly(vinyl) Alcohol–Phytagel Blends
Abstract
1. Introduction
2. Materials and Methods
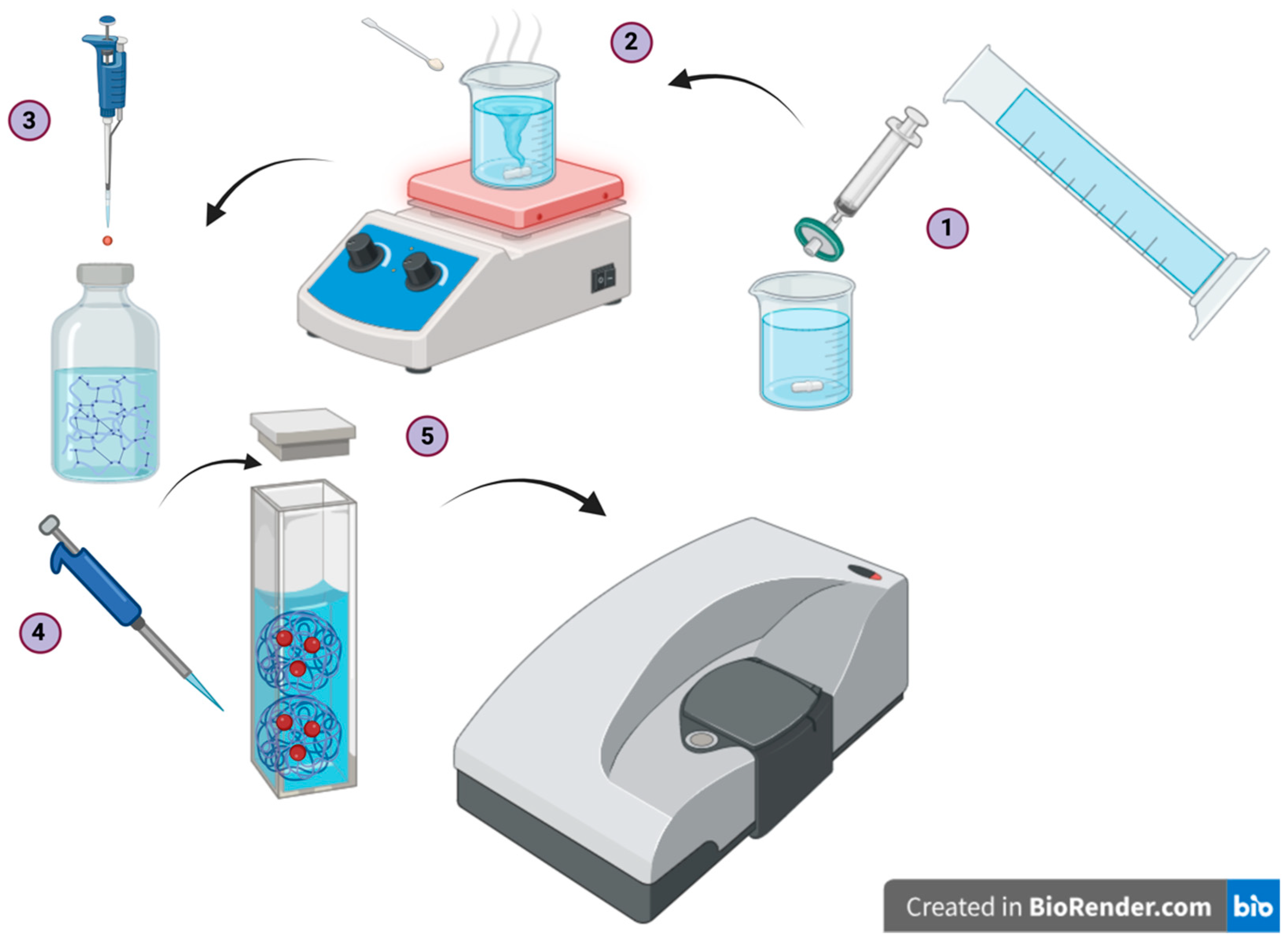
2.1. Sample Preparation
2.2. Dynamic Light Scattering Experiments
3. Theory
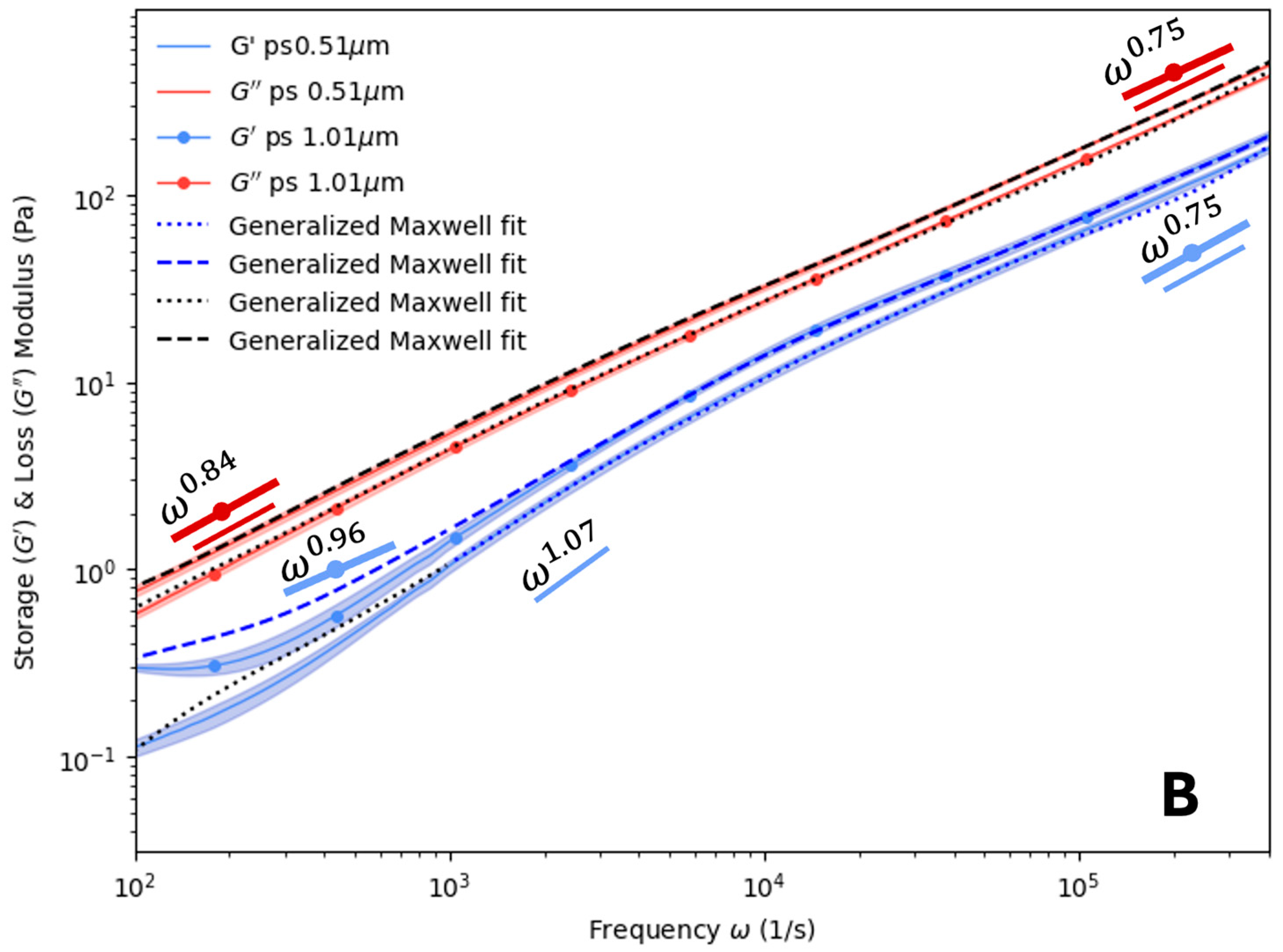
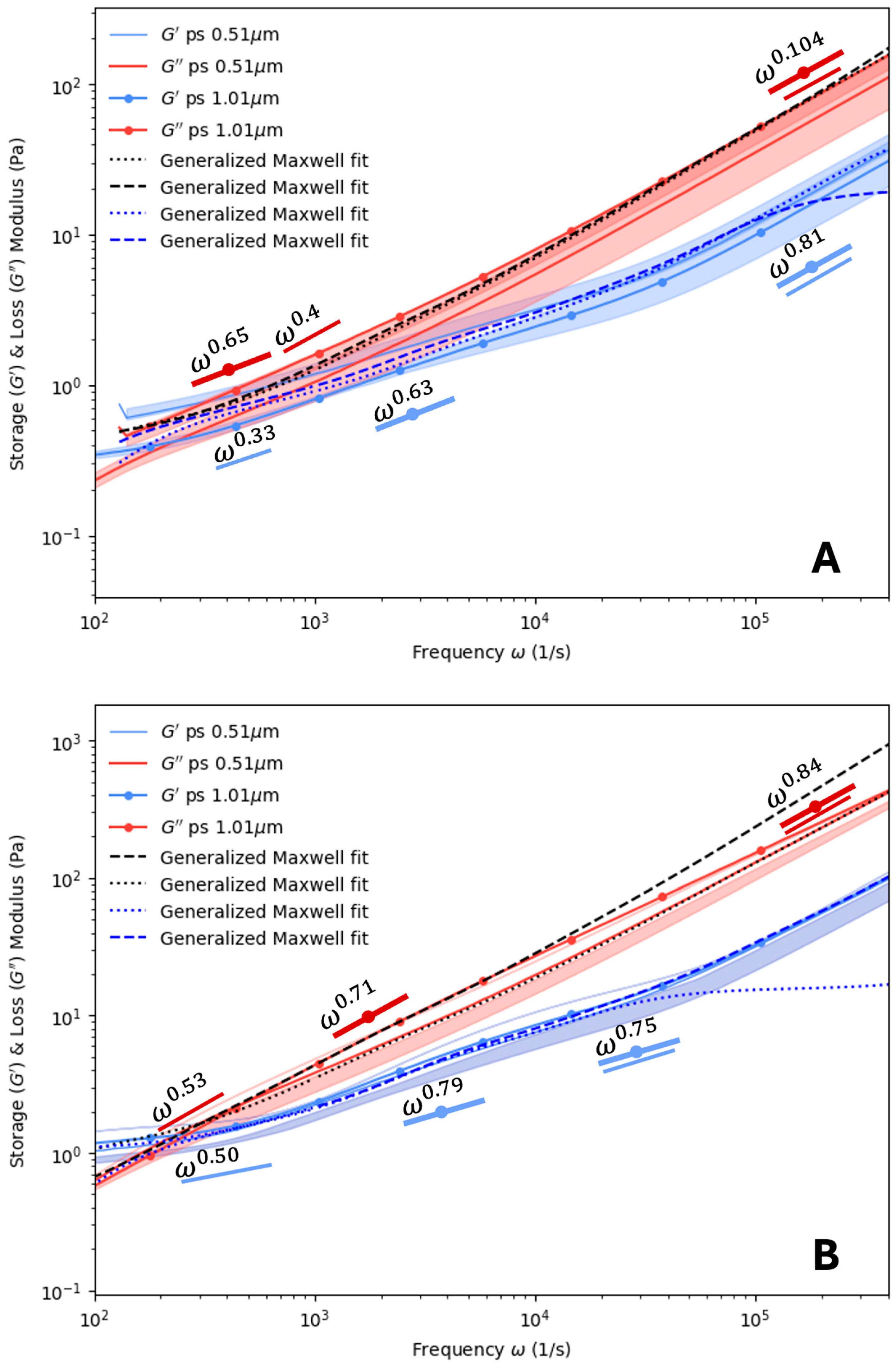
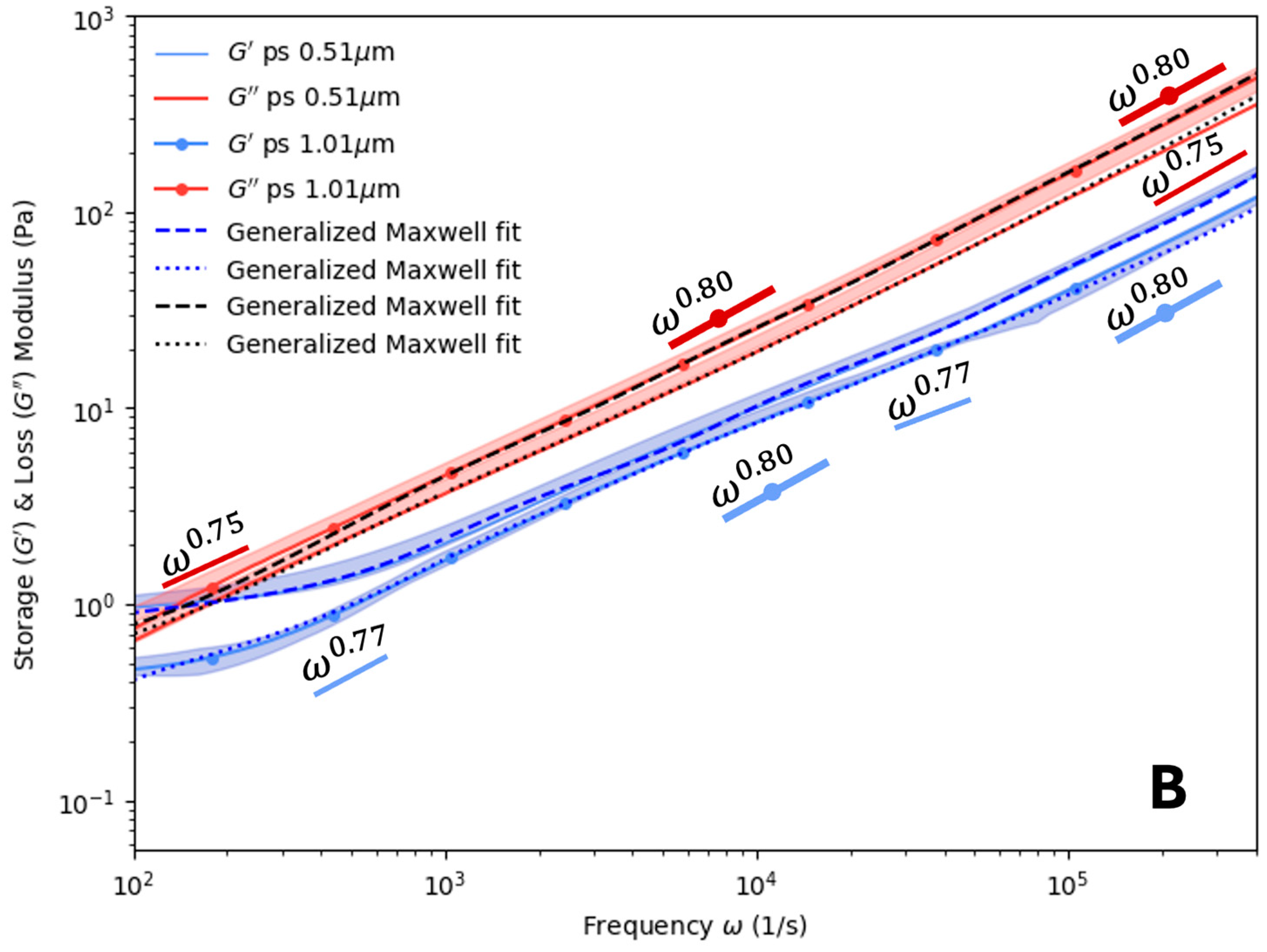
4. Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Chauhan, A. Gold Nanoparticles-Loaded Contact Lenses for Laser Protection and Meibomian Gland Dysfunction (MGD) Dry Eye Treatment. Colloids Surf. A Physicochem. Eng. Asp. 2022, 635, 128053. [Google Scholar] [CrossRef]
- Lochhead, R.Y. A Review of Recent Advances in the Polymeric Delivery of Attributes in Cosmetic and Personal Care Products. In Polymeric Delivery of Therapeutics; ACS Symposium Series; ACS Publications: Washington, DC, USA, 2010; Volume 1053, pp. 3–22. ISBN 978-0-8412-2583-1. [Google Scholar]
- Liu, G.; Feng, Y.; Zhao, N.; Chen, Z.; Shi, J.; Zhou, F. Polymer-Based Lubricating Materials for Functional Hydration Lubrication. Chem. Eng. J. 2022, 429, 132324. [Google Scholar] [CrossRef]
- Son, H.A.; Yoon, K.Y.; Lee, G.J.; Cho, J.W.; Choi, S.K.; Kim, J.W.; Im, K.C.; Kim, H.T.; Lee, K.S.; Sung, W.M. The Potential Applications in Oil Recovery with Silica Nanoparticle and Polyvinyl Alcohol Stabilized Emulsion. J. Pet. Sci. Eng. 2015, 126, 152–161. [Google Scholar] [CrossRef]
- Choi, Y.H.; Lee, S.S.; Lee, D.; Jeong, H.S.; Kim, S. Composite Microgels Created by Complexation between Polyvinyl Alcohol and Graphene Oxide in Compressed Double-Emulsion Drops. Small 2020, 16, 1903812. [Google Scholar] [CrossRef]
- Mafi, R.; Gray, C.; Pelton, R.; Ketelson, H.; Davis, J. On Formulating Ophthalmic Emulsions. Colloids Surf. B Biointerfaces 2014, 122, 7–11. [Google Scholar] [CrossRef]
- Agnihotri, S.A.; Aminabhavi, T.M. Development of Novel Interpenetrating Network Gellan Gum-Poly(Vinyl Alcohol) Hydrogel Microspheres for the Controlled Release of Carvedilol. Drug Dev. Ind. Pharm. 2005, 31, 491–503. [Google Scholar] [CrossRef]
- Jouenne, S.; Heurteux, G.; Levache, B. Online Monitoring for Measuring the Viscosity of the Injected Fluids Containing Polymer in Chemical Eor. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, OnePetro, Muscat, Oman, 21 March 2022. [Google Scholar]
- Dalle Fratte, E.; D’hooge, D.R.; Eeckhout, M.; Cardon, L. Principles and Guidelines for In-Line Viscometry in Cereal Extrusion. Polymers 2022, 14, 2316. [Google Scholar] [CrossRef] [PubMed]
- Malkin, A.Y.; Kulichikhin, V.G.; Gumennyi, I.V. Comparing Flow Characteristics of Viscoelastic Liquids in Long and Short Capillaries (Entrance Effects). Phys. Fluids 2021, 33, 013105. [Google Scholar] [CrossRef]
- Gupta, S.; Wang, W.S.; Vanapalli, S.A. Microfluidic Viscometers for Shear Rheology of Complex Fluids and Biofluids. Biomicrofluidics 2016, 10, 043402. [Google Scholar] [CrossRef]
- Ghanbari, A.; Mousavi, Z.; Heuzey, M.-C.; Patience, G.S.; Carreau, P.J. Experimental Methods in Chemical Engineering: Rheometry. Can. J. Chem. Eng. 2020, 98, 1456–1470. [Google Scholar] [CrossRef]
- Mackay, M.E. Rheological Measurements on Small Samples. In Rheological Measurement; Collyer, A.A., Clegg, D.W., Eds.; Springer: Dordrecht, The Netherlands, 1998; pp. 635–665. ISBN 978-94-011-4934-1. [Google Scholar]
- Hnyluchová, Z.; Bjalončíková, P.; Karas, P.; Mravec, F.; Halasová, T.; Pekař, M.; Kubala, L.; Víteček, J. A Simple Microviscometric Approach Based on Brownian Motion Tracking. Rev. Sci. Instrum. 2015, 86, 023710. [Google Scholar] [CrossRef] [PubMed]
- Shabaniverki, S.; Alvarez-Valdivia, A.; Juárez, J.J. Portable Imaging Viscometry for Quantitative Complex Fluid Measurements. Exp. Therm. Fluid Sci. 2019, 107, 29–37. [Google Scholar] [CrossRef]
- Chen, C.-J.; Chen, W.-L.; Phong, P.H.; Chuang, H.-S. Investigation of Micro-Volume Viscosity with Janus Microbeads Based on Rotational Brownian Motion. Sensors 2019, 19, 1217. [Google Scholar] [CrossRef] [PubMed]
- Hidema, R.; Yatabe, Z.; Takahashi, H.; Higashikawa, R.; Suzuki, H. Inverse Integral Transformation Method to Derive Local Viscosity Distribution Measured by Optical Tweezers. Soft Matter 2020, 16, 6826–6833. [Google Scholar] [CrossRef]
- Tassieri, M.; Giudice, F.D.; Robertson, E.J.; Jain, N.; Fries, B.; Wilson, R.; Glidle, A.; Greco, F.; Netti, P.A.; Maffettone, P.L.; et al. Microrheology with Optical Tweezers: Measuring the Relative Viscosity of Solutions ‘at a Glance’. Sci. Rep. 2015, 5, 8831. [Google Scholar] [CrossRef] [PubMed]
- Korzeniewska, A.K.; Drobczyński, S. Local Measurement of Liquid Viscosity in Optical Tweezers. Opt. Lasers Eng. 2023, 164, 107516. [Google Scholar] [CrossRef]
- Bera, S.; Paul, S.; Singh, R.; Ghosh, D.; Kundu, A.; Banerjee, A.; Adhikari, R. Fast Bayesian Inference of Optical Trap Stiffness and Particle Diffusion. Sci. Rep. 2017, 7, 41638. [Google Scholar] [CrossRef] [PubMed]
- Tassieri, M.; Evans, R.M.L.; Warren, R.L.; Bailey, N.J.; Cooper, J.M. Microrheology with Optical Tweezers: Data Analysis. New J. Phys. 2012, 14, 115032. [Google Scholar] [CrossRef]
- de Smidt, J.H.; Crommelin, D.J.A. Viscosity Measurement in Aqueous Polymer Solutions by Dynamic Light Scattering. Int. J. Pharm. 1991, 77, 261–264. [Google Scholar] [CrossRef]
- Mason, T.G.; Gang, H.; Weitz, D.A. Rheology of Complex Fluids Measured by Dynamic Light Scattering. J. Mol. Struct. 1996, 383, 81–90. [Google Scholar] [CrossRef]
- Mason, T.G.; Weitz, D.A. Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids. Phys. Rev. Lett. 1995, 74, 1250–1253. [Google Scholar] [CrossRef] [PubMed]
- Dhakal, S.; Chen, Z.; Estrin, D.; Morozova, S. Spatially-Resolved Network Dynamics of Poly(Vinyl Alcohol) Gels Measured with Dynamic Small Angle Light Scattering. Gels 2022, 8, 394. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Caciagli, A.; Yu, J.; Tang, X.; Ghosh, R.; Eiser, E. Dynamic Light Scattering Based Microrheology of End-Functionalised Triblock Copolymer Solutions. Polymers 2023, 15, 481. [Google Scholar] [CrossRef] [PubMed]
- Cai, P.C.; Krajina, B.A.; Kratochvil, M.J.; Zou, L.; Zhu, A.; Burgener, E.B.; Bollyky, P.L.; Milla, C.E.; Webber, M.J.; Spakowitz, A.J.; et al. Dynamic Light Scattering Microrheology for Soft and Living Materials. Soft Matter 2021, 17, 1929–1939. [Google Scholar] [CrossRef] [PubMed]
- Buzzaccaro, S.; Ruzzi, V.; Faleo, T.; Piazza, R. Microrheology of a Thermosensitive Gelling Polymer for Cell Culture. J. Chem. Phys. 2022, 157, 174901. [Google Scholar] [CrossRef] [PubMed]
- Cai, P.C.; Su, B.; Zou, L.; Webber, M.J.; Heilshorn, S.C.; Spakowitz, A.J. Rheological Characterization and Theoretical Modeling Establish Molecular Design Rules for Tailored Dynamically Associating Polymers. ACS Cent. Sci. 2022, 8, 1318–1327. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Bhatia, S.R. Dynamics and Microrheology of Colloidal Clay-Polymer Glasses and Gels: Size-Dependent Phenomena and Re-Entrant Behavior at Early Aging Times. J. Chem. Phys. 2023, 158, 054904. [Google Scholar] [CrossRef]
- Vega, J.F.; Fernández, M.; Cardil, A.; Calafel, I.; Martínez-Soroa, I.; Sarriegui, A.P.; Acera, A. Shedding Light on the Viscoelastic Behavior of Artificial and Human Tears: A Microrheological Approach. Phys. Fluids 2023, 35, 072008. [Google Scholar] [CrossRef]
- Forte, A.E.; Galvan, S.; Manieri, F.; Rodriguez, Y.; Baena, F.; Dini, D. A Composite Hydrogel for Brain Tissue Phantoms. Mater. Des. 2016, 112, 227–238. [Google Scholar] [CrossRef]
- Tejo-Otero, A.; Fenollosa-Artés, F.; Achaerandio, I.; Rey-Vinolas, S.; Buj-Corral, I.; Mateos-Timoneda, M.Á.; Engel, E. Soft-Tissue-Mimicking Using Hydrogels for the Development of Phantoms. Gels 2022, 8, 40. [Google Scholar] [CrossRef]
- Statnik, E.S.; Sorokina, E.A.; Larin, I.I.; Yu, K.; Salimon, A.I.; Kalyaev, V.Y.; Zherebtsov, D.D.; Zadorozhnyy, M.Y.; Korsunsky, A.M. The Characterization of PVA/PHY Hydrogels for 3D Printing Fabrication of Organ Phantoms. Mater. Today Proc. 2020, 33, 1874–1879. [Google Scholar] [CrossRef]
- Distler, T.; Schaller, E.; Steinmann, P.; Boccaccini, A.R.; Budday, S. Alginate-Based Hydrogels Show the Same Complex Mechanical Behavior as Brain Tissue. J. Mech. Behav. Biomed. Mater. 2020, 111, 103979. [Google Scholar] [CrossRef] [PubMed]
- Eble, S.K.; Hansen, O.B.; Chrea, B.; Cabe, T.N.; Garfinkel, J.; Drakos, M.C.; HSS Orthopaedic Foot and Ankle Surgery Group. Clinical Outcomes of the Polyvinyl Alcohol (PVA) Hydrogel Implant for Hallux Rigius. Sage Choice 2020, 41, 1056–1064. [Google Scholar] [CrossRef]
- Boudara, V.A.H.; Read, D.J.; Ramírez, J. Reptate Rheology Software: Toolkit for the Analysis of Theories and Experiments. J. Rheol. 2020, 64, 709–722. [Google Scholar] [CrossRef]
- Scheffold, F.; Skipetrov, S.E.; Romer, S.; Schurtenberger, P. Diffusing-Wave Spectroscopy of Nonergodic Media. Phys. Rev. E 2001, 63, 061404. [Google Scholar] [CrossRef]
- Pusey, P.N.; Megan, W.V. Dynamic Light Scattering by Non-Ergodic Media. Phys. A Stat. Mech. Appl. 1989, 157, 705–741. [Google Scholar] [CrossRef]
- Shabaniverki, S.; Juárez, J.J. Characterizing Gelatin Hydrogel Viscoelasticity with Diffusing Colloidal Probe Microscopy. J. Colloid Interface Sci. 2017, 497, 73–82. [Google Scholar] [CrossRef]
- Joosten, J.G.H.; Geladé, E.T.F.; Pusey, P.N. Dynamic Light Scattering by Nonergodic Media: Brownian Particles Trapped in Polyacrylamide Gels. Phys. Rev. A 1990, 42, 2161–2175. [Google Scholar] [CrossRef]
- van Megen, W.; Underwood, S.M. Dynamic-Light-Scattering Study of Glasses of Hard Colloidal Spheres. Phys. Rev. E 1993, 47, 248–261. [Google Scholar] [CrossRef]
- Fahimi, Z.; Aangenendt, F.J.; Voudouris, P.; Mattsson, J.; Wyss, H.M. Diffusing-Wave Spectroscopy in a Standard Dynamic Light Scattering Setup. Phys. Rev. E 2017, 96, 062611. [Google Scholar] [CrossRef]
- Mason, T.G. Estimating the Viscoelastic Moduli of Complex Fluids Using the Generalized Stokes–Einstein Equation. Rheol. Acta 2000, 39, 371–378. [Google Scholar] [CrossRef]
- Norton, A.B.; Hancocks, R.D.; Grover, L.M. Poly (Vinyl Alcohol) Modification of Low Acyl Gellan Hydrogels for Applications in Tissue Regeneration. Food Hydrocoll. 2014, 42, 373–377. [Google Scholar] [CrossRef]
- Furst, E.M.; Squires, T.M. Microrheology; Oxford University Press: Oxford, UK, 2017; ISBN 978-0-19-965520-5. [Google Scholar]





| PHY | 0.15 | 0.225 | 0.30 | ||
|---|---|---|---|---|---|
| PVA | |||||
| Blend 1 | 0.15 | (0.15, 0.15) | (0.15, 0.225) | (0.15, 0.30) | |
| Blend 2 | 0.225 | (0.225, 0.15) | (0.225, 0.225) | (0.225, 0.30) | |
| Blend 3 | 0.30 | (0.30, 0.15) | (0.30, 0.225) | (0.30, 0.30) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, R.; Bentil, S.A.; Juárez, J.J. Dynamic Light Scattering Microrheology of Phase-Separated Poly(vinyl) Alcohol–Phytagel Blends. Polymers 2024, 16, 2875. https://doi.org/10.3390/polym16202875
Ghosh R, Bentil SA, Juárez JJ. Dynamic Light Scattering Microrheology of Phase-Separated Poly(vinyl) Alcohol–Phytagel Blends. Polymers. 2024; 16(20):2875. https://doi.org/10.3390/polym16202875
Chicago/Turabian StyleGhosh, Richa, Sarah A. Bentil, and Jaime J. Juárez. 2024. "Dynamic Light Scattering Microrheology of Phase-Separated Poly(vinyl) Alcohol–Phytagel Blends" Polymers 16, no. 20: 2875. https://doi.org/10.3390/polym16202875
APA StyleGhosh, R., Bentil, S. A., & Juárez, J. J. (2024). Dynamic Light Scattering Microrheology of Phase-Separated Poly(vinyl) Alcohol–Phytagel Blends. Polymers, 16(20), 2875. https://doi.org/10.3390/polym16202875







