Glass Fibre-Reinforced Extrusion 3D-Printed Composites: Experimental and Numerical Study of Mechanical Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and 3D Printer Used
2.2. Investigated Parameters
2.3. Nozzle Diameter
2.4. Layer Height
2.5. Extruded Line cross-Section Area
2.6. Printing Temperature
2.7. Infill Orientation
2.8. Nozzle Types
2.9. Instruments
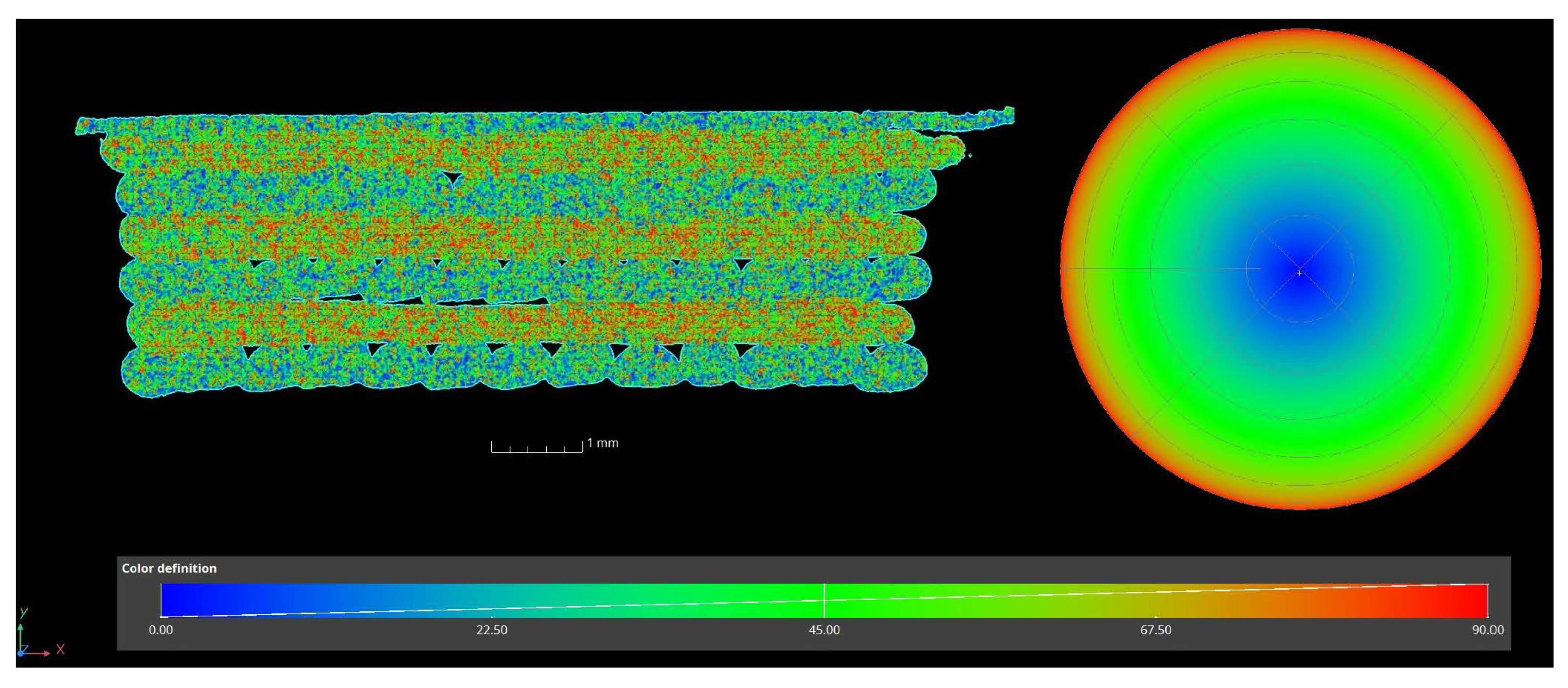
2.10. Scanning Electron Microscopy
2.11. Computed Tomography
3. Results and Discussion
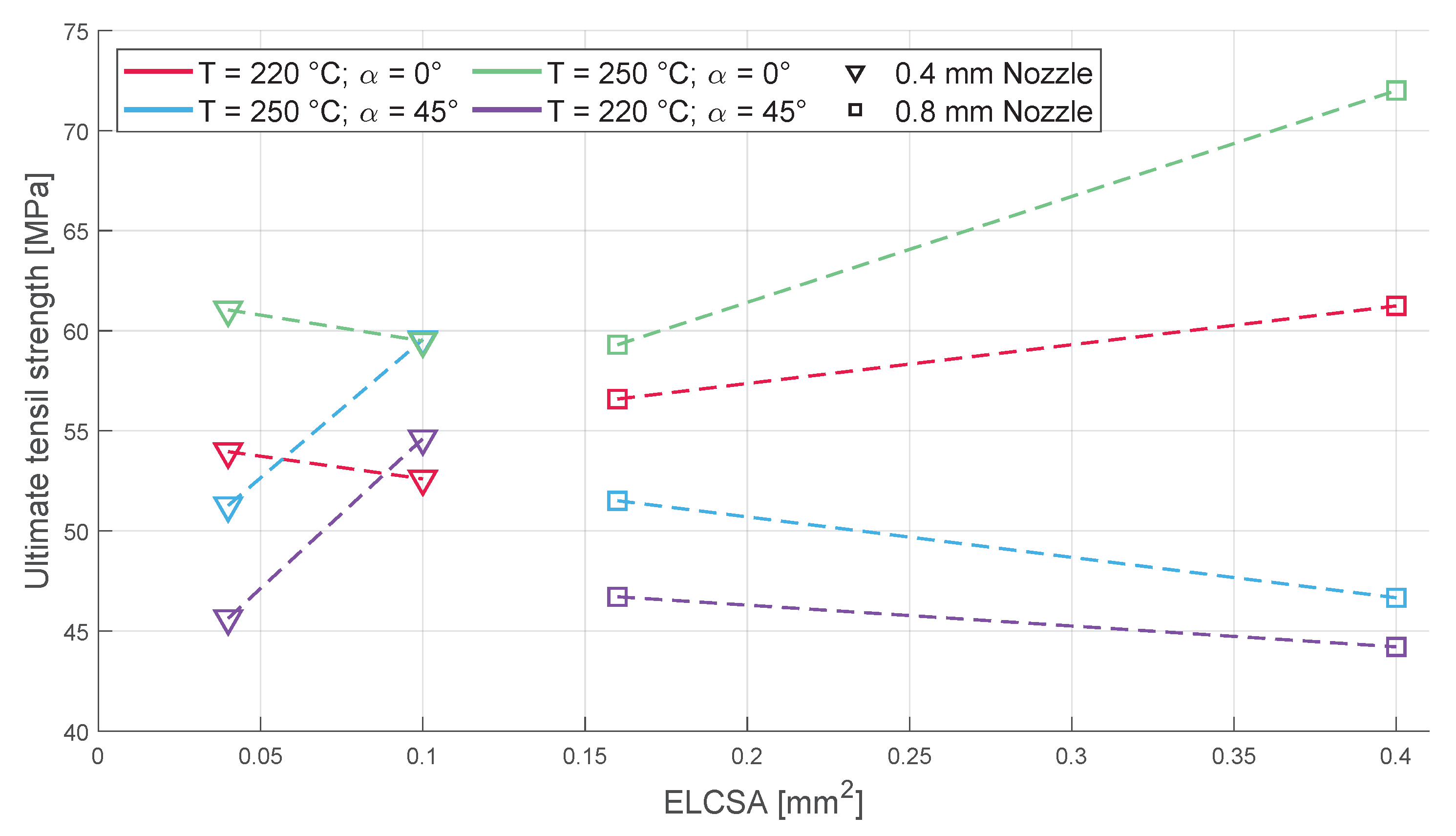
3.1. Tensile Strength
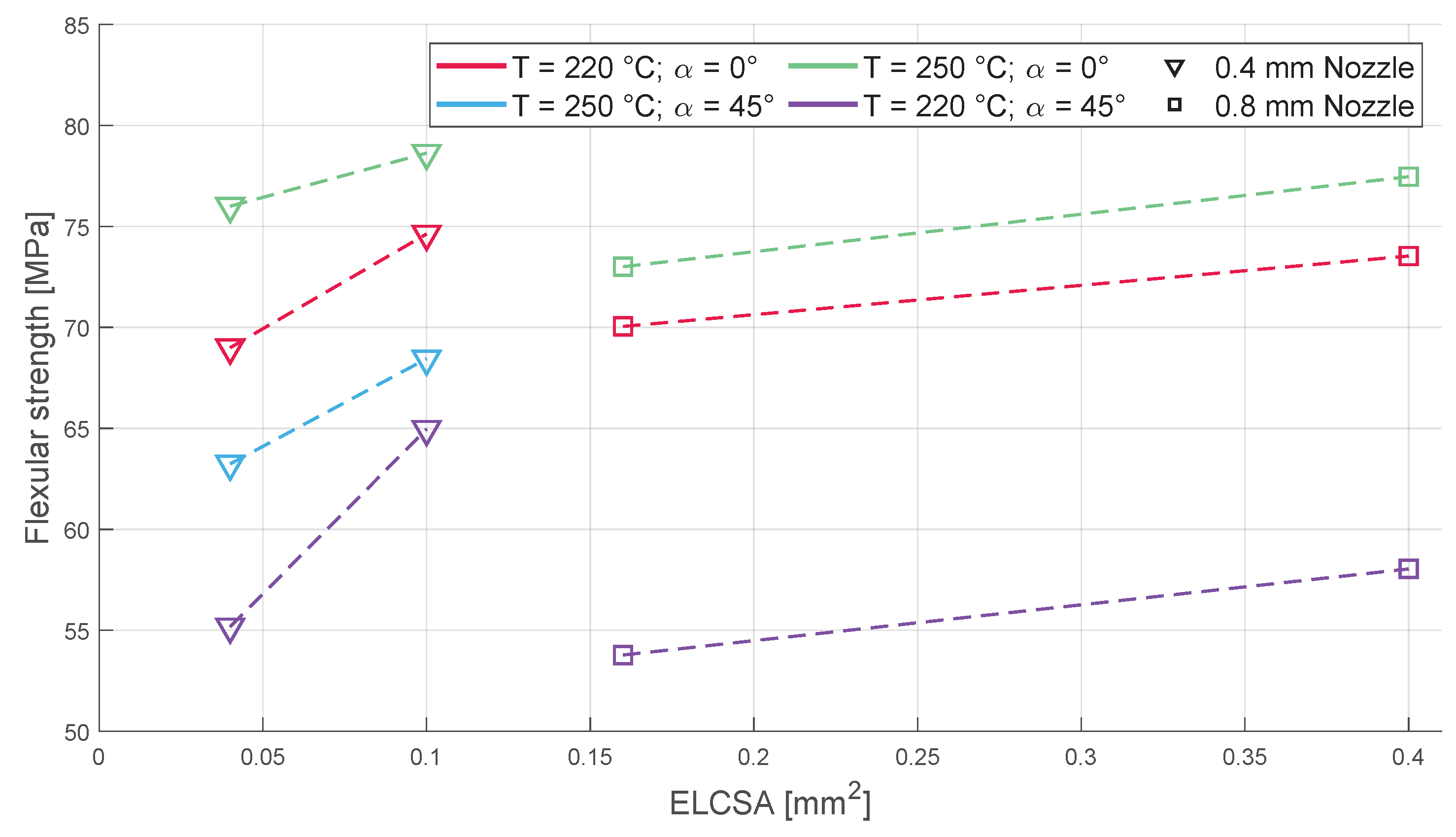
3.2. Flexural Strength
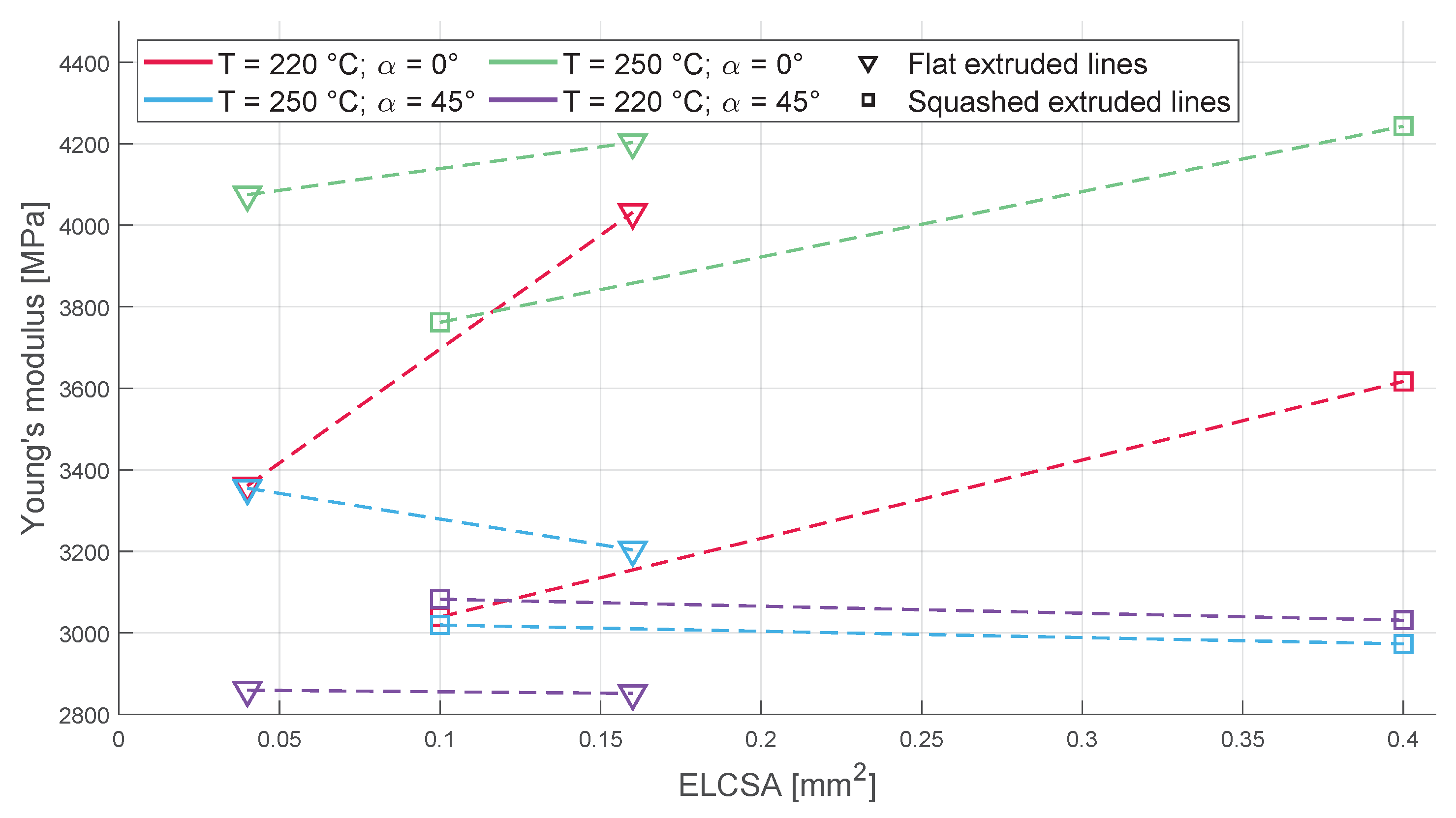
3.3. Young’s Modulus
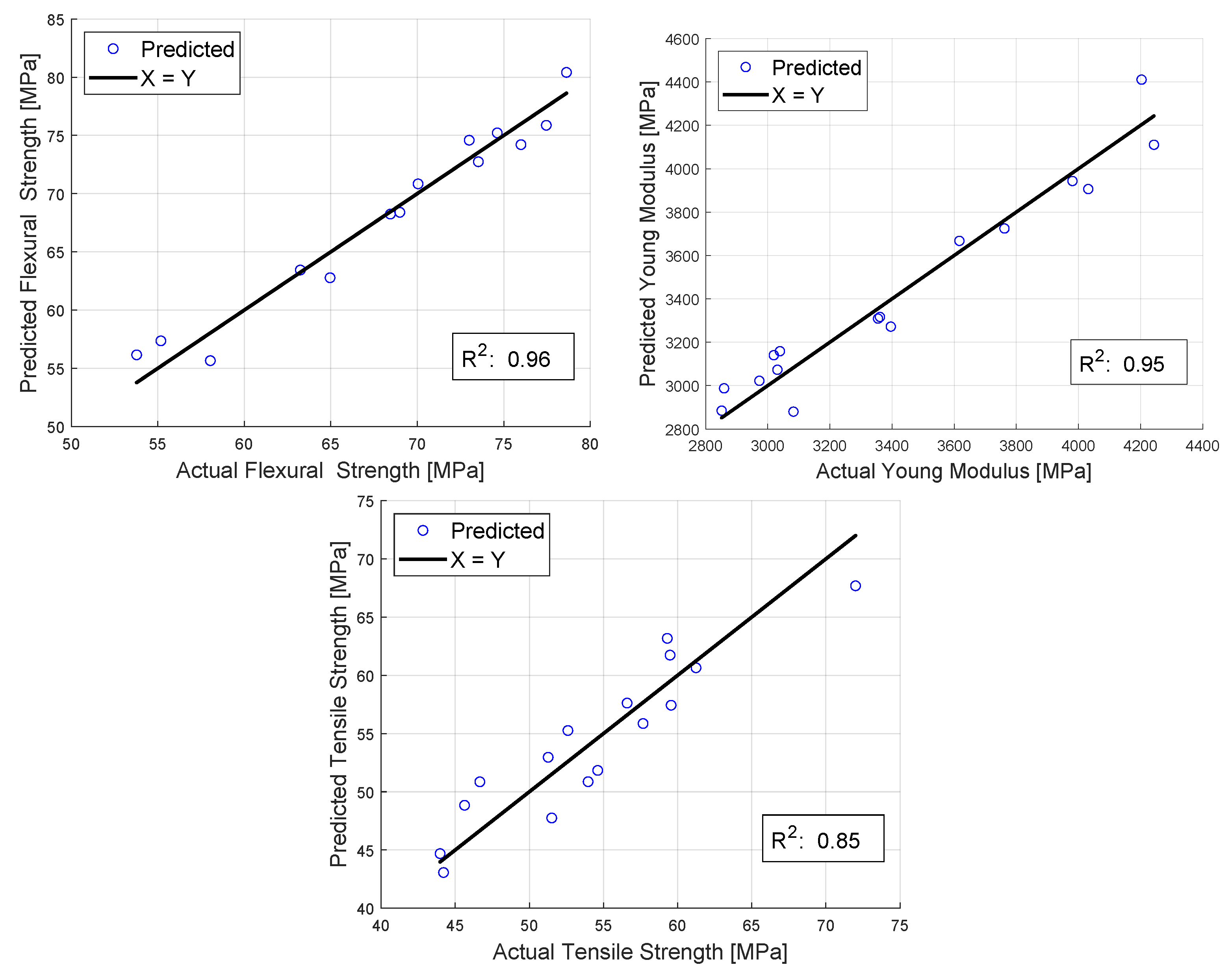
4. Modelling
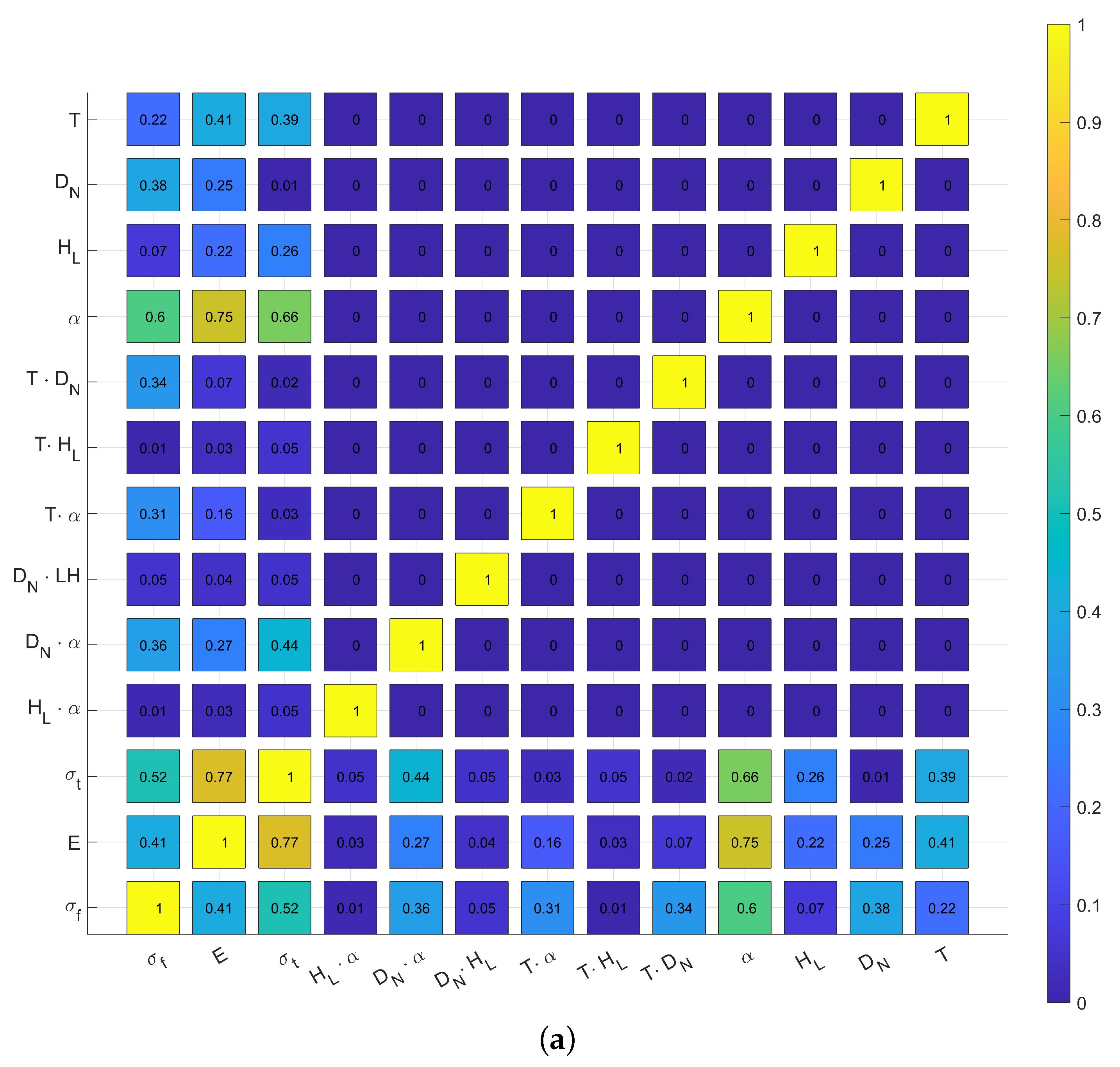
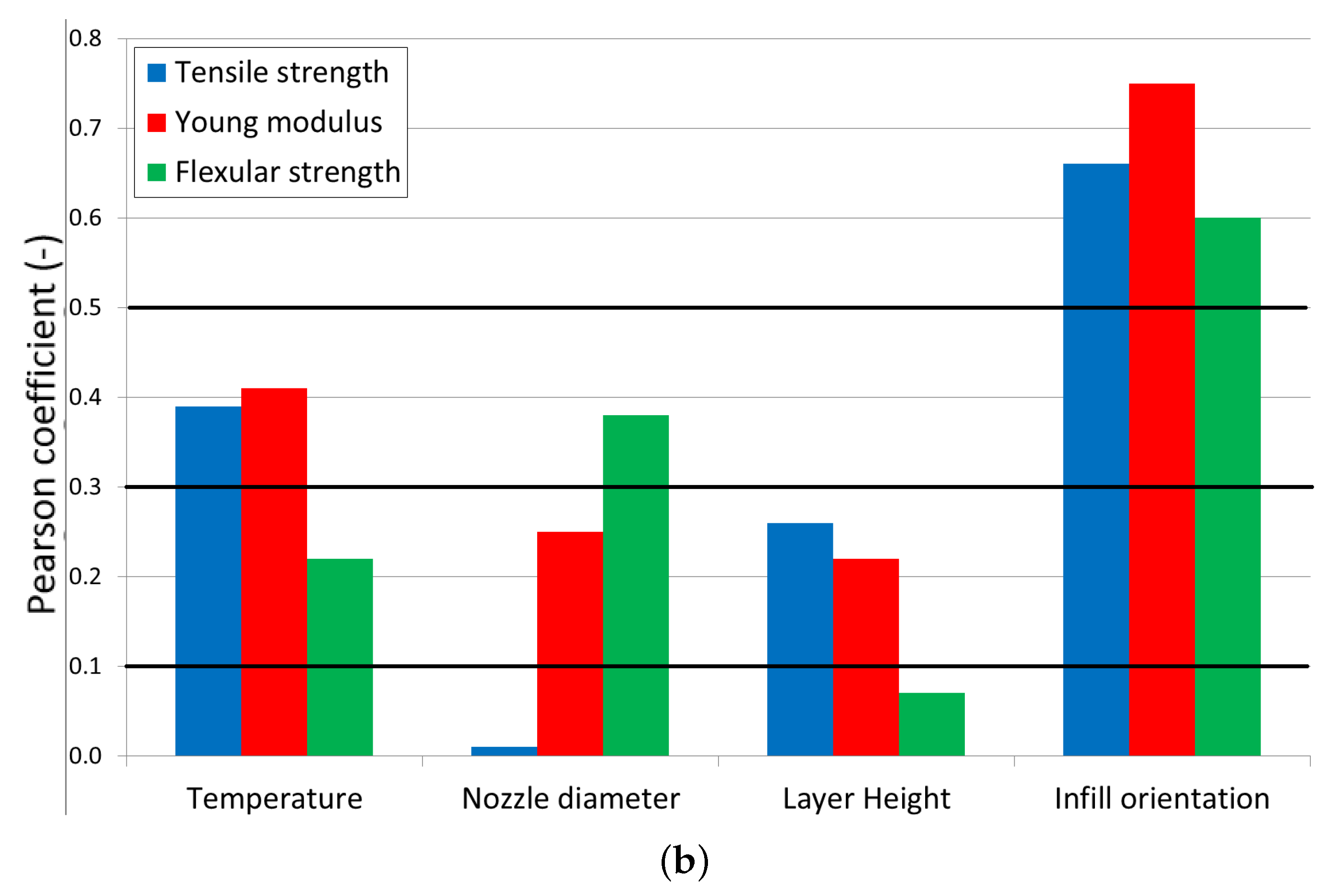
- No correlation between values of 0 and 0.1;
- A low correlation between values of 0.1 and 0.3;
- A medium correlation between values of 0.3 and 0.5;
- A strong correlation between values of 0.5 and 1.
The Effect of Studied Parameters
5. Conclusions
- A 0° infill orientation;
- A high temperature;
- A high layer height.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| T | Temperature | (°C) |
| Nozzle diameter | (mm) | |
| Layer height | (mm) | |
| Infill orientation | (°) | |
| Tensile strength | (MPa) | |
| Flexural strength | (MPa) | |
| E | Young’s modulus | (MPa) |
| Pearson coefficient | (-) | |
| N | Sizes of the data lines | (-) |
| P | Variables and measured data lines | (-) |
| Mean | (-) | |
| Standard deviation | (-) |
Appendix A. Measured vs. Computed Diagram
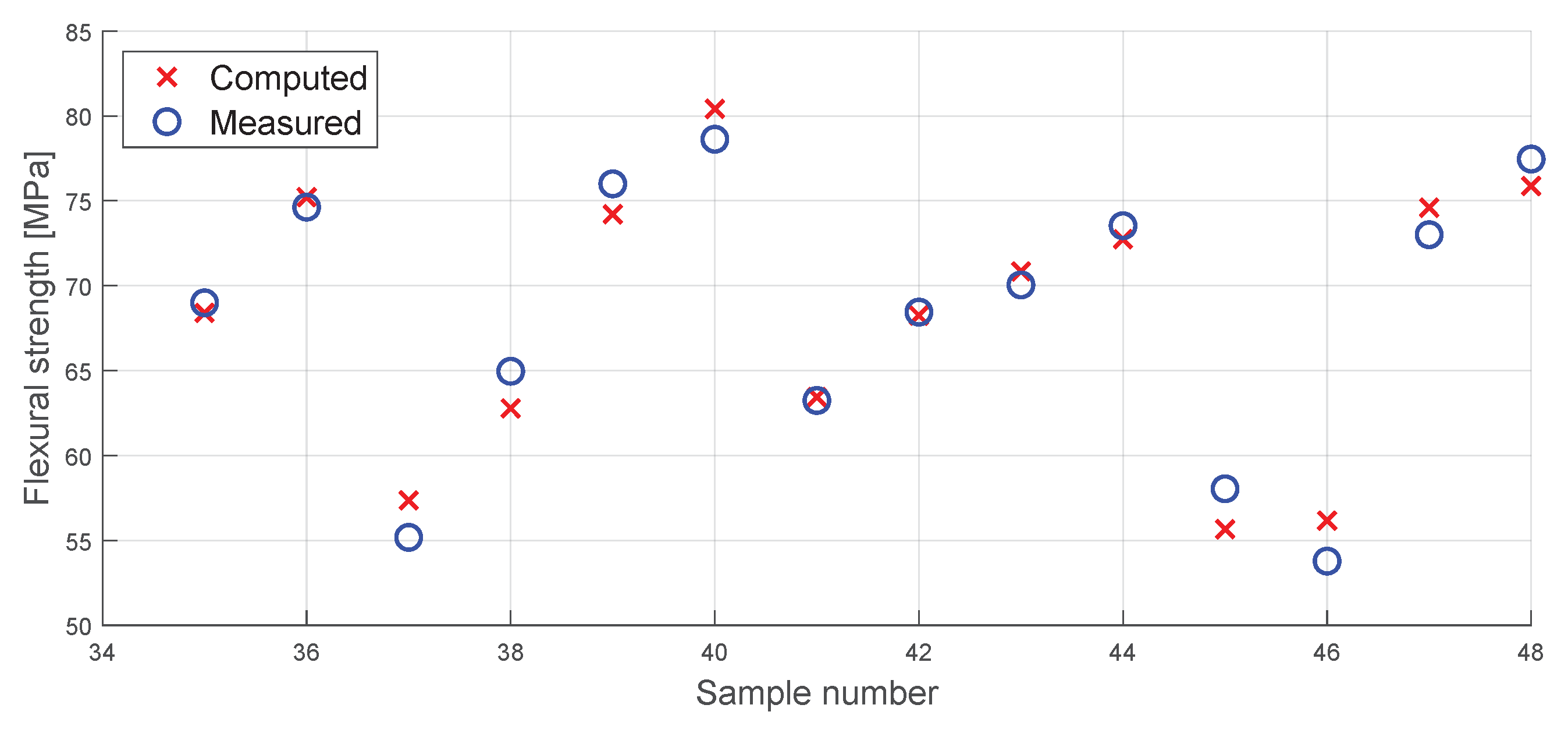
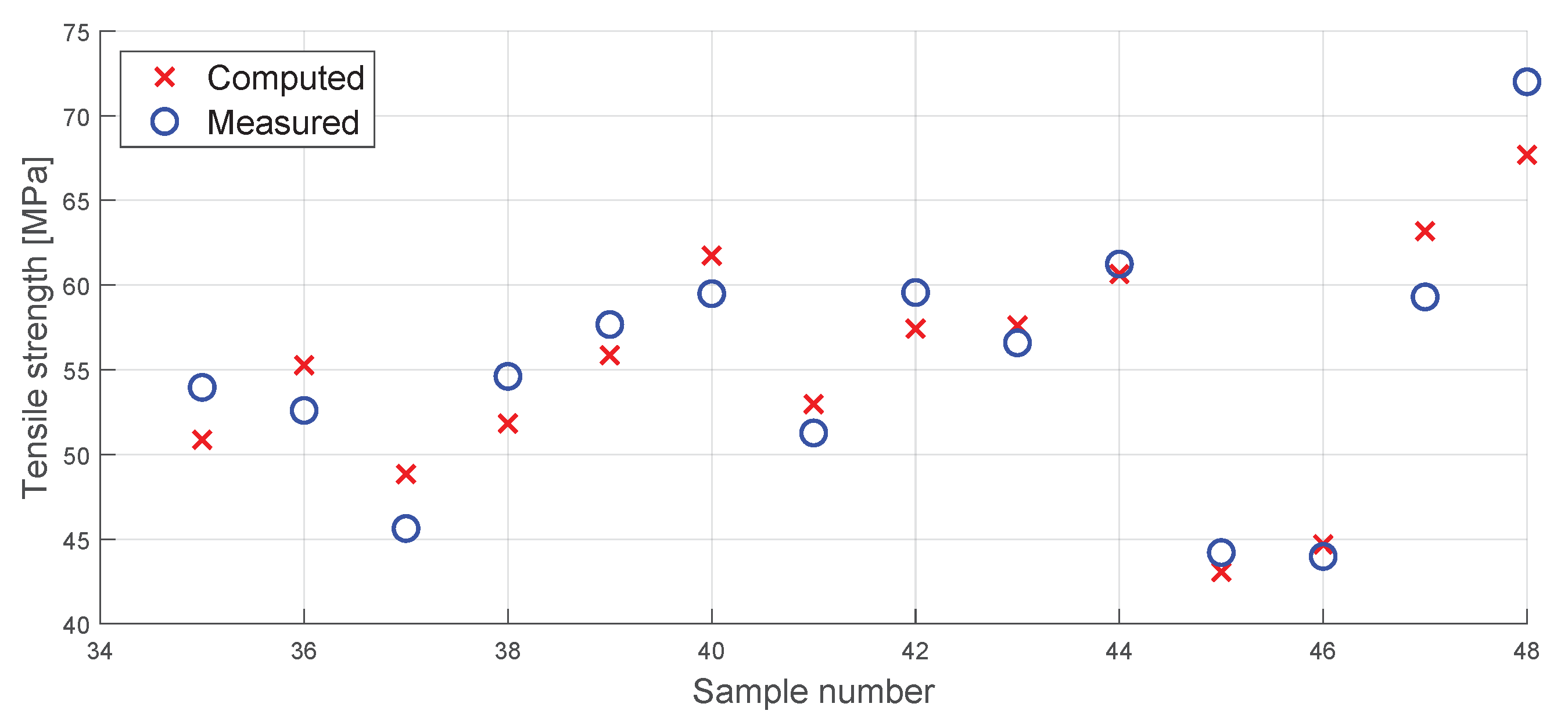
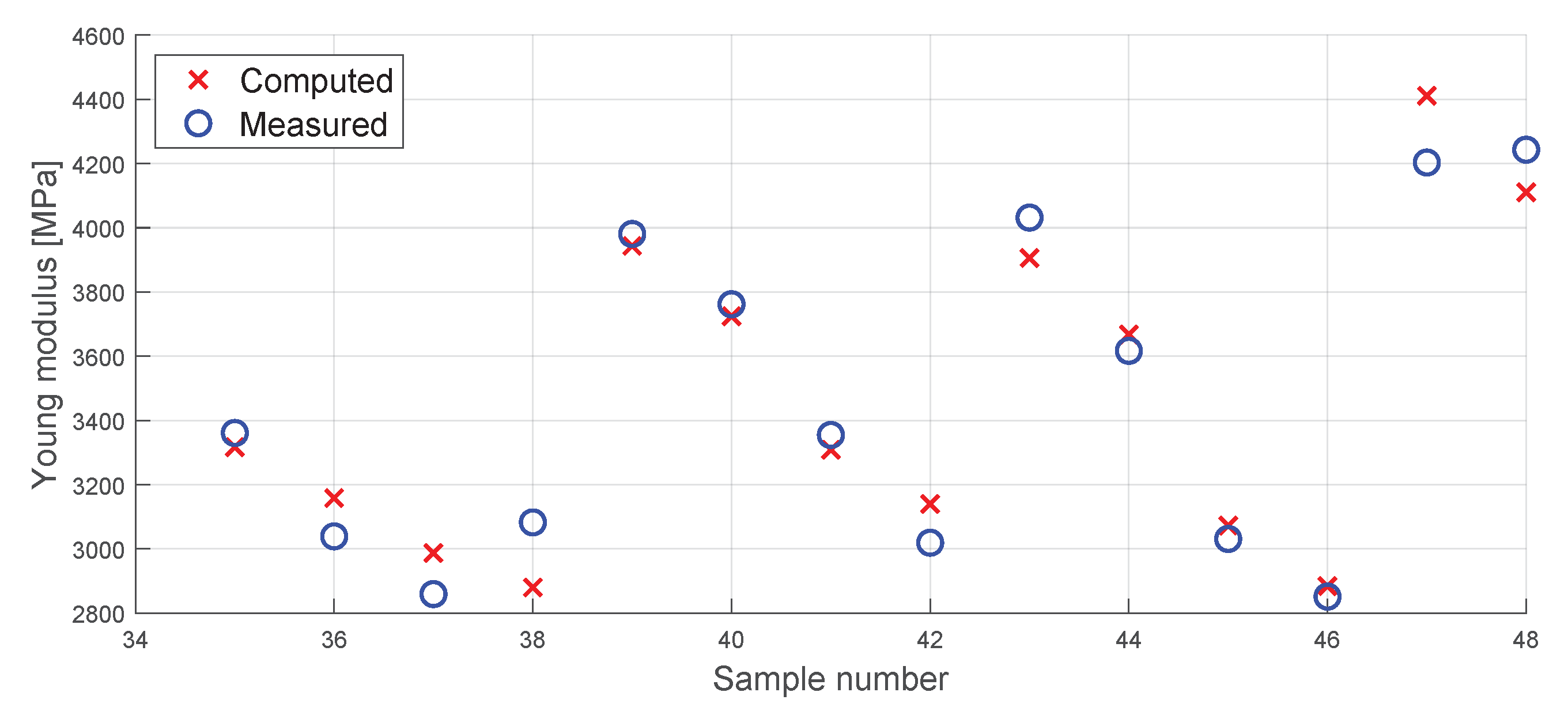
References
- Abas, M.; Habib, T.; Noor, S.; Salah, B.; Zimon, D. Parametric Investigation and Optimization to Study the Effect of Process Parameters on the Dimensional Deviation of Fused Deposition Modeling of 3D Printed Parts. Polymers 2022, 14, 3667. [Google Scholar] [CrossRef] [PubMed]
- Bochnia, J.; Blasiak, M.; Kozior, T. A Comparative Study of the Mechanical Properties of FDM 3D Prints Made of PLA and Carbon Fiber-Reinforced PLA for Thin-Walled Applications. Materials 2021, 14, 7062. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.F.M. A critical review on 3D printed continuous fiber-reinforced composites: History, mechanism, materials and properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- Hanemann, T.; Klein, A.; Baumgärtner, S.; Jung, J.; Wilhelm, D.; Antusch, S. Material Extrusion 3D Printing of PEEK-Based Composites. Polymers 2023, 15, 3412. [Google Scholar] [CrossRef] [PubMed]
- Majko, J.; Vaško, M.; Handrik, M.; Sága, M. Tensile Properties of Additively Manufactured Thermoplastic Composites Reinforced with Chopped Carbon Fibre. Materials 2022, 15, 4224. [Google Scholar] [CrossRef]
- Vakharia, V.S.; Singh, M.; Salem, A.; Halbig, M.C.; Salem, J.A. Effect of Reinforcements and 3-D Printing Parameters on the Microstructure and Mechanical Properties of Acrylonitrile Butadiene Styrene (ABS) Polymer Composites. Polymers 2022, 14, 2105. [Google Scholar] [CrossRef] [PubMed]
- Zainudin, E.; Sapuan, S.; Sulaiman, S.; Ahmad, M. Fiber orientation of short fiber reinforced injection molded thermoplastic composites: A review. J. Inject. Molding Technol. 2002, 6, 1–10. [Google Scholar]
- Teixeira, D.; Giovanela, M.; Gonella, L.; Crespo, J. Influence of injection molding on the flexural strength and surface quality of long glass fiber-reinforced polyamide 6.6 composites. Mater. Des. 2015, 85, 695–706. [Google Scholar] [CrossRef]
- Nguyen Thi, T.B.; Morioka, M.; Yokoyama, A.; Hamanaka, S.; Yamashita, K.; Nonomura, C. Measurement of fiber orientation distribution in injection-molded short-glass-fiber composites using X-ray computed tomography. J. Mater. Process. Technol. 2015, 219, 1–9. [Google Scholar] [CrossRef]
- Ferreira, R.T.L.; Amatte, I.C.; Dutra, T.A.; Bürger, D. Experimental characterization and micrography of 3D printed PLA and PLA reinforced with short carbon fibers. Compos. Part Eng. 2017, 124, 88–100. [Google Scholar] [CrossRef]
- Huang, P.; Xia, Z.; Cui, S. 3D printing of carbon fiber-filled conductive silicon rubber. Mater. Des. 2018, 142, 11–21. [Google Scholar] [CrossRef]
- Kaman, A.; Balogh, L.; Jakab, M.; Meszlenyi, A.; Levente Tarcsay, B.; Egedy, A. The Effect of 3D Printing Process Parameters on Nylon Based Composite Filaments: Experimental and Modelling Study. Chem. Eng. Trans. 2023, 100, 481–486. [Google Scholar] [CrossRef]
- Yao, T.; Zhang, K.; Deng, Z.; Ye, J. A novel generalized stress invariant-based strength model for inter-layer failure of FFF 3D printing PLA material. Mater. Des. 2020, 193, 108799. [Google Scholar] [CrossRef]
- Pervaiz, S.; Qureshi, T.A.; Kashwani, G.; Kannan, S. 3D Printing of Fiber-Reinforced Plastic Composites Using Fused Deposition Modeling: A Status Review. Materials 2021, 14, 4520. [Google Scholar] [CrossRef]
- Fisher, T.; Almeida, J.H.S., Jr.; Falzon, B.G.; Kazancı, Z. Tension and Compression Properties of 3D-Printed Composites: Print Orientation and Strain Rate Effects. Polymers 2023, 15, 1708. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Naeem, M.A.; Al Kouzbary, M.; Al Kouzbary, H.; Shasmin, H.N.; Arifin, N.; Abd Razak, N.A.; Abu Osman, N.A. Effect of Infill Parameters on the Compressive Strength of 3D-Printed Nylon-Based Material. Polymers 2023, 15, 255. [Google Scholar] [CrossRef] [PubMed]
- Venkatesh, R.; Jerold John Britto, J.; Amudhan, K.; Anbumalar, V.; Prabhakaran, R.; Thiyanesh Sakthi, R. Experimental investigation of mechanical properties on CF reinforced PLA, ABS and Nylon composite part. Mater. Today Proc. 2023, 76, 647–653. [Google Scholar] [CrossRef]
- Pulipaka, A.; Gide, K.M.; Beheshti, A.; Bagheri, Z.S. Effect of 3D printing process parameters on surface and mechanical properties of FFF-printed PEEK. J. Manuf. Process. 2023, 85, 368–386. [Google Scholar] [CrossRef]
- Klipper3d Team. Klipper Documentation—Kinematics. Available online: https://www.klipper3d.org/Kinematics.html (accessed on 19 July 2023).
- Klipper3d Team. Klipper Documentation—Skew Correction. Available online: https://www.klipper3d.org/Skew_Correction.html (accessed on 19 July 2023).
- Hackney, P.; Oppon, C. Fatigue Analysis of Additive Manufactured Long Fibre Reinforced Nylon Materials. Procedia Manuf. 2020, 51, 678–683. [Google Scholar] [CrossRef]
- Islam, M.N.; Baxevanakis, K.P.; Silberschmidt, V.V. Viscoelastic characterisation of additively manufactured composites with nylon matrix: Effects of type and orientation of fibres. Compos. Part Eng. 2023, 263, 110815. [Google Scholar] [CrossRef]
- Liu, Z.; Mazzei Capote, G.A.; Grubis, E.; Pandey, A.; Blanco Campos, J.C.; Hegge, G.R.; Osswald, T.A. Predicting Properties of Fused Filament Fabrication Parts through Sensors and Machine Learning. J. Manuf. Mater. Process. 2023, 7, 186. [Google Scholar] [CrossRef]
- Ismail, K.I.; Pang, R.; Ahmed, R.; Yap, T.C. Tensile Properties of In Situ 3D Printed Glass Fiber-Reinforced PLA. Polymers 2023, 15, 3436. [Google Scholar] [CrossRef] [PubMed]






| Sample No. (−) | Nozzle Diameter (mm) | Layer Height (mm) | Tempera Ture (°C) | Infill Orientation (°) | Tensile Strength (MPa) | Young’s Modulus (MPa) | Flexural Strength (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Average | Deviation | Average | Deviation | Average | Deviation | |||||
| 1 | 0.6 | 0.4 | 220 | 45 | 44.85 | 6.27 | 3322 | 906.03 | - | - |
| 2 | 0.6 | 0.4 | 250 | 45 | 39.17 | 1.86 | 2767 | 153.73 | - | - |
| 3 | 0.6 | 0.4 | 220 | 45 | 28.12 | 2.40 | 2417 | 97.83 | - | - |
| 4 | 0.6 | 0.15 | 220 | 45 | 30.29 | 1.15 | 2823 | 101.42 | - | - |
| 5 | 0.6 | 0.15 | 250 | 45 | 28.88 | 0.45 | 2497 | 94.67 | - | - |
| 6 | 0.6 | 0.15 | 220 | 45 | 31.01 | 2.55 | 3716 | 251.73 | - | - |
| 7 | 0.6 | 0.4 | 220 | 0 | 36.72 | 2.75 | 2943 | 189.45 | - | - |
| 8 | 0.6 | 0.15 | 220 | 0 | 34.77 | 2.87 | 3304 | 183.06 | - | - |
| 9 | 0.6 | 0.4 | 250 | 0 | 38.20 | 0.98 | 3018 | 33.38 | - | - |
| 10 | 0.6 | 0.15 | 250 | 0 | 43.33 | 1.55 | 3816 | 111.38 | - | - |
| 11 | 0.6 | 0.4 | 220 | 0 | 35.65 | 1.79 | 2789 | 215.70 | - | - |
| 12 | 0.6 | 0.15 | 220 | 0 | 37.25 | 12.39 | 3361 | 1018 | - | - |
| 13 | 0.6 | 0.4 | 220 | 45 | 35.05 | 5.08 | 2337 | 423.01 | - | - |
| 14 | 0.6 | 0.15 | 220 | 45 | 32.43 | 4.63 | 2308 | 293.98 | - | - |
| 15 | 0.6 | 0.4 | 250 | 90 | 36.86 | 2.69 | 2763 | 140.62 | - | - |
| 16 | 0.6 | 0.4 | 250 | 45 | 33.94 | 2.14 | 1854 | 124.32 | - | - |
| 17 | 0.6 | 0.15 | 250 | 0 | 32.71 | 2.12 | 2971 | 225.60 | - | - |
| 18 | 0.6 | 0.15 | 250 | 45 | 33.09 | 2.44 | 2265 | 209.53 | - | - |
| 19 | 0.3 | 0.2 | 220 | 45 | 36.09 | 0.84 | 2213 | 200.86 | - | - |
| 20 | 0.3 | 0.1 | 220 | 0 | 39.24 | 1.75 | 3951 | 460.87 | - | - |
| 21 | 0.3 | 0.2 | 220 | 0 | 35.00 | 3.91 | 2752 | 281.88 | - | - |
| 22 | 0.3 | 0.1 | 220 | 45 | 43.73 | 1.94 | 3400 | 167.57 | - | - |
| 23 | 0.3 | 0.1 | 220 | 0 | 28.94 | 3.01 | 2613 | 232.51 | - | - |
| 24 | 0.3 | 0.2 | 220 | 0 | 28.66 | 5.94 | 2270 | 421.09 | - | - |
| 25 | 0.3 | 0.1 | 220 | 45 | 27.08 | 1.14 | 1616 | 56.63 | - | - |
| 26 | 0.3 | 0.2 | 220 | 45 | 24.88 | 1.69 | 1353 | 100.76 | - | - |
| 27 | 0.3 | 0.2 | 250 | 45 | 36.50 | 0.99 | 2065 | 195.60 | - | - |
| 28 | 0.3 | 0.1 | 250 | 0 | 47.47 | 3.83 | 5409 | 508.06 | - | - |
| 29 | 0.3 | 0.2 | 250 | 0 | 36.81 | 1.29 | 2701 | 219.35 | - | - |
| 30 | 0.3 | 0.1 | 250 | 45 | 43.54 | 3.43 | 3802 | 364.11 | - | - |
| 31 | 0.3 | 0.1 | 250 | 0 | 40.29 | 1.66 | 3598 | 340.19 | - | - |
| 32 | 0.3 | 0.2 | 250 | 0 | 30.75 | 1.58 | 2176 | 147.28 | - | - |
| 33 | 0.3 | 0.2 | 250 | 45 | 31.37 | 0.75 | 1981 | 73.07 | - | - |
| 34 | 0.3 | 0.1 | 250 | 45 | 29.68 | 2.27 | 1738 | 275.94 | - | - |
| 35 | 0.4 | 0.10 | 220 | 0 | 53.96 | 3.73 | 3361 | 400.54 | 68.99 | 6.19 |
| 36 | 0.4 | 0.25 | 220 | 0 | 52.60 | 2.43 | 3039 | 139.61 | 74.62 | 3.79 |
| 37 | 0.4 | 0.10 | 220 | 45 | 45.63 | 0.72 | 2859 | 125.08 | 55.18 | 1.04 |
| 38 | 0.4 | 0.25 | 220 | 45 | 54.61 | 4.89 | 3083 | 61.63 | 64.96 | 3.64 |
| 39 | 0.4 | 0.10 | 250 | 0 | 57.67 | 3.98 | 3981 | 208.52 | 76.00 | 6.19 |
| 40 | 0.4 | 0.25 | 250 | 0 | 59.49 | 2.27 | 3762 | 112.57 | 78.63 | 1.75 |
| 41 | 0.4 | 0.10 | 250 | 45 | 51.27 | 3.84 | 3355 | 121.64 | 63.24 | 3.32 |
| 42 | 0.4 | 0.25 | 250 | 45 | 59.56 | 2.92 | 3019 | 223.98 | 68.44 | 3.19 |
| 43 | 0.8 | 0.20 | 220 | 0 | 56.59 | 6.51 | 4032 | 180.94 | 70.05 | 2.52 |
| 44 | 0.8 | 0.50 | 220 | 0 | 61.24 | 1.93 | 3617 | 168.38 | 73.53 | 3.92 |
| 45 | 0.8 | 0.50 | 220 | 45 | 44.21 | 3.80 | 3031 | 116.94 | 58.04 | 4.17 |
| 46 | 0.8 | 0.50 | 220 | 45 | 43.98 | 5.56 | 2852 | 371.12 | 53.78 | 3.92 |
| 47 | 0.8 | 0.20 | 250 | 0 | 59.30 | 3.96 | 4203 | 154.19 | 73.00 | 4.74 |
| 48 | 0.8 | 0.50 | 250 | 0 | 72.00 | 7.10 | 4243 | 198.44 | 77.46 | 5.92 |
| 49 | 0.8 | 0.20 | 250 | 45 | 51.51 | 3.67 | 3396 | 176.39 | - | - |
| 50 | 0.8 | 0.50 | 250 | 45 | 46.66 | 4.45 | 2973 | 113.84 | - | - |
| Parameter | Mechanical Property | ||
|---|---|---|---|
| a | 54.39 | 3425.33 | 67.20 |
| b | 2.79 | 191.17 | 2.30 |
| c | 0.04 | 117.95 | −1.56 |
| d | 1.88 | −101.90 | 1.68 |
| e | −4.71 | −354.35 | −6.84 |
| f | 0.14 | −30.64 | −0.52 |
| g | 0.37 | −15.28 | −0.15 |
| h | −0.22 | −76.36 | 0.07 |
| j | −0.34 | −20.27 | −1.23 |
| k | −3.13 | −126.04 | −1.04 |
| l | −0.35 | 12.57 | −0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kámán, A.; Balogh, L.; Tarcsay, B.L.; Jakab, M.; Meszlényi, A.; Turcsán, T.; Egedy, A. Glass Fibre-Reinforced Extrusion 3D-Printed Composites: Experimental and Numerical Study of Mechanical Properties. Polymers 2024, 16, 212. https://doi.org/10.3390/polym16020212
Kámán A, Balogh L, Tarcsay BL, Jakab M, Meszlényi A, Turcsán T, Egedy A. Glass Fibre-Reinforced Extrusion 3D-Printed Composites: Experimental and Numerical Study of Mechanical Properties. Polymers. 2024; 16(2):212. https://doi.org/10.3390/polym16020212
Chicago/Turabian StyleKámán, András, László Balogh, Bálint Levente Tarcsay, Miklós Jakab, Armand Meszlényi, Tamás Turcsán, and Attila Egedy. 2024. "Glass Fibre-Reinforced Extrusion 3D-Printed Composites: Experimental and Numerical Study of Mechanical Properties" Polymers 16, no. 2: 212. https://doi.org/10.3390/polym16020212
APA StyleKámán, A., Balogh, L., Tarcsay, B. L., Jakab, M., Meszlényi, A., Turcsán, T., & Egedy, A. (2024). Glass Fibre-Reinforced Extrusion 3D-Printed Composites: Experimental and Numerical Study of Mechanical Properties. Polymers, 16(2), 212. https://doi.org/10.3390/polym16020212






