Multiscale Analysis of Impact-Resistance in Self-Healing Poly(ethylene-co-methacrylic acid) (EMAA) Plain Woven Composites
Abstract
1. Introduction
2. Experimental Procedure
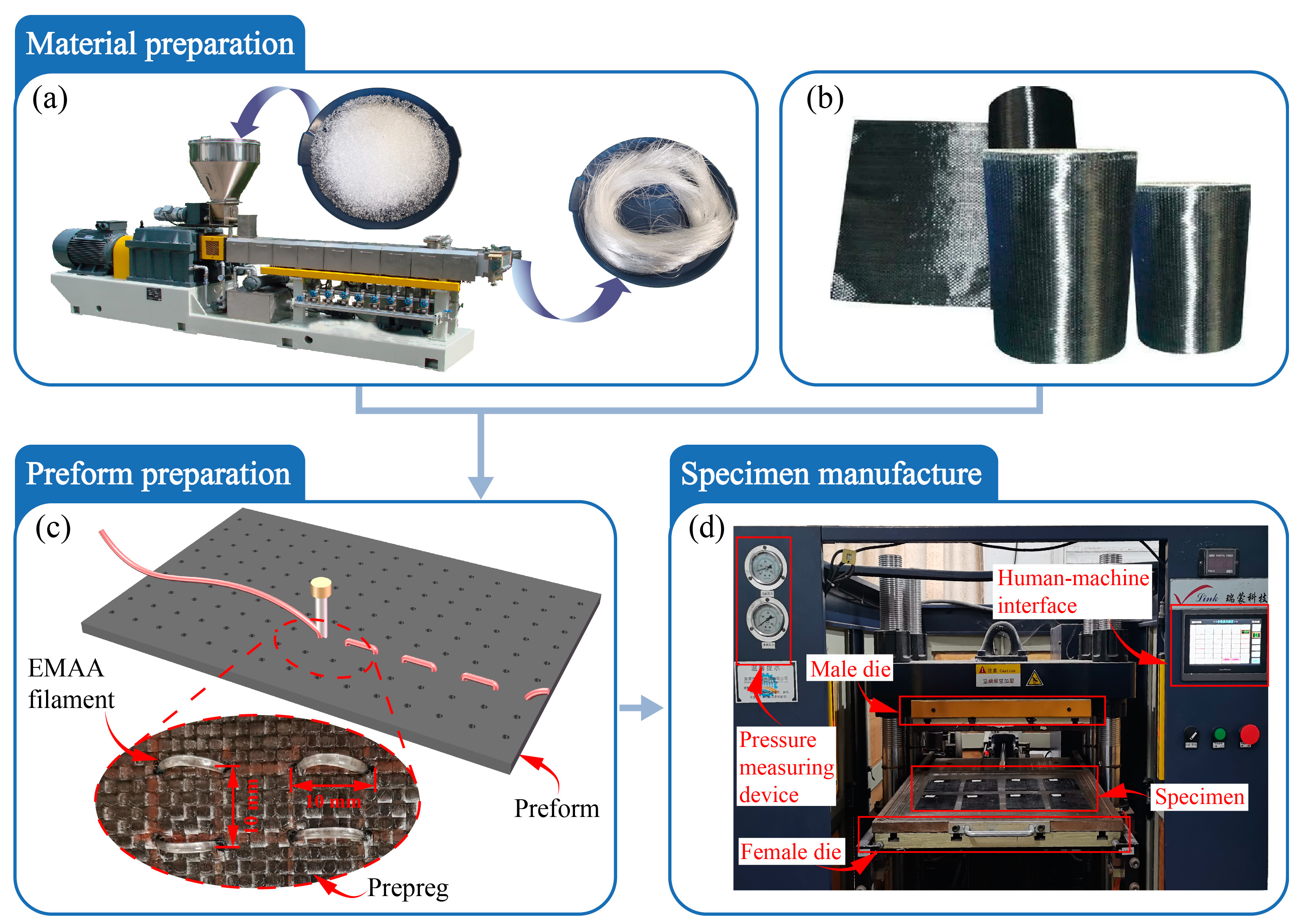
2.1. Specimen Preparation
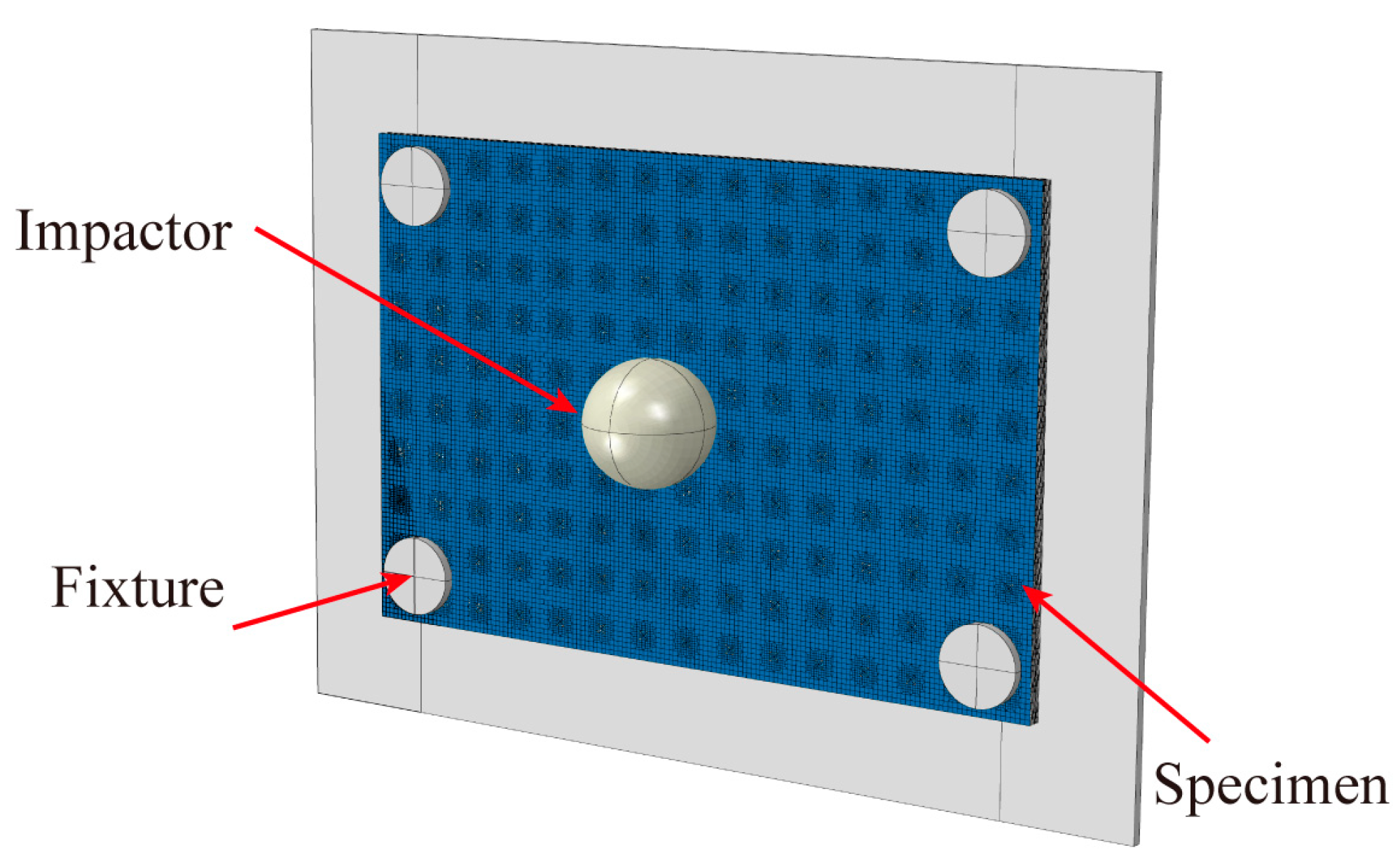
2.2. Low-Velocity Impact Test
2.3. Self-Healing Test
3. Multiscale Modeling of EWL
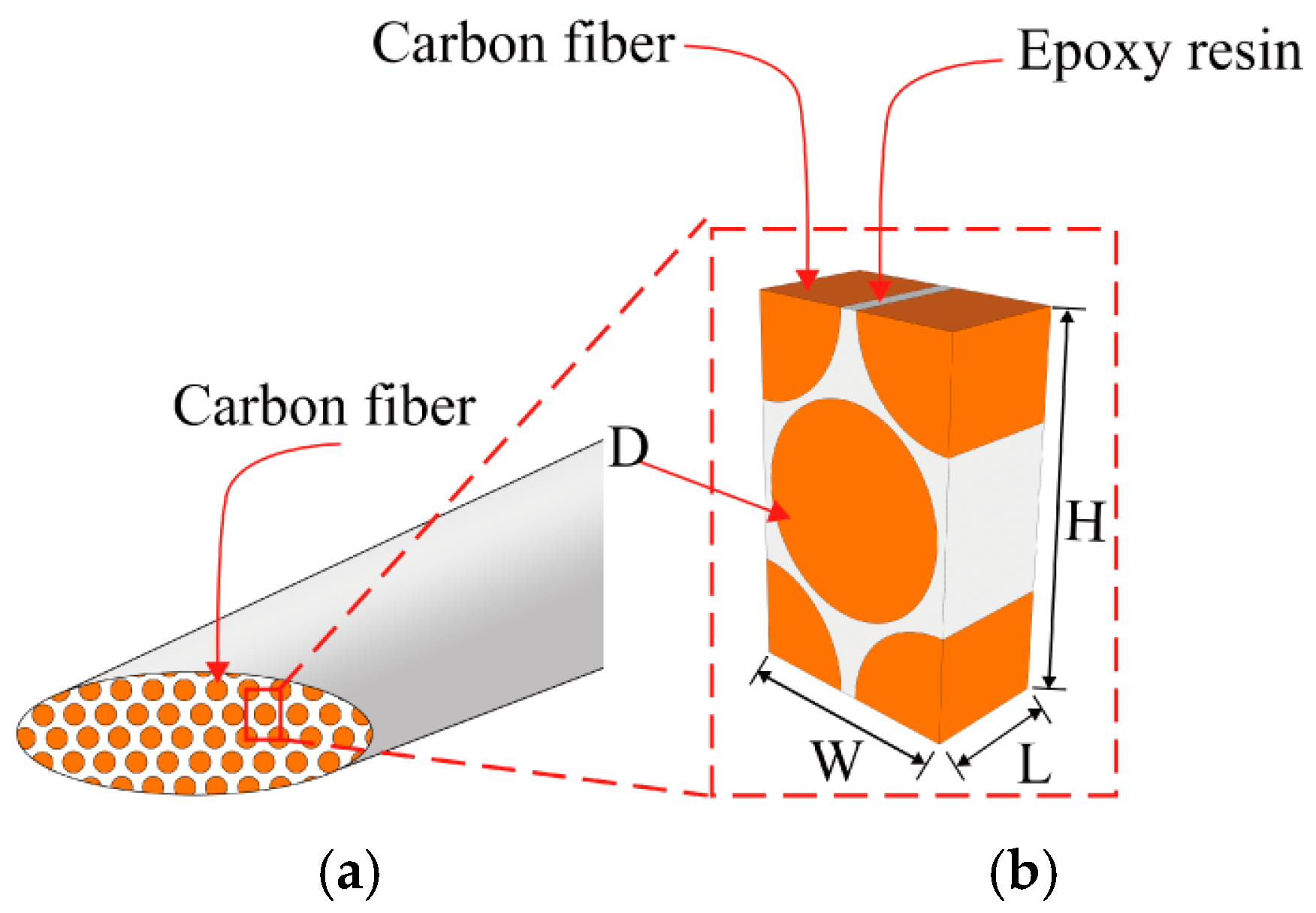
3.1. Microscale RVE Modeling
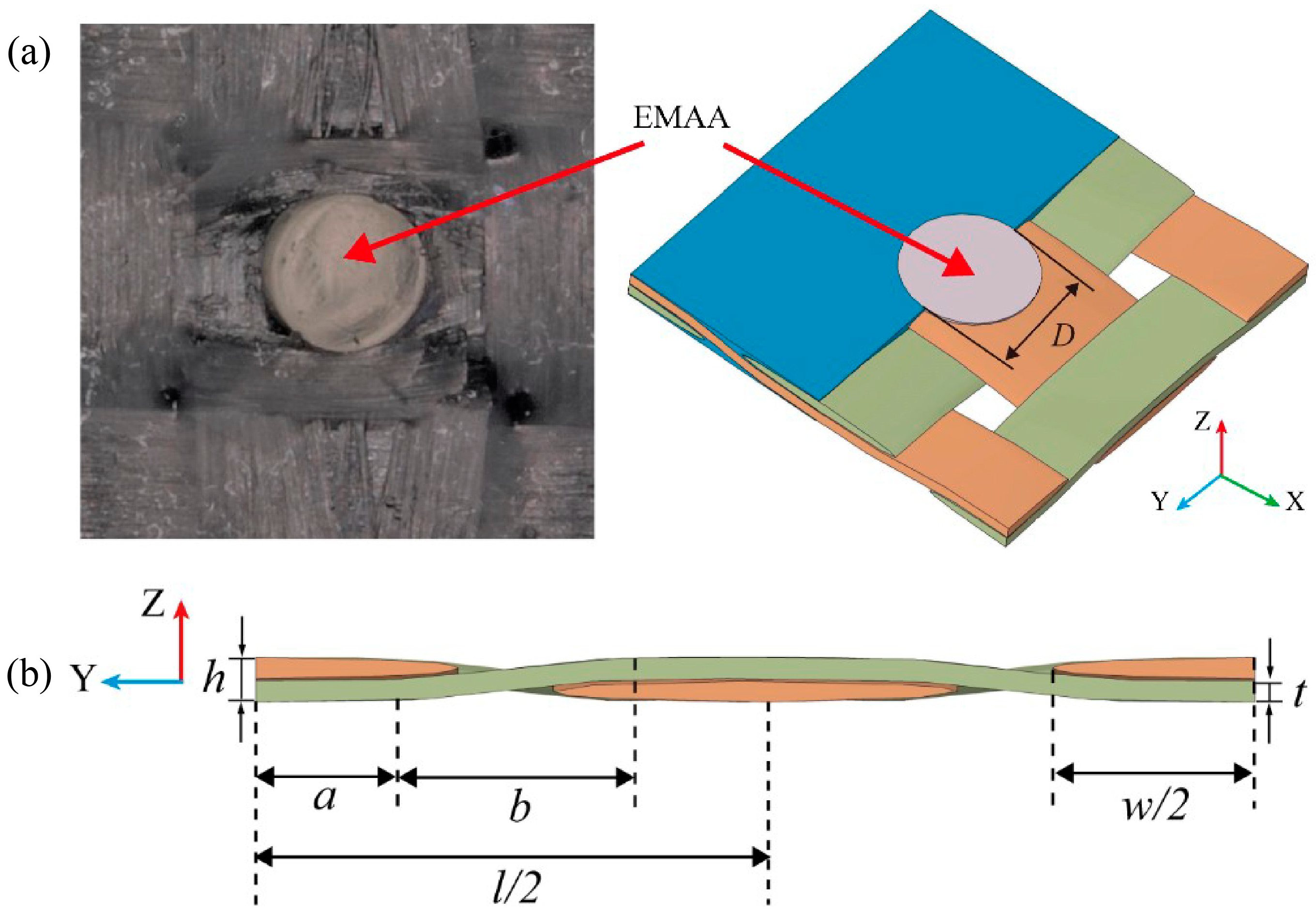
3.2. Mesoscale RVE Modeling
3.3. Local Homogenization Method
3.4. Macroscale Modeling
4. Results and Discussion
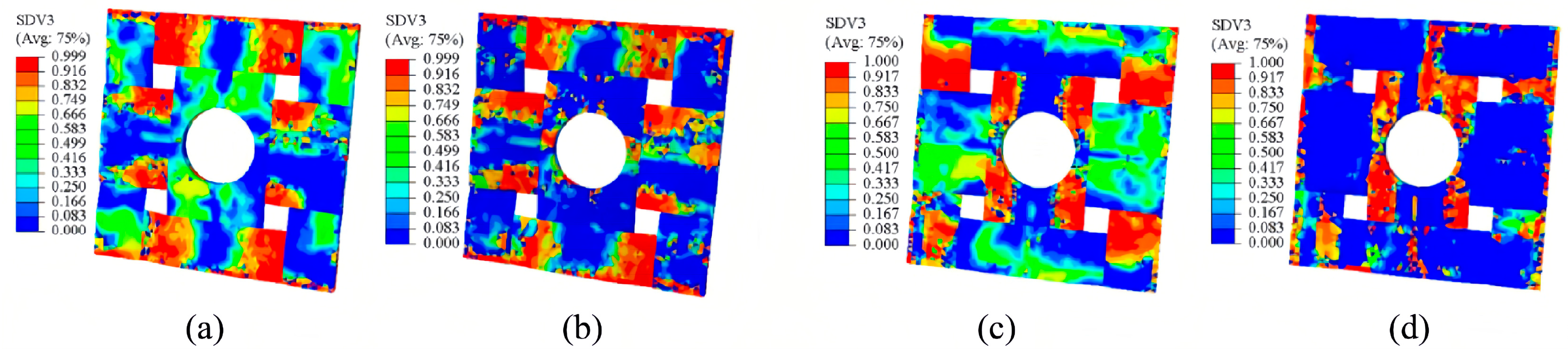
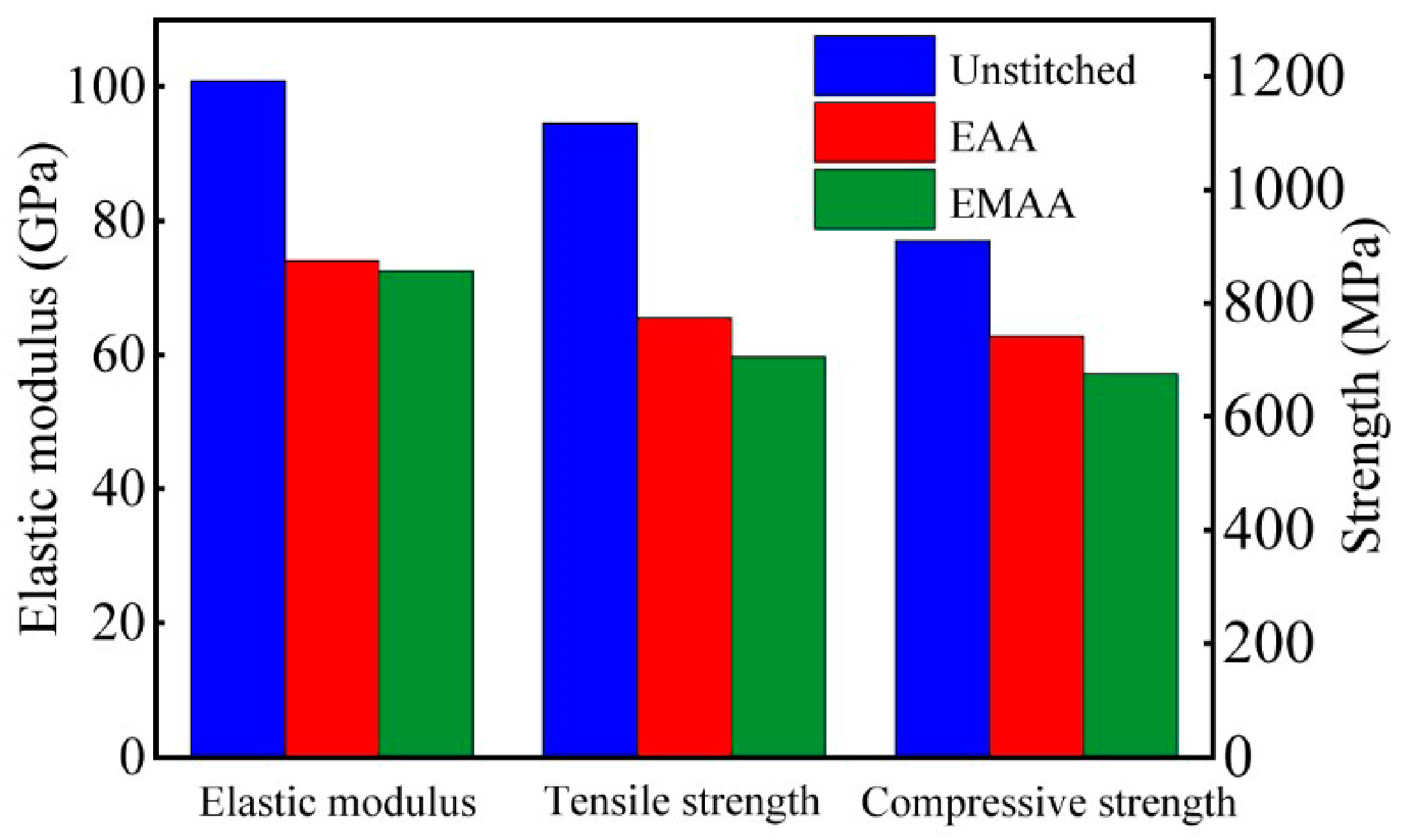
4.1. Effect of Stitching on the Mechanical Properties of the Mesoscale RVE Model
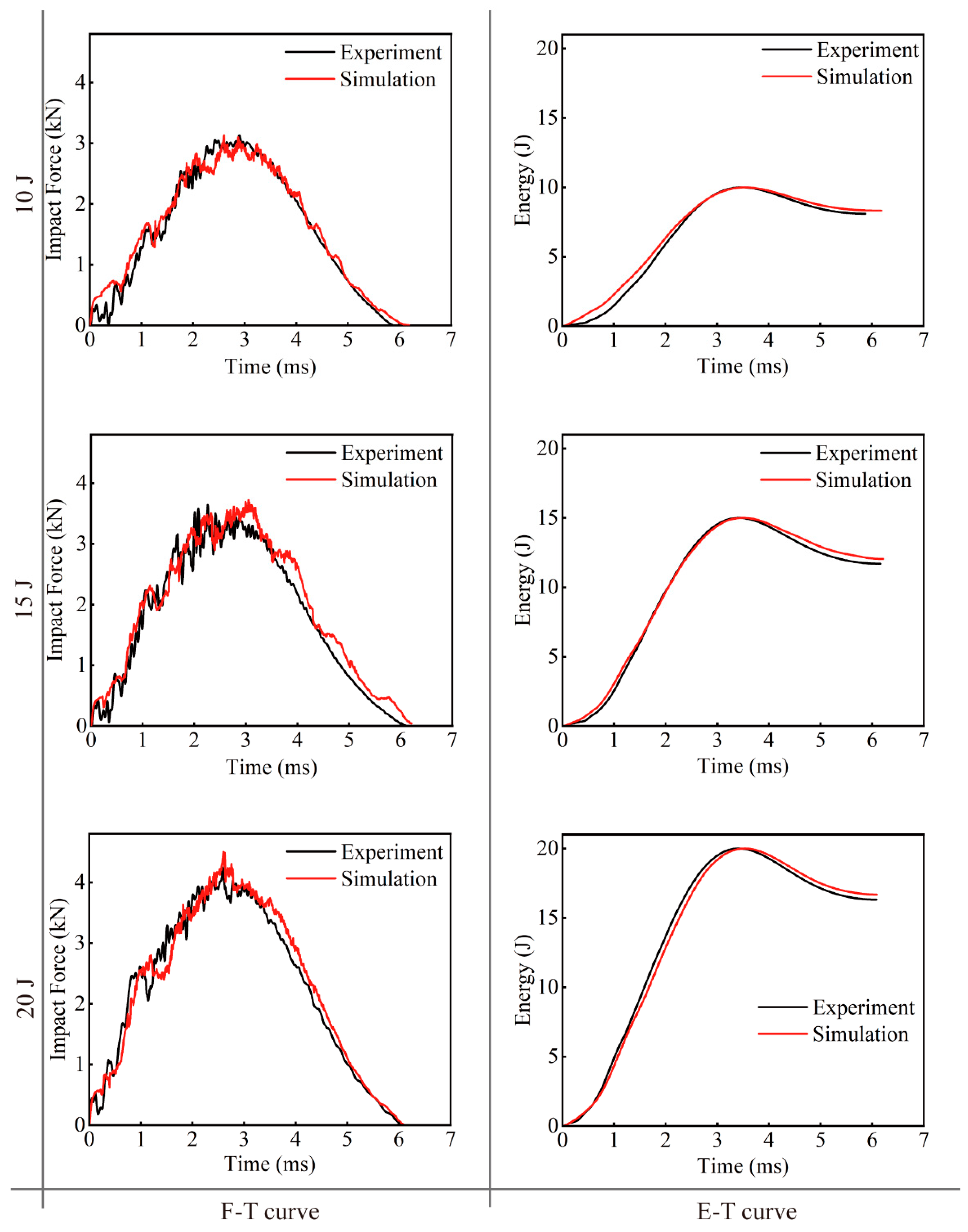
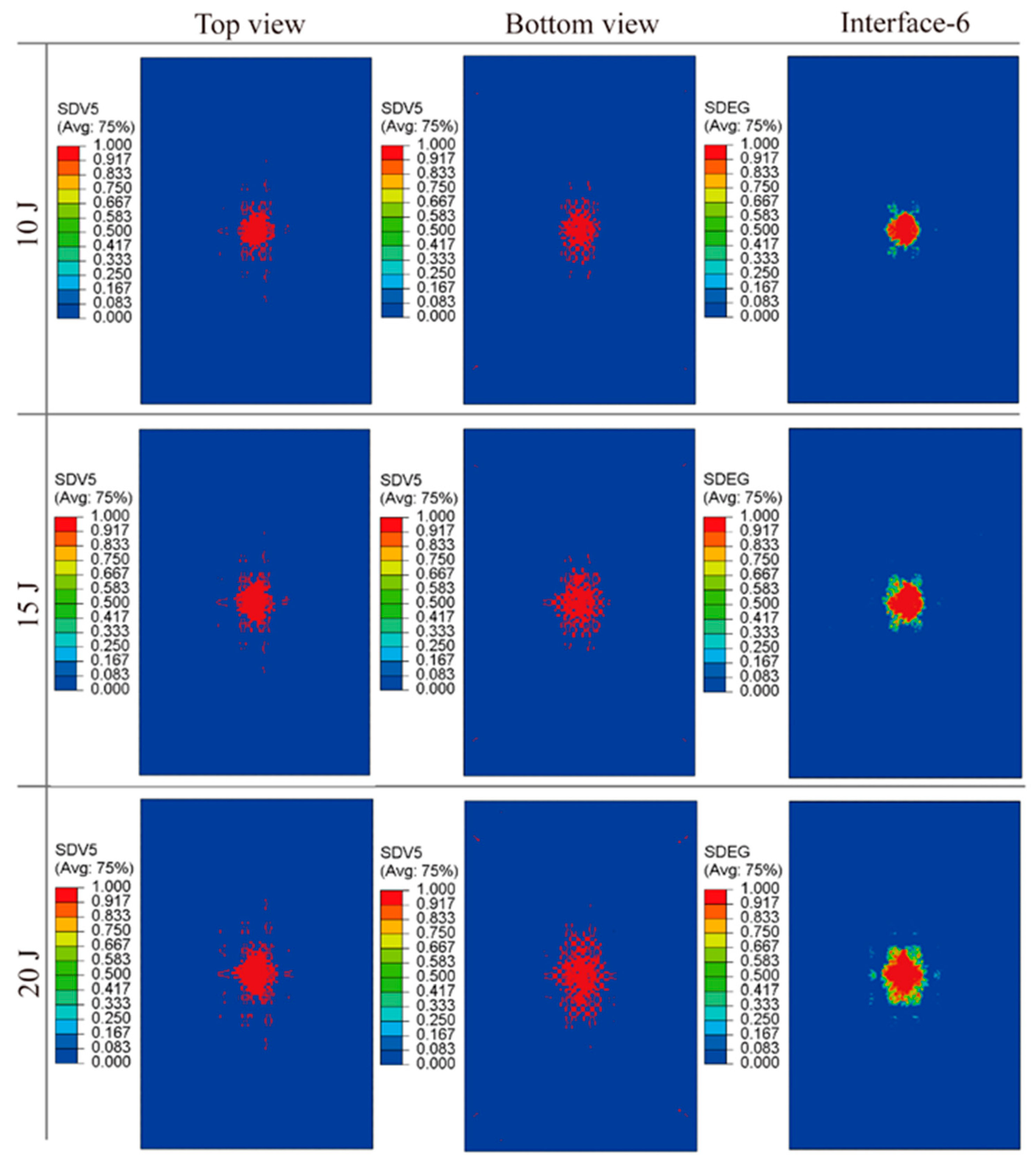
4.2. Multiscale Model Validation at Different LVI Energies
4.3. LVI Mechanical Response of EWL with Different Stitch Spacings
4.4. Mechanical Impact Response of EWL with Different Stitch Spacings after Self-Healing
5. Conclusions
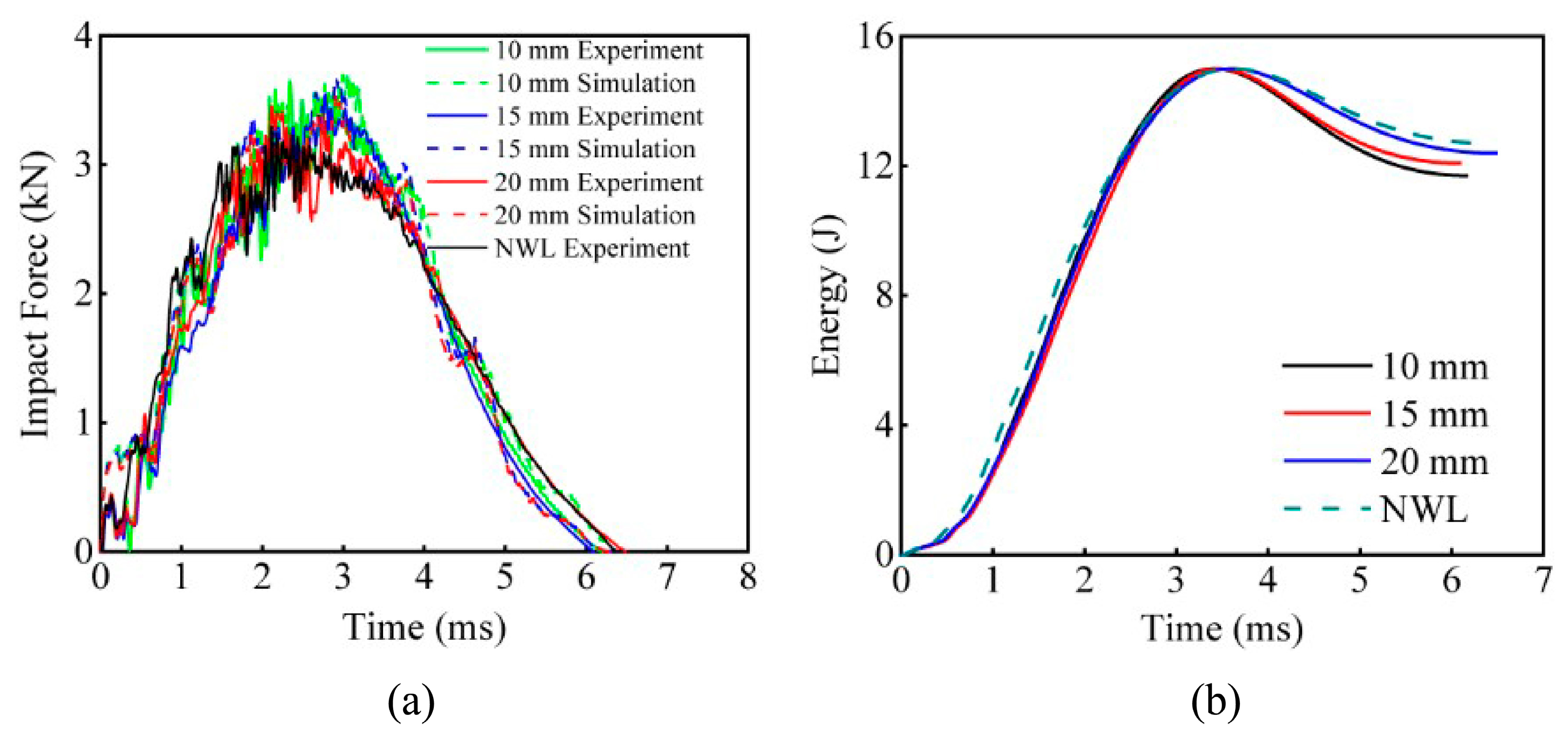
- F-T curves obtained from LVI experiments were compared with simulation calculations. The analysis reveals a high degree of congruence between the two sets of data, with discrepancies confined within an 8% margin. This substantiates the efficacy of the multiscale approach applied to the EWL model and indicates that matrix damage and delamination constitute the primary failure mechanisms.
- In the 15 J impact energy case, EWL with different stitch spacings offer enhanced performance in absorption of peak impact force and energy compared to NWL. The peak impact force increases to 0.31 kN with decreasing stitch spacing. The smaller the stitch spacing, the better the impact-resistance of the composite laminates.
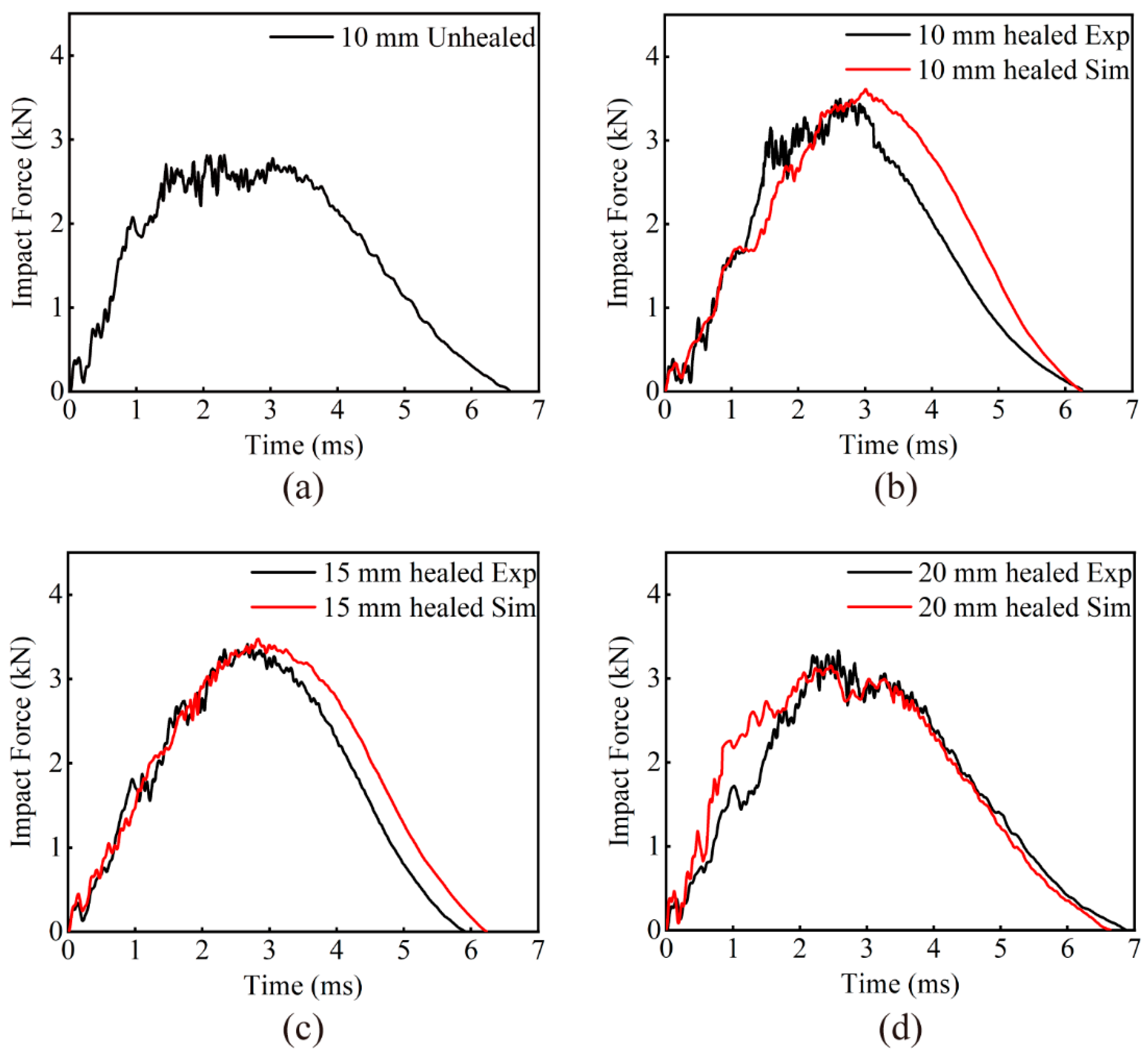
- After impact damage, EWL underwent a thermal compression process that activated the internal three-dimensional self-healing network. In the molten state, EMAA flowed into the damaged area and healed the cracks. The self-healing efficiency of EWL increased with decreasing stitch spacing, up to 98.28%. This effectively demonstrated the ability of EMAA to heal composite laminate damage.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ateeq, M.; Shafique, M.; Azam, A.; Rafiq, M. A review of 3D printing of the recycled carbon fiber reinforced polymer composites: Processing, potential, and perspectives. J. Mater. Res. Technol. 2023, 26, 2291–2309. [Google Scholar] [CrossRef]
- McGregor, C.; Vaziri, R.; Poursartip, A.; Xiao, X. Axial crushing of triaxially braided composite tubes at quasi-static and dynamic rates. Compos. Struct. 2016, 157, 197–206. [Google Scholar] [CrossRef]
- Gouveia, J.R.; Gonçalves, M.; Rocha, R.; Baptista, A.J.; Monteiro, H. Efficiency framework to assess aeronautic composite panel production: Tracking environmental and process performance. Sustain. Prod. Consum. 2022, 31, 419–431. [Google Scholar] [CrossRef]
- Döbrich, O.; Gereke, T.; Cherif, C. Modeling the mechanical properties of textile-reinforced composites with a near micro-scale approach. Compos. Struct. 2016, 135, 1–7. [Google Scholar] [CrossRef]
- Fu, K.; Ye, L.; Chang, L.; Yang, C.; Zhang, Z. Modelling of lightning strike damage to CFRP composites with an advanced protection system. Part I: Thermal–electrical transition. Compos. Struct. 2017, 165, 83–90. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, L.; Chen, Z.; Han, Y.; Jia, L.; Shang, J.; Yan, R. Combining acoustic emission and digital image correlation analysis for dynamic damage response of woven spacer structure reinforced sandwich composites. Compos. Struct. 2023, 319, 117162. [Google Scholar] [CrossRef]
- Rhead, A.T.; Butler, R.; Hunt, G.W. Compressive strength of composite laminates with delamination-induced interaction of panel and sublaminate buckling modes. Compos. Struct. 2017, 171, 326–334. [Google Scholar] [CrossRef]
- Panettieri, E.; Fanteria, D.; Montemurro, M.; Froustey, C. Low-velocity impact tests on carbon/epoxy composite laminates: A benchmark study. Compos. Part B Eng. 2016, 107, 9–21. [Google Scholar] [CrossRef]
- Zou, J.; Lei, Z.; Liu, D.; Hong, X.; Shang, Y.; Bai, R. Rapid prediction of compression after impact properties of composite structures: An equivalent strategy for impact damage. Compos. Struct. 2023, 307, 116655. [Google Scholar] [CrossRef]
- Yin, Z.; Tie, Y.; Duan, Y.; Li, C.; Chen, D. Impact damage assessment in patch-repaired carbon fiber-reinforced polymer laminates using the nonlinear Lamb wave-mixing technique. Polym. Compos. 2022, 43, 8152–8169. [Google Scholar] [CrossRef]
- Mohammadi, M.A.; Eslami-Farsani, R.; Ebrahimnezhad-Khaljiri, H. Experimental investigation of the healing properties of the microvascular channels-based self-healing glass fibers/epoxy composites containing the three-part healant. Polym. Test. 2020, 91, 106862. [Google Scholar] [CrossRef]
- Dhanaraju, G.; Golla, S.; Ben, B.S.; Vikram, K.A. Interfacial and matrix healing of thermally reversible bismaleimide infused Graphene Nano Platelets reinforced polymer nanocomposite through Diels-Alder bonding. Mater. Today Commun. 2022, 31, 103753. [Google Scholar] [CrossRef]
- Wang, J.T.; Tang, J.; Chen, D.; Xing, S.; Liu, X.; Hao, J. Intrinsic and extrinsic self-healing fiber-reinforced polymer composites: A review. Polym. Compos. 2023, 44, 6304–6323. [Google Scholar] [CrossRef]
- Wu, D.; Meure, S.; Solomon, D. Self-healing polymeric materials: A review of recent developments. Prog. Polym. Sci. 2008, 33, 479–522. [Google Scholar] [CrossRef]
- do Nascimento, A.A.; Fernandez, F.; da Silva, F.S.; Ferreira, E.P.C.; Melo, J.D.D.; Barbosa, A.P.C. Addition of poly (ethylene-co-methacrylic acid) (EMAA) as self-healing agent to carbon-epoxy composites. Composites. Part A Appl. Sci. Manuf. 2020, 137, 106016. [Google Scholar] [CrossRef]
- do Nascimento, A.A.; Trappe, V.; Melo, J.D.D.; Barbosa, A.P.C. Fatigue behavior of self-healing glass fiber/epoxy composites with addition of poly (ethylene-co-methacrylic acid) (EMAA). Polym. Test. 2023, 117, 107863. [Google Scholar] [CrossRef]
- Zhang, Z.; Tie, Y.; Li, C. Low-velocity impact and self-healing behavior of CFRP laminates with poly(ethylene-co-methacrylic acid) filament reinforcement. Polym. Compos. 2023, 44, 6012–6026. [Google Scholar] [CrossRef]
- Yang, T.; Wang, C.H.; Zhang, J.; He, S.; Mouritz, A.P. Toughening and self-healing of epoxy matrix laminates using mendable polymer stitching. Compos. Sci. Technol. 2012, 72, 1396–1401. [Google Scholar] [CrossRef]
- Pingkarawat, K.; Dell Olio, C.; Varley, R.J.; Mouritz, A.P. Poly(ethylene-co-methacrylic acid) (EMAA) as an efficient healing agent for high performance epoxy networks using diglycidyl ether of bisphenol A (DGEBA). Polymer 2016, 92, 153–163. [Google Scholar] [CrossRef]
- Varley, R.J.; Parn, G.P. Thermally activated healing in a mendable resin using a non woven EMAA fabric. Compos. Sci. Technol. 2012, 72, 453–460. [Google Scholar] [CrossRef]
- Peñas-Caballero, M.; Chemello, E.; Grande, A.M.; Santana, M.H.; Verdejo, R.; Lopez-Manchado, M.A. Poly(ethylene-co-methacrylic acid) coated carbon fiber for self-healing composites. Compos. Part A Appl. Sci. Manuf. 2023, 169, 107537. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, Y.; Sapanathan, T.; Meng, L.; Xu, Y. Multiscale modeling of the mechanical behavior of 3D braided CFRP composites under uniaxial tension. Compos. Struct. 2023, 306, 116601. [Google Scholar] [CrossRef]
- Li, H.; Khodaei, Z.S.; Aliabadi, M.H.F. Multiscale modelling of material degradation and failure in plain woven composites: A novel approach for reliable predictions enabled by meta-models. Compos. Sci. Technol. 2023, 233, 109910. [Google Scholar] [CrossRef]
- Zheng, T.; Guo, L.; Sun, R.; Wang, T.; Hong, C.; Benedictus, R.; Pascoe, J.A. Investigation on the effect of interface properties on compressive failure behavior of 3D woven composites through micromechanics-based multiscale damage model. Compos. Struct. 2023, 320, 117186. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, H. Multiscale modeling and failure analysis of an 8-harness satin woven composite. Compos. Struct. 2020, 242, 112186. [Google Scholar] [CrossRef]
- Zhang, D.; Waas, A.M.; Yen, C. Progressive damage and failure response of hybrid 3D textile composites subjected to flexural loading, part II: Mechanics based multiscale computational modeling of progressive damage and failure. Int. J. Solids Struct. 2015, 75–76, 321–335. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, H.; Dong, S.; Zhao, X.; Peng, Y.; Chen, J. Progressive failure analysis of needle-punched C/SiC composites based on multiscale finite element model. Compos. Struct. 2023, 310, 116774. [Google Scholar] [CrossRef]
- Ullah, Z.; Kaczmarczyk, L.; Pearce, C.J. Three-dimensional nonlinear micro/meso-mechanical response of the fibre-reinforced polymer composites. Compos. Struct. 2017, 161, 204–214. [Google Scholar] [CrossRef]
- ASTM D7136/D7136M-20; Standard Test Method for Measuring the Damage Resistance of a Fiber-Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event. ASTM International: West Conshohocken, PA, USA, 2020.
- Zhao, Q.; Wang, W.; Liu, Y.; Hou, Y.; Li, J.; Li, C. Multiscale modeling framework to predict the low-velocity impact and compression after impact behaviors of plain woven CFRP composites. Compos. Struct. 2022, 299, 116090. [Google Scholar] [CrossRef]
- Xia, Z.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef]
- Feng, Z.; Wang, X.; Wang, F. Implementation and its Application in Finite Element Analysis of Constitutive Model for ZWT Nonlinear Viscoelastic Material. J. Mater. Sci. Eng. 2007, 25, 269–272. [Google Scholar]
- Mulay, S.S.; Udhayaraman, R. On the constitutive modelling and damage behaviour of plain woven textile composite. Int. J. Solids Struct. 2019, 156–157, 73–86. [Google Scholar] [CrossRef]
- Hou, Y.; Meng, L.; Li, G.; Xia, L.; Xu, Y. A novel multiscale modeling strategy of the low-velocity impact behavior of plain woven composites. Compos. Struct. 2021, 274, 114363. [Google Scholar] [CrossRef]
- Pingkarawat, K.; Wang, C.H.; Varley, R.J.; Mouritz, A.P. Mechanical properties of mendable composites containing self-healing thermoplastic agents. Compos. Part A Appl. Sci. Manuf. 2014, 65, 10–18. [Google Scholar] [CrossRef]





| Carbon Fiber T300/3K | Epoxy Resin 7901 | ||
|---|---|---|---|
| /GPa | 230 | /GPa | 3.5 |
| /GPa | 40 | /GPa | 1.3 |
| /GPa | 24 | 0.35 | |
| /GPa | 14.3 | /MPa | 112 |
| 0.26 | /MPa | 241 | |
| 0.44 | /MPa | 89.6 | |
| /MPa | 3258 | /(N/mm2) | 1 |
| /MPa | 2470 | ||
| /(N/mm2) | 12.5 | ||
| Elastic Properties | Damage Properties | ||
|---|---|---|---|
| /GPa | 184.77 | /MPa | 2890 |
| /GPa | 19.17 | /MPa | 2059 |
| /GPa | 8.46 | /MPa | 92 |
| /GPa | 14.3 | /MPa | 185 |
| 0.27 | /MPa | 107 | |
| 0.42 | /MPa | 59 | |
| Parameter | l | h | D | b | a | w | t |
|---|---|---|---|---|---|---|---|
| Value/mm | 4 | 0.25 | 1.2 | 1.2 | 0.4 | 1.62 | 0.11 |
| Parameter | 0° Monolayer | 90° Monolayer |
|---|---|---|
| Young’s modulus, E11/GPa | 70,075 | 67,840 |
| Young’s modulus, E22, E33/GPa | 13,299 | 13,405 |
| Shear modulus, G12, G13/GPa | 1440 | 1632 |
| Shear modulus, G23/GPa | 2325 | 2148 |
| Poisson’s ratio, υ12, υ13 | 0.13 | 0.13 |
| Poisson’s ratio, υ23 | 0.43 | 0.4 |
| Tensile strength, XT/MPa | 705 | 658 |
| Compressive strength, XC/MPa | 675 | 587 |
| Tensile strength, YT/MPa | 182 | 172 |
| Compressive strength, YC/MPa | 76.2 | 92.4 |
| Shear strength, S12, S13/MPa | 30 | 36 |
| Shear strength, S23/MPa | 87 | 83 |
| Parameter | EAA | EMAA |
|---|---|---|
| Tensile modulus, E/MPa | 33.1 | 22.3 |
| Tensile strength, X/MPa | 18.6 | 16 |
| Poisson’s ratio, υ | 0.4 | 0.42 |
| Density, ρ/(g/cm3) | 0.91 | 0.90 |
| Energy/J | Peak Force/N | Healing Efficiency | |
|---|---|---|---|
| 15 | Unhealed | 2814 | / |
| 10 mm | 3551 | 98.28% | |
| 15 mm | 3447 | 97.26% | |
| 20 mm | 3268 | 94.67% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Tie, Y.; Fan, C.; Yin, Z.; Li, C. Multiscale Analysis of Impact-Resistance in Self-Healing Poly(ethylene-co-methacrylic acid) (EMAA) Plain Woven Composites. Polymers 2024, 16, 2740. https://doi.org/10.3390/polym16192740
Zhang Z, Tie Y, Fan C, Yin Z, Li C. Multiscale Analysis of Impact-Resistance in Self-Healing Poly(ethylene-co-methacrylic acid) (EMAA) Plain Woven Composites. Polymers. 2024; 16(19):2740. https://doi.org/10.3390/polym16192740
Chicago/Turabian StyleZhang, Zhenzhen, Ying Tie, Congjie Fan, Zhihao Yin, and Cheng Li. 2024. "Multiscale Analysis of Impact-Resistance in Self-Healing Poly(ethylene-co-methacrylic acid) (EMAA) Plain Woven Composites" Polymers 16, no. 19: 2740. https://doi.org/10.3390/polym16192740
APA StyleZhang, Z., Tie, Y., Fan, C., Yin, Z., & Li, C. (2024). Multiscale Analysis of Impact-Resistance in Self-Healing Poly(ethylene-co-methacrylic acid) (EMAA) Plain Woven Composites. Polymers, 16(19), 2740. https://doi.org/10.3390/polym16192740







