Calibration of Thermal Viscoelastic Material Models for the Dynamic Responses of PVB and SG Interlayer Materials
Abstract
1. Introduction
2. Experimental Program
2.1. Material Description
2.2. Specimen Preparations
2.3. Test Setups
2.4. Data Processing
2.5. Experimental Testing Matrix
3. Experimental Results
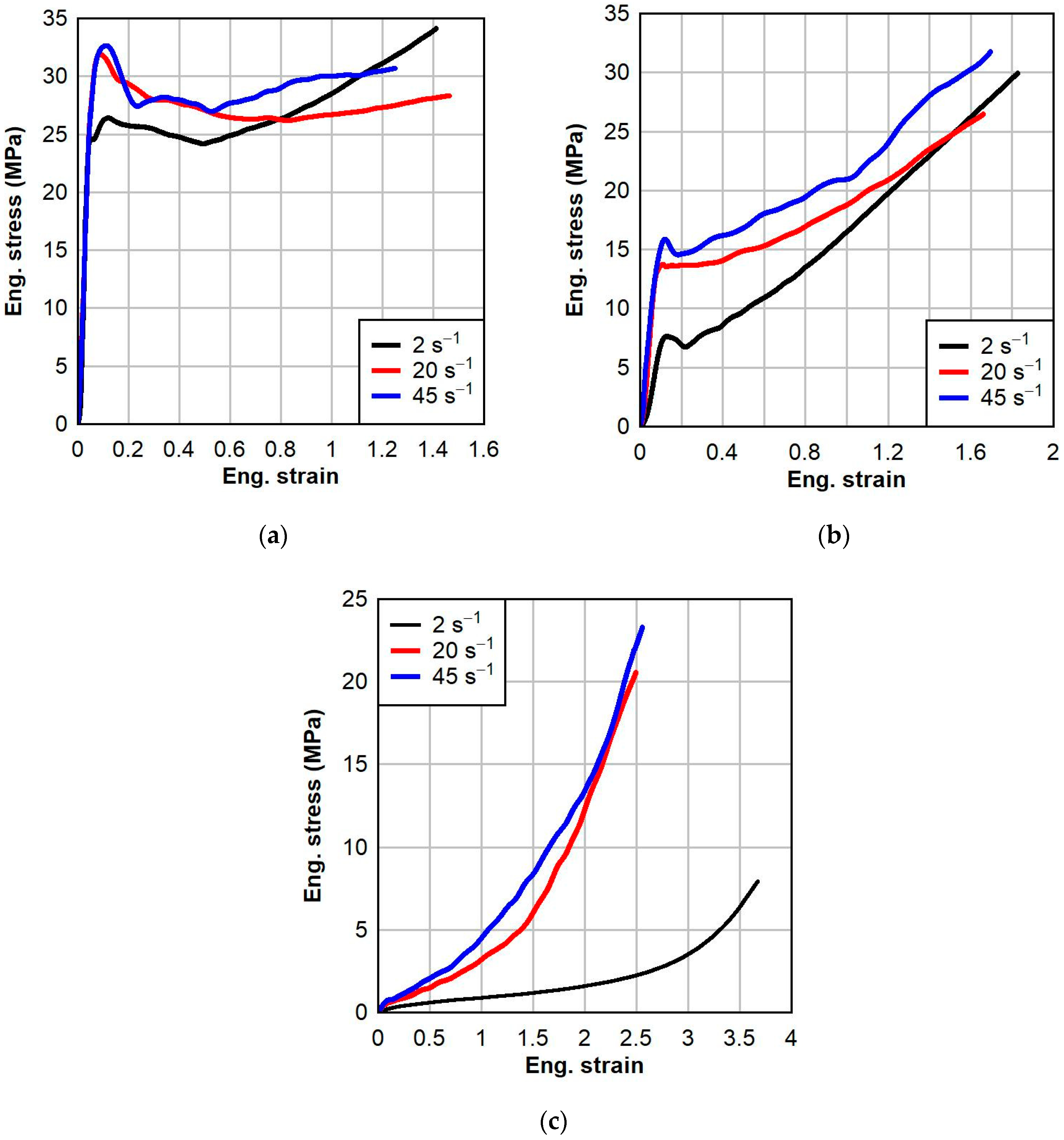
3.1. PVB Interlayer
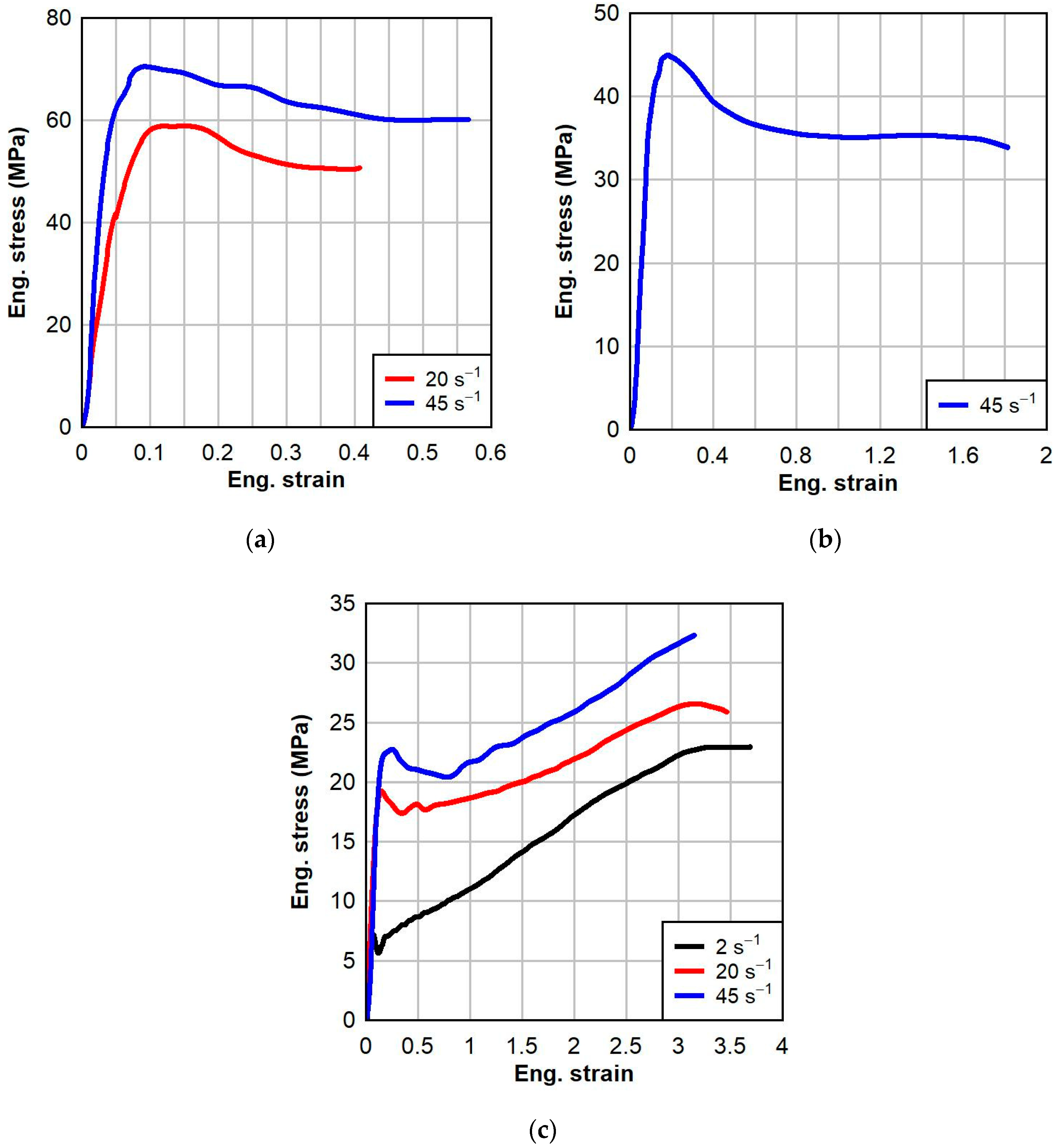
3.2. SG Interlayer
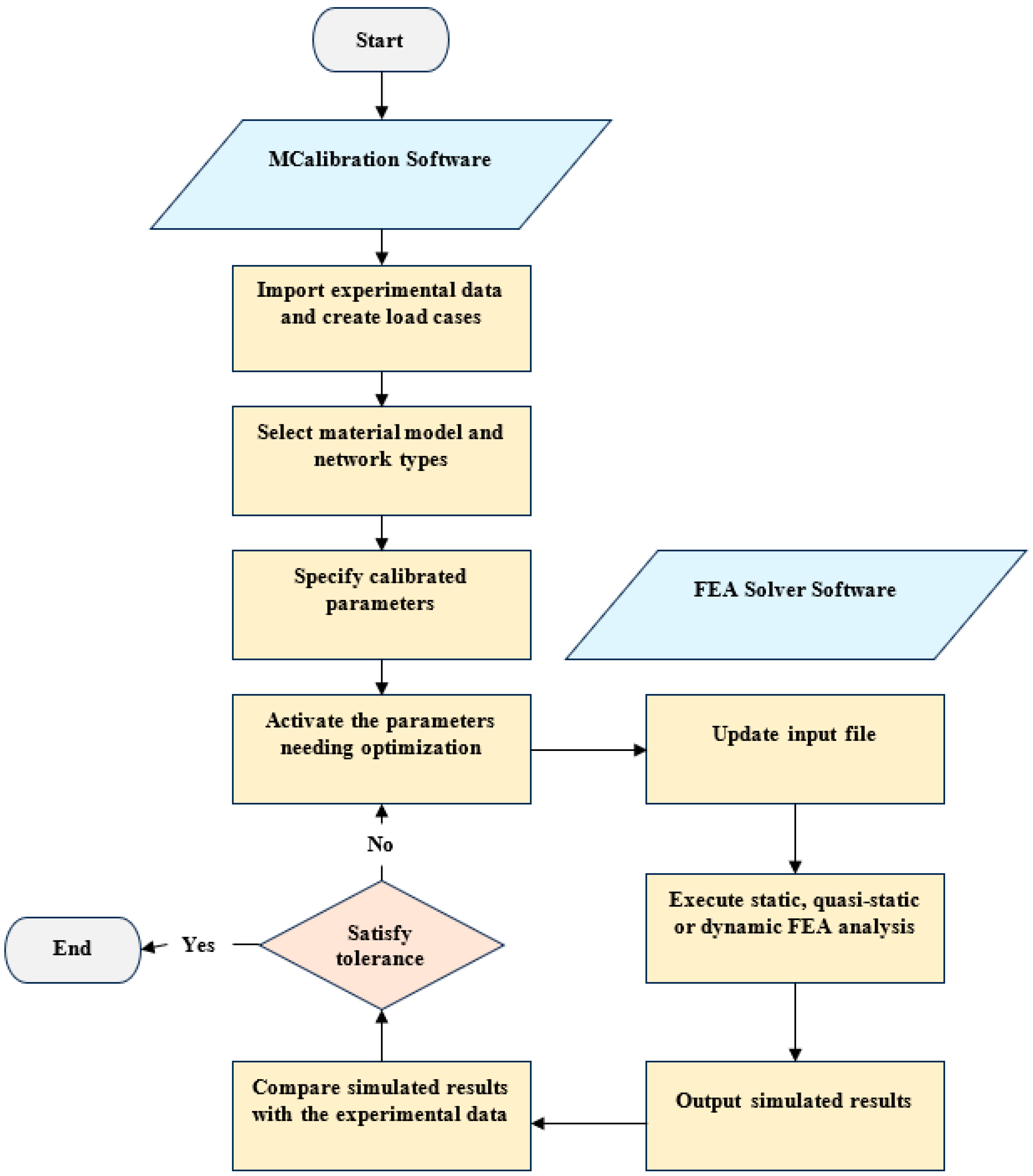
4. Numerical Modeling
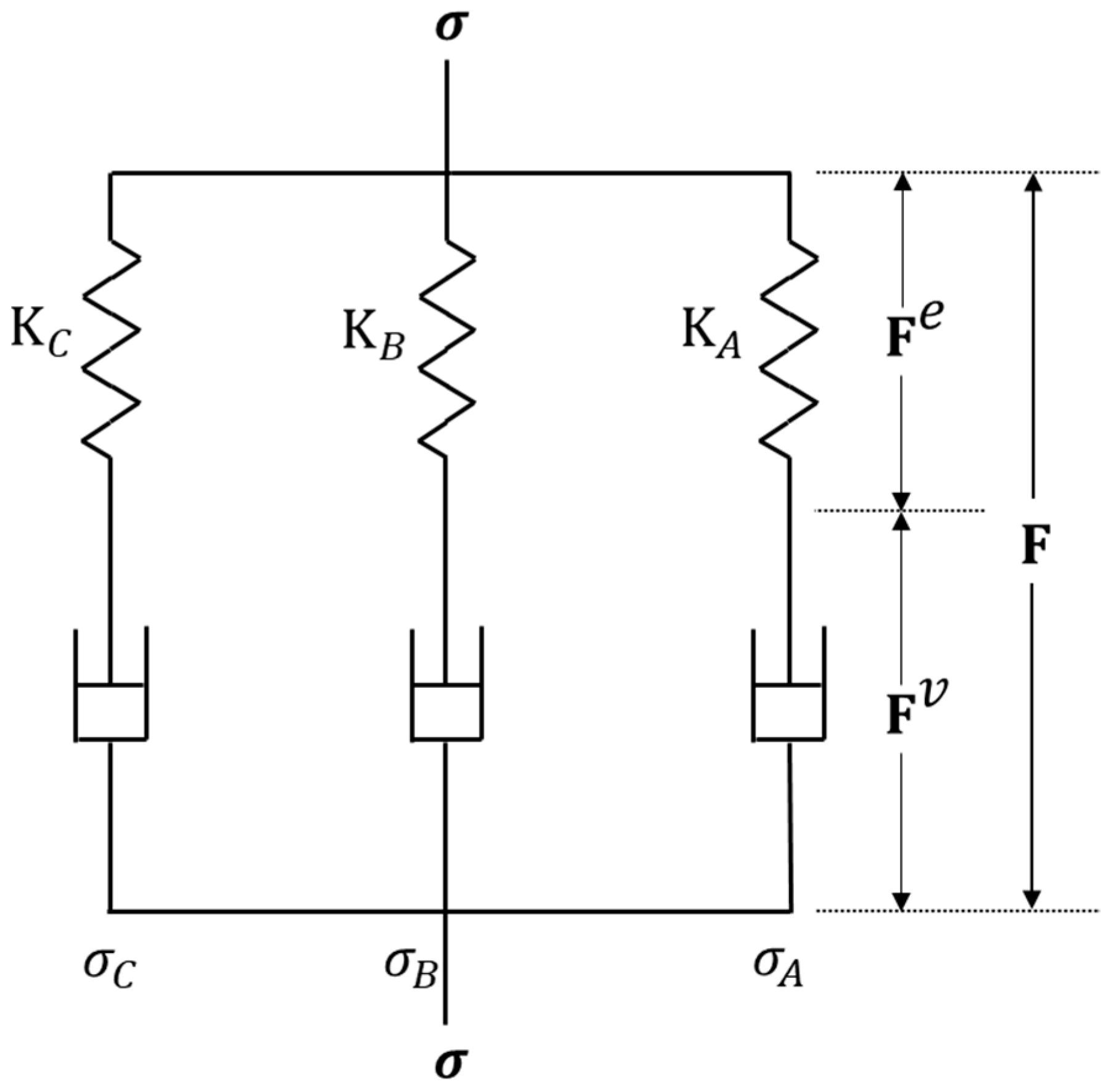
4.1. Material Constitutive Models
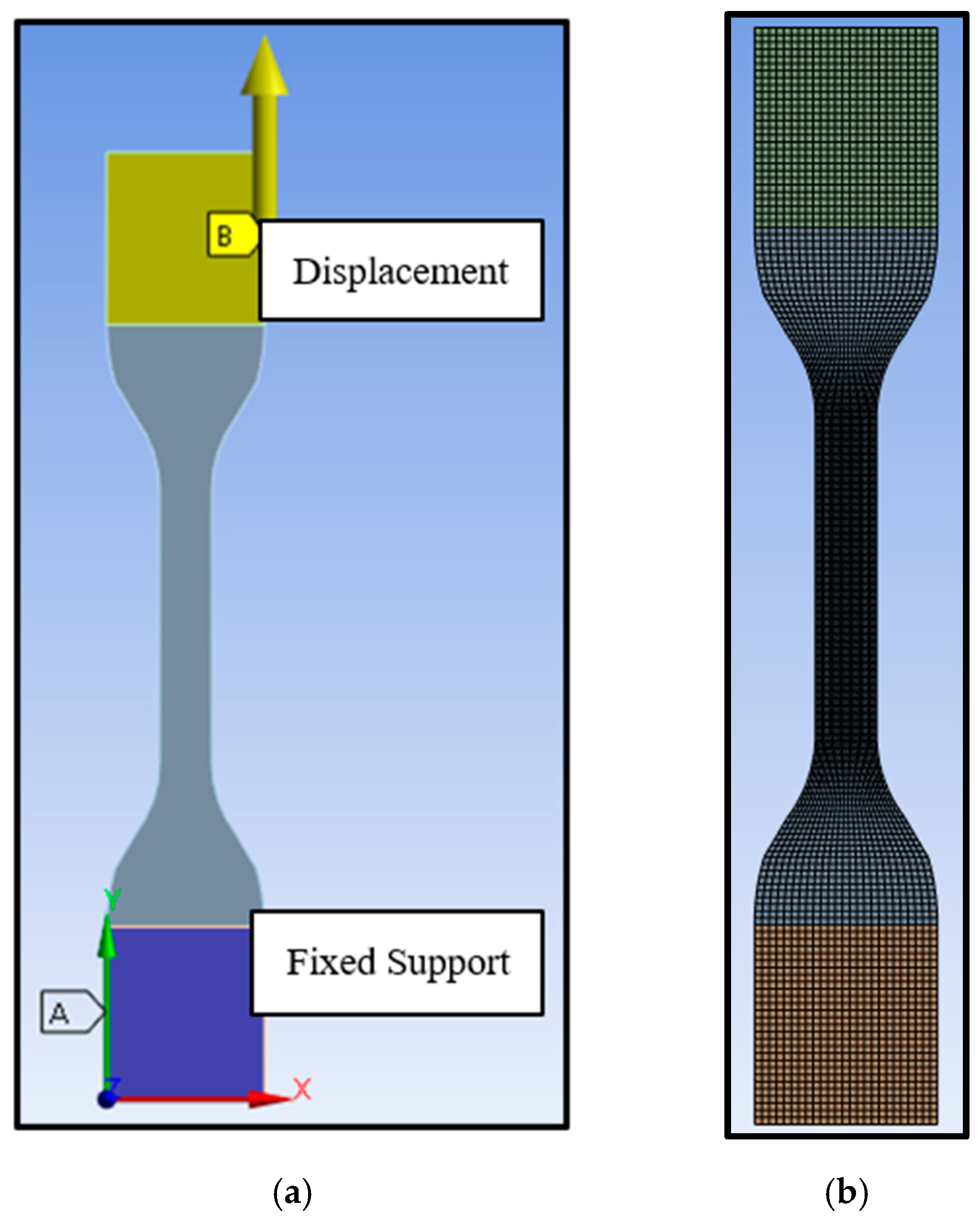
4.2. Finite Element Model Components
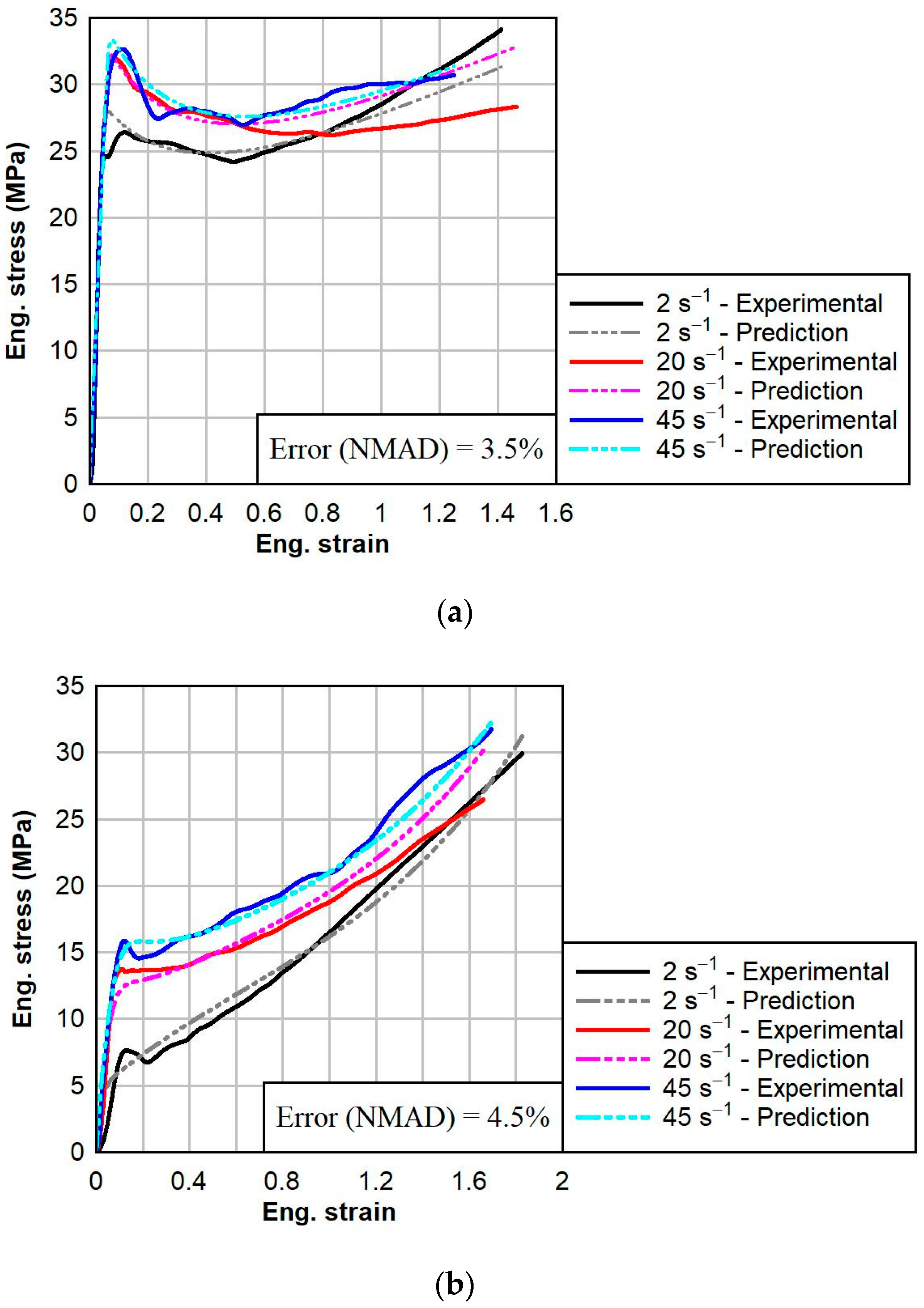
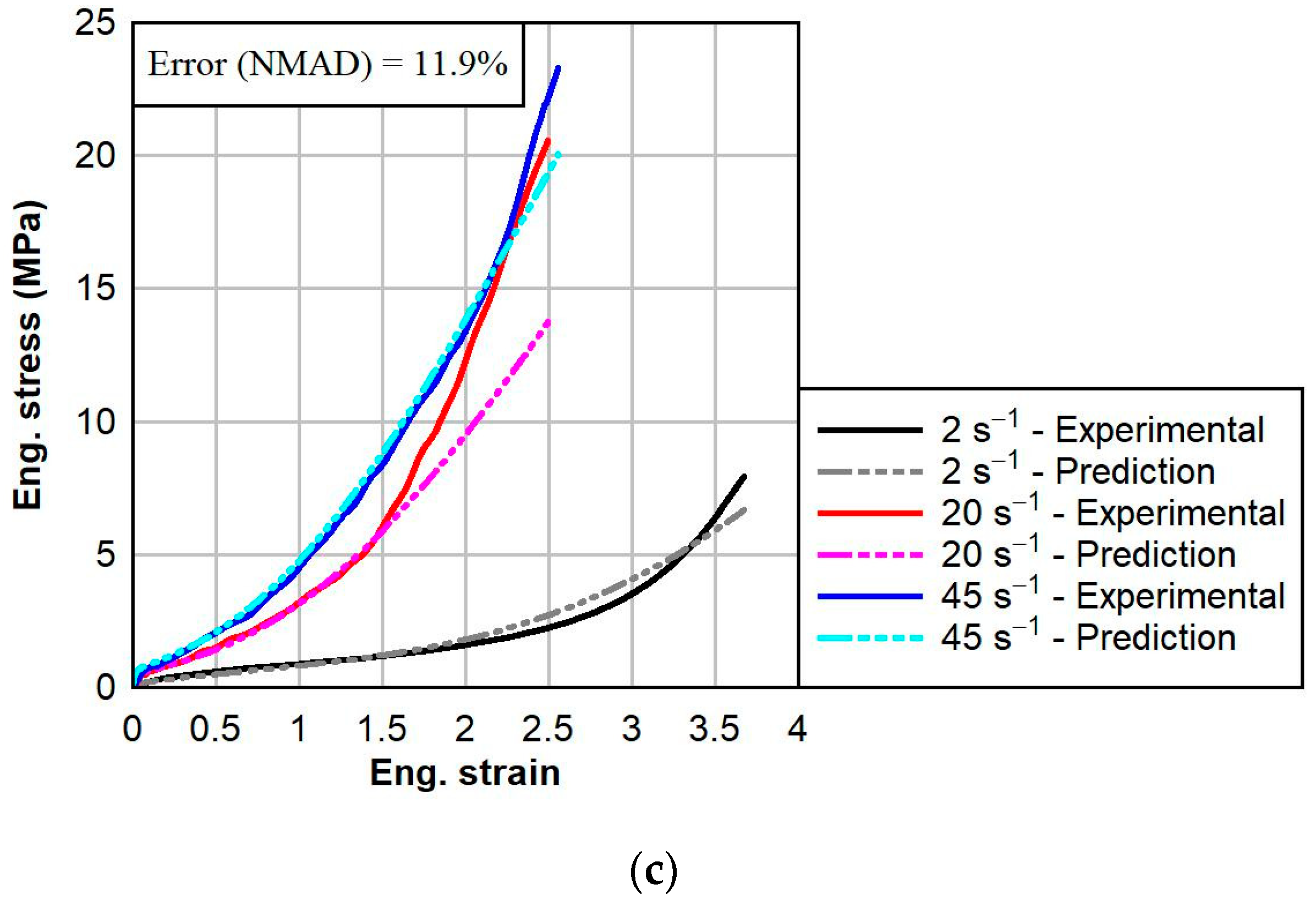
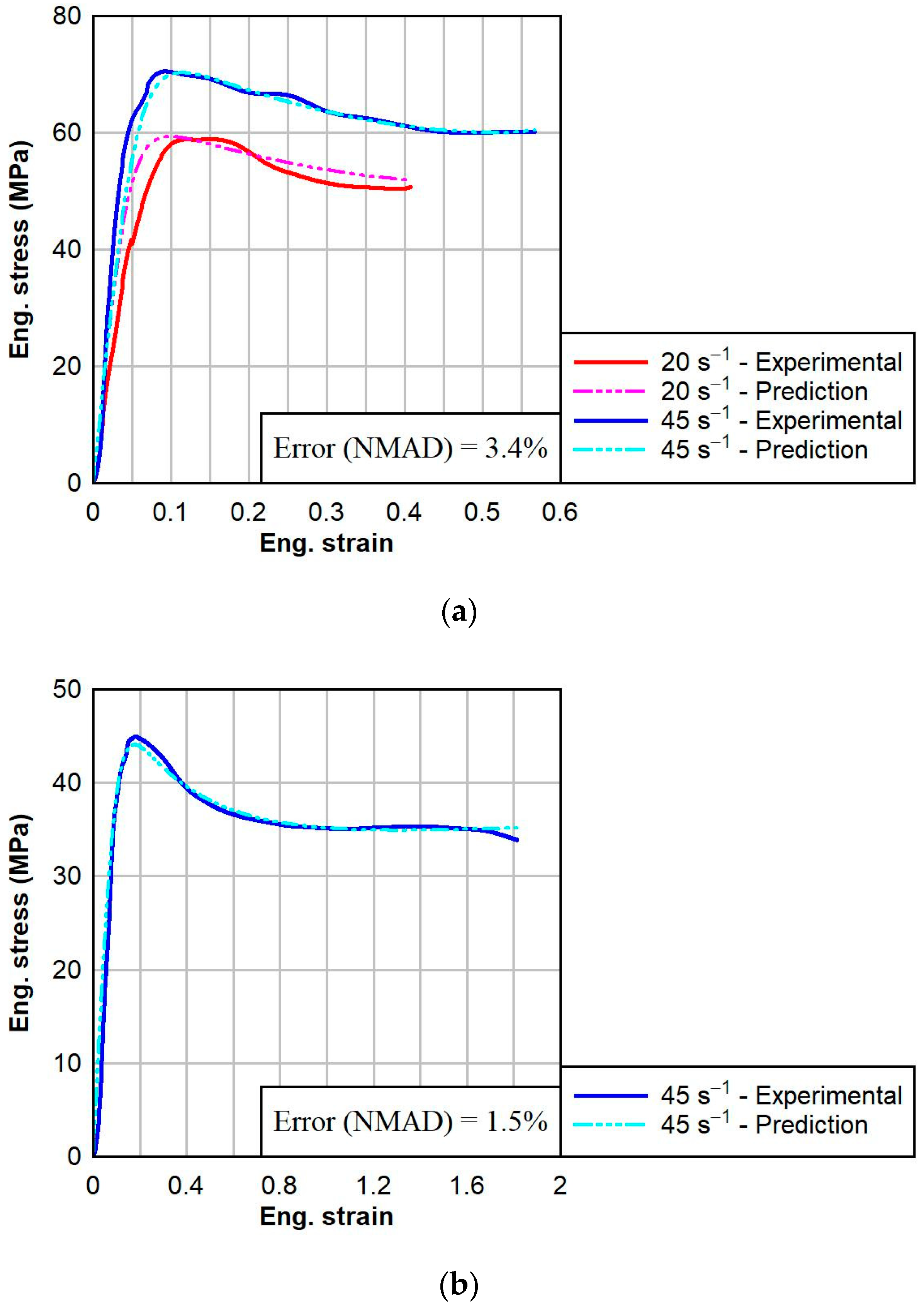
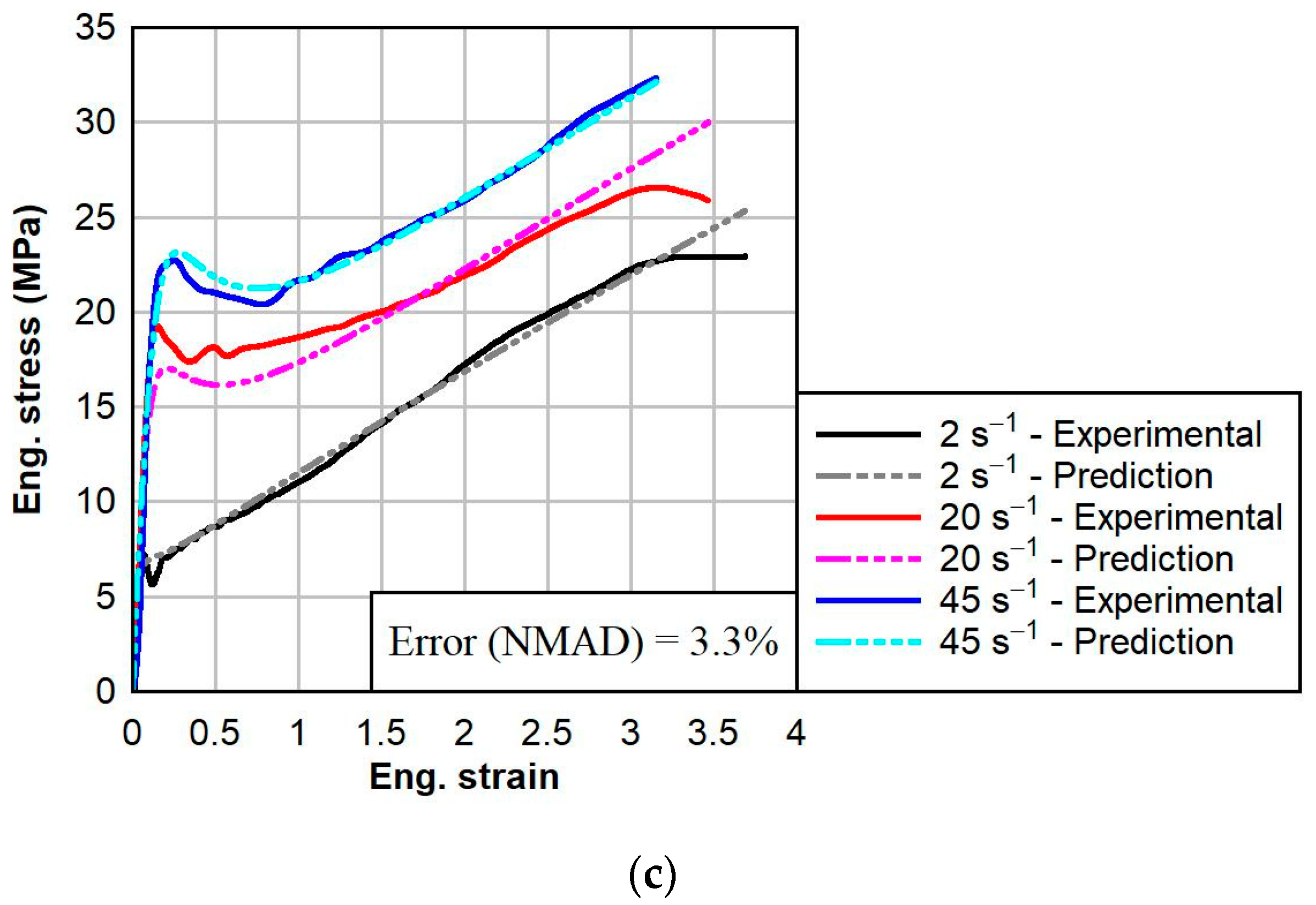
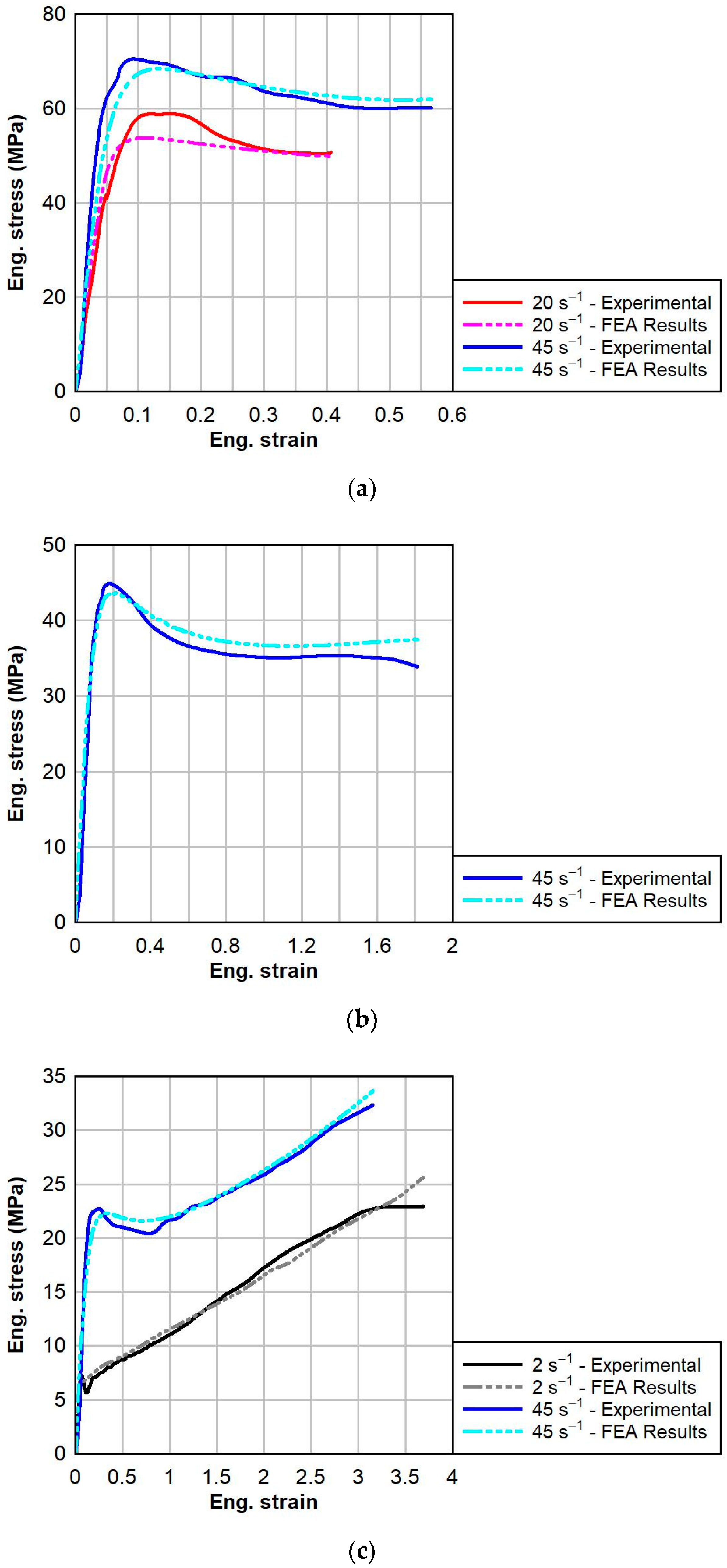
4.3. Material Model Validations and Discussion
5. Conclusions and Future Perspectives
- Strain rate predominantly affected the initial responses of PVB and SG. Initial modulus and yield stress increased with strain rate, resulting in increased toughness.
- Temperature affected the characteristic nature of the response of PVB, but not for SG. As temperature increased, the response of PVB transitioned from elastoplastic to bilinear to hyperelastic. At all temperatures, SG interlayer specimens exhibited a linear response followed by yield; strain softening; plastic flow; and, finally, strain hardening at large strains, achieved at elevated temperatures.
- In general, PVB and SG became stiffer and less ductile as the temperature decreases. The temperature effects were more pronounced in SG than in PVB. For a strain rate of 45 s−1, as the temperature decreased from 23 °C to 0 °C, the failure strain of SG decreased by 69% and the initial modulus increased by 418%, whereas for PVB, the failure strain decreased by 26% and the initial modulus increased by 200%.
- There was clear yielding and subsequent strain softening in the dynamic response of PVB at 0 °C and 23 °C, but not at 60 °C. The elevated temperature of 60 °C was greater than the glass transition temperature of PVB of about 50 °C, and therefore, the behavior was dominated by the viscous component of the viscoelastic response.
- Temperature- and strain rate-dependent material models for the dynamic responses of PVB and SG interlayer materials were calibrated using the three-network viscoplastic (TNV) model, with average normalized mean absolute differences (NMADs) between the experimental data and model predictions of 6.6% and 2.7% for PVB and SG, respectively.
- The FEA results based on the calibrated material models were successfully able to predict the thermal viscoelastic dynamic behaviors of PVB and SG interlayer materials under tensile loading, with average NMADs between the FEA results and experimental data of 6.0% and 4.9% for PVB and SG, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Norville, H.S.; Conrath, E.J. Blast-Resistant Glazing Design. J. Arch. Eng. 2006, 12, 129–136. [Google Scholar] [CrossRef]
- Wei, J.; Dharani, L. Fracture mechanics of laminated glass subjected to blast loading. Theor. Appl. Fract. Mech. 2005, 44, 157–167. [Google Scholar] [CrossRef]
- Edwards, D.; McMenemy, L.; Stapley, S.; Patel, H.; Clasper, J. 40 years of terrorist bombings—A meta-analysis of the casualty and injury profile. Injury 2015, 47, 646–652. [Google Scholar] [CrossRef]
- Hooper, P. Blast Performance of Silicone-Bonded Laminated Glass; Department of Mechanical Engineering: London, UK, 2011. [Google Scholar]
- Elbelbisi, A.; Elsisi, A.; Saffarini, M.H.; Salim, H.; Chen, Z. Enhanced Blast Response Simulation of LG Panels Using an Elasto-Damage Model with the Finite Element Method. Buildings 2023, 13, 3025. [Google Scholar] [CrossRef]
- Elbelbisi, A.; El-Sisi, A.; Knight, J.; Philipps, J.C.; Newberry, M.; Salim, H. Influence of panels size on the static and dynamic performance of laminated glass panels. Constr. Build. Mater. 2023, 399, 132562. [Google Scholar] [CrossRef]
- El-Sisi, A.; Elbelbisi, A.; Elemam, H.; Elkilani, A.; Newberry, M.; Salim, H. Effect of glass type and thickness on the static and blast response of LG panels. J. Build. Eng. 2024, 86, 108870. [Google Scholar] [CrossRef]
- López-Aenlle, M.; Pelayo, F. Static and dynamic effective thickness in five-layered glass plates. Compos. Struct. 2019, 212, 259–270. [Google Scholar] [CrossRef]
- Baraldi, D.; Cecchi, A.; Foraboschi, P. Broken tempered laminated glass: Non-linear discrete element modeling. Compos. Struct. 2016, 140, 278–295. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S.; Orlando, M.; Piscitelli, L.R.; Spinelli, P. Post-failure behavior of laminated glass beams using different interlayers. Compos. Struct. 2018, 202, 578–589. [Google Scholar] [CrossRef]
- Biolzi, L.; Orlando, M.; Piscitelli, L.R.; Spinelli, P. Static and dynamic response of progressively damaged ionoplast laminated glass beams. Compos. Struct. 2016, 157, 337–347. [Google Scholar] [CrossRef]
- López-Aenlle, M.; Noriega, A.; Pelayo, F. Mechanical characterization of polyvinil butyral from static and modal tests on laminated glass beams. Compos. Part B Eng. 2019, 169, 9–18. [Google Scholar] [CrossRef]
- Pelayo, F.; Lamela-Rey, M.; Muniz-Calvente, M.; López-Aenlle, M.; Álvarez-Vázquez, A.; Fernández-Canteli, A. Study of the time-temperature-dependent behaviour of PVB: Application to laminated glass elements. Thin-Walled Struct. 2017, 119, 324–331. [Google Scholar] [CrossRef]
- Andreozzi, L.; Bati, S.B.; Fagone, M.; Ranocchiai, G.; Zulli, F. Dynamic torsion tests to characterize the thermo-viscoelastic properties of polymeric interlayers for laminated glass. Constr. Build. Mater. 2014, 65, 1–13. [Google Scholar] [CrossRef]
- Serafinavičius, T.; Lebet, J.-P.; Louter, C.; Lenkimas, T.; Kuranovas, A. Long-term laminated glass four point bending test with PVB, EVA and SG interlayers at different temperatures. Procedia Eng. 2013, 57, 996–1004. [Google Scholar] [CrossRef]
- López-Aenlle, M.; Pelayo, F. Dynamic effective thickness in laminated-glass beams and plates. Compos. Part B Eng. 2014, 67, 332–347. [Google Scholar] [CrossRef]
- Larcher, M.; Solomos, G.; Casadei, F.; Gebbeken, N. Experimental and numerical investigations of laminated glass subjected to blast loading. Int. J. Impact Eng. 2012, 39, 42–50. [Google Scholar] [CrossRef]
- Kott, A.; Vogel, T. Safety of laminated glass structures after initial failure. Struct. Eng. Int. 2004, 14, 134–138. [Google Scholar] [CrossRef]
- Bennison, S.; Qin, M.; Davies, P. High-Performance Laminated Glass for Structurally Efficient Glazing; Innovative Light-Weight Structures and Sustainable Facades: Hongkong, China, 2008. [Google Scholar]
- Knight, J.T.; El-Sisi, A.A.; Elbelbisi, A.H.; Newberry, M.; Salim, H.A. Mechanical Behavior of Laminated Glass Polymer Interlayer Subjected to Environmental Effects. Polymers 2022, 14, 5113. [Google Scholar] [CrossRef]
- El-Sisi, A.; Newberry, M.; Knight, J.; Salim, H.; Nawar, M. Static and high strain rate behavior of aged virgin PVB. J. Polym. Res. 2022, 29, 1–12. [Google Scholar] [CrossRef]
- Bennison, S.; Sloan, J.G.; Kistunas, D.F.; Buehler, P.J.; Amos, T.; Smith, C.A. Laminated Glass for Blast Mitigation: Role of Interlayer Properties. In Proceedings of the Glass Processing Days, Tampere, Finland, 17–20 June 2005. [Google Scholar]
- Zhang, X.; Shi, Y.; Hao, H.; Cui, J. The mechanical properties of ionoplast interlayer material at high strain rates. Mater. Des. 2015, 83, 387–399. [Google Scholar] [CrossRef]
- Chen, S.; Lu, Y.; Zhang, Y.; Shao, X. Experimental and analytical study on uniaxial tensile property of ionomer interlayer at different temperatures and strain rates. Constr. Build. Mater. 2020, 262, 120058. [Google Scholar] [CrossRef]
- Santarsiero, M.; Louter, C.; Nussbaumer, A. The mechanical behaviour of SentryGlas®ionomer and TSSA silicon bulk materials at different temperatures and strain rates under uniaxial tensile stress state. Glas. Struct. Eng. 2016, 1, 395–415. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Wu, X. The mechanical behaviour of polyvinyl butyral at intermediate strain rates and different temperatures. Constr. Build. Mater. 2018, 182, 66–79. [Google Scholar] [CrossRef]
- Schuster, M. Determination of the linear viscoelastic material behaviour of interlayers with semi-crystalline structures shown by the example of a semi-crystalline ionomer. Glas. Struct. Eng. 2022, 7, 157–171. [Google Scholar] [CrossRef]
- Centelles, X.; Martín, M.; Solé, A.; Castro, J.R.; Cabeza, L.F. Tensile test on interlayer materials for laminated glass under diverse ageing conditions and strain rates. Constr. Build. Mater. 2020, 243, 118230. [Google Scholar] [CrossRef]
- Liu, B.; Sun, Y.; Li, Y.; Wang, Y.; Ge, D.; Xu, J. Systematic experimental study on mechanical behavior of PVB (polyvinyl butyral) material under various loading conditions. Polym. Eng. Sci. 2012, 52, 1137–1147. [Google Scholar] [CrossRef]
- Bergström, J. Large Strain Time-Dependent Behavior of Elastomeric Materials. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- Andreozzi, L.; Bati, S.B.; Fagone, M.; Ranocchiai, G.; Zulli, F. Weathering action on thermo-viscoelastic properties of polymer interlayers for laminated glass. Constr. Build. Mater. 2015, 98, 757–766. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S.; Orlando, M.; Piscitelli, L.R.; Spinelli, P. Constitutive relationships of different interlayer materials for laminated glass. Compos. Struct. 2020, 244, 112221. [Google Scholar] [CrossRef]
- Hidallana-Gamage, H.; Thambiratnam, D.; Perera, N. Influence of interlayer properties on the blast performance of laminated glass panels. Constr. Build. Mater. 2015, 98, 502–518. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Maharaj, C.; Zheng, M.; Mohagheghian, I.; Zhang, G.; Yan, Y.; Dear, J.P. Impact response of laminated glass with varying interlayer materials. Int. J. Impact Eng. 2020, 139, 103505. [Google Scholar] [CrossRef]
- Martín, M.; Centelles, X.; Solé, A.; Barreneche, C.; Fernández, A.I.; Cabeza, L.F. Polymeric interlayer materials for laminated glass: A review. Constr. Build. Mater. 2020, 230, 116897. [Google Scholar] [CrossRef]
- Morison, C.; Zobec, M.; Frenceschet, A. The measurement of {PVB} properties at high strain rates, and their application in the design of laminated glass under bomb blast. In Proceedings of the ISIEMS 2007, International Symposium on Interaction of the Effects of Munitions with Structures, Orlando, FL, USA, 17–21 September 2007. [Google Scholar]
- Nawar, M.; Salim, H.; Newberry, M.; El-Sisi, A. High strain rate response of laminated glass interlayer materials. Constr. Build. Mater. 2021, 299, 123934. [Google Scholar] [CrossRef]
- Elkilani, A.; El-Emam, H.; Elsisi, A.; Elbelbisi, A.; Salim, H. The Influence of Strain Rate Behavior on Laminated Glass Interlayer Types for Cured and Uncured Polymers. Polymers 2024, 16, 730. [Google Scholar] [CrossRef]
- Elbelbisi, A.; El-Sisi, A.; Mahmoud, M.E.; Newberry, M.; Salim, H. Influence of interlayer types and thicknesses on the blast performance of laminated glass panels. Structures 2023, 57, 105231. [Google Scholar] [CrossRef]
- Du Bois, P.; Kolling, S.; Fassnacht, W. Modelling of safety glass for crash simulation. Comput. Mater. Sci. 2003, 28, 675–683. [Google Scholar] [CrossRef]
- Timmel, M.; Kolling, S.; Osterrieder, P.; Du Bois, P. A finite element model for impact simulation with laminated glass. Int. J. Impact Eng. 2007, 34, 1465–1478. [Google Scholar] [CrossRef]
- Pyttel, T.; Liebertz, H.; Cai, J. Failure criterion for laminated glass under impact loading and its application in finite element simulation. Int. J. Impact Eng. 2010, 38, 252–263. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, J.; Deck, C.; Willinger, R. Finite element modeling of crash test behavior for windshield laminated glass. Int. J. Impact Eng. 2013, 57, 27–35. [Google Scholar] [CrossRef]
- El-Sisi, A.; Bowman, A.; Elbelbisi, A.; Elkilani, A.; Robert, S.; Salim, H.; Nawar, M. Performance of LG window systems with different materials under extreme static loading. Constr. Build. Mater. 2023, 409, 133923. [Google Scholar] [CrossRef]
- Lusk, B.; Salim, H.; Perry, K.; Nawar, M.; Wedding, W.C.; Kiger, S.; Ibrahim, A. Modeling and testing of laminated window systems under blast loading. In Proceedings of the Structures Congress 2011, Las Vegas, NV, USA, 14–16 April 2011. [Google Scholar]
- Hidallana-Gamage, H.; Thambiratnam, D.; Perera, N. Failure analysis of laminated glass panels subjected to blast loads. Eng. Fail. Anal. 2013, 36, 14–29. [Google Scholar] [CrossRef]
- Hidallana-Gamage, H.; Thambiratnam, D.; Perera, N. Numerical modelling and analysis of the blast performance of laminated glass panels and the influence of material parameters. Eng. Fail. Anal. 2014, 45, 65–84. [Google Scholar] [CrossRef]
- Molnár, G.; Vigh, L.G.; Stocker, G.; Dunai, L. Finite element analysis of laminated structural glass plates with polyvinyl butyral (PVB) interlayer. Period. Polytech. Civ. Eng. 2012, 56, 35. [Google Scholar] [CrossRef]
- Sable, L.; Skukis, E.; Japins, G.; Kalnins, K. Correlation between Numerical and Experimental Tests of Laminated Glass Panels with Visco-elastic Interlayer. Procedia Eng. 2017, 172, 945–952. [Google Scholar] [CrossRef]
- Iwasaki, R.; Sato, C.; Latailladeand, J.L.; Viot, P. Experimental study on the interface fracture toughness of PVB (polyvinyl butyral)/glass at high strain rates. Int. J. Crashworthiness 2007, 12, 293–298. [Google Scholar] [CrossRef]
- Hána, T.; Janda, T.; Schmidt, J.; Zemanová, A.; Šejnoha, M.; Eliášová, M.; Vokáč, M. Experimental and numerical study of viscoelastic properties of polymeric interlayers used for laminated glass: Determination of material parameters. Materials 2019, 12, 2241. [Google Scholar] [CrossRef] [PubMed]
- Centelles, X.; Pelayo, F.; Lamela-Rey, M.J.; Fernández, A.I.; Salgado-Pizarro, R.; Castro, J.R.; Cabeza, L.F. Viscoelastic characterization of seven laminated glass interlayer materials from static tests. Constr. Build. Mater. 2021, 279, 122503. [Google Scholar] [CrossRef]
- Almomani, A.; Deveci, S.; Mourad, A.-H.I.; Barsoum, I. Constitutive model calibration for the thermal viscoelastic-viscoplastic behavior of high density polyethylene under monotonic and cyclic loading. Polym. Test. 2023, 118, 107911. [Google Scholar] [CrossRef]
- Bergström, J. Bergström, Mechanics of Solid Polymers: Theory and Computational Modeling; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Shahin, A.; Barsoum, I.; Islam, M.D. Constitutive model calibration of the time and temperature-dependent behavior of high density polyethylene. Polym. Test. 2020, 91, 106800. [Google Scholar] [CrossRef]
- Lai, J.; Bakker, A. Analysis of the non-linear creep of high-density polyethylene. Polymer 1995, 36, 93–99. [Google Scholar] [CrossRef]
- Elleuch, R.; Taktak, W. Prediction of compressive creep and relaxation of HDPE. Int. J. Model. Simul. 2006, 26, 344–349. [Google Scholar] [CrossRef]
- Roff, W.; Scott, J. Fibres, Films, Plastics and Rubbers; Elsevier: Amsterdam, The Netherlands, 1971. [Google Scholar]
- Stojak, K.; Pal, S.; Srikanth, H.; Morales, C.; Dewdney, J.; Weller, T.; Wang, J. Polymer nanocomposites exhibiting magnetically tunable microwave properties. Nanotechnology 2011, 22, 135602. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Chen, S.; Li, G.-Q. Experimental investigation on the blast resistance of framed PVB-laminated glass. Int. J. Impact Eng. 2020, 149, 103788. [Google Scholar] [CrossRef]
- ASTM-D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM Standards: West Conshohocken, PA, USA, 2014.
- Canonsburg, T.D. ANSYS Mechanical APDL Material Reference. Knowl. Creat. Diffus. Util. 2012, 13, 15317. [Google Scholar]

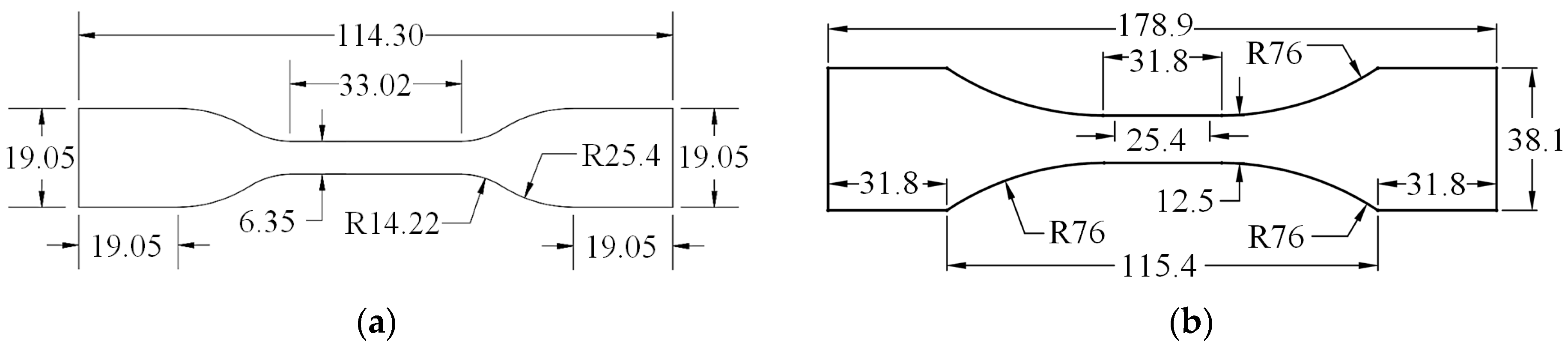




| Material/Manufacturer | Temperature (°C) | Strain Rates (s−1) |
|---|---|---|
| PVB (RA41)/Eastman (Eastman Chemical Company, Kingsport, TN, USA) | 0 | 2, 20, 45 |
| 23 | 2, 20, 45 | |
| 60 | 2, 20, 45 | |
| SG5000/Kuraray (kuraray, Houstan, TX, USA) | 0 | 20, 45 |
| 23 | 45 | |
| 60 | 2, 20, 45 |
| Polymer | Temperature (°C) | Strain Rate (s−1) | Yield Stress (MPa) | Yield Strain (mm/mm) | Failure Stress (MPa) | Failure Strain (mm/mm) | Young’s Modulus (MPa) | Toughness (MPa-mm/mm) |
|---|---|---|---|---|---|---|---|---|
| PVB | 0 | 2 s−1 | 26.4 | 0.122 | 34.1 | 1.412 | 519 | 37.9 |
| 20 s−1 | 31.9 | 0.088 | 28.3 | 1.464 | 573 | 39.6 | ||
| 45 s−1 | 32.7 | 0.111 | 30.7 | 1.249 | 586 | 35.5 | ||
| 23 | 2 s−1 | 7.6 | 0.129 | 30.0 | 1.828 | 63.2 | 29.2 | |
| 20 s−1 | 13.8 | 0.108 | 26.5 | 1.661 | 194 | 29.6 | ||
| 45 s−1 | 15.9 | 0.120 | 31.8 | 1.694 | 195 | 35.1 | ||
| 60 | 2 s−1 | - | - | 7.9 | 3.677 | 2.3 | 7.8 | |
| 20 s−1 | - | - | 20.6 | 2.496 | 7.0 | 16.4 | ||
| 45 s−1 | - | - | 23.3 | 2.558 | 8.7 | 20.8 | ||
| SG5000 | 0 | 20 s−1 | 58.8 | 0.120 | 50.7 | 0.407 | 1035 | 20.3 |
| 45 s−1 | 70.5 | 0.092 | 60.2 | 0.567 | 2203 | 34.9 | ||
| 23 | 45 s−1 | 45.0 | 0.128 | 33.9 | 1.814 | 425 | 64.9 | |
| 60 | 2 s−1 | 7.3 | 0.067 | 22.9 | 3.690 | 165 | 58.1 | |
| 20 s−1 | 19.3 | 0.147 | 25.9 | 3.468 | 191 | 73.9 | ||
| 45 s−1 | 22.7 | 0.249 | 32.3 | 3.154 | 242 | 77.2 |
| 0 °C | 23 °C | 60 °C | ||||||
|---|---|---|---|---|---|---|---|---|
| Description | Symbol | Units | Network A | Network B | Network A | Network B | Network A | Network B |
| Yeoh parameter 1 | MPa | 5.24 | 90.1 | 3.39 | 39.3 | 0.169 | 132 | |
| Yeoh parameter 2 | MPa | 0 | 0 | 0 | 0 | 0 | 0 | |
| Yeoh parameter 3 | MPa | 1.92 × 10−5 | 0 | 0.021 | 0 | 1.32 × 10−7 | 0 | |
| Bulk modulus 1 | MPa | 922 | 922 | 242 | 242 | 3.87 | 3.87 | |
| Bulk moduli 2 and 3 | MPa | 0 | 0 | 0 | 0 | 0 | 0 | |
| Flow resistance of network | MPa | 0 | 20.7 | 0 | 1.69 | 0 | 0.035 | |
| Initial stress exponent | - | 0 | 15.7 | 0 | 2.40 | 0 | 1.72 | |
| Final stress exponent | 0 | 20 | 0 | 5.31 | 0 | 0.064 | ||
| Transition strain power exponent | 0 | 0.548 | 0 | 1.19 | 0 | 0.85 | ||
| Volumetric flow coefficient | - | 0 | 0 | 0 | 0 | 0 | 0 | |
| Pressure dependence of flow | - | 0 | 0 | 0 | 0 | 0 | 0 | |
| Yield evolution | - | 0 | 0.100 | 0 | 1.48 | 0 | 1.64 | |
| Yield evolution strain | - | 0 | 0.550 | 0 | 0.010 | 0 | 0.013 | |
| Flow damage strain | - | 0 | 0.1 | 0 | 0.1 | 0 | 0.1 | |
| Flow damage final state | - | 0 | 1 | 0 | 1 | 0 | 1 | |
| Strength of flow cessation | 0 | 1 | 0 | 1 | 0 | 0.994 | ||
| Normalized cutoff orientation for flow cessation | 0 | 0 | 0 | 0 | 0 | 0.180 | ||
| 0 °C | 23 °C | 60 °C | ||||||
|---|---|---|---|---|---|---|---|---|
| Description | Symbol | Units | Network A | Network B | Network A | Network B | Network A | Network B |
| Yeoh parameter 1 | MPa | 2.44 | 229 | 1.82 | 84.2 | 2.44 | 32.5 | |
| Yeoh parameter 2 | MPa | 0 | 0 | 0 | 0 | 0 | 0 | |
| Yeoh parameter 3 | MPa | 1.35 | 0 | 0.0009 | 0 | 5.02 × 10−8 | 0 | |
| Bulk modulus 1 | MPa | 2050 | 2050 | 837 | 837 | 338 | 338 | |
| Bulk moduli 2 and 3 | MPa | 0 | 0 | 0 | 0 | 0 | 0 | |
| Flow resistance of network | MPa | 0 | 15.4 | 0 | 11.9 | 0 | 3.47 | |
| Initial stress exponent | - | 0 | 2.89 | 0 | 3.25 | 0 | 3.97 | |
| Final stress exponent | 0 | 4.41 | 0 | 3.25 | 0 | 2.22 | ||
| Transition strain power exponent | 0 | 2.93 | 0 | 0.039 | 0 | 1.27 × 10−4 | ||
| Volumetric flow coefficient | - | 0 | 0 | 0 | 0 | 0 | 0 | |
| Pressure dependence of flow | - | 0 | 0 | 0 | 0 | 0 | 0 | |
| Yield evolution | - | 0 | 0.955 | 0 | 0.257 | 0 | 0.341 | |
| Yield evolution strain | - | 0 | 0.431 | 0 | 0.885 | 0 | 0.498 | |
| Flow damage strain | - | 0 | 0.1 | 0 | 0.1 | 0 | 0.1 | |
| Flow damage final state | - | 0 | 1 | 0 | 1 | 0 | 1 | |
| Strength of flow cessation | 0 | 0.730 | 0 | 0.996 | 0 | 1 | ||
| Normalized cutoff orientation for flow cessation | 0 | 0.054 | 0 | 0 | 0 | 0 | ||
| Polymer | Temperature (°C) | Strain Rate (s−1) | Normalized Mean Absolute Difference, NMAD (%) |
|---|---|---|---|
| PVB | 0 | 2 s−1 | 4.37 |
| 45 s−1 | 2.28 | ||
| 23 | 2 s−1 | 7.72 | |
| 45 s−1 | 4.28 | ||
| 60 | 2 s−1 | 9.80 | |
| 45 s−1 | 7.23 | ||
| SG5000 | 0 | 20 s−1 | 6.47 |
| 45 s−1 | 4.40 | ||
| 23 | 45 s−1 | 5.88 | |
| 60 | 2 s−1 | 4.33 | |
| 45 s−1 | 3.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knight, J.; Salim, H.; Elemam, H.; Elbelbisi, A. Calibration of Thermal Viscoelastic Material Models for the Dynamic Responses of PVB and SG Interlayer Materials. Polymers 2024, 16, 1870. https://doi.org/10.3390/polym16131870
Knight J, Salim H, Elemam H, Elbelbisi A. Calibration of Thermal Viscoelastic Material Models for the Dynamic Responses of PVB and SG Interlayer Materials. Polymers. 2024; 16(13):1870. https://doi.org/10.3390/polym16131870
Chicago/Turabian StyleKnight, Jon, Hani Salim, Hesham Elemam, and Ahmed Elbelbisi. 2024. "Calibration of Thermal Viscoelastic Material Models for the Dynamic Responses of PVB and SG Interlayer Materials" Polymers 16, no. 13: 1870. https://doi.org/10.3390/polym16131870
APA StyleKnight, J., Salim, H., Elemam, H., & Elbelbisi, A. (2024). Calibration of Thermal Viscoelastic Material Models for the Dynamic Responses of PVB and SG Interlayer Materials. Polymers, 16(13), 1870. https://doi.org/10.3390/polym16131870







