Microstructures and Rheological Properties of Short-Side-Chain Perfluorosulfonic Acid in Water/2-Propanol
Abstract
1. Introduction
2. Experimental Section
2.1. Materials
2.2. Preparation of Dispersions
2.3. Macrorheology
2.4. Diffusing Wave Spectroscopy Microrheology
2.5. Small-Angle X-ray Scattering (SAXS)
3. Results and Discussion
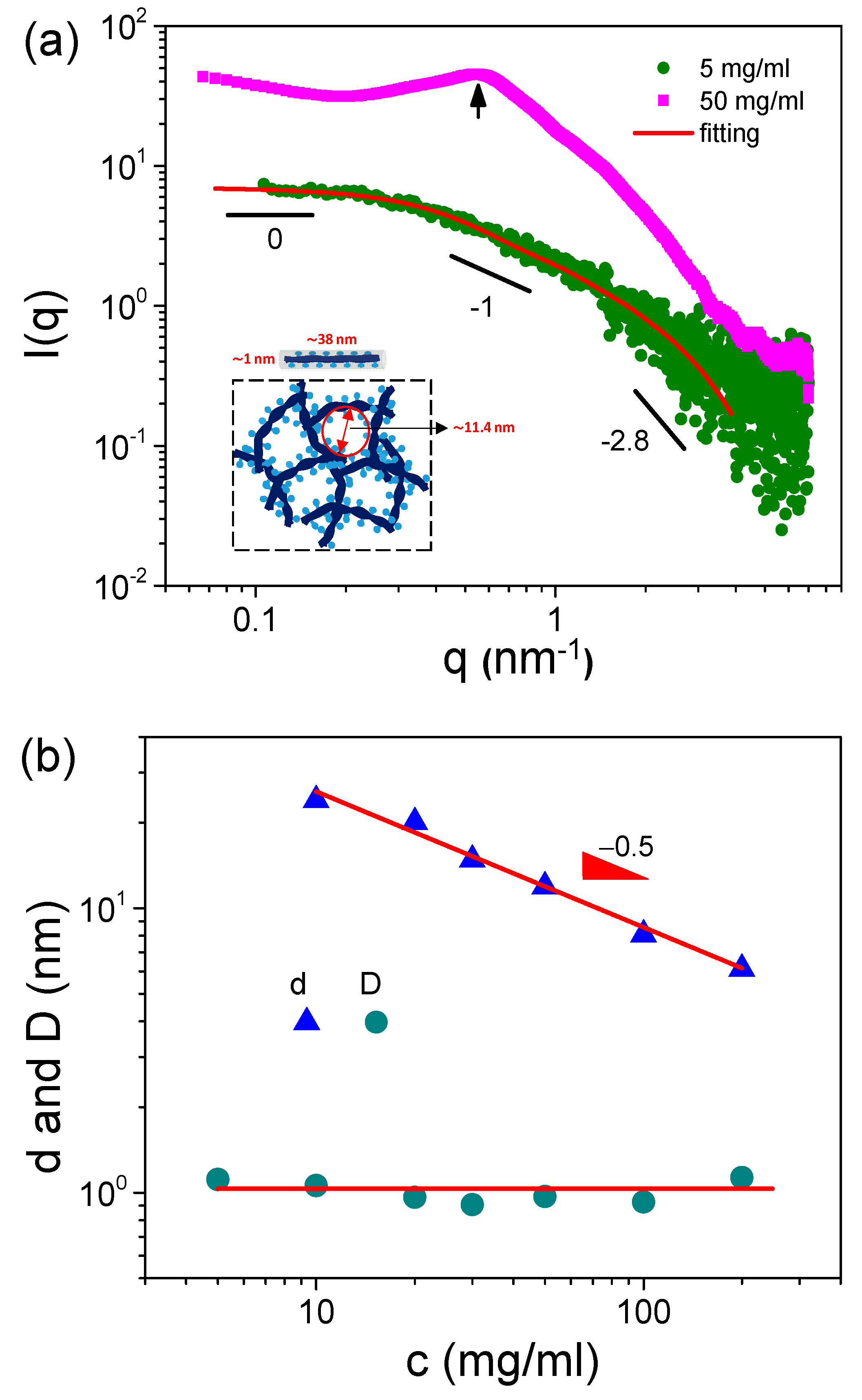
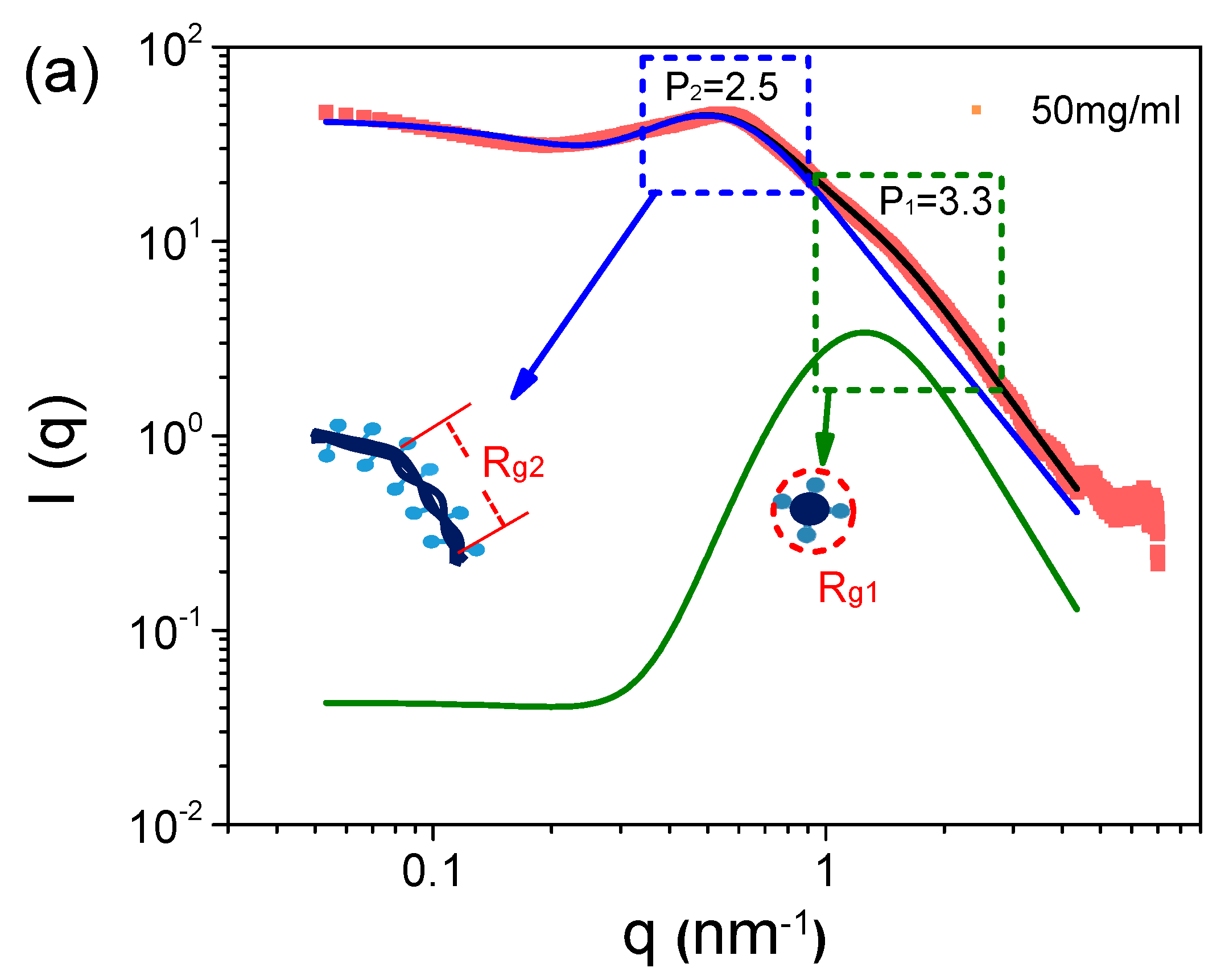
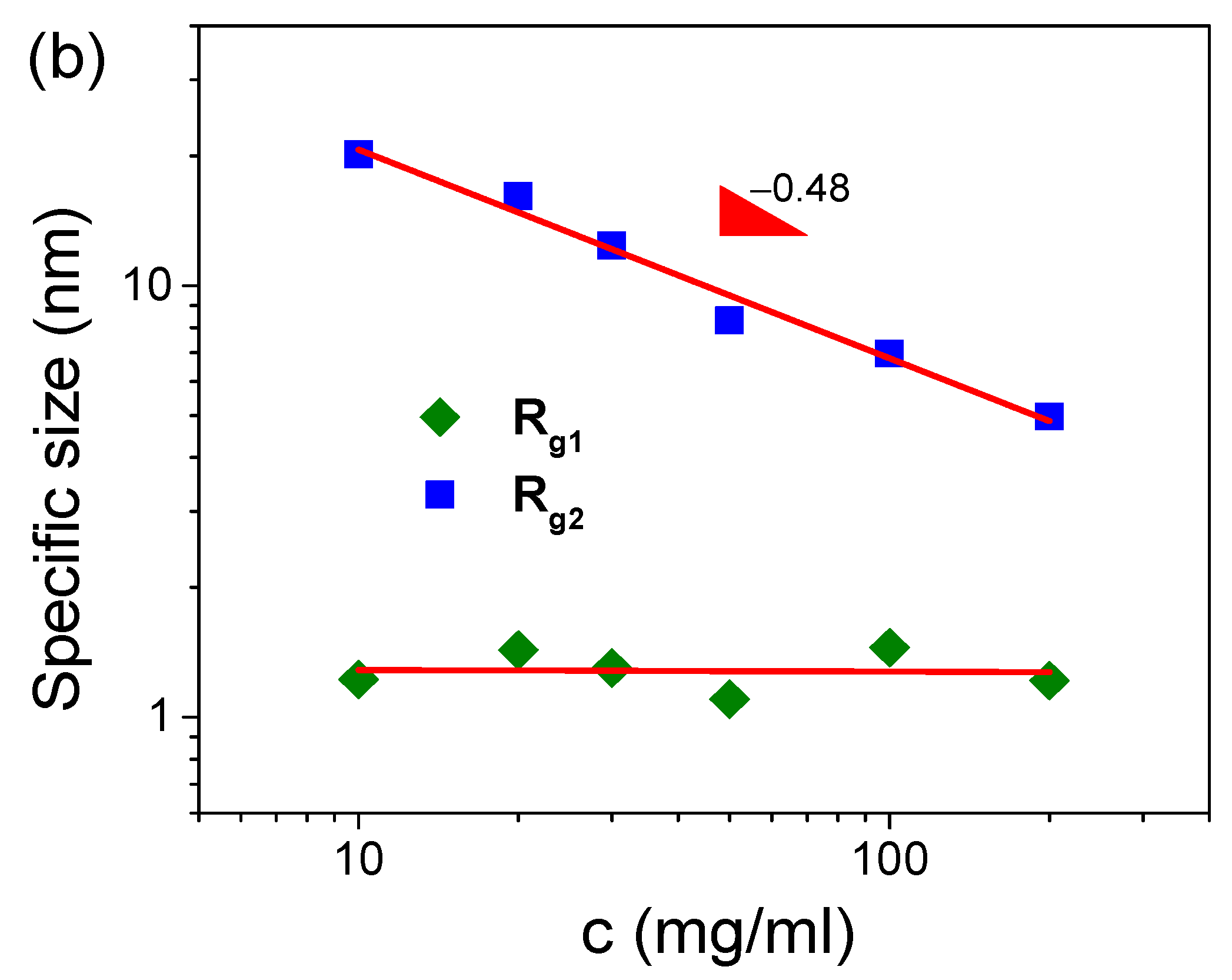
3.1. Microstructure of S-PFSA
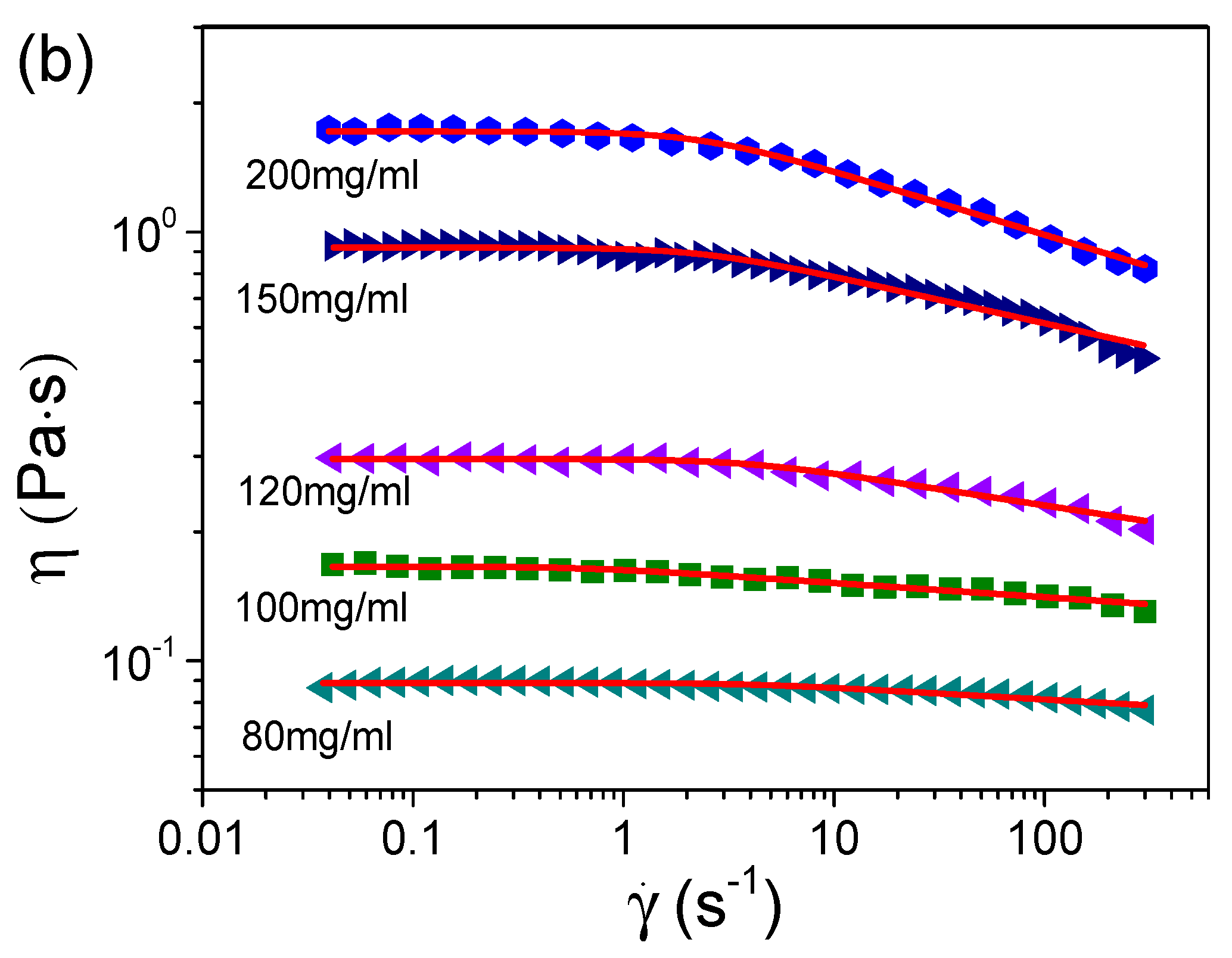
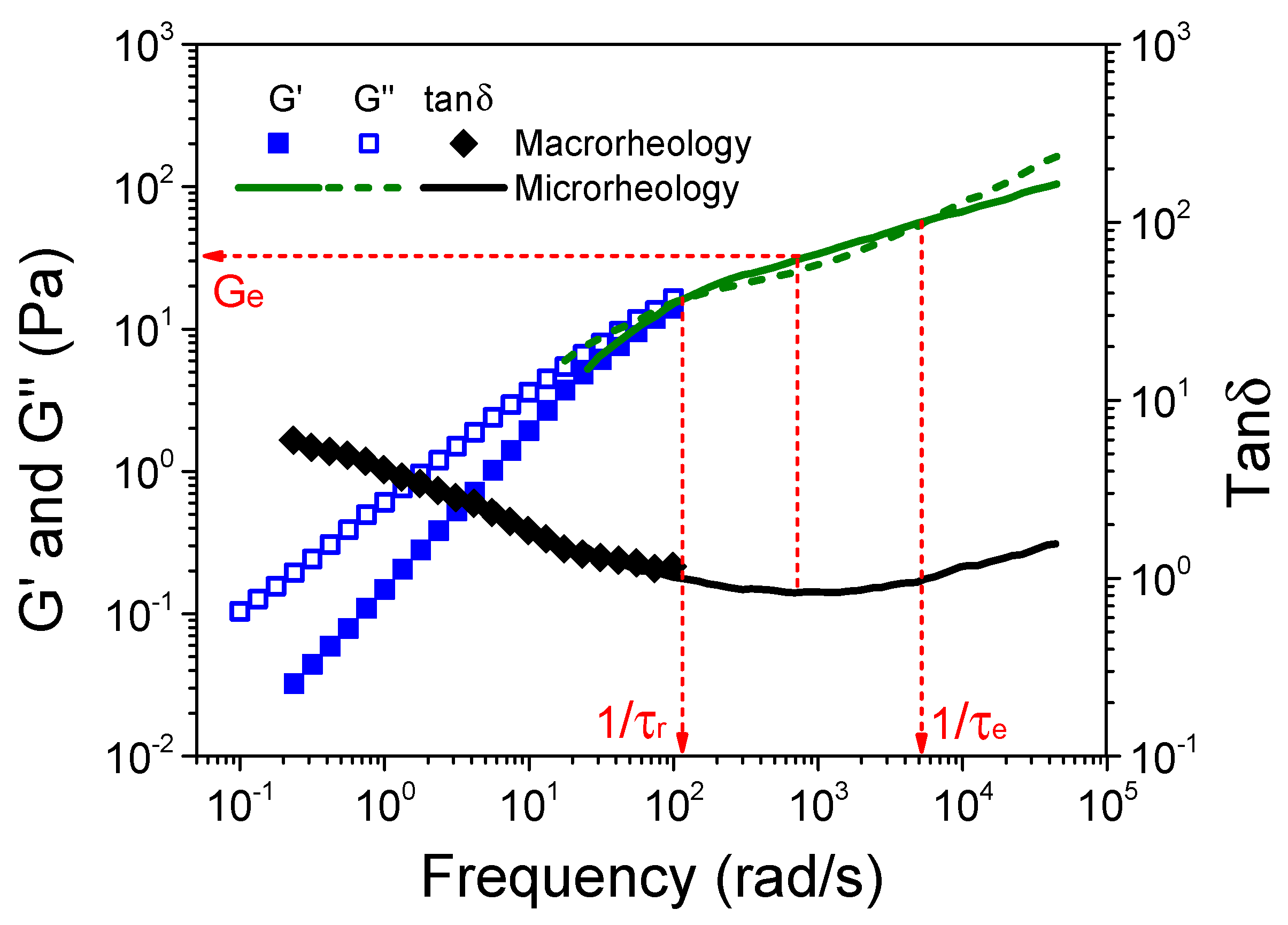
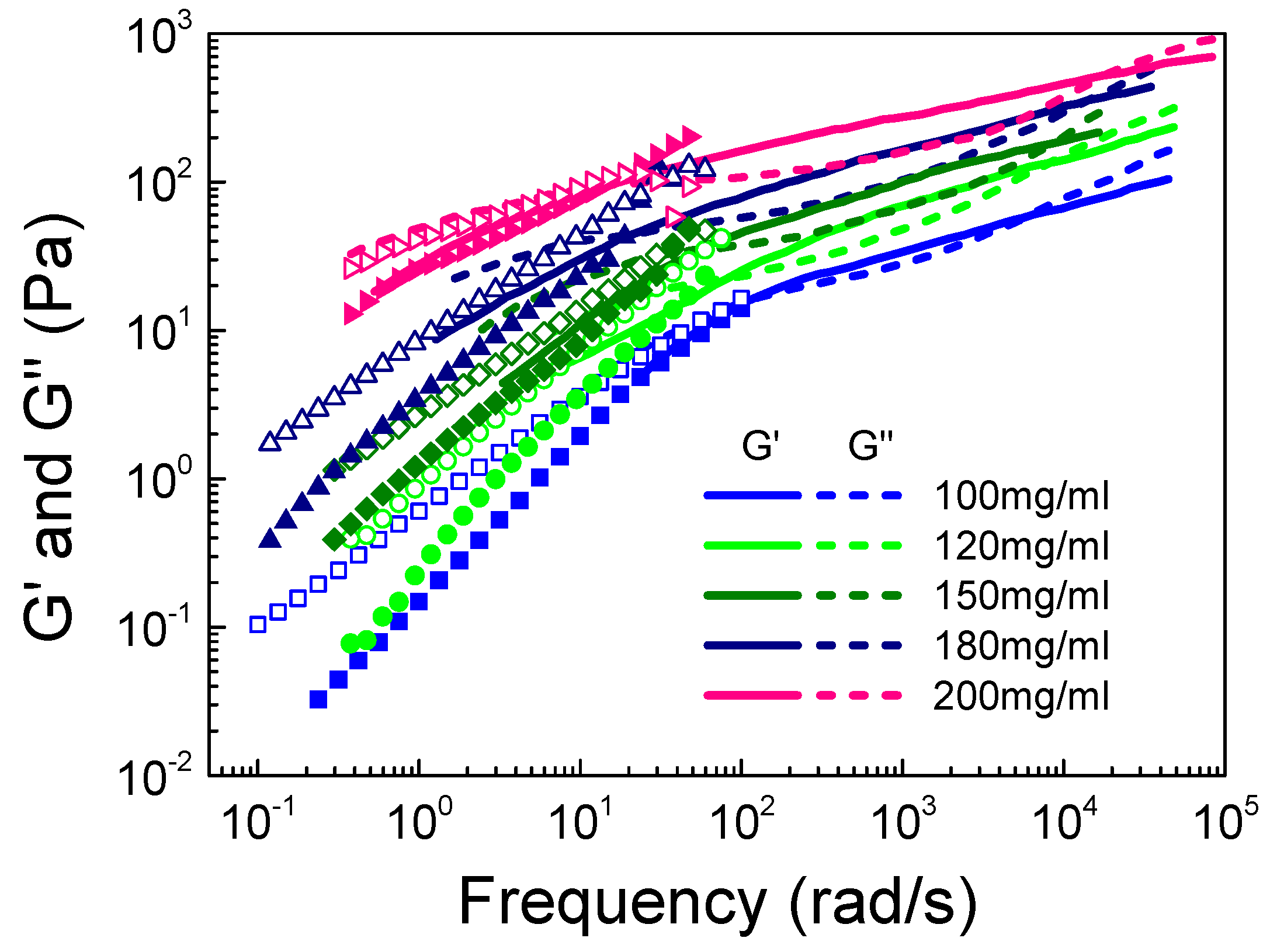
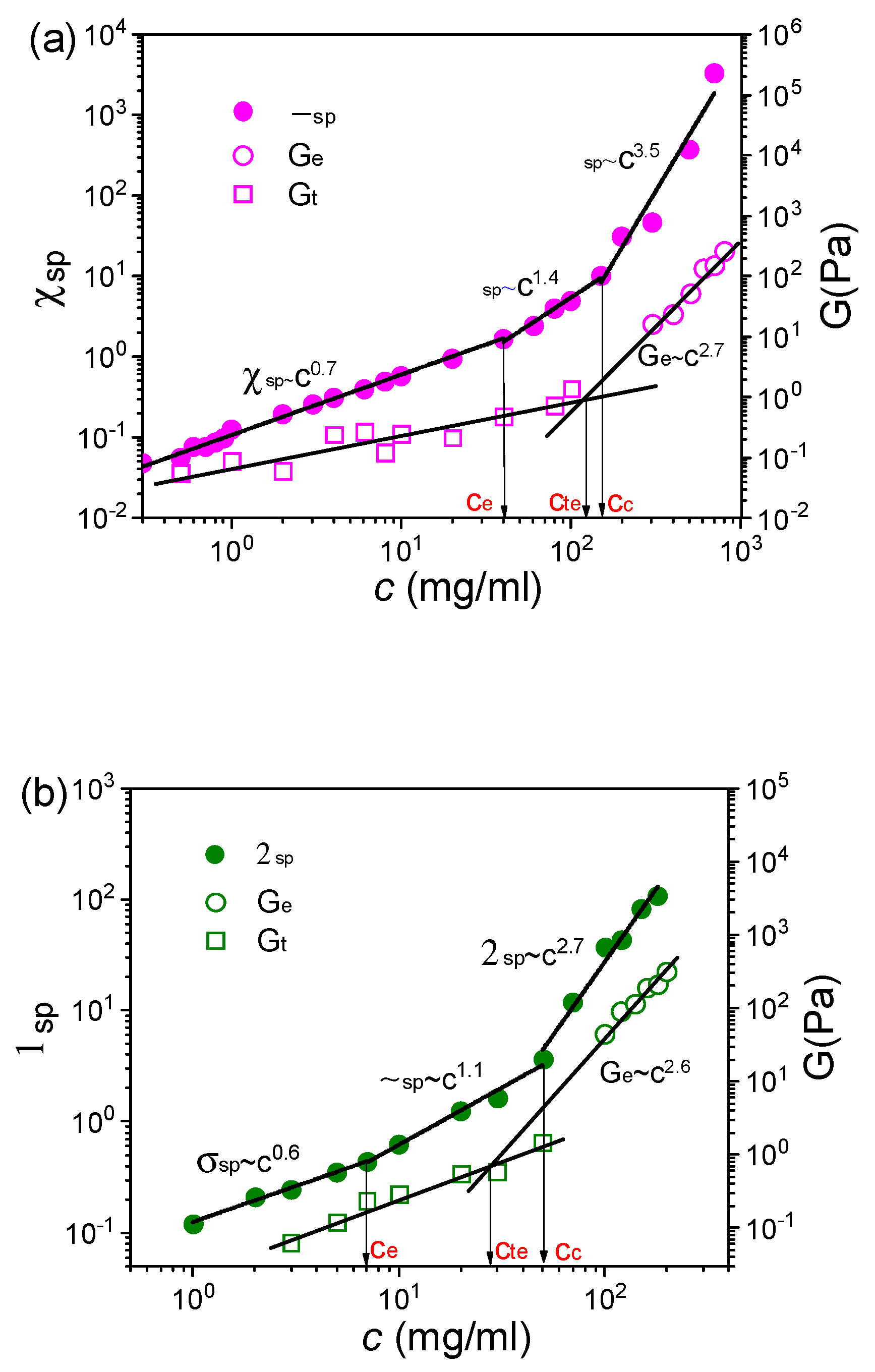
3.2. Rheological Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Philipp, B.; Dautzenberg, H.; Linow, K.J.; Kötz, J.; Dawydoff, W. Polyelectrolyte complexes—Recent developments and open problems. Prog. Polym. Sci. 1989, 14, 91–172. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Theory of polyelectrolytes in solutions and at surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Ballauff, M. Spherical polyelectrolyte brushes. Prog. Polym. Sci. 2007, 32, 1135–1151. [Google Scholar] [CrossRef]
- Muthukumar, M. 50th Anniversary Perspective: A Perspective on Polyelectrolyte Solutions. Macromolecules 2017, 50, 9528–9560. [Google Scholar] [CrossRef]
- Yethiraj, A.; Shew, C.Y. Structure of polyelectrolyte solutions. Phys. Rev. Lett. 1996, 77, 3937–3940. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Theory of viscoelastic properties of polyelectrolyte solutions. Polymer 2001, 42, 5921–5923. [Google Scholar] [CrossRef]
- Chen, G.; Perazzo, A.; Stone, H.A. Electrostatics, conformation, and rheology of unentangled semidilute polyelectrolyte solutions. J. Rheol. 2021, 65, 507–526. [Google Scholar] [CrossRef]
- Jimenez, L.N.; Martínez Narváez, C.D.V.; Sharma, V. Solvent Properties Influence the Rheology and Pinching Dynamics of Polyelectrolyte Solutions: Thickening the Pot with Glycerol and Cellulose Gum. Macromolecules 2022, 55, 8117–8132. [Google Scholar] [CrossRef]
- Dou, S.; Colby, R.H. Charge density effects in salt-free polyelectrolyte solution rheology. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2001–2013. [Google Scholar] [CrossRef]
- Ganesan, M.; Knier, S.; Younger, J.G.; Solomon, M.J. Associative and Entanglement Contributions to the Solution Rheology of a Bacterial Polysaccharide. Macromolecules 2016, 49, 8313–8321. [Google Scholar] [CrossRef]
- Kujawa, P.; Audibert-Hayet, A.; Selb, J.; Candau, F. Effect of ionic strength on the rheological properties of multisticker associative polyelectrolytes. Macromolecules 2006, 39, 384–392. [Google Scholar] [CrossRef]
- Esquenet, C.; Buhler, E. Phase behavior of associating polyelectrolyte polysaccharides. 1. Aggregation process in dilute solution. Macromolecules 2001, 34, 5287–5294. [Google Scholar] [CrossRef]
- Elliot, J.H.; Ganz, A.J. Some rheological properties of sodium carboxymethylcellulose solutions and gels. Rheol. Acta 1974, 13, 670–674. [Google Scholar] [CrossRef]
- Su, Y.-X.; Xu, L.; Xu, X.-H.; Hou, X.-H.; Liu, N.; Wu, Z.-Q. Controlled Synthesis of Densely Grafted Bottlebrushes That Bear Helical Polyisocyanide Side Chains on Polyisocyanide Backbones and Exhibit Greatly Increased Viscosity. Macromolecules 2020, 53, 3224–3233. [Google Scholar] [CrossRef]
- Zhang, W.; Du, Z.; Wang, W.; Li, G. Aggregation behavior of amphiphic comb-like copolymer containing poly(ethylene oxide) methyl ether grafts. Colloids Surf. Physicochem. Eng. Asp. 2012, 395, 175–182. [Google Scholar] [CrossRef]
- Liu, Z.; Shang, Y.; Feng, J.; Peng, C.; Liu, H.; Hu, Y. Effect of Hydrophilicity or Hydrophobicity of Polyelectrolyte on the Interaction between Polyelectrolyte and Surfactants: Molecular Dynamics Simulations. J. Phys. Chem. B 2012, 116, 5516–5526. [Google Scholar] [CrossRef]
- Lisal, M.; Limpouchova, Z.; Prochazka, K. The self-assembly of copolymers with one hydrophobic and one polyelectrolyte block in aqueous media: A dissipative particle dynamics study. Phys. Chem. Chem. Phys. 2016, 18, 16127–16136. [Google Scholar] [CrossRef]
- Esquenet, C.; Terech, P.; Boué, F.; Buhler, E. Structural and rheological properties of hydrophobically modified polysaccharide associative networks. Langmuir 2004, 20, 3583–3592. [Google Scholar] [CrossRef]
- Li, J.; Pan, M.; Tang, H. Understanding short-side-chain perfluorinated sulfonic acid and its application for high temperature polymer electrolyte membrane fuel cells. RSC Adv. 2014, 4, 3944–3965. [Google Scholar] [CrossRef]
- Economou, N.J.; O’Dea, J.R.; McConnaughy, T.B.; Buratto, S.K. Morphological differences in short side chain and long side chain perfluorosulfonic acid proton exchange membranes at low and high water contents. RSC Adv. 2013, 3, 19525–19532. [Google Scholar] [CrossRef]
- Siracusano, S.; Baglio, V.; Stassi, A.; Merlo, L.; Moukheiber, E.; Arico, A.S. Performance analysis of short-side-chain Aquivion® perfluorosulfonic acid polymer for proton exchange membrane water electrolysis. J. Membr. Sci. 2014, 466, 1–7. [Google Scholar] [CrossRef]
- Ren, H.; Meng, X.; Lin, Y.; Shao, Z. Structural stability of catalyst ink and its effects on the catalyst layer microstructure and fuel cell performance. J. Power Sources 2022, 517, 230698. [Google Scholar] [CrossRef]
- Zhao, N.; Shi, Z.; Girard, F. Superior proton exchange membrane fuel cell (Pemfc) performance using short-side-chain perfluorosulfonic acid (pfsa) membrane and ionomer. Materials 2022, 15, 78. [Google Scholar] [CrossRef] [PubMed]
- Neeshma, M.; Dhanasekaran, P.; Unni, S.M.; Bhat, S.D. Short side chain perfluorosulfonic acid composite membrane with covalently grafted cup stacked carbon nanofibers for polymer electrolyte fuel cells. J. Membr. Sci. 2023, 668, 121240. [Google Scholar] [CrossRef]
- Pellegrino, J.; Wang, D.; Rabago, R.; Noble, R.; Koval, C. Gas transport properties of solution-cast perfluorosulfonic acid ionomer films containing ionic surfactants. J. Membr. Sci. 1993, 84, 161–169. [Google Scholar] [CrossRef]
- Chung, R.J.; Chin, T.S.; Chen, L.C.; Hsieh, M.F. Preparation of gradually componential metal electrode on solution-casted Nafion™ membrane. Biomol. Eng. 2007, 24, 434–437. [Google Scholar] [CrossRef] [PubMed]
- Luan, Y.; Zhang, H.; Zhang, Y.; Li, L.; Li, H.; Liu, Y. Study on structural evolution of perfluorosulfonic ionomer from concentrated DMF-based solution to membranes. J. Membr. Sci. 2008, 319, 91–101. [Google Scholar] [CrossRef]
- Zammali, M.; Liu, S.; Yu, W. Symmetry breakdown in the sol-gel transition of a Guar gum transient physical network. Carbohydr. Polym. 2021, 258, 117689. [Google Scholar] [CrossRef] [PubMed]
- Szajdzinska-Pietek, E.; Wolszczak, M.; Plonka, A.; Schlick, S. Structure and dynamics of micellar aggregates in aqueous nafion solutions reported by electron spin resonance and fluorescence probes. Macromolecules 1999, 32, 7454–7460. [Google Scholar] [CrossRef]
- Loppinet, B.; Gebel, G. Rodlike colloidal structure of short pendant chain perfluorinated ionomer solutions. Langmuir 1998, 14, 1977–1983. [Google Scholar] [CrossRef]
- Martin, J.E.; Hurd, A.J. Scattering from fractals. J. Appl. Crystallogr. 1987, 20, 61–78. [Google Scholar] [CrossRef]
- Kassapidou, K.; Jesse, W.; Kuil, M.E.; Lapp, A.; Egelhaaf, S.; van der Maarel, J.R.C. Structure and Charge Distribution in DNA and Poly(styrenesulfonate) Aqueous Solutions. Macromolecules 1997, 30, 2671–2684. [Google Scholar] [CrossRef]
- Burchard, W. Solubility and solution structure of cellulose derivatives. Cellulose 2003, 10, 213–225. [Google Scholar] [CrossRef]
- Sundblom, A.; Oliveira, C.L.P.; Palmqvist, A.E.C.; Pedersen, J.S. Modeling in Situ Small-Angle X-ray Scattering Measurements Following the Formation of Mesostructured Silica. J. Phys. Chem. C 2009, 113, 7706–7713. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Matsunaga, T.; Amemiya, K.; Ohira, A.; Hasegawa, N.; Shinohara, K.; Ando, M.; Yoshida, T. Dispersion of rod-like particles of nafion in salt-free water/1-propanol and water/ethanol solutions. J. Phys. Chem. B 2014, 118, 14922–14928. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Zhang, H.; Ilavsky, J.; Stanciu, L.; Ho, D.; Justice, M.J.; Petrache, H.I.; Xie, J. Investigation of a catalyst ink dispersion using both ultra-small-angle X-ray scattering and cryogenic TEM. Langmuir 2010, 26, 19199–19208. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.G.; Rogers, S.E.; Colby, R.H.; Graham, P.; Cabral, J.T. Structure of sodium carboxymethyl cellulose aqueous solutions: A SANS and rheology study. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 492–501. [Google Scholar] [CrossRef]
- Justice, R.S.; Schaefer, D.W.; Vaia, R.A.; Tomlin, D.W.; Bunning, T.J. Interface morphology and phase separation in polymer-dispersed liquid crystal composites. Polymer 2005, 46, 4465–4473. [Google Scholar] [CrossRef]
- Beaucage, G. Approximations Leading to a Unified Exponential/Power-Law Approach to Small-Angle Scattering. J. Appl. Crystallogr. 1995, 28, 717–728. [Google Scholar] [CrossRef]
- Beaucage, G.; Schaefer, D.W. Structural studies of complex systems using small-angle scattering: A unified Guinier/power-law approach. J. Non-Cryst. Solids 1994, 172–174, 797–805. [Google Scholar] [CrossRef]
- Beaucage, G.; Ulibarri, T.; Black, E.; Schaefer, D. Multiple Size Scale Structures in Silica-Siloxane Composites Studied by Small-Angle Scattering; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1995; pp. 97–111. [Google Scholar]
- Hammouda, B. Analysis of the Beaucage model. J. Appl. Crystallogr. 2010, 43, 1474–1478. [Google Scholar] [CrossRef]
- Boucard, N.; David, L.; Rochas, C.; Montembault, A.; Viton, C.; Domard, A. Polyelectrolyte microstructure in chitosan aqueous and alcohol solutions. Biomacromolecules 2007, 8, 1209–1217. [Google Scholar] [CrossRef] [PubMed]
- Popa-Nita, S.; Rochas, C.; David, L.; Domard, A. Structure of Natural Polyelectrolyte Solutions: Role of the Hydrophilic/Hydrophobic Interaction Balance. Langmuir 2009, 25, 6460–6468. [Google Scholar] [CrossRef] [PubMed]
- Dou, S.; Colby, R.H. Solution rheology of a strongly charged polyelectrolyte in good solvent. Macromolecules 2008, 41, 6505–6510. [Google Scholar] [CrossRef]
- Liao, Q.; Dobrynin, A.V.; Rubinstein, M. Molecular dynamics simulations of polyelectrolyte solutions: Nonuniform stretching of chains and scaling behavior. Macromolecules 2003, 36, 3386–3398. [Google Scholar] [CrossRef]
- Matsumoto, A.; Del Giudice, F.; Rotrattanadumrong, R.; Shen, A.Q. Rheological Scaling of Ionic-Liquid-Based Polyelectrolytes in Ionic Liquid Solutions. Macromolecules 2019, 52, 2759–2771. [Google Scholar] [CrossRef]
- Tam, K.C.; Tiu, C. Steady and Dynamic Shear Properties of Aqueous Polymer Solutions. J. Rheol. 1989, 33, 257–280. [Google Scholar] [CrossRef]
- Schunk, P.R.; Scriven, L.E. Constitutive Equation for Modeling Mixed Extension and Shear in Polymer Solution Processing. J. Rheol. 1990, 34, 1085–1119. [Google Scholar] [CrossRef]
- Clasen, C.; Kulicke, W.M. Determination of viscoelastic and rheo-optical material functions of water-soluble cellulose derivatives. Prog. Polym. Sci. 2001, 26, 1839–1919. [Google Scholar] [CrossRef]
- Kulicke, W.M.; Kull, A.H.; Kull, W.; Thielking, H.; Engelhardt, J.; Pannek, J.B. Characterization of aqueous carboxymethylcellulose solutions in terms of their molecular structure and its influence on rheological behaviour. Polymer 1996, 37, 2723–2731. [Google Scholar] [CrossRef]
- Boris, D.C.; Colby, R.H. Rheology of sulfonated polystyrene solutions. Macromolecules 1998, 31, 5746–5755. [Google Scholar] [CrossRef]
- Lopez, C.G. Entanglement of semiflexible polyelectrolytes: Crossover concentrations and entanglement density of sodium carboxymethyl cellulose. J. Rheol. 2020, 64, 191–204. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Colby, R.H.; Rubinstein, M. Scaling Theory of Polyelectrolyte Solutions. Macromolecules 1995, 28, 1859–1871. [Google Scholar] [CrossRef]
- Lopez, C.G.; Colby, R.H.; Cabral, J.T. Electrostatic and Hydrophobic Interactions in NaCMC Aqueous Solutions: Effect of Degree of Substitution. Macromolecules 2018, 51, 3165–3175. [Google Scholar] [CrossRef]
- Liu, C.; He, J.; Ruymbeke, E.V.; Keunings, R.; Bailly, C. Evaluation of different methods for the determination of the plateau modulus and the entanglement molecular weight. Polymer 2006, 47, 4461–4479. [Google Scholar] [CrossRef]
- Graessley, W.W.; Edwards, S.F. Entanglement Interactions in Polymers and the Chain Contour Concentration. Polymer 1981, 22, 1329–1334. [Google Scholar] [CrossRef]
- Matsumoto, A.; Zhang, C.; Scheffold, F.; Shen, A.Q. Microrheological Approach for Probing the Entanglement Properties of Polyelectrolyte Solutions. ACS Macro Lett. 2022, 11, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Han, A.; Colby, R.H. Rheology of Entangled Polyelectrolyte Solutions. Macromolecules 2021, 54, 1375–1387. [Google Scholar] [CrossRef]
- Pinder, D.N.; Swanson, A.J.; Hebraud, P.; Hemar, Y. Micro-rheological investigation of dextran solutions using diffusing wave spectroscopy. Food Hydrocoll. 2006, 20, 240–244. [Google Scholar] [CrossRef]
- Ilyin, S.O.; Malkin, A.Y.; Kulichikhin, V.G.; Denisova, Y.I.; Krentsel, L.B.; Shandryuk, G.A.; Litmanovich, A.D.; Litmanovich, E.A.; Bondarenko, G.N.; Kudryavtsev, Y.V. Effect of Chain Structure on the Rheological Properties of Vinyl Acetate–Vinyl Alcohol Copolymers in Solution and Bulk. Macromolecules 2014, 47, 4790–4804. [Google Scholar] [CrossRef]
- Mason, T.G. Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation. Rheol. Acta 2000, 39, 371–378. [Google Scholar] [CrossRef]
- Mason, T.G.; Ganesan, K.; van Zanten, J.H.; Wirtz, D.; Kuo, S.C. Particle Tracking Microrheology of Complex Fluids. Phys. Rev. Lett. 1997, 79, 3282–3285. [Google Scholar] [CrossRef]
- Mason, T.G.; Weitz, D.A. Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids. Phys. Rev. Lett. 1995, 74, 1250–1253. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.R.; Ji, C.H.; Xue, S.M.; Xu, Z.L.; Yang, H.; Ma, X.H. Enhanced pervaporation performance of SA-PFSA/ceramic hybrid membranes for ethanol dehydration. Sep. Purif. Technol. 2018, 206, 218–225. [Google Scholar] [CrossRef]
- Fang, X.; Shen, P.K.; Song, S.; Stergiopoulos, V.; Tsiakaras, P. Degradation of perfluorinated sulfonic acid films: An in-situ infrared spectro-electrochemical study. Polym. Degradation Stab. 2009, 94, 1707–1713. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Y.; Zhao, X.; Li, H.; Liu, S.; Yu, W. Microstructures and Rheological Properties of Short-Side-Chain Perfluorosulfonic Acid in Water/2-Propanol. Polymers 2024, 16, 1863. https://doi.org/10.3390/polym16131863
Qiu Y, Zhao X, Li H, Liu S, Yu W. Microstructures and Rheological Properties of Short-Side-Chain Perfluorosulfonic Acid in Water/2-Propanol. Polymers. 2024; 16(13):1863. https://doi.org/10.3390/polym16131863
Chicago/Turabian StyleQiu, Yan, Xinyang Zhao, Hong Li, Sijun Liu, and Wei Yu. 2024. "Microstructures and Rheological Properties of Short-Side-Chain Perfluorosulfonic Acid in Water/2-Propanol" Polymers 16, no. 13: 1863. https://doi.org/10.3390/polym16131863
APA StyleQiu, Y., Zhao, X., Li, H., Liu, S., & Yu, W. (2024). Microstructures and Rheological Properties of Short-Side-Chain Perfluorosulfonic Acid in Water/2-Propanol. Polymers, 16(13), 1863. https://doi.org/10.3390/polym16131863








