Effects of Testing Methods and Sample Configuration on the Flexural Properties of Extruded Polystyrene
Abstract
1. Introduction
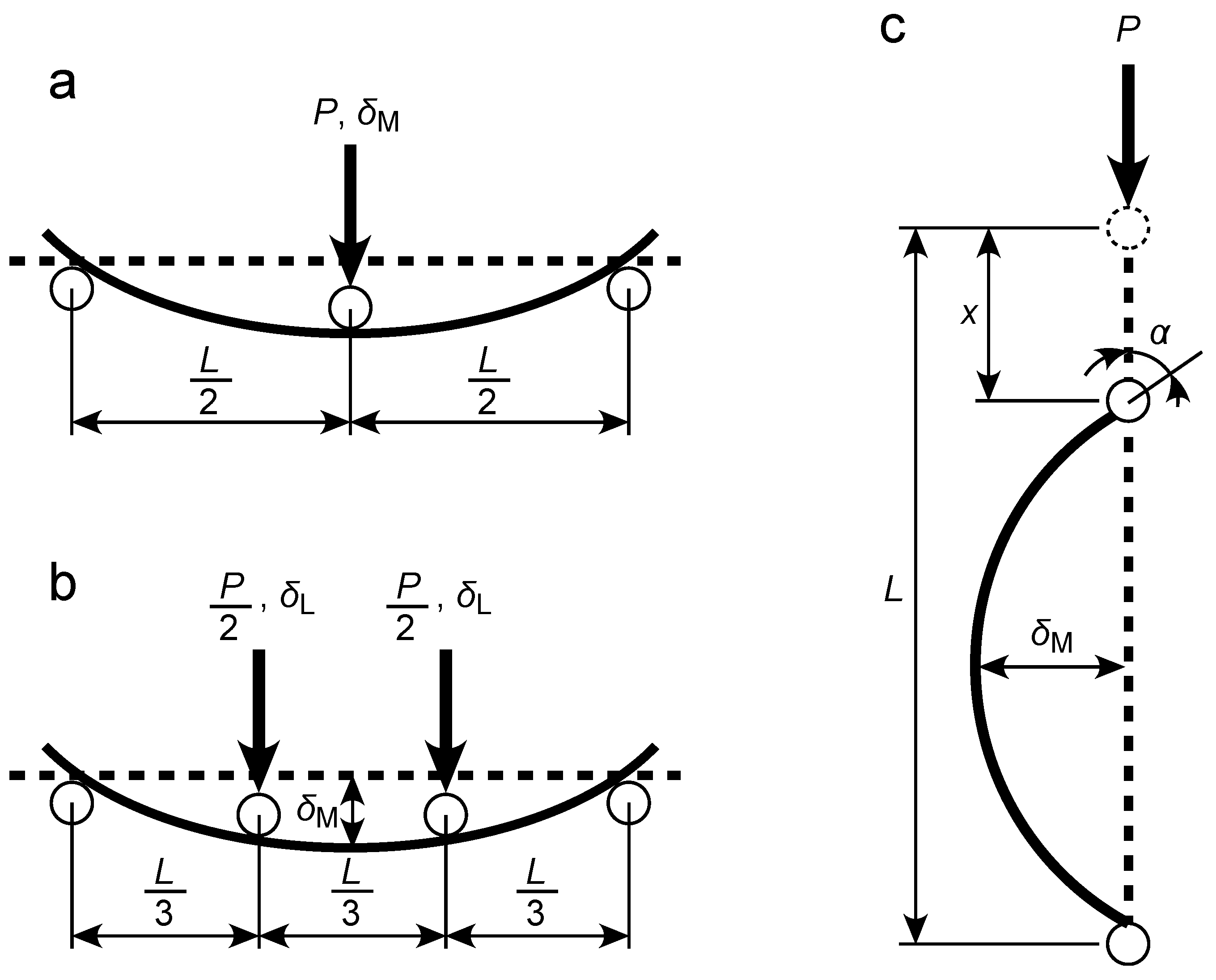
2. Theoretical Background
3. Materials and Methods
3.1. Materials
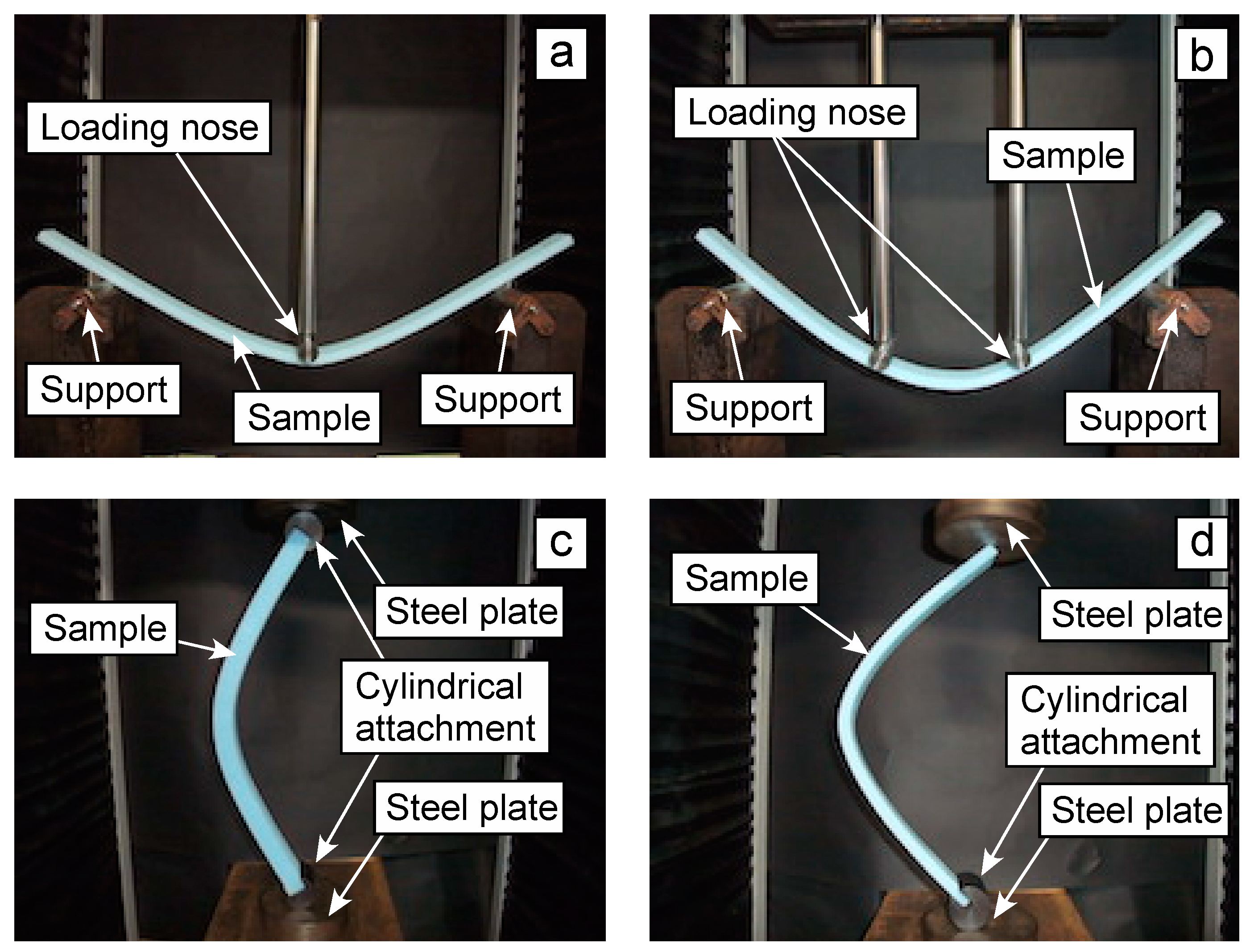
3.2. TPB, FPB, and CB Tests
4. Results and Discussion
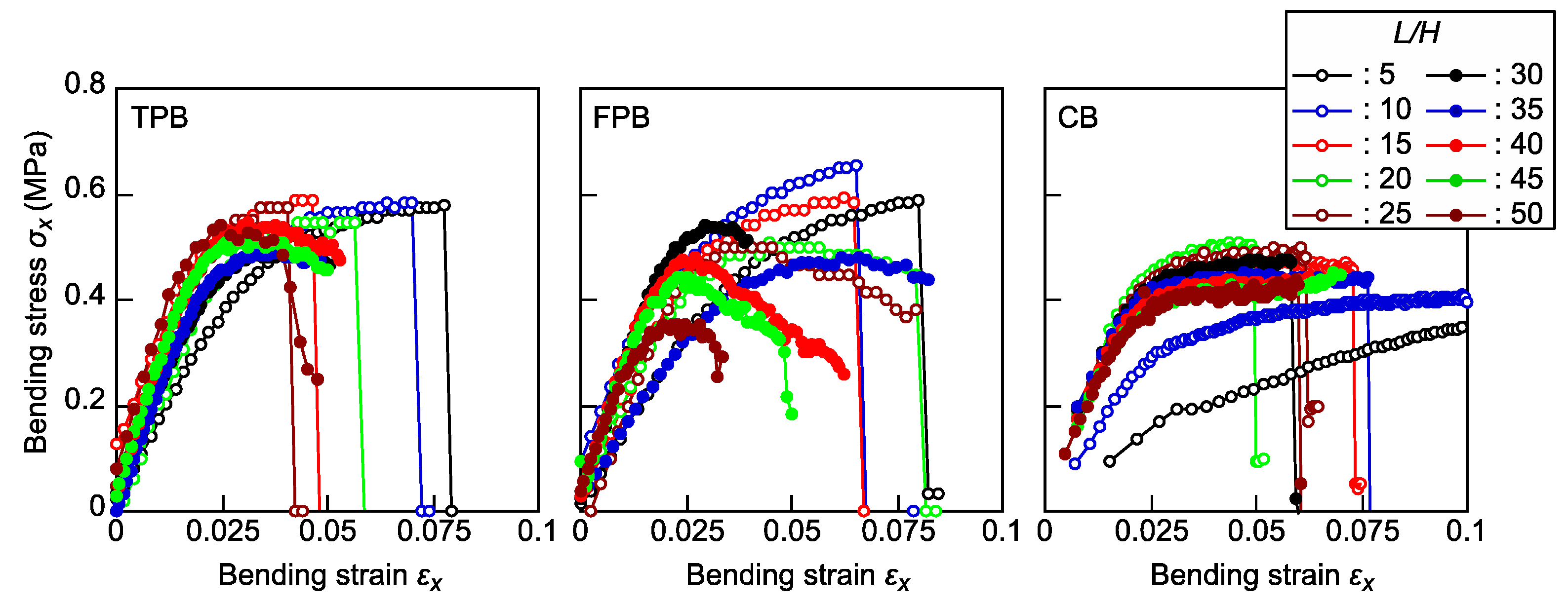
4.1. Experimental Results Obtained from the TPB, FPB, and CB Tests
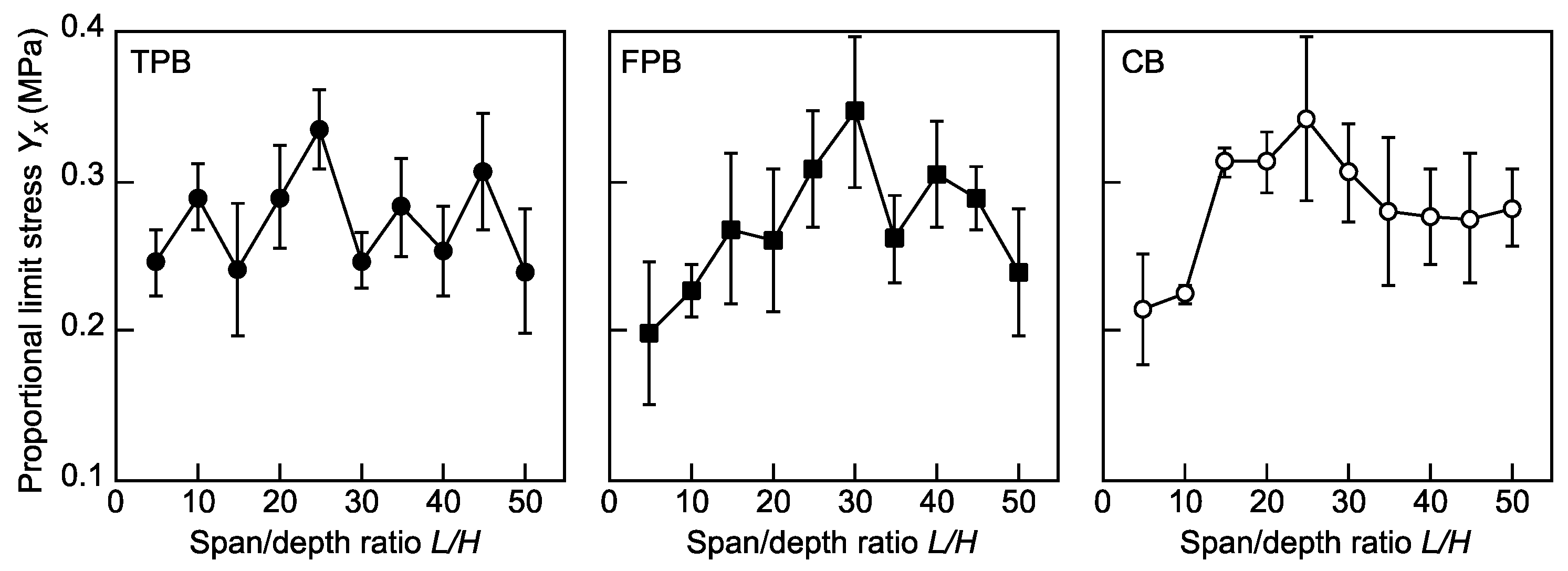
4.2. Statistical Analyses of the Testing Results
5. Conclusions
- (1)
- In the TPB and FPB tests, Young’s modulus increased continuously as the span/depth ratio increased because of the slippage between the sample and supporting point, as well as the effect of deflection caused by the shearing force. In the CB test, the Young’s modulus was lower in the small span/depth ratio range where material nonlinearity was induced by axial loading prior to bending deformation. Except for this span/depth ratio range, Young’s modulus could be obtained while reducing the effect of the sample configuration.
- (2)
- The effect of the span/depth ratio on the proportional limit stress was not observed in the TPB test results; in contrast, the effect was found in the results obtained from the FPB and CB tests.
- (3)
- To determine the samples’ bending strength by using the TPB test, the methods for correcting the large defection determined in ASTM D 790-17 and JIS K 7074-1988 were effective; the correction methods for the FPB test determined in ASTM 6272-17 and JIS K 7074-1988 were not sufficient, however. In contrast, the effect of the span/depth ratio was not significant in the CB test results.
- (4)
- From the experimental results, the use of TPB and CB tests is recommended over the FPB test to determine the bending properties of XPS samples. However, the properties determined via the TPB and CB tests were different. Therefore, further research should be conducted to explore the source of these differences in more detail.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.; You, Y.-C. Composite behavior of a novel insulated concrete sandwich wall panel reinforced with GFRP shear grids: Effects of insulation types. Materials 2015, 8, 899–913. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Zhang, B.; Cremaschi, L. Review of moisture behavior and thermal performance of polystyrene insulation in building applications. Build. Environ. 2017, 123, 50–65. [Google Scholar] [CrossRef]
- Li, Q.; Wei, H.; Han, L.; Wang, F.; Zhang, Y.; Han, S. Feasibility of using modified silty clay and extruded polystyrene (XPS) board as the subgrade thermal insulation layer in a seasonally frozen region, Northeast China. Sustainability 2019, 11, 804. [Google Scholar] [CrossRef]
- Aksit, M.; Zhao, C.; Klose, B.; Kreger, K.; Schmidt, H.-W.; Altstädt, V. Extruded polystyrene foams with enhanced insulation and mechanical properties by a benzene-trisamide-based additive. Polymers 2019, 11, 268. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Wei, H.; Zhou, P.; Zhang, Y.; Han, L.; Han, S. Experimental and numerical research on utilizing modified silty clay and extruded polystyrene (XPS) board as the subgrade thermal insulation layer in a seasonally frozen region, Northeast China. Sustainability 2019, 11, 3495. [Google Scholar] [CrossRef]
- Seto, H.; Saito, I.; Onuki, A.; Takeuchi, M.; Tsuchiya, T. Presumption of the source of indoor air pollution. Amounts of styrene and butanol generation from construction materials. Annu. Rep. Tokyo Metrop. Res. Lab. Public Health 2000, 51, 219–222. [Google Scholar]
- Aoyagi, R.; Matsunobu, K.; Matsumura, T. Development of continuous vapor generation for calibration styrene with permeation tube method. Indoor Environ. 2009, 52, 97–102. [Google Scholar] [CrossRef][Green Version]
- Matsumoto, T.; Iwamae, A.; Wakana, S.; Mihara, N. Effect of the temperature-humidity condition in the room and under the floor by heat insulation tatami and flooring. In Summaries of Technical Papers of Annual Meeting, Kobe, Japan, 13 September 2014; Architectural Institute of Japan (Environmental Engineering II): Tokyo, Japan, 2014. [Google Scholar]
- Vinson, J.R. Sandwich structures. Appl. Mech. Rev. 2001, 54, 201–214. [Google Scholar] [CrossRef]
- Hu, Y.; Nakao, T.; Nakai, T.; Gu, J.; Wang, F. Dynamic properties of three types of wood-based composites. J. Wood Sci. 2005, 51, 7–12. [Google Scholar] [CrossRef]
- Hu, Y.; Nakao, T.; Nakai, T.; Gu, J.; Wang, F. Vibrational properties of wood plastic plywood. J. Wood Sci. 2005, 51, 13–17. [Google Scholar] [CrossRef]
- Kawasaki, T.; Kawai, S. Thermal insulation properties of wood-based sandwich panel for use as structural insulated walls and floors. J. Wood Sci. 2005, 52, 75–83. [Google Scholar] [CrossRef]
- Kilar, V.; Koren, D.; Bokan-Bosiljkov, V. Evaluation of the performance of extruded polystyrene boards—Implications for their application in earthquake engineering. Polym. Test. 2014, 40, 234–244. [Google Scholar] [CrossRef]
- Vitau, C.; Dudescu, M.C. Investigation of mechanical behaviour of expanded polystyrene under compressive and bending loadings. Mater. Plast. 2020, 57, 199–207. [Google Scholar]
- Tang, N.; Lei, D.; Huang, D.; Xiao, R. Mechanical performance of polystyrene foam (EPS): Experimental and numerical analysis. Polym. Test. 2019, 73, 359–365. [Google Scholar] [CrossRef]
- Yoshihara, H.; Ataka, N.; Maruta, M. Measurement of the Young’s modulus and shear modulus of extruded polystyrene foam by the longitudinal and flexural vibration methods. J. Cell. Plast. 2018, 54, 199–216. [Google Scholar] [CrossRef]
- Yoshihara, H.; Wakahara, M.; Yoshinobu, M.; Maruta, M. Torsional vibration tests of extruded polystyrene with improved accuracy in determining the shear modulus. Polymers 2022, 14, 1148. [Google Scholar] [CrossRef] [PubMed]
- Yoshihara, H.; Maruta, M. Measurement of the shear properties of extruded polystyrene foam by in-plane shear and asymmetric four-point bending tests. Polymers 2020, 12, 47. [Google Scholar] [CrossRef] [PubMed]
- ISO 1209-02-2007; Rigid Cellular Plastics—Determination of Flexural Properties—Part 2: Determination of Flexural Strength and Apparent Flexural Modulus of Elasticity. International Organization for Standardization: Geneva, Switzerland, 2007.
- JIS K 7221-2:2006; Rigid Cellular Plastics—Determination of Flexural Properties—Part 2: Determination of Flexural Strength and Apparent Flexural Modulus of Elasticity. Japan Standards Association: Tokyo, Japan, 2006.
- Wang, G.; Chen, X.; Liu, P.; Bai, S. Flame-retardant mechanism of expandable polystyrene foam with a macromolecular nitrogen-phosphorus intumescent flame retardant. J. Appl. Poym. Sci. 2017, 134, 1. [Google Scholar] [CrossRef]
- Iyer, S.V.; Chatterjee, R.; Ramya, M.; Suresh, E.; Padmanabhan, K. A comparative study of the three point and four point bending behaviour of rigid foam core glass/epoxy face sheet sandwich composites. Mater. Today Proc. 2018, 5, 12083–12090. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, S.; Chen, Z. Influence of particle size and addition of recycling phenolic foam on mechanical and flame retardant properties of wood-phenolic composites. Constr. Build. Mater. 2018, 168, 1–10. [Google Scholar] [CrossRef]
- Fukuda, H. A new bending test method of advanced composites. Exp. Mech. 1989, 29, 330–335. [Google Scholar] [CrossRef]
- Fukuda, H.; Katoh, H.; Uesugi, H. A modified procedure to measure bending strength and modulus of advanced composites by means of compression bending. J. Compos. Mater. 1995, 29, 195–207. [Google Scholar] [CrossRef]
- Fukuda, H.; Itabashi, M. Simplified compression bending test method for advanced composites. Compos. A 1999, 30, 249–256. [Google Scholar] [CrossRef]
- Yoshihara, H.; Oka, S. Measurement of bending properties of wood by compression bending tests. J. Wood Sci. 2001, 47, 262–268. [Google Scholar] [CrossRef]
- Yoshihara, H. Bending properties of medium-density fiberboard and plywood obtained by compression bending test. For. Prod. J. 2010, 61, 56–63. [Google Scholar] [CrossRef]
- Santabárbara, A.G.; Carrió, J.M.; Sastre, R.S.; Sakata, H. Determination of bending properties of lauan plywood by compression bending tests. In Proceedings of the 6th International Conference on Technological Innovation in Buildin (CITE 2021), Madrid, Spain, 25 March 2021. [Google Scholar]
- Yoshihara, H.; Yoshinobu, M.; Maruta, M. Bending stiffness and moment capacity of cardboard obtained from three-point and elastica bending tests. Nord. Pulp Pap. Res. J. 2023, 38, 73–85. [Google Scholar] [CrossRef]
- Kurauchi, T.; Negi, K. Energy absorption of foamed rigid polyurethane under compressive deformation. J. Soc. Mater. Sci. Jpn. 1984, 33, 986–991. [Google Scholar] [CrossRef]
- Nakajima, T.; Nogami, R.; Teragishi, Y.; Takada, T. Relationship between stress and strain in polyethylene foam. A consideration of compressive properties based on a simulation model. J. Soc. Mater. Sci. Jpn. 1992, 41, 28–33. [Google Scholar] [CrossRef][Green Version]
- Gholampour, S.; Hajirayat, K.; Erfanian, A.; Zali, A.R.; Shakouri, E. Investigating the role of helmet layers in reducing the stress applied during head injury using FEM. Int. Clin. Neurosci. J. 2017, 4, 4–11. [Google Scholar]
- ASTM D790-17; Standard Test Methods for Flexural Properties of unreinforced and Reinforced Plastics and Electrical Insulating Materials. ASTM International: West Conshohocken, PA, USA, 2017.
- JIS K 7074-2:1988; Testing Methods for Flexural Properties of Carbon Fiber Reinforced Plastics. Japan Standards Association: Tokyo, Japan, 1988.
- ASTM D6272-17; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials by Four-Point Bending. ASTM International: West Conshohocken, PA, USA, 2017.
- Adams, D.F.; Carlsson, L.A.; Pipes, R.B. Lamina flexural response. In Experimental Characterization of Advanced Composite Materials, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 121–130. [Google Scholar]
- Davies, P.; Blackman, B.R.K.; Brunner, A.J. Mode II delamination. In Fracture Mechanics Testing Methods for Polymers Adhesives and Composites; Moore, D.R., Pavan, A., Williams, J.G., Eds.; ESIS Publication 28; Elsevier: Amsterdam, The Netherland, 2001; pp. 307–333. [Google Scholar]
- Yoshihara, H.; Kubojima, Y.; Ishimoto, T. Several examinations on the static bending test methods of wood by using todomatsu (Japanese fir). For. Prod. J. 2003, 53, 39–44. [Google Scholar]
- Yoshihara, H.; Itoh, A. Influence of large deflection on the measurement of bending properties of veneer by three-point static bending tests. Wood Fiber Sci. 2003, 35, 293–300. [Google Scholar]
- Free Statistical Software: EZR (Easy R). Available online: https://www.jichi.ac.jp/saitama-sct/SaitamaHP.files/statmedEN.html (accessed on 16 June 2024).


| H (mm) | 20 | 10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L (mm) | 100 | 200 | 300 | 400 | 500 | 300 | 350 | 400 | 450 | 500 |
| L/H | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| TPB | 5.0 | 20.0 | 45.0 | 80.0 | 125 | 90.0 | 123 | 160 | 203 | 250 |
| FPB | 6.39 | 25.6 | 57.5 | 102 | 160 | 115 | 156 | 205 | 259 | 319 |
| CB | 0.902 | 7.19 | 24.2 | 57.3 | 112 | 96.4 | 153 | 228 | 324 | 445 |
| L/H | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|
| TPB | A | AB | AC | ACD | BCDE | BCDE | BCDE | E | BDE | E |
| FPB | A | AB | ABC | B | BD | BD | CD | D | CD | CD |
| CB | A | B | B | B | B | AB | AB | B | B |
| L/H | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|
| TPB | A | A | A | A | A | A | A | A | A | A |
| FPB | A | AB | AC | AD | BCD | CD | ACD | BCD | ACD | AD |
| CB | A | AB | C | C | C | BC | AC | ABC | ABC | ABC |
| L/H | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|
| TPB, EBT | A | AB | ABC | ABC | ABC | BC | BC | ABC | C | ABC |
| TPB, ASTM | A | A | A | A | A | A | A | A | A | A |
| TPB, JIS | A | A | A | A | A | A | A | A | A | A |
| FPB EBT | A | A | AB | BC | C | C | C | C | CD | D |
| FPB, ASTM | A | AB | A | AC | AC | AC | BC | BC | CD | D |
| FPB, JIS | A | AB | A | AC | AC | AC | BC | BC | CD | C |
| CB | A | A | A | A | A | A | A | A | A | A |
| Method | Ex (MPa) | Yx (MPa) | Fx EBT (MPa) | Fx ASTM (MPa) | Fx JIS (MPa) |
|---|---|---|---|---|---|
| TPB | 24.8 ± 3.5 | 0.273 ± 0.049 | 0.520 ± 0.045 | 0.606 ± 0.047 | 0.593 ± 0.046 |
| FPB | 23.9 ± 3.0 | 0.287 ± 0.049 | 0.490 ± 0.043 | 0.551 ± 0.042 | 0.602 ± 0.070 |
| CB | 18.1 ± 2.5 | 0.298 ± 0.040 | 0.457 ± 0.046 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshihara, H.; Yoshinobu, M.; Maruta, M. Effects of Testing Methods and Sample Configuration on the Flexural Properties of Extruded Polystyrene. Polymers 2024, 16, 1857. https://doi.org/10.3390/polym16131857
Yoshihara H, Yoshinobu M, Maruta M. Effects of Testing Methods and Sample Configuration on the Flexural Properties of Extruded Polystyrene. Polymers. 2024; 16(13):1857. https://doi.org/10.3390/polym16131857
Chicago/Turabian StyleYoshihara, Hiroshi, Masahiro Yoshinobu, and Makoto Maruta. 2024. "Effects of Testing Methods and Sample Configuration on the Flexural Properties of Extruded Polystyrene" Polymers 16, no. 13: 1857. https://doi.org/10.3390/polym16131857
APA StyleYoshihara, H., Yoshinobu, M., & Maruta, M. (2024). Effects of Testing Methods and Sample Configuration on the Flexural Properties of Extruded Polystyrene. Polymers, 16(13), 1857. https://doi.org/10.3390/polym16131857






