Artificial Neural Network Study on the Pyrolysis of Polypropylene with a Sensitivity Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. The Experiments
2.2. ANNs Topology
3. Results and Discussion
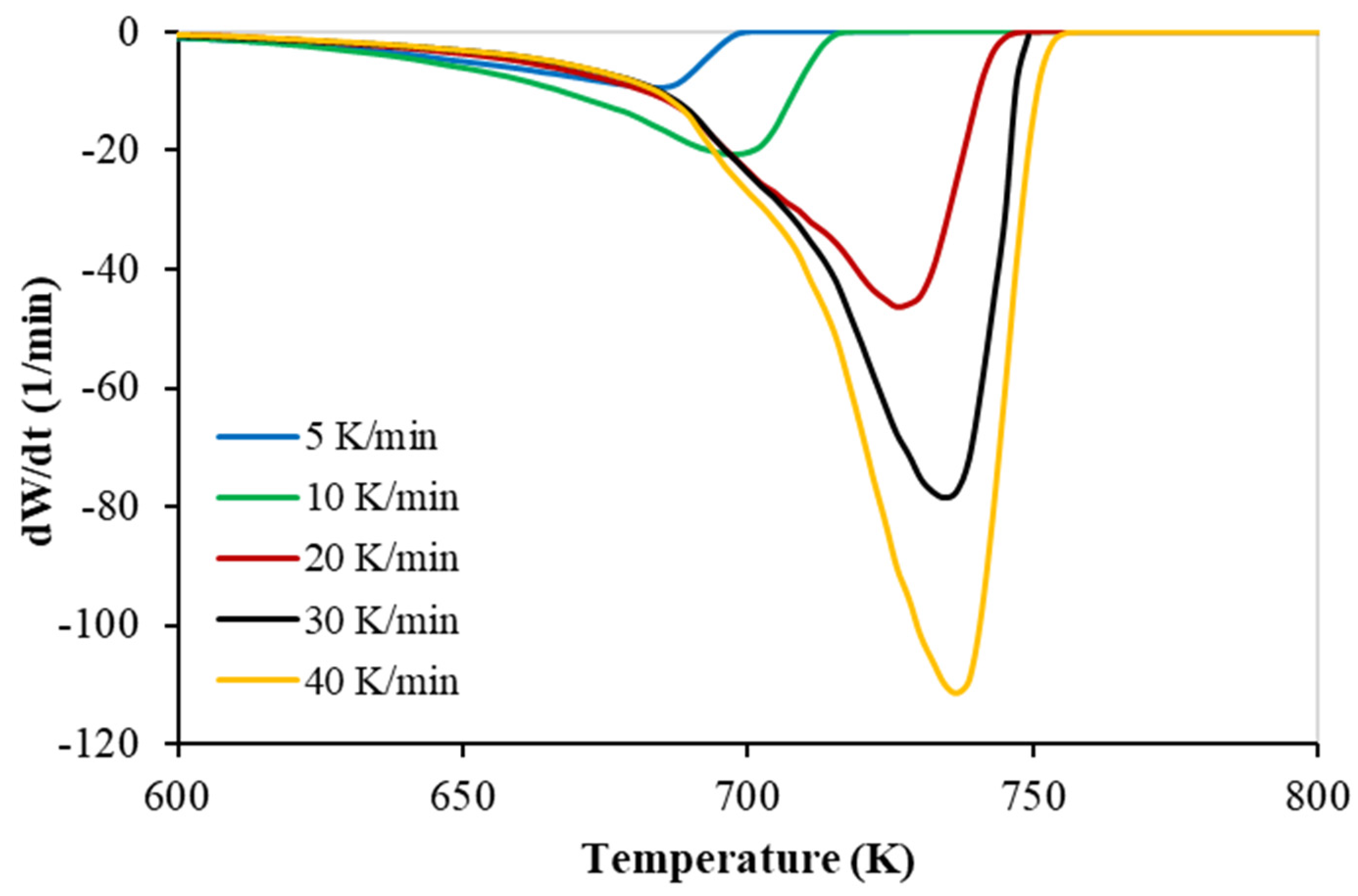
3.1. Thermogravimetric Analysis of PP
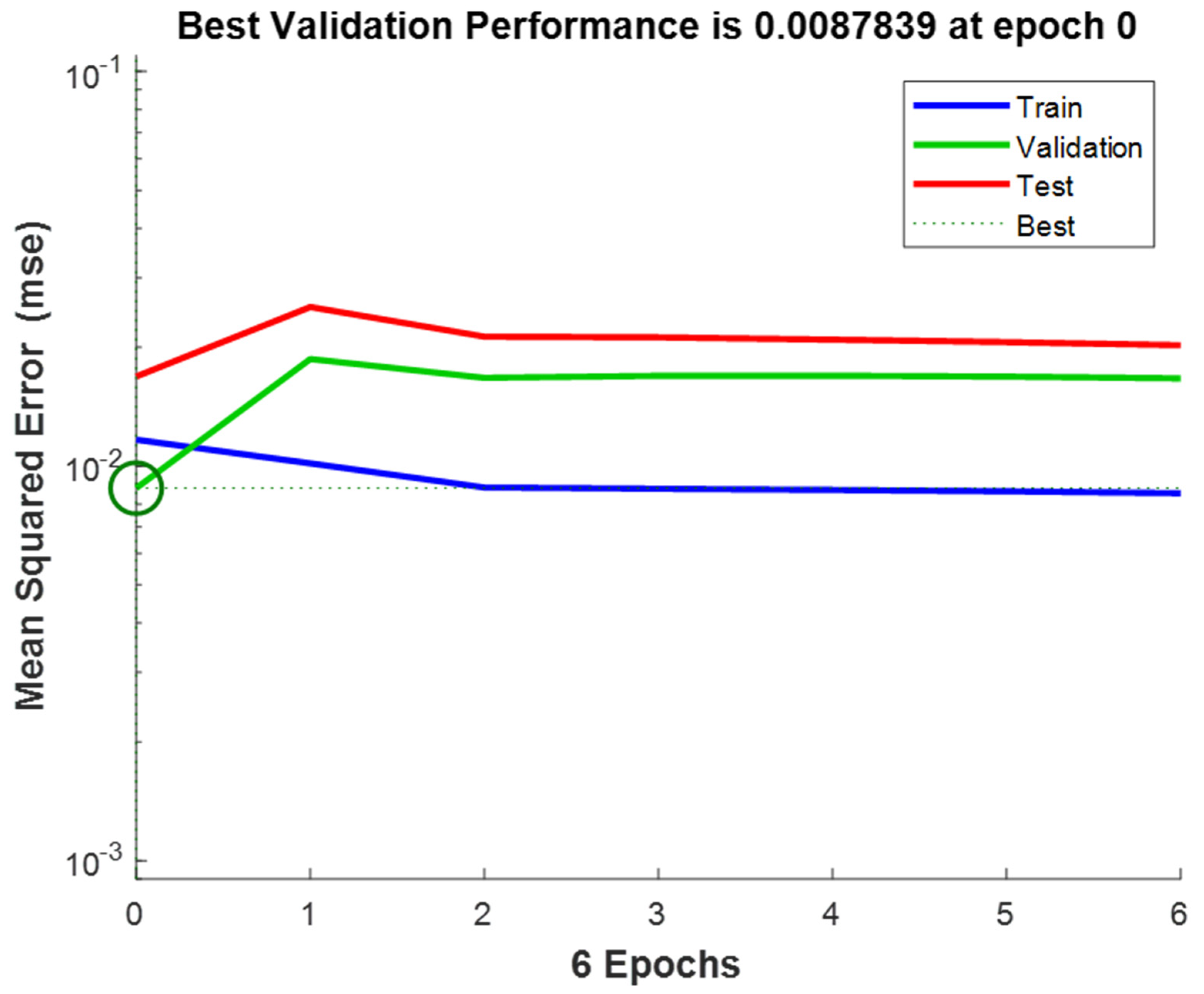
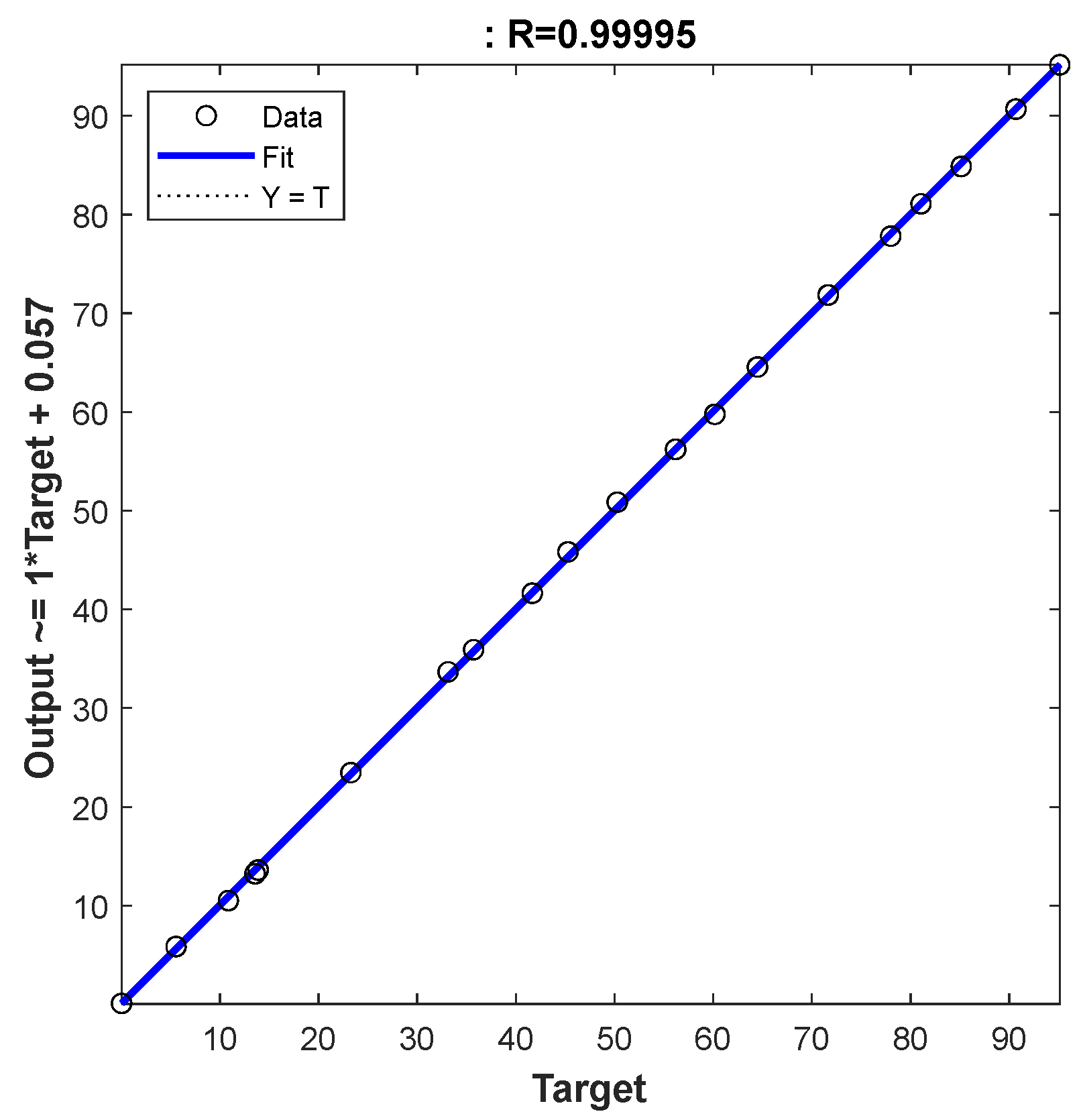
3.2. Pyrolysis Prediction by ANN Model
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muravyev, N.V.; Luciano, G.; Ornaghi, H.L.J.; Svoboda, R.; Vyazovkin, S. Artificial neural networks for pyrolysis, thermal analysis, and thermokinetic studies: The status quo. Molecules 2021, 26, 3727. [Google Scholar] [CrossRef] [PubMed]
- Conesa, J.A.; Caballero, J.A.; Labarta, J.A. Artificial neural network for modelling thermal decompositions. J. Anal. Appl. Pyrolysis 2004, 71, 343–352. [Google Scholar] [CrossRef]
- Zaker, A.; Chen, Z.; Zaheer-Uddin, M. Catalytic pyrolysis of sewage sludge with HZSM5 and sludge-derived activated char: A comparative study using TGA-MS and artificial neural networks. J. Environ. Chem. Eng. 2021, 9, 105891. [Google Scholar] [CrossRef]
- Dubdub, I. Pyrolysis study of mixed polymers for non-isothermal TGA: Artificial neural networks application. Polymers 2022, 14, 2638. [Google Scholar] [CrossRef] [PubMed]
- Khan, N.; Taqvi, S.A.A. Machine learning an intelligent approach in process industries: A perspective and overview. ChemBioEng Rev. 2023, 10, 1–28. [Google Scholar] [CrossRef]
- Verma, A.K.; Singh, T.N. Prediction of water quality from simple field parameters. Environ. Earth Sci. 2012, 69, 821–829. [Google Scholar] [CrossRef]
- Gonzalez-Aguilar, A.M.; Cabrera-Madera, V.P.; Vera-Rozo, J.R.; Riesco-Ávila, J.M. Effects of heating rate and temperature on the thermal pyrolysis of expanded polystyrene post-industrial waste. Polymers 2022, 14, 4957. [Google Scholar] [CrossRef]
- Demir, P. Thermal degradation kinetics, mechanism, thermodynamics, shape memory properties and artificial neural network application study of polycaprolactone (PCL)/polyvinyl chloride (PVC) blends. Polym. Bull. 2022. [Google Scholar] [CrossRef]
- Ai, Z.; Zhang, W.; Yang, L.; Chen, H.; Xu, Z.; Leng, L.; Li, H. Investigation and prediction of co-pyrolysis between oily sludge and high-density polyethylene via in-situ DRIFTS, TGA, and artificial neural network. J. Anal. Appl. Pyrolysis 2022, 166, 105610. [Google Scholar] [CrossRef]
- Balsora, H.K.; Kartik, S.; Dua, V.; Joshi, J.B.; Kataria, G.; Sharma, A.; Chakinala, A.G. Machine learning approach for the prediction of biomass pyrolysis kinetics from preliminary analysis. J. Environ. Chem. Eng. 2022, 10, 108025. [Google Scholar] [CrossRef]
- Jacob, G.A.; Prabhakaran, S.P.S.; Swaminathan, G.; Joseyphus, R.J. Thermal kinetic analysis of mustard biomass with equiatomic iron–nickel catalyst and its predictive modeling. Chemosphere 2022, 286, 131901. [Google Scholar] [CrossRef]
- Kartal, F.; Özveren, U. Prediction of activation energy for combustion and pyrolysis by means of machine learning. Therm. Sci. Eng. Prog. 2022, 33, 101346. [Google Scholar] [CrossRef]
- Khodaparasti, M.S.; Shirazvatan, M.R.; Tavakoli, O.; Khodadadi, A.A. Co-pyrolysis of municipal sewage sludge and microalgae Chlorella Vulgaris: Products’ optimization; thermo-kinetic study, and ANN modeling. Energy Convers. Manag. 2022, 254, 115258. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Chen, S.; Xu, K.; Fan, B.; Yang, D.; Geng, L.; Qiao, H. Investigation on the co-pyrolysis of agricultural waste and high-density polyethylene using TG-FTIR and artificial neural network modelling. Process Saf. Environ. Prot. 2022, 160, 341–353. [Google Scholar] [CrossRef]
- Nawaz, A.; Kumar, P. Pyrolysis behavior of low value biomass (Sesbania bispinosa) to elucidate its bioenergy potential: Kinetic, thermodynamic and prediction modelling using artificial neural network. Renew. Energy 2022, 200, 257–270. [Google Scholar] [CrossRef]
- Postawa, K.; Fałtynowicz, H.; Pstrowska, K.; Szczygieł, J.; Marek Kułażyński, M. Artificial neural networks to differentiate the composition and pyrolysis kinetics of fresh and long-stored maize. Bioresour. Technol. 2022, 364, 128137. [Google Scholar] [CrossRef]
- Al-Yaari, M.; Dubdub, I. Pyrolytic behavior of polyvinyl chloride: Kinetics, mechanisms, thermodynamics, and artificial neural network application. Polymers 2021, 13, 4359. [Google Scholar] [CrossRef]
- Dubdub, I. Kinetics study of polypropylene pyrolysis by non-isothermal thermogravimetric analysis. Materials 2023, 16, 584. [Google Scholar] [CrossRef]
- Quantrille, T.E.; Liu, Y.A. Artificial Intelligence in Chemical Engineering; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Halali, M.A.; Azari, V.; Arabloo, M.; Mohammadi, A.H.; Bahadori, A. Application of a radial basis function neural network to estimate pressure gradient in water–oil pipelines. J. Taiwan Inst. Chem. Eng. 2016, 58, 189–202. [Google Scholar] [CrossRef]
- Govindan, B.; Jakka, S.C.B.; Radhakrishnan, T.K.; Tiwari, A.K.; Sudhakar, T.M.; Shanmugavelu, P.; Kalburgi, A.K.; Sanyal, A.; Sarkar, S. Investigation on kinetic parameters of combustion and oxy-combustion of calcined pet coke employing thermogravimetric analysis coupled to artificial neural network modeling. Energy Fuels 2018, 32, 3995–4007. [Google Scholar] [CrossRef]
- Bar, N.; Bandyopadhyay, T.K.; Biswas, M.N.; Das, S.K. Prediction of pressure drop using artificial neural network for non-Newtonian liquid flow through piping components. J. Pet. Sci. Eng. 2010, 71, 187–194. [Google Scholar] [CrossRef]
- Al-Wahaibi, T.; Mjalli, F.S. Prediction of horizontal oil-water flow pressure gradient using artificial intelligence techniques. Chem. Eng. Commun. 2014, 201, 209–224. [Google Scholar] [CrossRef]
- Osman, E.A.; Aggour, M.A. Artificial neural network model for accurate prediction of pressure drop in horizontal and near-horizontal-multiphase flow. Pet. Sci. Technol. 2002, 20, 1–15. [Google Scholar] [CrossRef]
- Qinghua, W.; Honglan, Z.; Wei, L.; Junzheng, Y.; Xiaohong, W.; Yan, W. Experimental study of horizontal gas-liquid two-phase flow in two medium-diameter pipes and prediction of pressure drop through BP neural networks. Int. J. Fluid Mach. Syst. 2018, 11, 255–264. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox TM User’s Guide; MathWorks: Natick, MA, USA, 2018. [Google Scholar]
- Alkasseh, J.M.A.; Adlan, M.N.; Abustan, I.; Aziz, H.A.; Hanif, A.B. Applying minimum night flow to estimate water loss using statistical modeling: A case study in Kinta Valley, Malaysia. Water Resour. Manag. 2013, 27, 1439–1455. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Akbari, M.; Tahani, M.; Farhani, F. Sensitivity analysis of the artificial neural network outputs in friction stir lap joining of aluminum to brass. Adv. Mater. Sci. Eng. 2013, 1–7. [Google Scholar] [CrossRef]
- Dubdub, I.; Rushd, S.; Al-Yaari, M.; Gadri, E. Application of ANN to model the friction losses in lubricated pipe flow of non-conventional oils. Chem. Eng. Commun. 2020, 209, 47–61. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of mixed plastic waste: I. kinetic study. Materials 2020, 13, 4912. [Google Scholar] [CrossRef]
- Johnson, V.E. Revised standards for statistical evidence. Proc. Natl. Acad. Sci. USA 2013, 110, 19313–19317. [Google Scholar] [CrossRef]
- Krzywinski, M.; Altman, N. Points of significance: Significance, P values and t-tests. Nat. Methods 2013, 10, 1041–1042. [Google Scholar] [CrossRef]
- Sham, P.C.; Purcell, S.M. Statistical power and significance testing in large-scale genetic studies. Nat. Rev. Genet. 2014, 15, 335–346. [Google Scholar] [CrossRef]
- Kempel, F.; Schartel, B.; Linteris, G.T.; Stanislav, I.; Stoliarov, R.E.; Lyon, R.N.; Walters, A.H. Prediction of the mass loss rate of polymer materials: Impact of residue formation. Combust. Flame 2012, 159, 2974–2984. [Google Scholar] [CrossRef]
- Stoliarov, S.I.; Walters, R.N. Determination of the heats of gasification of polymers using differential scanning calorimetry. Polym. Degrad. Stab. 2008, 93, 422–427. [Google Scholar] [CrossRef]




| Parameters | Number |
|---|---|
| Number of inputs | 2 (heating rate K min−1, temperature K) |
| Number of outputs | 1 (weight left %) |
| Number of hidden layers | 2 |
| Network | 2-10-10-1 |
| Transfer functions (hidden layers) | Logsig–Tansig |
| Transfer function (output layer) | Linear |
| Validation checks | 50 |
| Learning algorithms | TRAINLM |
| Performance function | MSE |
| Data division function | Dividerand |
| Data division and number (training–validation–testing) | 70%-15%-15% |
| 657-141-141 |
| Set | Statistical Parameters | |||
|---|---|---|---|---|
| R | RMSE | MAE | MBE | |
| Training | 1.0 | 0.107977 | 0.052428 | −0.001664 |
| Validation | 1.0 | 0.093722 | 0.050369 | 0.000012 |
| Test | 1.0 | 0.129828 | 0.064604 | −0.005936 |
| All | 1.0 | 0.109579 | 0.053947 | −0.002054 |
| No. | Input Data | Output Data | |
|---|---|---|---|
| Heating Rate (K/min) | Temperature (K) | Mass % | |
| 1 | 5 | 605.553 | 90.67025 |
| 2 | 5 | 668.192 | 41.66792 |
| 3 | 5 | 657.612 | 56.18587 |
| 4 | 5 | 702.357 | 0.05542216 |
| 5 | 10 | 651.17 | 81.05005 |
| 6 | 10 | 689.612 | 35.71684 |
| 7 | 10 | 670.339 | 64.48985 |
| 8 | 10 | 700.2 | 13.88899 |
| 9 | 20 | 698.027 | 71.65227 |
| 10 | 20 | 725.982 | 23.28277 |
| 11 | 20 | 691.698 | 77.98775 |
| 12 | 20 | 730.234 | 13.58366 |
| 13 | 30 | 717.712 | 60.16715 |
| 14 | 30 | 738.684 | 10.87517 |
| 15 | 30 | 693.819 | 85.1306 |
| 16 | 30 | 730.234 | 33.13463 |
| 17 | 40 | 725.982 | 50.282 |
| 18 | 40 | 742.871 | 5.571741 |
| 19 | 40 | 670.339 | 95.11706 |
| 20 | 40 | 728.123 | 45.28695 |
| Set | Statistical Parameters | |||
|---|---|---|---|---|
| R | RMSE | MAE | MBE | |
| simulated | 0.99995 | 0.294390 | 0.230408 | 0.043524 |
| Weight-Left % (Output Parameter) | |
|---|---|
| Temperature (1st input parameter) | −0.79722 |
| Heating rate (2nd input parameter) | 0.04101 |
| Input Parameter | Temperature | Heating Rate |
|---|---|---|
| p-value | <0.05 | >0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubdub, I. Artificial Neural Network Study on the Pyrolysis of Polypropylene with a Sensitivity Analysis. Polymers 2023, 15, 494. https://doi.org/10.3390/polym15030494
Dubdub I. Artificial Neural Network Study on the Pyrolysis of Polypropylene with a Sensitivity Analysis. Polymers. 2023; 15(3):494. https://doi.org/10.3390/polym15030494
Chicago/Turabian StyleDubdub, Ibrahim. 2023. "Artificial Neural Network Study on the Pyrolysis of Polypropylene with a Sensitivity Analysis" Polymers 15, no. 3: 494. https://doi.org/10.3390/polym15030494
APA StyleDubdub, I. (2023). Artificial Neural Network Study on the Pyrolysis of Polypropylene with a Sensitivity Analysis. Polymers, 15(3), 494. https://doi.org/10.3390/polym15030494






