Simulation Analysis of Equibiaxial Tension Tests for Rubber-like Materials
Abstract
:1. Introduction
2. Constitutive Model of Hyperelastic Membrane Based on Equibiaxial Tension
2.1. Mooney–Rivlin Model
2.2. Yeoh Model
2.3. Ogden Model
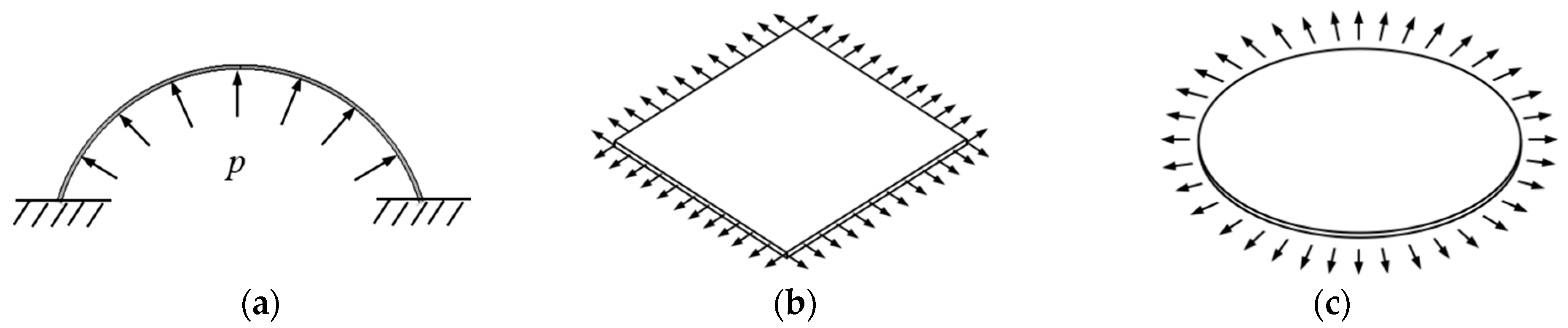
2.4. Mechanical Behavior Based on Equibiaxial Tension
3. Equibiaxial Tension Tests and Their Simulations for Hyperelastic Membrane
3.1. Inflation Tension
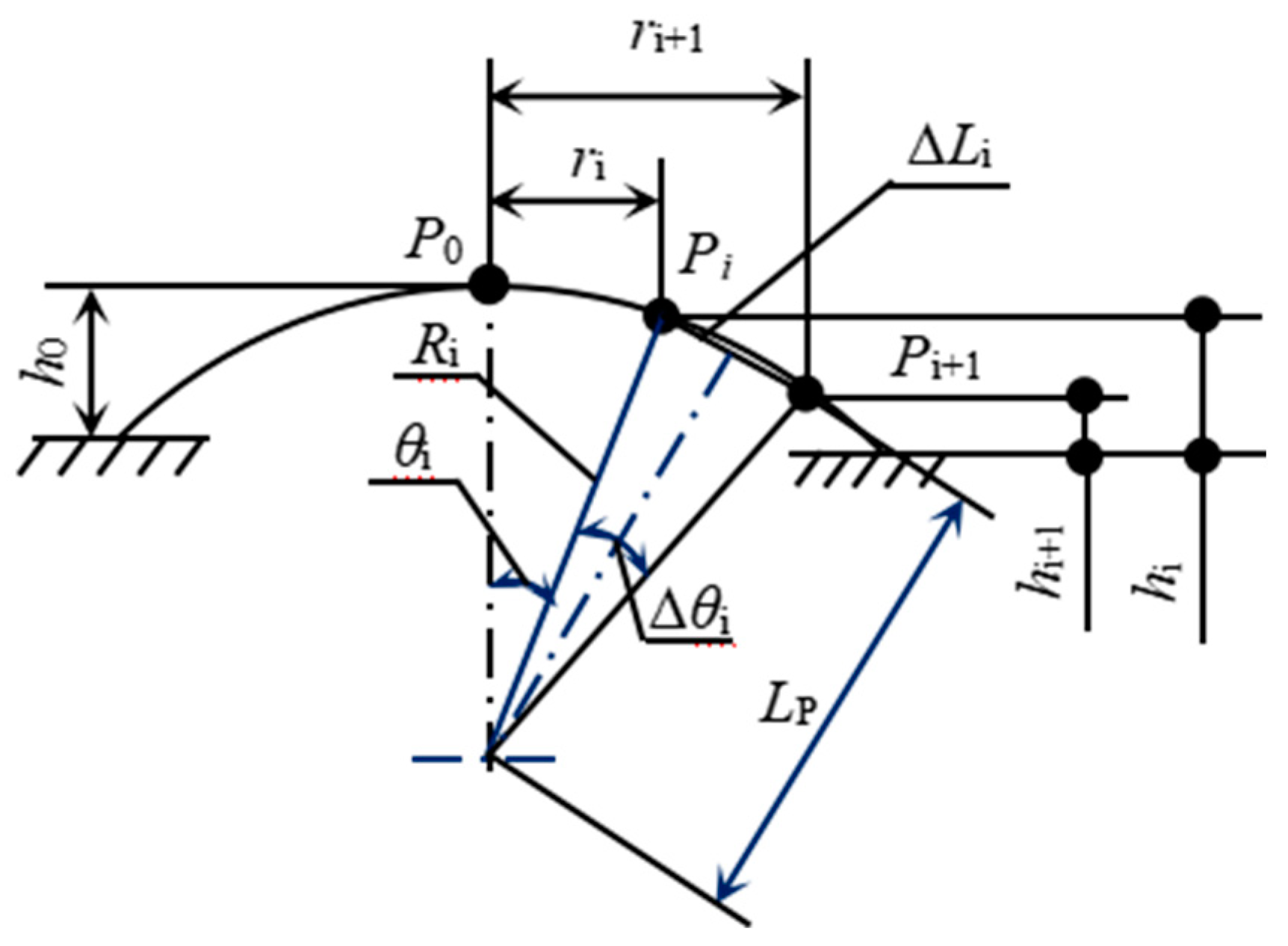
3.1.1. Deformation of Inflation Tension
3.1.2. Stress of Inflation Tension
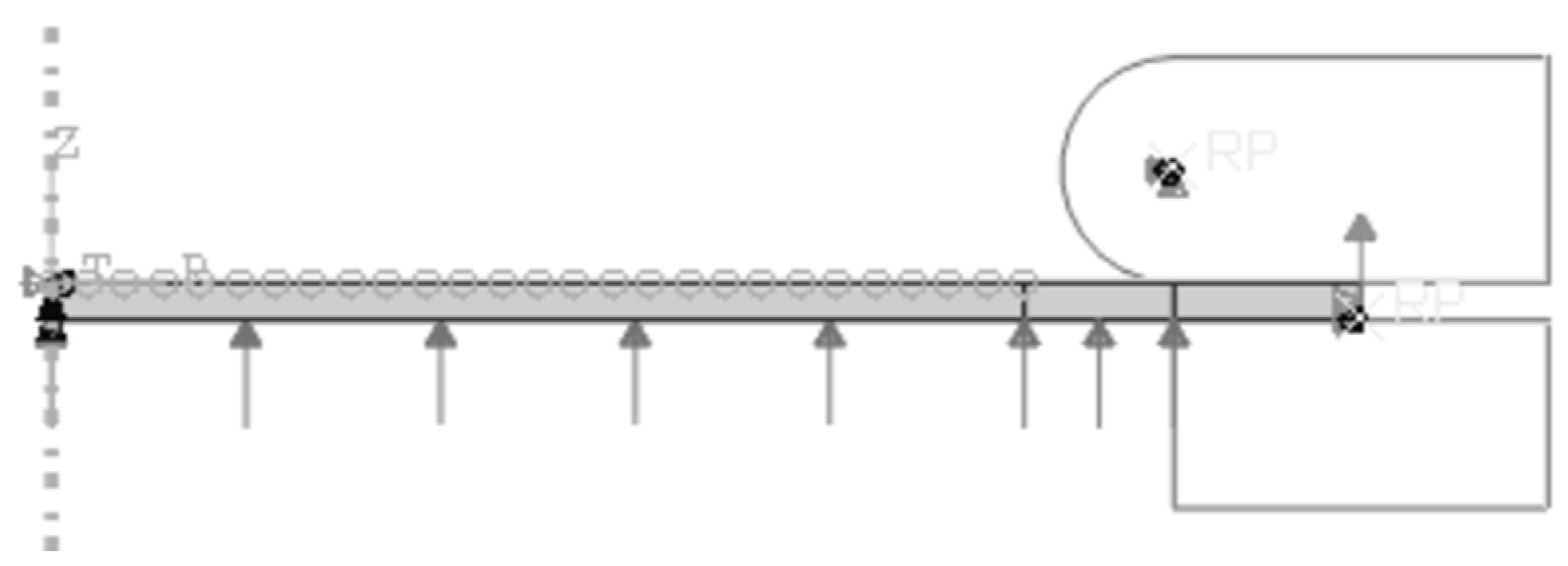
3.1.3. Simulation of Inflation Tension
3.2. Equibiaxial Planar Tension Test
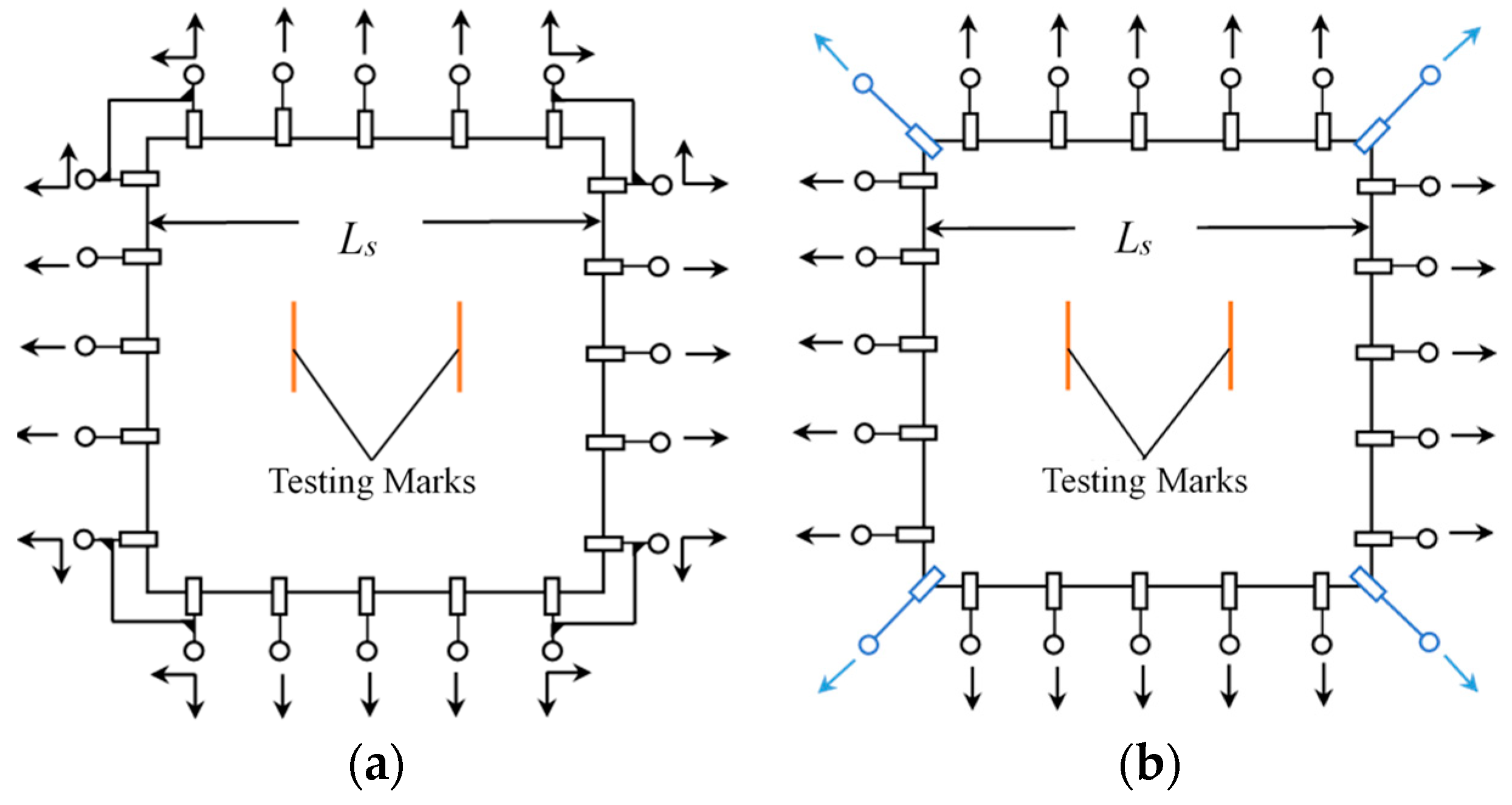
3.2.1. Equibiaxial Planar Tension Method
3.2.2. Simulation of Equibiaxial Planar Tension
3.3. Radial Tension Test
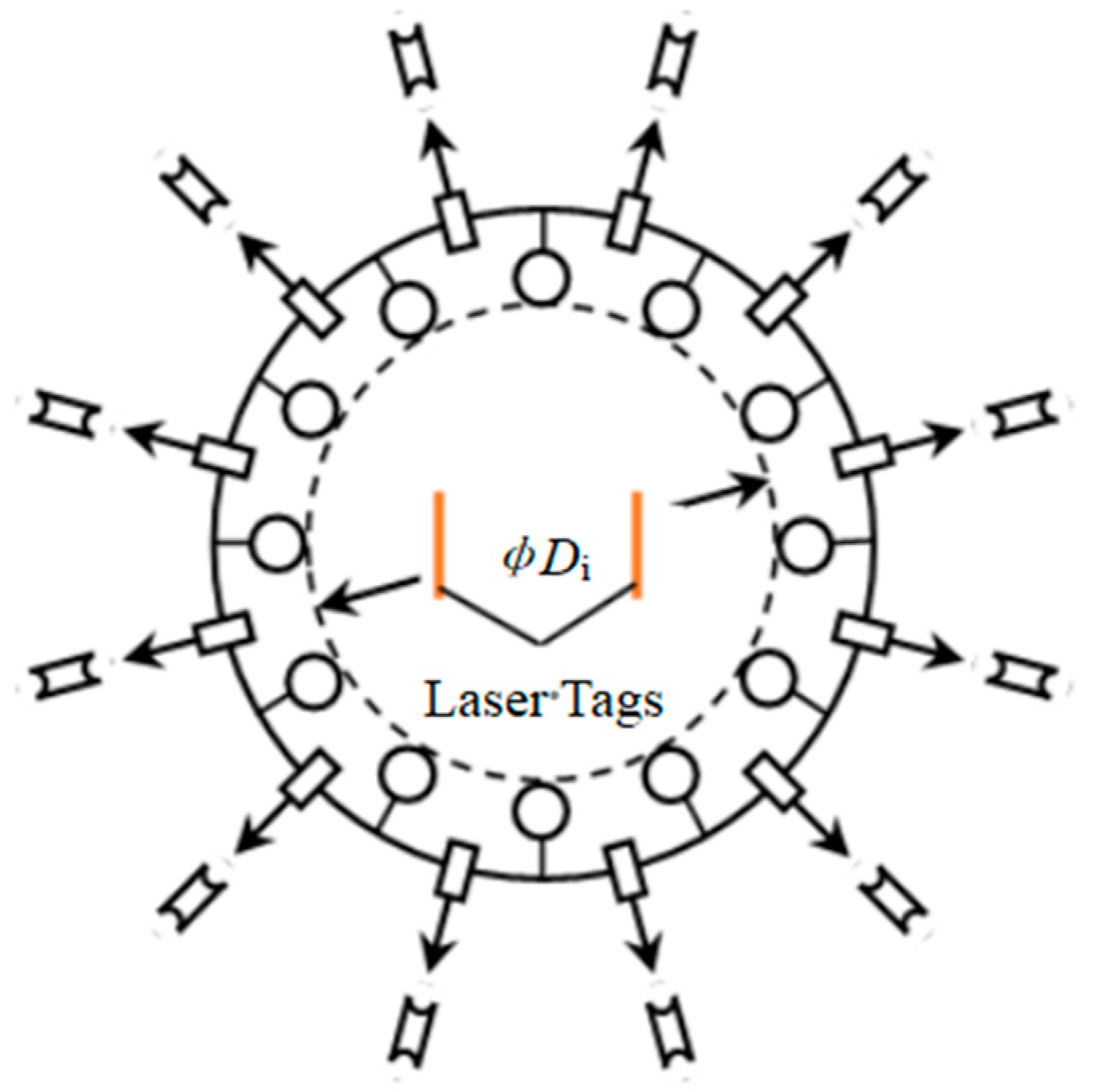
3.3.1. Radial Tension Method
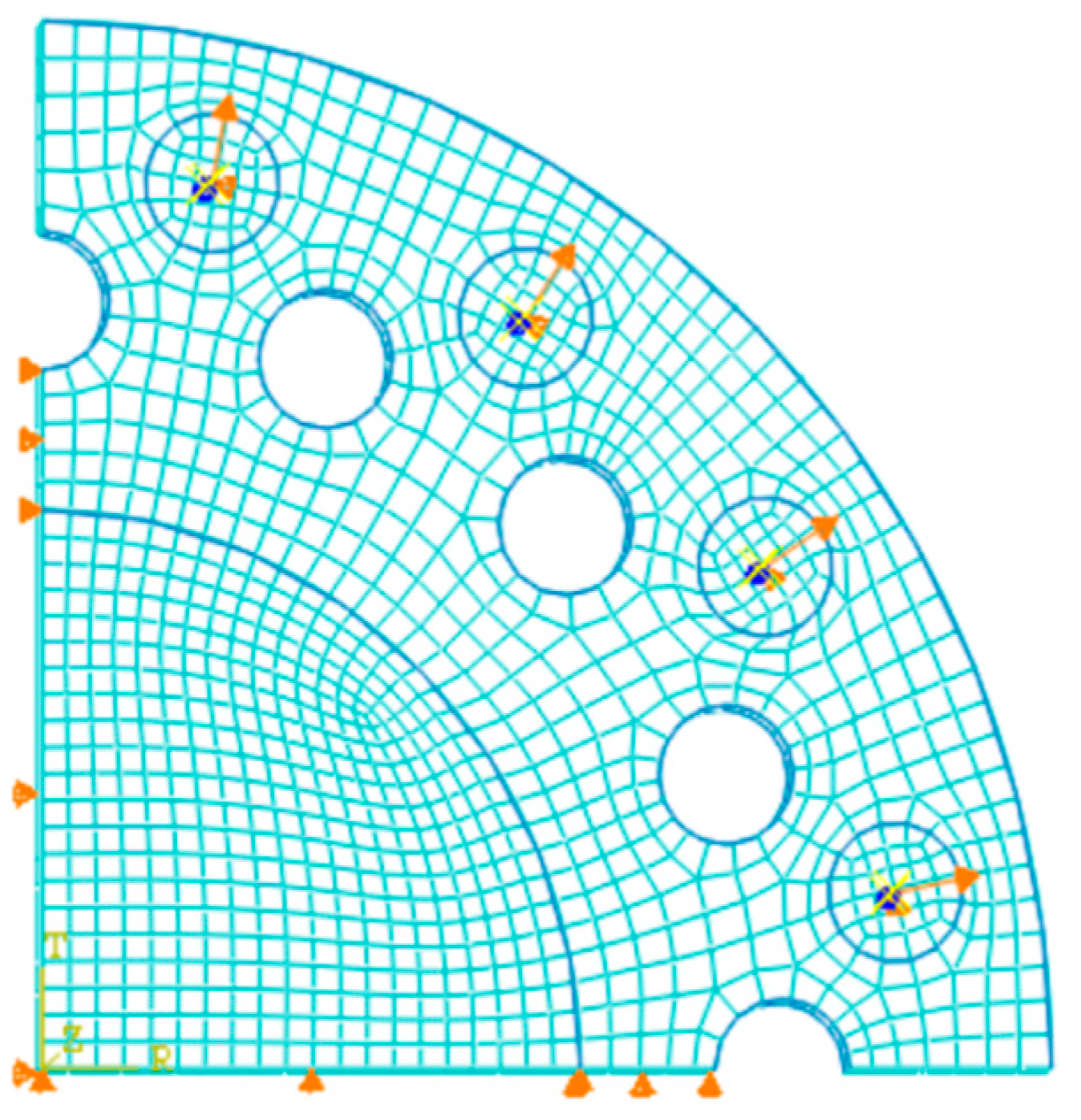
3.3.2. Radial Tension Simulation
4. Results and Discussion
4.1. Equibiaxial Inflation Tension
4.1.1. Deformation Profile
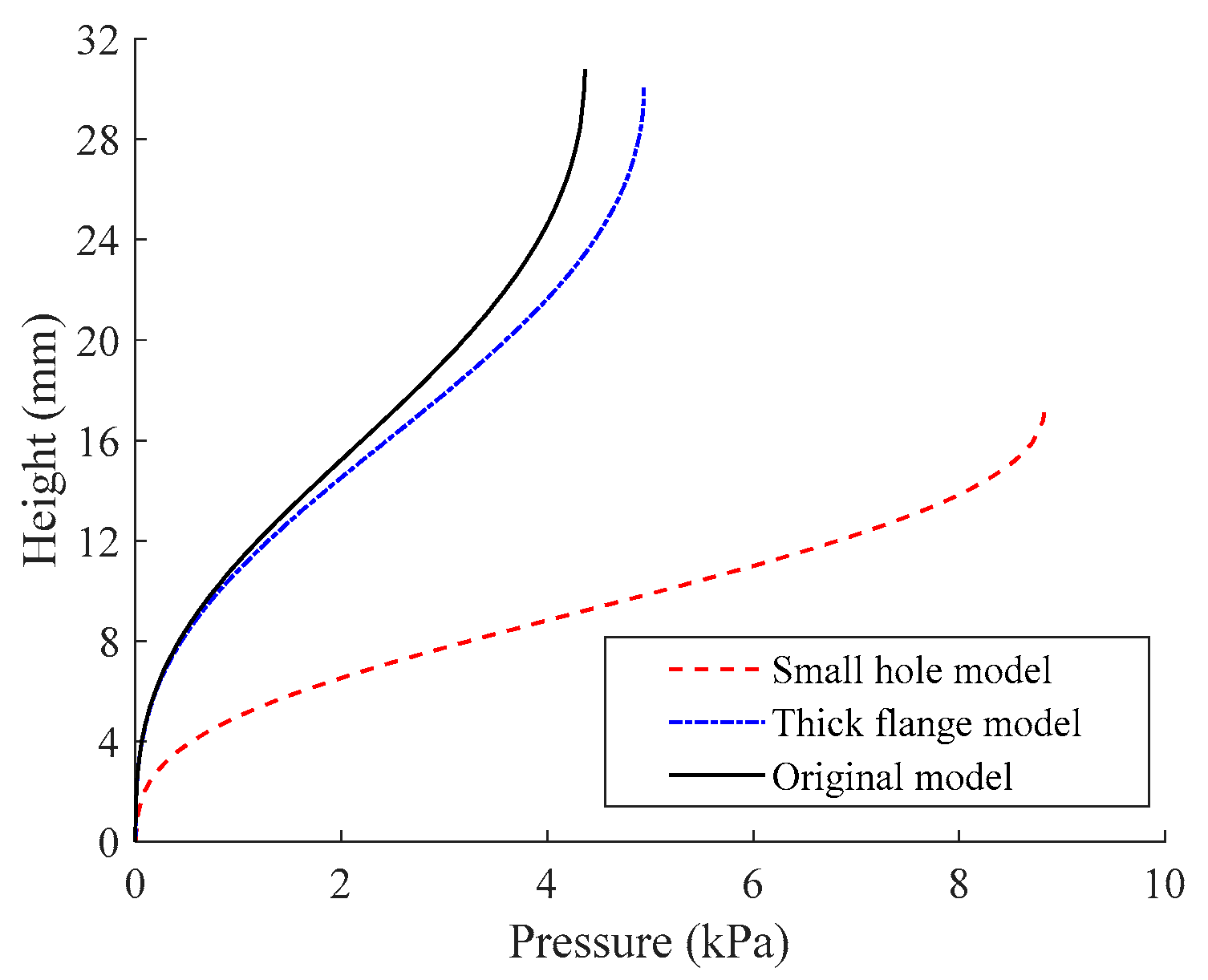
4.1.2. Influence of Structure Dimensions
- Original model: The test apparatus model has the same dimensions as the original structure.
- Thick flange model: According to the original model, the thickness of the upper flange is doubled.
- Small hole model: Based on the original model, the inflation hole of the structure is halved.
4.1.3. Deformation Range during Inflation Tension Simulation
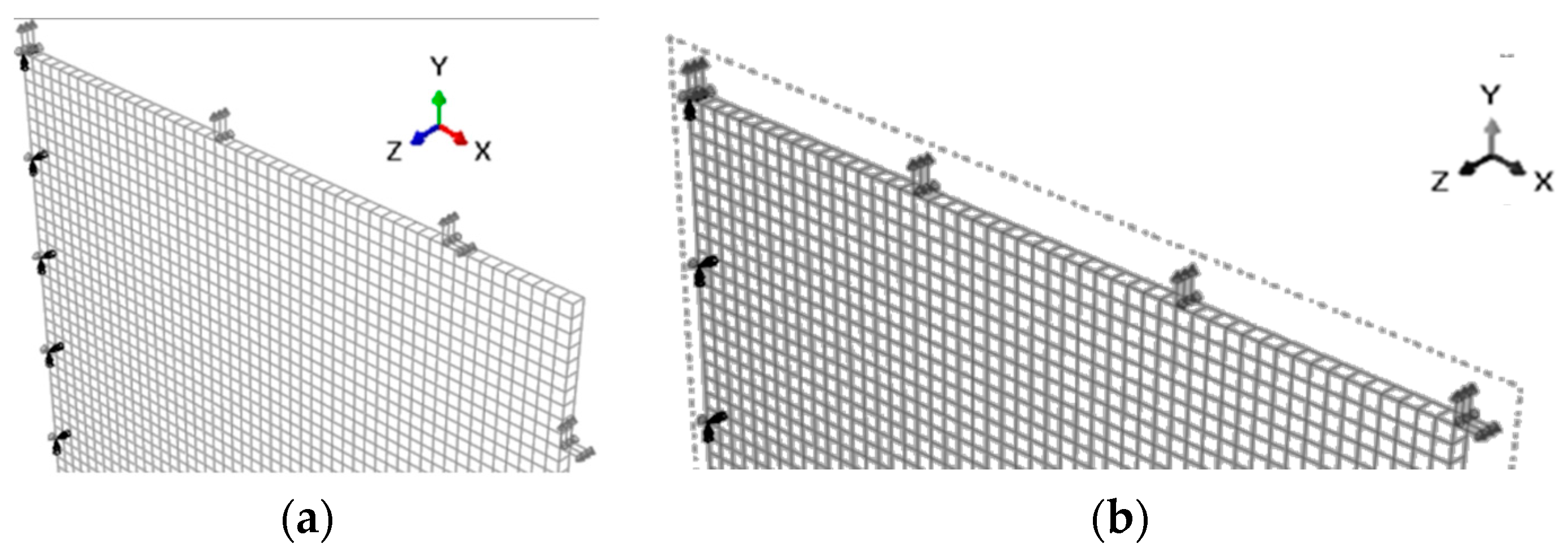
4.2. Equibiaxial Planar Tension Simulation
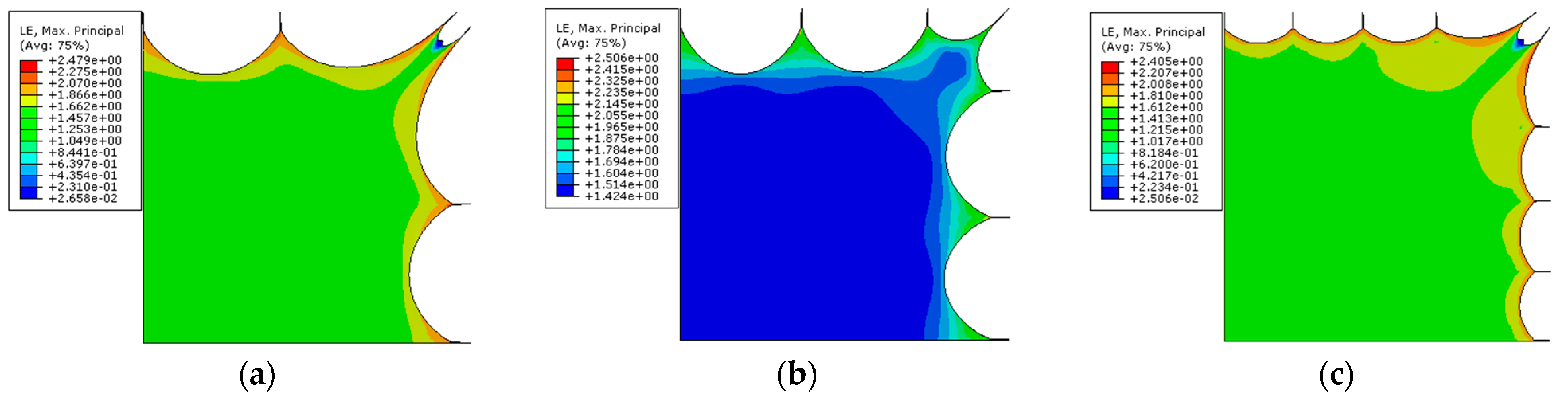
4.2.1. Strain Distribution
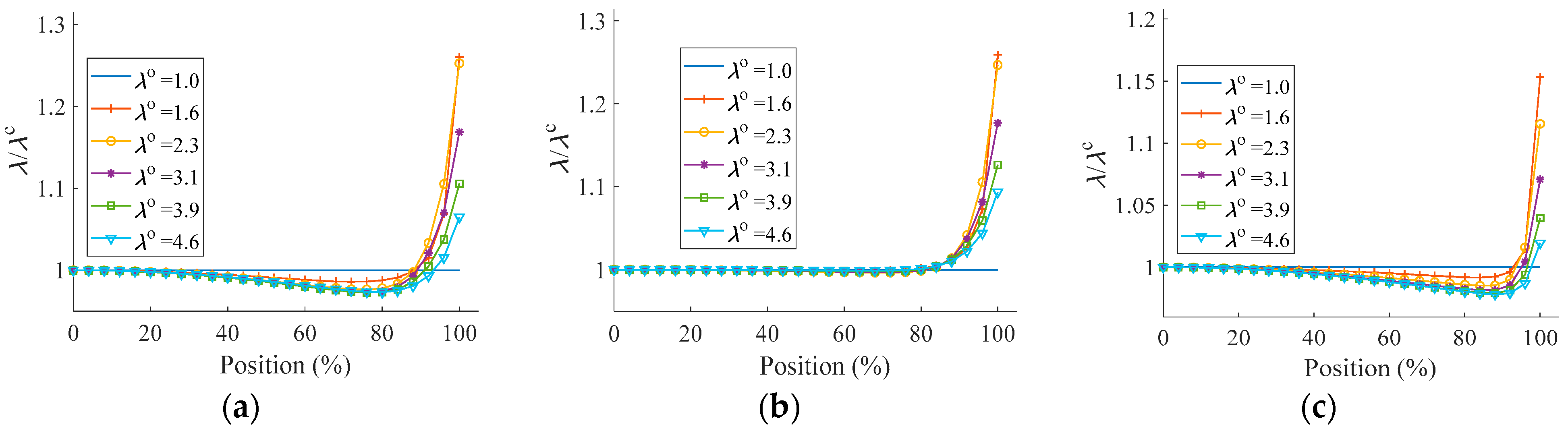
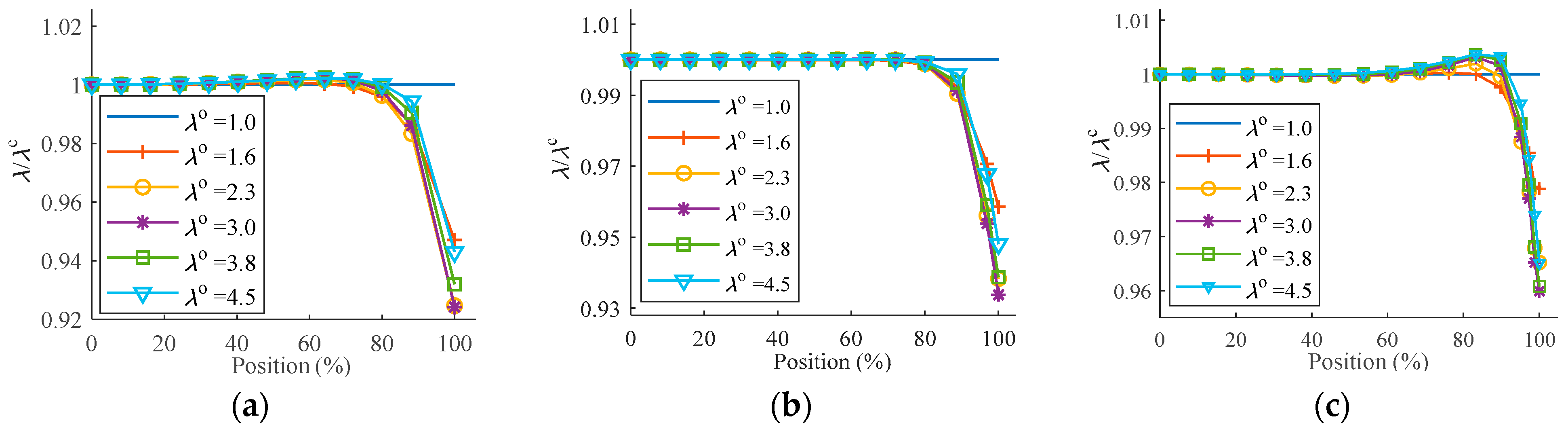
4.2.2. Deformation along Symmetry Axis
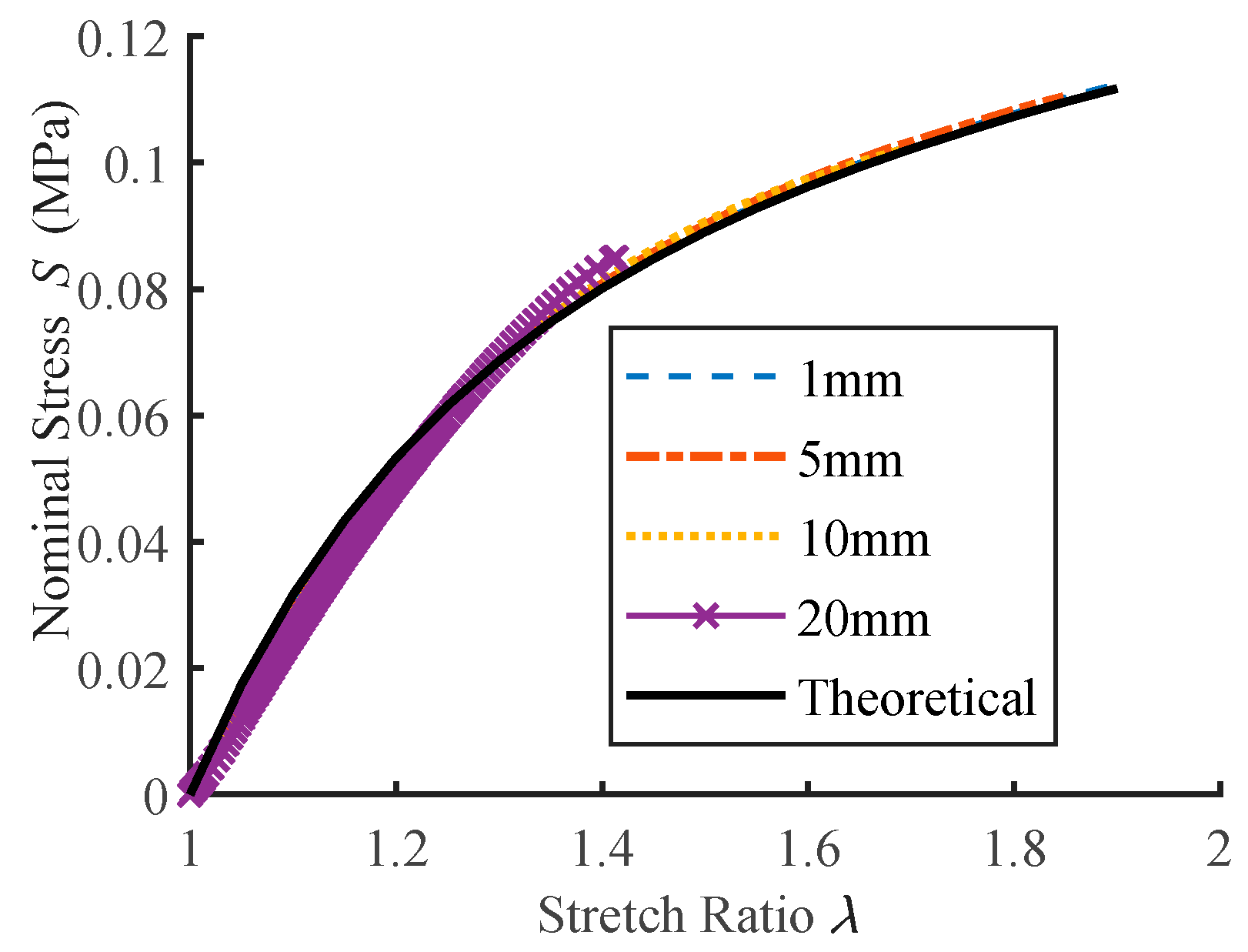
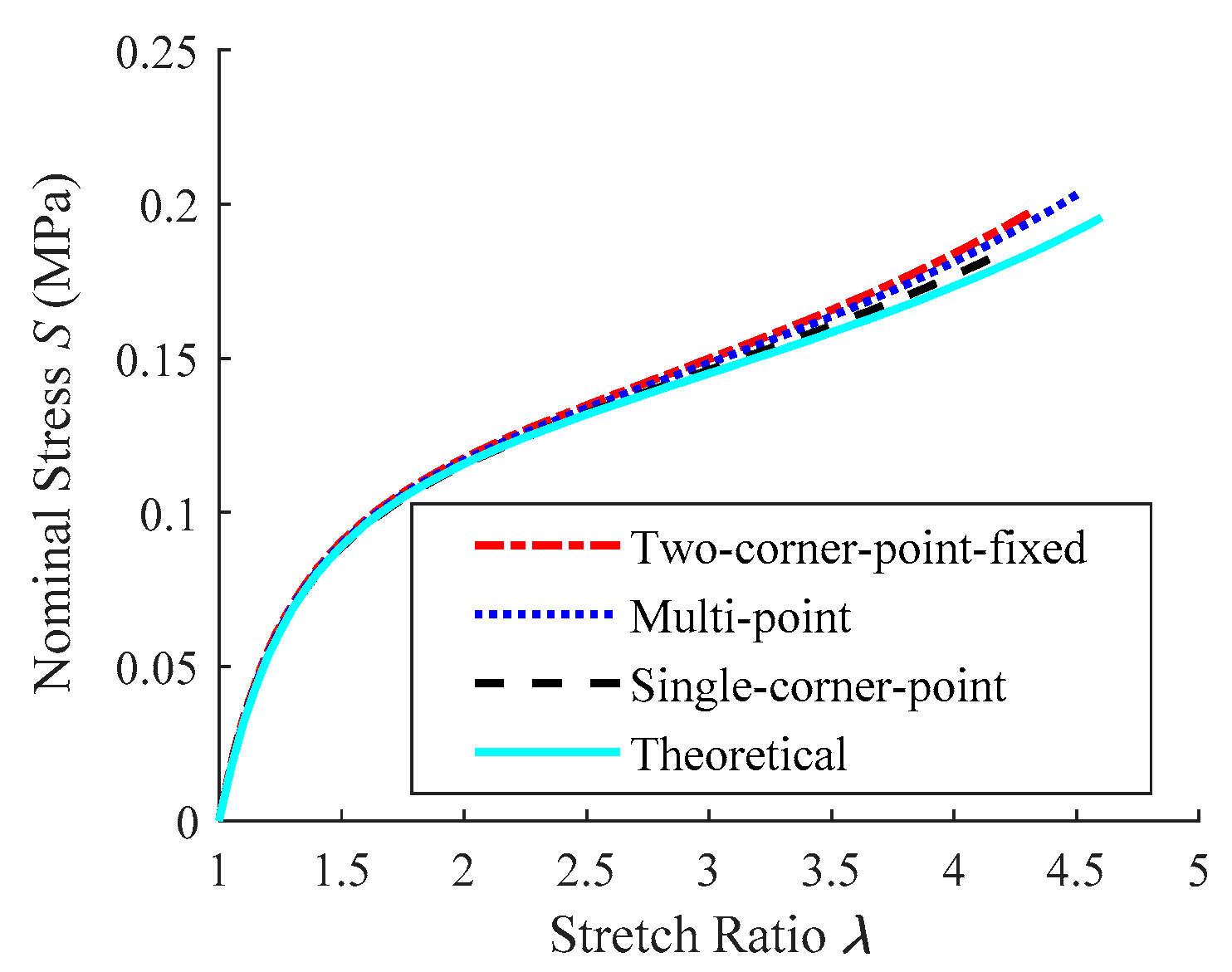
4.2.3. The Relationship between Stress and Stretch Ratio in Equibiaxial Planar Tension
4.3. Radial Tension
4.3.1. Deformation in Radial Tension
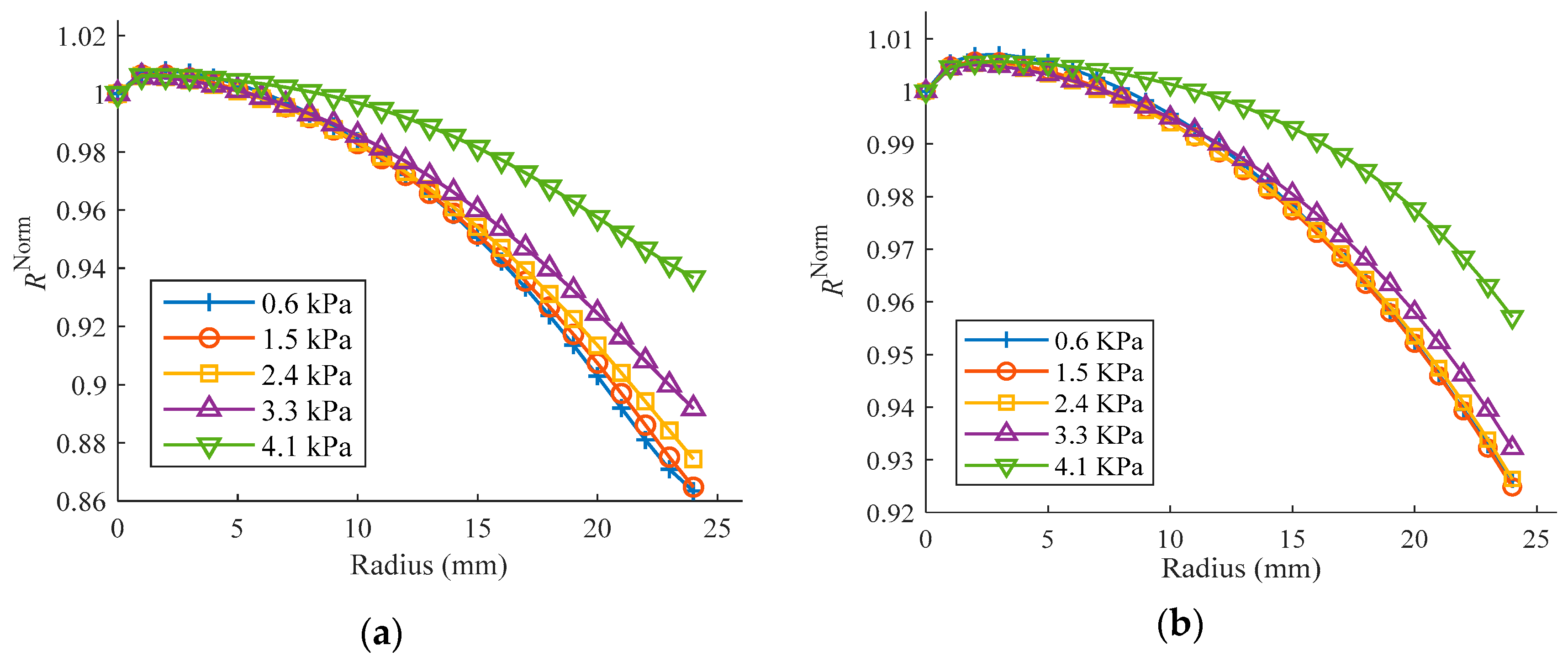
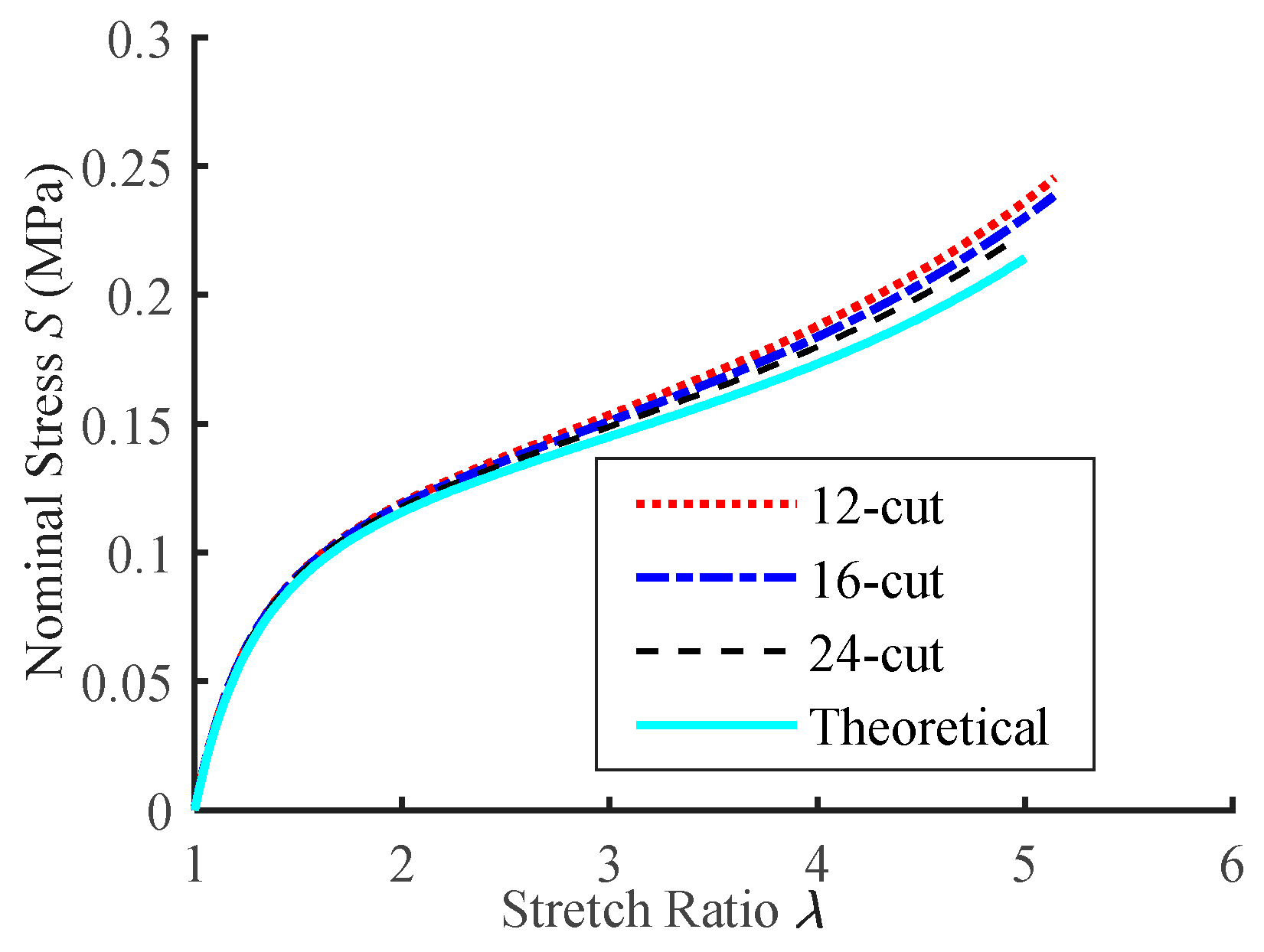
4.3.2. The Relationship between Stress and Stretch Ratio in Radial Tension
4.3.3. Influence of the Punched Hole Size
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mansouri, M.R.; Darijani, H.; Baghani, M. On the correlation of FEM and experiments for hyperelastic elastomers. Exp. Mech. 2017, 57, 195–206. [Google Scholar] [CrossRef]
- Keerthiwansa, R.; Javořík, J.; Kledrowetz, J.; Nekoksa, P. Hyperelastic material characterization: A method of reducing the error of using only uniaxial data for fitting the Mooney-Rivlin curve. Mater. Sci. Forum 2018, 919, 292–298. [Google Scholar] [CrossRef]
- Luo, H.; Zhu, Y.; Zhao, H.; Ma, L.; Zhang, J. Equibiaxial Planar Tension Test Method and the Simulation Analysis for Hyperelastic EAP Membrane. Adv. Polym. Technol. 2023, 2023, 7343992. [Google Scholar] [CrossRef]
- Park, J.; Kim, Y.; Yoon, J.W.; So, H.; Ko, S. Finite element modeling and durability evaluation for rubber pad forming process. IOP Conf. Ser. Mater. Sci. Eng. 2019, 651, 012096. [Google Scholar] [CrossRef]
- Treloar, L.R.G. Strains in an inflated rubber sheet and the mechanism of bursting. Trans. Inst. Rubber Ind. 1944, 19, 201–212. [Google Scholar]
- Rivlin, R.S.; Saunders, D.W. Large elastic deformations of isotropic materials. VII. Experiments on the deformation of rubber. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1951, 243, 251–288. [Google Scholar]
- Adkins, J.E.; Rivlin, R.S. Large elastic deformations of isotropic materials. IX. The deformation of thin shells. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1952, 244, 505–531. [Google Scholar]
- Hart-Smith, L.J.; Crisp, J.D.C. Large elastic deformations of thin rubber membranes. Int. J. Eng. Sci. 1967, 5, 1–24. [Google Scholar] [CrossRef]
- Fox, J.W. Electromechanical Characterization of the Static and Dynamic Response of Dielectric Elastomer Membranes. Master’s Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2007. [Google Scholar]
- Sasso, M.; Palmieri, G.; Chiappini, G.; Amodio, D. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods. Polym. Test. 2008, 27, 995–1004. [Google Scholar] [CrossRef]
- Lanir, Y.; Fung, Y.C. Two-dimensional mechanical properties of rabbit skin—I. Experimental system. J. Biomech. 1974, 7, 29–34. [Google Scholar] [CrossRef]
- Zemánek, M.; Burša, J.; Děták, M. Biaxial tension tests with soft tissues of arterial wall. Eng. Mech. 2009, 16, 3–11. [Google Scholar]
- Genovese, K.; Lamberti, L.; Pappalettere, C. Mechanical characterization of hyperelastic materials with fringe projection and optimization techniques. Opt. Lasers Eng. 2006, 44, 423–442. [Google Scholar] [CrossRef]
- Chevalier, L.; Marco, Y. Tools for multiaxial validation of behavior laws chosen for modeling hyperelasticity of rubber-like materials. Polym. Eng. Sci. 2010, 42, 280–298. [Google Scholar] [CrossRef]
- Luo, H.; Wang, H.; You, Y. Experimental methods of equiaxial tension of hyperelastic membrane and corresponding simulations. J. South China Univ. Technol. 2011, 39, 56–61. [Google Scholar]
- Blatz, P.J.; Paul, J. Application of finite elastic theory to the deformation of rubbery materials. J. Rheol. 1962, 6, 223–252. [Google Scholar] [CrossRef]
- Obata, Y.; Kawabata, S.; Kawai, H. Mechanical properties of natural rubber vulcanizates in finite deformation. J. Polym. Sci. Part A-2 1970, 8, 903–919. [Google Scholar] [CrossRef]
- Jacobs, N.T.; Cortes, D.H.; Vresilovic, E.J.; Elliott, D.M. Biaxial tension of fibrous tissue: Using finite element methods to address experimental challenges arising from boundary conditions and anisotropy. J. Biomech. Eng. 2013, 135, 021004. [Google Scholar] [CrossRef]
- Miller, K. Testing elastomer for hyperelastic material models in finite element analysis. In Axel Products Testing and Analysis Report; Axel Products Inc.: Ann Arbor, MI, USA, 2000. [Google Scholar]
- Li, Y.; Wu, J.; Sato, H. Agile and resilient insect-scale robot. Soft Robot. 2018, 5, 365–374. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, S.; Ren, Z.; Chirarattananon, P. Collision resilient insect-scale soft-actuated aerial robots with high agility. IEEE Trans. Robot. 2021, 37, 1752–1764. [Google Scholar] [CrossRef]
- Zhu, Y.; Hua, C.; Su, X.; Geng, L.; Hu, Z.; Su, H. Investigation on flexible pressure sensor array and signal acquisition system. Trans. Chin. Soc. Agric. Mach. 2020, 51, 400–405. [Google Scholar]
- Son, S.; Goulbourne, N.C. Large strain analysis of a soft polymer electromechanical sensor coupled to an arterial segment. J. Intell. Mater. Syst. Struct. 2012, 23, 575–586. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, S.; Zhong, M.; Zhang, L.; Ning, N.; Tian, M. Optimizing energy harvesting performance of cone dielectric elastomer generator based on VHB elastomer. Nano Energy 2020, 71, 104606. [Google Scholar] [CrossRef]
- Carpi, F.; Rossi, D.D.; Kornbluh, R.; Pelrine, R.; Sommer-Larsen, P. Dielectric Elastomers as Electromechanical Transducers: Fundamentals, Materials, Devices, Models and Applications of an Emerging Electroactive Polymer Technology; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Boyce, M.C.; Arruda, E.M. Constitutive models of rubber elasticity: A review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhong, D.; Rudykh, S.; Zhou, H.; Qu, S.; Yang, W. A review of physically based and thermodynamically based constitutive models for soft materials. J. Appl. Mech. 2020, 87, 110801. [Google Scholar] [CrossRef]
- Raheem, H.M.; Al-Mukhtar, A.M. Experimental and analytical study of the hyperelastic behavior of the hydrogel under unconfined compression. Procedia Struct. Integr. 2020, 25, 3–7. [Google Scholar] [CrossRef]
- Raheem, H.M.; Al-Mukhtar, A.M. Experimental investigation of the effects of infusing a foam into hydrogels on the hyperelastic coefficients. Mater. Des. Process. Commun. 2020, 3, e180. [Google Scholar] [CrossRef]
- Maiti, A.; Small, W.; Lewicki, J.P.; Chinn, S.C.; Wilson, T.S.; Saab, A.P. Age-aware constitutive materials model for a 3D printed polymeric foam. Sci. Rep. 2019, 9, 15923. [Google Scholar] [CrossRef]
- Lou, W.; Xie, C.; Guan, X. Thermal-aging constitutive model for a silicone rubber foam under compression. Polym. Degrad. Stab. 2022, 198, 109873. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Thomas, A.G. Large elastic deformations of isotropic materials. VIII. Strain distribution around a hole in a sheet. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1951, 243, 289–298. [Google Scholar]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 2012, 63, 792–805. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity-on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. 1972, A326, 565–584. [Google Scholar] [CrossRef]
- Íñiguez-Macedo, S.; Lostado-Lorza, R.; Escribano-García, R.; Martínez-Calvo, M. Finite element model updating combined with multi-response optimization for hyper-elastic materials characterization. Materials 2019, 12, 1019. [Google Scholar] [CrossRef] [PubMed]





| The Second-Order Ogden Model (Abaqus Form) [9] | The First-Order Mooney–Rivlin Model a | ||
|---|---|---|---|
| μ1 (kPa) | 64.7 | C01 (kPa) | 21.56 |
| α1 | 1.39689 | ||
| μ2 (kPa) | 0.0457 | C10 (kPa) | 0.0815 |
| α2 | 5.8638 | ||
| Tension Method | Two-Corner-Point-Fixed Tension | Single-Corner-Point Tension | Multi-Point Tension |
|---|---|---|---|
| Stress error (%) | 6.2 | 2.1 | 4.6 |
| ηλ (%) | 93.9 | 91.4 | 98.1 |
| Specimen | 12-Cut | 16-Cut | 24-Cut |
|---|---|---|---|
| Stress error (%) | 8.48(8.59) | 6.05(8.46) | 3.83(4.65) |
| ηλ (%) | 101.52(98.03) | 101.12(99.55) | 96.72(100.04) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Zhu, Y.; Zhao, H.; Ma, L.; Zhang, J. Simulation Analysis of Equibiaxial Tension Tests for Rubber-like Materials. Polymers 2023, 15, 3561. https://doi.org/10.3390/polym15173561
Luo H, Zhu Y, Zhao H, Ma L, Zhang J. Simulation Analysis of Equibiaxial Tension Tests for Rubber-like Materials. Polymers. 2023; 15(17):3561. https://doi.org/10.3390/polym15173561
Chicago/Turabian StyleLuo, Huaan, Yinlong Zhu, Haifeng Zhao, Luqiang Ma, and Jingjing Zhang. 2023. "Simulation Analysis of Equibiaxial Tension Tests for Rubber-like Materials" Polymers 15, no. 17: 3561. https://doi.org/10.3390/polym15173561
APA StyleLuo, H., Zhu, Y., Zhao, H., Ma, L., & Zhang, J. (2023). Simulation Analysis of Equibiaxial Tension Tests for Rubber-like Materials. Polymers, 15(17), 3561. https://doi.org/10.3390/polym15173561







