Analysis of the Warpage Phenomenon of Micro-Sized Parts with Precision Injection Molding by Experiment, Numerical Simulation, and Grey Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental
2.1.1. Precision Injection Molding (PIM)
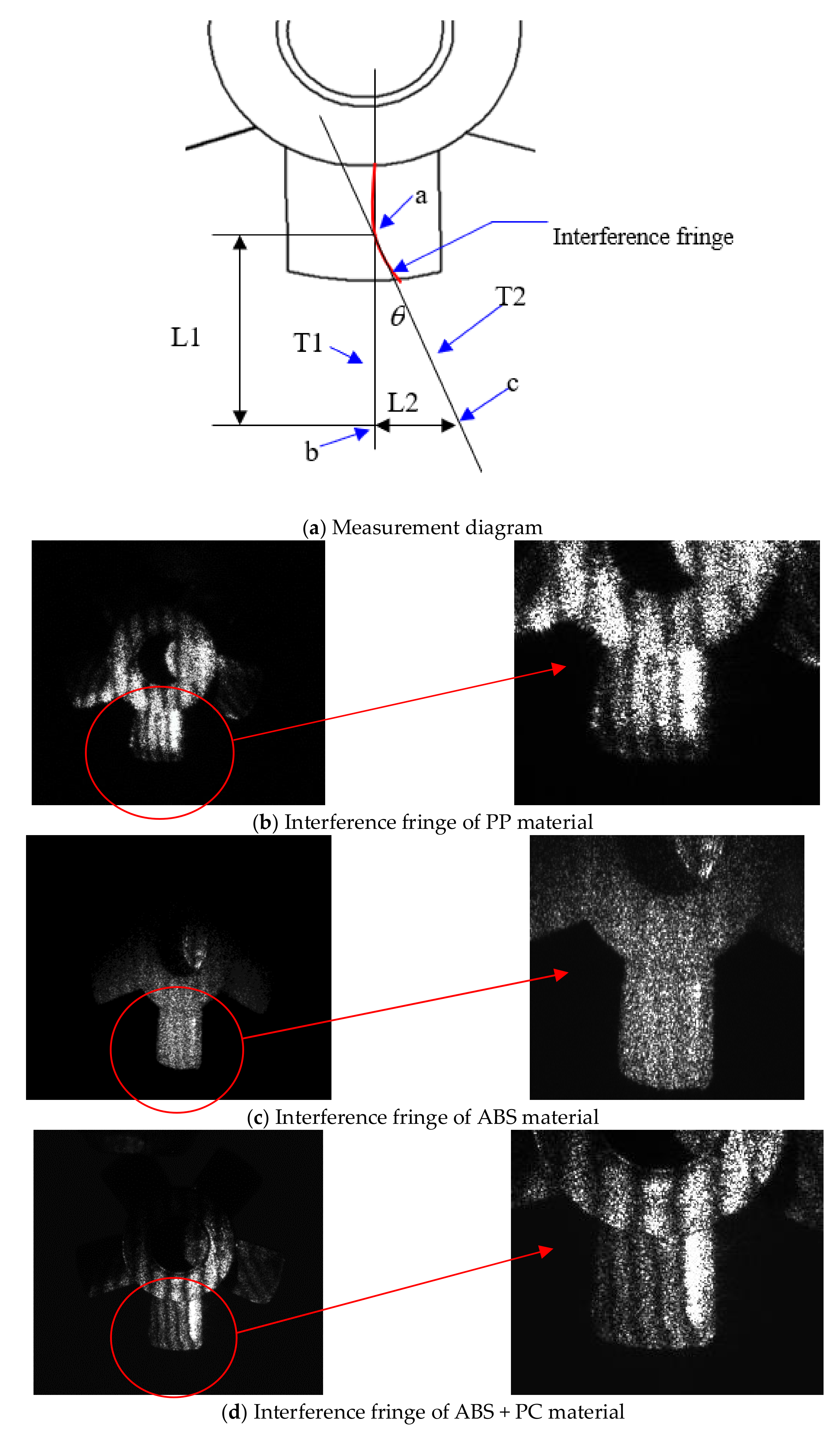
2.1.2. Measurement (Warpage)
2.2. Numerical Simulation
2.3. Grey Theory
2.3.1. Grey Relational Analysis of Optimal Processing Parameters
- (1)
- Grey relational space.
- (2)
- The effect of the measurement method.
- (a)
- Maximum: measurement of the upper-limit effect
- (b)
- Minimum: measurement of the lower-limit effect
- (c)
- Median: measurement of moderate effects-measurement of central effects
- (3)
- Grey correlation measurement.where and are the grey correlation coefficient and degree, respectively.
- (a)
- Locality when only is the reference sequence and the other is the comparison sequence.where and are reference sequence and a specific comparison sequence, respectively. ξ is the identification coefficient, and its value is between 0 and 1.
- (b)
- Integrity: when any is a reference sequence.is the absolute value.
- (4)
- Grey correlation.
2.3.2. Grey Decision Analysis of Suitable Material
- (1)
- Situation where is an event, and is a countermeasure.
- (2)
- The target is an index for evaluating the situation effect (countermeasure effect), and an evaluation scale by an analytical hierarchy (AHP) table is shown in Table 3.
- (3)
- Effect measurement for evaluating targets can be divided into three types.
- (a)
- Measurement of the benefit target (upper-limit effect measurement)where is the situation, and is the actual effect.
- (b)
- Measurement of the cost target (lower-limit effect measurement)
- (c)
- Measurement of a specific target (specific-center effect measurement)where is the actual effect.
- (4)
- For situation , under the corresponding M, , if there is one target (p = 1, 2, …, l), where , is called the comprehensive effect measurement, it is recorded as .
- (5)
- Let be the comprehensive effect measurement vector of event . If there are conditions, , that meet , it is called a satisfactory situation . n is also called a satisfactory strategy, , to deal with event . A satisfactory is the optimal situation.
- Values of five materials in the evaluation criteria were sampled.
- Events, countermeasures, situations, goals, and samples were identified.Event: The material of the micro-sized part for PIM was selected as an event.Countermeasure: Schemes A, B, C, D, and E represent the POM, ABS, PP, PA, and ABS + PC materials, respectively.Therefore, plan A (b1), B (b2), …, E (b5).Situation:S11 = (a1, b1), material selection (scheme A)S12 = (a1, b2), material selection (scheme B)S13 = (a1, b3), material selection (scheme C)S14 = (a1, b4), material selection (scheme D)S15 = (a1, b5), material selection (scheme E)
- Make effect measurements of effect samples.
- Decide.Finally, we determined which material was the best mold material.
3. Results and Discussion
3.1. Numerical Simulation (Also Compared to the Experiment on the Short Shot Situation)
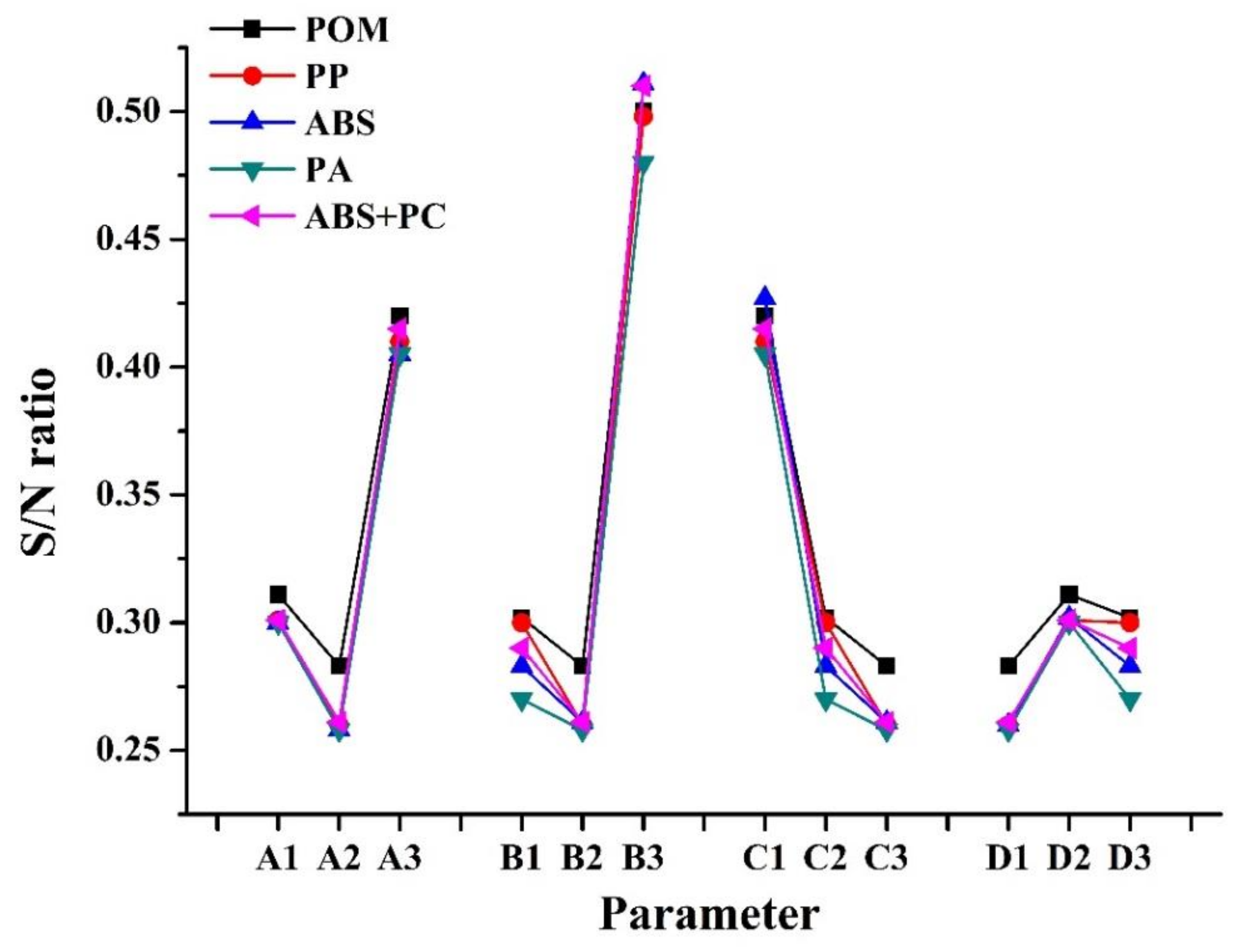
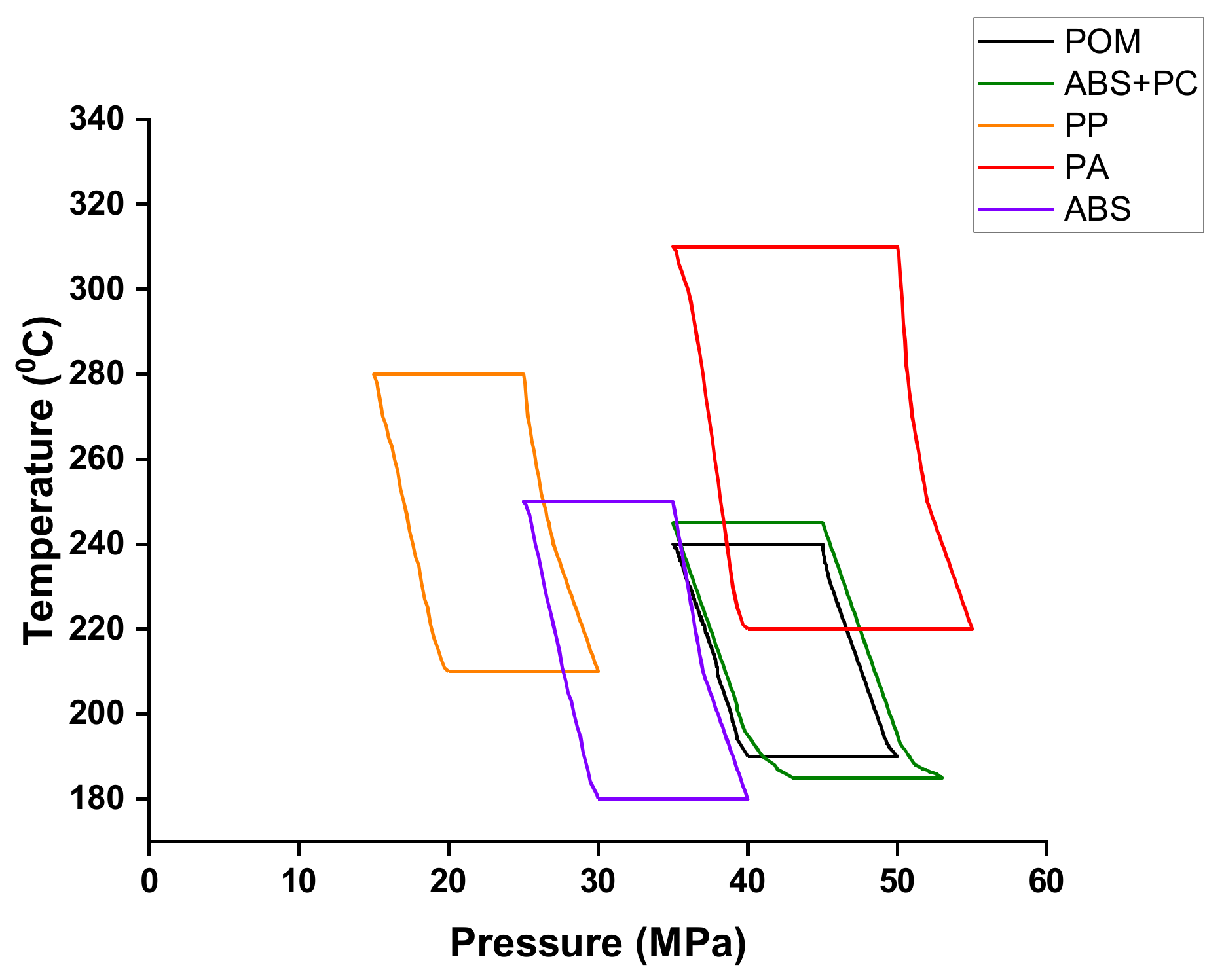
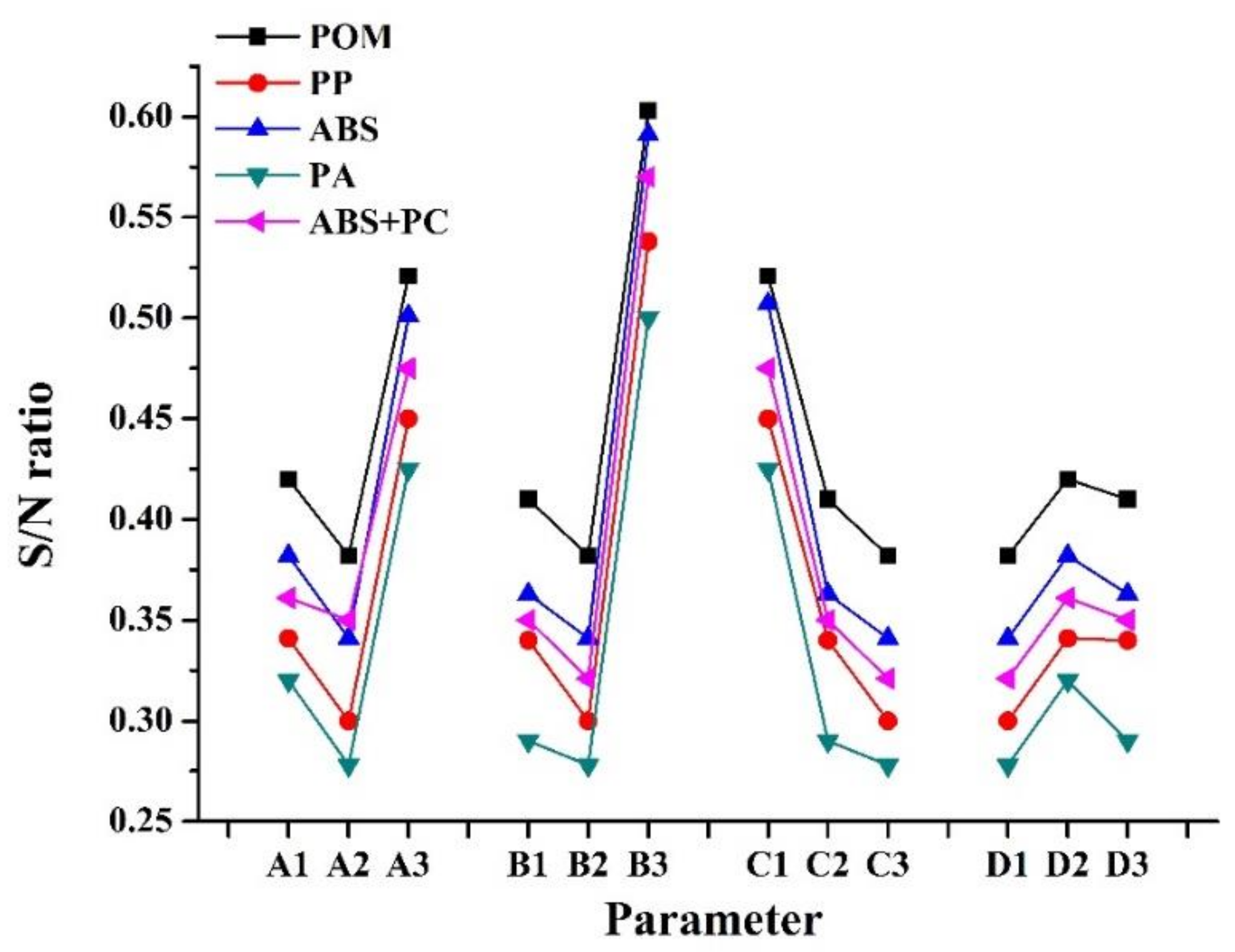
3.2. Experimentation and Measurement (of the Warpage and Mold Window)
3.3. Grey Theory
3.3.1. Grey Relational Analysis in Grey-Theory-Optimal Process Parameters
- r(x0(1), x1(1)) = 0.5000, r(x0(2), x1(2)) = 0.5000, r(x0(3), x1(3)) = 0.3333, r(x0(4), x1(4)) = 0.9804
- r(x0(1), x2(1)) = 0.5000, r(x0(2), x2(2)) = 1.0000, r(x0(3), x2(3)) = 0.5000, r(x0(4), x2(4)) = 1.0000
- r(x0(1), x3(1)) = 0.5000, r(x0(2), x3(2)) = 0.5000, r(x0(3), x3(3)) = 1.0000, r(x0(4), x3(4)) = 0.9804
- r(x0(1), x4(1)) = 1.0000, r(x0(2), x4(2)) = 0.5000, r(x0(3), x4(3)) = 0.5000, r(x0(4), x4(4)) = 0.9804
- r(x0(1), x5(1)) = 1.0000, r(x0(2), x5(2)) = 1.0000, r(x0(3), x5(3)) = 1.0000, r(x0(4), x5(4)) = 0.9804
- r(x0(1), x6(1)) = 1.0000, r(x0(2), x6(2)) = 0.5000, r(x0(3), x6(3)) = 0.3333, r(x0(4), x6(4)) = 1.0000
- r(x0(1), x7(1)) = 0.5000, r(x0(2), x7(2)) = 0.5000, r(x0(3), x7(3)) = 1.0000, r(x0(4), x7(4)) = 1.0000
- r(x0(1), x8(1)) = 0.5000, r(x0(2), x8(2)) = 1.0000, r(x0(3), x8(3)) = 0.3333, r(x0(4), x8(4)) = 0.9804
- r(x0(1), x9(1)) = 0.5000, r(x0 (2), x9(2)) = 0.5000, r(x0(3), x9(3)) = 0.5000, r(x0(4), x9(4)) = 0.9804
3.3.2. Grey Decision Analysis in Grey-Theory-Suitable Material
3.4. Molded Product
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Manzione, L.T. Process studies in precision injection molding. I: Process parameters and precision. Polym. Eng. Sci. 1996, 36, 1–9. [Google Scholar] [CrossRef]
- Yoshii, M.; Kuramoto, H.; Kawana, T.; Kato, K. The observation and origin of micro flow marks in the precision injection molding of poIycarbonate. Polym. Eng. Sci. 1996, 36, 819–826. [Google Scholar] [CrossRef]
- Tsai, K.M.; Hsieh, C.Y.; Lo, W.C. A study of the effects of process parameters for injection molding on surface quality of optical lenses. J. Mater. Processing Technol. 2009, 209, 3469–3477. [Google Scholar] [CrossRef]
- Weng, C.; Lee, W.B.; To, S.; Jiang, B.Y. Numerical simulation of residual stress and birefringence in the precision injection molding of plastic microlens arrays. Int. Commun. Heat Mass Transf. 2009, 36, 213–219. [Google Scholar] [CrossRef]
- Yang, C.; Su, L.; Huang, C.N.; Huang, H.X.; Castro, J.M.; Yi, A.Y. Effect of packing pressure on refractive index variation in injection molding of precision plastic optical len. Adv. Polym. Technol. 2011, 34, 51–61. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, Z.; Tan, J.R. Multiobjective optimization of injection molding parameters based on soft computing and variable complexity method. Int. J. Adv. Manuf. Technol. 2013, 66, 907–916. [Google Scholar] [CrossRef]
- Fang, F.Z.; Zhang, N.; Zhang, X.D. Precision injection molding of freeform optics. Adv. Opt. Technol. 2016, 5, 303–324. [Google Scholar] [CrossRef]
- Liu, J.H.; Chen, X.D.; Lin, Z.Q.; Diao, S.P. Multiobjective optimization of injection molding process parameters for the precision manufacturing of plastic optical lens. Math. Probl. Eng. 2017, 17, 2834013. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.D.; Zhang, Y.; Mao, T.; Zhou, H.M. Monitoring and dynamic control of quality stability for injection molding process. J. Mater. Processing Technol. 2017, 249, 358–366. [Google Scholar] [CrossRef]
- Ogorodnyka, O.; Martinsen, K. Monitoring and control for thermoplastics injection molding a Review. Procedia CIRP 2018, 67, 380–385. [Google Scholar] [CrossRef]
- Calaon, M.; Baruffi, F.; Fantoni, G.; Cirri, I.; Santochi, M.; Nørgaard, H.; Tosello, G. Functional analysis validation of micro and conventional injection molding machines performances based on process precision and accuracy for micro manufacturing. Micromachines 2020, 11, 1115. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.B.; Xu, H.; Liu, Y.; Yang, Z.G.; Kormakov, S.; Wu, D.; Sun, J.Y. Overview of injection molding technology for processing polymers and their composites. ES Mater. Manuf. 2020, 8, 3–23. [Google Scholar]
- Chen, J.C.; Guo, G.G.; Wang, W.N. Artificial neural network-based online defect detection system with in-mold temperature and pressure sensors for high precision injection molding. Int. J. Adv. Manuf. Technol. 2020, 110, 2023–2033. [Google Scholar] [CrossRef]
- Zhao, P.; Dong, Z.Y.; Zhang, J.F.; Zhang, Y.; Cao, M.Y.; Zhu, Z.; Zhou, H.W.; Fu, J.Z. Optimization of injection-molding process parameters for weight control: Converting optimization problem to classification problem. Adv. Polym. Technol. 2020, 20, 7654249. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, J.F.; Dong, Z.Y.; Huang, J.Y.; Zhou, H.W.; Fu, J.Z.; Turng, L.S. Intelligent injection molding on sensing, optimization, and control. Adv. Polym. Technol. 2020, 16, 7023616. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chen, J.C.; Ali, W.M. Process optimization and in-mold sensing enabled dimensional prediction for high precision injection molding. Int. J. Interact. Des. Manuf. 2021, 1–17. [Google Scholar] [CrossRef]
- Mahshid, R.; Zhang, Y.; Nørgaard, H.; Slocum, A.H. Effect of mold compliance on dimensional variations of precision molded components in multi-cavity injection molding. J. Manuf. Processes 2021, 67, 12–22. [Google Scholar] [CrossRef]
- Chena, J.Y.; Hung, P.H.; Huang, M.S. Determination of process parameters based on cavity pressure characteristics to enhance quality uniformity in injection molding. Int. J. Heat Mass Transf. 2021, 180, 121788. [Google Scholar] [CrossRef]
- Hopmann, C.; Xiao, C.L.; Kahve, C.E.; Fellerhoff, J. Prediction and validation of the specific volume for inline warpage control in injection molding. Polym. Test. 2021, 104, 107393. [Google Scholar] [CrossRef]
- Shen, Y.K. Comparison of height replication properties of precision injection molding and micro-njection compression molding for production of microstructures on lightguiding plate. Plast. Rubber Compos. 2007, 36, 37–84. [Google Scholar] [CrossRef]
- Packianather, M.; Griffiths, C.; Kadir, W. Micro injection moulding process parameter tuning. Procedia CIRP 2015, 33, 400–405. [Google Scholar] [CrossRef] [Green Version]
- Baruffi, F.; Gülçür, M.; Calaon, M.; Romano, J.M.; Penchev, P.; Dimov, S.; Whiteside, B.; Tosello, G. Correlating nano-scale surface replication accuracy and cavity temperature in micro-injection moulding using in-line process control and high-speed thermal imaging. J. Manuf. Processes 2019, 47, 367–381. [Google Scholar] [CrossRef]
- Surace, R.; Bellantone, V.; Trotta, G.; Fassi, I. Replicating capability investigation of micro features in injection moulding process. J. Manuf. Processes 2017, 28, 351–361. [Google Scholar] [CrossRef]
- Maghsoudi, K.; Jafari, R.; Momen, G.; Farzaneh, M. Micro-nanostructured polymer surfaces using injection molding: A review. Mater. Today Commun. 2017, 13, 126–143. [Google Scholar] [CrossRef]
- Speranza, V.; Liparoti, S.; Calaon, M.; Tosello, G.; Pantani, R.; Titomanlio, G. Replication of micro and nano-features on iPP by injection molding with fast cavity surface temperature evolution. Mater. Des. 2017, 133, 559–569. [Google Scholar] [CrossRef] [Green Version]
- Repisoa, P.G.; Soto, M.S.; Pinto, S.S.; Maspoch, M.L. Improvement of the replication quality of randomly micro-textured injection-moulding components using a multi-scale surface analysis. J. Manuf. Processes 2019, 42, 67–81. [Google Scholar] [CrossRef]
- Yang, C.; Li, L.; Huang, H.; Castro, J.M.; Yi, A.Y. Replication characterization of microribs fabricated by combining ultraprecision machining and microinjection molding. Polym. Eng. Sci. 2010, 50, 2021–2030. [Google Scholar] [CrossRef]
- Hakimian, E.; Sulong, A.B. Analysis of warpage and shrinkage properties of injection-molded micro gears polymer composites using numerical simulations assisted by the Taguchi method. Mater. Des. 2012, 42, 62–71. [Google Scholar] [CrossRef]
- Singh, G.; Pradhan, M.K.; Verma, A. Multi response optimization of injection molding process parameters to reduce cycle time and warpage. Mater. Today Proc. 2018, 5, 8398–8405. [Google Scholar] [CrossRef]
- Sanchez, R.; Aisa, J.; Martinez, A.; Mercado, D. On the relationship between cooling setup and warpage in injection molding. Measurement 2012, 45, 1051–1056. [Google Scholar] [CrossRef]
- Sudsawat, S.; Sriseubasi, W. Optimized plastic injection molding process and minimized the warpage and volume shrinkage by response surface methodology with genetic algorithm and firefly algorithm techniques. Indian J. Eng. Mater. Sci. 2017, 24, 228–238. [Google Scholar]
- Sudsawat, S.; Sriseubasi, W. Warpage reduction through optimized process parameters and annealed process of injection-molded parts. J. Mech. Sci. Technol. 2018, 32, 4787–4799. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Hwang, C.J.; Lee, B.K. Numerical investigation of warpage in insert injection-molded lightweight hybrid products. Int. J. Precis. Eng. Manuf. 2017, 18, 187–195. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, G. An innovative surrogate-based searching method for reducing warpage and cycle time in injection molding. Adv. Polym. Technol. 2016, 35, 21554. [Google Scholar] [CrossRef]
- Hidayah, M.H.N.; Shayfull, Z.; Noriman, N.Z.; Fathullah, M.; Norshahira, R.; Miza, A.T.N.A. Optimization of warpage on plastic part by using response surface methodology (RSM). AIP Conf. 2018, 30, 020155. [Google Scholar]
- Masato, D.; Rathore, J.; Sorgato, M.; Carmignato, S.; Lucchetta, G. Analysis of the shrinkage of injection-molded fiber-reinforced thin-wall parts. Mater. Des. 2017, 132, 496–504. [Google Scholar] [CrossRef]
- Sreedharan, J.; Jeevanantham, A.K. Analysis of shrinkage in ABS injection molding parts for automobile applications. Mater. Today Proc. 2018, 5, 12744–12749. [Google Scholar] [CrossRef]
- Taghizadeh, S.; Ozdemir, A.; Uluer, O. Warpage prediction in plastic injection molded part using artificial neural network. IJST Trans. Mech. Eng. 2013, 37, 149–160. [Google Scholar]
- Kennedy, R.J. A refinement of the Michelson-morley experiment. Physics 1926, 12, 621–629. [Google Scholar] [CrossRef] [Green Version]
- Tsuda, H.; Takahashi, J.; Urabe, K.; Ikeguchi, T. Damage monitoring of carbon fiber-reinforced plastics with Michelson interferometric fiber-optic sensors. J. Mater. Sci. 1999, 34, 4163–4172. [Google Scholar] [CrossRef]
- Hlubina, P. White-light spectral interferometry with the uncompensated Michelson interferometer and the group refractive index dispersion in fused silica. Opt. Commun. 2001, 193, 1–7. [Google Scholar] [CrossRef]
- Sutter, J.P.; Ishikawa, T.; Kuetgens, U.; Materlik, G.; Nishino, Y.; Rostomyan, A.; Tamasaku, K.; Yabashi, M. An X-ray BBB Michelson interferometer. J. Synchrotron Radiat. 2004, 11, 378–385. [Google Scholar] [CrossRef] [PubMed]
- Langangen, Ø.; Vaskinn, A.; Skagerstam, B.S. Interference of light in a Michelson-Morley interferometer: A quantum optical approach. Int. J. Opt. 2012, 16, 408067. [Google Scholar] [CrossRef]
- Li, P.F.; Yan, H.T.; Zhang, H.J. Highly sensitive liquid level sensor based on an optical fiber Michelson interferometer with core-offset structure. Optik 2018, 171, 781–785. [Google Scholar] [CrossRef]
- Tan, D.; Lim, K.S.; Zaini, M.K.; Yeong, C.H.; Wong, Y.H.; Yang, H.Z.; Ahmada, H. Phase derivative thermo-spatiogram for distributed temperature sensing based on chirped grating-Michelson Interferometer. Sens. Actuators A Phys. 2018, 278, 43–47. [Google Scholar] [CrossRef]
- Liu, Y.G.; Liu, X.; Ma, C.J.; Zhou, Y.M. Micro-structured optical fiber sensor for simultaneous measurement of temperature and refractive index. Opt. Fiber Technol. 2018, 41, 168–172. [Google Scholar] [CrossRef]
- Ye, T.M.; Xu, Y.F.; Hu, W.X. Generation of narrowband Lamb waves based on the Michelson interference technique. Chin. Phys. B 2018, 27, 054301. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Ng, D.K.W. Grey system and grey relational model. ACM SIGICE Bull. 1994, 20, 1–9. [Google Scholar] [CrossRef]
- Chiang, K.T.; Chang, F.P. Application of grey-fuzzy logic on the optimal process design of an injection-molded part with a thin shell feature. Int. Commun. Heat Mass Transf. 2006, 33, 94–101. [Google Scholar] [CrossRef]
- Shen, Y.K.; Chien, H.W.; Lin, Y. Optimization of the precision injection molding process using grey relational analysis and MoldFlow analysis. J. Reinf. Plast. Compos. 2004, 23, 1799–1814. [Google Scholar] [CrossRef]
- Chiang, K.T. The optimal process conditions of an injection-molded thermoplastic part with a thin shell feature using grey-fuzzy logic: A case study on machining the PC/ABS cell phone shell. Mater. Des. 2007, 28, 1851–1860. [Google Scholar] [CrossRef]
- Khalilpourazarya, S.; Payam, N. Optimization of the injection molding process of Derlin 500 composite using ANOVA and grey relational analysis. J. Comput. Appl. Res. Mech. Eng. 2016, 6, 39–50. [Google Scholar]
- Lin, C.M.; Chen, Y.W. Grey optimization of injection molding processing of plastic optical lens based on joint consideration of aberration and birefringence effects. Microsyst. Technol. 2019, 25, 621–631. [Google Scholar] [CrossRef]
- Lin, C.M.; Chen, Y.W. Optimization of injection-molding processing conditions for plastic double-convex Fresnel lens using grey-based Taguchi method. Microsyst. Technol. 2020, 26, 2575–2588. [Google Scholar] [CrossRef]
- Taguchi, G. Introduction to Quality Engineering; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Chiang, Y.C.; Cheng, H.C.; Huang, C.F.; Lee, J.J.; Lin, Y.; Shen, Y.K. Warpage phenomenon of thin-wall injection molding. Int. J. Adv. Manuf. Technol. 2011, 55, 517–526. [Google Scholar] [CrossRef]
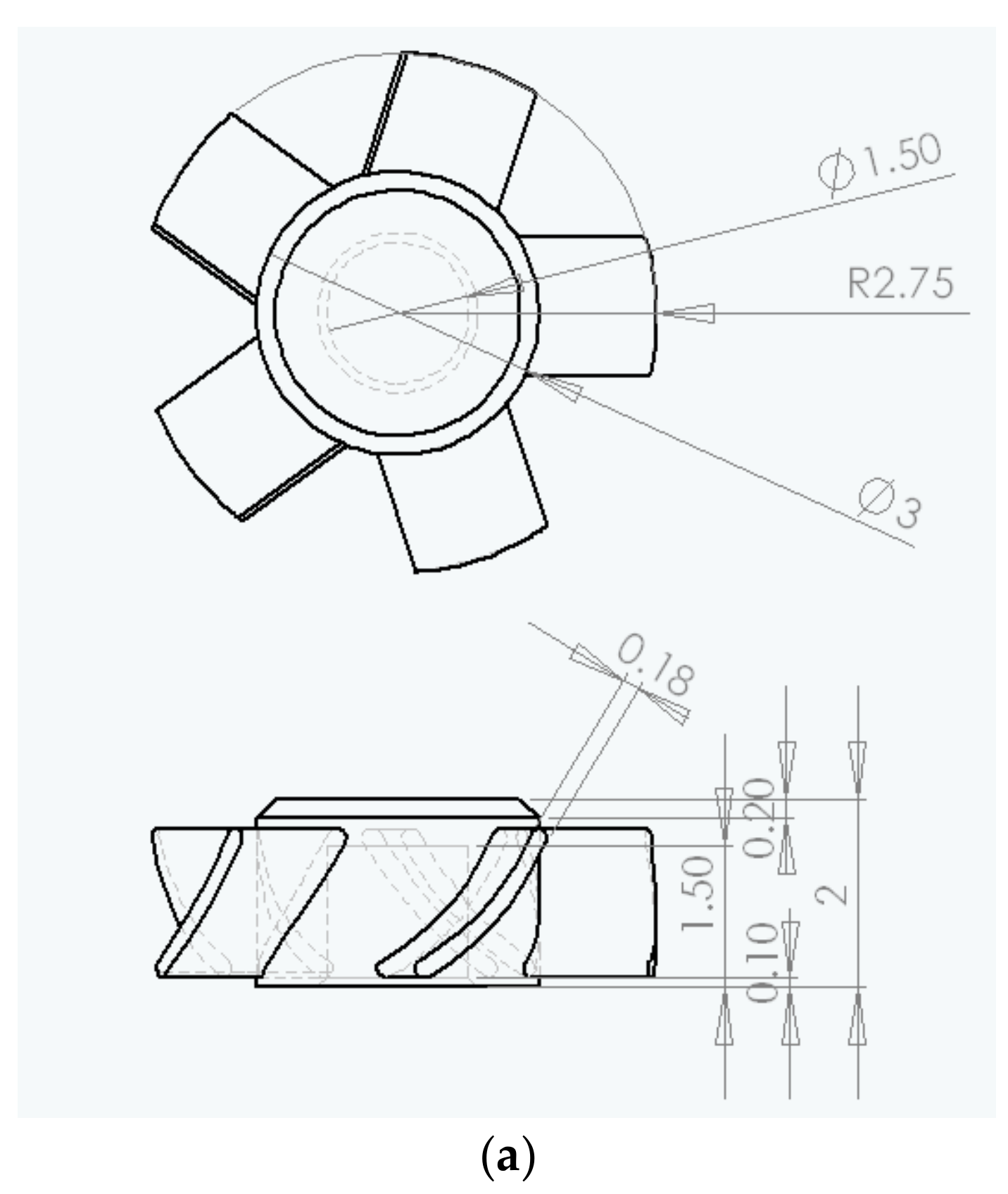
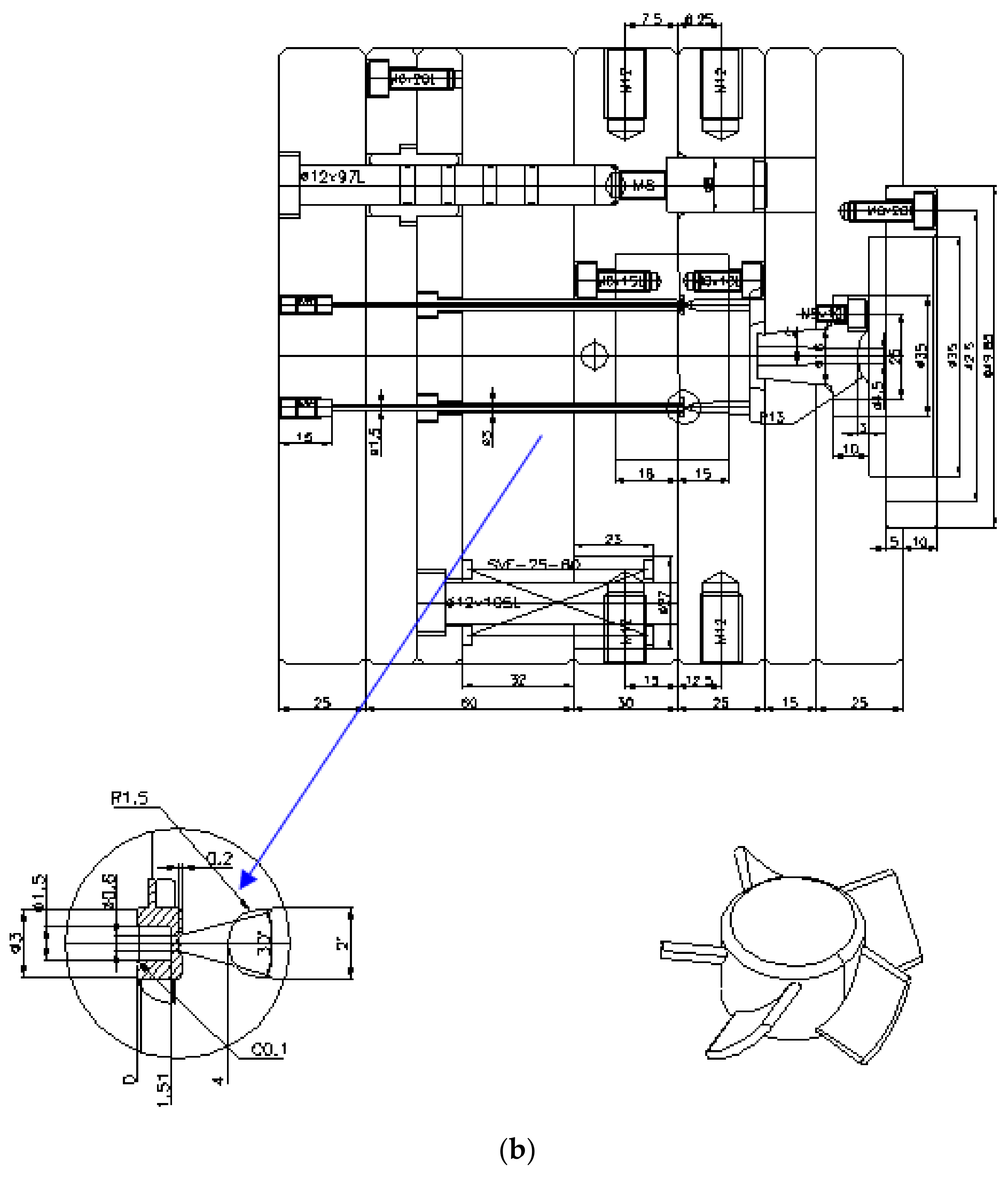

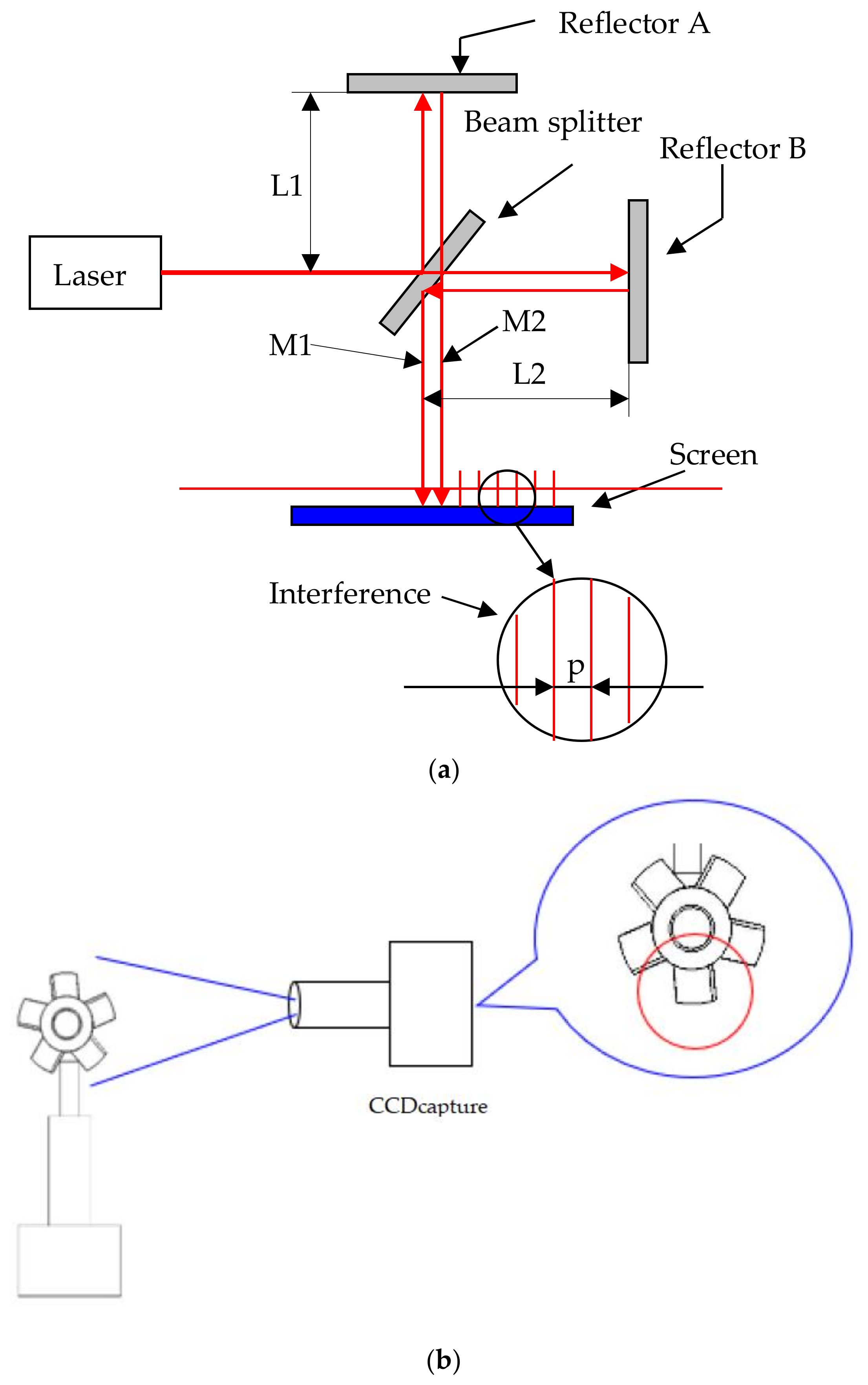

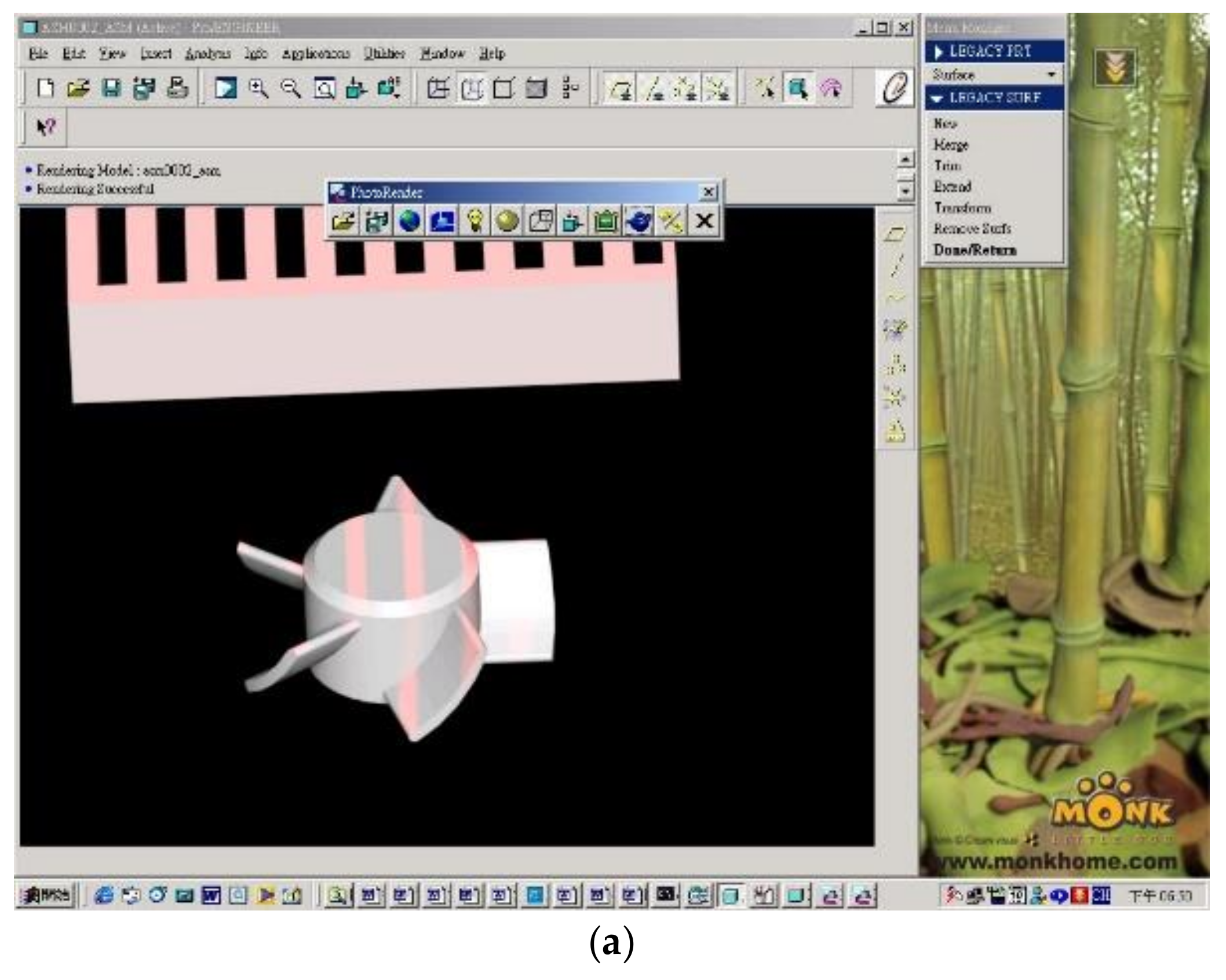









| Level Parameter | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| A. Melt temp. (°C) | 225/230/270/295/240 | 230/235/275/300/245 | 235/240/280/305/250 |
| B. Mold temp. (°C) | 80/80/50/70/55 | 85/85/55/75/60 | 90/90/60/80/65 |
| C. Injection press. (MPa) | 40/40/15/45/30 | 45/45/20/50/35 | 50/50/25/55/40 |
| D. Filling time (s) | 1/0.5/0.1/0.1/1 | 1.5/1/0.2/0.2/1.5 | 2/1.5/0.3/0.3/2 |
| Run | Melt Temp. (A) | Mold Temp. (B) | Injection Press. (C) | Filling Time (D) |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 |
| 4 | 2 | 1 | 2 | 3 |
| 5 | 2 | 2 | 3 | 1 |
| 6 | 2 | 3 | 1 | 2 |
| 7 | 3 | 1 | 3 | 2 |
| 8 | 3 | 2 | 1 | 3 |
| 9 | 3 | 3 | 2 | 1 |
| Assessment Scale | Definition | Explanation |
|---|---|---|
| 1 | Equally important | The contribution of the two comparison schemes is of equal importance (equal strength) |
| 3 | Slightly important | Experience and judgment tend to prefer a certain plan (slightly stronger) |
| 5 | Quite important | Experience and judgment strongly favor a certain plan (very strong) |
| 7 | Extremely important | Very strong tendency to favor a certain plan (very strong) |
| 9 | Absolutely important | There is enough evidence to definitely favor a certain plan (very strong) |
| 2, 4, 6, 8 | Median of adjacent scales | When a compromise value is needed |
| Runs. | Warpage (mm) |
|---|---|
| L1 | 0.427/0.412/0.450/0.410/0.430 |
| L2 | 0.311/0.301/0.302/0.300/0.301 |
| L3 | 0.500/0.498/0.575/0.480/0.510 |
| L4 | 0.302/0.300/0.283/0.270/0.290 |
| L5 | 0.283/0.260/0.261/0.258/0.261 |
| L6 | 0.600/0.510/0.511/0.505/0.510 |
| L7 | 0.425/0.410/0.427/0.408/0.415 |
| L8 | 0.420/0.410/0.427/0.405/0.415 |
| L9 | 0.560/0.500/0.552/0.498/0.523 |
| Average | 0.429/0.400/0.420/0.392/0.406 |
| Runs | Warpage (mm) |
|---|---|
| L1 | 0.527/0.452/0.530/0.430/0.490 |
| L2 | 0.420/0.341/0.382/0.320/0.361 |
| L3 | 0.603/0.538/0.655/0.500/0.570 |
| L4 | 0.410/0.340/0.363/0.290/0.350 |
| L5 | 0.382/0.300/0.341/0.278/0.321 |
| L6 | 0.710/0.550/0.591/0.525/0.570 |
| L7 | 0.530/0.450/0.501/0.428/0.475 |
| L8 | 0.521/0.450/0.507/0.425/0.475 |
| L9 | 0.670/0.540/0.632/0.518/0.583 |
| Average | 0.505/0.440/0.500/0.413/0.466 |
| Run | Grey Correlation | Sort |
|---|---|---|
| 1 | 0.7273/0.5833/0.5784/0.5784/0.5606 | 6/9/9/9/9 |
| 2 | 0.7500/0.7273/0.7500/0.7500/0.7500 | 4/4/2/2/2 |
| 3 | 0.5606/0.7273/0.7451/0.7451/0.7273 | 9/5/5/5/5 |
| 4 | 0.7273/0.7273/0.7451/0.7451/0.7273 | 5/3/4/4/4 |
| 5 | 0.8106/0.9773/0.9951/0.9951/0.9773 | 3/1/1/1/1 |
| 6 | 0.8750/0.7083/0.7083/0.7083/0.7083 | 1/6/6/6/6 |
| 7 | 0.5833/0.7500/0.7500/0.7500/0.7500 | 8/2/3/3/3 |
| 8 | 0.8523/0.6856/0.7034/0.7034/0.6856 | 2/7/7/7/7 |
| 9 | 0.6023/0.6023/0.6201/0.6201/0.6023 | 7/8/8/8/8 |
| Material | Run | Optimal Set of Processing Parameters | |||
|---|---|---|---|---|---|
| A. Melt Temp. (°C) | B. Mold Temp. (°C) | C. Injection Press. (MPa) | D. Filling Time (s) | ||
| POM | 6 | 230 | 80 | 15 | 1.5 |
| ABS | 5 | 235 | 85 | 50 | 1 |
| PP | 5 | 235 | 55 | 25 | 0.1 |
| PA | 5 | 300 | 75 | 55 | 0.5 |
| ABS + PC | 5 | 245 | 60 | 45 | 1 |
| Target | Sample | Target Polarity | POM Scheme A | ABS Scheme B | PP Scheme C | PA Scheme D | ABS + PC Scheme E |
|---|---|---|---|---|---|---|---|
| 1 | Melt temp. | Minimum | 195 | 230 | 230 | 295 | 240 |
| 2 | Mold temp. | Minimum | 70 | 80 | 50 | 70 | 55 |
| 3 | Injection Press. | Minimum | 15 | 40 | 15 | 45 | 30 |
| 4 | Filling time | Minimum | 1 | 1 | 1 | 1 | 1 |
| 5 | Specific weight | Minimum | 3 | 7 | 9 | 5 | 7 |
| 6 | Shrinkage rate | Minimum | 5 | 7 | 5 | 9 | 5 |
| 7 | Tensile strength | Minimum | 7 | 5 | 5 | 9 | 5 |
| Target | Sample | Target Polarity | POM Scheme A | ABS Scheme B | PP Scheme C | PA Scheme D | ABS + PC Scheme E |
|---|---|---|---|---|---|---|---|
| 1 | Melt temp. | Minimum | 1 | 0.85 | 1 | 0.49 | 0.96 |
| 2 | Mold temp. | Minimum | 0.71 | 0.63 | 1 | 0.71 | 0.91 |
| 3 | Injection Press. | Minimum | 1 | 0.38 | 1 | 0.34 | 0.5 |
| 4 | Filling time | Minimum | 1 | 1 | 1 | 1 | 1 |
| 5 | Specific weight | Minimum | 1 | 0.43 | 0.34 | 0.6 | 0.43 |
| 6 | Shrinkage rate | Minimum | 1 | 0.71 | 1 | 0.56 | 1 |
| 7 | Tensile strength | Minimum | 0.71 | 1 | 1 | 0.56 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.-C.; Fan, F.-Y.; Huang, C.-F.; Shen, Y.-K.; Wang, H. Analysis of the Warpage Phenomenon of Micro-Sized Parts with Precision Injection Molding by Experiment, Numerical Simulation, and Grey Theory. Polymers 2022, 14, 1845. https://doi.org/10.3390/polym14091845
Lin W-C, Fan F-Y, Huang C-F, Shen Y-K, Wang H. Analysis of the Warpage Phenomenon of Micro-Sized Parts with Precision Injection Molding by Experiment, Numerical Simulation, and Grey Theory. Polymers. 2022; 14(9):1845. https://doi.org/10.3390/polym14091845
Chicago/Turabian StyleLin, Wei-Chun, Fang-Yu Fan, Chiung-Fang Huang, Yung-Kang Shen, and Hao Wang. 2022. "Analysis of the Warpage Phenomenon of Micro-Sized Parts with Precision Injection Molding by Experiment, Numerical Simulation, and Grey Theory" Polymers 14, no. 9: 1845. https://doi.org/10.3390/polym14091845
APA StyleLin, W.-C., Fan, F.-Y., Huang, C.-F., Shen, Y.-K., & Wang, H. (2022). Analysis of the Warpage Phenomenon of Micro-Sized Parts with Precision Injection Molding by Experiment, Numerical Simulation, and Grey Theory. Polymers, 14(9), 1845. https://doi.org/10.3390/polym14091845











