A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates
Abstract
1. Introduction
- Describe the theory of the proposed FDM, main hypothesis and assumptions;
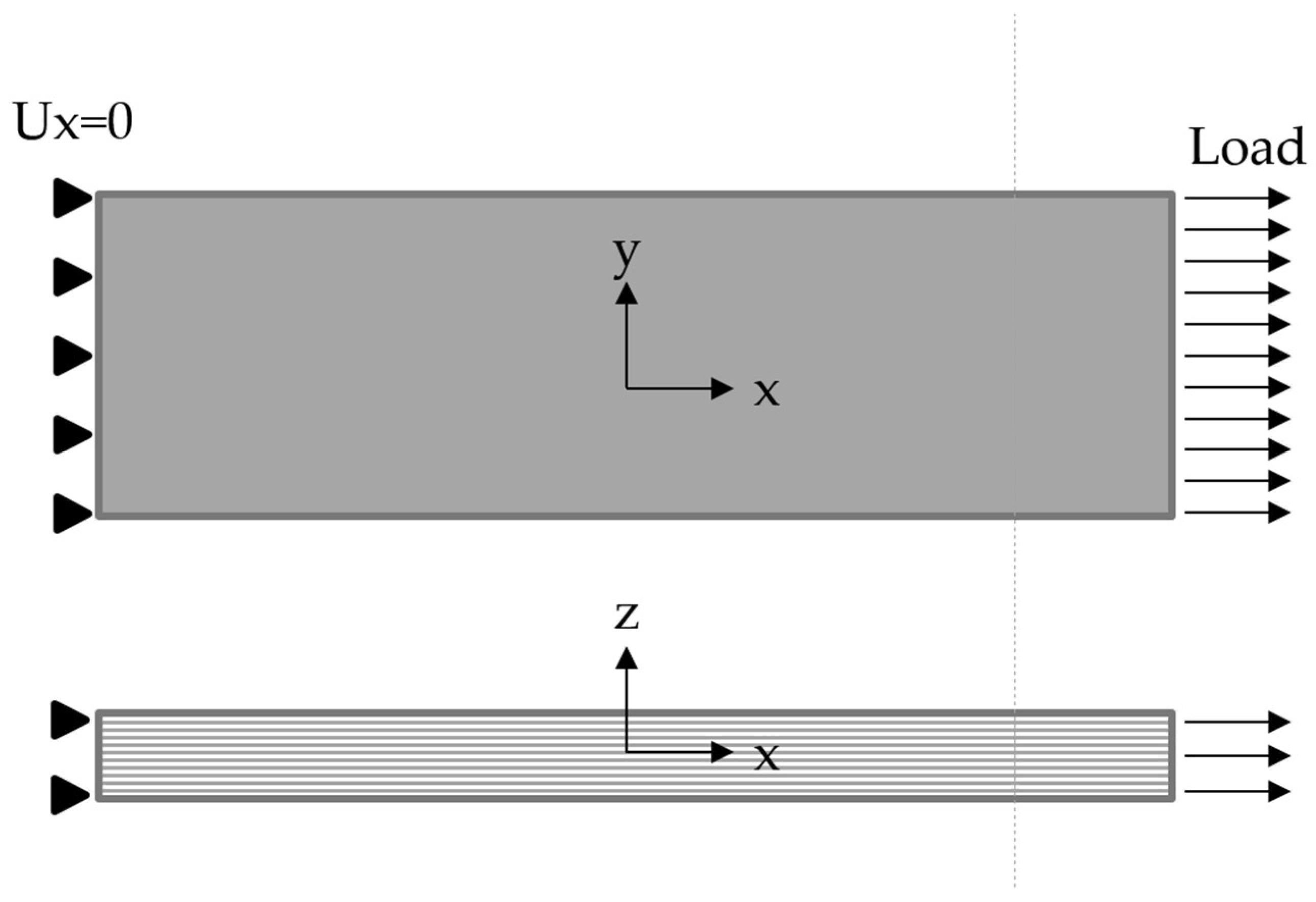
- Detail FEA implementation features;
- Present the comparison between the FDM predictions and the experimental data, discuss the prediction flaws.
2. Materials and Methods
2.1. Theoretical Background of the FDM
2.2. Initial Data
- Zero-degree-oriented CLD to determine a strength degradation along fibers;
- Forty-five-degree-oriented CLD to determine a degradation of shear strength;
- Ninety-degree-oriented CLD to determine a strength degradation across fibers.
3. Results
4. Discussion
- The various scatter of the experimental fatigue data for different stress ratios and lay-ups that implies errors to the model identification;
- Applicability of the chosen failure criteria for a variety of lay-ups and stress states.
5. Conclusions
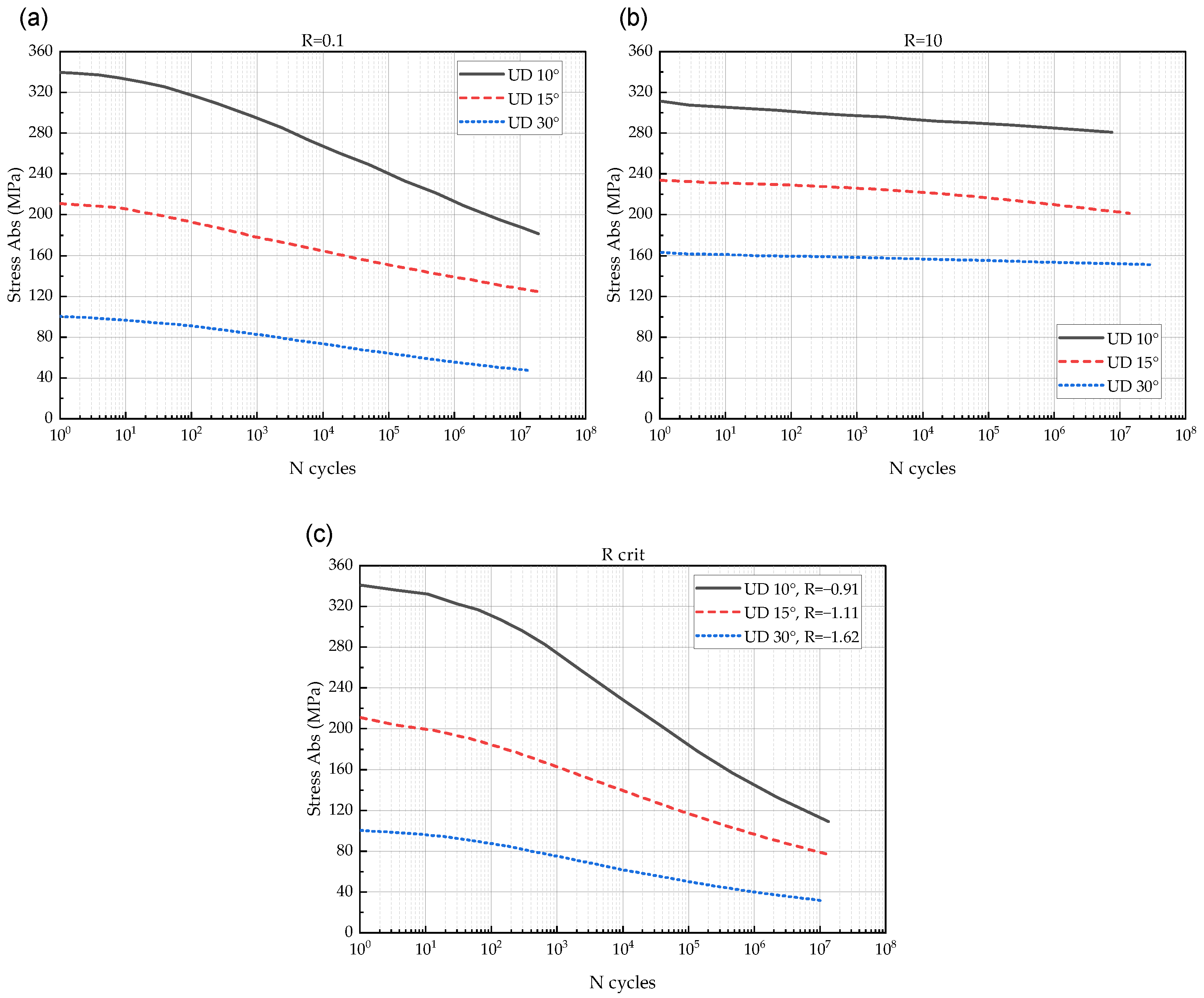
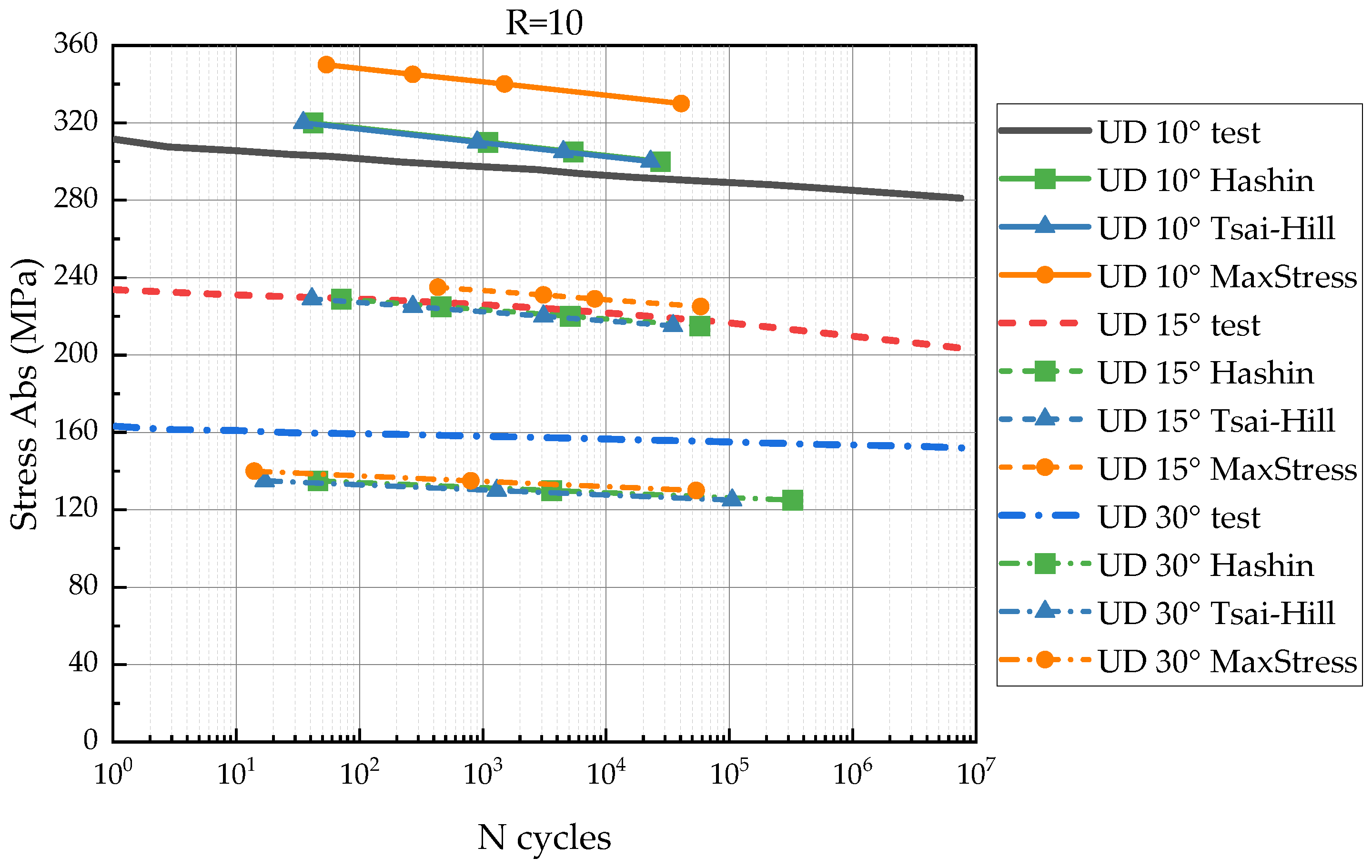
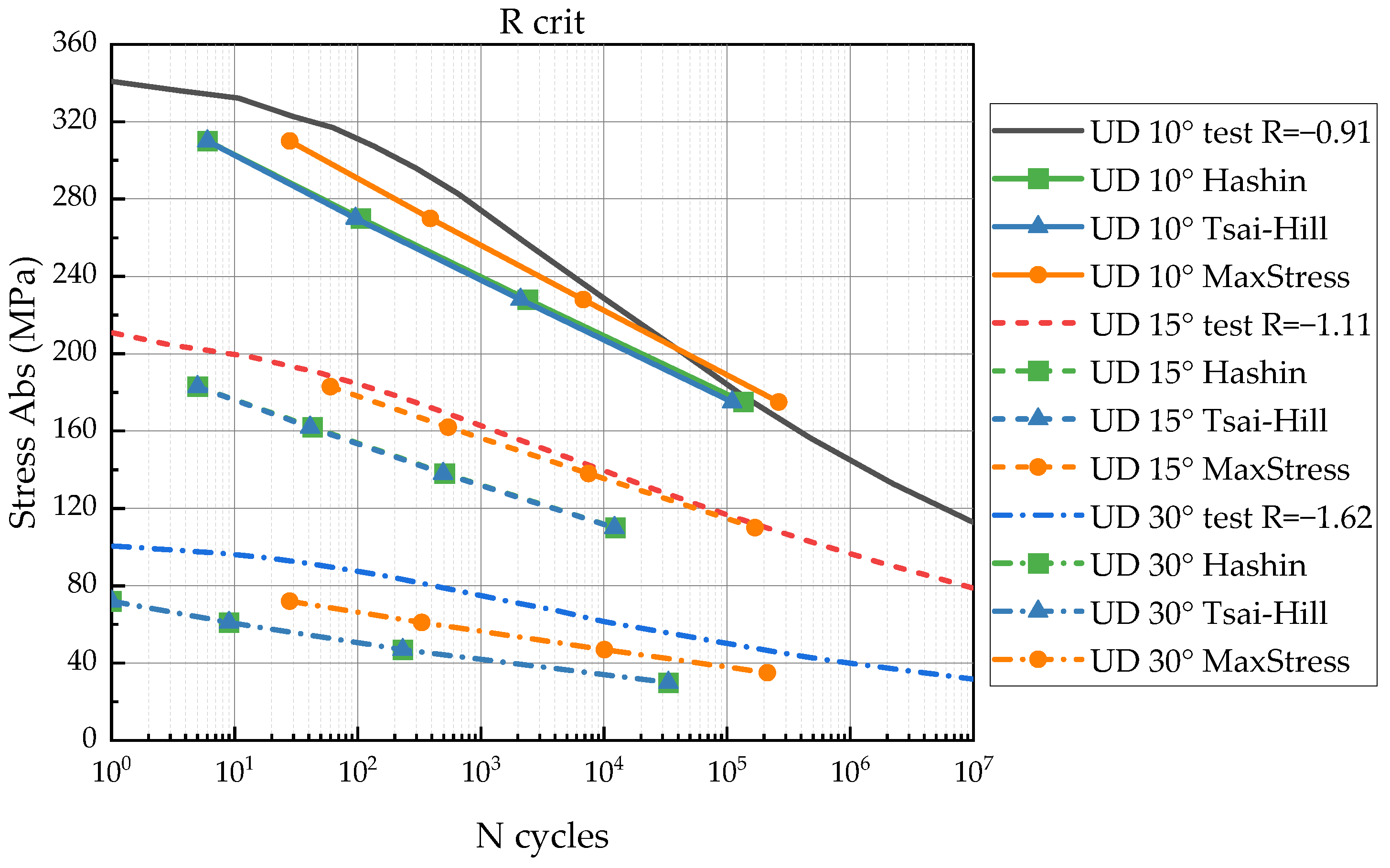
- Comparison between the reference fatigue data (nine S-N curves of UD 10°, 15°, and 30°) and the predictions showed a resemblance. Therefore, the hypothesis assumed was valid for fatigue life predictions of FRP laminates with those lay-ups;
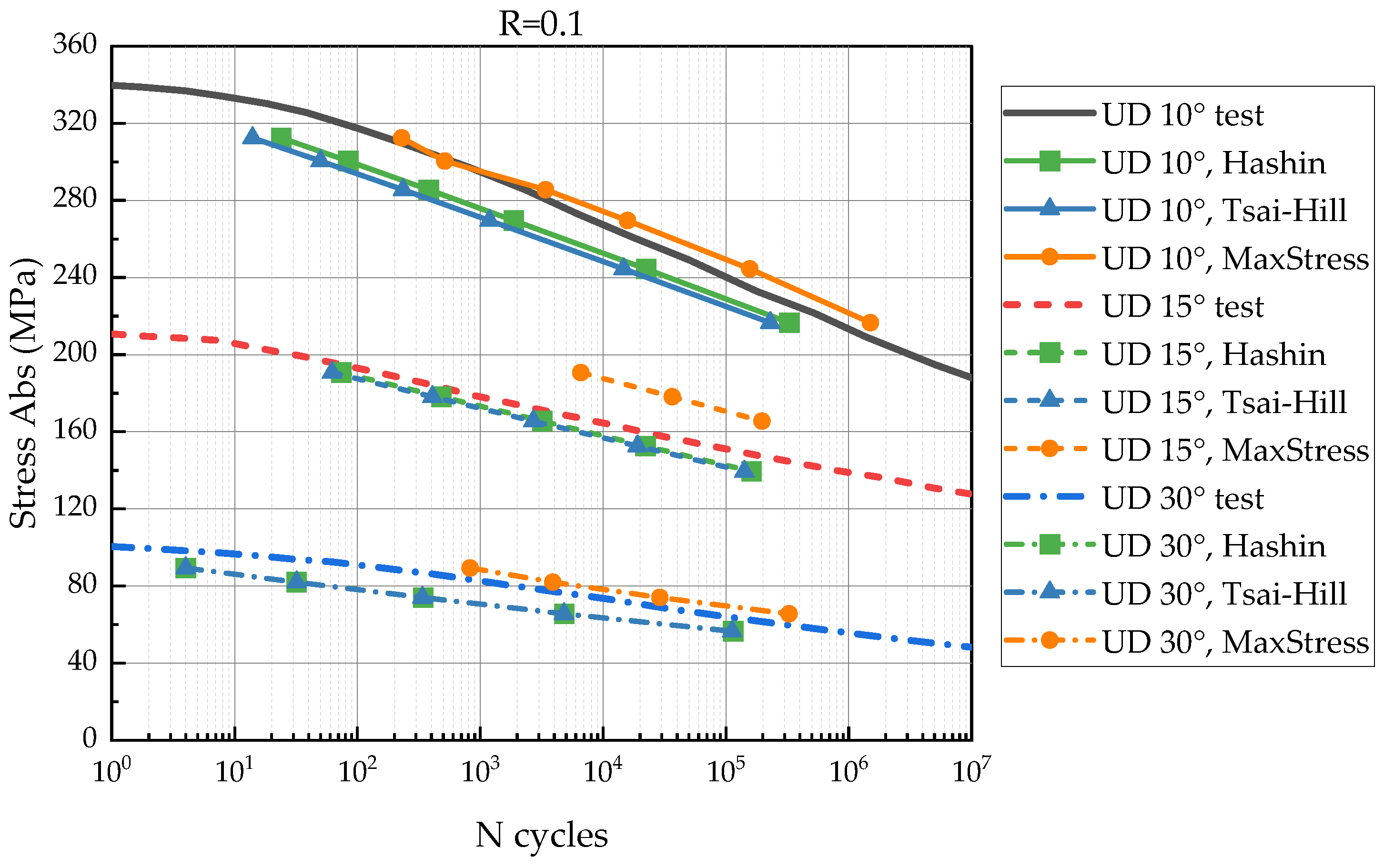
- The failure criteria influence the predicted number of loading cycles, but the strength degradation rate depends only on the input approximated S-N curves. Tsai–Hill and Hashin failure criteria provide conservative predictions in the most cases;
- The FDM is able to estimate the fatigue life under arbitrary non-constant stress ratios and various stress magnitudes.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maskepatil, L.P.; Gandigude, A.U.; Kale, S.A. Selection of Material for Wind Turbine Blade by Analytic Hierarchy Process (AHP) Method. Appl. Mech. Mater. 2014, 612, 145–150. [Google Scholar] [CrossRef]
- Sergeichev, I.; Fedulov, B.; Fedorenko, A.; Zershchikov, K.; Lomakin, E.; Akhatov, I. Constitutive material model for the design and virtual testing of pressure vessel service equipment manufactured from thermoplastic fiber-reinforced polymer composites. Int. J. Press. Vessel. Pip. 2021, 193, 104475. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue 2020, 134, 105512. [Google Scholar] [CrossRef]
- Deng, Q.-Y.; Zhu, S.-P.; He, J.-C.; Li, X.-K.; Carpinteri, A. Multiaxial fatigue under variable amplitude loadings: Review and solutions. Int. J. Struct. Integr. 2022, 13, 349–393. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Qian, G. Multiaxial fatigue analysis of notched components using combined critical plane and critical distance approach. Int. J. Mech. Sci. 2019, 160, 38–50. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Hua, F.; He, Y.; Wang, X. Critical plane-based fatigue life model under multiaxial random loading. Int. J. Struct. Integr. 2022, 13, 845–856. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Yu, Z.-Y.; Correia, J.; De Jesus, A.; Berto, F. Evaluation and comparison of critical plane criteria for multiaxial fatigue analysis of ductile and brittle materials. Int. J. Fatigue 2018, 112, 279–288. [Google Scholar] [CrossRef]
- Ma, S.; Markert, B.; Yuan, H. Multiaxial fatigue life assessment of sintered porous iron under proportional and non-proportional loadings. Int. J. Fatigue 2017, 97, 214–226. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Stress concentration factors in tubular X-connections retrofitted with FRP under compressive load. Ocean Eng. 2021, 229, 108562. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. SCFs in tubular X-connections retrofitted with FRP under in-plane bending load. Compos. Struct. 2021, 274, 114314. [Google Scholar] [CrossRef]
- Colombo, C.; Vergani, L. Influence of delamination on fatigue properties of a fibreglass composite. Compos. Struct. 2014, 107, 325–333. [Google Scholar] [CrossRef]
- Naebe, M.; Abolhasani, M.M.; Khayyam, H.; Amini, A.; Fox, B. Crack damage in polymers and composites: A review. Polym. Rev. 2016, 56, 31–69. [Google Scholar] [CrossRef]
- Reifsnider, K.L. Fatigue of Composite Materials; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Brod, M.; Dean, A.; Scheffler, S.; Gerendt, C.; Rolfes, R. Numerical modeling and experimental validation of fatigue damage in Cross-Ply CFRP composites under inhomogeneous stress states. Compos. Part B: Eng. 2020, 200, 108050. [Google Scholar] [CrossRef]
- Stinchcomb, W.W.; Bakis, C.E. Chapter 4—Fatigue Behavior of Composite Laminates. In Composite Materials Series; Reifsnider, K.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1991; Volume 4, pp. 105–180. [Google Scholar]
- Gough, H.J. Cantor Lectures-“Fatigue Phenomena, With Special Reference to Single Crystals”: I. RSA J. 1928, 76, 1025–1044. [Google Scholar]
- Moore, H.F.; Kommers, J.B. The Fatigue of Metals: With Chapters on the Fatigue of Wood and of Concrete; McGraw-Hill Book Company, Incorporated: New York, NY, USA, 1927. [Google Scholar]
- Goodman, J. Mechanics Applied to Engineering; Longmans, Green: London, UK, 1919. [Google Scholar]
- Sendeckyj, G.P. History of Constant Life Diagrams; The Minerals, Metals and Materials Society: Warrendale, PA, USA, 1997. [Google Scholar]
- Sutherland, H.; Mandell, J. Optimized Goodman Diagram for the Analysis of Fiberglass Composites Used in Wind Turbine Blades. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 196. [Google Scholar]
- Kawai, M.; Murata, T. A three-segment anisomorphic constant life diagram for the fatigue of symmetric angle-ply carbon/epoxy laminates at room temperature. Compos. Part A: Appl. Sci. Manuf. 2010, 41, 1498–1510. [Google Scholar] [CrossRef]
- Degrieck, J.; Van Paepegem, W. Fatigue damage modeling of fibre-reinforced composite materials. Appl. Mech. Rev. 2001, 54, 279–300. [Google Scholar] [CrossRef]
- Brunbauer, J.; Pinter, G. Fatigue life prediction of carbon fibre reinforced laminates by using cycle-dependent classical laminate theory. Compos. Part B: Eng. 2015, 70, 167–174. [Google Scholar] [CrossRef]
- D’Amore, A.; Giorgio, M.; Grassia, L. Modeling the residual strength of carbon fiber reinforced composites subjected to cyclic loading. Int. J. Fatigue 2015, 78, 31–37. [Google Scholar] [CrossRef]
- Pfanner, D. Zur Degradation von Stahlbetonbauteilen Unter Ermüdungsbeanspruchung; VDI-Verlag: Düsseldorf, Germany, 2003. [Google Scholar]
- Krüger, H.; Rolfes, R. A physically based fatigue damage model for fibre-reinforced plastics under plane loading. Int. J. Fatigue 2015, 70, 241–251. [Google Scholar] [CrossRef]
- De-guang, S.; De-jun, W. A new multiaxial fatigue damage model based on the critical plane approach. Int. J. Fatigue 1998, 20, 241–245. [Google Scholar] [CrossRef]
- Khan, A.I.; Venkataraman, S.; Miller, I. Predicting Fatigue Damage of Composites Using Strength Degradation and Cumulative Damage Model. J. Compos. Sci. 2018, 2, 9. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. A unified multiaxial fatigue damage model for isotropic and anisotropic materials. Int. J. Fatigue 2007, 29, 347–359. [Google Scholar] [CrossRef]
- Brunbauer, J.; Arbeiter, F.; Stelzer, S.; Pinter, G. Stiffness Based Fatigue Characterisation of CFRP. In Proceedings of the Advanced Materials Research, Solo, Indonesia, 16–17 September 2014; pp. 166–171. [Google Scholar]
- Häusler, S.; Fink, R.; Benz, C.; Sander, M. An investigation of the residual stiffness of a glass fibre reinforced composite in high cycle fatigue experiments. Procedia Struct. Integr. 2022, 38, 230–237. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Palmgren, A. Die Lebensdauer von Kugellagern Zeitschrift des Vereines Deutscher Ingenieure. Sci. Res. 1924, 68, 339–341. [Google Scholar]
- Kawai, M.; Teranuma, T. A multiaxial fatigue failure criterion based on the principal constant life diagrams for unidirectional carbon/epoxy laminates. Compos. Part A: Appl. Sci. Manuf. 2012, 43, 1252–1266. [Google Scholar] [CrossRef]
- Association, J.I. Testing Method for Compressive Properties of Carbon Fiber-Reinforced Plastics, Japanese Industrial Standard. JIS K7076; 1991. Available online: https://webdesk.jsa.or.jp/books/W11M0090/index/?bunsyo_id=JIS+K+7076%3A1991 (accessed on 19 October 2022).
- Association, J.I. Testing Method for Constant-Load Amplitude Tension-Tension Fatigue of Carbon Fibre Reinforced Plastics, Japanese Industrial Standard. JIS K7083; 1993. Available online: https://webdesk.jsa.or.jp/books/W11M0090/index/?bunsyo_id=JIS+K+7083%3A1993 (accessed on 19 October 2022).
- Kim, H.S.; Zhang, J. Fatigue damage and life prediction of glass/vinyl ester composites. J. Reinf. Plast. Compos. 2001, 20, 834–848. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue failure criteria for unidirectional fiber composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Rao, P.M.; Subba Rao, V. Degradation model based on Tsai-Hill factors to model the progressive failure of fiber metal laminates. J. Compos. Mater. 2011, 45, 1783–1792. [Google Scholar] [CrossRef]
- Ansari, M.T.A.; Singh, K.K.; Azam, M.S. Fatigue damage analysis of fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2018, 37, 636–654. [Google Scholar] [CrossRef]
- Barbosa, J.F.; Correia, J.A.; Freire Junior, R.; Zhu, S.-P.; De Jesus, A.M. Probabilistic SN fields based on statistical distributions applied to metallic and composite materials: State of the art. Adv. Mech. Eng. 2019, 11, 1687814019870395. [Google Scholar] [CrossRef]
- Burhan, I.; Kim, H.S. SN curve models for composite materials characterisation: An evaluative review. J. Compos. Sci. 2018, 2, 38. [Google Scholar] [CrossRef]
- Orifici, A.C.; Herszberg, I.; Thomson, R.S. Review of methodologies for composite material modelling incorporating failure. Compos. Struct. 2008, 86, 194–210. [Google Scholar] [CrossRef]
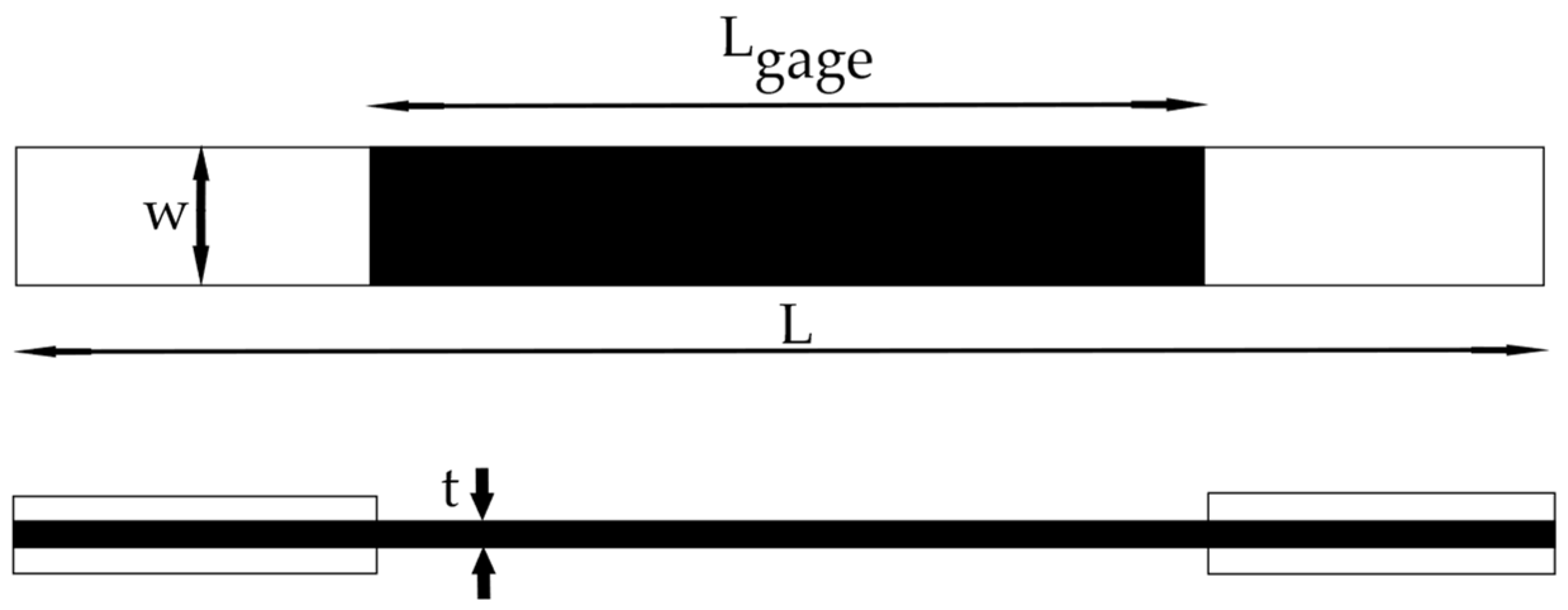

| Type of a Sample | The Long Sample, According to JIS K7076 [35] | The Short Sample, According to JIS K7083 [36] |
|---|---|---|
| t (thickness) [mm] | 3.1 | 3.1 |
| W (width) [mm] | 20 | 10 |
| L (length) [mm] | 200 | 100 |
| Lgage (gage length) [mm] | 100 | 10 |
| Young’s modulus along X [GPa] | 132 |
| Young’s modulus along Y [GPa] | 10.3 |
| Young’s modulus along Z [GPa] | 10.3 |
| Poisson’s ratio XY | 0.25 |
| Poisson’s ratio XZ | 0.25 |
| Poisson’s ratio YZ | 0.38 |
| Shear modulus XY [GPa] | 6.5 |
| Shear modulus XZ [GPa] | 6.5 |
| Shear modulus YZ [GPa] | 3.9 |
| Tensile strength along X [MPa] | 1860 |
| Tensile strength along Y [MPa] | 31 |
| Tensile strength along Z [MPa] | 31 |
| Compression strength along X [MPa] | 800 |
| Compression strength along Y [MPa] | 155 |
| Compression strength along Z [MPa] | 155 |
| Tensile strength of UD 45° (pseudo shear) [MPa] | 61 |
| Compression strength UD 45° (pseudo shear) [MPa] | 150.5 |
| Lay−up | R | A | B | C |
|---|---|---|---|---|
| UD [0°] | 0.5 | 1529 | −0.0219 | 364.1 |
| 0.1 | 2180 | −0.03561 | −265.5 | |
| −1 | 845.5 | −0.03549 | −47.58 | |
| −0.43 (Rcrit) | 1710 | −0.0826 | 146.3 | |
| 10 | 2322 | −0.004905 | −1529 | |
| 2 | −101.8 | 0.04086 | 891.3 | |
| UD [45°] | 0.5 | −27.98 | 0.03497 | 90.81 |
| 0.1 | −70.35 | 0.02127 | 132.4 | |
| −1 | 326.7 | −0.008352 | −261.2 | |
| −2.46 (Rcrit) | 107 | −0.04319 | −36.06 | |
| 10 | −14.87 | 0.05726 | 166 | |
| 2 | −9.357 | 0.05288 | 160.3 | |
| UD [90°] | 0.5 | 33.42 | −0.02427 | −2.161 |
| 0.1 | 35.76 | −0.04479 | −4.292 | |
| −1 | 33.31 | −0.06944 | −0.483 | |
| −5.12 (Rcrit) | 33.22 | −0.0948 | −0.3134 | |
| 10 | −31.23 | 0.02087 | 182.1 | |
| 2 | −47.35 | 0.009497 | 197.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elkin, A.; Gaibel, V.; Dzhurinskiy, D.; Sergeichev, I. A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates. Polymers 2022, 14, 4985. https://doi.org/10.3390/polym14224985
Elkin A, Gaibel V, Dzhurinskiy D, Sergeichev I. A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates. Polymers. 2022; 14(22):4985. https://doi.org/10.3390/polym14224985
Chicago/Turabian StyleElkin, Aleksandr, Viktor Gaibel, Dmitry Dzhurinskiy, and Ivan Sergeichev. 2022. "A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates" Polymers 14, no. 22: 4985. https://doi.org/10.3390/polym14224985
APA StyleElkin, A., Gaibel, V., Dzhurinskiy, D., & Sergeichev, I. (2022). A Multiaxial Fatigue Damage Model Based on Constant Life Diagrams for Polymer Fiber-Reinforced Laminates. Polymers, 14(22), 4985. https://doi.org/10.3390/polym14224985






